ResSANet: Learning Geometric Information for Point Cloud Processing
Abstract
1. Introduction
- A novel operation is presented based on geometric primitives for point clouds that could better capture local geometric features of point cloud while still maintaining permutation invariance;
- Two point-based skip connection modules are devised in the network, Res-SA and Res-SA-2, which can fuse multi-level features to raise accuracy and efficiency in point-cloud processing;
2. Related Work
2.1. Point-Cloud Processing Networks
2.2. Deep Learning on Geometry
3. Approach
3.1. Geometric Primitives
3.2. ResSANet for Point-Cloud Processing
3.3. Res-SA Module
3.4. Res-SA-2 Module
4. Evaluation
4.1. Dataset and Implementation
4.2. Classification
4.3. Shape Retrieval
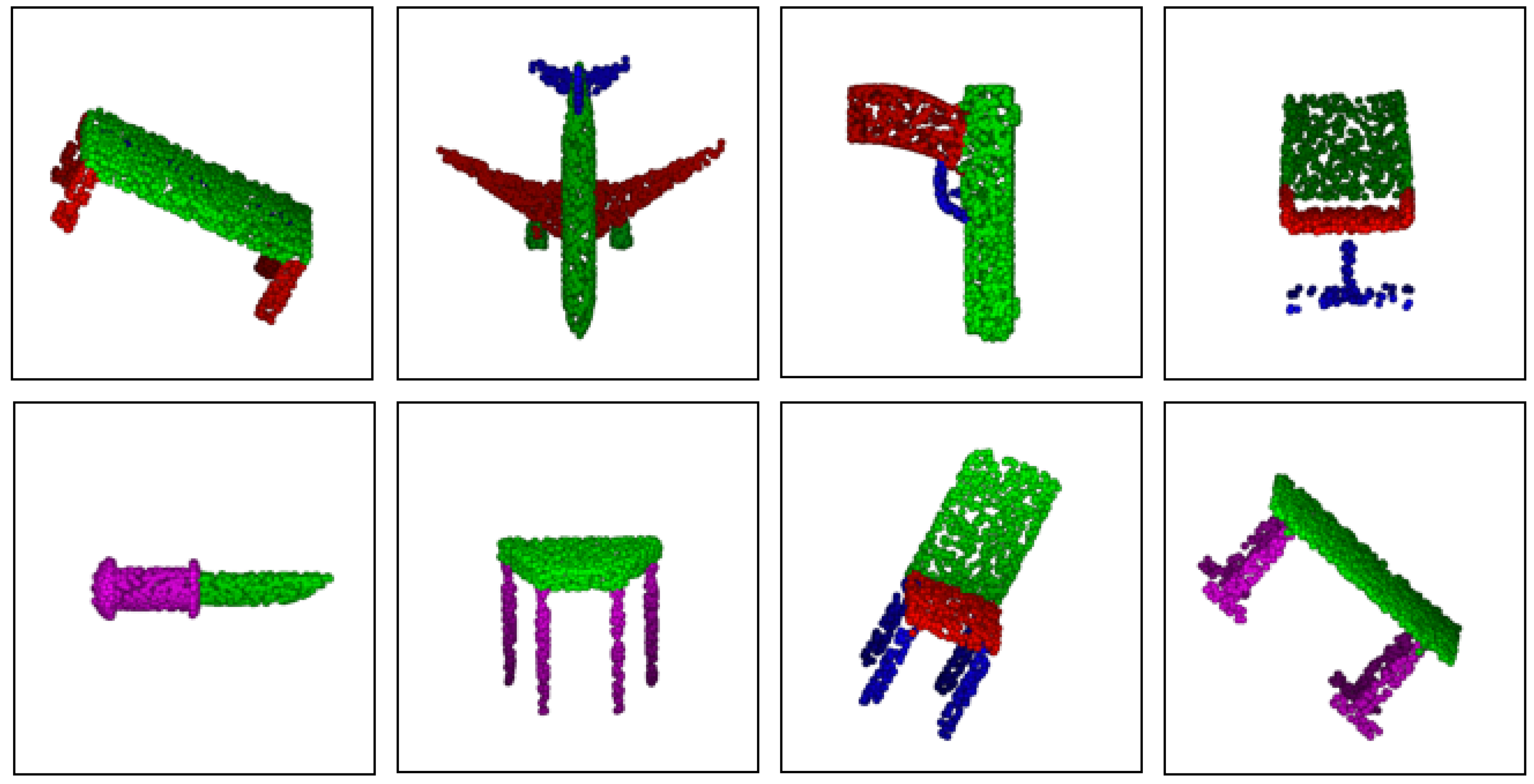
4.4. Part Segmentation
4.5. Model Complexity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum pointnets for 3d object detection from rgb-d data. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 918–927. [Google Scholar]
- Liang, H.; Ma, X.; Li, S.; Gorner, M.; Tang, S.; Fang, B.; Sun, F.; Zhang, J. Pointnetgpd: Detecting grasp configurations from point sets. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3629–3635. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv 2017, arXiv:1706.02413. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Chiu, C.-C.; Sainath, T.N.; Wu, Y.; Prabhavalkar, R.; Nguyen, P.; Chen, Z.; Kannan, A.; Weiss, R.J.; Rao, K.; Gonina, E.; et al. State-of-the-art speech recognition with sequence-to-sequence models. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 4774–4778. [Google Scholar]
- Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-transformed points. Adv. Neural Inf. Process. Syst. 2018, 31, 820–830. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic graph cnn for learning on point clouds. ACM Trans. Graph. (TOG) 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Fu, C.W.; Jia, J. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 July 2019; pp. 5565–5573. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Savva, M.; Yu, F.; Su, H.; Aono, M.; Chen, B.; Cohen-Or, D.; Deng, W.; Su, H.; Bai, S.; Bai, X.; et al. Shrec16 track: Largescale 3d shape retrieval from shapenet core55. In Proceedings of the Eurographics Workshop on 3D Object Retrieval, Lisbon, Portugal, 8 May 2016; pp. 89–98. [Google Scholar]
- Zhang, W.; Xiao, C. PCAN: 3d attention map learning using contextual information for point cloud based retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 12436–12445. [Google Scholar]
- Liu, Y.; Fan, B.; Xiang, S.; Pan, C. Relation-shape convolutional neural network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 8895–8904. [Google Scholar]
- Lan, S.; Yu, R.; Yu, G.; Davis, L.S. Modeling local geometric structure of 3d point clouds using geo-cnn. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 998–1008. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Jian, S. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision & Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar]
- Feng, Y.; Zhang, Z.; Zhao, X.; Ji, R.; Gao, Y. Gvcnn: Group-view convolutional neural networks for 3d shape recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 264–272. [Google Scholar]
- Maturana, D.; Scherer, S. Voxnet: A 3d convolutional neural network for real-time object recognition. In Proceedings of the 2015 IEEERSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar]
- Zhou, Y.; Tuzel, O. Voxelnet: End-to-end learning for point cloud based 3d object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4490–4499. [Google Scholar]
- Liu, Y.; Fan, B.; Meng, G.; Lu, J.; Xiang, S.; Pan, C. Densepoint: Learning densely contextual representation for efficient point cloud processing. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 5239–5248. [Google Scholar]
- Lei, H.; Akhtar, N.; Mian, A. Octree guided cnn with spherical kernels for 3d point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9631–9640. [Google Scholar]
- Komarichev, A.; Zhong, Z.; Hua, J. A-cnn: Annularly convolutional neural networks on point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7421–7430. [Google Scholar]
- Shen, Y.; Feng, C.; Yang, Y.; Tian, D. Mining point cloud local structures by kernel correlation and graph pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4548–4557. [Google Scholar]
- Chen, C.; Li, G.; Xu, R.; Chen, T.; Wang, M.; Lin, L. Clusternet: Deep hierarchical cluster network with rigorously rotation-invariant representation for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4994–5002. [Google Scholar]
- Long, H.; Suk-Hwan, L.; Ki-Ryong, K. A Deep Learning Method for 3D Object Classification and Retrieval Using the Global Point Signature Plus and Deep Wide Residual Network. Sensors 2021, 21, 2644. [Google Scholar]
- Ben-Shabat, Y.; Lindenbaum, M.; Fischer, A. 3DmFV: Three-Dimensional Point Cloud Classification in Real-Time Using Convolutional Neural Networks. IEEE Robot. Autom. Lett. 2018, 3, 3145–3152. [Google Scholar] [CrossRef]
- Christian, M.; Andreas, B. Visual Object Categorization Based on Hierarchical Shape Motifs Learned From Noisy Point Cloud Decompositions. J. Intell. Robot. Syst. 2020, 97, 313–338. [Google Scholar]
- Cui, Y.M.; Liu, X.; Liu, H.M.; Zhang, J.Y.; Zare, A. Geometric attentional dynamic graph convolutional neural networks for point cloud analysis. Neurocomputing 2021, 432, 300–310. [Google Scholar] [CrossRef]
- Guo, R.; Zhou, Y.; Zhao, J.Q.; Liu, M.J.; Liu, B. Point cloud classification by dynamic graph CNN with adaptive feature fusion. IET Comput. Vis. 2021, 15, 235–244. [Google Scholar] [CrossRef]
- Yi, L.; Kim, V.G.; Ceylan, D.; Shen, I.-C.; Yan, M.; Su, H.; Lu, C.; Huang, Q.; Sheffer, A.; Guibas, L. A scalable active frame-work for region annotation in 3d shape collections. ACM Trans. Graph. (TOG) 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Xie, S.; Liu, S.; Chen, Z.; Tu, Z. Attentional shapecontextnet for point cloud recognition. In Proceedings of the IEEE Confer-ence on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4606–4615. [Google Scholar]
- Klokov, R.; Lempitsky, V. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 863–872. [Google Scholar]
- Hermosilla, P.; Ritschel, T.; Vazquez, P.P.; Vinacua, A.; Ropinski, T. Monte carlo convolution for learning on non-uniformly sampled point clouds. In SIGGRAPH Asia 2018 Technical Papers; ACM: New York, NY, USA, 2018; p. 235. [Google Scholar]
- Gadelha, M.; Wang, R.; Maji, S. Multiresolution tree networks for 3d point cloud processing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 103–118. [Google Scholar]
- Wang, C.; Samari, B.; Siddiqi, K. Local spectral graph convolution for point set feature learning. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 52–66. [Google Scholar]
- Atzmon, M.; Maron, H.; Lipman, Y. Point convolutional neural networks by extension operators. arXiv 2018, arXiv:1803.10091. [Google Scholar] [CrossRef]
- Liu, X.; Han, Z.; Liu, Y.-S.; Zwicker, M. Point2sequence: Learning the shape representation of 3d point clouds with an atten-tion-based sequence to sequence network. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8778–8785. [Google Scholar]
- Zhang, K.; Hao, M.; Wang, J.; de Silva, C.W.; Fu, C. Linked dynamic graph cnn: Learning on point cloud via linking hierar-chical features. arXiv 2019, arXiv:1904.10014. [Google Scholar]
- Yan, X.; Zheng, C.; Li, Z.; Wang, S.; Cui, S. Pointasnl: Robust point clouds processing using nonlocal neural networks with adaptive sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Yang, Y.; Feng, C.; Shen, Y.; Tian, D. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 206–215. [Google Scholar]
- Li, J.; Chen, B.M.; Lee, G.H. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9397–9406. [Google Scholar]
- Wu, W.; Qi, Z.; Fuxin, L. Pointconv: Deep convolutional networks on 3d point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9621–9630. [Google Scholar]
- Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep learning on point sets with parameterized convolutional filters. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 87–102. [Google Scholar]
- Jiang, J.; Bao, D.; Chen, Z.; Zhao, X.; Gao, Y. Mlvcnn: Multi-loop-view convolutional neural network for 3d shape retrieval. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8513–8520. [Google Scholar]
- You, H.; Feng, Y.; Ji, R.; Gao, Y. Pvnet: A joint convolutional network of point cloud and multi-view for 3d shape recogni-tion. In Proceedings of the 2018 ACM Multimedia Conference on Multimedia Conference, Seoul, Korea, 22–26 October 2018; pp. 1310–1318. [Google Scholar]
- Bai, S.; Bai, X.; Zhou, Z.; Zhang, Z.; jan Latecki, L. Gift: A real-time and scalable 3d shape search engine. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 5023–5032. [Google Scholar]
- Sfikas, K.; Pratikakis, I.; Theoharis, T. Ensemble of panorama-based convolutional neural networks for 3d model classifica-tion and retrieval. Comput. Graph. 2018, 71, 208–218. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhou, Z.; Bai, S.; Bai, X. Triplet-center loss for multi-view 3d object retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1945–1954. [Google Scholar]
- Han, Z.; Shang, M.; Liu, Z.; Vong, C.-M.; Liu, Y.-S.; Zwicker, M.; Han, J.; Chen, C.P. Seqviews2seqlabels: Learning 3d global features via aggregating sequential views by rnn with attention. IEEE Trans. Image Process. 2018, 28, 658–672. [Google Scholar] [CrossRef] [PubMed]
- Te, G.; Hu, W.; Zheng, A.; Guo, Z. Rgcnn: Regularized graph cnn for point cloud segmentation. In Proceedings of the 2018 ACM Multimedia Conference on Multimedia Conference, Seoul, Korea, 22–26 October 2018; pp. 746–754. [Google Scholar]








| Algorithm | Input | Points | Accuracy |
|---|---|---|---|
| ClusterNet [24] | xyz | 1024 | 87.1% |
| PointNet [3] | xyz | 1024 | 89.2% |
| SCN [31] | xyz | 1024 | 90.0% |
| Kd-Net [32] | xyz | 1024 | 90.6% |
| PointNet++ [4] | xyz | 1024 | 90.7% |
| MCConv [33] | xyz | 1024 | 90.9% |
| KCNet [23] | xyz | 1024 | 91.0% |
| MRTNet [34] | xyz | 1024 | 91.2% |
| Spec-GCN [35] | xyz | 1024 | 91.5% |
| W-CNN [21] | xyz | 1024 | 92.0% |
| DGCNN [8] | xyz | 1024 | 92.2% |
| PointCNN [7] | xyz | 1024 | 92.2% |
| PCNN [36] | xyz | 1024 | 92.3% |
| PointWeb [9] | xyz | 1024 | 92.3% |
| Point2Sequence [37] | xyz | 1024 | 92.6% |
| A-CNN [22] | xyz | 1024 | 92.6% |
| LDGCNN [38] | xyz | 1024 | 92.9% |
| PointASNL [39] | xyz | 1024 | 92.9% |
| Ours | xyz | 1024 | 93.2% |
| FoldingNet [40] | xyz | 2048 | 88.4% |
| SO-Net [41] | xyz | 2048 | 90.9% |
| Spec-GCN [35] | xyz + n | 1024 | 91.8% |
| Pointconv [42] | xyz + n | 1024 | 92.5% |
| Geo-CNN [14] | xyz + n | 1024 | 93.4% |
| SpiderCNN [43] | xyz + n | 5000 | 92.4% |
| LDGCNN [38] | xyz + n | 5000 | 92.9% |
| MLVCNN [44] | xyz + n | 5000 | 92.9% |
| SO-Net [41] | xyz + n | 5000 | 93.4% |
| PVNet [45] | xyz + n | 1024 | 93.2% |
| Modality | Algorithm | Points/Views | mAP |
|---|---|---|---|
| points | PointNet [3] | 1 k | 70.5 |
| points | PointCNN [7] | 1 k | 83.8 |
| points | DGCNN [8] | 1 k | 85.3 |
| points | Ours | 1 k | 87.4 |
| Images | 3D ShapeNet [10] | - | 49.2 |
| Images | MVCNN [16] | 12 | 80.2 |
| Images | GIFT [46] | 12 | 81.9 |
| Images | GVCNN [17] | 12 | 85.7 |
| Images | PANORAMA-ENN [47] | - | 86.3 |
| Images | Triplet [48] | 12 | 88.0 |
| Images | SeqViews [49] | 12 | 89.1 |
| Algorithm | Ours | PointNet | KCNet | DGCNN | PCNN |
|---|---|---|---|---|---|
| points | 2048 | 2048 | 2048 | 2048 | 2048 |
| Class | 83.3 | 80.4 | 82.2 | 82.3 | 81.8 |
| Instance | 85.3 | 83.7 | 84.7 | 85.1 | 85.1 |
| airplane | 82.0 | 83.4 | 82.8 | 84.2 | 82.4 |
| bag | 85.7 | 78.7 | 81.5 | 83.7 | 80.1 |
| cap | 87.2 | 82.5 | 86.4 | 84.4 | 85.5 |
| car | 78.1 | 74.9 | 77.6 | 77.1 | 79.5 |
| chair | 90.5 | 89.6 | 90.3 | 90.9 | 90.8 |
| earphone | 78.9 | 73.0 | 76.8 | 78.5 | 73.2 |
| guitar | 91.2 | 91.5 | 91.0 | 91.5 | 91.3 |
| knife | 86.8 | 85.9 | 87.2 | 87.3 | 86.0 |
| lamp | 85.2 | 80.8 | 84.5 | 82.9 | 85.0 |
| laptop | 95.6 | 95.3 | 95.5 | 96.0 | 95.7 |
| motorbike | 71.9 | 65.2 | 69.2 | 67.8 | 73.2 |
| mug | 94.5 | 93.0 | 94.4 | 93.3 | 94.8 |
| pistol | 83.1 | 81.2 | 81.6 | 82.6 | 83.3 |
| rocket | 61.4 | 57.9 | 60.1 | 59.7 | 51.0 |
| skateboard | 77.4 | 72.8 | 75.2 | 75.5 | 75.0 |
| table | 82.6 | 80.6 | 81.3 | 82.0 | 81.8 |
| Algorithm | Params | FLOPs |
|---|---|---|
| PCNN [7] | 8.20 M | 294 M |
| PointNet [3] | 3.50 M | 440 M |
| RGCNN [50] | 2.24 M | 750 M |
| SpecGCN [7] | 2.05 M | 1112 M |
| DGCNN [7] | 1.84 M | 2767 M |
| PointNet++ [7] | 1.48 M | 1684 M |
| RSCNN [13] | 1.41 M | 295 M |
| Ours (L = 3) | 1.59 M | 450 M |
| Ours (L = 2) | 1.31 M | 409 M |
| Ours (L = 1) | 1.04 M | 286 M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Zhang, Z.; Ruan, J.; Liu, H.; Sun, H. ResSANet: Learning Geometric Information for Point Cloud Processing. Sensors 2021, 21, 3227. https://doi.org/10.3390/s21093227
Zhu X, Zhang Z, Ruan J, Liu H, Sun H. ResSANet: Learning Geometric Information for Point Cloud Processing. Sensors. 2021; 21(9):3227. https://doi.org/10.3390/s21093227
Chicago/Turabian StyleZhu, Xiaojun, Zheng Zhang, Jian Ruan, Houde Liu, and Hanxu Sun. 2021. "ResSANet: Learning Geometric Information for Point Cloud Processing" Sensors 21, no. 9: 3227. https://doi.org/10.3390/s21093227
APA StyleZhu, X., Zhang, Z., Ruan, J., Liu, H., & Sun, H. (2021). ResSANet: Learning Geometric Information for Point Cloud Processing. Sensors, 21(9), 3227. https://doi.org/10.3390/s21093227





