Braille Block Detection via Multi-Objective Optimization from an Egocentric Viewpoint
Abstract
1. Introduction
- A Braille block detection framework with the egocentric images as input is proposed.
- We formulate the block detection as a multi-objective optimization problem by considering both the geometric and the appearance features.
- A Braille block detection dataset is originally built with annotations.
2. Related Work
3. Detection of Braille Block
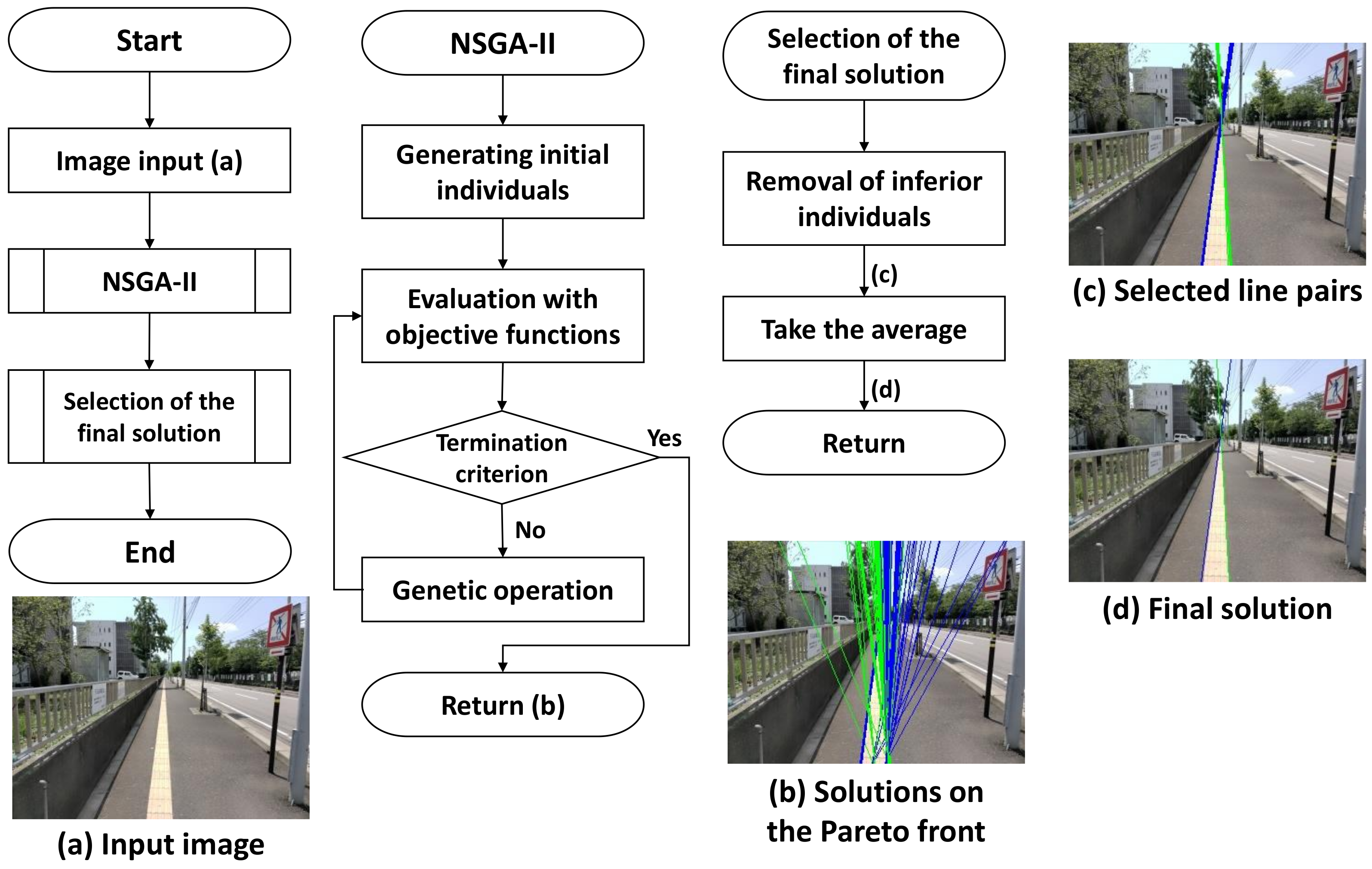
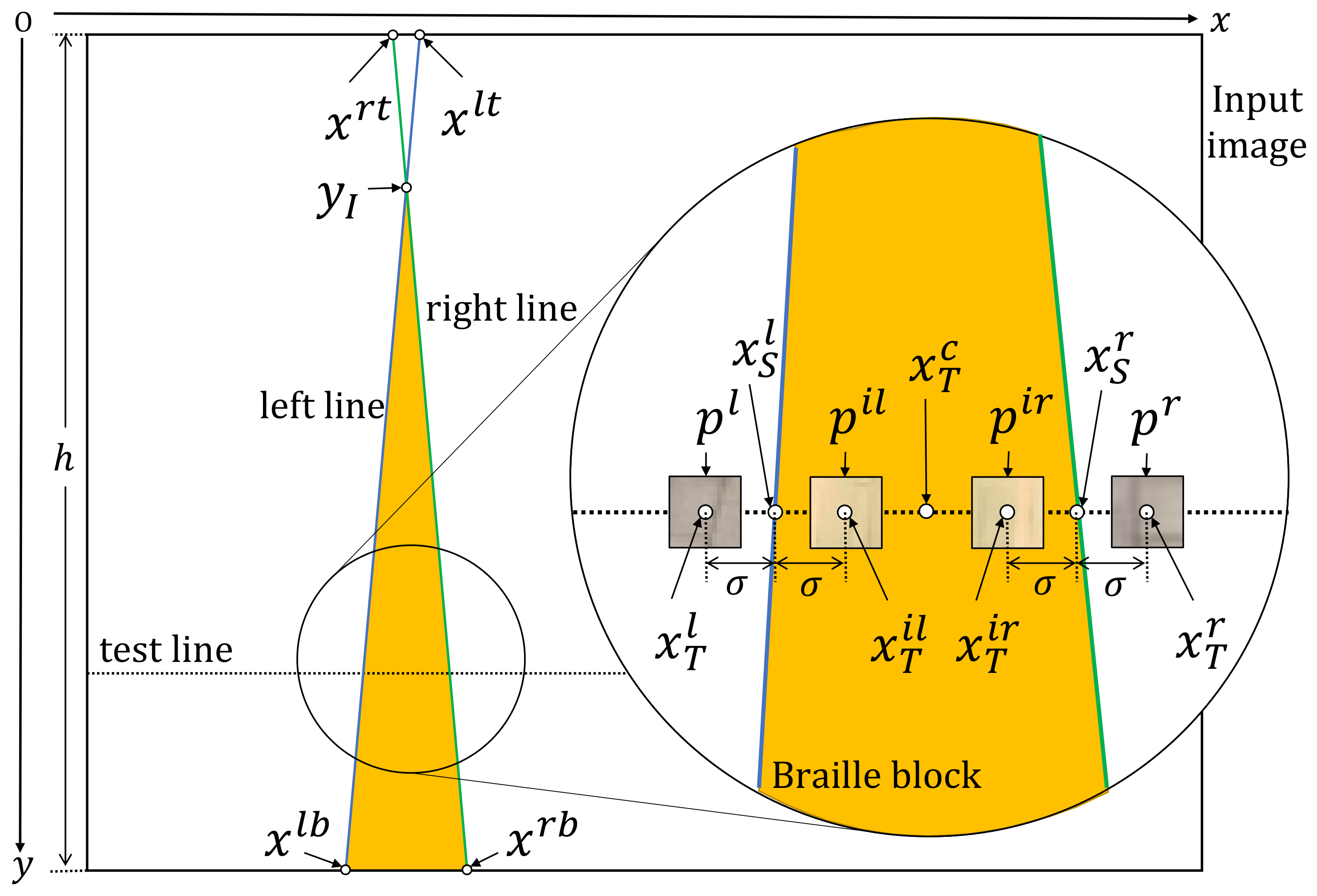
3.1. Problem Setting and Overview
3.2. Individual Representation and Population Initialization
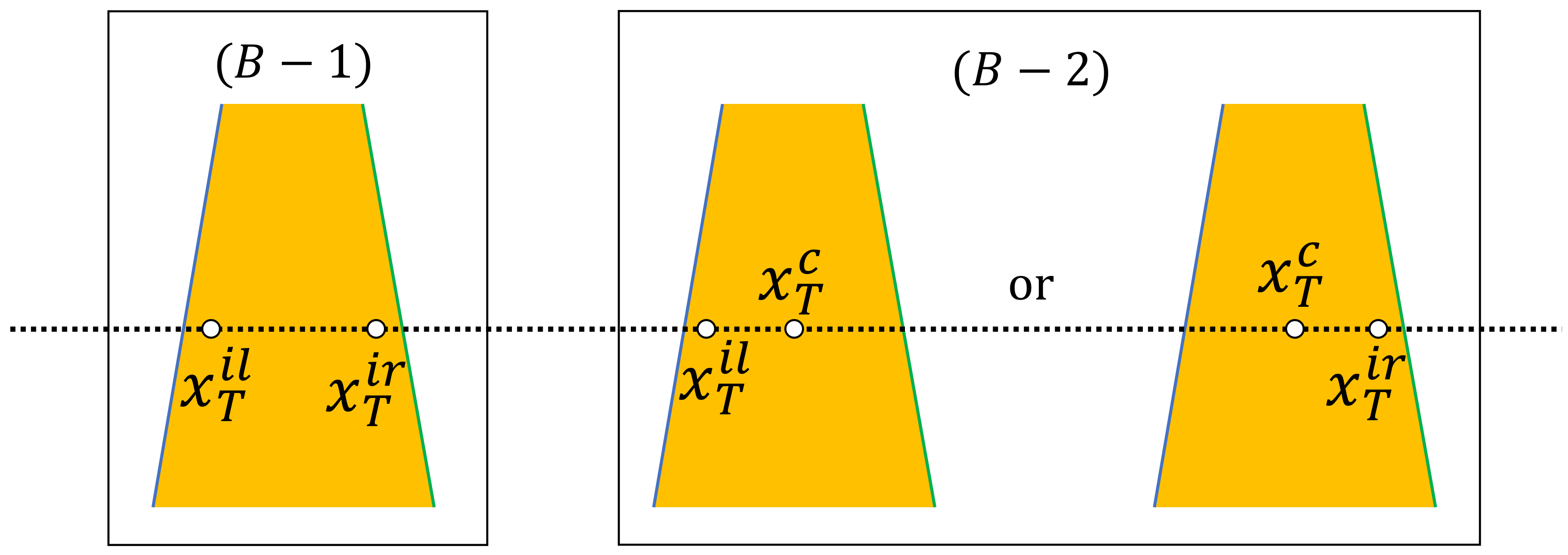
3.3. Objective Functions
| Algorithm 1: Objective Function 1 |
 |
| Algorithm 2: Objective Function 2 |
 |
3.4. Genetic Operators and Termination Criterion
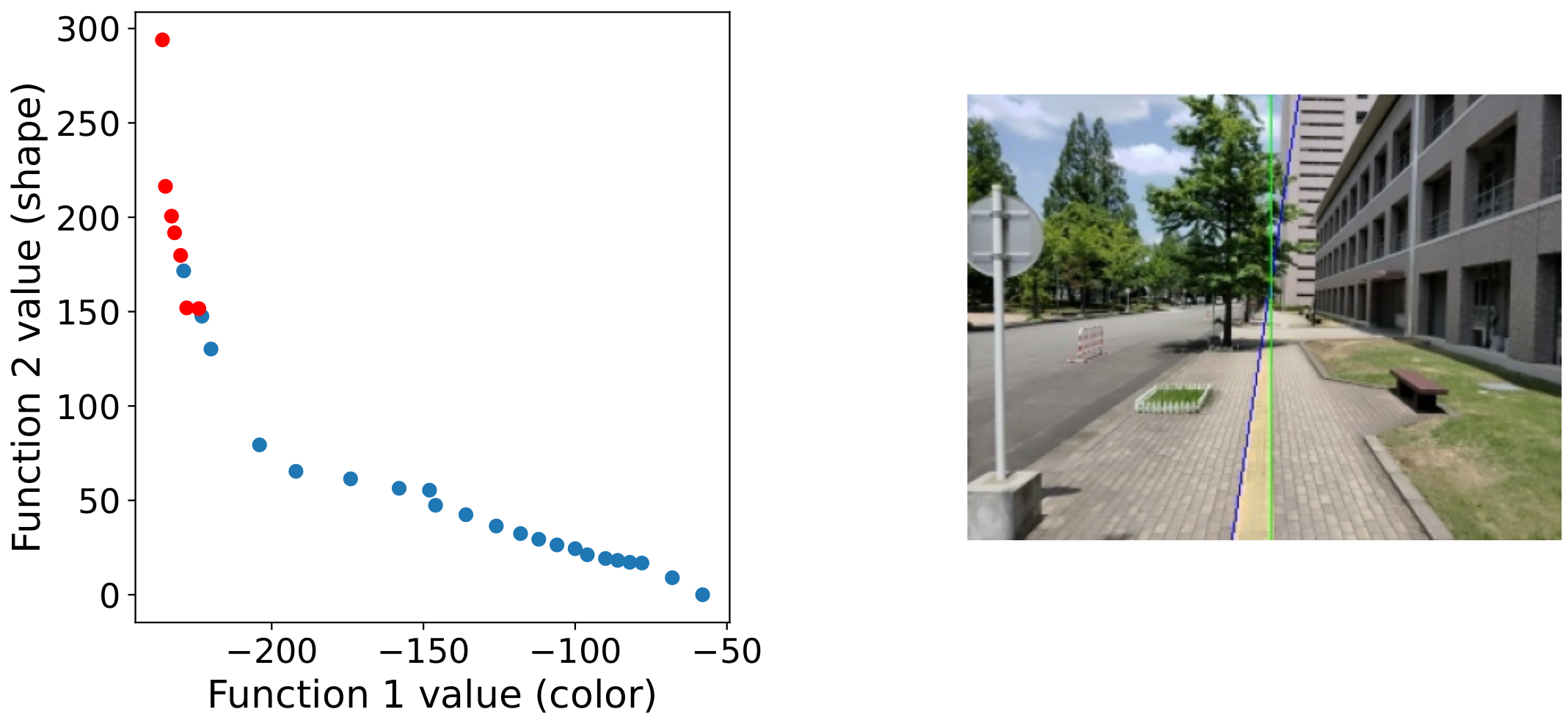
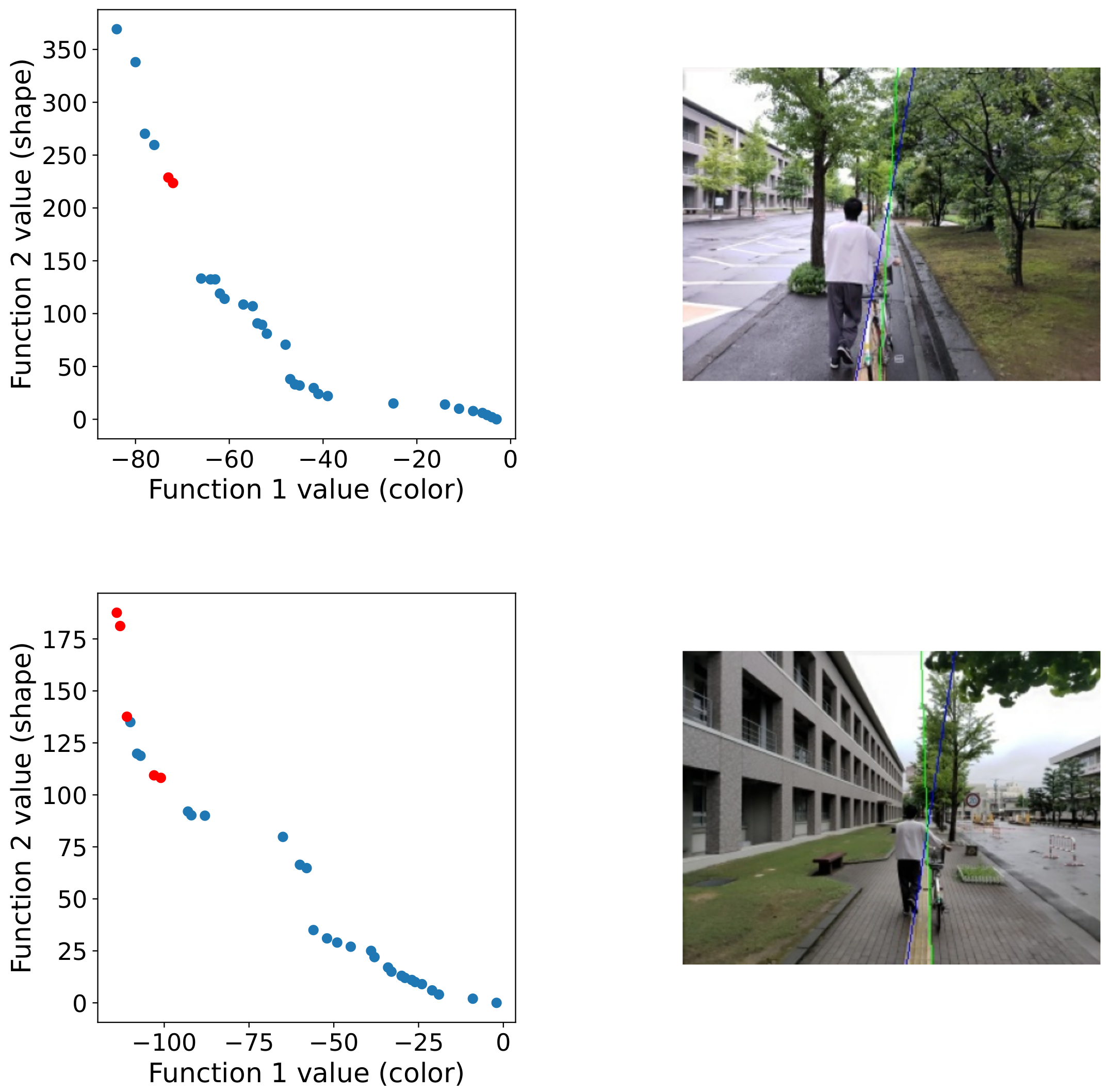
3.5. Selection of the Final Solution
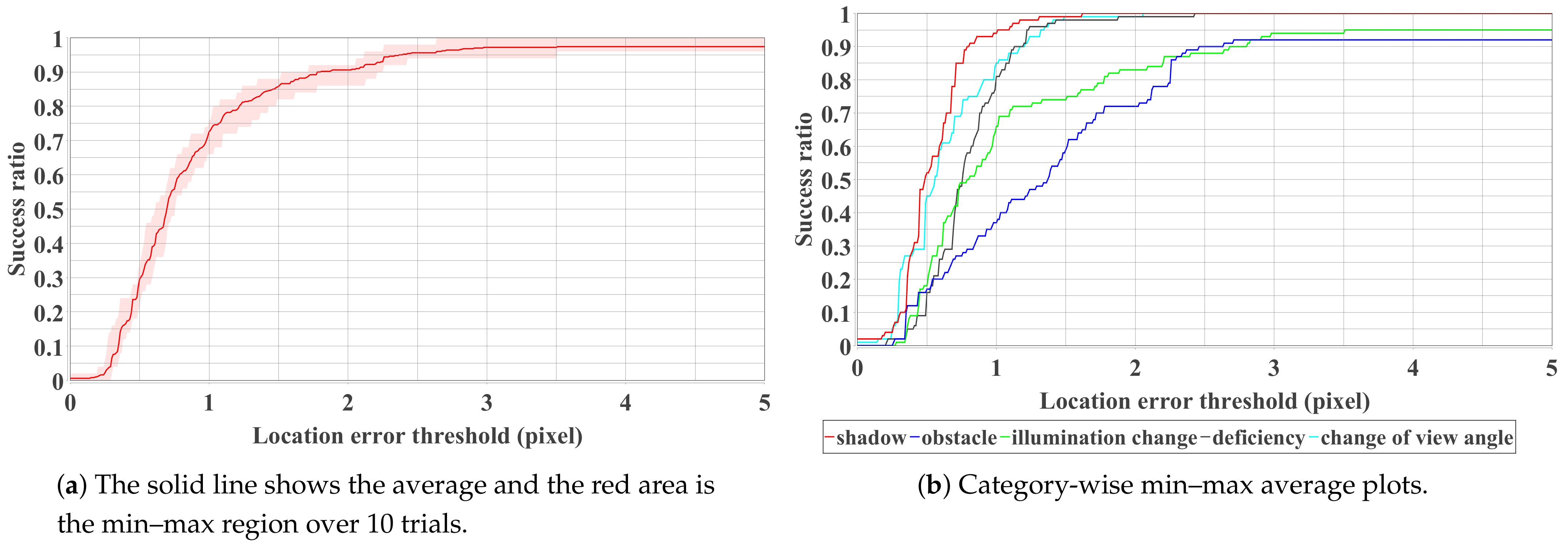
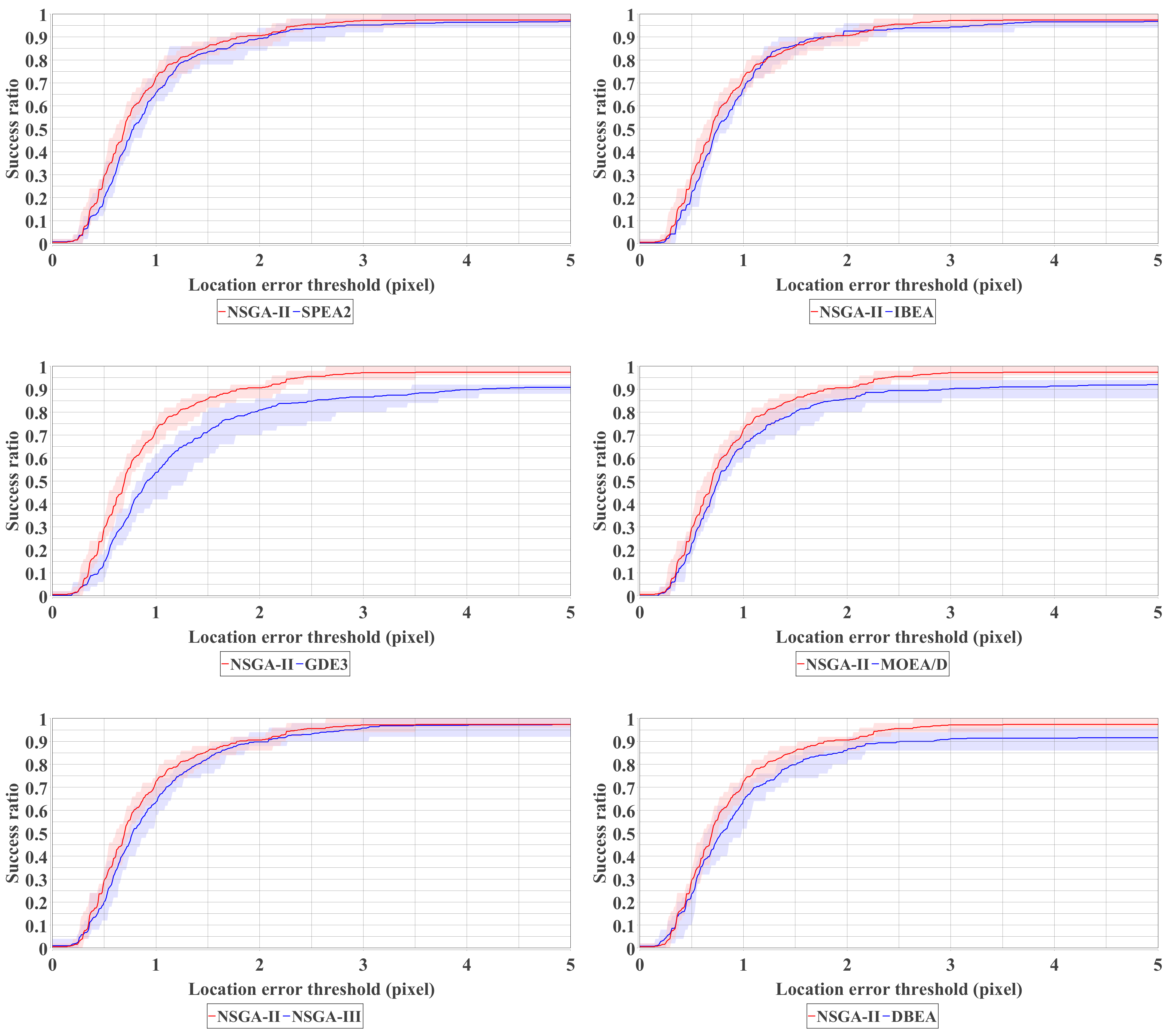
4. Experimental Results
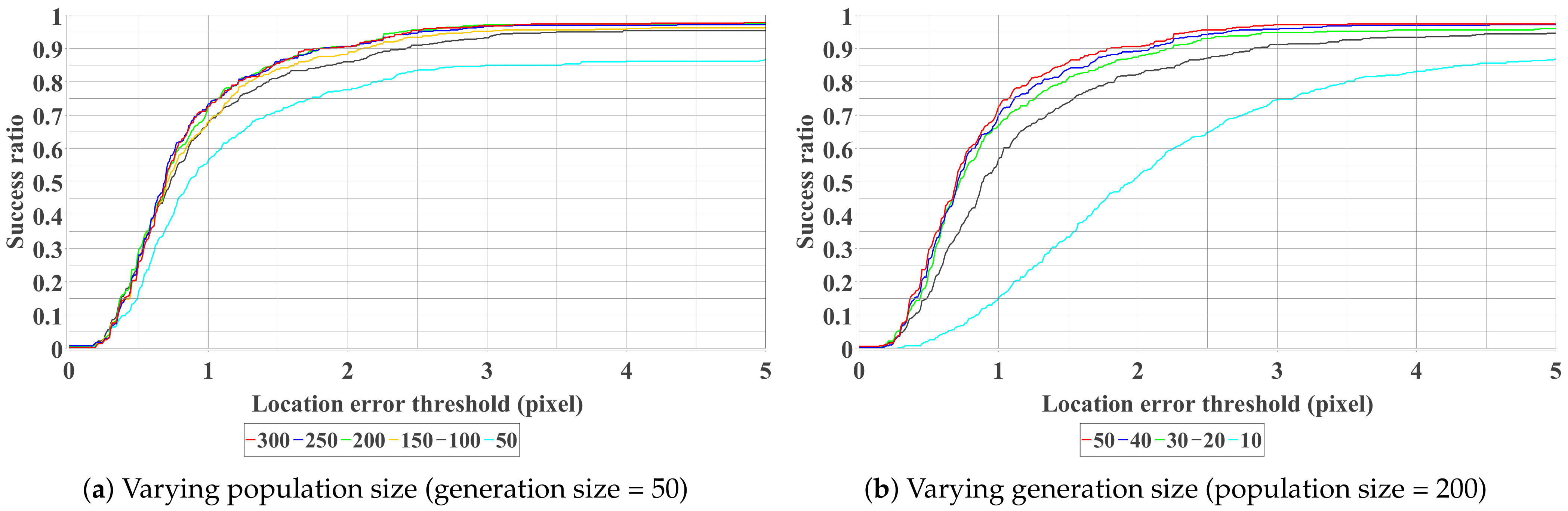
4.1. Parameter Tuning
4.2. Performance Evaluation and Limitation Analysis
4.3. Comparison over Different MOEAs
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bhowmick, A.; Hazarika, S.M. An insight into assistive technology for the visually impaired and blind people: State-of-the-art and future trends. J. Multimodal User Interfaces 2017, 11, 149–172. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ren, X.; Philipose, M. Egocentric recognition of handled objects: Benchmark and analysis. In Proceedings of the 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Ren, X.; Gu, C. Figure-ground segmentation improves handled object recognition in egocentric video. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 3137–3144. [Google Scholar] [CrossRef]
- Fathi, A.; Ren, X.; Rehg, J.M. Learning to recognize objects in egocentric activities. In Proceedings of the CVPR 2011, Colorado, CO, USA, 20–25 June 2011; pp. 3281–3288. [Google Scholar] [CrossRef]
- Kang, H.; Hebert, M.; Kanade, T. Discovering object instances from scenes of daily living. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 762–769. [Google Scholar] [CrossRef]
- Liu, Y.; Jang, Y.; Woo, W.; Kim, T.K. Video-based object recognition using novel set-of-sets representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Columbus, OH, USA, 24–27 June 2014; pp. 519–526. [Google Scholar]
- Abbas, A.M. Object Detection on Large-Scale Egocentric Video Dataset; University of Stirling: Stirling, UK, 2018. [Google Scholar]
- Yoshida, T.; Ohya, A. Autonomous mobile robot navigation using braille blocks in outdoor environment. J. Robot. Soc. Jpn. 2004, 22, 469–477. [Google Scholar] [CrossRef][Green Version]
- Okamoto, T.; Shimono, T.; Tsuboi, Y.; Izumi, M.; Takano, Y. Braille Block Recognition Using Convolutional Neural Network and Guide for Visually Impaired People. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 487–492. [Google Scholar] [CrossRef]
- Roth, G.; Levine, M.D. Extracting geometric primitives. CVGIP Image Underst. 1993, 58, 1–22. [Google Scholar] [CrossRef]
- Roth, G.; Levine, M.D. Geometric primitive extraction using a genetic algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 901–905. [Google Scholar] [CrossRef]
- Chai, J.; Jiang, T.; De Ma, S. Evolutionary tabu search for geometric primitive extraction. In Soft Computing in Engineering Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 1998; pp. 190–198. [Google Scholar] [CrossRef]
- Yao, J.; Kharma, N.; Grogono, P. Fast robust GA-based ellipse detection. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 26–26 August 2004; Volume 2, pp. 859–862. [Google Scholar] [CrossRef]
- Yao, J.; Kharma, N.; Grogono, P. A multi-population genetic algorithm for robust and fast ellipse detection. Pattern Anal. Appl. 2005, 8, 149–162. [Google Scholar] [CrossRef]
- Ayala-Ramirez, V.; Garcia-Capulin, C.H.; Perez-Garcia, A.; Sanchez-Yanez, R.E. Circle detection on images using genetic algorithms. Pattern Recognit. Lett. 2006, 27, 652–657. [Google Scholar] [CrossRef]
- Değirmenci, M. Complex geometric primitive extraction on graphics processing unit. J. WSCG 2010, 18, 129–134. [Google Scholar]
- Raja, M.M.R.; Ganesan, R. VLSI Implementation of Robust Circle Detection On Image Using Genetic Optimization Technique. Asian J. Sci. Appl. Technol. (AJSAT) 2014, 2, 17–20. [Google Scholar]
- Lutton, E.; Martinez, P. A genetic algorithm with sharing for the detection of 2D geometric primitives in images. In European Conference on Artificial Evolution; Springer: Berlin/Heidelberg, Germany, 1995; pp. 287–303. [Google Scholar] [CrossRef]
- Mirmehdi, M.; Palmer, P.; Kittler, J. Robust line segment extraction using genetic algorithms. In Proceedings of the 1997 Sixth International Conference on Image Processing and Its Applications, IET, Dublin, Ireland, 14–17 July 1997; Volume 1, pp. 141–145. [Google Scholar] [CrossRef]
- Kahlouche, S.; Achour, K.; Djekoune, O. Extracting geometric primitives from images compared with genetic algorithms approach. Comput. Eng. Syst. Appl. 2003. [Google Scholar]
- Dong, N.; Wu, C.H.; Ip, W.H.; Chen, Z.Q.; Chan, C.Y.; Yung, K.L. An opposition-based chaotic GA/PSO hybrid algorithm and its application in circle detection. Comput. Math. Appl. 2012, 64, 1886–1902. [Google Scholar] [CrossRef]
- Dasgupta, S.; Das, S.; Biswas, A.; Abraham, A. Automatic circle detection on digital images with an adaptive bacterial foraging algorithm. Soft Comput. 2010, 14, 1151–1164. [Google Scholar] [CrossRef]
- Cuevas, E.; Sención-Echauri, F.; Zaldivar, D.; Pérez-Cisneros, M. Multi-circle detection on images using artificial bee colony (ABC) optimization. Soft Comput. 2012, 16, 281–296. [Google Scholar] [CrossRef]
- Das, S.; Dasgupta, S.; Biswas, A.; Abraham, A. Automatic circle detection on images with annealed differential evolution. In Proceedings of the 2008 Eighth International Conference on Hybrid Intelligent Systems IEEE, Barcelona, Spain, 10–12 September 2008; pp. 684–689. [Google Scholar] [CrossRef]
- Cuevas, E.; Zaldivar, D.; Pérez-Cisneros, M.; Ramírez-Ortegón, M. Circle detection using discrete differential evolution optimization. Pattern Anal. Appl. 2011, 14, 93–107. [Google Scholar] [CrossRef]
- Cuevas, E.; Santuario, E.L.; Zaldívar, D.; Perez-Cisneros, M. Automatic circle detection on images based on an evolutionary algorithm that reduces the number of function evaluations. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Fourie, J. Robust circle detection using harmony search. J. Optim. 2017, 2017. [Google Scholar] [CrossRef]
- Kharma, N.; Moghnieh, H.; Yao, J.; Guo, Y.P.; Abu-Baker, A.; Laganiere, J.; Rouleau, G.; Cheriet, M. Automatic segmentation of cells from microscopic imagery using ellipse detection. IET Image Process. 2007, 1, 39–47. [Google Scholar] [CrossRef]
- Soetedjo, A.; Yamada, K. Fast and robust traffic sign detection. In Proceedings of the 2005 IEEE International Conference on Systems, Man and Cybernetics IEEE, Waikoloa, HI, USA, 12 October 2005; Volume 2, pp. 1341–1346. [Google Scholar] [CrossRef]
- Cuevas, E.; Díaz, M.; Manzanares, M.; Zaldivar, D.; Perez-Cisneros, M. An improved computer vision method for white blood cells detection. Comput. Math. Methods Med. 2013, 2013. [Google Scholar] [CrossRef]
- Alwan, S.; Caillec, J.M.; Meur, G. Detection of Primitives in Engineering Drawing using Genetic Algorithm. In Proceedings of the ICPRAM 2019, Prague, Czech Republic, 9–21 February 2019; pp. 277–282. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-Report 2001, 103. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar] [CrossRef]
- Kukkonen, S.; Lampinen, J. GDE3: The third evolution step of generalized differential evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, IEEE, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 443–450. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2008, 13, 284–302. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Asafuddoula, M.; Ray, T.; Sarker, R. A decomposition-based evolutionary algorithm for many objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 445–460. [Google Scholar] [CrossRef]
- Nakane, T.; Bold, N.; Sun, H.; Lu, X.; Akashi, T.; Zhang, C. Application of evolutionary and swarm optimization in computer vision: A literature survey. IPSJ Trans. Comput. Vis. Appl. 2020, 12, 1–34. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Maulik, U.; Mukhopadhyay, A. Multiobjective Genetic Clustering for Pixel Classification in Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1506–1511. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Maulik, U.; Bandyopadhyay, S. Multiobjective Genetic Clustering with Ensemble Among Pareto Front Solutions: Application to MRI Brain Image Segmentation. In Proceedings of the 2009 Seventh International Conference on Advances in Pattern Recognition, Kolkata, India, 4–6 February 2009; pp. 236–239. [Google Scholar] [CrossRef]
- Nakib, A.; Oulhadj, H.; Siarry, P. Image thresholding based on Pareto multiobjective optimization. Eng. Appl. Artif. Intell. 2010, 23, 313–320. [Google Scholar] [CrossRef]
- Shanmugavadivu, P.; Balasubramanian, K. Particle swarm optimized multi-objective histogram equalization for image enhancement. Opt. Laser Technol. 2014, 57, 243–251. [Google Scholar] [CrossRef]
- De, S.; Bhattacharyya, S.; Chakraborty, S. Color Image Segmentation by NSGA-II Based ParaOptiMUSIG Activation Function. In Proceedings of the 2013 International Conference on Machine Intelligence and Research Advancement, Katra, India, 21–23 December 2013; pp. 105–109. [Google Scholar] [CrossRef]
- Zhang, M.; Jiao, L.; Ma, W.; Ma, J.; Gong, M. Multi-objective evolutionary fuzzy clustering for image segmentation with MOEA/D. Appl. Soft Comput. 2016, 48, 621–637. [Google Scholar] [CrossRef]
- Wang, J.; Peng, H.; Shi, P. An optimal image watermarking approach based on a multi-objective genetic algorithm. Inf. Sci. 2011, 181, 5501–5514. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, R. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1994, 9, 115–148. [Google Scholar]
- Deb, K.; Goyal, M. A Combined Genetic Adaptive Search (GeneAS) for Engineering Design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Bandyopadhyay, S.; Bhattacharya, R. Applying modified NSGA-II for bi-objective supply chain problem. J. Intell. Manuf. 2013, 24, 707–716. [Google Scholar] [CrossRef]
- Kalaivani, L.; Subburaj, P.; Willjuice Iruthayarajan, M. Speed control of switched reluctance motor with torque ripple reduction using non-dominated sorting genetic algorithm (NSGA-II). Int. J. Electr. Power Energy Syst. 2013, 53, 69–77. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Imada, R.; Setoguchi, Y.; Nojima, Y. Performance comparison of NSGA-II and NSGA-III on various many-objective test problems. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3045–3052. [Google Scholar] [CrossRef]




| MOEA | POP | GEN | SR | PR | DIV | OS | DR | DS | NS | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NSGA-II [2] | 200 | 50 | 1.0 | 0.25 | - | - | - | - | - | - | - |
| SPEA2 [33] | 200 | 50 | 1.0 | 0.25 | - | 200 | - | - | - | - | - |
| IBEA [34] | 200 | 50 | 1.0 | 0.25 | - | - | - | - | - | - | - |
| GDE3 [35] | 200 | 50 | - | - | - | - | 0.1 | 0.5 | - | - | - |
| MOEA/D [36] | 200 | 50 | 1.0 | 0.25 | - | - | - | - | 20 | 0.9 | 2 |
| NSGA-III [37] | 200 | 50 | 1.0 | 0.25 | 4 | - | - | - | - | - | - |
| DBEA [38] | 200 | 50 | 1.0 | 0.25 | 4 | - | - | - | - | - | - |
| Par. | Description |
|---|---|
| POP | Population size. |
| GEN | Generation size. |
| SR | Crossover rate of the simulated binary crossover. |
| PR | Mutation rate of the polynomial mutation. |
| DIV | Number of divisions. |
| OS | Number of offspring generated per iteration. |
| DR | Crossover rate for differential evolution. |
| DS | Size of each step taken by differential evolution. |
| NS | Size of the neighborhood for mating. |
| Probability of mating with an individual from the neighborhood versus the entire population. | |
| Maximum number of spots in the population that an offspring can replace. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takano, T.; Nakane, T.; Akashi, T.; Zhang, C. Braille Block Detection via Multi-Objective Optimization from an Egocentric Viewpoint. Sensors 2021, 21, 2775. https://doi.org/10.3390/s21082775
Takano T, Nakane T, Akashi T, Zhang C. Braille Block Detection via Multi-Objective Optimization from an Egocentric Viewpoint. Sensors. 2021; 21(8):2775. https://doi.org/10.3390/s21082775
Chicago/Turabian StyleTakano, Tsubasa, Takumi Nakane, Takuya Akashi, and Chao Zhang. 2021. "Braille Block Detection via Multi-Objective Optimization from an Egocentric Viewpoint" Sensors 21, no. 8: 2775. https://doi.org/10.3390/s21082775
APA StyleTakano, T., Nakane, T., Akashi, T., & Zhang, C. (2021). Braille Block Detection via Multi-Objective Optimization from an Egocentric Viewpoint. Sensors, 21(8), 2775. https://doi.org/10.3390/s21082775






