From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems
Abstract
1. Introduction
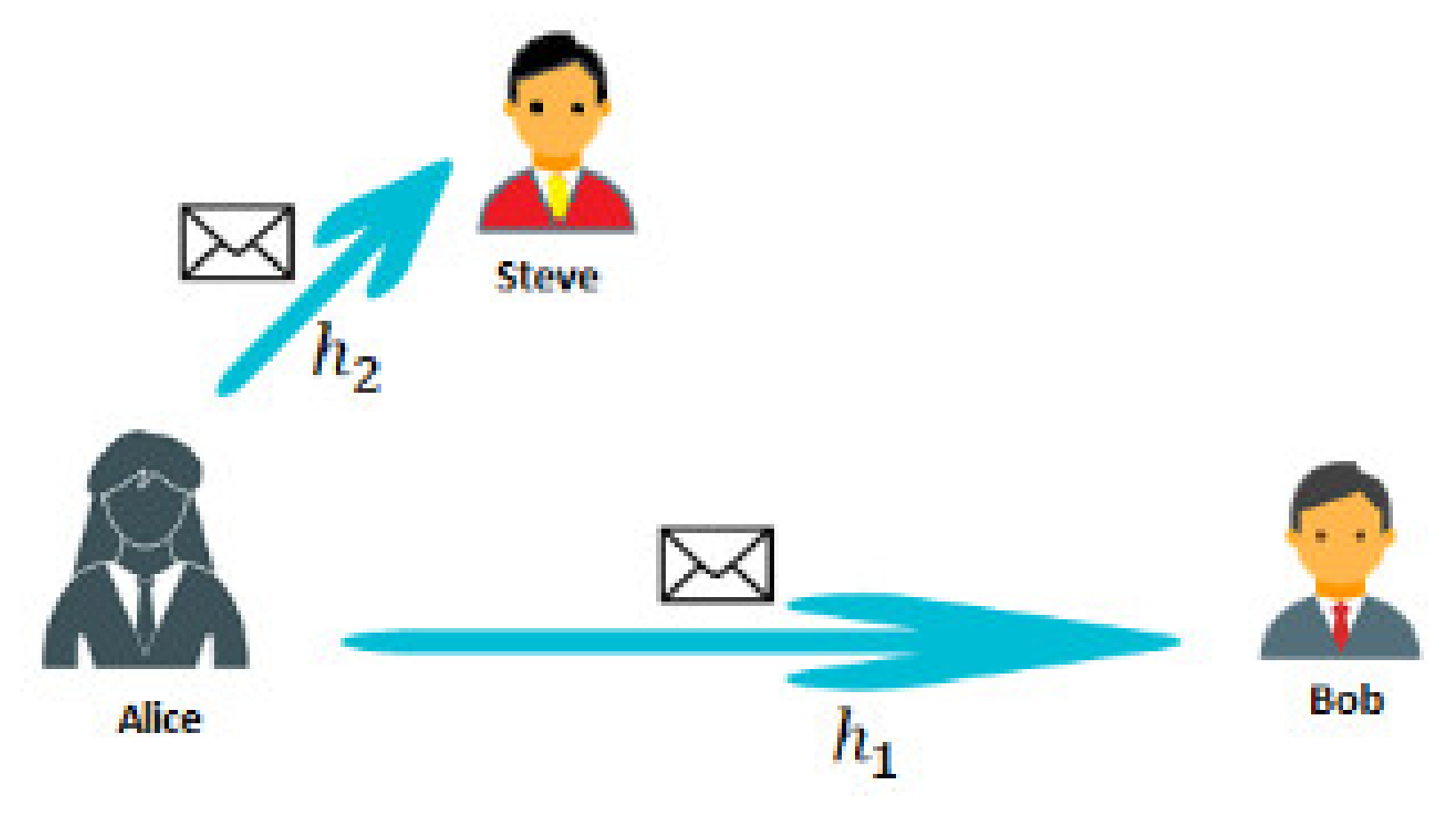
2. Superposition of Signals as a Watermarking
3. Superposition of Signals as a Covert Channel
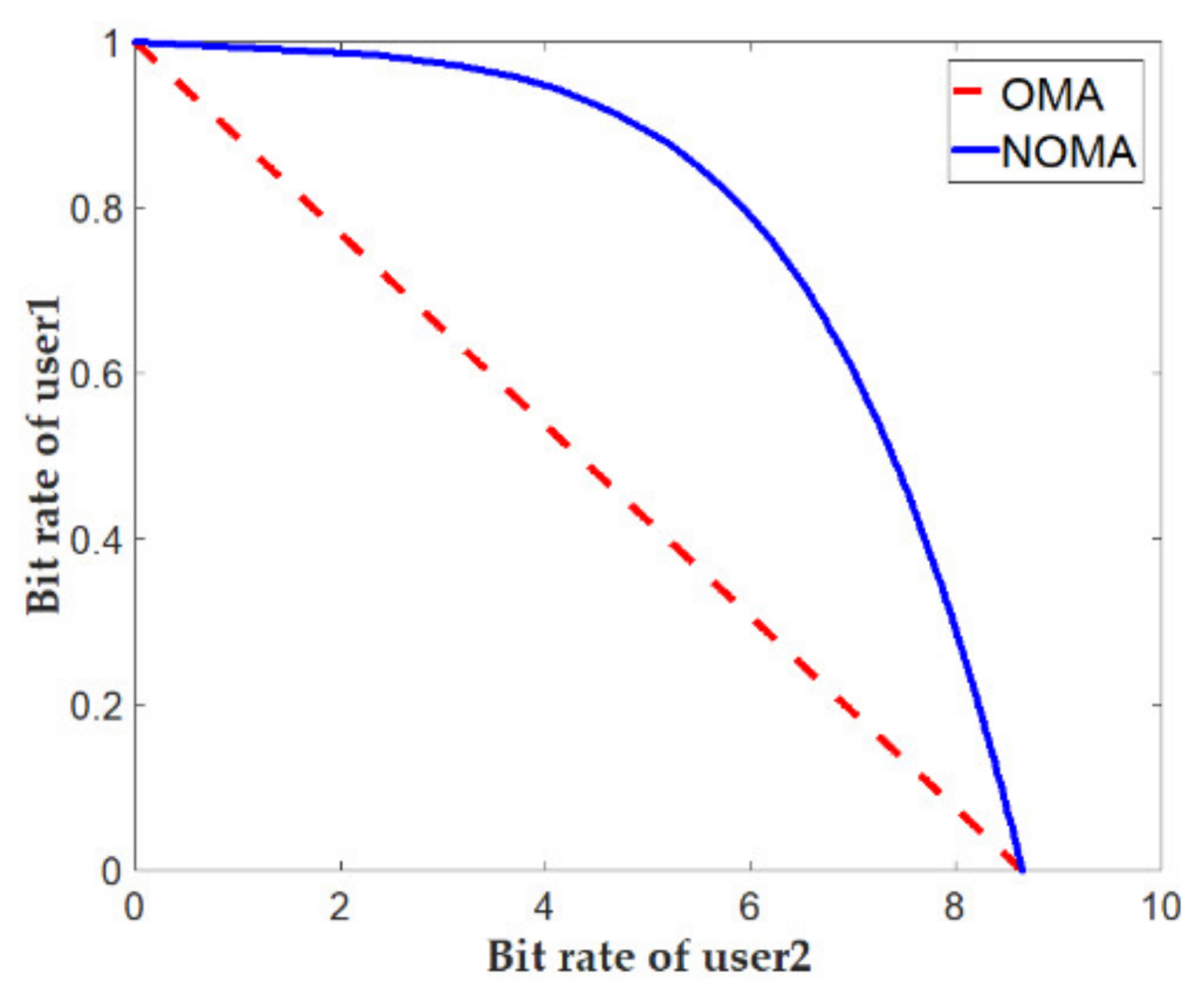
4. Superposition of Signals as a Multi-Access Systems NOMA
5. Security Aspects of Watermarking, Covert Channels and NOMA
5.1. PLS
5.2. LPD
- (a)
- Calculation of the AUR where AUR = 0.5 corresponds to a random detector.
- (b)
- Calculation of the minimum sum of the binary detector for false positive and negative errors, defined as or , where is false positive and is false negative.
6. Current Issues and Future Research Direction
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NR; Base Station (BS). Radio Transmission and Reception (3GPP TS 38.104 Version 15.5.0 Release 15); ETSI, 3GPP: Sophia-Antipolis, France, 2019. [Google Scholar]
- Miridakis, N.I.; Vergados, D.D. A Survey on the Successive Interference Cancellation Performance for Single-Antenna and Multiple-Antenna OFDM Systems. IEEE Commun. Surv. Tutor. 2012, 15, 312–335. [Google Scholar] [CrossRef]
- Costa, M. Writing on dirty paper (Corresp.). IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Zaidi, A.; Piantanida, P.; Duhamel, P. Broadcast- and MAC-Aware Coding Strategies for Multiple User Information Embedding. IEEE Trans. Signal Process. 2007, 55, 2974–2992. [Google Scholar] [CrossRef]
- Zaidi, A.; Vandendorpe, L. Coding Schemes for Relay-Assisted Information Embedding. IEEE Trans. Inf. Forensics Secur. 2009, 4, 70–85. [Google Scholar] [CrossRef]
- Piotrowski, Z.; Kelner, J.M. Steganografia radiowa—Zagrożenia i wyzwania, Przegląd Telekomunikacyjny + Wiadomości Telekomunikacyjne. Radio Steganogr. Threat. Chall. Telecommun. Rev. Telecommun. News 2017, 6, 165–172. [Google Scholar]
- Park, J.-M.; Reed, J.H.; Beex, A.A.; Clancy, T.C.; Kumar, V.; Bahrak, B. Security and Enforcement in Spectrum Sharing. Proc. IEEE 2014, 102, 270–281. [Google Scholar] [CrossRef]
- Yu, P.L.; Baras, J.S.; Sadler, B.M. Physical-Layer Authentication. IEEE Trans. Inf. Forensics Secur. 2008, 3, 38–51. [Google Scholar] [CrossRef]
- Kleider, J.E.; Gifford, S.; Chuprun, S.; Fette, B. Radio frequency watermarking for OFDM wireless networks. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; p. 397. [Google Scholar]
- Yu, P.L.; Verma, G.; Sadler, B.M. Wireless physical layer authentication via fingerprint embedding. IEEE Commun. Mag. 2015, 53, 48–53. [Google Scholar] [CrossRef]
- Verma, G.; Yu, P.; Sadler, B.M. Physical Layer Authentication via Fingerprint Embedding Using Software-Defined Radios. IEEE Access 2015, 3, 81–88. [Google Scholar] [CrossRef]
- Tan, X.; Borle, K.; Du, W.; Chen, B. Cryptographic Link Signatures for Spectrum Usage Authentication in Cognitive Radio. In Proceedings of the Fourth ACM Conference on Recommender Systems—RecSys ’10; ACM: New York, NY, USA, 2011; pp. 79–90. [Google Scholar]
- Jiang, T.; Zeng, H.; Yan, Q.; Lou, W.; Hou, Y.T. On the Limitation of Embedding Cryptographic Signature for Primary Transmitter Authentication. IEEE Wirel. Commun. Lett. 2012, 1, 324–327. [Google Scholar] [CrossRef]
- Xu, Z.; Yuan, W. Watermark BER and Channel Capacity Analysis for QPSK-Based RF Watermarking by Constellation Dithering in AWGN Channel. IEEE Signal Process. Lett. 2017, 24, 1068–1072. [Google Scholar] [CrossRef]
- Lampson, W. A note on the connement problem. Commun. ACM 1973, 16, 613–615. [Google Scholar] [CrossRef]
- Chen, O.; Meadows, C.; Trivedi, G. Stealthy Protocols: Metrics and Open Problems. In Concurrency, Security, and Puzzles; Lecture Notes in Computer Science; Springer: Cham, Germany, 2017; pp. 1–17. ISBN 978-3-319-51045-3. [Google Scholar]
- Hijaz, Z.; Frost, V.S. Exploiting OFDM systems for covert communication. In Proceedings of the 2010 Military Communications Conference (MILCOM), San Jose, CA, USA, 31 October–3 November 2010; pp. 2149–2155. [Google Scholar]
- Classen, J.; Schulz, M.; Hollick, M. Practical covert channels for WiFi systems. In Proceedings of the 2015 IEEE Conference on Communications and Network Security (CNS), Florence, Italy, 28–30 September 2015; pp. 209–217. [Google Scholar]
- Dutta, A.; Saha, D.; Grunwald, D.; Sicker, D. Secret agent radio: Covert communication through dirty constellations. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 2012; pp. 160–175. [Google Scholar]
- Cao, P.; Liu, W.; Liu, G.; Ji, X.; Zhai, J.; Dai, Y. A Wireless Covert Channel Based on Constellation Shaping Modulation. Secur. Commun. Netw. 2018, 2018, 1214681. [Google Scholar] [CrossRef]
- D’Oro, S.; Restuccia, F.; Melodia, T. Hiding Data in Plain Sight: Undetectable Wireless Communications through Pseudo-Noise Asymmetric Shift Keying. In Proceedings of the 2019 38th IEEE Conference on Computer Communications (INFOCOM), Paris, France, 29 April–2 May 2019; IEEE: New York, NY, USA; pp. 1585–1593. [Google Scholar]
- Benjebboour, A.; Li, A.; Saito, Y.; Kishiyama, Y.; Harada, A.; Nakamura, T. System-level performance of downlink NOMA for future LTE enhancements. In Proceedings of the 2013 IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 66–70. [Google Scholar]
- Islam, S.R.; Zeng, M.; Dobre, O.A.; Kwak, K.S. Non-Orthogonal Multiple Access (NOMA): How It Meets 5G and Beyond; Wiley 5G Ref: Hoboken, NJ, USA, 2019. [Google Scholar]
- Yan, S.; Zhou, X.; Hu, J.; Hanly, S.V. Low Probability of Detection Communication: Opportunities and Challenges. IEEE Wirel. Commun. 2019, 26, 19–25. [Google Scholar] [CrossRef]
- Simmons, G.J. The Prisoners’ Problem and the Subliminal Channel. Adv. Cryptol. 1984, 51–67. [Google Scholar] [CrossRef]
- Yang, N.; Wang, L.; Geraci, G.; Elkashlan, M.; Yuan, J.; Di Renzo, M. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 2015, 53, 20–27. [Google Scholar] [CrossRef]
- Zhao, N.; Yu, F.R.; Li, M.; Yan, Q.; Leung, V.C.M. Physical layer security issues in interference- alignment-based wireless networks. IEEE Commun. Mag. 2016, 54, 162–168. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z.; Zhou, C.; Zhang, Y. Physical-Layer Security in Space Information Networks: A Survey. IEEE Internet Things J. 2020, 7, 33–52. [Google Scholar] [CrossRef]
- Sanchez, J.D.V.; Urquiza-Aguiar, L.; Paredes, M.C.P. Physical Layer Security for 5G Wireless Networks: A Comprehensive Survey. In Proceedings of the 2019 3rd Cyber Security in Networking Conference (CSNet), Quito, Ecuador, 23–25 October 2019; pp. 122–129. [Google Scholar]
- Furqan, H.M.; Hamamreh, J.; Arslan, H. Physical Layer Security for NOMA: Requirements, Merits, Challenges, and Recommendations. arXiv 2019, arXiv:1905.05064. [Google Scholar]
- Subramanian, A.; Suresh, A.T.; Raj, S.; Thangaraj, A.; Bloch, M.; McLaughlin, S. Strong and weak secrecy in wiretap channels. In Proceedings of the 2010 6th International Symposium on Turbo Codes & Iterative Information Processing, Brest, France, 6–10 September 2010; pp. 30–34. [Google Scholar] [CrossRef]
- Shannon, E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Wyner, D. The wire-tap channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Güvenkaya, E.; Hamamreh, J.M.; Arslan, H. On physical-layer concepts and metrics in secure signal transmission. Phys. Commun. 2017, 25, 14–25. [Google Scholar] [CrossRef]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and Applications of Physical Layer Security Techniques for Confidentiality: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless Information-Theoretic Security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Wang, L. Physical Layer Security in Wireless Cooperative Networks; Metzler, J.B., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Prabhu, V.U.; Rodrigues, M.R.D. On Wireless Channels with M-Antenna Eavesdroppers: Characterization of the Outage Probability and Outage Secrecy Capacity. In 2010 IEEE Global Telecommunications Conference GLOBECOM 2010; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Ding, Z.; Zhao, Z.; Peng, M.; Poor, H.V. On the Spectral Efficiency and Security Enhancements of NOMA Assisted Multicast-Unicast Streaming. IEEE Trans. Commun. 2017, 65, 3151–3163. [Google Scholar] [CrossRef]
- Feng, Y.; Yan, S.; Yang, Z.; Yang, N.; Yuan, J. Beamforming Design and Power Allocation for Secure Transmission with NOMA. IEEE Trans. Wirel. Commun. 2019, 18, 2639–2651. [Google Scholar] [CrossRef]
- Xiao, K.; Gong, L.; Kadoch, M. Opportunistic Multicast NOMA with Security Concerns in a 5G Massive MIMO System. IEEE Commun. Mag. 2018, 56, 91–95. [Google Scholar] [CrossRef]
- Satrya, G.; Shin, S. Enhancing security of SIC algorithm on non-orthogonal multiple access (NOMA) based systems. Phys. Commun. 2019, 33, 16–25. [Google Scholar] [CrossRef]
- Bash, B.A.; Goeckel, D.; Towsley, D.; Guha, S. Hiding information in noise: Fundamental limits of covert wireless communication. IEEE Commun. Mag. 2015, 53, 26–31. [Google Scholar] [CrossRef]
- Bash, B.A.; Goeckel, D.; Towsley, D. Limits of reliable communication with low probability of detection on AWGN channels. IEEE J. Sel. Areas Commun. 2013, 31, 1921–1930. [Google Scholar] [CrossRef]
- Bloch, M.R. Covert Communication over Noisy Channels: A Resolvability Perspective. IEEE Trans. Inf. Theory 2016, 62, 2334–2354. [Google Scholar] [CrossRef]
- Wang, L.; Wornell, G.W.; Zheng, L. Fundamental Limits of Communication with Low Probability of Detection. IEEE Trans. Inf. Theory 2016, 62, 3493–3503. [Google Scholar] [CrossRef]
- Chandramouli, R. A mathematical framework for active steganalysis. Multimed. Syst. 2003, 9, 303–311. [Google Scholar] [CrossRef]
- Sullivan, K.; Bi, Z.; Madhow, U.; Chandrasekaran, S.; Manjunath, B. Steganalysis of Quantization Index Modulation Data Hiding. In Proceedings of the 2004 International Conference on Image Processing, 2004. ICIP ′04, Singapore, 24–27 October 2004; Volume 2, pp. 1165–1168. [Google Scholar] [CrossRef]
- Anderson, R. Stretching the limits of steganography. In International Workshop on Information Hiding; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1174, pp. 39–48. [Google Scholar]
- Lee, S.; Baxley, R.J.; Weitnauer, M.A.; Walkenhorst, B. Achieving Undetectable Communication. IEEE J. Sel. Top. Signal Process. 2015, 9, 1195–1205. [Google Scholar] [CrossRef]
- Sobers, T.V.; Bash, B.A.; Guha, S.; Towsley, D.; Goeckel, D. Covert Communication in the Presence of an Uninformed Jammer. IEEE Trans. Wirel. Commun. 2017, 16, 6193–6206. [Google Scholar] [CrossRef]
- Shahzad, K.; Zhou, X.; Yan, S.; Hu, J.; Shu, F.; Li, J. Achieving Covert Wireless Communications Using a Full-Duplex Receiver. IEEE Trans. Wirel. Commun. 2018, 17, 8517–8530. [Google Scholar] [CrossRef]
- Tandra, R.; Sahai, A. SNR Walls for Signal Detection. IEEE J. Sel. Top. Signal Process. 2008, 2, 4–17. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Z.; Zhong, C.; Ng, D.W.K.; Jia, R. Exploiting Inter-User Interference for Secure Massive Non-Orthogonal Multiple Access. IEEE J. Sel. Areas Commun. 2018, 36, 788–801. [Google Scholar] [CrossRef]
- Shahzad, K.; Zhou, X.; Yan, S. Covert Communication in Fading Channels under Channel Uncertainty. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, NSW, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Tao, L.; Yang, W.; Yan, S.; Wu, D.; Guan, X.; Chen, D. Covert Communication in Downlink NOMA Systems with Random Transmit Power. IEEE Wirel. Commun. Lett. 2020, 9, 2000–2004. [Google Scholar] [CrossRef]
- Ta, H.Q. Physical-Layer Secrecy and Privacy of Wireless Communication. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 2020. [Google Scholar]
- Cabuk, S.; Brodley, C.; Shields, C. IP covert timing channels: Design and detection. In Proceedings of the 2004 ACM Conference on Computer and Communications Security; ACM: New York, NY, USA, 2004. [Google Scholar]
- Ker, A.D.; Pevný, T.; Kodovský, J.; Fridrich, J. The square root law of steganographic capacity. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security; Association for Computing Machinery (ACM): New York, NY, USA, 2008; pp. 107–116. [Google Scholar]
- Melki, R.; Noura, H.N.; Chehab, A. Physical layer security for NOMA: Limitations, issues, and recommendations. Ann. Telecommun. 2020, 1–23. [Google Scholar] [CrossRef]
- Anh, L.; Kong, H. Secrecy performance of an uplink-downlink cooperative PD-NOMA DF network in PLS. Int. J. Electron. 2020, 107, 1861–1886. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, J. Physical-Layer Security for Mobile Users in NOMA-Enabled Visible Light Communication Networks. IEEE Access 2020, 8, 205411–205423. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.-H.; Wang, L. Physical Layer Security for Next Generation Wireless Networks: Theories, Technologies, and Challenges. IEEE Commun. Surv. Tutor. 2016, 19, 347–376. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzesiak, K.; Piotrowski, Z. From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems. Sensors 2021, 21, 2752. https://doi.org/10.3390/s21082752
Grzesiak K, Piotrowski Z. From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems. Sensors. 2021; 21(8):2752. https://doi.org/10.3390/s21082752
Chicago/Turabian StyleGrzesiak, Krystian, and Zbigniew Piotrowski. 2021. "From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems" Sensors 21, no. 8: 2752. https://doi.org/10.3390/s21082752
APA StyleGrzesiak, K., & Piotrowski, Z. (2021). From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems. Sensors, 21(8), 2752. https://doi.org/10.3390/s21082752






