Low-Velocity Impact Localization on a Honeycomb Sandwich Panel Using a Balanced Projective Dictionary Pair Learning Classifier
Abstract
:1. Introduction
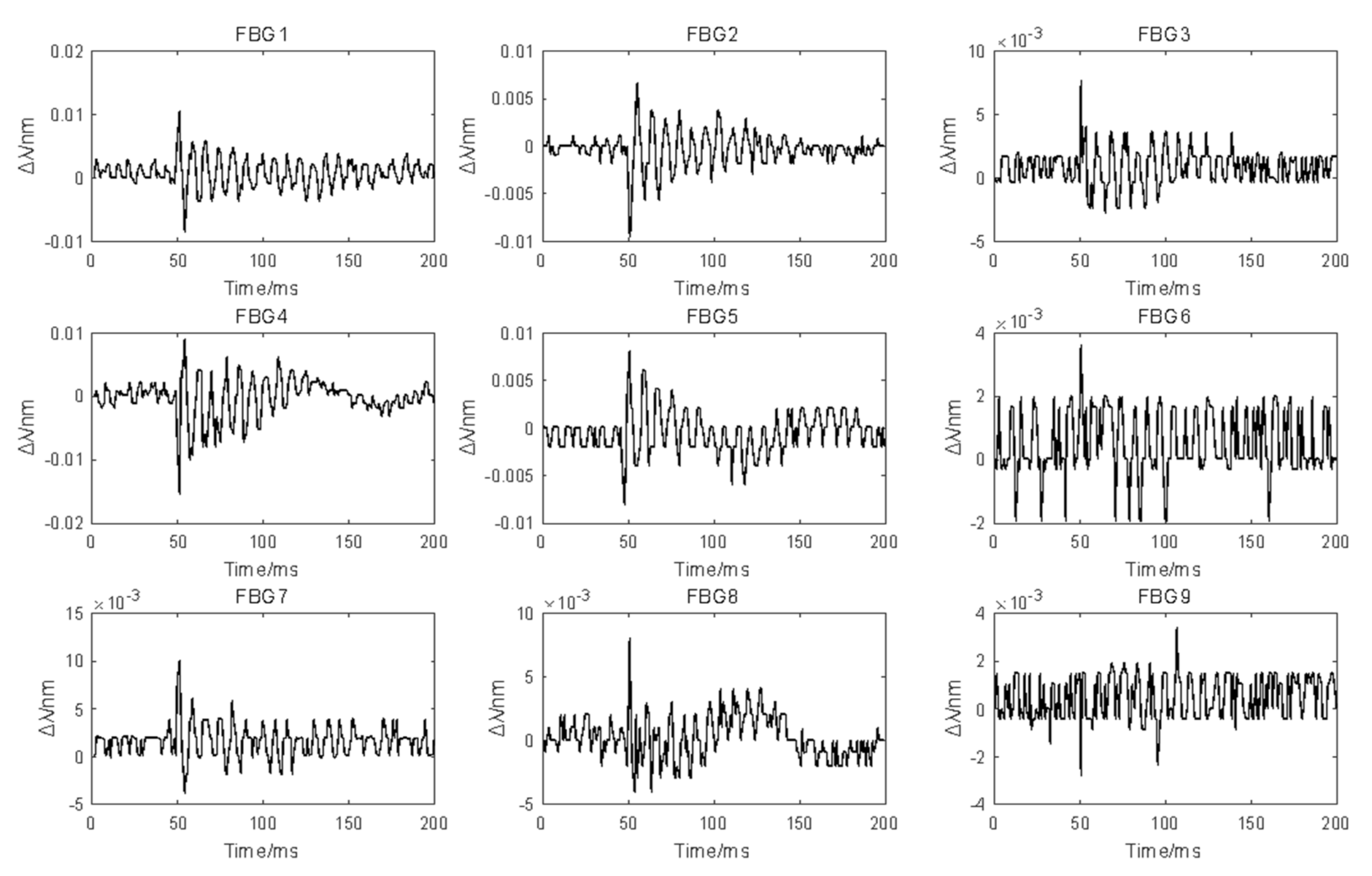
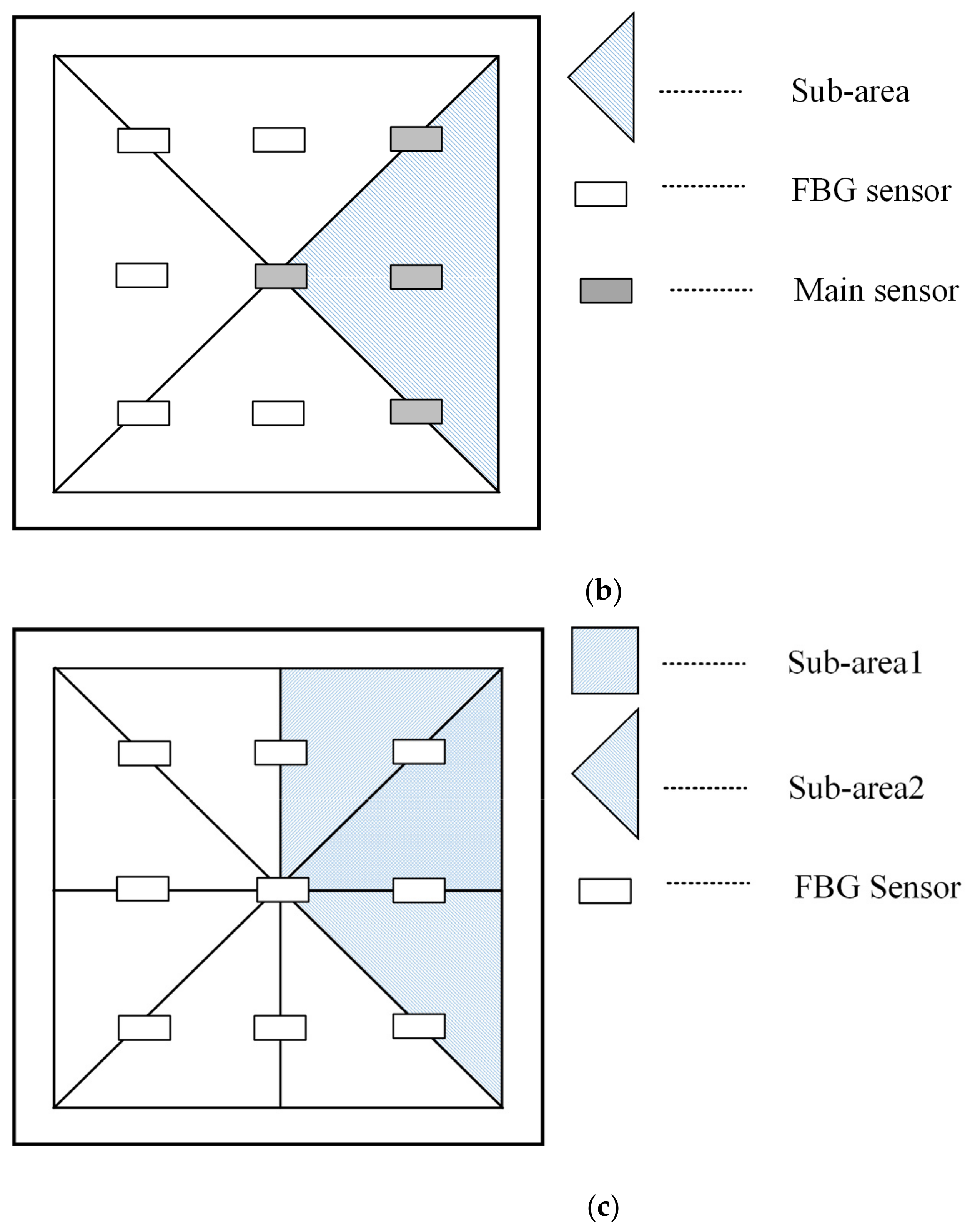
2. FBG Sensing Technique
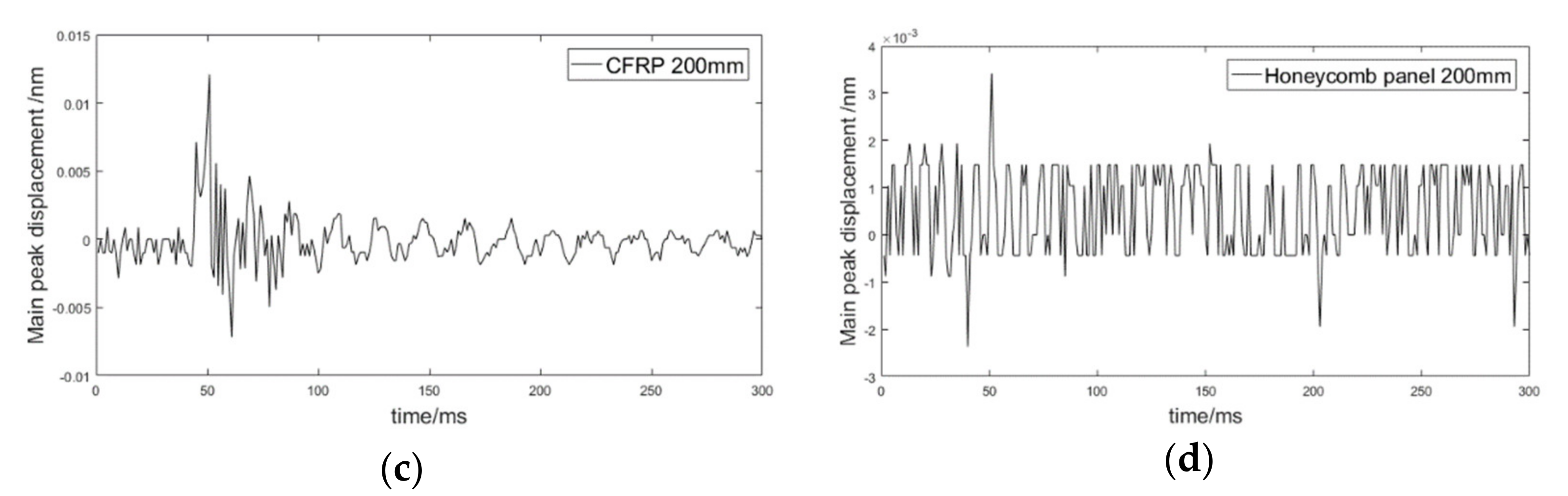
3. Experimental Setup and Specimen Analysis
4. Sparse Representation Classifier Based on Balanced-DPL
4.1. DPL Algorithm
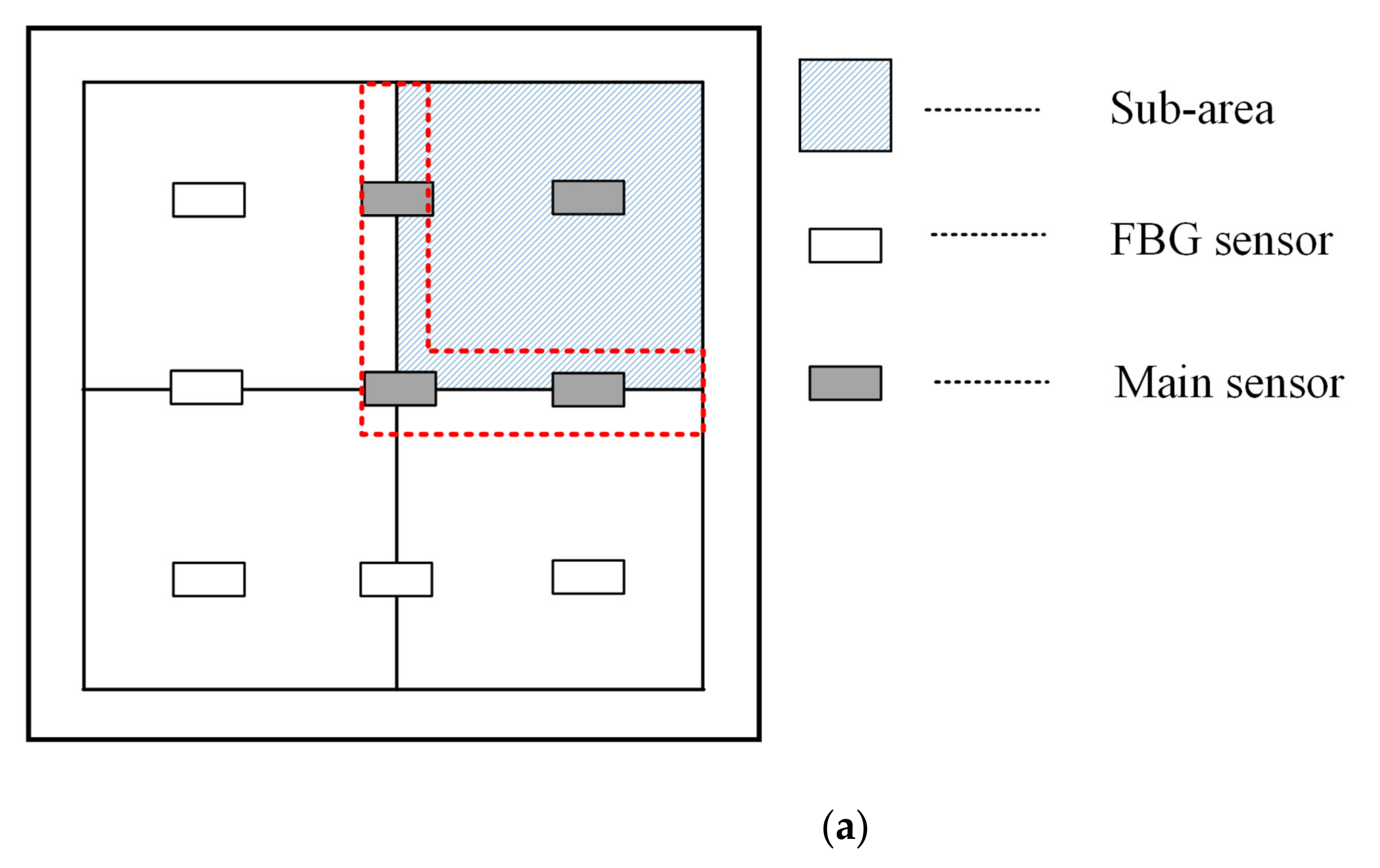
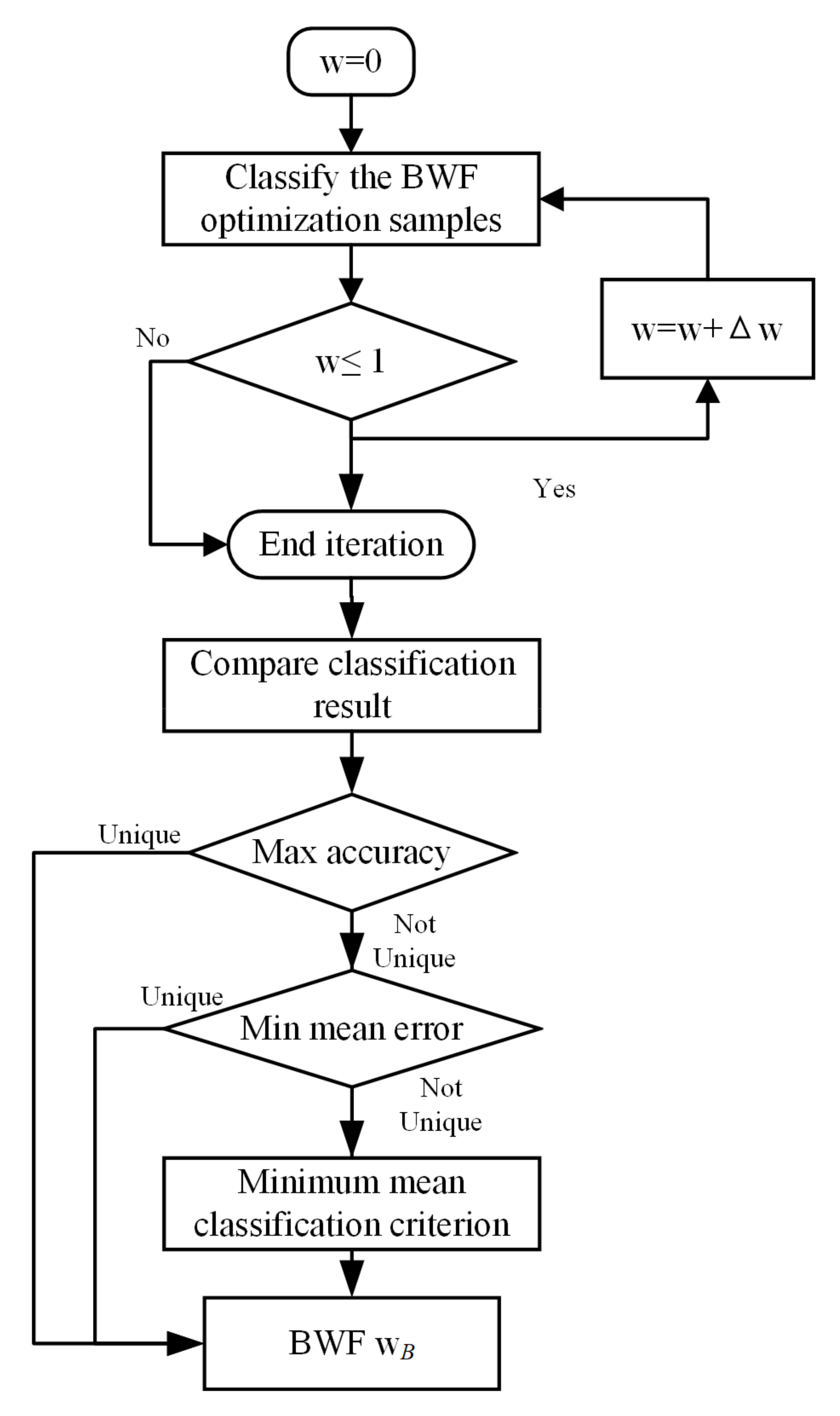
4.2. Balanced-DPL Classifier
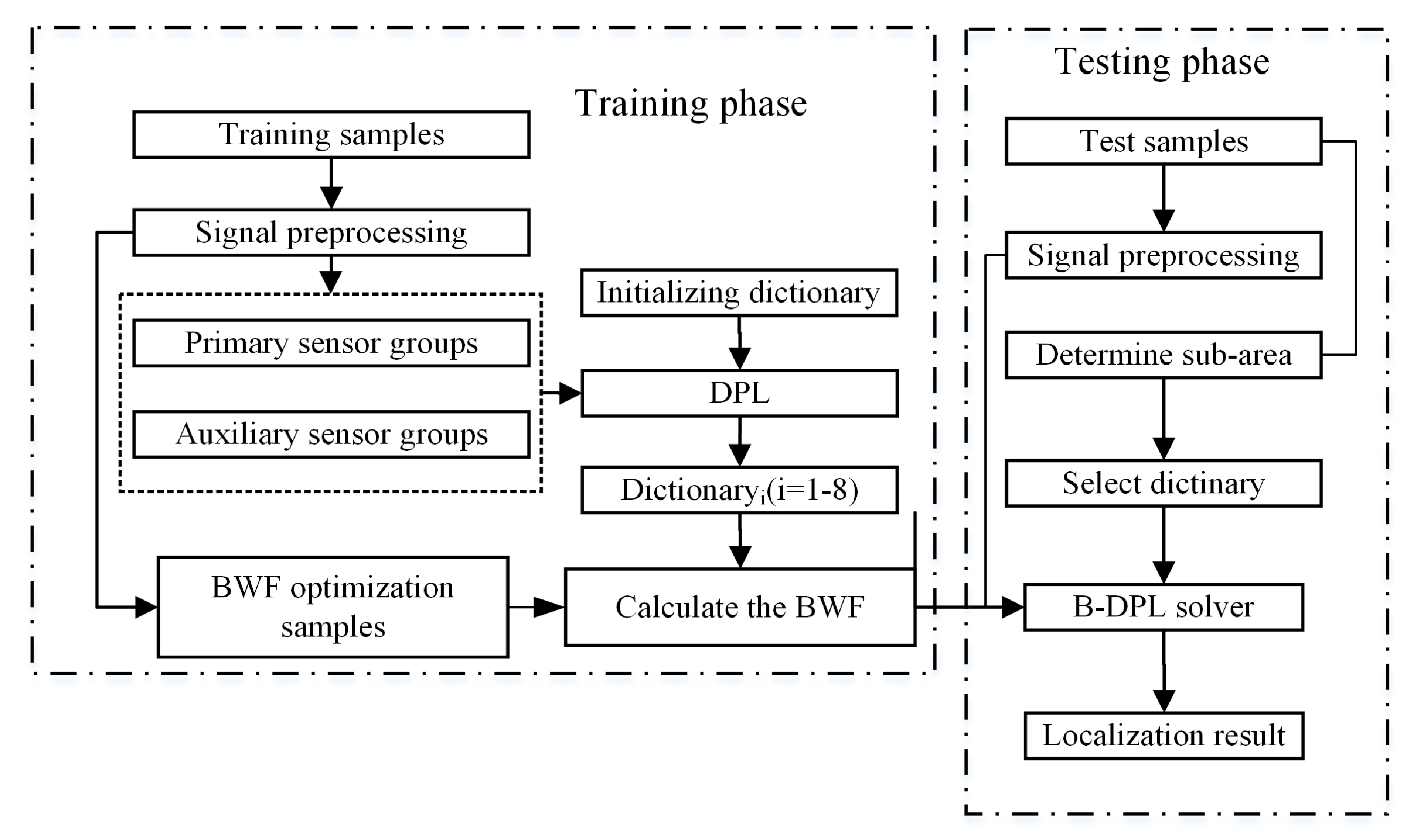
4.3. Method Processing
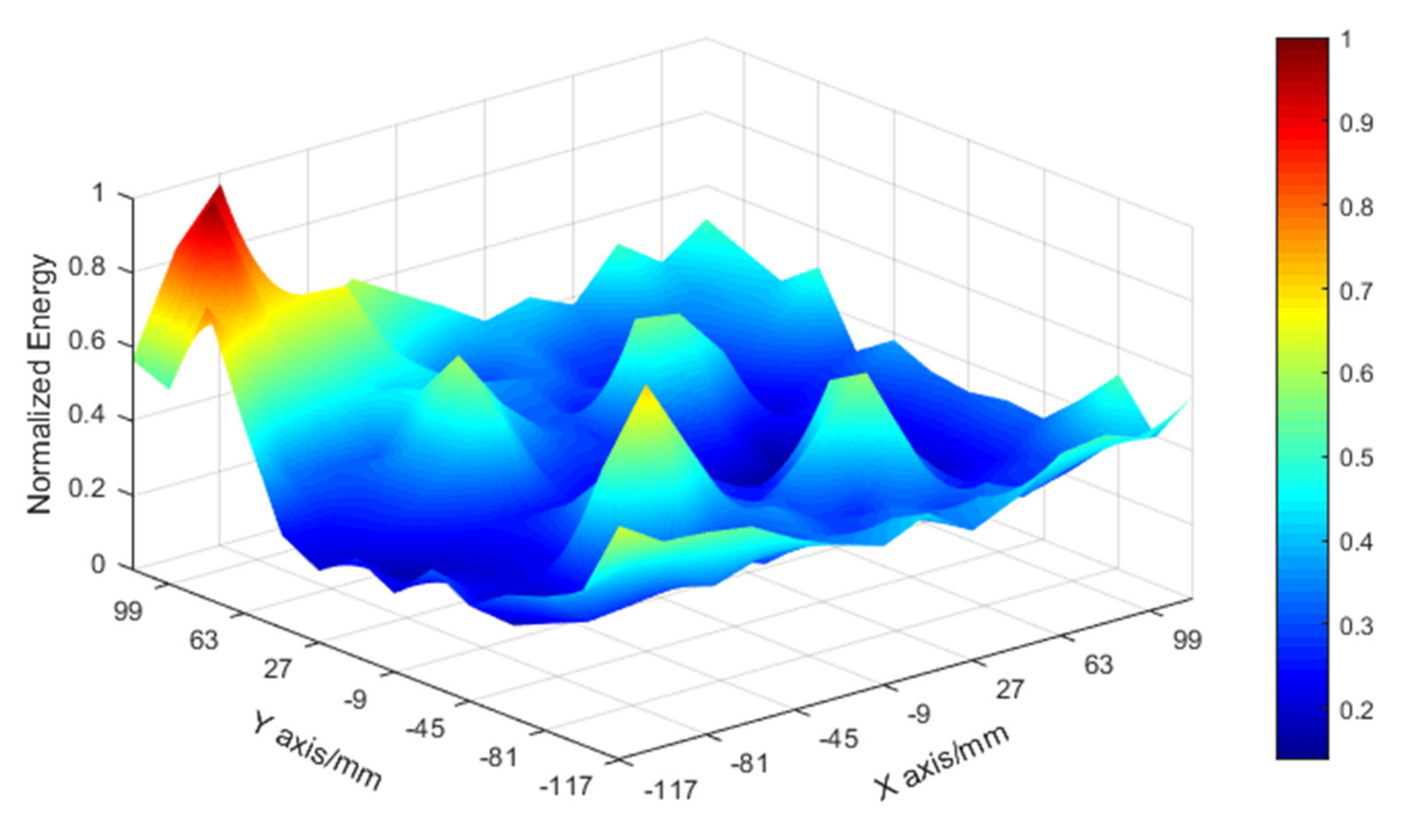
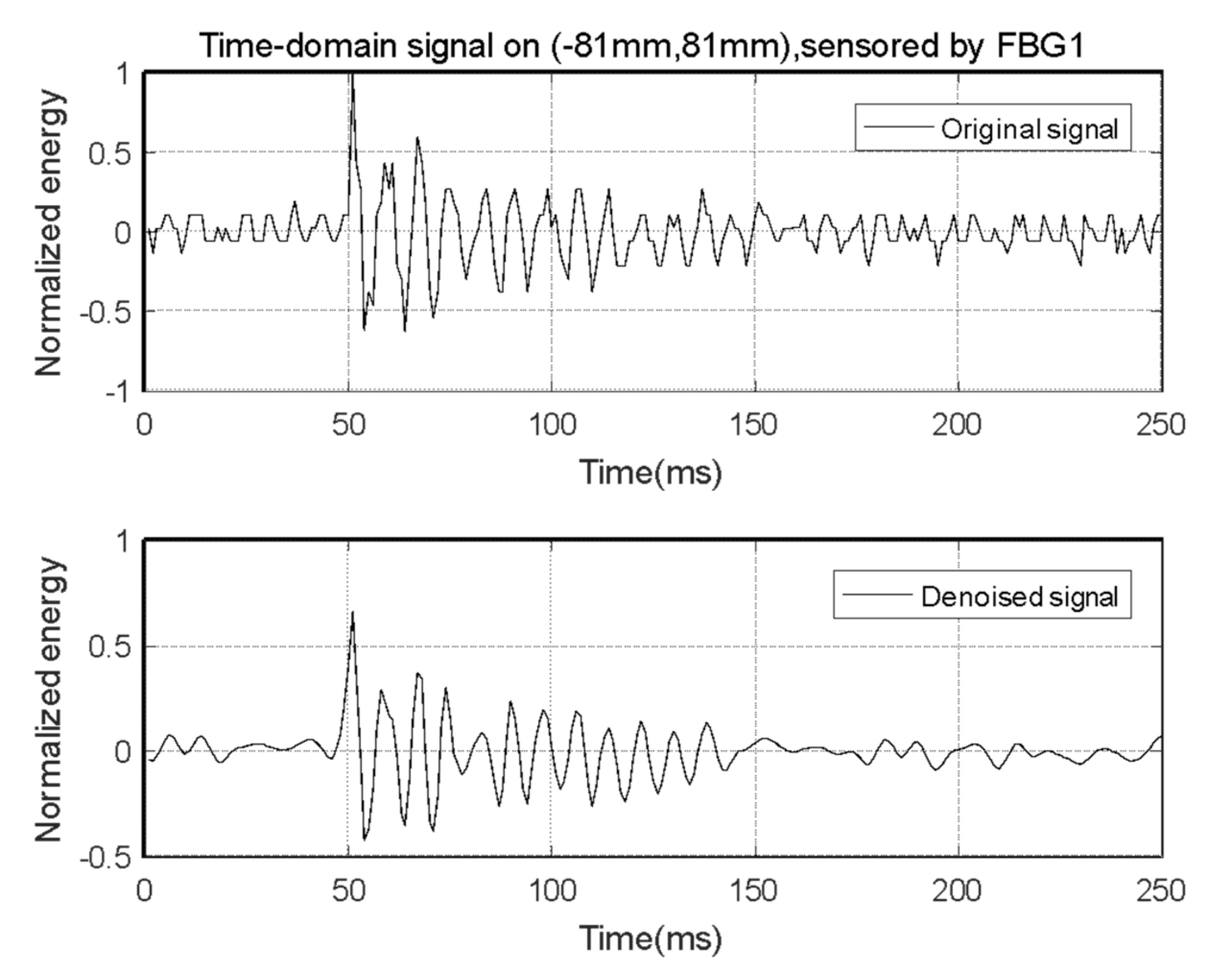
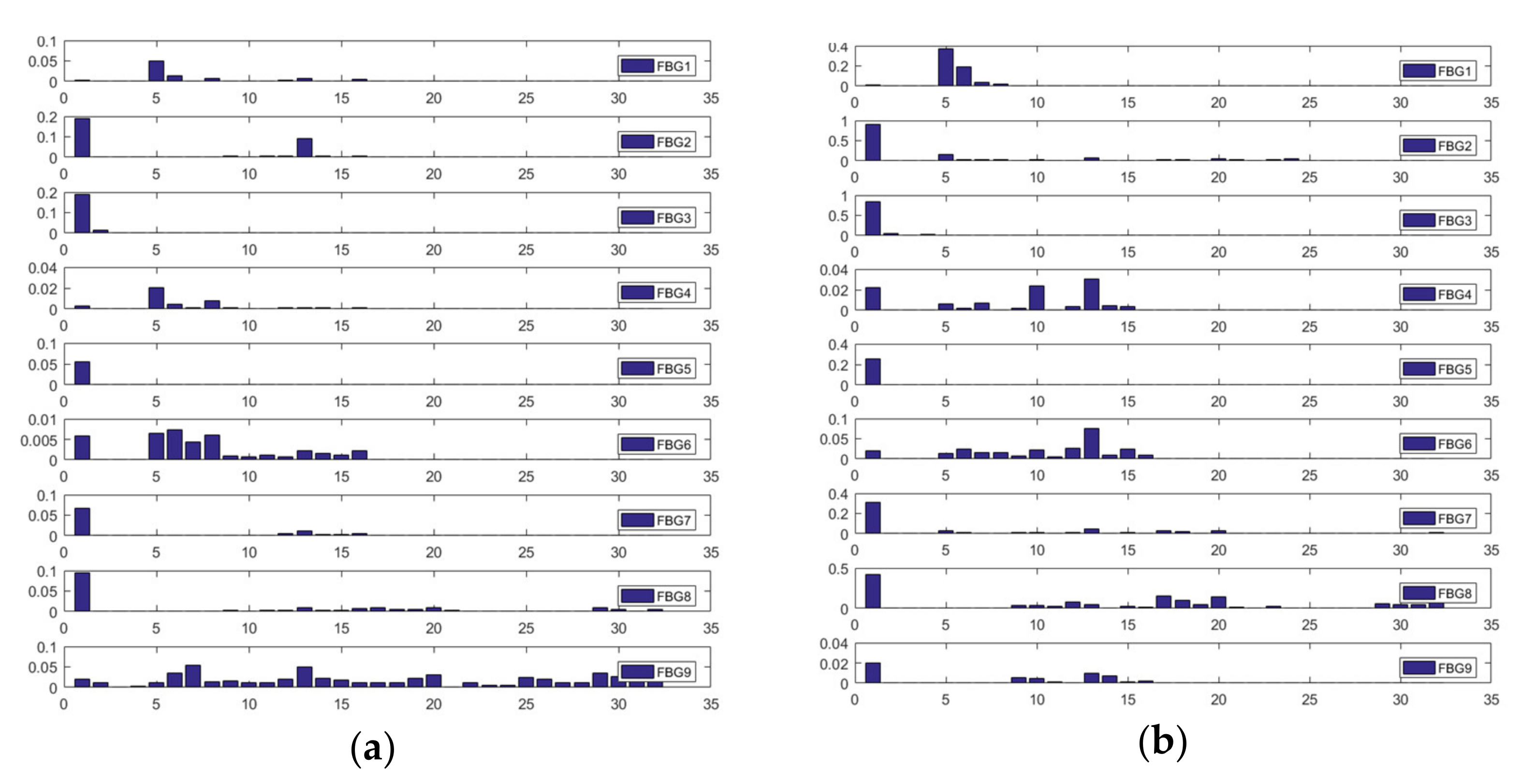
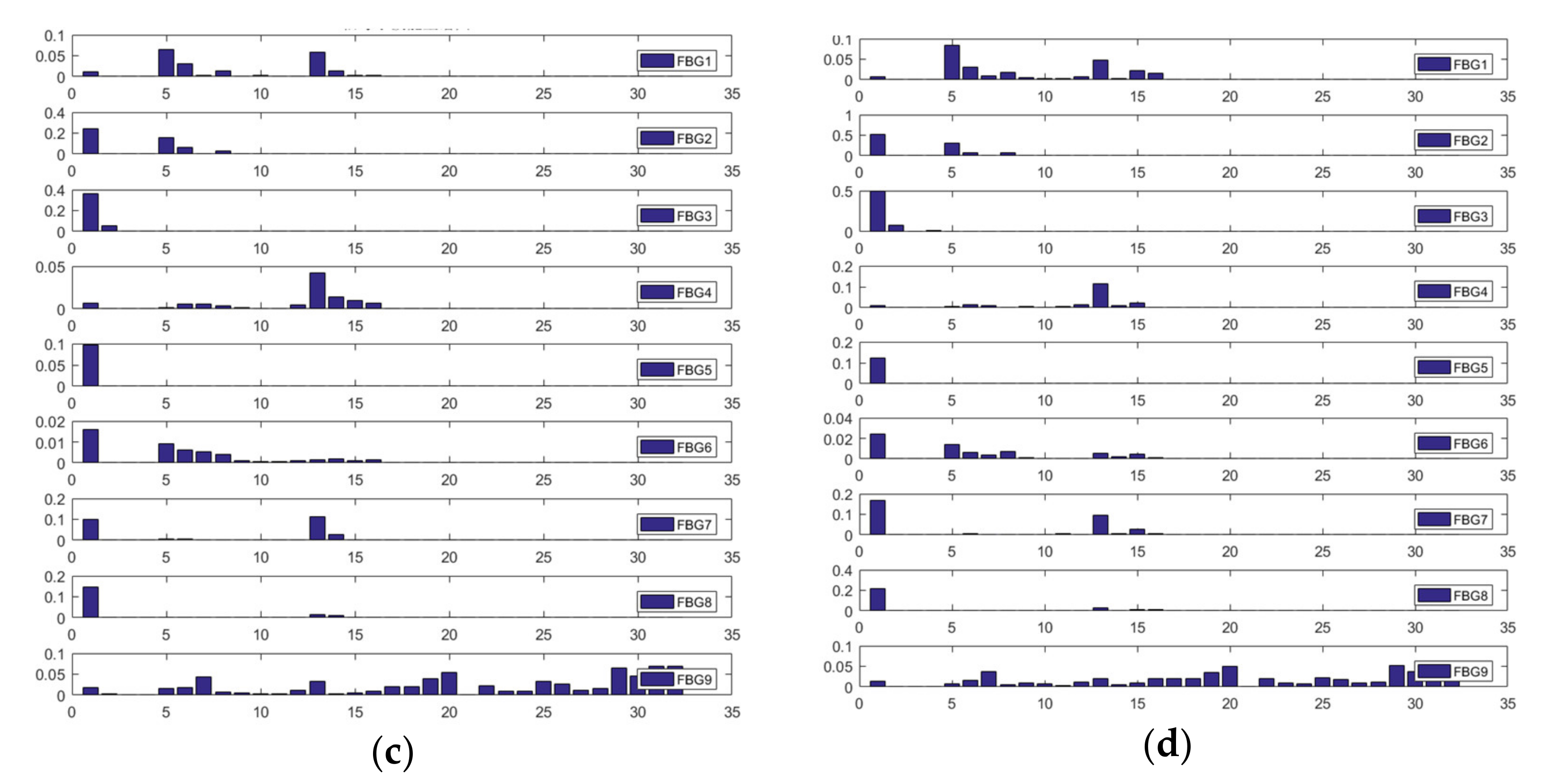
4.4. Signal Preprocessing and Feature Extraction
5. Experiment and Results
5.1. Sample Collection and Selection
5.2. Parameter Selection
5.3. Control-Group Settings
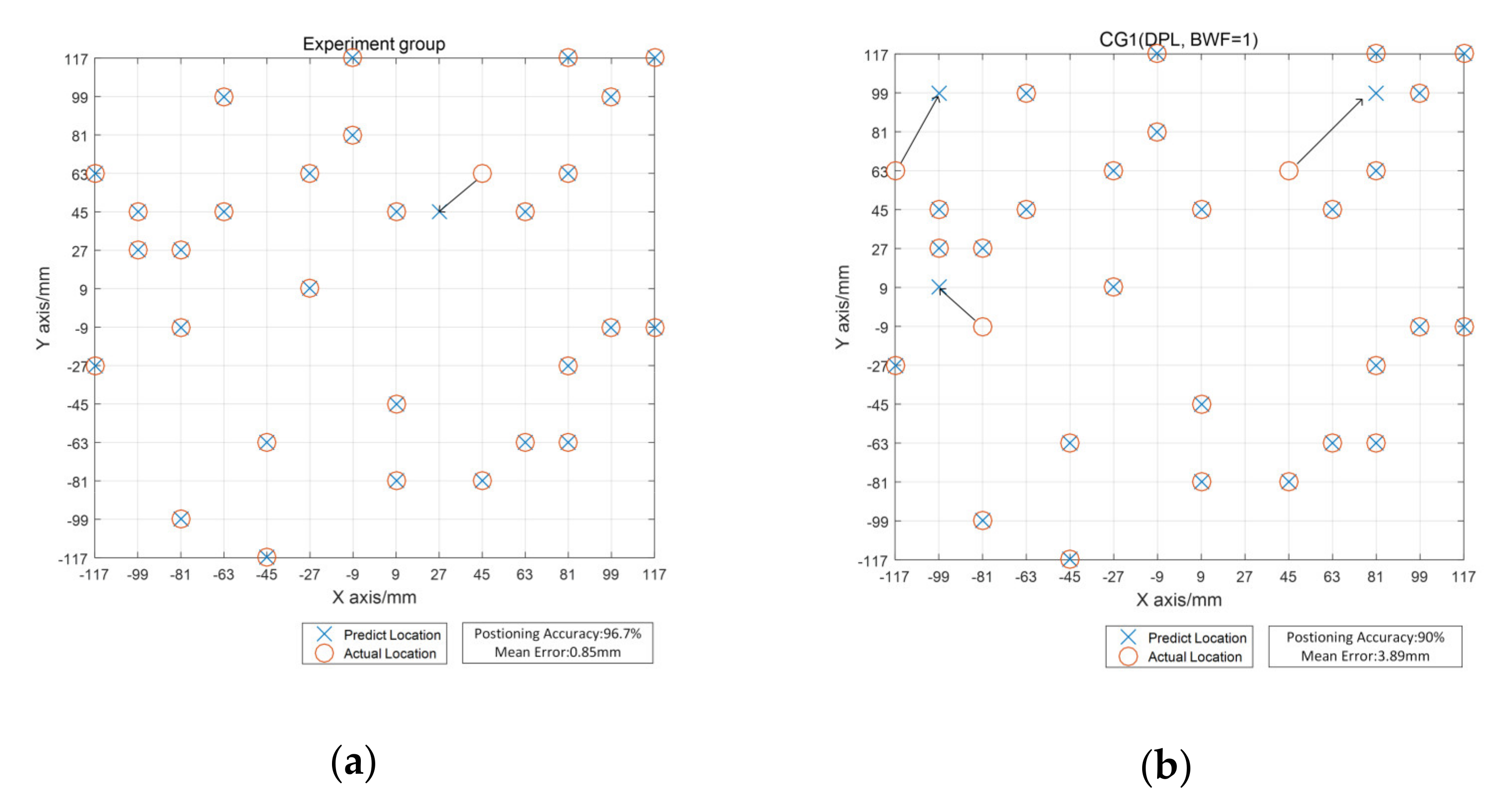
- CG1 involved DPL with . In this group, the positioning algorithm model degenerated to the original DPL. The measurement area was not divided, and all the sensors had the same weight in the classifier.
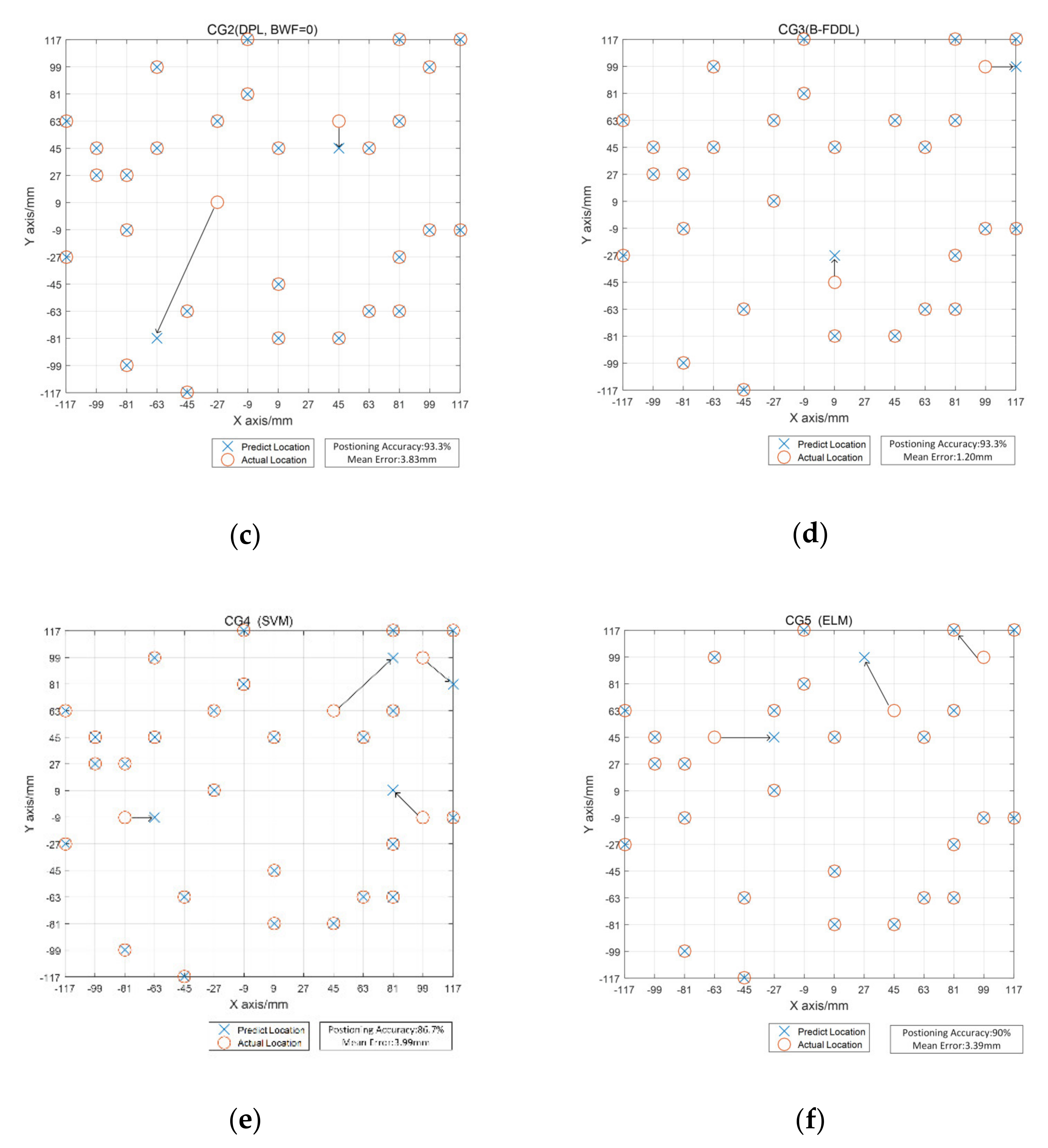
- CG2 involved DPL with . In this group, the measurements were divided in the same way as in the experiment group, but when the sub-area of impact was determined, only the main sensors were selected to obtain the impact response signal.
- CG3 involved the FDDL algorithm. In this group, the measurements were divided in the same way as in the experiment group. The global mode classifier was chosen, and the FDDL algorithm was optimized with BWF (hereinafter referred to simply as B-FDDL). The classification solution was as follows:
- CG4 involved the SVM algorithm, which was used in the research of Lu et al. [12]. The layout of the sensors, grid setting, and feature exaction of GC3 were the same as this method. In GC3 the measurement area was not divided.
- CG5 involved the ELM algorithm, which was used in the research of Jiang et al. [15]. The layout of the sensors, grid setting, and feature exaction of GC3 were the same as this method. In GC3 the measurement area was not divided.
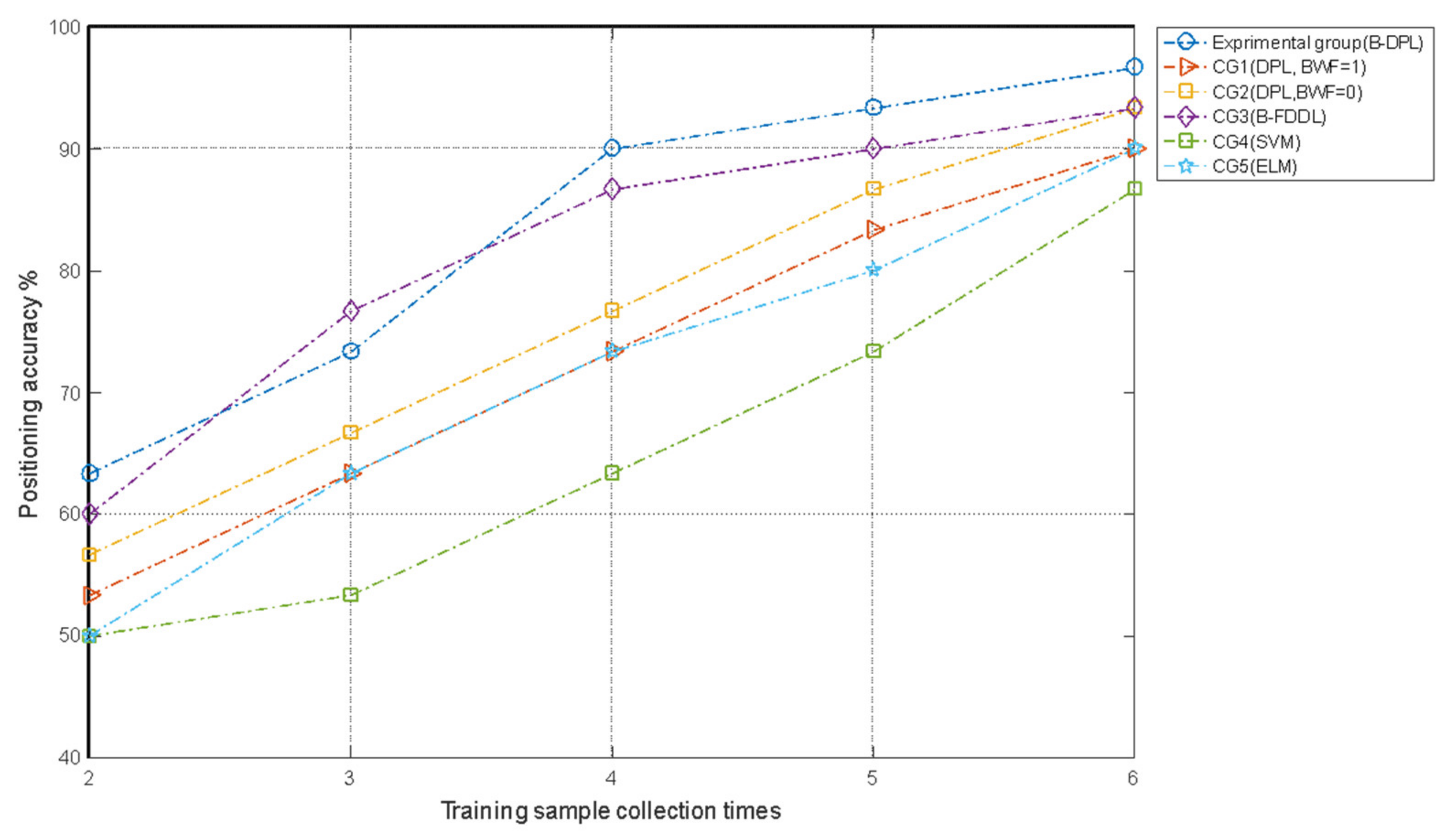
5.4. Results and Discussion
6. Conclusions
- The division of the measurement area and the introduction of BWF can improve the performance of the localization method.
- Original DPL, FDDL and ELM algorithms have achieved decent results but the result of SVM is not satisfactory. The results of B-DPL and B-FDDL are better than that of the above methods.
- The increase in training samples can improve the classification performance of all the algorithms in the experiment. Among them, B-DPL and B-FDDL have the least dependence on the number of training samples.
- Compared with B-FDDL, B-DPL has a faster calculation speed and is more suitable for impact positioning scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Bragg wavelength of FBG | |
| Shifting of Bragg wavelength | |
| Average refractive index of the fiber | |
| Pockel coefficients of the stress-optic tensor | |
| Poisson’s ratio of the fiber | |
| Thermal expansion coefficient of the fiber | |
| Strain on the sensor | |
| Change in temperature | |
| Elasto-optic coefficient | |
| Initial center wavelength | |
| Training sample | |
| Training sample of each category | |
| Test sample | |
| Synthesis dictionary | |
| Sub synthesis dictionary | |
| Learned synthesis dictionary | |
| Coding coefficient matrix | |
| Learned coding coefficient matrix | |
| Learned analysis dictionary | |
| Sub analysis dictionary | |
| Learned analysis dictionary | |
| Constraint item related to the discriminative ability | |
| k | Number of categories |
| Number of atoms in each category | |
| Adjusts weight | |
| Scalar constant of reconstruction error | |
| Balancing weight factor | |
| Balancing weight vector |
References
- Wu, K.; Yang, H.; Jia, L.; Pan, Y.; Hao, Y.; Zhang, K.; Du, K.; Hu, G. Smart construction of 3D N-doped graphene honeycombs with (NH4)2SO4 as a multifunctional template for Li-ion battery anode:“A choice that serves three purposes”. Green Chem. 2019, 21, 1472–1483. [Google Scholar] [CrossRef]
- Kang, S.; Soo, Y.; Kim, N.; Oh, J.; Park, M.; Chung, K.; Lee, S.; Lee, J.; Son, J. Stretchable Lithium-Ion Battery Based on Re-entrant Micro-honeycomb Electrodes and Cross-Linked Gel Electrolyte. ACS Nano 2020, 14, 3660–3668. [Google Scholar] [CrossRef] [PubMed]
- Abdulhamid, M.; Park, S.; Zhou, Z.; Ladner, D.; Szekely, G. Surface engineering of intrinsically microporous poly (ether-ether-ketone) membranes: From flat to honeycomb structures. J. Membr. Sci. 2021, 621, 118997. [Google Scholar] [CrossRef]
- Teng, L.; Zheng, X.D.; Jin, Z.H. Performance Optimization and Verification of a New Type of Solar Panel for Microsatellites. Int. J. Aerosp. Eng. 2019, 2019, 2846491. [Google Scholar] [CrossRef]
- Boudjemai, A.; Mankour, A.; Salem, H.; Amri, R.; Hocine, R.; Chouchaoui, B. Inserts thermal coupling analysis in hexagonal honeycomb plates used for satellite structural design. Appl. Therm. Eng. 2014, 67, 352–361. [Google Scholar] [CrossRef]
- Hazizan, A.; Cantwell, W.J. The low velocity impact response of an aluminium honeycomb sandwich structure. Compos. Part B Eng. 2003, 34, 679–687. [Google Scholar] [CrossRef]
- Nguyen, M.Q.; Jacombs, S.S.; Thomson, R.S.; Hachenberg, D.; Scott, M.L. Simulation of impact on sandwich structures. Compos. Struct. 2005, 67, 217–227. [Google Scholar] [CrossRef]
- Meo, M.; Vignjevic, R.; Marengo, G. The response of honeycomb sandwich panels under low-velocity impact loading. Int. J. Mech. Sci. 2005, 47, 1301–1325. [Google Scholar] [CrossRef]
- Chen, B.; Shin, C. An Improved Impact Source Locating System Using FBG Rosette Array. Sensors 2019, 16, 3543. [Google Scholar] [CrossRef] [Green Version]
- Jang, B.; Lee, Y.; Kim, J.; Kim, Y.; Kim, C. Real-time impact identification algorithm for composite structures using fiber Bragg grating sensors. Struct. Control Health Monit. 2012, 19, 580–591. [Google Scholar] [CrossRef]
- Garrett, R.C.; Peters, K.J.; Zikry, M.A. In-situ impact-induced damage assessment of woven composite laminates through a fibre Bragg grating sensor network. Aeronaut. J. 2009, 113, 357–370. [Google Scholar] [CrossRef]
- Lu, J.Y.; Wang, B.F.; Liang, D.K. Wavelet packet energy characterization of low velocity impacts and load localization by optical fiber Bragg grating sensor technique. Appl. Opt. 2013, 52, 2346–2352. [Google Scholar] [CrossRef]
- Shrestha, P.; Park, Y.; Kwon, H.; Kim, C. Error outlier with weighted Median Absolute Deviation threshold algorithm and FBG sensor based impact localization on composite wing structure. Compos. Struct. 2017, 180, 412–419. [Google Scholar] [CrossRef]
- Zhao, G.; Li, S.; Hu, H.; Zhong, Y.; Li, K. Impact localization on composite laminates using fiber Bragg grating sensors and a novel technique based on strain amplitude. Opt. Fiber Technol. 2018, 40, 172–179. [Google Scholar] [CrossRef]
- Jiang, M.; Lu, S.; Sui, Q.; Dong, H.; Sai, Y.; Jia, L. Low velocity impact localization on CFRP based on FBG sensors and ELM algorithm. IEEE Sens. J. 2015, 15, 4451–4456. [Google Scholar] [CrossRef]
- Lu, S.Z.; Jiang, M.S.; Sui, Q.M.; Sai, Y.Z.; Jia, L. Low velocity impact localization system of CFRP using fiber Bragg grating sensors. Opt. Fiber Technol. 2015, 21, 13–19. [Google Scholar] [CrossRef]
- Baid, H.; Schaal, C.; Samajder, H.; Mal, A. Dispersion of Lamb waves in a honeycomb composite sandwich panel. Ultrasonics 2015, 56, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Projective dictionary pair learning for pattern classification. Adv. Neural Inf. Process. Syst. 2014, 27, 793–801. [Google Scholar]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust Face Recognition via Sparse Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 31, 210–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kreutz-Delgado, K.; Murray, J.F.; Rao, B.D.; Engan, K.; Lee, T.W.; Sejnowski, T.J. Dictionary Learning Algorithms for Sparse Representation. Neural Comput. 2003, 15, 349–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, B. Discriminative K-SVD for dictionary learning in face recognition. In Proceedings of the Twenty-Third IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Jiang, Z.; Zhe, L.; Davis, L.S. Label consistent K-SVD: Learning a discriminative dictionary for recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2651–2664. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhang, L.; Feng, X.; Zhang, D. Sparse representation based fisher discrimination dictionary learning for image classification. Int. J. Comput. Vis. 2014, 109, 209–232. [Google Scholar] [CrossRef]
- Valencia, D.; Orejuela, D.; Salazar, J.; Valencia, J. Comparison analysis between rigrsure, sqtwolog, heursure and minimaxi techniques using hard and soft thresholding methods. In Proceedings of the 2016 XXI Symposium on Signal Processing, Images and Artificial Vision (STSIVA), Bucaramanga, Colombia, 31 August–2 September 2016. [Google Scholar]
- Torkkola, K. Feature extraction by non-parametric mutual information maximization. J. Mach. Learn. Res. 2003, 3, 1415–1438. [Google Scholar]
- Juha, K.; Jyrki, J. Representation and separation of signals using nonlinear PCA type learning. Neural Netw. 1994, 7, 113–127. [Google Scholar]
- Oja, E. Principal components, minor components, and linear neural networks. Neural Netw. 1992, 5, 927–935. [Google Scholar] [CrossRef]




| FBG No. | Initial Center Wavelength λ [nm] | Position [mm] |
|---|---|---|
| FBG1 | 1529.823 | (−72, 72) |
| FBG2 | 1560.032 | (0, 72) |
| FBG4 | 1535.023 | (−72, 0) |
| FBG7 | 1549.933 | (−72, −72) |
| FBG10 | 1544.421 | Temperature compensation |
| FBG3 | 1524.961 | (72, 72) |
| FBG5 | 1560.097 | (0, 0) |
| FBG6 | 1529.788 | (72, 0) |
| FBG8 | 1555.114 | (0, −72) |
| FBG9 | 1549.760 | (72, −72) |
| Sub-Area | Main Sensors | Auxiliary Sensors |
|---|---|---|
| 1 | FBG2, FBG3, FBG5, FBG6 | FBG1, FBG4, FBG7, FBG8, FBG9 |
| 2 | FBG3, FBG5, FBG6, FBG9 | FBG1, FBG2, FBG4, FBG7, FBG8 |
| 3 | FBG5, FBG6, FBG8, FBG9 | FBG1, FBG2, FBG3, FBG4, FBG7 |
| 4 | FBG5, FBG7, FBG8, FBG9 | FBG1, FBG2, FBG3, FBG4, FBG6 |
| 5 | FBG4, FBG5, FBG7, FBG8 | FBG1, FBG2, FBG3, FBG6, FBG9 |
| 6 | FBG1, FBG4, FBG5, FBG7 | FBG2, FBG3, FBG6, FBG8, FBG9 |
| 7 | FBG1, FBG2, FBG4, FBG5 | FBG3, FBG6, FBG7, FBG8, FBG9 |
| 8 | FBG1, FBG2, FBG3, FBG5 | FBG4, FBG6, FBG7, FBG8, FBG9 |
| Sub-Area | Features of Main Sensors | Feature Ratio% | Features of Auxiliary Sensors | Feature Ratio% |
|---|---|---|---|---|
| 1 | 42/1024 | 90.29 | 37/1280 | 90.42 |
| 2 | 45/1024 | 90.43 | 39/1280 | 90.08 |
| 3 | 41/1024 | 90.88 | 38/1280 | 90.77 |
| 4 | 42/1024 | 90.31 | 40/1280 | 90.36 |
| 5 | 39/1024 | 90.27 | 39/1280 | 90.51 |
| 6 | 40/1024 | 90.13 | 34/1280 | 90.34 |
| 7 | 44/1024 | 90.15 | 40/1280 | 90.31 |
| 8 | 41/1024 | 90.42 | 38/1280 | 90.02 |
| Sub-Area | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| BWF | 0.35 | 0.25 | 0.35 | 0.30 | 0.30 | 0.40 | 0.35 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Z.; Lu, J.; Liang, D. Low-Velocity Impact Localization on a Honeycomb Sandwich Panel Using a Balanced Projective Dictionary Pair Learning Classifier. Sensors 2021, 21, 2602. https://doi.org/10.3390/s21082602
Zheng Z, Lu J, Liang D. Low-Velocity Impact Localization on a Honeycomb Sandwich Panel Using a Balanced Projective Dictionary Pair Learning Classifier. Sensors. 2021; 21(8):2602. https://doi.org/10.3390/s21082602
Chicago/Turabian StyleZheng, Zhaoyu, Jiyun Lu, and Dakai Liang. 2021. "Low-Velocity Impact Localization on a Honeycomb Sandwich Panel Using a Balanced Projective Dictionary Pair Learning Classifier" Sensors 21, no. 8: 2602. https://doi.org/10.3390/s21082602
APA StyleZheng, Z., Lu, J., & Liang, D. (2021). Low-Velocity Impact Localization on a Honeycomb Sandwich Panel Using a Balanced Projective Dictionary Pair Learning Classifier. Sensors, 21(8), 2602. https://doi.org/10.3390/s21082602






