A Data Fusion Method for Non-Destructive Testing by Means of Artificial Neural Networks
Abstract
1. Introduction
2. Method
2.1. Simulated Data Base for EC and US Testing in the Presence of Side Drill Holes (SDHs)
2.1.1. Finite Elements EC Simulations
2.1.2. Ultrasonic (US) Testing Simulations
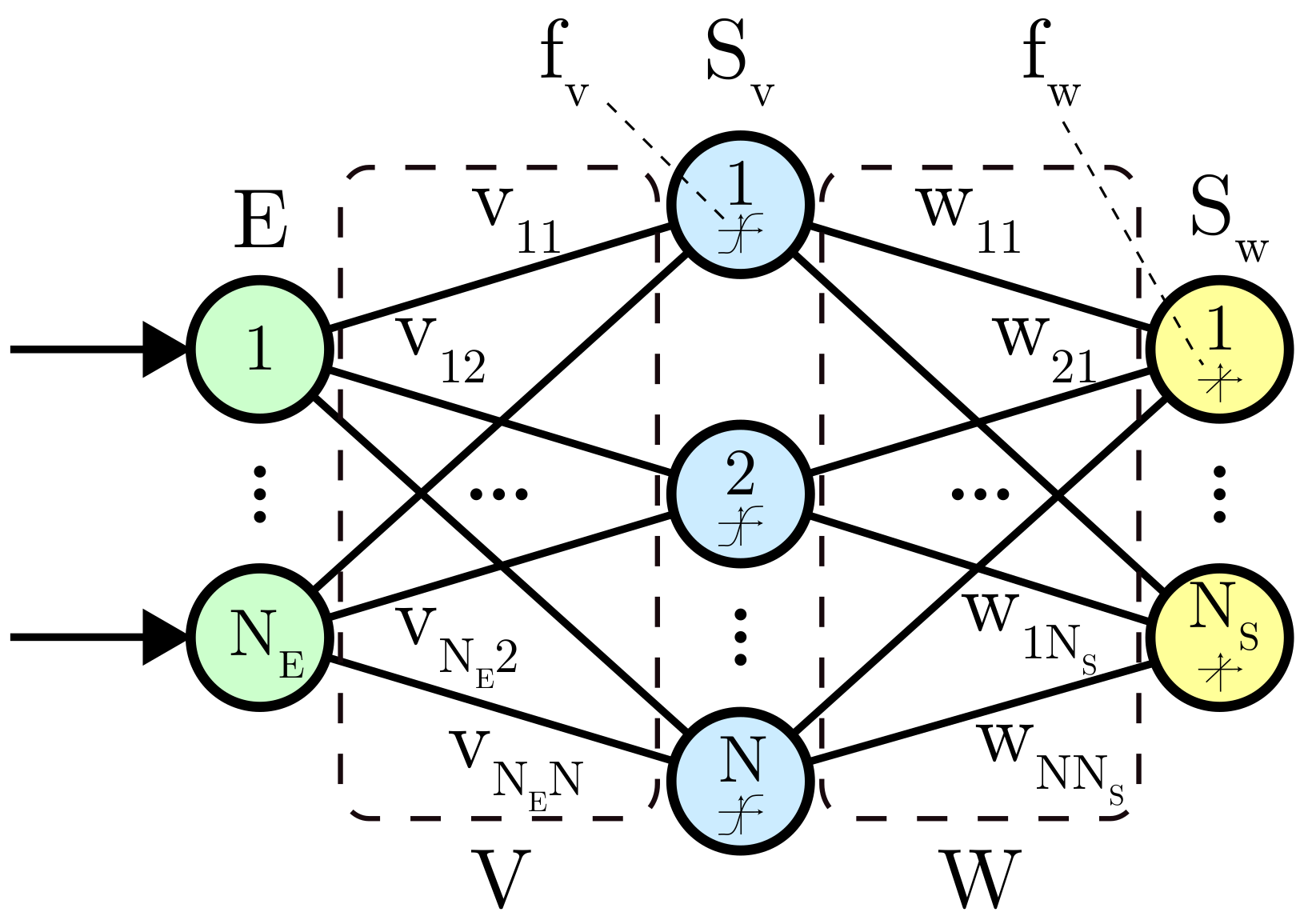
2.2. Artificial Neural Network for Data Fusion
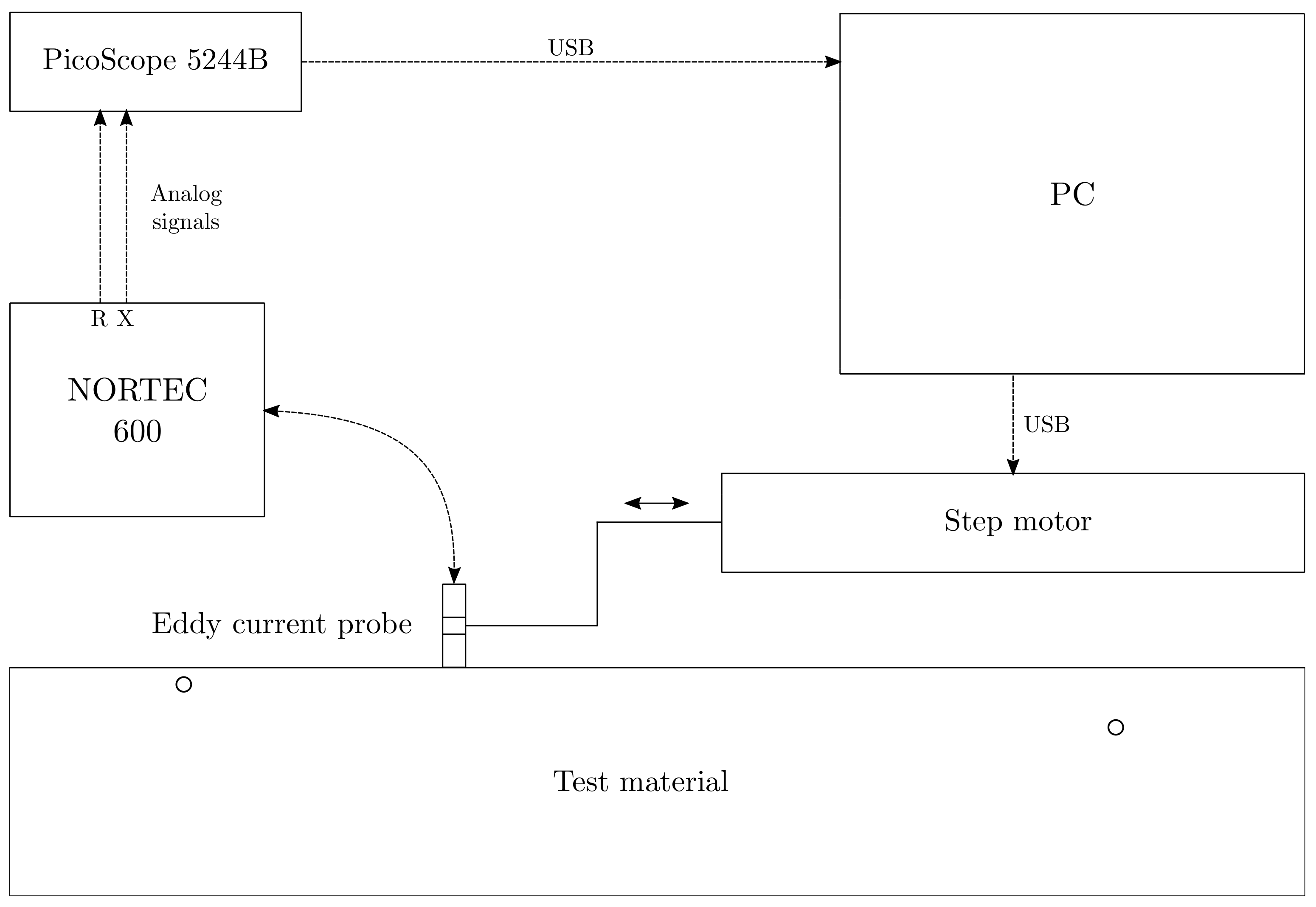
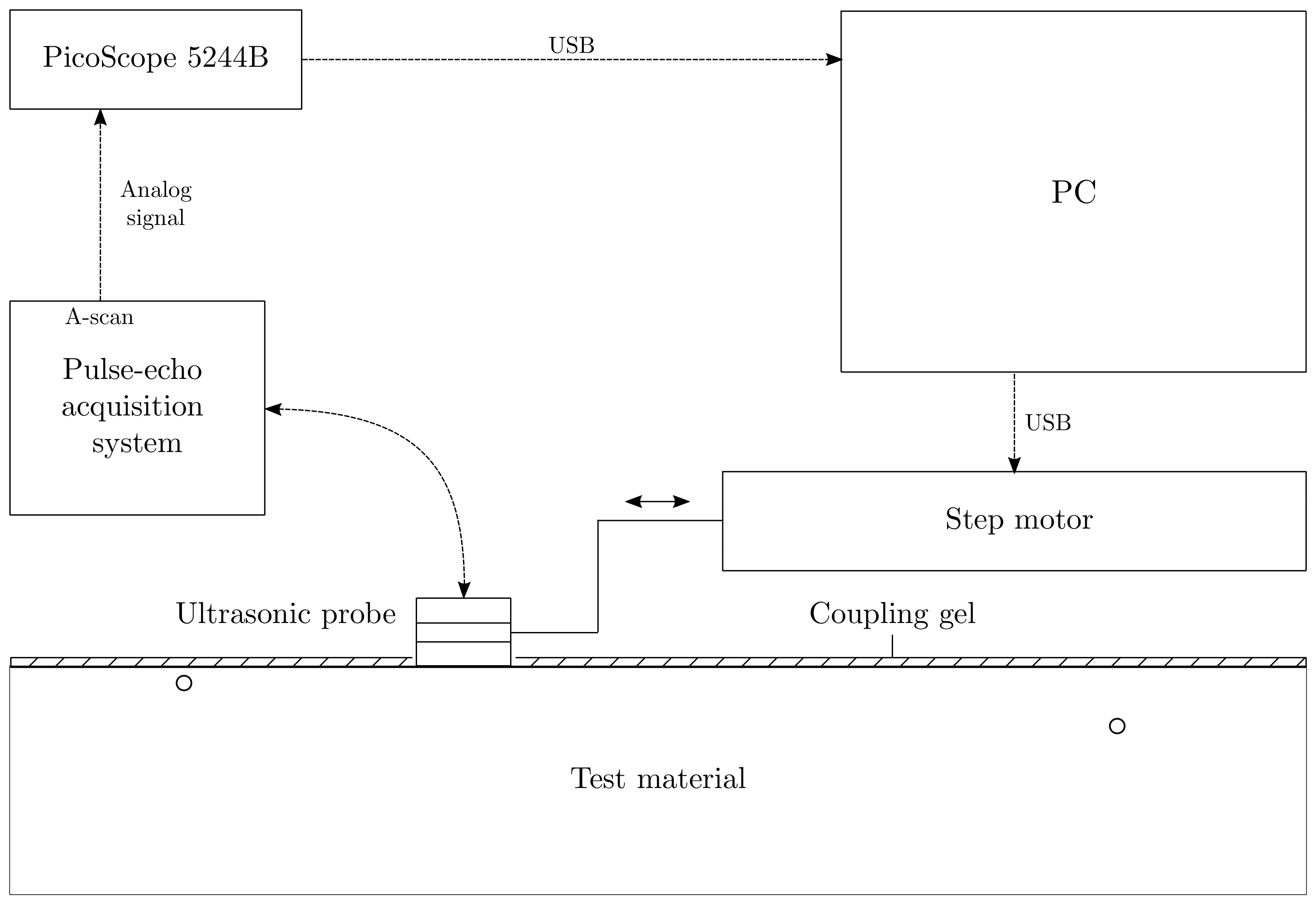
2.3. Experimental Set-Up
2.3.1. Experimental Set-Up for EC Measurements
2.3.2. Experimental Set-Up for US Measurements
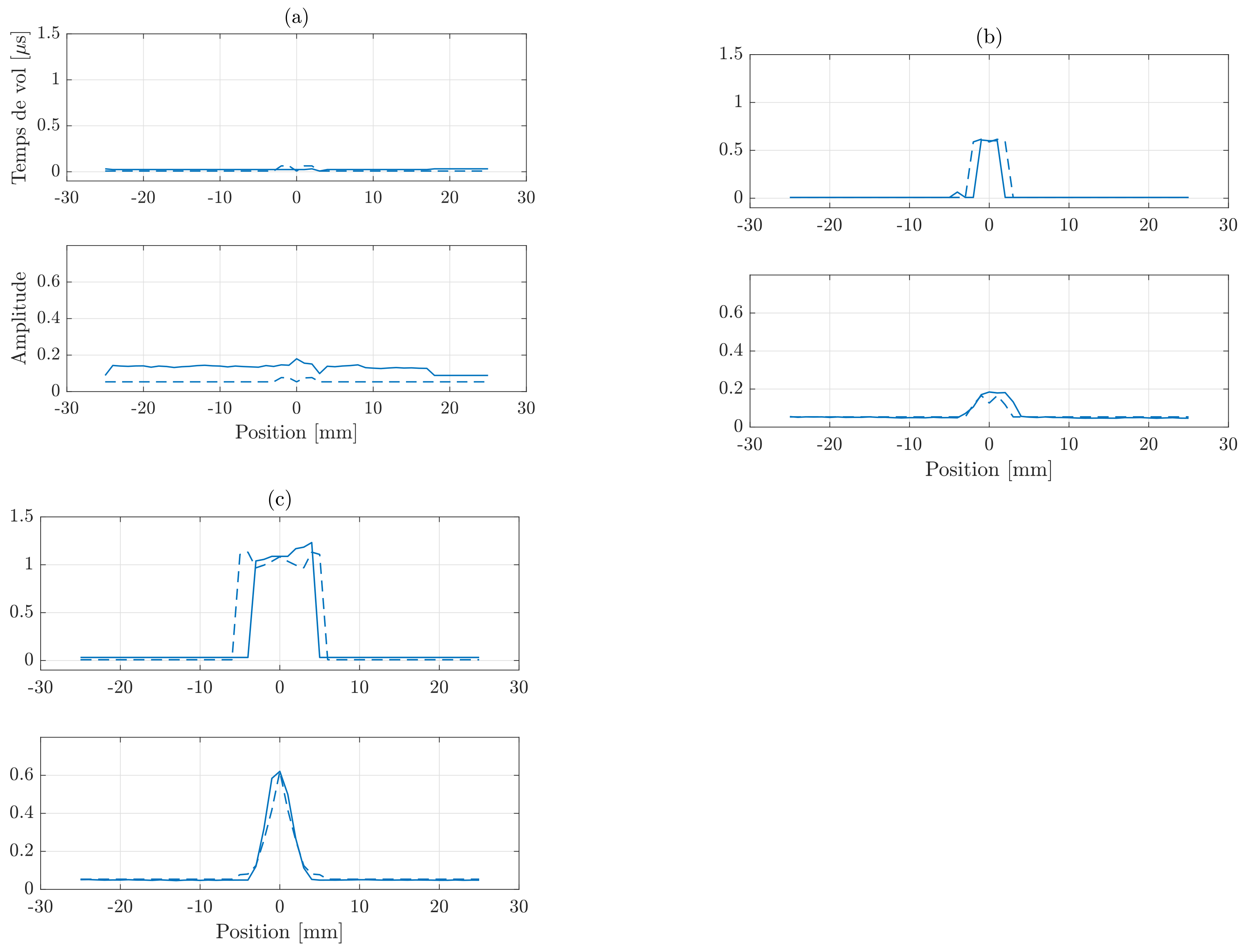
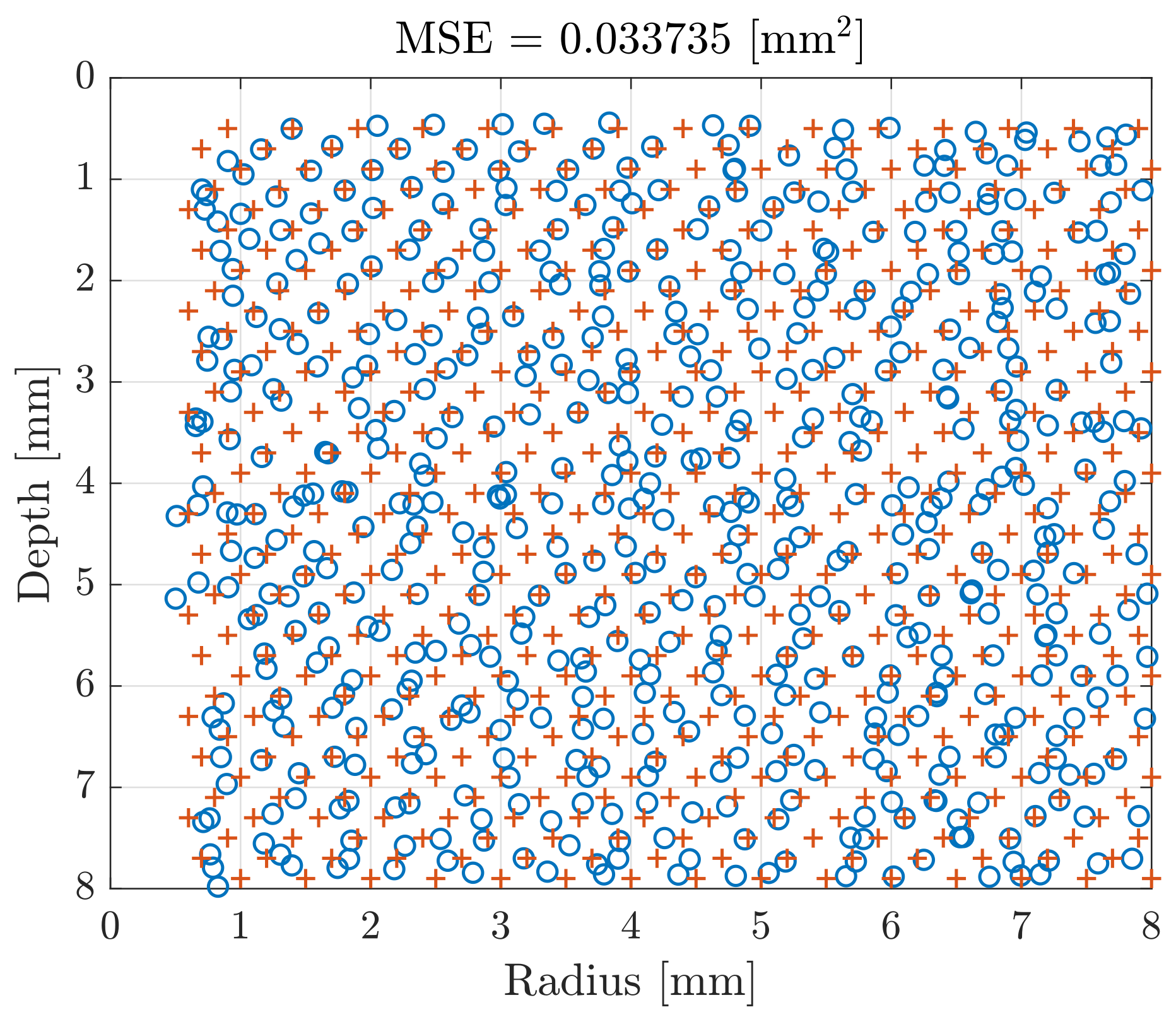
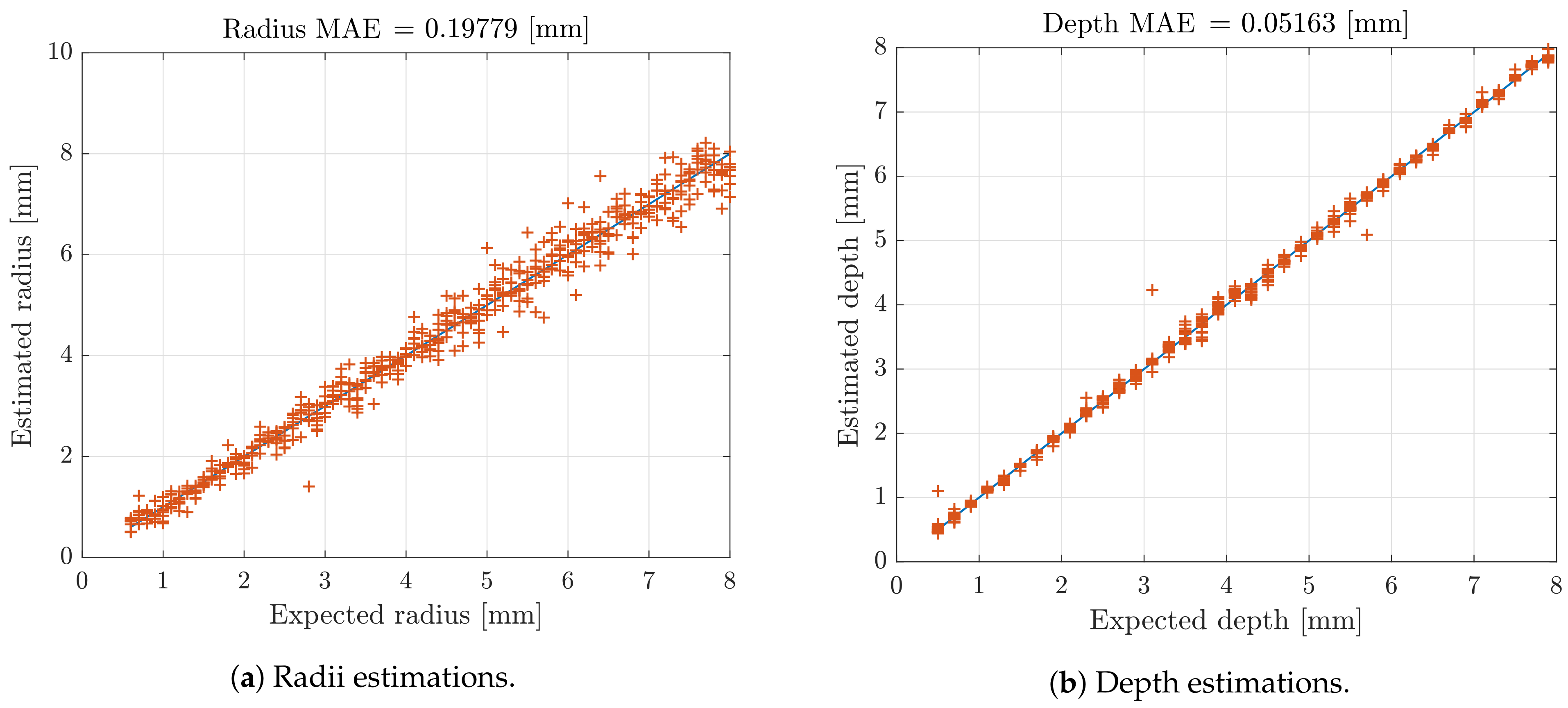
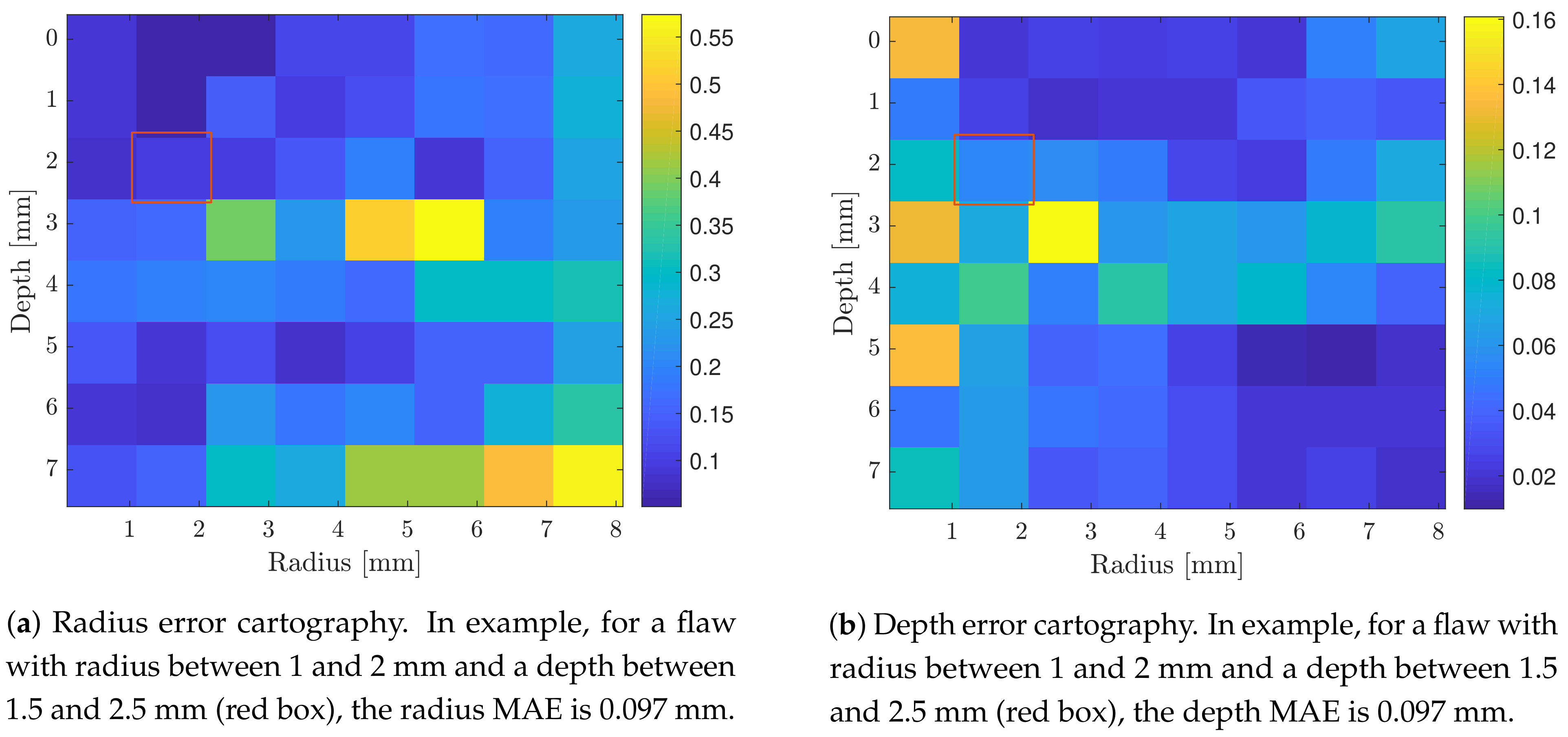
3. Results and Discussion
3.1. Preliminary Results Using Simulated Data
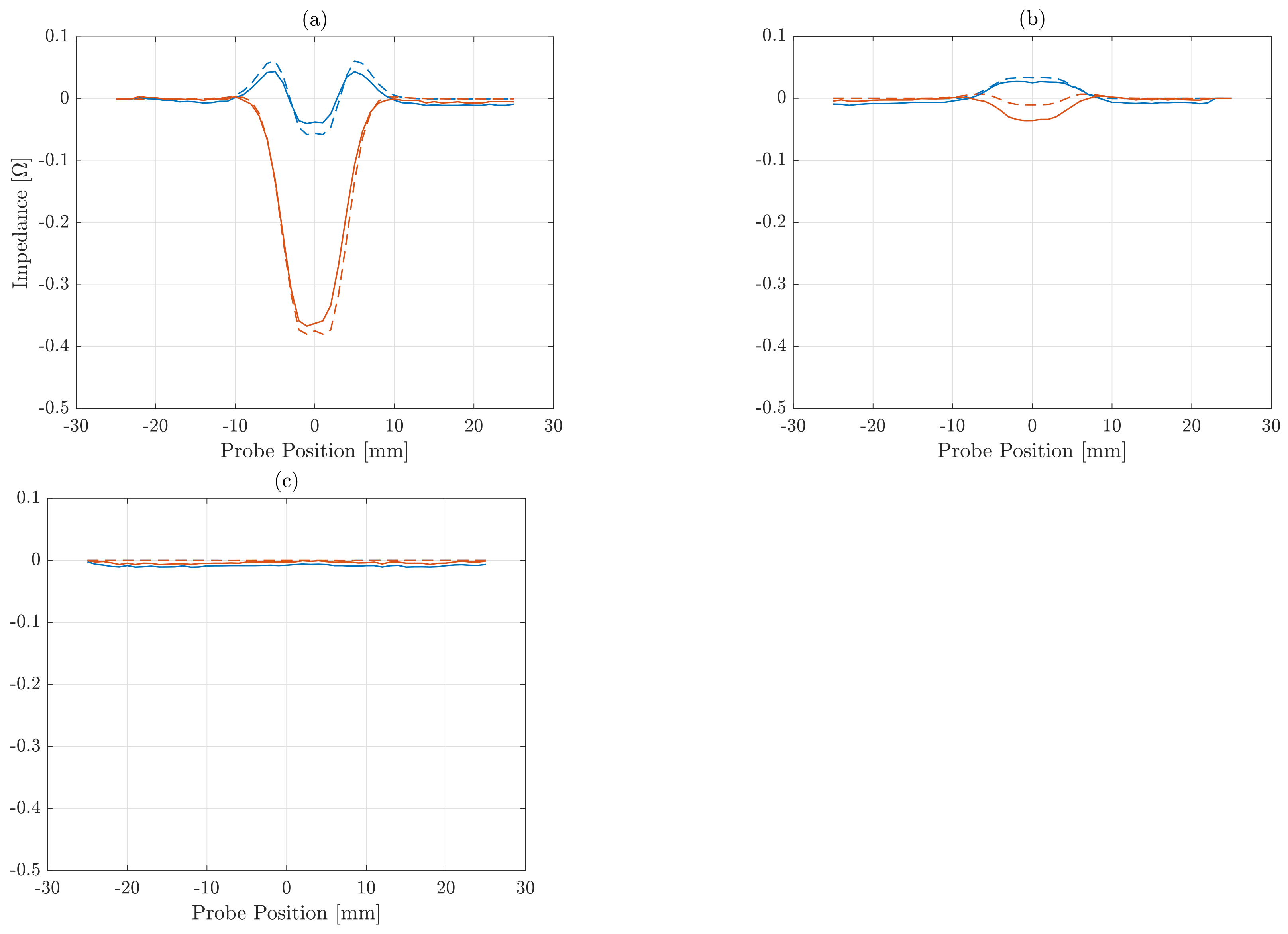
3.2. Final Results Using Experimental Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hellier, C. Handbook of Non Destructive Evaluation; McGraw-Hill Professional: New York, NY, USA, 2001; p. 603. [Google Scholar]
- Heideklang, R.; Shokouhi, P. Application of Data Fusion in Nondestructive Testing (NDT). In Proceedings of the 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 835–841. [Google Scholar]
- IAEA. Training Guidelines in Non-Destructive Testing Techniques: Leak Testing at Level 2; International Atomic Energy Agency: Vienna, Austria, 2012. [Google Scholar]
- Chen, C.H. Ultrasonic and Advanced Methods for Nondestructive Testing and Material Characterization; World Scientific Publishing: Hackensack, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Krautkrämer, J.; Krautkrämer, H. Ultrasonic Testing of Materials; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Langenberg, K.J.; Marklein, R.M.; Mayer, K.M. Ultrasonic Nondestructive Testing of Materials; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Schmerr, L.W.; Song, S.J. Ultrasonic Nondestructive Evaluation Systems: Models and Measurements; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Auld, B.A. Acoustic Fields and Waves in Solids, Volumes I and II; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar] [CrossRef]
- Babaei, A.; Suratgar, A.A.; Salemi, A.H. Dimension estimation of rectangular cracks using impedance changes of the eddy current probe with a neural network. J. Appl. Res. Technol. 2013, 11, 397–401. [Google Scholar] [CrossRef]
- He, Y.; Gao, B.; Sophian, A.; Yang, R. Transient Electromagnetic-Thermal Nondestructive Testing; Jonathan Simpson: Oxford, UK, 2017. [Google Scholar]
- Sabbagh, H.A.; Murphy, R.K.; Sabbagh, E.H.; Aldrin, J.C.; Knopp, J.S. Computational Electromagnetics and Model-Based Inversion; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Rodríguez, A.A.; Valli, A. Eddy Current Approximation of Maxwell Equations: Theory, Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Raol, J.R. Data Fusion Mathematics: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Hall, D.L.; Llinas, J. Handbook of Multisensor Data Fusion; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Postorino, M.N.; Versaci, M. A Geometric Fuzzy-Based Approach for Airport Clustering. Adv. Fuzzy Syst. 2014, 2014, 201243. [Google Scholar] [CrossRef]
- Gros, X.E. NDT Data Fusion; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Gros, X.E. Applications of NDT Data Fusion; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar] [CrossRef]
- Liu, Z.; Forsyth, D.S.; Komorowski, J.P.; Hanasaki, K.; Kirubarajan, T. Survey: State of the art in NDE data fusion techniques. IEEE Trans. Instrum. Meas. 2007, 56, 2435–2451. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Alfaro, S.C.A.; Cayo, E.H. Sensoring fusion data from the optic and acoustic emissions of electric arcs in the GMAW-S process for welding quality assessment. Sensors 2012, 12, 6953–6966. [Google Scholar] [CrossRef] [PubMed]
- Habibalahi, A.; Safizadeh, M.S. Pulsed eddy current and ultrasonic data fusion applied to stress measurement. Meas. Sci. Technol. 2014, 25, 1–10. [Google Scholar] [CrossRef]
- Horn, D.; Mayo, W.R. NDE reliability gains from combining eddy-current and ultrasonic testing. NDT E Int. 2000, 33, 351–362. [Google Scholar] [CrossRef]
- Jing, L.; Wang, T.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef] [PubMed]
- Osman, A.; Kaftandjian, V.; Hassler, U. Application of Data Fusion Theory and Support Vector Machine To X-ray Castings Inspection. In Proceedings of the 10th European Conference on Non-Destructive Testing, Moscow, Russia, 7–11 June 2010; pp. 7–11. [Google Scholar]
- Shih, Y.F.; Wang, Y.R.; Lin, K.L.; Chen, C.W. Improving non-destructive concrete strength tests using support vector machines. Materials 2015, 8, 7169–7178. [Google Scholar] [CrossRef] [PubMed]
- Bernieri, A.; Ferrigno, L.; Laracca, M.; Molinara, M. Crack shape reconstruction in Eddy current testing using machine learning systems for regression. IEEE Trans. Instrum. Meas. 2008, 57, 1958–1968. [Google Scholar] [CrossRef]
- Chelabi, M.; Hacib, T.; Le Bihan, Y. Eddy Current Testing Using Support Vector Machines. In Proceedings of the 7th Int’l Workshop-NDT Signal Processing, Quebec City, QC, Canada, 31 July–2 August 2013; pp. 63–68. [Google Scholar]
- Zhu, P.; Cheng, Y.; Banerjee, P.; Tamburrino, A.; Deng, Y. A novel machine learning model for eddy current testing with uncertainty. NDT E Int. 2019, 101, 104–112. [Google Scholar] [CrossRef]
- Chen, W.; Liu, T.; Wang, B. Ultrasonic image classification based on support vector machine with two independent component features. Comput. Math. Appl. 2011, 62, 2696–2703. [Google Scholar] [CrossRef]
- Hoshyar, A.N.; Rashidi, M.; Samali, B.; Liyanapathirana, R. Algorithm development for the non-destructive testing of structural damage. Appl. Sci. 2019, 9, 2810. [Google Scholar] [CrossRef]
- Meng, M.; Chua, Y.J.; Wouterson, E.; Ong, C.P.K. Ultrasonic signal classification and imaging system for composite materials via deep convolutional neural networks. Neurocomputing 2017, 257, 128–135. [Google Scholar] [CrossRef]
- Henneron, T. Contribution à la prise en compte des Grandeurs Globales dans les Problèmes d’Electromagnétisme résolus avec la Méthode des Eléments Finis. Ph.D. Thesis, Université Lille 1—Sciences et Technologies, Lille, France, 2004. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Firouzi, K.; Cox, B.T.; Treeby, B.E.; Saffari, N. A first-order k-space model for elastic wave propagation in heterogeneous media. J. Acoust. Soc. Am. 2012, 132, 1271–1283. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.; Cox, B.; Jaros, J. k-Wave, A MATLAB Toolbox for the Time Domain Simulation of Acoustic Wave Field. 2012. Available online: http://www.k-wave.org/acousticsoftware.php (accessed on 6 April 2021).
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesus, O. Neural Network Design, 2nd ed.; Martin Hagan: 1995. Available online: https://hagan.okstate.edu/NNDesign.pdf (accessed on 5 April 2021). [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]

| MSE | |
|---|---|
| Training data set | 0.038 ± 0.002 mm |
| Validation data set | 0.038 ± 0.005 mm |
| Test data set | 0.040 ± 0.007 mm |
| Flaw 1 | Radius | Depth |
|---|---|---|
| True values | 2.5 | 1 |
| Data fusion estimation | 2.52 ± 0.18 | 1.08 ± 0.07 |
| Flaw 2 | Radius | Depth |
|---|---|---|
| True values | 2.5 | 3 |
| Data fusion estimation | 2.56 ± 0.27 | 2.55 ± 0.29 |
| Flaw 3 | Radius | Depth |
|---|---|---|
| True values | 2.5 | 7.5 |
| Data fusion estimation | 1.91 ± 0.18 | 7.59 ± 0.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cormerais, R.; Duclos, A.; Wasselynck, G.; Berthiau, G.; Longo, R. A Data Fusion Method for Non-Destructive Testing by Means of Artificial Neural Networks. Sensors 2021, 21, 2598. https://doi.org/10.3390/s21082598
Cormerais R, Duclos A, Wasselynck G, Berthiau G, Longo R. A Data Fusion Method for Non-Destructive Testing by Means of Artificial Neural Networks. Sensors. 2021; 21(8):2598. https://doi.org/10.3390/s21082598
Chicago/Turabian StyleCormerais, Romain, Aroune Duclos, Guillaume Wasselynck, Gérard Berthiau, and Roberto Longo. 2021. "A Data Fusion Method for Non-Destructive Testing by Means of Artificial Neural Networks" Sensors 21, no. 8: 2598. https://doi.org/10.3390/s21082598
APA StyleCormerais, R., Duclos, A., Wasselynck, G., Berthiau, G., & Longo, R. (2021). A Data Fusion Method for Non-Destructive Testing by Means of Artificial Neural Networks. Sensors, 21(8), 2598. https://doi.org/10.3390/s21082598






