Work-Related Risk Assessment According to the Revised NIOSH Lifting Equation: A Preliminary Study Using a Wearable Inertial Sensor and Machine Learning
Abstract
1. Introduction
2. Materials and Methods
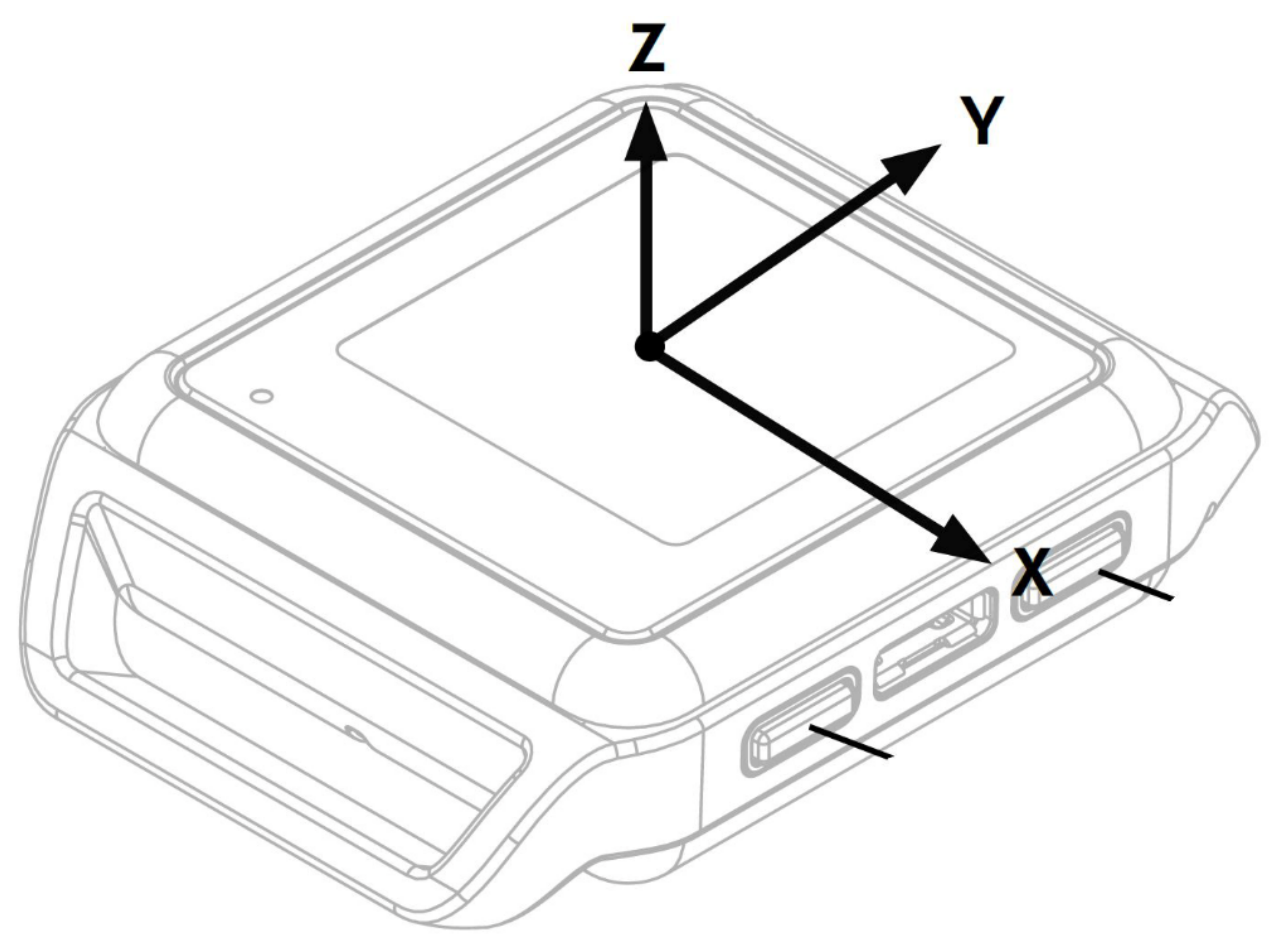
2.1. IMU-Based Motion Capture Wearable System: The OPAL System
2.2. Revised NIOSH Lifting Equation
- LC: Load Constant = 25/20 kg (males, <45/>45 years old respectively), 20/15 kg (females, <45/>45 years old respectively);
- HM: Horizontal Multiplier;
- VM: Vertical Multiplier;
- DM: Distance Multiplier;
- AM: Asymmetric Multiplier; and
- FM: Frequency Multiplier.
2.3. Study Population
2.4. Study Protocol
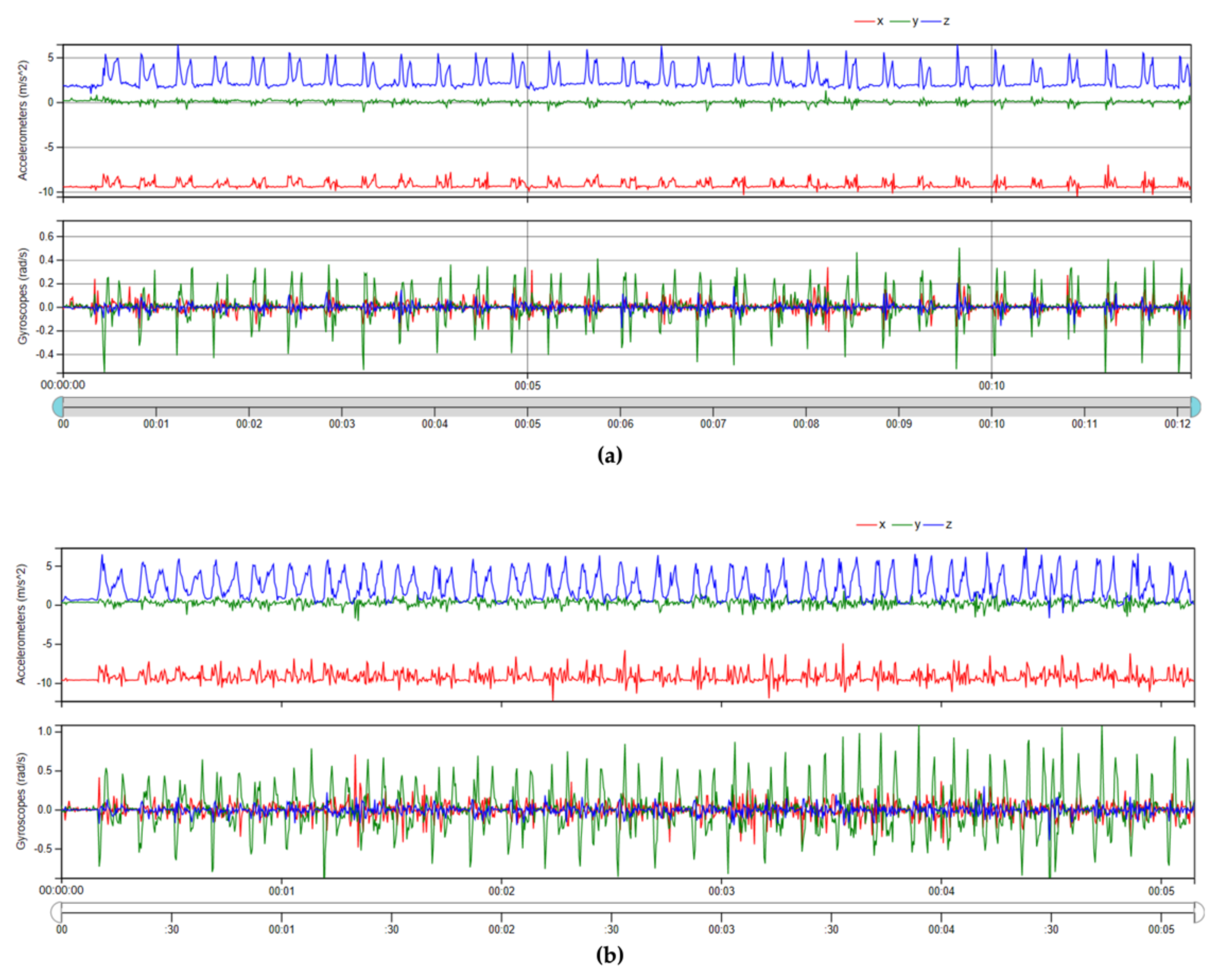
2.5. Feature Extraction
- root mean square (RMS),
- standard deviation (SD),
- minimum (MIN) and
- maximum (MAX).
2.6. Machine Learning and Tools
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marras, W.S.; Lavender, S.A.; Leurgans, S.E.; Fathallah, F.A.; Ferguson, S.A.; Allread, W.G.; Rajulu, S.L. Biomechanical risk factors for occupationally related low back disorders. Ergonomics 1995, 38, 377–410. [Google Scholar] [CrossRef] [PubMed]
- Musculoskeletal Disorders and Workplace Factors; A Critical Review of Epidemiologic Evidence for Work-Related Musculoskeletal Disorders of The Neck, Upper Extremity, and Low Back. Available online: https://www.cdc.gov/niosh/docs/97-141/default.html (accessed on 27 January 2021).
- Punnett, L.; Fine, L.J.; Keyserling, W.M.; Herrin, G.D.; Chaffin, D.B. Back disorders and nonneutral trunk postures of automobile assembly workers. Scand. J. Work. Environ. Heath 1991, 17, 337–346. [Google Scholar] [CrossRef]
- Keyserling, W.; Brouwer, M.; Silverstein, B. A checklist for evaluating ergonomic risk factors resulting from awkward postures of the legs, trunk and neck. Int. J. Ind. Ergon. 1992, 9, 283–301. [Google Scholar] [CrossRef]
- Radwin, R.G.; Marras, W.S.; Lavender, S.A. Biomechanical aspects of work-related musculoskeletal disorders. Theor. Issues Ergon. Sci. 2001, 2, 153–217. [Google Scholar] [CrossRef]
- Winkel, J.; Mathiassen, S.E. Assessment of physical work load in epidemiologic studies: Concepts, issues and operational considerations. Ergonomics 1994, 37, 979–988. [Google Scholar] [CrossRef] [PubMed]
- Buchholz, B.; Paquet, V.; Punnett, L.; Lee, D.; Moir, S. PATH: A work sampling-based approach to ergonomic job analysis for construction and other non-repetitive work. Appl. Ergon. 1996, 27, 177–187. [Google Scholar] [CrossRef]
- Karhu, O.; Kansi, P.; Kuorinka, I. Correcting working postures in industry: A practical method for analysis. Appl. Ergon. 1977, 8, 199–201. [Google Scholar] [CrossRef]
- McAtamney, L.; Corlett, E.N. RULA: A survey method for the investigation of work-related upper limb disorders. Appl. Ergon. 1993, 24, 91–99. [Google Scholar] [CrossRef]
- Hignett, S.; McAtamney, L. Rapid Entire Body Assessment (REBA). Appl. Ergon. 2000, 31, 201–205. [Google Scholar] [CrossRef]
- Battevi, N.; Menoni, O.; Ricci, M.G.; Cairoli, S. MAPO index for risk assessment of patient manual handling in hospital wards: A validation study. Ergonomics 2006, 49, 671–687. [Google Scholar] [CrossRef]
- Waters, T.R.; Putz-Anderson, V.; Garg, A.; Fine, L.J. Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics 1993, 36, 749–776. [Google Scholar] [CrossRef] [PubMed]
- Takala, E.-P.; Pehkonen, I.; Forsman, M.; Hansson, G.-Å.; Mathiassen, S.E.; Neumann, W.P.; Sjøgaard, G.; Veiersted, K.B.; Westgaard, R.H.; Winkel, J. Systematic evaluation of observational methods assessing biomechanical exposures at work. Scand. J. Work. Environ. Health 2009, 36, 3–24. [Google Scholar] [CrossRef] [PubMed]
- Ranavolo, A.; Draicchio, F.; Varrecchia, T.; Silvetti, A.; Iavicoli, S. Wearable Monitoring Devices for Biomechanical Risk Assessment at Work: Current Status and Future Challenges—A Systematic Review. Int. J. Environ. Res. Public Health 2018, 15, 2001. [Google Scholar] [CrossRef]
- Lim, S.; D’Souza, C. A narrative review on contemporary and emerging uses of inertial sensing in occupational ergonomics. Int. J. Ind. Ergon. 2020, 76, 102937. [Google Scholar] [CrossRef]
- David, G.C. Ergonomic methods for assessing exposure to risk factors for work-related musculoskeletal disorders. Occup. Med. 2005, 55, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Luinge, H.J. Inertial Sensing of Human Movement. Ph.D. Thesis, University of Twente, Twente, The Netherlands, 30 October 2002. [Google Scholar]
- Zheng, H.; Black, N.D.; Harris, N.D. Position-sensing technologies for movement analysis in stroke rehabilitation. Med. Biol. Eng. Comput. 2005, 43, 413–420. [Google Scholar] [CrossRef]
- Faber, G.; Koopman, A.; Kingma, I.; Chang, C.; Dennerlein, J.; Van Dieën, J. Continuous ambulatory hand force monitoring during manual materials handling using instrumented force shoes and an inertial motion capture suit. J. Biomech. 2018, 70, 235–241. [Google Scholar] [CrossRef]
- Yang, C.-C.; Hsu, Y.-L. A Review of Accelerometry-Based Wearable Motion Detectors for Physical Activity Monitoring. Sensors 2010, 10, 7772–7788. [Google Scholar] [CrossRef]
- Caputo, F.; Greco, A.; Egidio, D.A.; Notaro, I.; Spada, S. Imu-based motion capture wearable system for ergonomic assessment in industrial environment. In Proceedings of the AHFE 2018 International Conferences on Human Factors and Wearable Technologies, and Human Factors in Game Design and Virtual Environments, Orlando, FL, USA, 21–25 July 2018; Ahram, T.Z., Ed.; Springer: Cham, Switzerland, 2019; pp. 215–225. [Google Scholar] [CrossRef]
- Scott, K.A.; Browning, R.C. Occupational physical activity assessment for chronic disease prevention and management: A review of methods for both occupational health practitioners and researchers. J. Occup. Environ. Hyg. 2016, 13, 451–463. [Google Scholar] [CrossRef]
- Muro-de-la-Herran, A.; Garcia-Zapirain, B.; Mendez-Zorrilla, A. Gait analysis methods: An overview of wearable and non-wearable systems, highlighting clinical applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef]
- Hlucny, S.D.; Novak, D. Characterizing Human Box-Lifting Behavior Using Wearable Inertial Motion Sensors. Sensors 2020, 20, 2323. [Google Scholar] [CrossRef] [PubMed]
- Giannini, P.; Bassani, G.; Avizzano, C.A.; Filippeschi, A. Wearable Sensor Network for Biomechanical Overload Assessment in Manual Material Handling. Sensors 2020, 20, 3877. [Google Scholar] [CrossRef]
- Akhmad, S.; Arendra, A.; Findiastuti, W.; Lumintu, I.; Pramudita, Y.D.; Mualim. Wearable IMU Wireless Sensors Network for Smart Instrument of Ergonomic Risk Assessment. In Proceedings of the 6th Information Technology International Seminar (IT IS, 2020), Surabaya, Indonesia, 14–16 October 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 213–218. [Google Scholar]
- Conforti, I.; Mileti, I.; Del Prete, Z.; Palermo, E. Measuring Biomechanical Risk in Lifting Load Tasks Through Wearable System and Machine-Learning Approach. Sensors 2020, 20, 1557. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.L.; Barim, M.S.; Feng, S.; Hughes, G.; Hayden, M.; Werren, D. Development of a Wearable IMU System for Automatically Assessing Lifting Risk Factors. In Proceedings of the International Conference on Human-Computer Interaction, Copenhagen, Denmark, 19–24 July 2020; Duffy, V.G., Ed.; Springer: Cham, Switzerland, 2020; pp. 194–213. [Google Scholar] [CrossRef]
- Lu, M.-L.; Feng, S.; Hughes, G.; Barim, M.S.; Hayden, M.; Werren, D. Development of an Algorithm for Automatically Assessing Lifting Risk Factors Using Inertial Measurement Units. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2019, 63, 1334–1338. [Google Scholar] [CrossRef]
- O’Reilly, M.; Caulfield, B.; Ward, T.; Johnston, W.; Doherty, C. Wearable Inertial Sensor Systems for Lower Limb Exercise Detection and Evaluation: A Systematic Review. Sports Med. 2018, 48, 1221–1246. [Google Scholar] [CrossRef] [PubMed]
- Donisi, L.; Pagano, G.; Cesarelli, G.; Coccia, A.; Amitrano, F.; D’Addio, G. Benchmarking between two wearable inertial systems for gait analysis based on a different sensor placement using several statistical approaches. Measurement 2021, 173, 108642. [Google Scholar] [CrossRef]
- Mancini, M.; Horak, F.B. Potential of APDM mobility lab for the monitoring of the progression of Parkinson’s disease. Expert Rev. Med. Devices 2016, 13, 455–462. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.; Stuart, S.; McBarron, G.; Fino, P.C.; Mancini, M.; Curtze, C. Validity of Mobility Lab (version 2) for gait assessment in young adults, older adults and Parkinson’s disease. Physiol. Meas. 2019, 40, 095003. [Google Scholar] [CrossRef]
- Schmitz-Hübsch, T.; Brandt, A.U.; Pfueller, C.; Zange, L.; Seidel, A.; Kühn, A.A.; Paul, F.; Minnerop, M.; Doss, S. Accuracy and repeatability of two methods of gait analysis—GaitRite™ und Mobility Lab™—in subjects with cerebellar ataxia. Gait Posture 2016, 48, 194–201. [Google Scholar] [CrossRef]
- Pagano, G.; D’Addio, G.; De Campi, M.; Donisi, L.; Biancardi, A.; Cesarelli, M. Rehabilitation Outcome in Patients undergone Hip or Knee Replacement Surgery using Inertial Technology for Gait Analysis. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bari, Italy, 1 June–1 July 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020. 5p. [Google Scholar] [CrossRef]
- Coccia, A.; Lanzillo, B.; Donisi, L.; Amitrano, F.; Cesarelli, G.; D’Addio, G. Repeatability of Spatio-Temporal Gait Measurements in Parkinson’s Disease. In Proceedings of the 2020 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Bary, Italy, 1 June–1 July 2020; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Cleland, I.; Kikhia, B.; Nugent, C.; Boytsov, A.; Hallberg, J.; Synnes, K.; McClean, S.; Finlay, D. Optimal Placement of Accelerometers for the Detection of Everyday Activities. Sensors 2013, 13, 9183–9200. [Google Scholar] [CrossRef]
- Matijevich, E.S.; Volgyesi, P.; Zelik, K.E. A Promising Wearable Solution for the Practical and Accurate Monitoring of Low Back Loading in Manual Material Handling. Sensors 2021, 21, 340. [Google Scholar] [CrossRef]
- Waters, T.R.; Lu, M.-L.; Piacitelli, L.A.; Werren, D.; Deddens, J.A. Efficacy of the Revised NIOSH Lifting Equation to Predict Risk of Low Back Pain Due to Manual Lifting. J. Occup. Environ. Med. 2011, 53, 1061–1067. [Google Scholar] [CrossRef]
- Spector, J.T.; Lieblich, M.; Bao, S.; McQuade, K.; Hughes, M. Automation of Workplace Lifting Hazard Assessment for Musculoskeletal Injury Prevention. Ann. Occup. Environ. Med. 2014, 26, 15. [Google Scholar] [CrossRef]
- Applications Manual for the Revised NIOSH Lifting Equation. Available online: https://stacks.cdc.gov/view/cdc/5434 (accessed on 27 January 2021).
- Waters, T.R.; Baron, S.L.; Piacitelli, L.A.; Anderson, V.P.; Skov, T.; Haring-Sweeney, M.; Wall, D.K.; Fine, L.J. Evaluation of the Revised NIOSH Lifting Equation. Spine 1999, 24, 386–394. [Google Scholar] [CrossRef] [PubMed]
- Brandt, M.; Madeleine, P.; Samani, A.; Jakobsen, M.D.; Skals, S.; Vinstrup, J.; Andersen, L.L. Accuracy of identification of low or high risk lifting during standardised lifting situations. Ergonomics 2017, 61, 710–719. [Google Scholar] [CrossRef]
- Long, X.; Yin, B.; Aarts, R.M. Single-accelerometer-based daily physical activity classification. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2009; Volume 2009, pp. 6107–6110. [Google Scholar]
- Arif, M.; Kattan, A. Physical Activities Monitoring Using Wearable Acceleration Sensors Attached to the Body. PLoS ONE 2015, 10, e0130851. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Murthy, S.K. Automatic Construction of Decision Trees from Data: A Multi-Disciplinary Survey. Data Min. Knowl. Discov. 1998, 2, 345–389. [Google Scholar] [CrossRef]
- Sheng, P.; Chen, L.; Tian, J. Learning-based road crack detection using gradient boost decision tree. In Proceedings of the 2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, China, 31 May–2 June 2018; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2018; pp. 1228–1232. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. J. Mach. Learn. Res. 2009, 10, 207–244. [Google Scholar]
- Sun, S.; Huang, R. An adaptive k-nearest neighbor algorithm. In Proceedings of the 2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery, Yantai, China, 10–12 August 2010; Li, M., Liang, Q., Wang, L., Eds.; IEEE: Piscataway, NJ, USA, 2010; Volume 1, pp. 91–94. [Google Scholar]
- Al-Aidaroos, K.M.; Abu Bakar, A.; Othman, Z. Naïve bayes variants in classification learning. In Proceedings of the 2010 International Conference on Information Retrieval & Knowledge Management (CAMP), Shah Alam, Malaysia, 17–18 March 2010; Abu Bakar, Z., Tengku Sembok, T.M., Eds.; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2010; pp. 276–281. [Google Scholar]
- Pal, S.; Mitra, S. Multilayer perceptron, fuzzy sets, and classification. IEEE Trans. Neural Netw. 1992, 3, 683–697. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. In Emerging Artificial Intelligence Applications in Computer Engineering; Maglogiannis, I., Karpouzis, K., Wallace, B.A., Soldatos, J., Eds.; IoS Press: Amsterdam, The Netherlands, 2007; pp. 3–24. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Stoltzfus, J.C. Logistic Regression: A Brief Primer. Acad. Emerg. Med. 2011, 18, 1099–1104. [Google Scholar] [CrossRef] [PubMed]
- Anguita, D.; Ghelardoni, L.; Ghio, A.; Oneto, L.; Ridella, S. The ‘K’ in K-fold Cross Validation. In Proceedings of the 20th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2012), Bruges, Belgium, 25–27 April 2012; ESANN: Louvain-la-Neuve, Belgium; pp. 441–446. [Google Scholar]
- Sechidis, K.; Tsoumakas, G.; Vlahavas, I. On the stratification of multi-label data. In Proceedings of the Joint European Conference on Machine Learning (ECML) and Knowledge Discovery in Databases (PKDD), Athens, Greece, 5–9 September 2011; Gunopulos, D., Hofmann, T., Eds.; Springer: Berlin, Germany, 2011; pp. 145–158. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Res. 2011, 2, 37–63. [Google Scholar]
- Lei, S. A Feature Selection Method Based on Information Gain and Genetic Algorithm. In Proceedings of the 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; O’ Conner, L., Ed.; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2012; Volume 2, pp. 355–358. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Scrutinio, D.; Ricciardi, C.; Donisi, L.; Losavio, E.; Battista, P.; Guida, P.; Cesarelli, M.; Pagano, G.; D’Addio, G. Machine learning to predict mortality after rehabilitation among patients with severe stroke. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Tougui, I.; Jilbab, A.; El Mhamdi, J. Heart disease classification using data mining tools and machine learning techniques. Health Technol. 2020, 10, 1137–1144. [Google Scholar] [CrossRef]
- Mannini, A.; Sabatini, A.M. Machine Learning Methods for Classifying Human Physical Activity from On-Body Accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef]
- Varrecchia, T.; De Marchis, C.; Rinaldi, M.; Draicchio, F.; Serrao, M.; Schmid, M.; Conforto, S.; Ranavolo, A. Lifting activity assessment using surface electromyographic features and neural networks. Int. J. Ind. Ergon. 2018, 66, 1–9. [Google Scholar] [CrossRef]
- Varrecchia, T.; De Marchis, C.; Draicchio, F.; Schmid, M.; Conforto, S.; Ranavolo, A. Lifting Activity Assessment Using Kinematic Features and Neural Networks. Appl. Sci. 2020, 10, 1989. [Google Scholar] [CrossRef]
- Ranavolo, A.; Varrecchia, T.; Iavicoli, S.; Marchesi, A.; Rinaldi, M.; Serrao, M.; Conforto, S.; Cesarelli, M.; Draicchio, F. Surface electromyography for risk assessment in work activities designed using the e “revisedNIOSH lifting equation”. Int. J. Ind. Ergon. 2018, 68, 34–45. [Google Scholar] [CrossRef]
- Snyder, K.; Thomas, B.; Lu, M.-L.; Jha, R.; Barim, M.S.; Hayden, M.; Werren, D. A deep learning approach for lower back-pain risk prediction during manual lifting. PLoS ONE 2021, 16, e0247162. [Google Scholar] [CrossRef] [PubMed]
- Snyder, K. Utilizing Convolutional Neural Networks for Specialized Activity Recognition: Classifying Lower Back Pain Risk Prediction During Manual Lifting. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 3 June 2020. [Google Scholar]
- Veiga, J.J.D.; O’Reilly, M.; Whelan, D.; Caulfield, B.; Ward, T.E. Feature-Free Activity Classification of Inertial Sensor Data with Machine Vision Techniques: Method, Development, and Evaluation. JMIR mHealth uHealth 2017, 5, e115. [Google Scholar] [CrossRef] [PubMed]



| Age (years) | 27.71 | ± | 1.60 |
| Height (cm) | 167.40 | ± | 4.86 |
| Weight (kg) | 69.00 | ± | 69.00 |
| Body Mass Index (kg/m2) | 24.51 | ± | 24.51 |
| First Trial LI < 1 (0.5) | Second Trial LI > 1 (1.3) | |||||||
|---|---|---|---|---|---|---|---|---|
| Displacement [Start–End] (cm) | Frequency (Lifts/min) | Weight Lifted (kg) | Displacement [Start–End] (cm) | Frequency (Lifts/min) | Weight Lifted (kg) | |||
| m & f | m | f | m | f | m | f | ||
| [50–125] | 2.5 | 7 | 5 | [50–125] | 6 | 4 | 15 | 10 |
| [30–125] | 2.5 | 5 | 4 | [30–125] | 5 | 3 | 13 | 8 |
| [50–150] | 2.5 | 5 | 4 | [50–150] | 5 | 3 | 13 | 8 |
| Algorithms | Accuracy | Sensitivity | Specificity | AucRoc |
|---|---|---|---|---|
| DT | 0.97 ± 0.05 | 0.97 ± 0.04 | 0.97 ± 0.05 | 0.97 ± 0.03 |
| RF | 0.98 ± 0.02 | 0.98 ± 0.03 | 0.99 ± 0.02 | 0.99 ± 0.01 |
| GB | 0.97 ± 0.04 | 0.98 ± 0.03 | 0.96 ± 0.06 | 0.98 ± 0.02 |
| AB | 0.98 ± 0.02 | 0.98 ± 0.02 | 0.98 ± 0.04 | 0.97 ± 0.03 |
| kNN | 0.90 ± 0.09 | 0.88 ± 0.10 | 0.91 ± 0.11 | 0.94 ± 0.06 |
| NB | 0.96 ± 0.03 | 0.96 ± 0.04 | 0.96 ± 0.04 | 0.99 ± 0.01 |
| MLP | 0.95 ± 0.06 | 0.93 ± 0.07 | 0.96 ± 0.06 | 0.97 ± 0.03 |
| SVM | 0.83 ± 0.20 | 0.83 ± 0.29 | 0.82 ± 0.37 | 0.85 ± 0.22 |
| LR | 0.79 ± 0.15 | 0.79 ± 0.14 | 0.79 ± 0.19 | 0.84 ± 0.13 |
| Algorithms | Accuracy | Sensitivity | Specificity | AucRoc |
|---|---|---|---|---|
| DT | 0.88 ± 0.11 | 0.87 ± 0.14 | 0.88 ± 0.08 | 0.88 ± 0.12 |
| RF | 0.90 ± 0.11 | 0.90 ± 0.13 | 0.89 ± 0.09 | 0.94 ± 0.10 |
| GB | 0.89 ± 0.13 | 0.90 ± 0.14 | 0.88 ± 0.13 | 0.92 ± 0.09 |
| AB | 0.89 ± 0.14 | 0.89 ± 0.16 | 0.89 ± 0.12 | 0.92 ± 0.12 |
| kNN | 0.82 ± 0.10 | 0.81 ± 0.14 | 0.82 ± 0.09 | 0.88 ± 0.09 |
| NB | 0.86 ± 0.12 | 0.83 ± 0.17 | 0.89 ± 0.08 | 0.92 ± 0.08 |
| MLP | 0.90 ± 0.12 | 0.88 ± 0.16 | 0.92 ± 0.09 | 0.94 ± 0.08 |
| SVM | 0.68 ± 0.19 | 0.91 ± 0.13 | 0.44 ± 0.42 | 0.82 ± 0.16 |
| LR | 0.84 ± 0.08 | 0.84 ± 0.13 | 0.84 ± 0.05 | 0.90 ± 0.07 |
| Algorithms | Accuracy | Sensitivity | Specificity | AucRoc |
|---|---|---|---|---|
| DT | 0.91 | 0.89 | 0.92 | 0.93 |
| RF | 0.95 | 0.94 | 0.95 | 0.99 |
| GB | 0.95 | 0.94 | 0.96 | 0.99 |
| AB | 0.80 | 0.72 | 0.87 | 0.90 |
| kNN | 0.84 | 0.83 | 0.85 | 0.91 |
| NB | 0.67 | 0.63 | 0.71 | 0.75 |
| MLP | 0.91 | 0.91 | 0.91 | 0.97 |
| SVM | 0.71 | 0.70 | 0.71 | 0.79 |
| LR | 0.66 | 0.67 | 0.66 | 0.68 |
| NO RISK | YES RISK | |
|---|---|---|
| NO RISK | 197 | 13 |
| YES RISK | 8 | 202 |
| Algorithms | Accuracy | Sensitivity | Specificity | AucRoc |
|---|---|---|---|---|
| DT | 0.88 | 0.93 | 0.83 | 0.88 |
| RF | 0.88 | 0.97 | 0.80 | 0.97 |
| GB | 0.75 | 0.97 | 0.53 | 0.92 |
| AB | 0.88 | 0.97 | 0.80 | 0.96 |
| kNN | 0.50 | 0.00 | 1.00 | 0.48 |
| NB | 0.82 | 0.97 | 0.67 | 0.97 |
| MLP | 0.73 | 0.97 | 0.50 | 0.87 |
| SVM | 0.77 | 0.97 | 0.57 | 0.82 |
| LR | 0.70 | 0.97 | 0.43 | 0.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Donisi, L.; Cesarelli, G.; Coccia, A.; Panigazzi, M.; Capodaglio, E.M.; D’Addio, G. Work-Related Risk Assessment According to the Revised NIOSH Lifting Equation: A Preliminary Study Using a Wearable Inertial Sensor and Machine Learning. Sensors 2021, 21, 2593. https://doi.org/10.3390/s21082593
Donisi L, Cesarelli G, Coccia A, Panigazzi M, Capodaglio EM, D’Addio G. Work-Related Risk Assessment According to the Revised NIOSH Lifting Equation: A Preliminary Study Using a Wearable Inertial Sensor and Machine Learning. Sensors. 2021; 21(8):2593. https://doi.org/10.3390/s21082593
Chicago/Turabian StyleDonisi, Leandro, Giuseppe Cesarelli, Armando Coccia, Monica Panigazzi, Edda Maria Capodaglio, and Giovanni D’Addio. 2021. "Work-Related Risk Assessment According to the Revised NIOSH Lifting Equation: A Preliminary Study Using a Wearable Inertial Sensor and Machine Learning" Sensors 21, no. 8: 2593. https://doi.org/10.3390/s21082593
APA StyleDonisi, L., Cesarelli, G., Coccia, A., Panigazzi, M., Capodaglio, E. M., & D’Addio, G. (2021). Work-Related Risk Assessment According to the Revised NIOSH Lifting Equation: A Preliminary Study Using a Wearable Inertial Sensor and Machine Learning. Sensors, 21(8), 2593. https://doi.org/10.3390/s21082593









