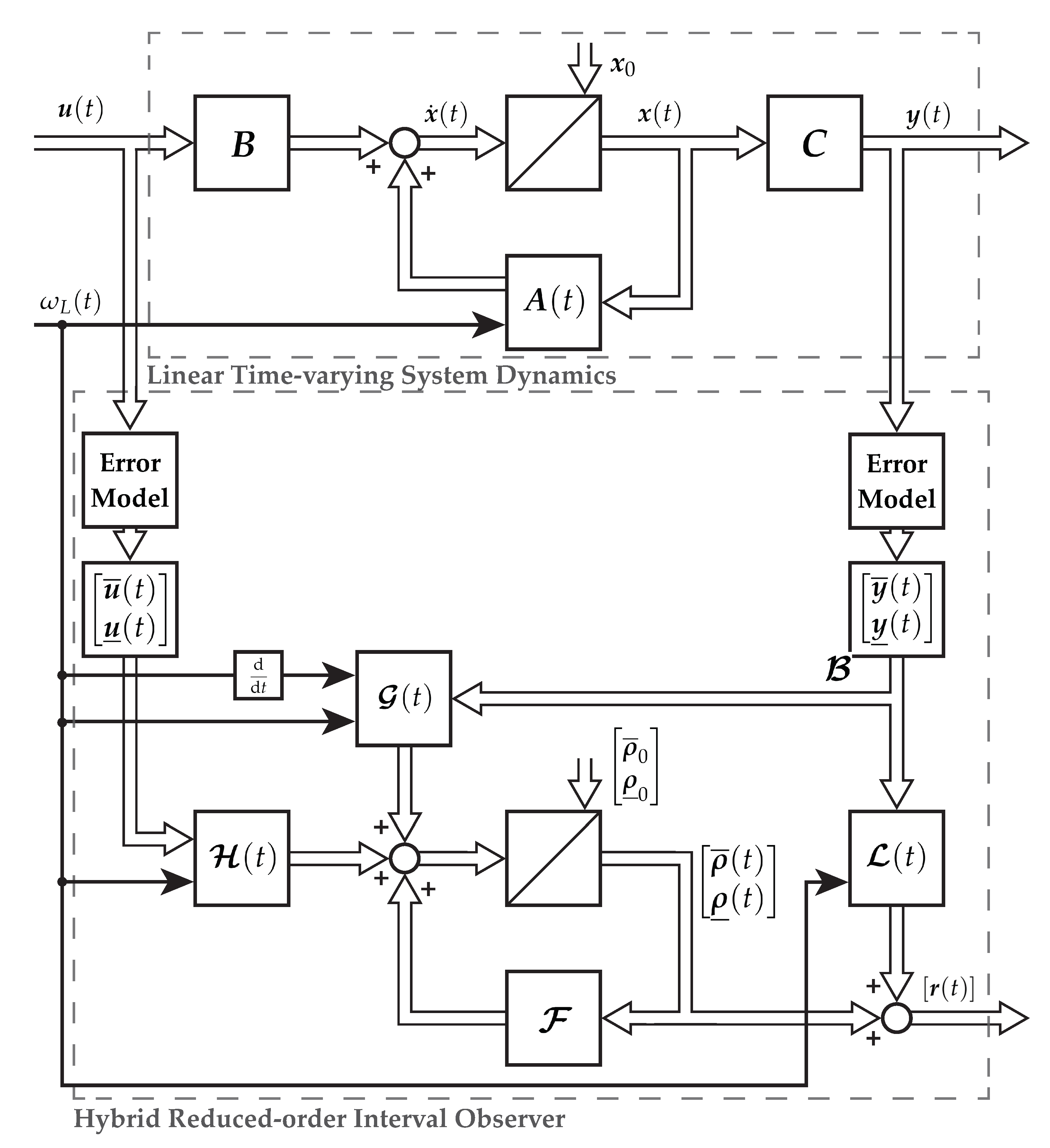
1. Motivation and Overview
Guaranteed state estimation of uncertain linear continuous time dynamical systems with time-varying parameters is of increasing interest in various technical applications. Firstly presented for the induction machine in [
1], a reduced-order hybrid interval observer for the verified state estimation was designed. Its main advantage is the provision of guarantees regarding the estimated states. A major disadvantage is the relatively wide interval width resulting in practical inapplicability. To tackle this challenge, a bundle of interval observers with optimal adaptive gains regarding the operation point of the plant is designed within this paper leading to a significant reduction of the estimated interval widths.
Challenges for guaranteed state estimation are the growing complexity of technical systems in combination with a great demand for functional safety, e.g., autonomous driving [
2], which results in requirements for fault detection and fault diagnosis applications guaranteeing the safe and reliable operation of the system [
3,
4]. Furthermore, in the presence of undesirable effects such as failures in the actuators or sensors, it is desired that the control system is responsive and adaptive to such failures and adjustable to recover the system from anomalies and failures [
5]. Therefore, the aim of a diagnosis system is to detect faults as early as possible while, at the same time, false alarms, e.g., due to measurement noise or parameter uncertainties exceeding acceptable bounds, have to be avoided to minimize unnecessary system shutdowns and maximize system reliability and dependability [
6]. For these mentioned challenges and applications, guaranteed state estimation using real-time capable interval observers are an appropriate choice. An overview about interval estimation applied to the diagnosis and control of uncertain systems is given in Raissi et al. [
7].
One way to achieve guaranteed enclosure is the observation of system states by considering input and output noise as well as parameter uncertainties in a model-based estimation setup resulting in essential signals for fault diagnosis and other applications. Under certain conditions and restrictions, the estimation of the important system states gives guaranteed results leading to safety diagnosis based on guaranteed intervals for the signals instead of a measurement value trend or threshold comparison [
8].
However, approaches like the extended Luenberger Observer, the extended Kalman Filter, the High-Gain Observer, the Sliding Mode Observer, the
Observer, or the
-Gain Observer are not directly applicable with a priori assumptions on probability distributions or models of the uncertainties, because these are often unknown for practical applications. Furthermore, such methods, e.g., Sun et al. [
9], cannot be used because they do not provide necessary guaranteed error bounds [
10]. Therefore, it is reasonable to utilize methods that assume that the uncertainties are unknown but their boundaries are specified, which is usually given for practical applications.
In the literature, there are two approaches which should be emphasized considering bounded intervals for the uncertainties, namely set-membership estimators and interval observers [
11,
12]. Both aim at providing sets or intervals containing all the possible state vectors consistent with the model structure, and input and output uncertainties as well as uncertainties in initial states and the parameters.
Set-membership estimators are based on a predictor-corrector structure with different descriptions of uncertainties, e.g., zonotopes, parallelotopes, subpavings, and ellipsoids [
6,
13]. These approaches have issues with real-time capability due to excessive computational effort for the complex and guaranteed description of the uncertainties. Hence, these methods are not suitable for systems with relatively small time constants like the induction machine. However, in Zbranek and Vesely [
14], a set-membership estimator for a permanent magnet synchronous machine based on a nonlinear model with four states is designed. The results show that this approach is only suitable for online operations under restrictive conditions. In the case of a induction machine with similar time constants, the coupling of such state estimators to a bundle to improve the performance is not feasible.
In contrast, interval observers are based on the classical observer structure. For each state a lower and an upper bound is estimated. Due to a less complex description of the set of possible states, i.e., just a box, the computational effort is lower than with the aforementioned approach. This method is divided into cooperative-based and hybrid interval observers [
12].
The idea behind the so-called hybrid interval observer is to design dynamical systems with monotone error dynamics that are activated on certain switching conditions guarding the states which change the monotonicity of the system [
10,
15]. These systems enclose all the state trajectories, generated by the original uncertain system, by estimating a lower and an upper boundary for each state in a guaranteed way [
16,
17]. The derivatives of the error dynamics activate a subsequent system, keeping monotonicity of the error dynamics [
18]. Finally, switching conditions describe the change of these derivatives. This leads to a cooperative system [
19] for the error dynamics, resulting in an inclusion of the real state.
Both approaches, set-membership estimators and hybrid interval observers, face the key challenge of finding a suitable parametrization for the observer or the estimator in order to get a sufficient tight interval for the estimated states. With the task of considering input and output noise as well as parameter uncertainties, these methods tend to give conservative intervals widths. Especially for electric machines whereby the system dynamics have time-varying parameters, thus the parametrization of the observer is a crucial task.
Due to the basic idea of a guaranteed enclosure of states, every interval observer limits the range of the actual value. Therefore, the actual value has to be below each upper bound and above each lower bound of the considered interval observers. Due to the fact that interval observers have to bound the same value, even with different parameterizations, these interval observers allow a comparison among themselves regarding the narrowest enclosure of the actual value for the current operating point. This allows that the envelope to be composed by the lowest upper bound and the highest lower bound chosen out of each interval observer considered in the estimation setup.
Following this idea, a so-called bundle of interval observers, for which several observers are run in parallel and the resulting interval is arranged with the most suitable upper and lower boundary, can be developed. Furthermore, within a bundle, it is possible to generate interval observers with unstable dynamics, called framers [
20], which simply bound the estimated state without the assurance of stability. Finally, a better convergence rate as well as smaller interval widths are expected. Interval observer bundles, predominantly applied to bioprocessess, are presented in [
21,
22,
23]. Furthermore, a similar approach is named a bank of observers. Hereby, the main difference between a bundle of observers and a bank of observers is the used methodical approach for a single observer as well as the underlying system description. If estimation with zonotopes is considered, the resulting guaranteed enclosure is the intersection of the solutions [
24]. Hence, this would be the set-membership approach pendant to the bundle approach presented in this paper. Secondly, if uncertain switching functions are considered to maintain guaranteed interval enclosure for nonlinear systems, the so-called global solution would be the over-approximation of activated interval observers [
25]. This stabilizes the guaranteed boundaries but does not minimize the error bounds.
However, most publications on interval observers and bundle of observers do neither investigate the selection of observer gains, the behavior of unstable observer dynamics, or an algorithm to determine feasible configurations with respect to an improvement of the interval width. Their focus is on the design for a suitable structure of a single interval observer. This strongly depends on the underlying model, hence, this usually is a challenging task. A subsequent arrangement to a bundle of observers is made using an arbitrary or a not precisely specified parametrization of the observer gain, which is not discussed in detail.
In this contribution, to tackle the gap between using a bundle of interval observers to improve state estimation and obtain an optimal solution for the given task, scenario-based optimization for the reduced-order hybrid interval observer’s parametrization for a linear time-varying model of the induction machine is discussed. Hereby, unstable observer dynamics are considered. Moreover, the results of an offline optimization are used online to adapt the observer gains during runtime.
Within previously published guaranteed interval estimation techniques [
1,
10,
15,
26,
27], realistic sensor errors have not been considered and interval widths need to be minimized further in order to be applied for a practical algorithm (e.g., fault detection). For such practical usage of guaranteed interval estimation, the interval width needs to be as small as possible. Hence, to improve the interval widths for guaranteed state estimation with a bundle of observers, the reduced-order interval observer approach has been chosen. However, all these approaches are capable of being used in an observer bundle as presented within this contribution.
This paper is organized as follows: First, some necessary interval arithmetics, coordinate transformations, and matrix operations are given. Afterwards, the design of the reduced-order hybrid interval observer is presented. A description of an interval observer bundle using some preliminary work out of Moisan et al. [
23] as well as the necessary definitions for the hybrid interval observer and the re-initialization approach with an overview of some re-initialization conditions are introduced. In
Section 3, a model of the induction machine in
-coordinates is presented. The
Section 4 deals with the design and implementation of the reduced-order hybrid interval observer and the combination to the interval observer bundle. A general time-invariant as well as a time-varying observer gain are specified. Furthermore, an algorithm for the parametrization of the observer bundle as well as the reduced-order interval observers with a scenario-based optimization is also presented in the
Section 4. In the process, resulting lookup tables and a switching algorithm suitable for the adaptive gain are presented.
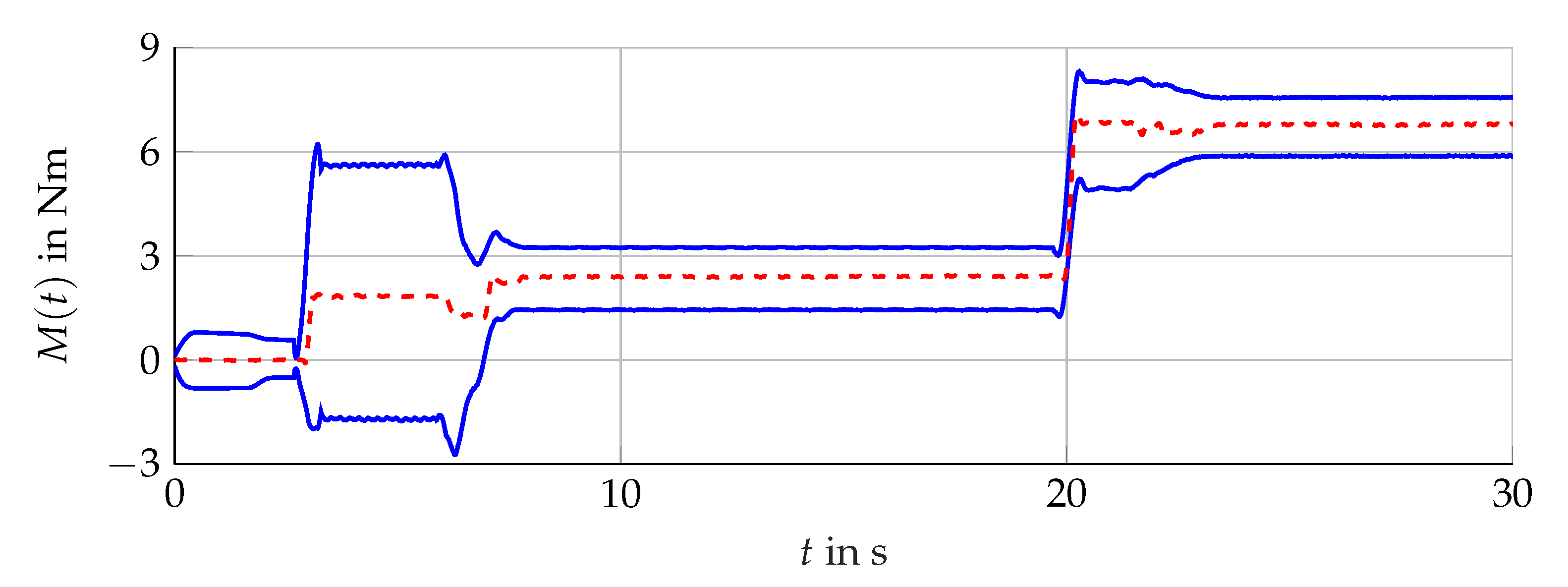
The validation of the interval observer bundle is executed by comparing the measured torque with the one calculated with the stator currents under consideration of the respective uncertainties and the estimated magnetizing current intervals. This is reasonable since the measurement of the magnetic flux is usually a sophisticated and expensive task.
Finally, the implementation of the whole system along with the re-initialization process is discussed for the induction machine with simulations and measurement data in
Section 5.
5. Results
The simulation and experimental results are obtained by considering an induction machine with a rated power of 2
, a rated torque of
, and a rated speed of 3000
. The numerical values of the parameters listed in
Table 1 are assumed to be known exactly. A lookup table for the torque control as well as a cascaded PI controller for the current control followed by an ideal voltage source inverter, with a DC link voltage of 48
arrange the control system of the induction machine. As load, a speed regulated synchronous machine with a maximum torque of 32
is used. The angular velocity
is obtained by an incremental encoder and assumed to be known exactly. Within the simulation, the setpoint of the output torque is given as
and Equation (
56) is used to calculate the output torque of the induction machine. Hence, only the interval inclusion of the measured torque
against the calculated interval with Equation (
56) and the estimations are presented. Within the experimental setup, the input voltages
can not be measured directly. Therefore, these values have to be calculated with the controllers output signals and the ideal model of a voltage source converter leading to the necessary input voltages
.
The simulation scenario is shown in
Figure 11. For the analysis with measurement data, the scenario presented in
Figure 12 is considered. The comparison of the bundle of observers against the benchmark interval observer
given by [
10] is shown in
Figure 13 (simulation) and
Figure 14 (measurement data). With (
56) and the measured output torque, the validation is presented in
Figure 15.
The results are presented for the interval estimation of . Qualitatively, the same results are obtained for .
5.1. Interval Width Improvement
Compared with the single interval observer, the bundle is able to suppress the initial overshoot and to achieve a fast convergence for different operation areas. The narrowing of the envelope
shows significant improvement presented in
Figure 16 (simulation) and
Figure 17 (measurement data). Furthermore, the influence of the angular velocity’s amplitude during periods with constant
is nearly decoupled from the resulting interval width. The bundle of observers shows its full potential in the neighborhood around
. In this operation area, the influence of the interval arithmetic operations is decisive but minimized with the optimized observer configurations. Nevertheless, the combination of rapid changes and zero crossings of
challenge the interval observers for the induction machine. Hereby, the interval observers implemented with (
59) are able to reduce the interval width, which is presented in
Figure 18, but still, a temporarily widening can not be avoided with the established configuration.
A similar improvement is obtained with measurement data, see
Figure 19. However, the resulting interval width is not suitable, which can mainly be attributed to a too large input uncertainty, due to the interval model of the inverter that is adding additional interval calculations within the chain of the estimation algorithm. Hereby, each zero crossing of the stator currents within the used interval model of the inverter contributes the deterioration of the interval width. The principle improvement of the guaranteed state estimation with measurement data is shown.
The validation of the reduced-order interval observer and the observer bundle is successful. The calculated interval of the output torque follows the measured torque’s dynamics and enclosures the real value for the whole simulation (see
Figure 15).
5.2. Reinitalization & Unstable Configurations
Firstly, the periodical re-initialization has not shown improvements on the interval widths. Hence, the re-initialization process is mainly driven by the second case of (
43). Nevertheless, the re-initialization process is used to take advantage of unstable configurations and is necessary for the implementation of the unstable interval observers.
The presented optimization achieves two different types of results for the parameters and :
- (i)
The eigenvalues of the resulting system matrices are negative, which also yields stable and bounded error dynamics in case of
together with Proposition
Section 2.3;
- (ii)
Considering the optimization and the results with parameters it can be observed that the optimization algorithm shifts one off-diagonal element or of the system matrix to zero. The matching main diagonal element or then results in an unstable eigenvalue. Hence, the dynamics of this unstable eigenvalue does not affect the dynamics of the stable eigenvalue. The remaining optimization parameters, in case of the induction machine three, are used to minimize the interval width. Since the optimization and estimation is done separately for each unmeasurable state, this procedure leads to appropriate results. Further improvements could be made by setting one off-diagonal element a priori to zero and starting the optimization using this knowledge about the behavior and the considered scenario.
5.3. Real-Time Capability
The interval observer bundle presented in this paper was successfully tested at the test bench sketched in
Section 5 and [
10]. For the investigation of the discussed methods, the number of implemented interval observers within the bundle was gradually increased until the real-time controller (dSPACE ds1005 Controller Board) was unable to perform the algorithm in real-time. It resulted in a total number of 15 reduced-order hybrid interval observers with the whole extensions established in this paper capable of running in parallel. Hereby, none of the possible combinations with the prior proposed 20 interval observers are tested. Such a procedure needs to be done if the bundle of observers is applied to a specific technical system, whereby, the overall performances needs to be optimal.
For the experimental setup, the sampling frequency of the whole test bench is not known. Furthermore, the numerical discretization scheme, e.g., the Runge–Kutta method, as well as the implementation of interval operations in real-time environment is done with default settings of Simulink Embedded Coder. Hence, potential in order to speed up the algorithms or to increase the accuracy exist.
However, real-time capability has been shown up to a certain number of reduced-order interval observers. This may be improved with a detailed look into implementation as well as a real setup on which the bundle has to perform.
Additionally, with a detailed study about the interval observers within the bundle and the corresponding lookup tables with the parameters concerning the best enclosure for certain scenarios, interval observers with little improvement can be removed from the observer bundle which is then capable for practical use in real-time setup.
6. Conclusions
The design procedure for guaranteed state estimation of unmeasurable states is a challenging task. Hereby, the determination of an optimal observer gain depends on the chosen interval observer structure, the system properties, and the range of operation. The presented interval observer bundle’s underlying reduced-order hybrid interval observer does not restrict the configuration of the observer gain, but neither does it give specific statements about the resulting interval widths with respect to the eigenvalues nor the observer gain itself, especially not in case of parameter-varying systems. Therefore, a bundle of interval observers was proposed which overcomes the difficulty to choose an optimal observer gain by introducing a set of configurations covering the most important operating points with respect to the time-varying parameters.
The proposed methodical approach made huge improvements on the estimated interval widths of the induction machine’s magnetizing currents. The underlying reduced-order interval observers with their low computational effort yielded the possibility to supplement a bundle of interval observers for the given induction machine model with its small time constants. Furthermore, the offline optimization with its objective function’s decomposition and the adaptive gain give the potential to optimize the estimation for a priori considered operation areas, whereby, the continuity conditions are met.
Due to the continuity of the observer gain parameters, the switching of the configuration can not be done immediately. Therefore, the effect of the adaptive gains are delayed. Nevertheless, real-time capability as well as the verification of the proposed methods are successfully tested with measurement data of an induction machine and show a significant decrease of the estimated state’s interval width.
The applied number of interval observers within a bundle of observers as well as global optimization leading to a guaranteed and optimal enclosure of the estimated states should be considered for practical tasks.
Furthermore, the results within a real-time setup will be improved by applying instrumentation to measure the input voltages of the induction machine. Moreover, instrumentation with small measurement errors lead to an improvement of the interval widths for single observers and thus also for a bundle of observers.
A drawback of the proposed interval observer is the influence of the wrapping effect [
33]. The over-approximation due to the interval calculations is amplified by the shape of the state-space representation, which also affects the calculation of the initial values at the time steps of re-initialization, which is attributed to the necessary transformation of the reduced-order observer.
Future work will be the consideration of uncertain parameters like the angular velocity . It is expected that the interval width can be kept within a feasible envelope for further applications like machine control or fault diagnosis.