Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
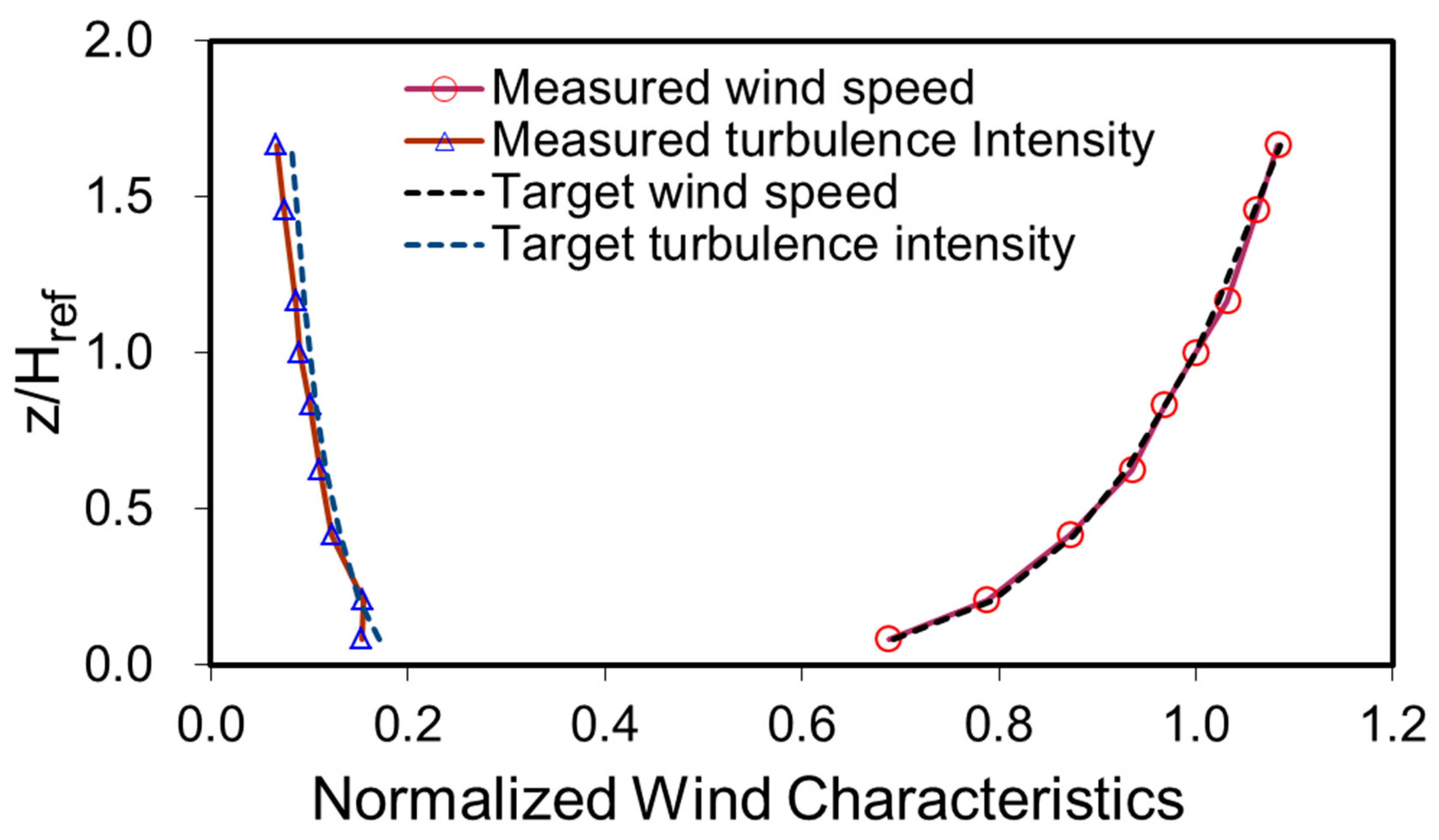
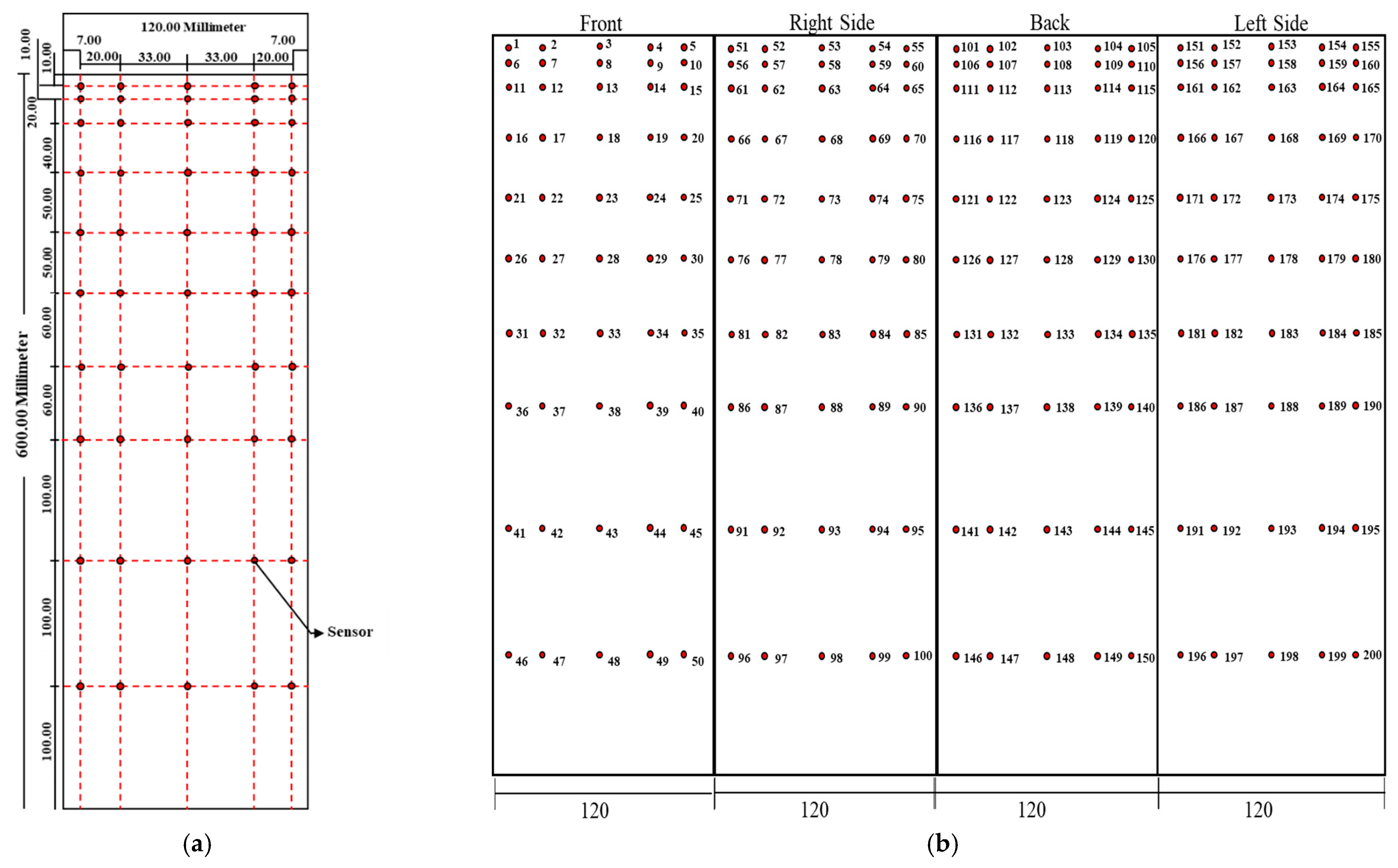
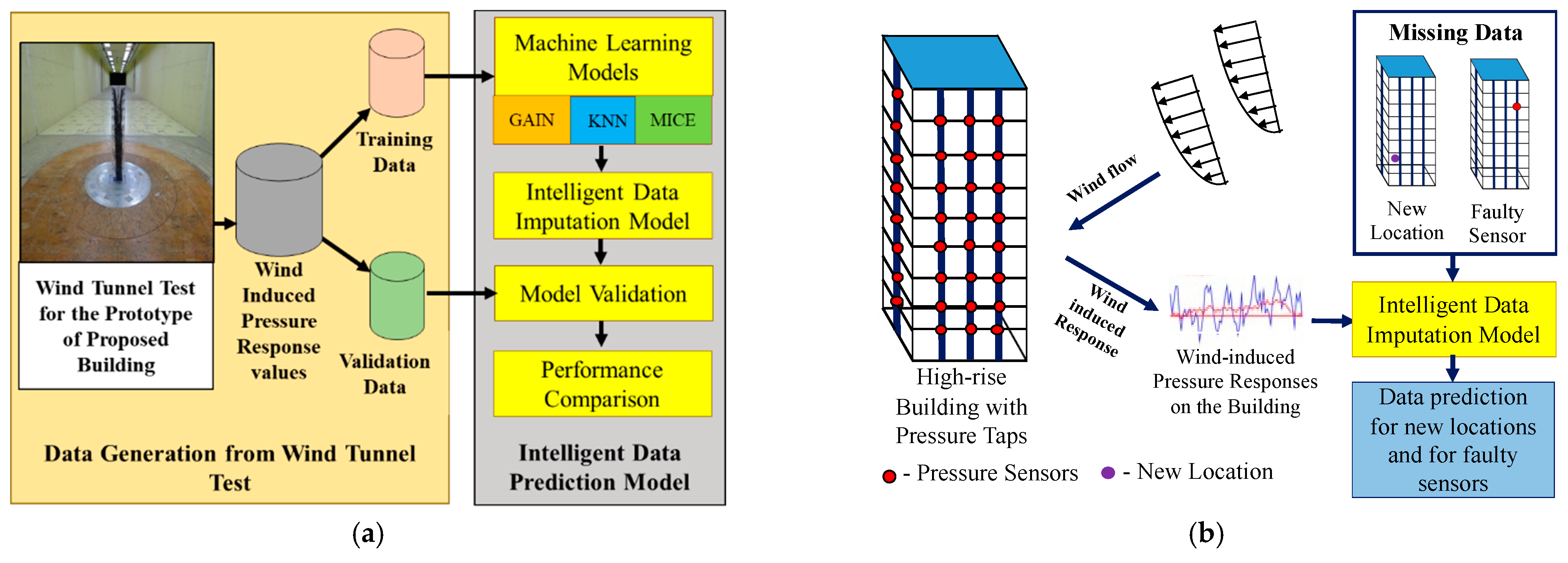
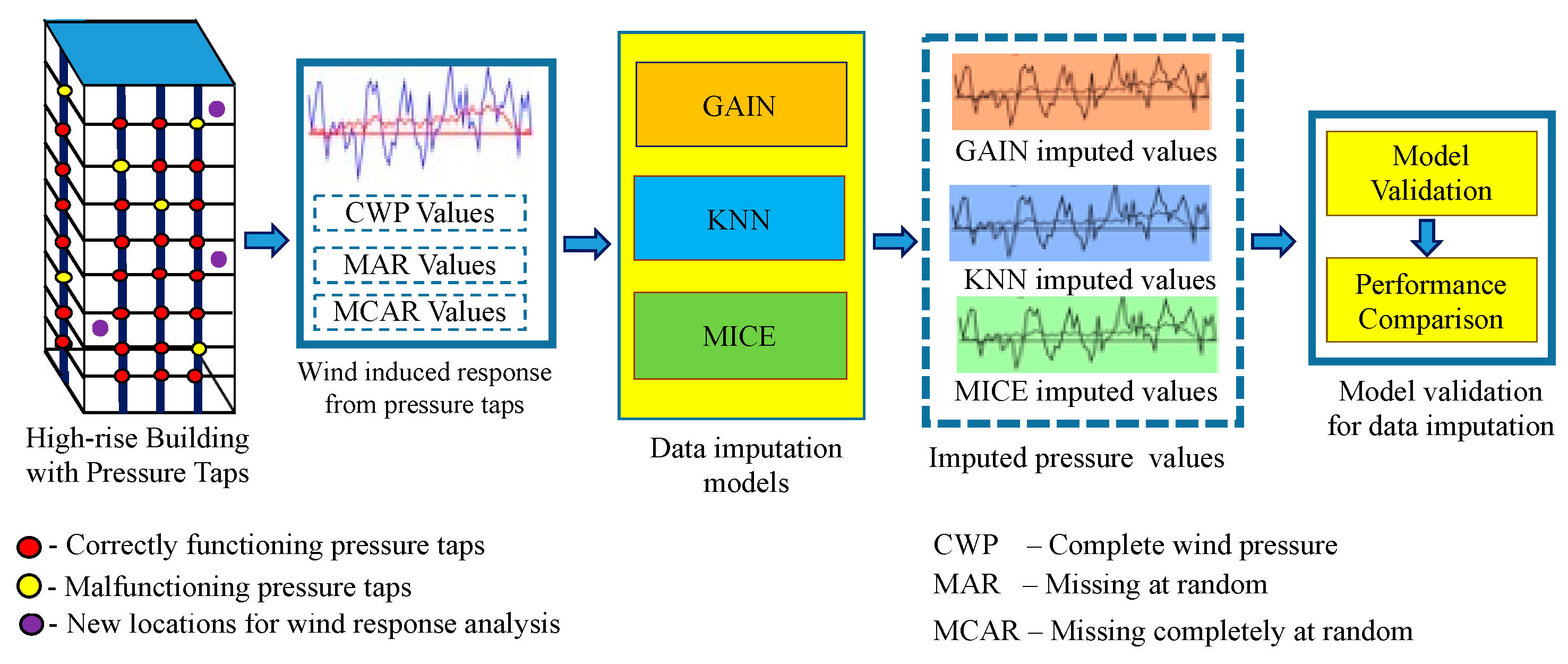
3.1. Wind Tunnel Test and Wind Pressure Data
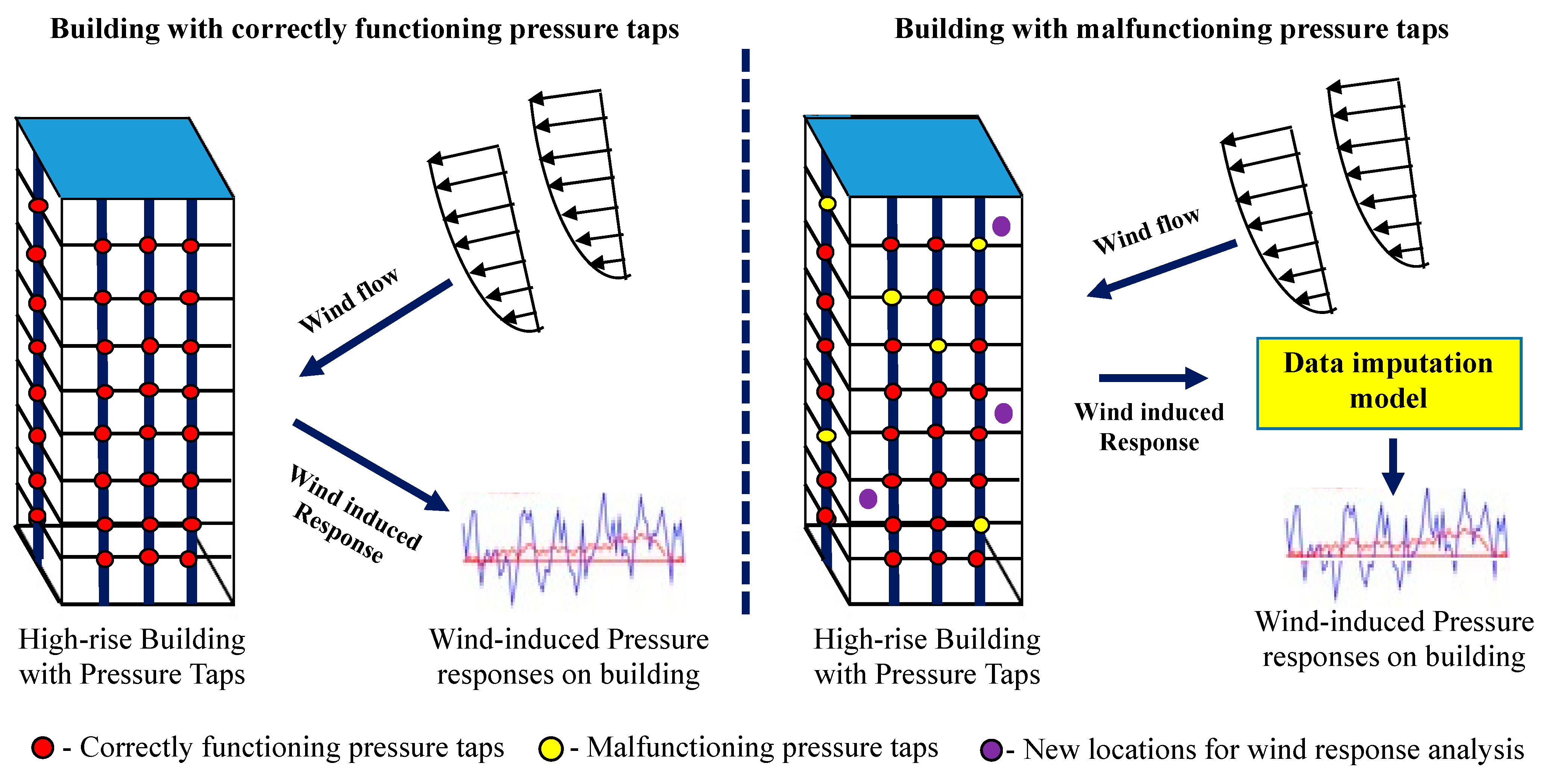
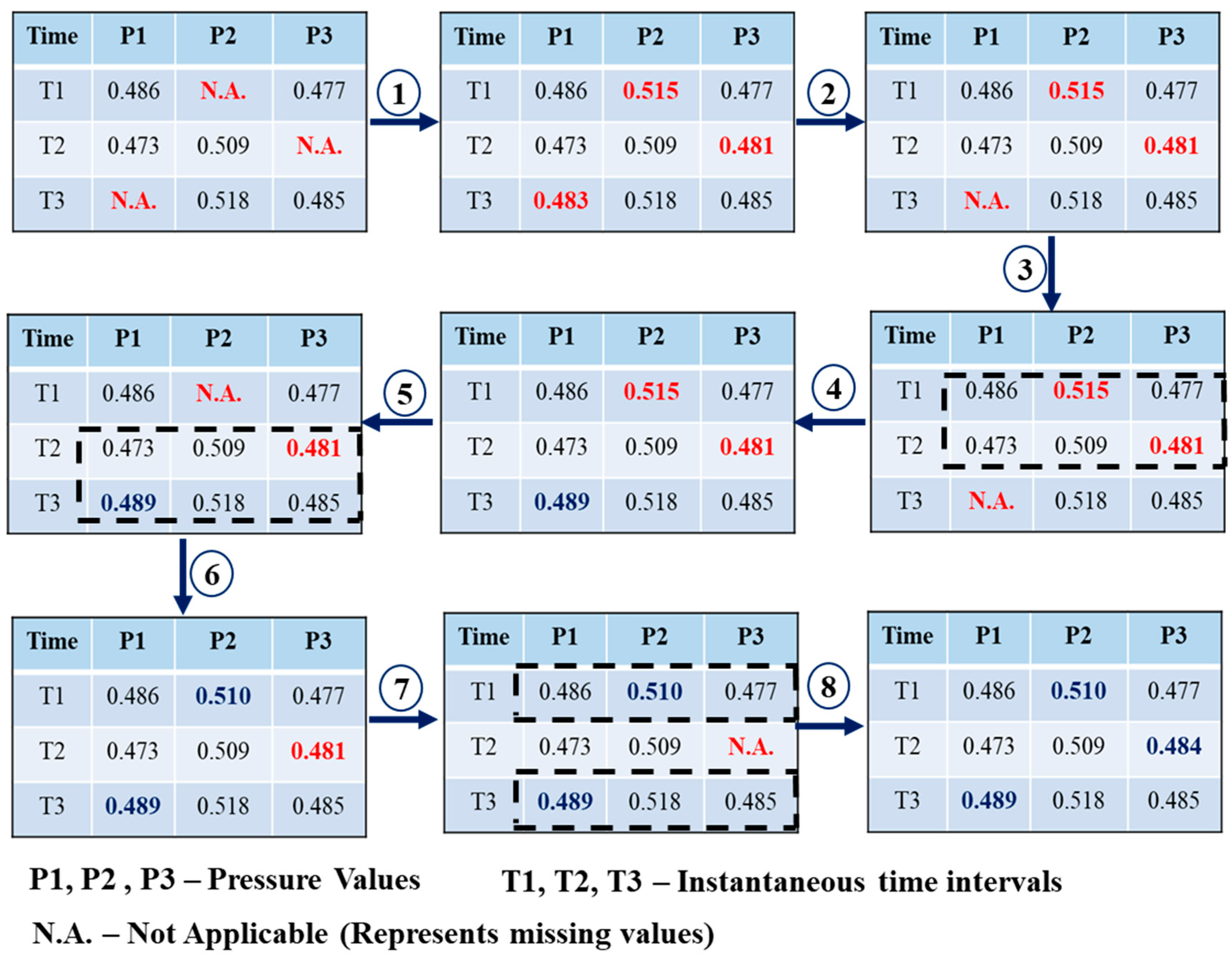
3.2. Intelligent Data Prediction Model
4. Construction of Wind-Induced Pressure Prediction Model
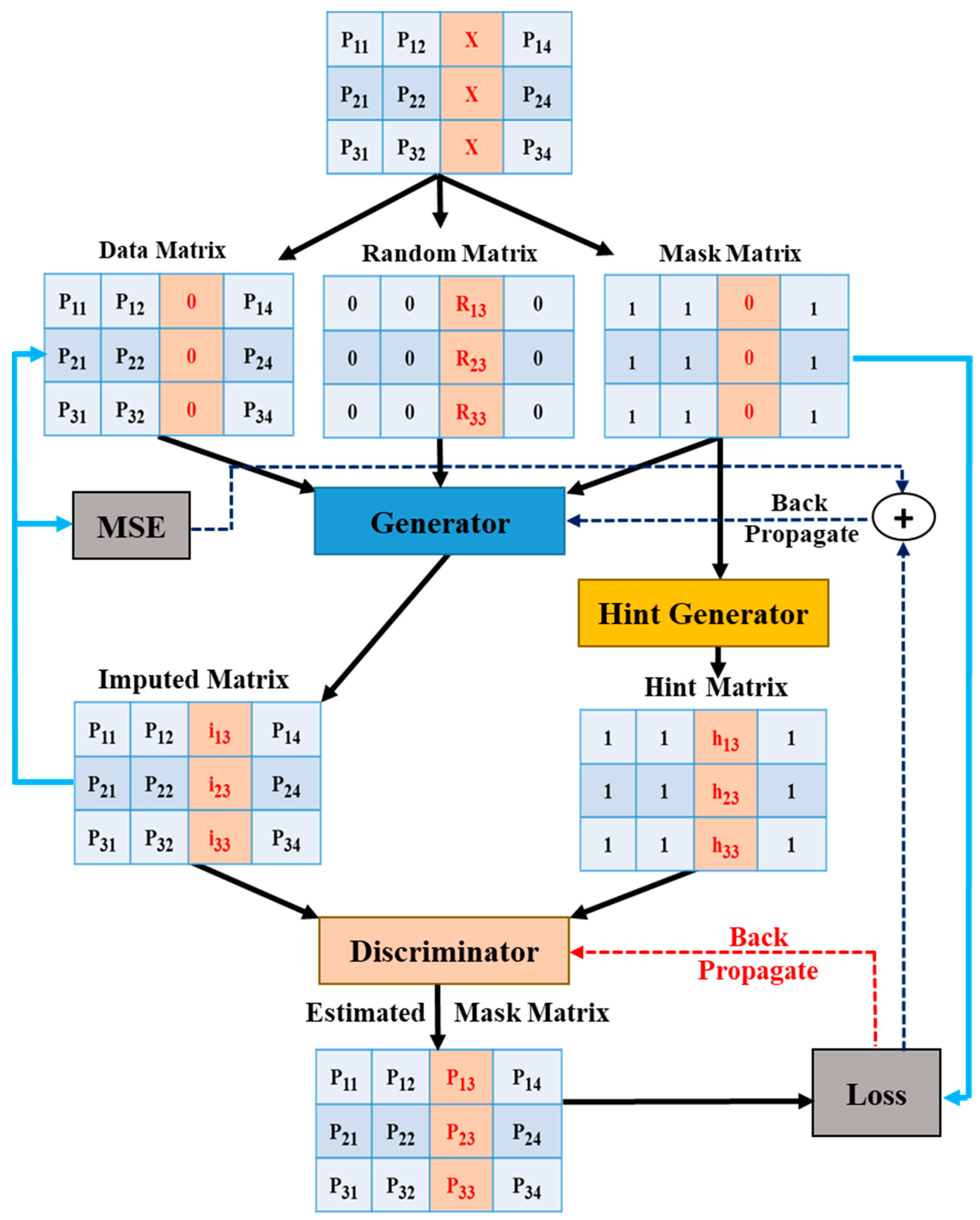
4.1. GAIN
Missing Data Imputation Using GAIN
| Algorithms 1 GAIN for data imputation. |
| 1. While training loss has not converged do 2. Discriminator (D) 3. Get samples from the dataset 4. Get independent and identically distributed samples of Z 5. Get independent and identically distributed samples of B 6. For j = 1… do 7. 8. 9. 10. End for 11. Update D using adaptive moment estimation optimization (Adam) using the loss obtained from the loss function of D 12. 13. Generator (G) 14. Draw samples from the dataset 15. Draw independent and identically distributed samples of Z 16. Draw independent and identically distributed samples of B 17. For j = 1… do 18. 19. End for 20. Update G using Adam (for fixed D) based on the loss obtained from the loss function of G 21. 22. End while |
4.2. MICE
4.3. KNN
5. Performance Discussions
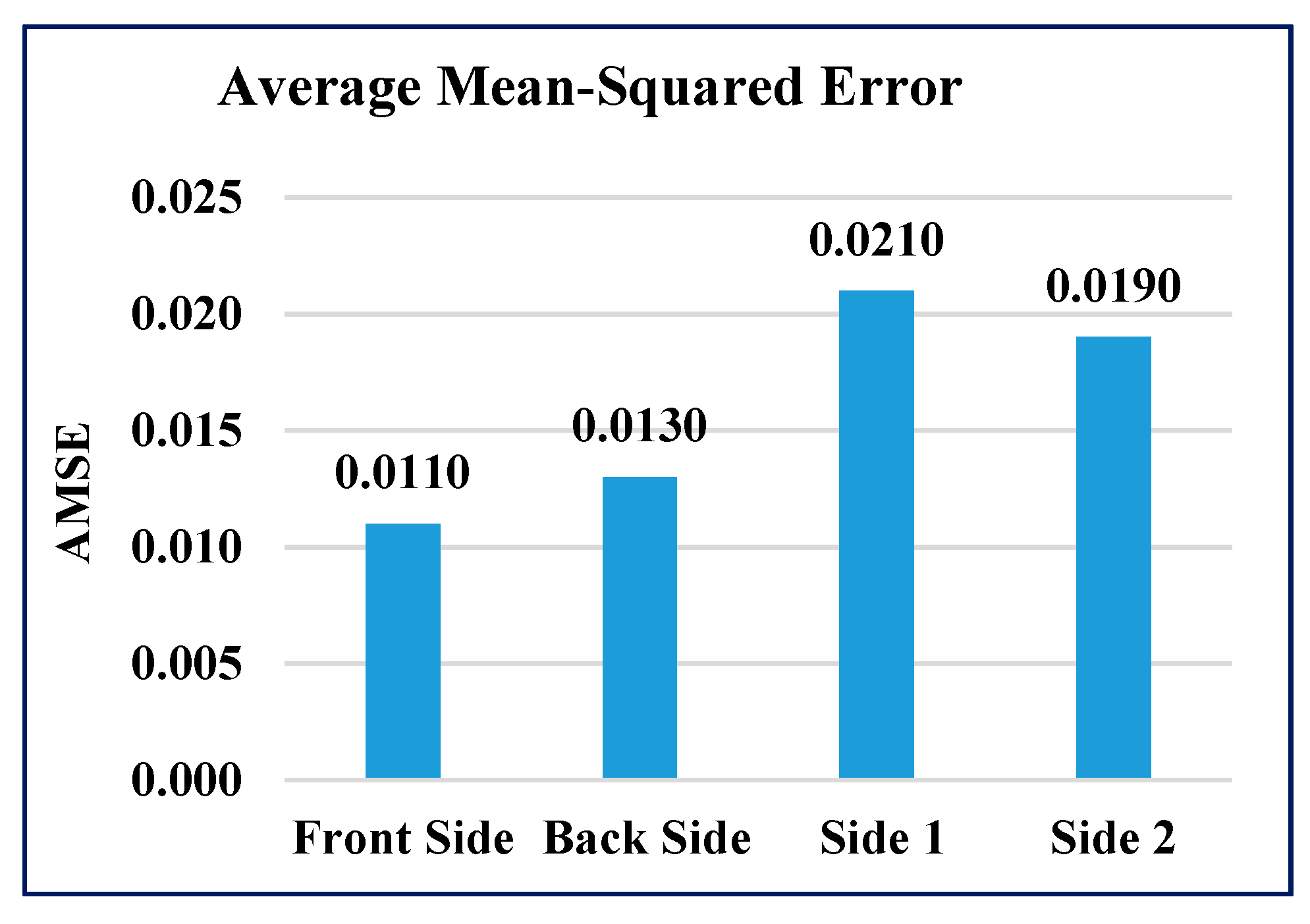
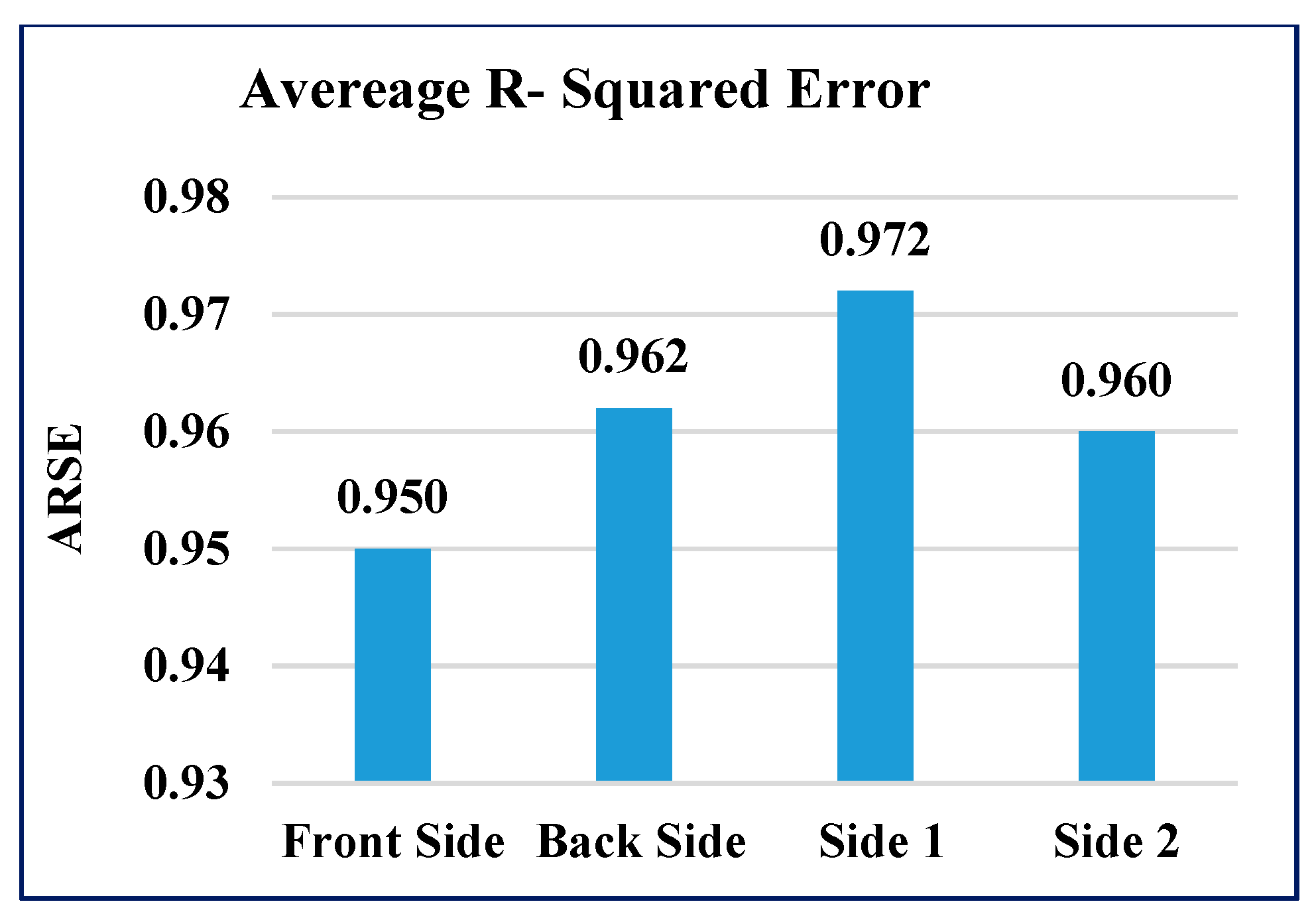
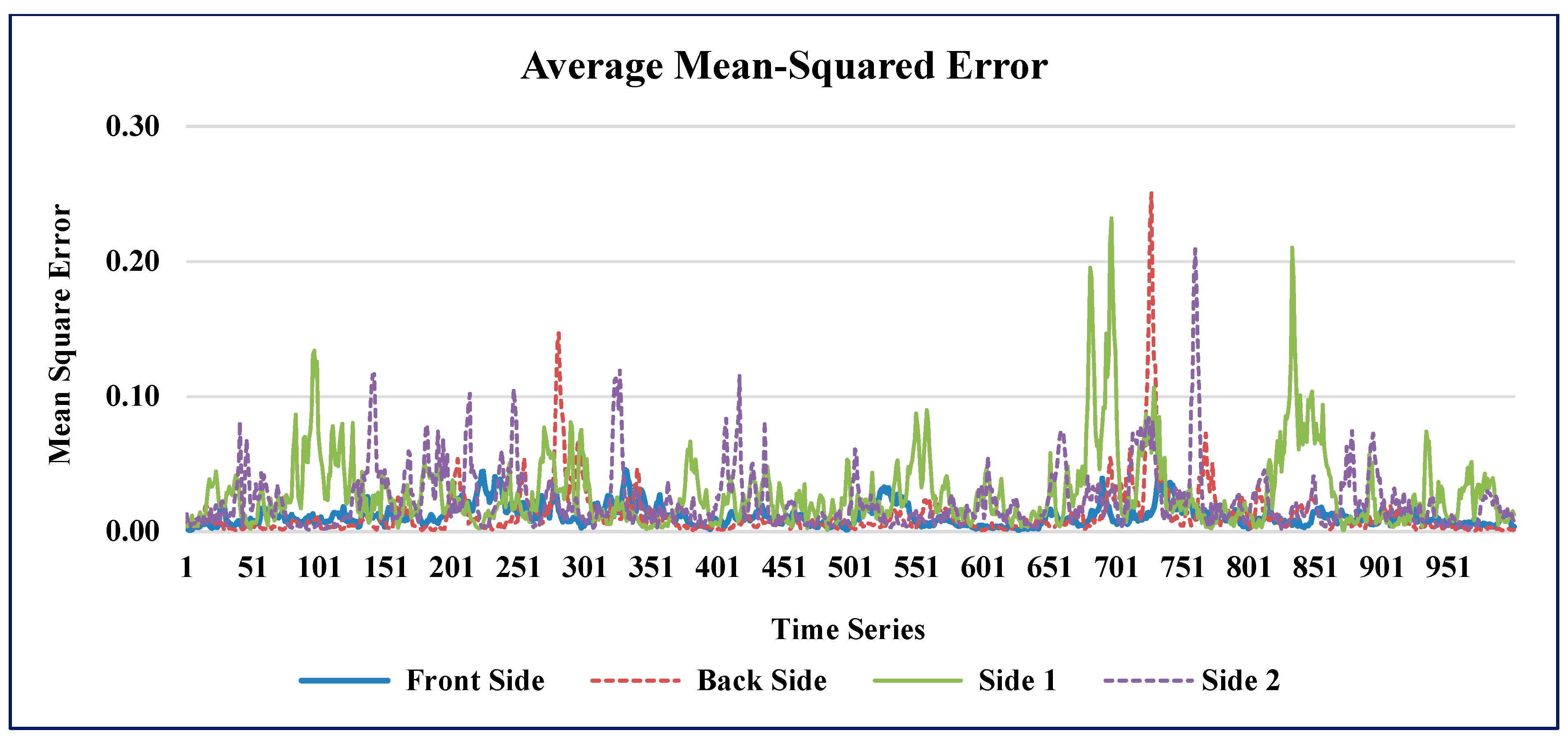
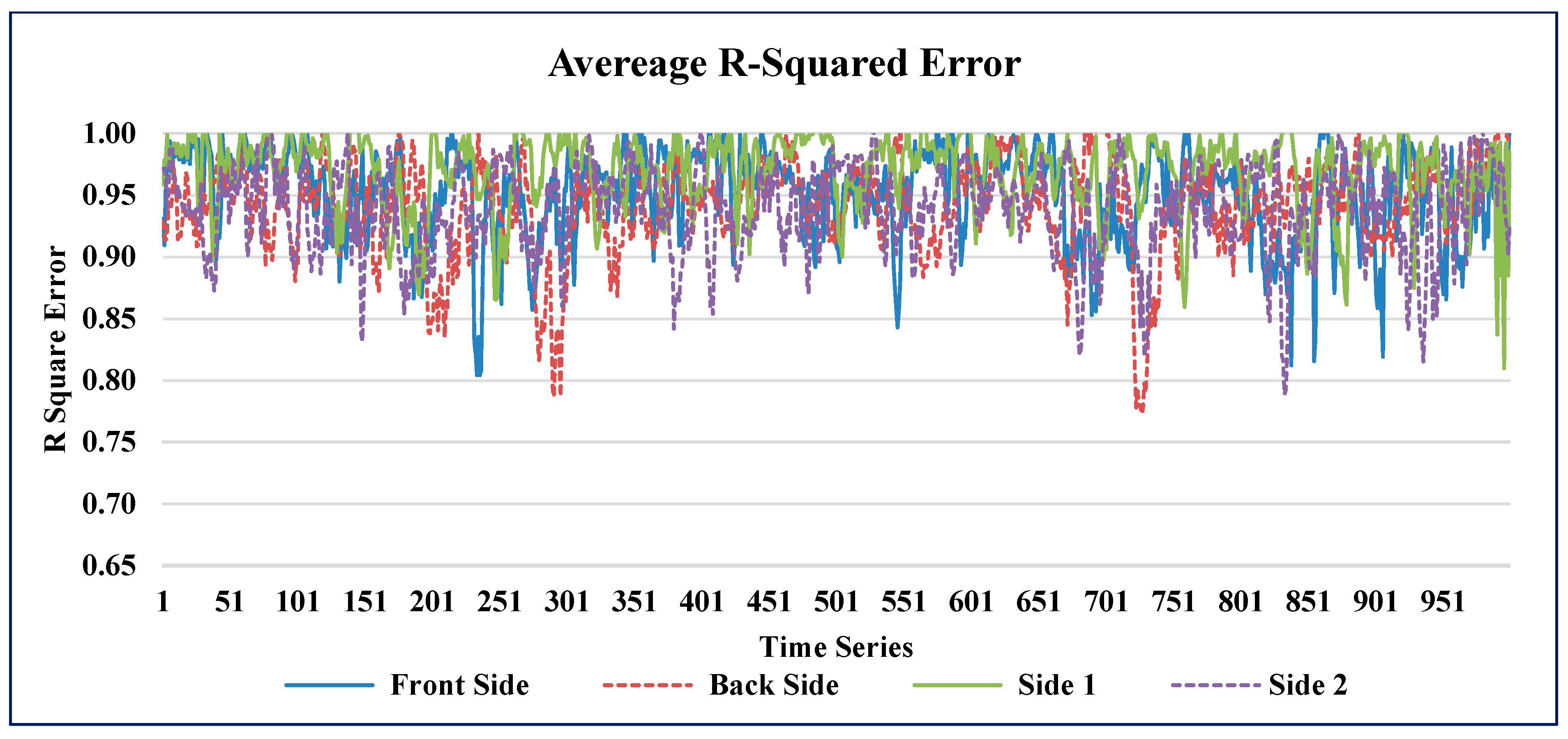
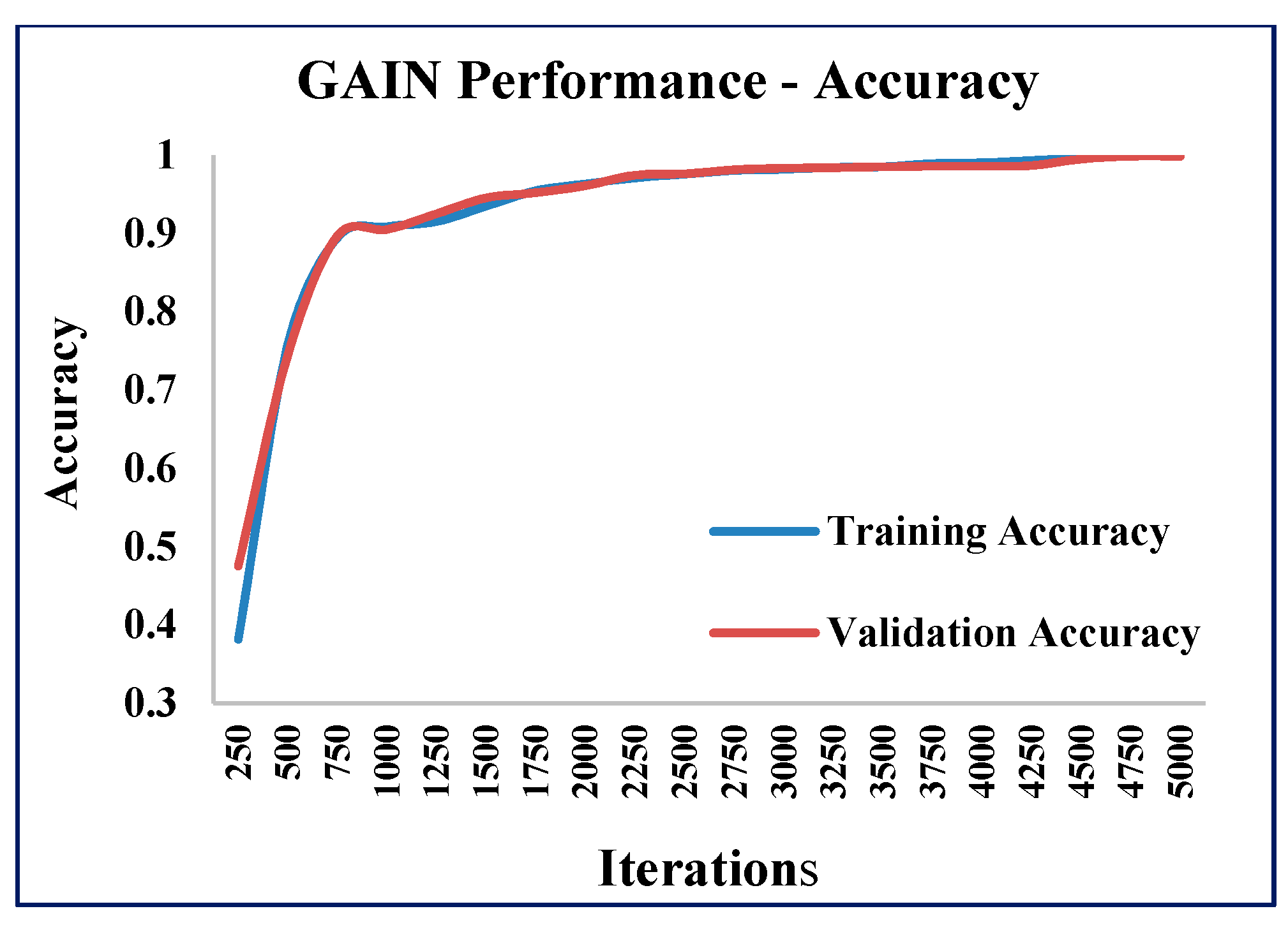
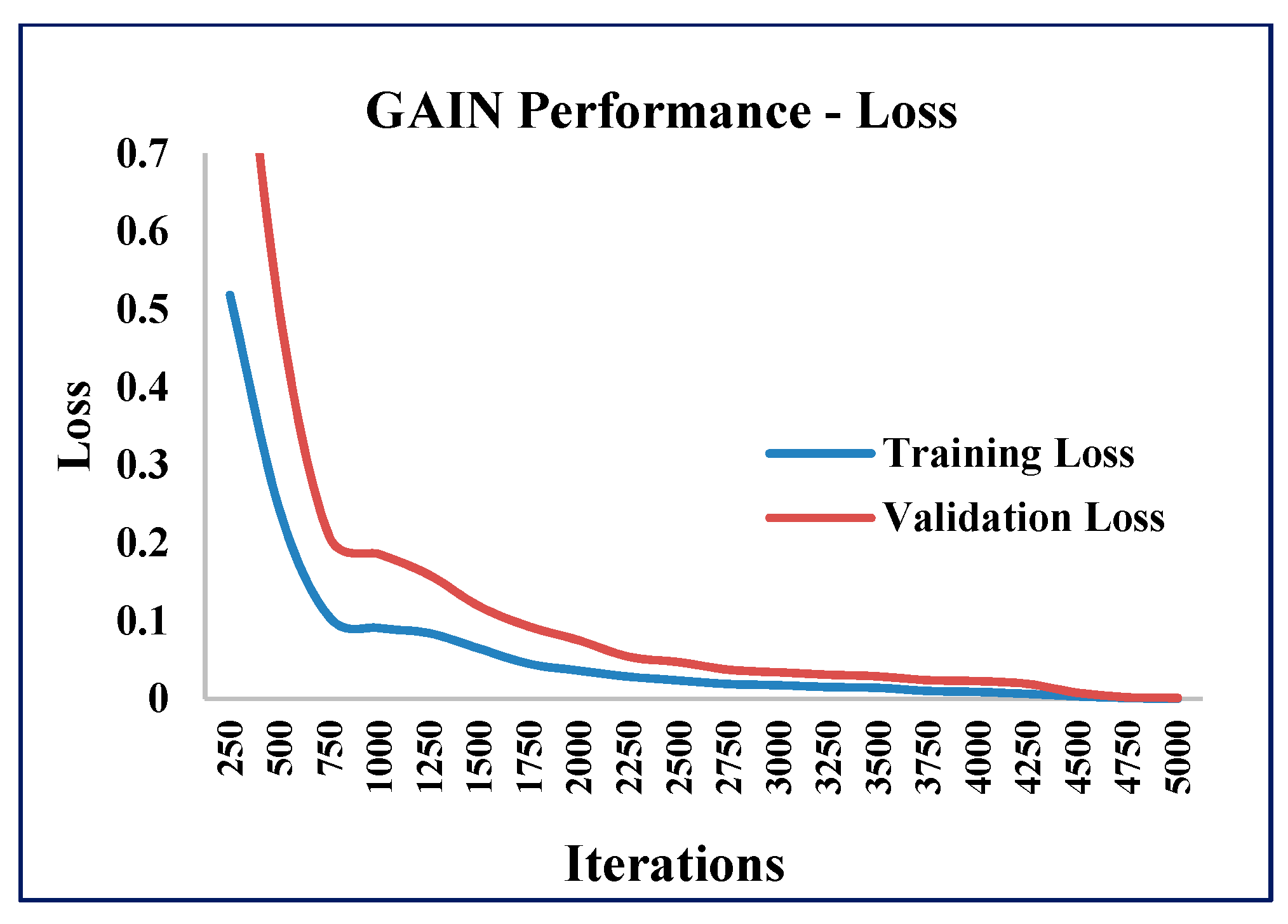
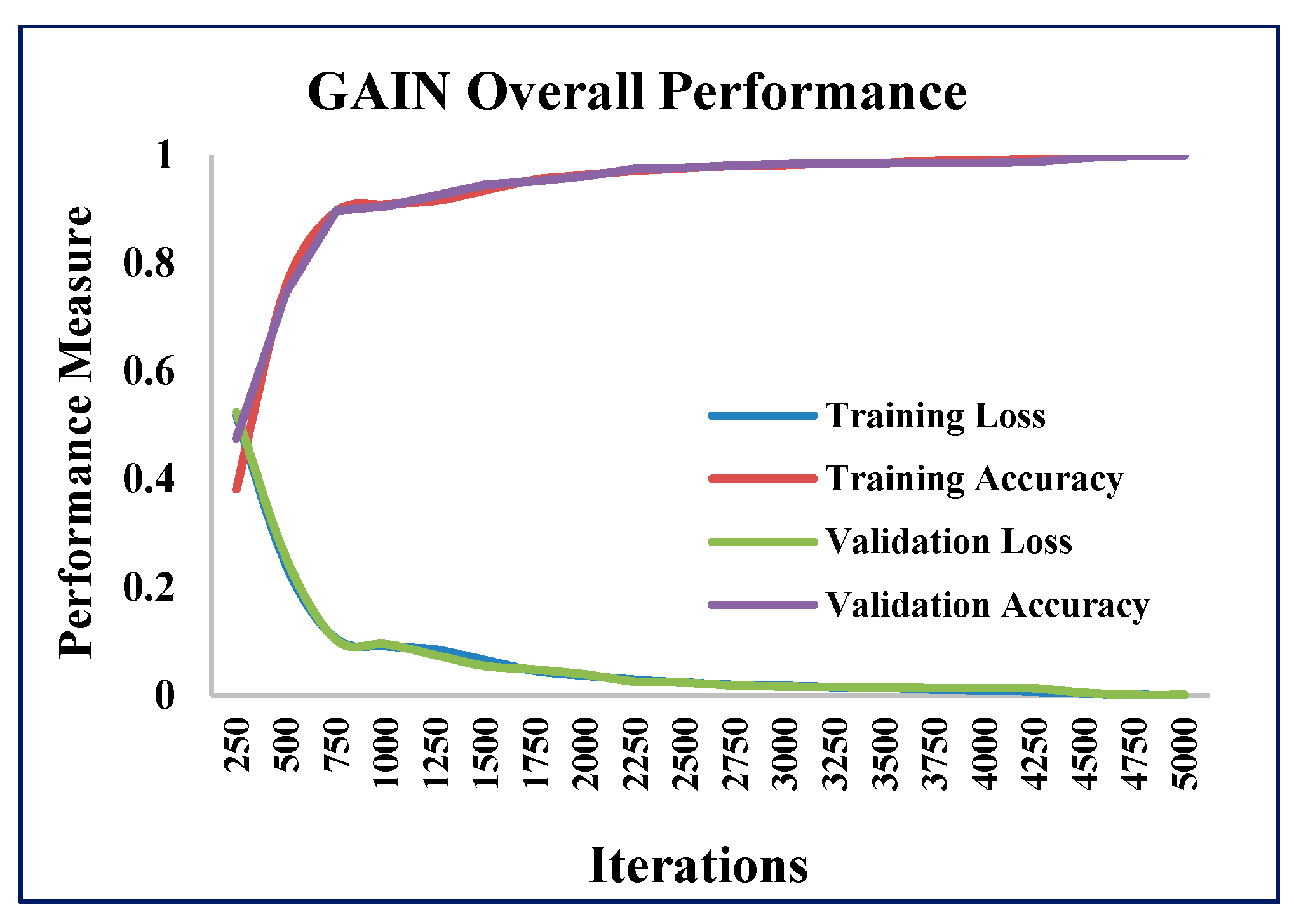
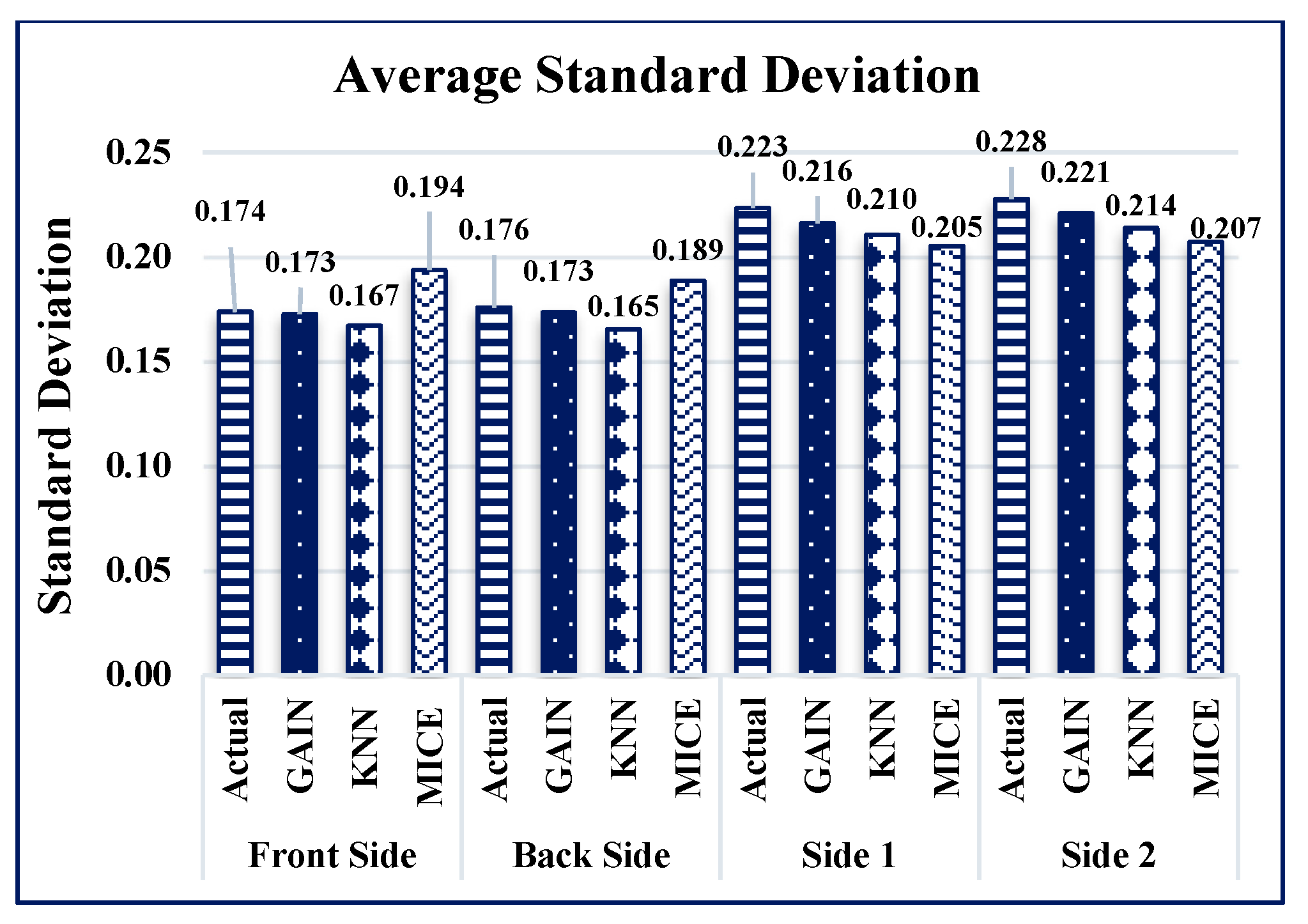
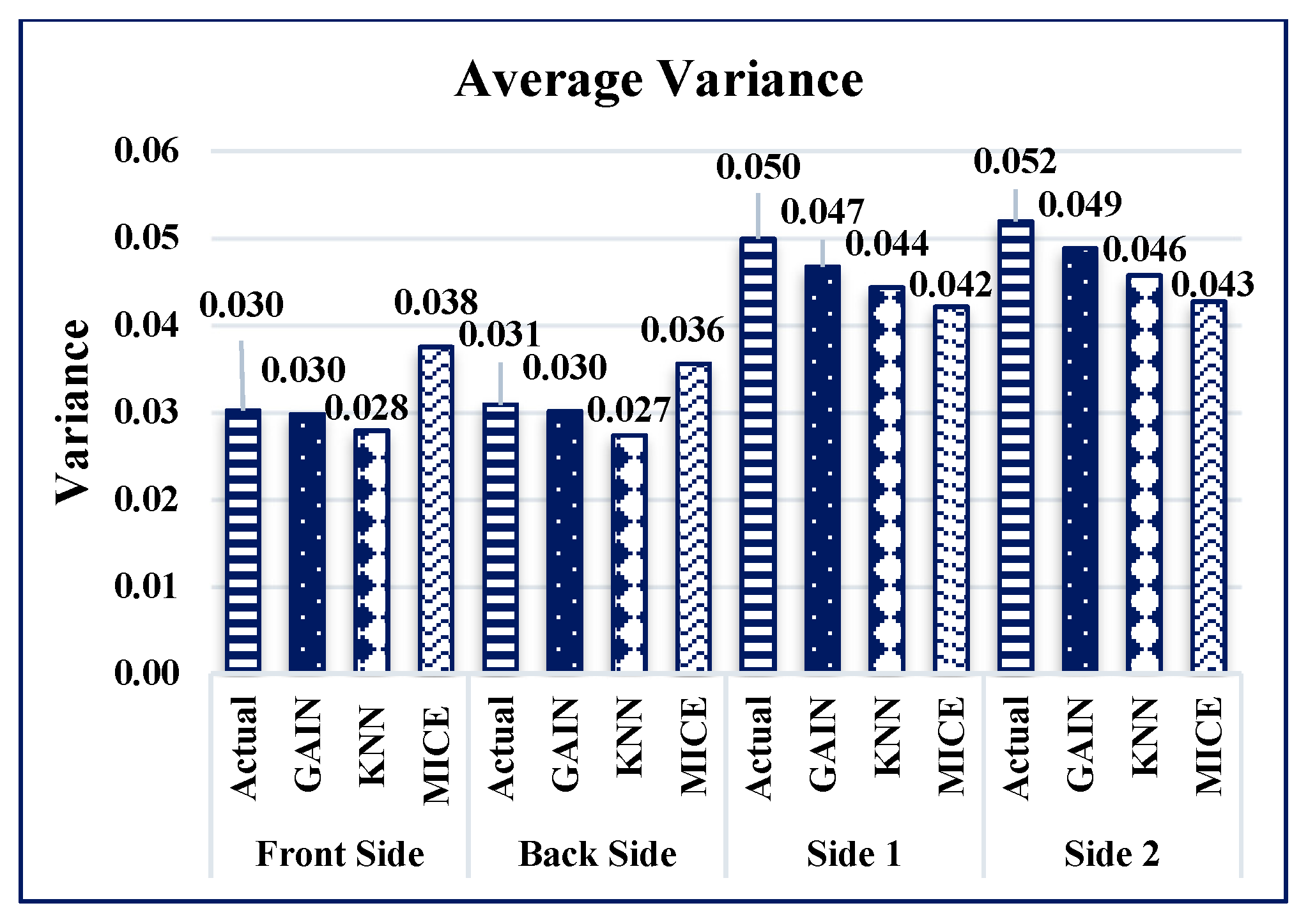
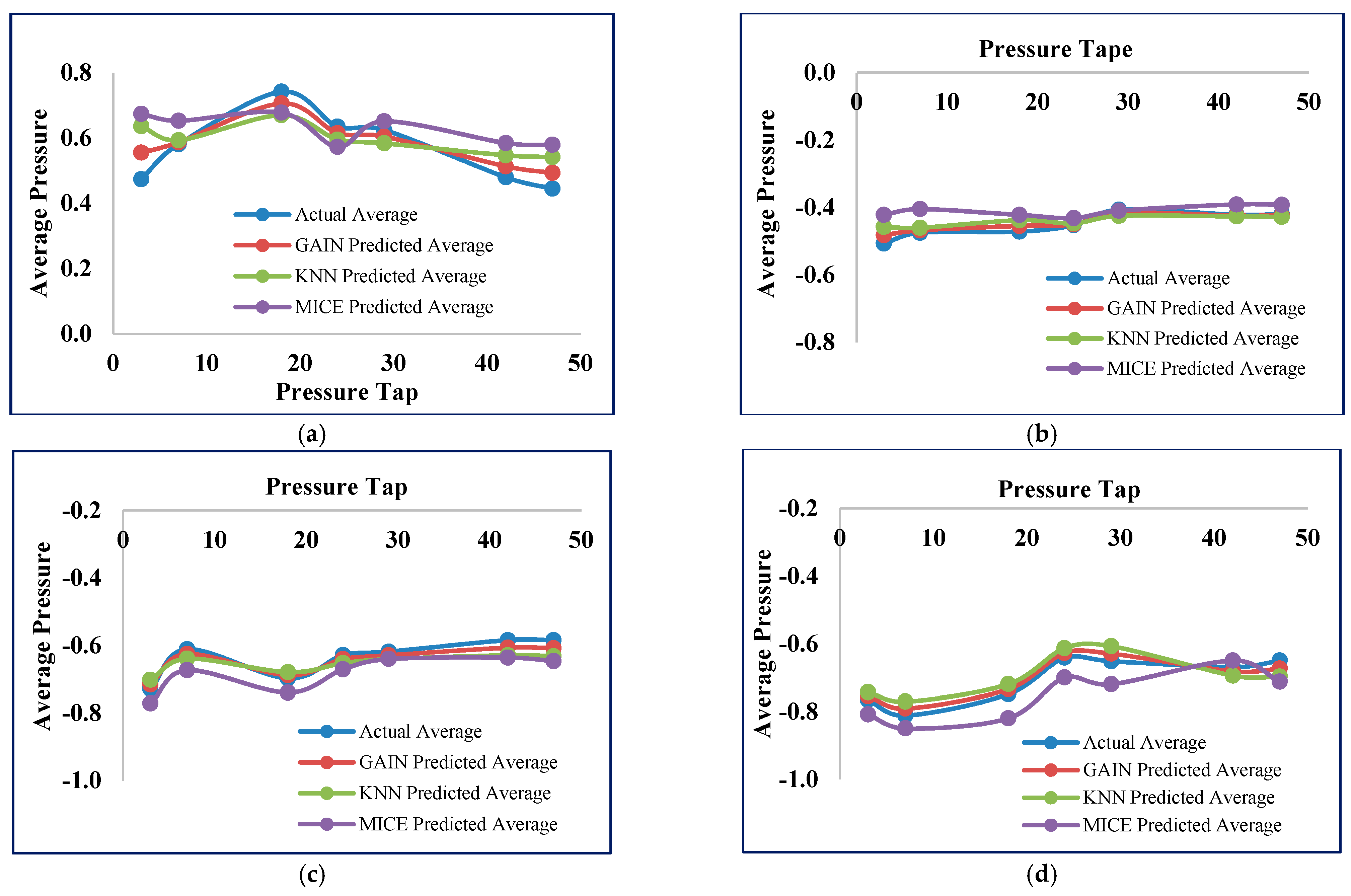
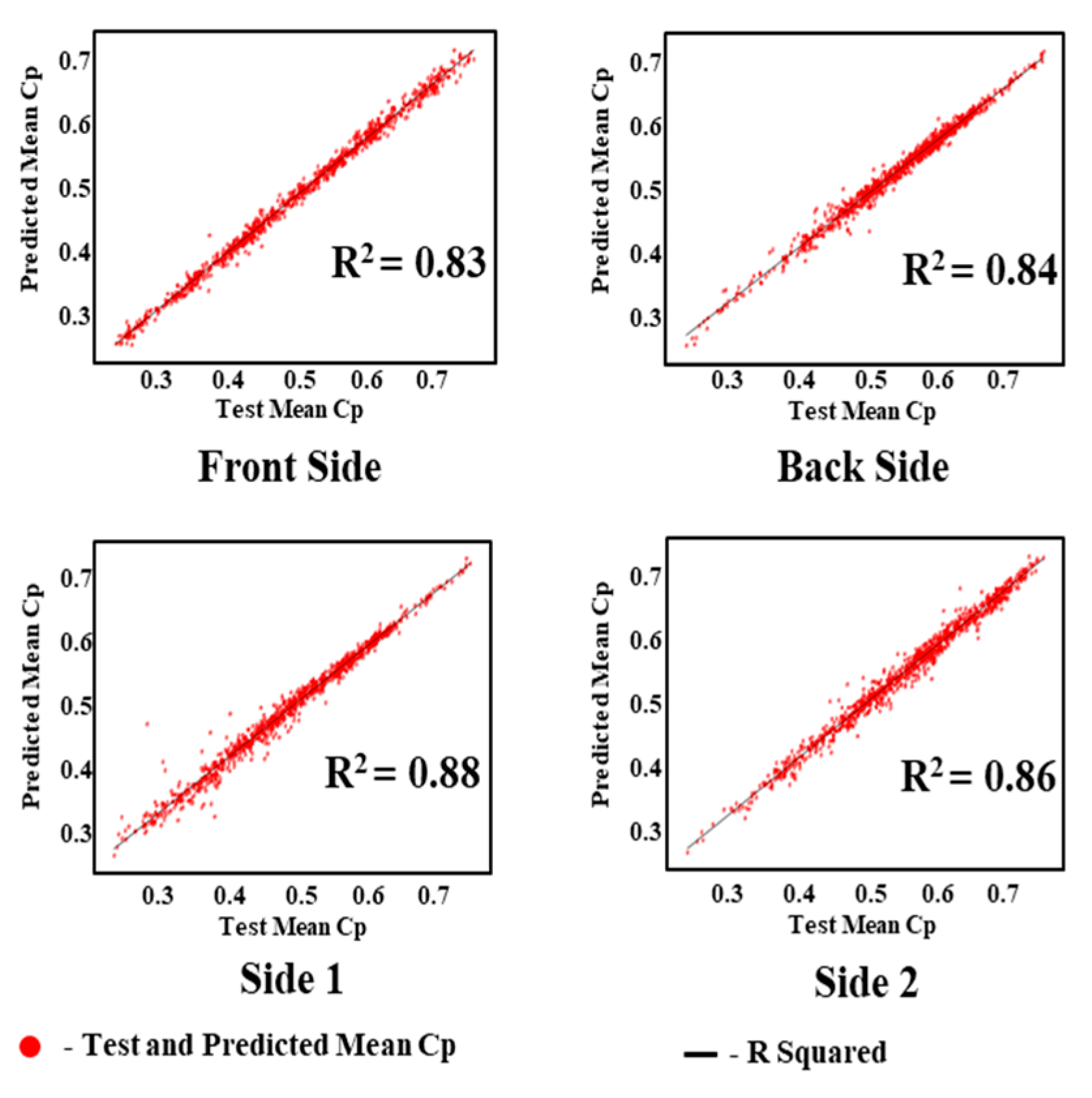
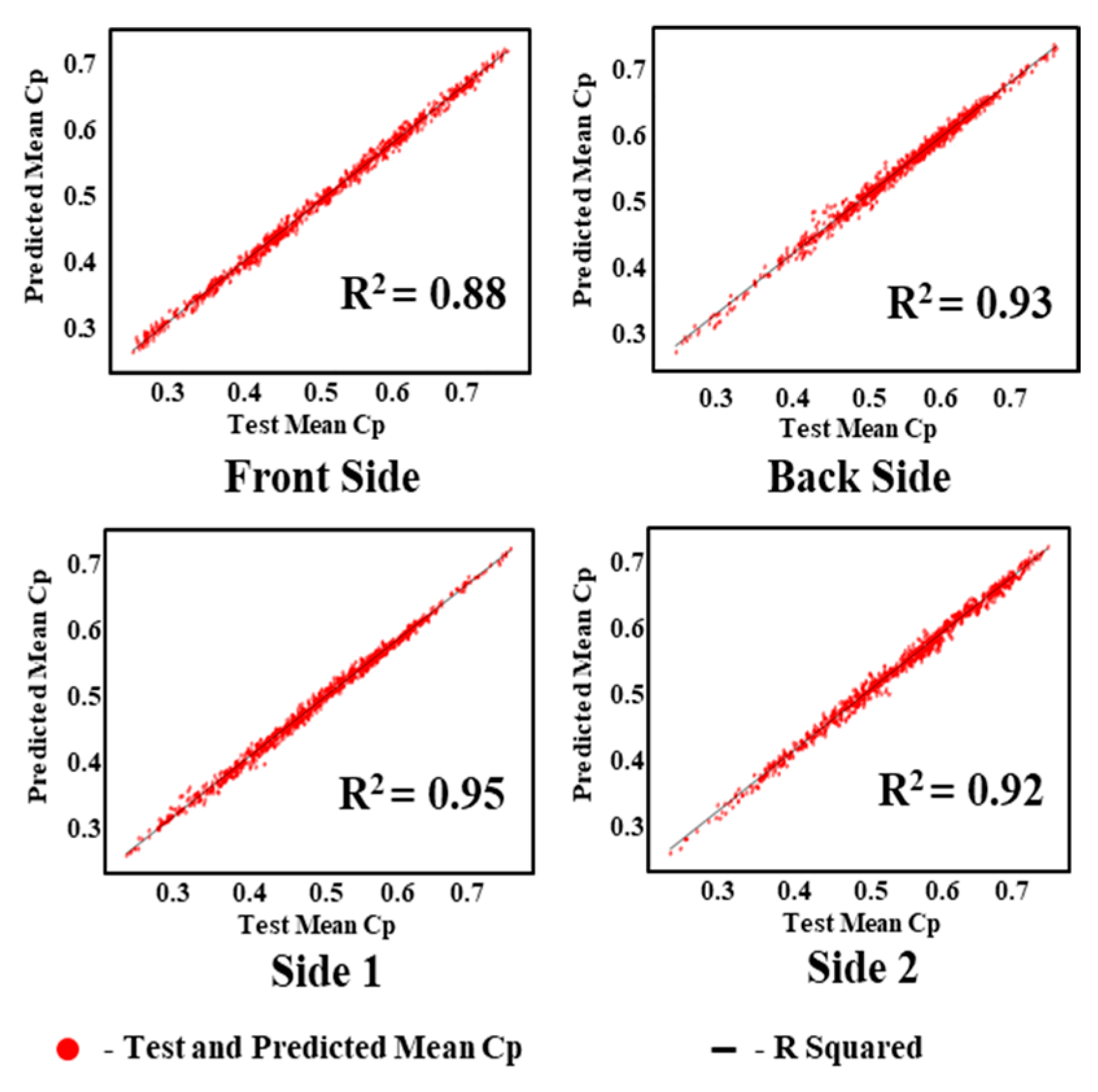
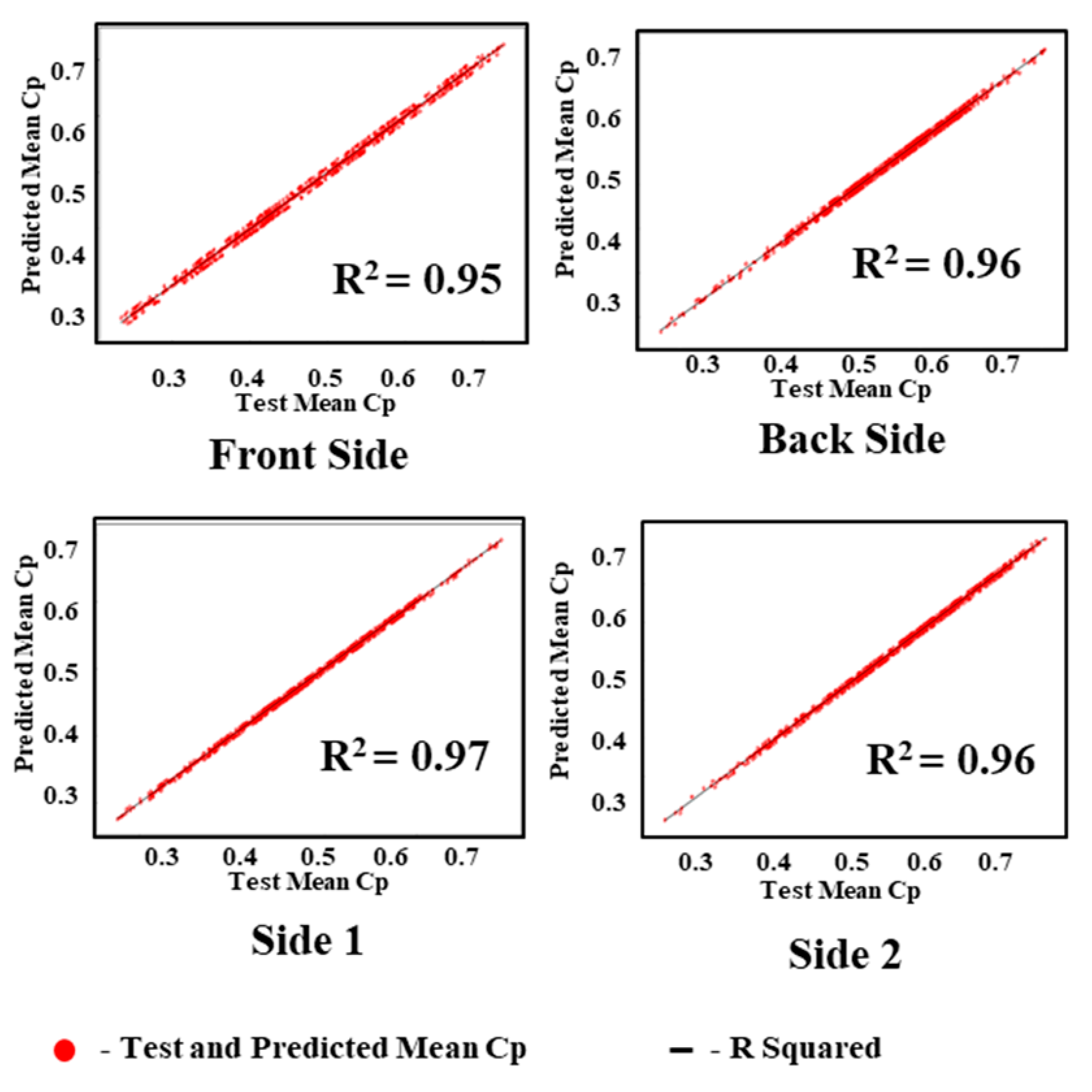
5.1. Experimental Results of GAIN
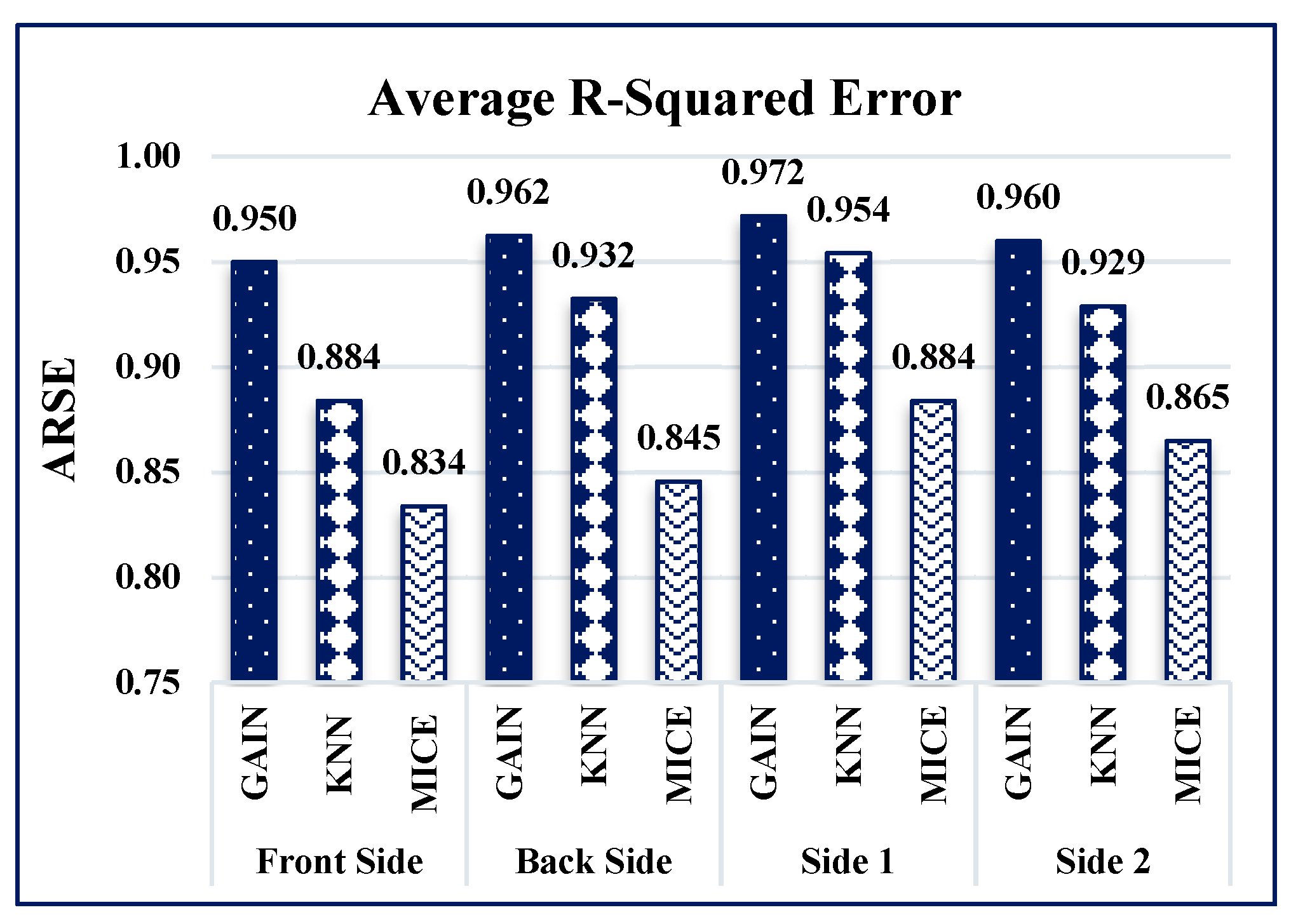
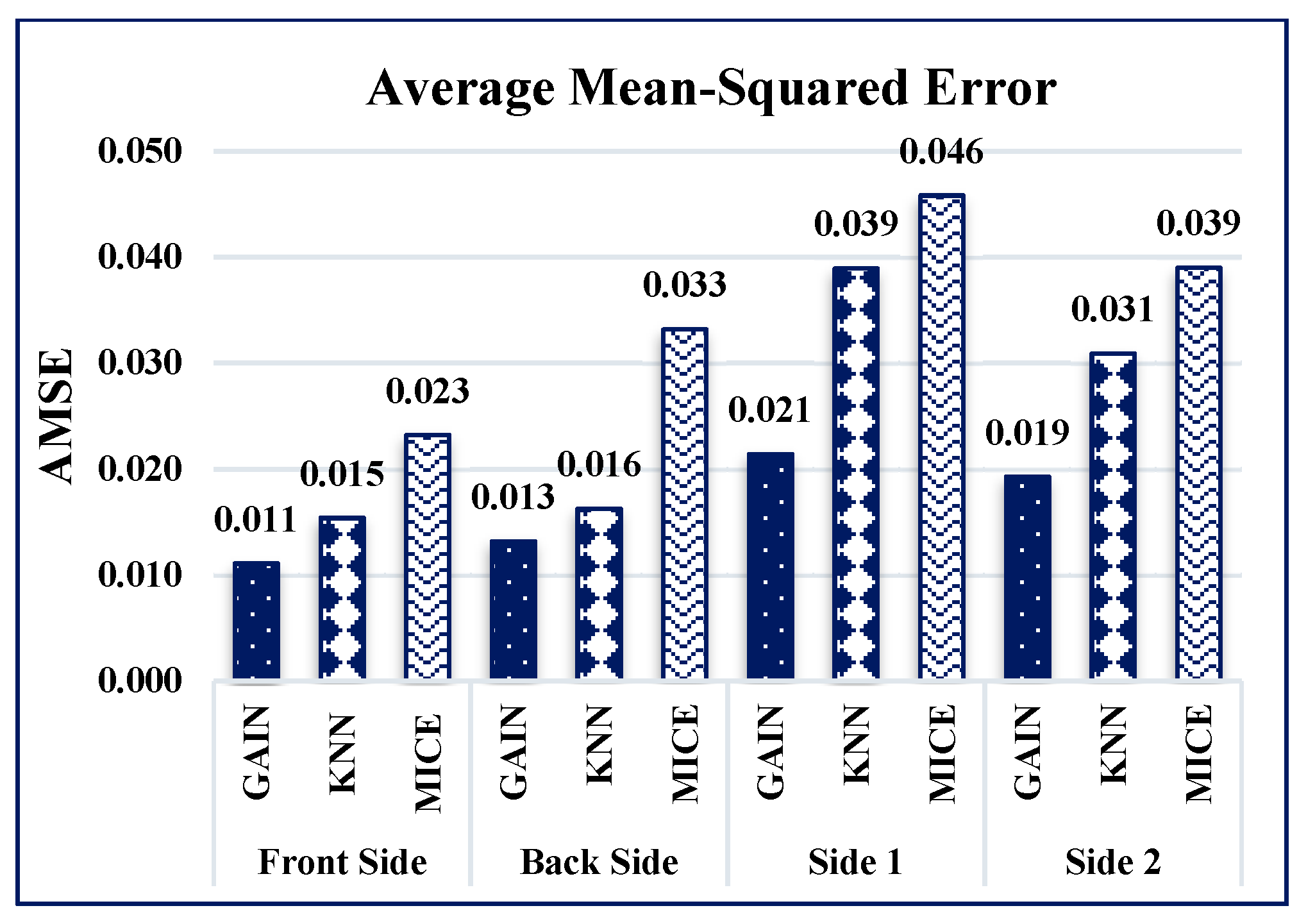
5.2. Experimental Comparisons
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dongmei, H.; Shiqing, H.; Xuhui, H.; Xue, Z. Prediction of wind loads on high-rise building using a BP neural network combined with POD. J. Wind. Eng. Ind. Aerodyn. 2017, 170, 1–17. [Google Scholar] [CrossRef]
- Kwok, K.C.S.; Hitchcock, P.A.; Burton, M.D. Perception of vibration and occupant comfort in wind-excited tall buildings. J. Wind. Eng. Ind. Aerodyn. 2009, 97, 368–380. [Google Scholar] [CrossRef]
- Tse, K.; Zhang, X.; Weerasuriya, A.; Li, S.; Kwok, K.; Mak, C.M.; Niu, J. Adopting ‘lift-up’ building design to improve the surrounding pedestrian-level wind environment. Build. Environ. 2017, 117, 154–165. [Google Scholar] [CrossRef]
- Zhang, X.; Tse, K.; Weerasuriya, A.; Li, S.; Kwok, K.; Mak, C.M.; Niu, J.; Lin, Z. Evaluation of pedestrian wind comfort near ‘lift-up’ buildings with different aspect ratios and central core modifications. Build. Environ. 2017, 124, 245–257. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.; Yoshida, A.; Chen, Z.; Van Phuc, P.; Park, H.S. Investigation of flow visualization around linked tall buildings with circular sections. Build. Environ. 2019, 153, 60–76. [Google Scholar] [CrossRef]
- Weerasuriya, A.; Tse, K.; Zhang, X.; Li, S. A wind tunnel study of effects of twisted wind flows on the pedestrian-level wind field in an urban environment. Build. Environ. 2018, 128, 225–235. [Google Scholar] [CrossRef]
- Aly, A.M. Pressure integration technique for predicting wind-induced response in high-rise buildings. Alex. Eng. J. 2013, 52, 717–731. [Google Scholar] [CrossRef]
- Weerasuriya, A.; Tse, K.; Zhang, X.; Kwok, K. Integrating twisted wind profiles to Air Ventilation Assessment (AVA): The current status. Build. Environ. 2018, 135, 297–307. [Google Scholar] [CrossRef]
- Beranek, W.J. Wind environment around single buildings of rectangular shape. Heron 1984, 29, 3–31. [Google Scholar]
- Weerasuriya, A.; Hu, Z.; Zhang, X.; Tse, K.; Li, S.; Chan, P. New inflow boundary conditions for modeling twisted wind profiles in CFD simulation for evaluating the pedestrian-level wind field near an isolated building. Build. Environ. 2018, 132, 303–318. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y. Ventilation strategy and air change rates in idealized high-rise compact urban areas. Build. Environ. 2010, 45, 2754–2767. [Google Scholar] [CrossRef]
- Ng, E. Policies and technical guidelines for urban planning of high-density citiesair ventilation assessment (AVA) of Hong Kong. Build. Environ. 2009, 44, 1478–1488. [Google Scholar] [CrossRef] [PubMed]
- Yim, S.; Fung, J.; Lau, A.; Kot, S. Air ventilation impacts of the “wall effect” resulting from the alignment of high-rise buildings. Atmos. Environ. 2009, 43, 4982–4994. [Google Scholar] [CrossRef]
- Tsang, C.; Kwok, K.; Hitchcock, P. Wind tunnel study of pedestrian level wind environment around tall buildings: Effects of building dimensions, separation and podium. Build. Environ. 2012, 49, 167–181. [Google Scholar] [CrossRef]
- Niu, Y.; Fritzen, C.-P.; Jung, H.; Buethe, I.; Ni, Y.-Q.; Wang, Y.-W. Online Simultaneous Reconstruction of Wind Load and Structural Responses-Theory and Application to Canton Tower. Comput. Civ. Infrastruct. Eng. 2015, 30, 666–681. [Google Scholar] [CrossRef]
- Graf, K.; Müller, O. Photogrammetric Investigation of the Flying Shape of Spinnakers in a Twisted Flow Wind Tunnel. In Proceedings of the 19th Chesapeake Sailing Yacht Symposium, Annapolis, MD, USA, 20–21 March 2009. [Google Scholar]
- Kato, Y.; Kanda, M. Development of a modified hybrid aerodynamic vibration technique for simulating aerodynamic vibration of structures in a wind tunnel. J. Wind. Eng. Ind. Aerodyn. 2014, 135, 10–21. [Google Scholar] [CrossRef]
- Lam, K.M.; Li, A. Mode shape correction for wind-induced dynamic responses of tall buildings using time-domain computation and wind tunnel tests. J. Sound Vib. 2009, 322, 740–755. [Google Scholar] [CrossRef]
- Tse, K.; Hitchcock, P.; Kwok, K. Mode shape linearization for HFBB analysis of wind-excited complex tall buildings. Eng. Struct. 2009, 31, 675–685. [Google Scholar] [CrossRef]
- Ho, T.C.E.; Surry, D. Factory Mutual-High Resolution Pressure Measurements on Roof Panels; Boundary Layer Wind Tunnel Laboratory Report; The University of Western Ontario: London, ON, Canada, 2000. [Google Scholar]
- Park, H.S.; Sohn, H.G.; Kim, I.S.; Park, J.H. Application of GPS to monitoring of wind-induced responses of high-rise buildings. Struct. Des. Tall Spéc. Build. 2008, 17, 117–132. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Park, H.S.; Adeli, H. A novel methodology for modal parameters identification of large smart structures using MUSIC, empirical wavelet transform, and Hilbert transform. Eng. Struct. 2017, 147, 148–159. [Google Scholar] [CrossRef]
- Xia, Y.; Ni, Y.-Q.; Zhang, P.; Liao, W.-Y.; Ko, J.-M. Stress Development of a Supertall Structure during Construction: Field Monitoring and Numerical Analysis. Comput. Civ. Infrastruct. Eng. 2011, 26, 542–559. [Google Scholar] [CrossRef]
- Amezquita-Sanchez, J.P.; Adeli, H. Signal Processing Techniques for Vibration-Based Health Monitoring of Smart Structures. Arch. Comput. Methods Eng. 2016, 23, 1–15. [Google Scholar] [CrossRef]
- Gao, Y.; Mosalam, K.M. Deep Transfer Learning for Image-Based Structural Damage Recognition. Comput. Civ. Infrastruct. Eng. 2018, 33, 748–768. [Google Scholar] [CrossRef]
- Rafiei, M.H.; Adeli, H. A novel unsupervised deep learning model for global and local health condition assessment of structures. Eng. Struct. 2018, 156, 598–607. [Google Scholar] [CrossRef]
- Tsogka, C.; Daskalakis, E.; Comanducci, G.; Ubertini, F. The Stretching Method for Vibration-Based Structural Health Monitoring of Civil Structures. Comput. Civ. Infrastruct. Eng. 2017, 32, 288–303. [Google Scholar] [CrossRef]
- Ni, Y.Q.; Xia, Y.; Liao, W.Y.; Ko, J.M. Technology innovation in developing the structural health monitoring system for Guangzhou New TV Tower. Struct. Control. Health Monit. 2009, 16, 73–98. [Google Scholar] [CrossRef]
- Yuvaraj, N.; Kim, B.; Preethaa, S.; Transfer, K.R. Learning based Real-Time Crack Detection Using Unmanned Arial System. Int. J. High Rise Build. 2021, 9, 4. [Google Scholar] [CrossRef]
- Hu, G.; Kwok, K. Predicting wind pressures around circular cylinders using machine learning techniques. J. Wind. Eng. Ind. Aerodyn. 2020, 198, 104099. [Google Scholar] [CrossRef]
- Lee, K.J.; Carlin, J.B. Multiple Imputation for Missing Data: Fully Conditional Specification Versus Multivariate Normal Imputation. Am. J. Epidemiol. 2010, 171, 624–632. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, Y. Restoring method for missing data of spatial structural stress monitoring based on correlation. Mech. Syst. Signal Process. 2017, 91, 266–277. [Google Scholar] [CrossRef]
- Yang, Y.; Nagarajaiah, S. Harnessing data structure for recovery of randomly missing structural vibration responses time history: Sparse representation versus low-rank structure. Mech. Syst. Signal Process. 2016, 74, 165–182. [Google Scholar] [CrossRef]
- Yu, Y.; Han, F.; Bao, Y.; Ou, J. A Study on Data Loss Compensation of WiFi-Based Wireless Sensor Networks for Structural Health Monitoring. IEEE Sens. J. 2015, 16, 3811–3818. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.L.; Courville, A.; Bengio, Y. Generative adversarial nets. arXiv 2014, arXiv:1406.2661v1. [Google Scholar]
- Preethaa, K.R.S.; Sabari, A. Intelligent video analysis for enhanced pedestrian detection by hybrid metaheuristic approach. Soft Comput. 2020, 24, 12303–12311. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository. 2013. Available online: http://archive.ics.uci.edu/ml (accessed on 18 January 2021).
- Bre, F.; Gimenez, J.M.; Fachinotti, V.D. Prediction of wind pressure coefficients on building surfaces using artificial neural networks. Energy Build. 2018, 158, 1429–1441. [Google Scholar] [CrossRef]
- Chen, Y.; Kopp, G.; Surry, D. Prediction of pressure coefficients on roofs of low buildings using artificial neural networks. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 423–441. [Google Scholar] [CrossRef]
- Fu, J.; Liang, S.; Li, Q. Prediction of wind-induced pressures on a large gymnasium roof using artificial neural networks. Comput. Struct. 2007, 85, 179–192. [Google Scholar] [CrossRef]
- Thrun, M.C.; Ultsch, A.; Breuer, L. Explainable AI Framework for Multivariate Hydrochemical Time Series. Mach. Learn. Knowl. Extr. 2021, 3, 170–205. [Google Scholar] [CrossRef]
- Oh, B.K.; Glisic, B.; Kim, Y.; Park, H.S. Convolutional neural network-based wind-induced response estimation model for tall buildings. Comput. Civ. Infrastruct. Eng. 2019, 34, 843–858. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Lv, W.; Wang, D. Image recognition of wind turbine blade damage based on a deep learning model with transfer learning and an ensemble learning classifier. Renew. Energy 2021, 163, 386–397. [Google Scholar] [CrossRef]
- Zhang, C.; Patras, P.; Haddadi, H. Deep Learning in Mobile and Wireless Networking: A Survey. IEEE Commun. Surv. Tutor. 2019, 21, 2224–2287. [Google Scholar] [CrossRef]
- Kim, B.; Yuvaraj, N.; Preethaa, K.R.S.; Pandian, R.A. Surface crack detection using deep learning with shallow CNN architecture for enhanced computation. Neural Comput. Appl. 2021, 1–17. [Google Scholar] [CrossRef]
- Dong, M.; Wu, H.; Hu, H.; Azzam, R.; Zhang, L.; Zheng, Z.; Gong, X. Deformation Prediction of Unstable Slopes Based on Real-Time Monitoring and DeepAR Model. Sensors 2020, 21, 14. [Google Scholar] [CrossRef] [PubMed]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Kim, B.; Yuvaraj, N.; Preethaa, K.R.S.; Santhosh, R.; Sabari, A. Enhanced pedestrian detection using optimized deep convolution neural network for smart building surveillance. Soft Comput. 2020, 24, 17081–17092. [Google Scholar] [CrossRef]
- Lee, S.-J.; Yoon, H.-K. Discontinuity Predictions of Porosity and Hydraulic Conductivity Based on Electrical Resistivity in Slopes through Deep Learning Algorithms. Sensors 2021, 21, 1412. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Ahmed, R.; El Sayed, M.; Gadsden, S.A.; Tjong, J.; Habibi, S. Automotive Internal-Combustion-Engine Fault Detection and Classification Using Artificial Neural Network Techniques. IEEE Trans. Veh. Technol. 2014, 64, 21–33. [Google Scholar] [CrossRef]
- Royston, P.; Carlin, J.B.; White, I.R. Multiple Imputation of Missing Values: New Features for Mim. Stata J. Promot. Commun. Stat. Stata 2009, 9, 252–264. [Google Scholar] [CrossRef]
- Yuvaraj, N.; SriPreethaa, K.R. Diabetes prediction in healthcare systems using machine learning algorithms on Hadoop cluster. Clust. Comput. 2017, 22, 1–9. [Google Scholar] [CrossRef]
- Thakker, D.; Mishra, B.K.; Abdullatif, A.; Mazumdar, S.; Simpson, S. Explainable Artificial Intelligence for Developing Smart Cities Solutions. Smart Cities 2020, 3, 1353–1382. [Google Scholar] [CrossRef]
- Jin, X.; Cheng, P.; Chen, W.-L.; Wen-Li, C. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Farahmandpour, Z.; Seyedmahmoudian, M.; Stojcevski, A.; Moser, I.; Schneider, J.-G. Cognitive Service Virtualisation: A New Machine Learning-Based Virtualisation to Generate Numeric Values. Sensors 2020, 20, 5664. [Google Scholar] [CrossRef]
- Park, H.; Son, J.-H. Machine Learning Techniques for THz Imaging and Time-Domain Spectroscopy. Sensors 2021, 21, 1186. [Google Scholar] [CrossRef] [PubMed]
- Dou, J.; Yunus, A.P.; Bui, D.T.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Han, Z.; Pham, B.T. Improved landslide assessment using support vector machine with bagging, boosting, and stacking ensemble machine learning framework in a mountainous watershed, Japan. Landslides 2020, 17, 641–658. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, C.; Khan, K.U.J. Application and comparison of different ensemble learning machines combining with a novel sampling strategy for shallow landslide susceptibility mapping. Stoch. Environ. Res. Risk Assess. 2020, 1–14. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Do, D.T.; Chiu, F.-Y.; Yapp, E.K.Y.; Yeh, H.-Y.; Chen, C.-Y. XGBoost Improves Classification of MGMT Promoter Methylation Status in IDH1 Wildtype Glioblastoma. J. Pers. Med. 2020, 10, 128. [Google Scholar] [CrossRef] [PubMed]
- White, I.R.; Royston, P.; Wood, A.M. Multiple imputation using chained equations: Issues and guidance for practice. Stat. Med. 2010, 30, 377–399. [Google Scholar] [CrossRef]
- Enişer, H.F.; Sen, A. Virtualization of stateful services via machine learning. Softw. Qual. J. 2019, 28, 283–306. [Google Scholar] [CrossRef]
- Loyola-Gonzalez, O.; Gutierrez-Rodriguez, A.E.; Medina-Perez, M.A.; Monroy, R.; Martinez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; Garcia-Borroto, M. An Explainable Artificial Intelligence Model for Clustering Numerical Databases. IEEE Access 2020, 8, 52370–52384. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.P.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Wen, Y.; Song, M.; Wang, J. A combined AR-kNN model for short-term wind speed forecasting. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 6342–6346. [Google Scholar]
- Dasgupta, S.; Frost, N.; Moshkovitz, M.; Rashtchian, C. Explainable k-Means and k-Medians Clustering. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020. [Google Scholar]
- Thrun, M.C.; Ultsch, A. Using Projection-Based Clustering to Find Distance- and Density-Based Clusters in High-Dimensional Data. J. Classif. 2020, 1–33. [Google Scholar] [CrossRef]
- Hu, G.; Liu, L.; Tao, D.; Song, J.; Tse, K.; Kwok, K. Deep learning-based investigation of wind pressures on tall building under interference effects. J. Wind. Eng. Ind. Aerodyn. 2020, 201, 104138. [Google Scholar] [CrossRef]
- Stivaktakis, R.; Tsagkatakis, G.; Tsakalides, P. Semantic Predictive Coding with Arbitrated Generative Adversarial Networks. Mach. Learn. Knowl. Extr. 2020, 2, 307–326. [Google Scholar] [CrossRef]
- Allen, A.; Li, W. Generative Adversarial Denoising Autoencoder for Face Completion. 2016. Available online: https://www.cc.gatech.edu/˜hays/7476/projects/Avery_Wenchen/ (accessed on 18 January 2021).
- Chen, Z.; Fu, X.; Xu, Y.; Li, C.Y.; Kim, B.; Tse, K. A perspective on the aerodynamics and aeroelasticity of tapering: Partial reattachment. J. Wind. Eng. Ind. Aerodyn. 2021, 212, 104590. [Google Scholar] [CrossRef]
- Chen, Z.; Tse, K.; Kwok, K.; Kareem, A.; Kim, B. Measurement of unsteady aerodynamic force on a galloping prism in a turbulent flow: A hybrid aeroelastic-pressure balance. J. Fluids Struct. 2021, 102, 103232. [Google Scholar] [CrossRef]
- Tse, K.T.; Hu, G.; Song, J.; Park, H.S.; Kim, B. Effects of corner modifications on wind loads and local pressures on walls of tall buildings. Build. Simul. 2020, 1–18. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.; Chen, Z.; Park, H.S. Multi-objective optimization of a structural link for a linked tall building system. J. Build. Eng. 2020, 31, 101382. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, Y.; Tse, K.; Hu, L.; Kwok, K.; Kim, B. Non-wind-induced nonlinear damping and stiffness on slender prisms: A forced vibration-pressure balance. Eng. Struct. 2020, 207, 110107. [Google Scholar] [CrossRef]
- Chen, Z.; Tse, K.; Kwok, K.; Kim, B.; Kareem, A. Modelling unsteady self-excited wind force on slender prisms in a turbulent flow. Eng. Struct. 2020, 202, 109855. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.; Yoshida, A.; Tamura, Y.; Chen, Z.; Van Phuc, P.; Park, H.S. Statistical analysis of wind-induced pressure fields and PIV measurements on two buildings. J. Wind. Eng. Ind. Aerodyn. 2019, 188, 161–174. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K. POD analysis of aerodynamic correlations and wind-induced responses of two tall linked buildings. Eng. Struct. 2018, 176, 369–384. [Google Scholar] [CrossRef]
- Kim, B.; Tse, K.; Tamura, Y. POD analysis for aerodynamic characteristics of tall linked buildings. J. Wind. Eng. Ind. Aerodyn. 2018, 181, 126–140. [Google Scholar] [CrossRef]
| Technique | Learning Scenarios | Functionality | Pros | Cons |
|---|---|---|---|---|
| ANN/MLP | Supervised, unsupervised, reinforcement | Modeling data with simple correlations | Naïve structure, easy to build | Slow convergence rate, high complexity, and not suitable for heavy applications |
| BPNN | Supervised, unsupervised | Modeling the learning derivatives | Fast and simple, efficient for a clean dataset | Sensitive to noisy data, difficult to fix the learning rate |
| CNN | Supervised, unsupervised, reinforcement | Spatial data modeling | Weight sharing, customizable layer stack arrangement | High computational cost, difficult to optimize the hyperparameters |
| RCNN | Supervised, unsupervised, reinforcement | Sequential data modeling | Good in capturing the temporal dependencies | Heavily complex model, stuck with vanishing gradient, exploding problems occurs on complex data |
| ARN | Supervised, unsupervised | Modeling time series and interpretable model | Operates on variety of data and various conditions | Generating variable length output is difficult |
| Autoencoder | Unsupervised | Dimensionality reduction, compression | Very effective in computation, powerful for unsupervised learning | Pretraining is expensive Stuck with performance for timeseries data |
| DNN–LSTM | Supervised, unsupervised, reinforcement | Control problems with high dimensional inputs | Fully connected layer arrangement, can overcome vanishing gradient problem. | Depends on large amount of data, very expensive in computation |
| XG-Boost | Supervised, unsupervised | Modelling less feature engineering applications | Fast in operations, less overfitting | Difficult to optimize the hyperparameters |
| Randomforest | Supervised, unsupervised | Modelling applications for feature selection | Very effective in highly correlated features | Depend on highly correlated features |
| KNN | Supervised, unsupervised | Modelling instance-based applications | Easy implementation, evolving model for new data points | Depends on homogeneous features |
| MICE | Supervised, unsupervised | Data imputations | Flexible, can handle variables of varying types | Sensitive to outliers, depends on homogeneous features |
| GAIN | Supervised, unsupervised | Data generations | Effective in generating the similar patterns | Convergence is difficult |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.; Yuvaraj, N.; Sri Preethaa, K.R.; Hu, G.; Lee, D.-E. Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network. Sensors 2021, 21, 2515. https://doi.org/10.3390/s21072515
Kim B, Yuvaraj N, Sri Preethaa KR, Hu G, Lee D-E. Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network. Sensors. 2021; 21(7):2515. https://doi.org/10.3390/s21072515
Chicago/Turabian StyleKim, Bubryur, N. Yuvaraj, K. R. Sri Preethaa, Gang Hu, and Dong-Eun Lee. 2021. "Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network" Sensors 21, no. 7: 2515. https://doi.org/10.3390/s21072515
APA StyleKim, B., Yuvaraj, N., Sri Preethaa, K. R., Hu, G., & Lee, D.-E. (2021). Wind-Induced Pressure Prediction on Tall Buildings Using Generative Adversarial Imputation Network. Sensors, 21(7), 2515. https://doi.org/10.3390/s21072515








