A Redundancy Metric Set within Possibility Theory for Multi-Sensor Systems †
Abstract
1. Introduction
- At the level of single sensor measurements, lack of information, e.g., about the sensor’s detailed characteristics, tolerances, or physical limits, results in imprecise readings. Thus, a sensor is only able to give an approximate measurement. As a result of this, information is often provided in intervals, fuzzy intervals, or uncertainty distributions (either probabilistic or possibilistic) [13].
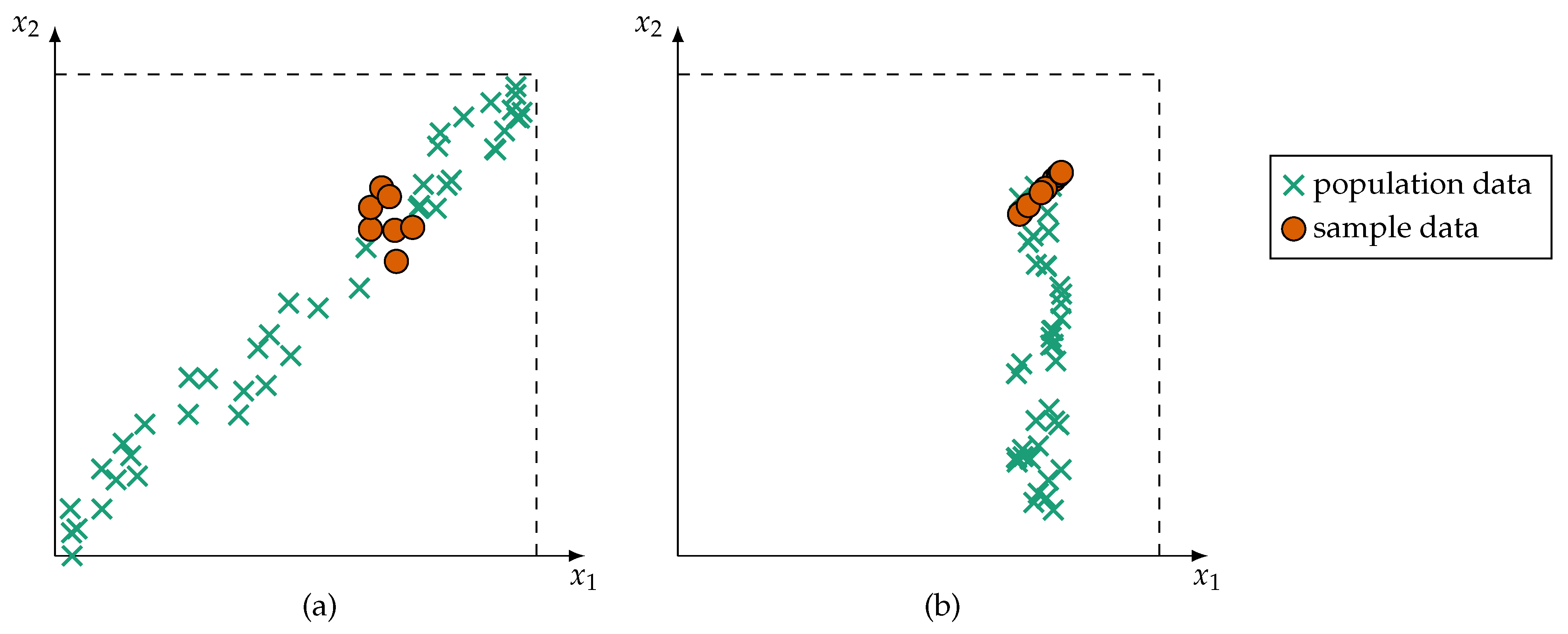
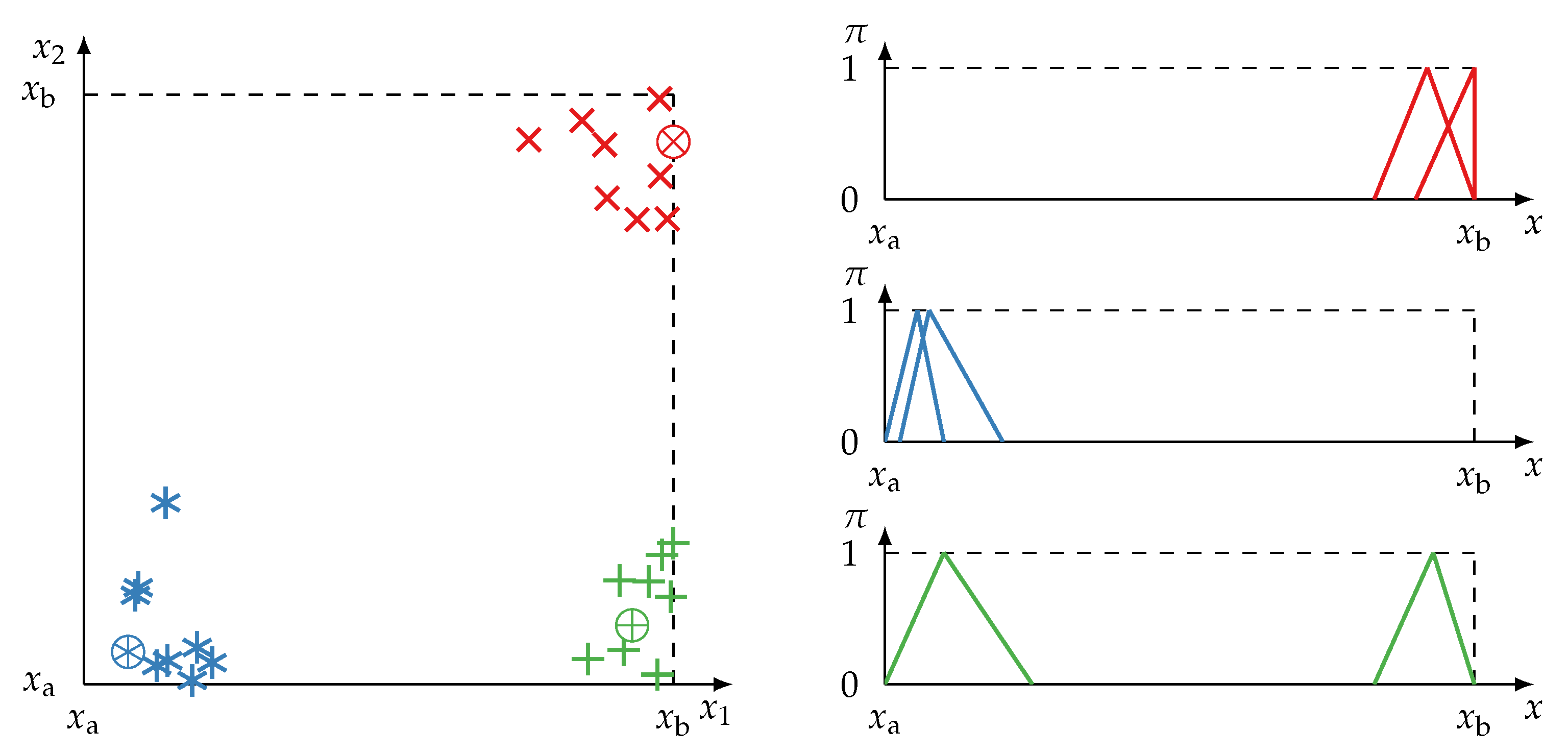
- Furthermore, during training, the monitored process may only by observable in specific states. For example, a production machine may create a lot of training data, but these data often originate from the same machine state, that is, data about states of failure are rare. This leads to ambiguous and fuzzy classes [14] as well as premature detection of interrelations (such as redundancy) between sensors. The risk of detecting spurious correlations [15] is greatly amplified in intelligent technical or cyber–physical systems. Two examples of premature detection of variable interrelation are shown in Figure 1.
2. Redundancy in Related Work
3. Possibility Theory
3.1. Basics of Possibility Theory
3.2. Possibility Theory in Comparison to Probability Theory
- The application of PosT does not require statistical data to be available. Consequently, it is easier and takes less effort to construct sound possibility distributions than probability distributions (cf. [54] for methods to construct possibility distributions).
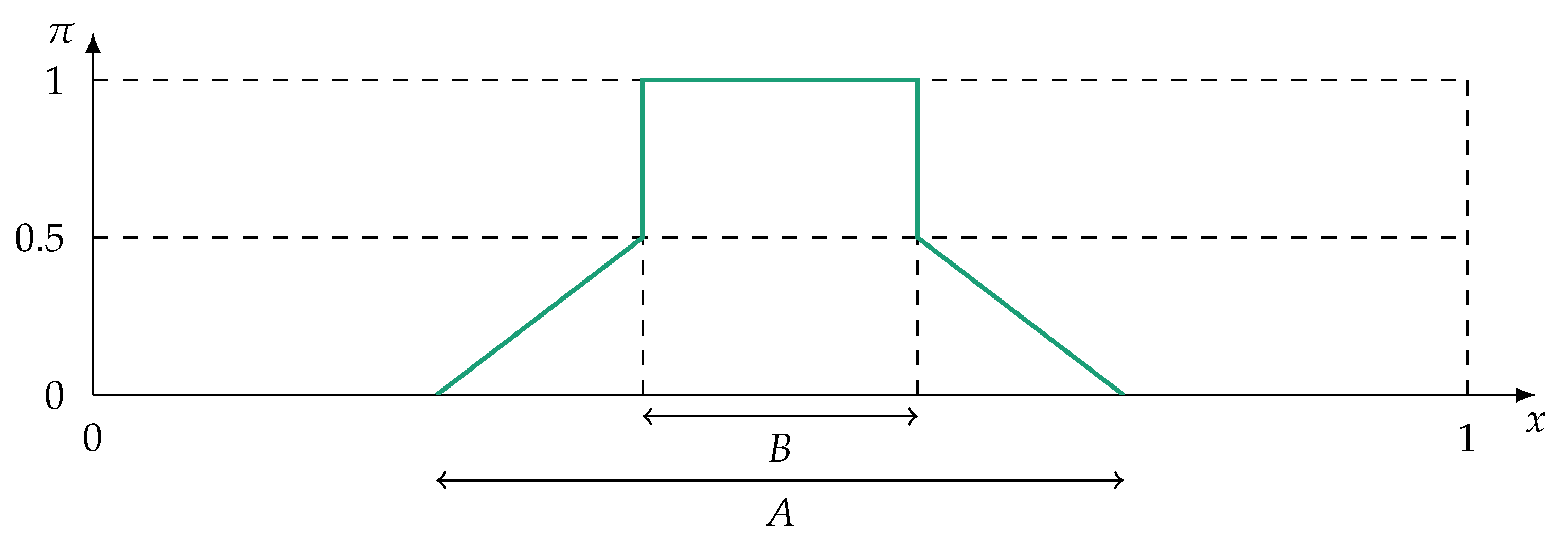
- In contrast to ProbT, both imprecision and confidence can be modelled distinctly within a possibility distribution. Imprecision is modeled by allowing multiple alternatives to be possible, e.g., it may be known that , but not which value v takes within A precisely. Confidence is expressed by the degree of possibility assigned to a value x, i.e., if , it is uncertain if is fully possible. It follows directly that confidence is also represented in the duality measure of and N as can be seen in the three extreme epistemic situations [50]: (i) if is certain, and , (ii) if is certain, and , and (iii) in case of ignorance, and .
3.3. Fusion within Possibility Theory
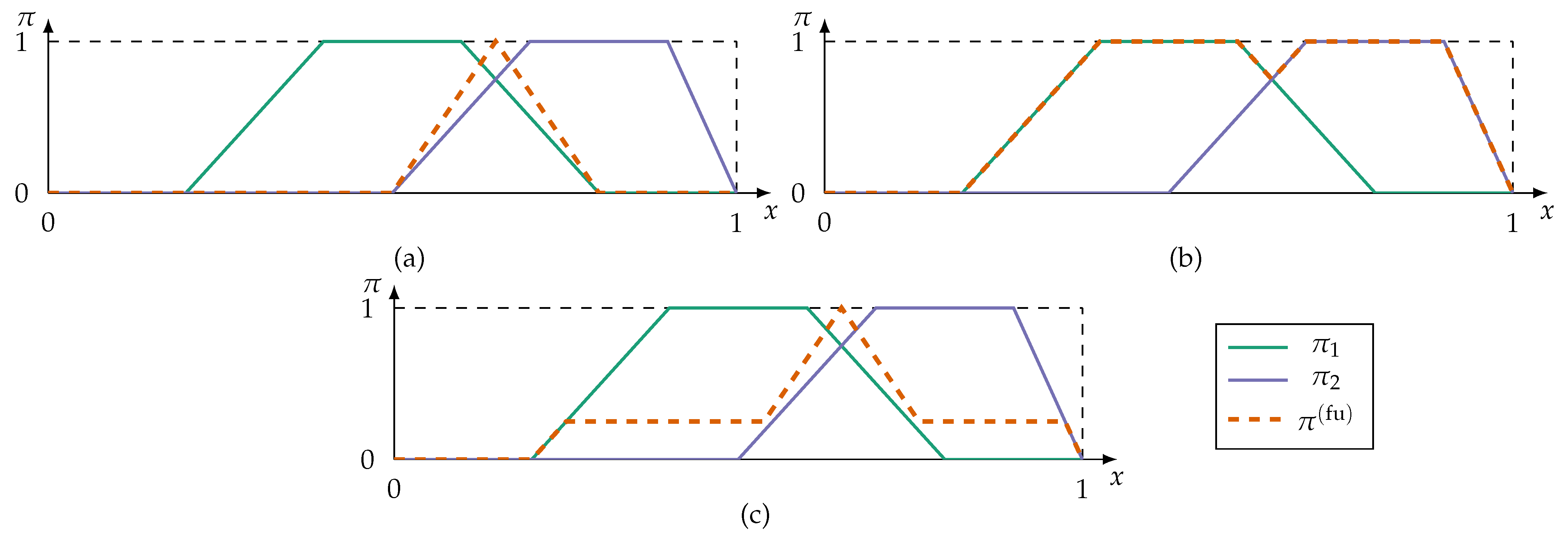
- Conjunctive fusion modes implement the principle of minimal specificity most strongly. By applying a triangular norm (t-norm),conjunctive fusion reduces the information to alternatives all sources can agree on. An overview of t-norms, and their counterpart s-norms (also referred to as t-conorms), can be found in [68]. If at least one source is inconsistent with the remaining sources, i.e., the sources cannot agree on a fully plausible alternative, then the fused possibility distribution is subnormal () or even empty. This violates the axiom (2) of PosT that at least one alternative in X must be fully plausible. A renormalisationprevents subnormal fusion results, but is numerically unstable if at least one source is fully inconsistent, i.e., .
- In case of fully inconsistent possibility distributions at least one information source must be unreliable. Assuming it is not known which source is unreliable, disjunctive fusion modes apply s-norms so that as much information is kept as possible:Disjunctive fusion is generally not desirable because the fusion does not result in more specific information.
- Adaptive fusion modes combine conjunctive and disjunctive fusion methods. These modes switch from conjunctive to disjunctive aggregation depending on which of the alternatives the sources are inconsistent for. An adaptive fusion mode, proposed in [69], isThus, fusion results in a global level of conflict () for all alternatives the sources cannot agree on. Otherwise the adaptive fusion reinforces by conjunction.
- A majority-guided fusion searches for the alternatives which are supported by most sources. This is similar to a voting style consensus. Majority-guided fusion requires the identification of a majority subset—usually the subset with highest consistency and maximum number of sources. The possibility distributions of this subset are fused conjunctively. Information outside of the majority subset is discarded which violates the fairness principle postulated in [4]. Applications of majority-guided fusion can be found in previous works of the authors of this contribution [6,7].
4. Quantifying Redundancy within the Possibility Theory
4.1. Redundant Information Items
- Boundaries: Information items can be minimally and maximally redundant. Therefore, is minimally and maximally bounded: .
- Inclusion (Upper Bound): An information item is fully redundant in relation to if it encloses (includes) .
- Lower Bound: An information item is non-redundant if it adds new information. Additionally, an item is fully non-redundant in relation to if and disagree completely on the state of affairs, i.e., in terms of possibility theory .
- Identity: Two identical information items are fully redundant, i.e., .
- Symmetry: A redundancy metric is symmetric in all its arguments, i.e., for any permutation p on .
- Non-Agreement (Lower Bound): Information items are fully non-redundant if they disagree completely on the state of affairs, i.e., they do not agree on at least one alternative in the frame of discernment to be possible, i.e., .
4.1.1. Redundancy Type I
- in case of total ignorance, i.e., .
- iff in case of complete knowledge, i.e., only one unique event is totally possible and all other events are impossible.
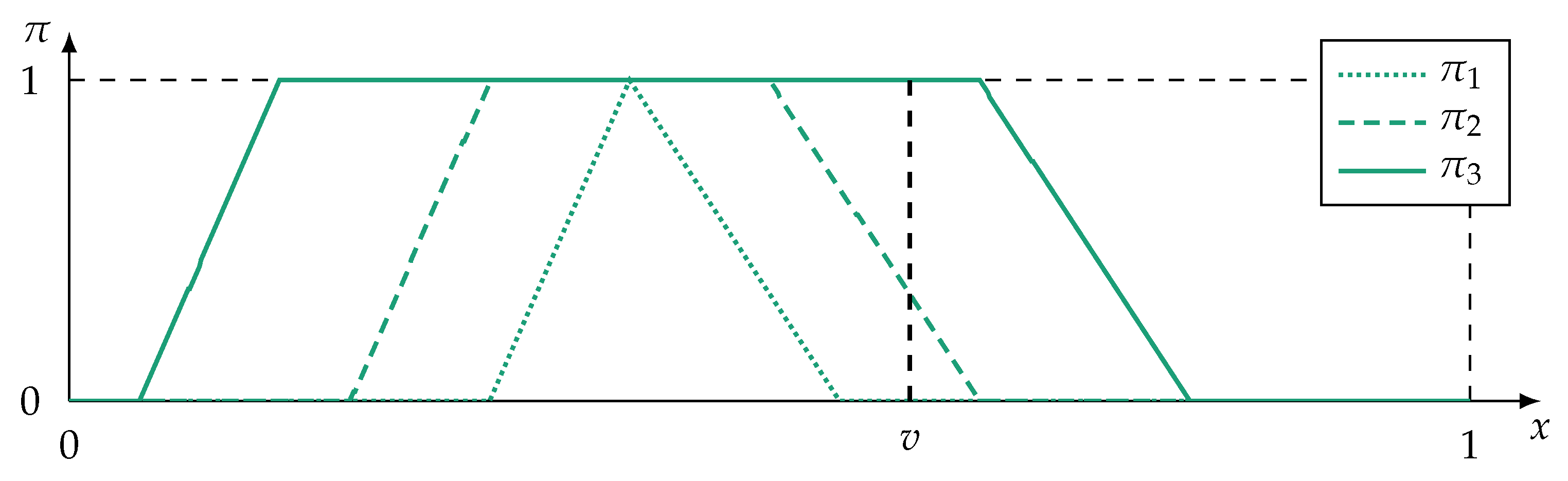
- A specificity measure de- and increases with the maximum value of , i.e., let be the kth largest possibility degree in , then .
- , i.e., the specificity decreases as the possibilities of other values approach the maximum value of .
4.1.2. Redundancy Type II
- Boundaries: It is reasonable to assume that possibility distributions can be minimally and maximally similar. The measure is therefore bounded. It is normalized if .
- Identity relation (upper bound): A set of possibility distributions is maximally similar if they are identical, i.e., for any π. The reverse is not necessarily to be true. A set of possibility distributions with does not imply that all are identical.
- Non-agreement (lower bound): The non-agreement property defines that any set of possibility distributions which cannot agree on a common alternative x to be possible are maximal dissimilar, i.e.,
- Least agreement: A set of possibility distributions is at most as similar as the least similar pair :
- Symmetry: A similarity measure is a symmetric function in all its arguments, that is, for any permutation p on .
- Inclusion: For any , if , then and .
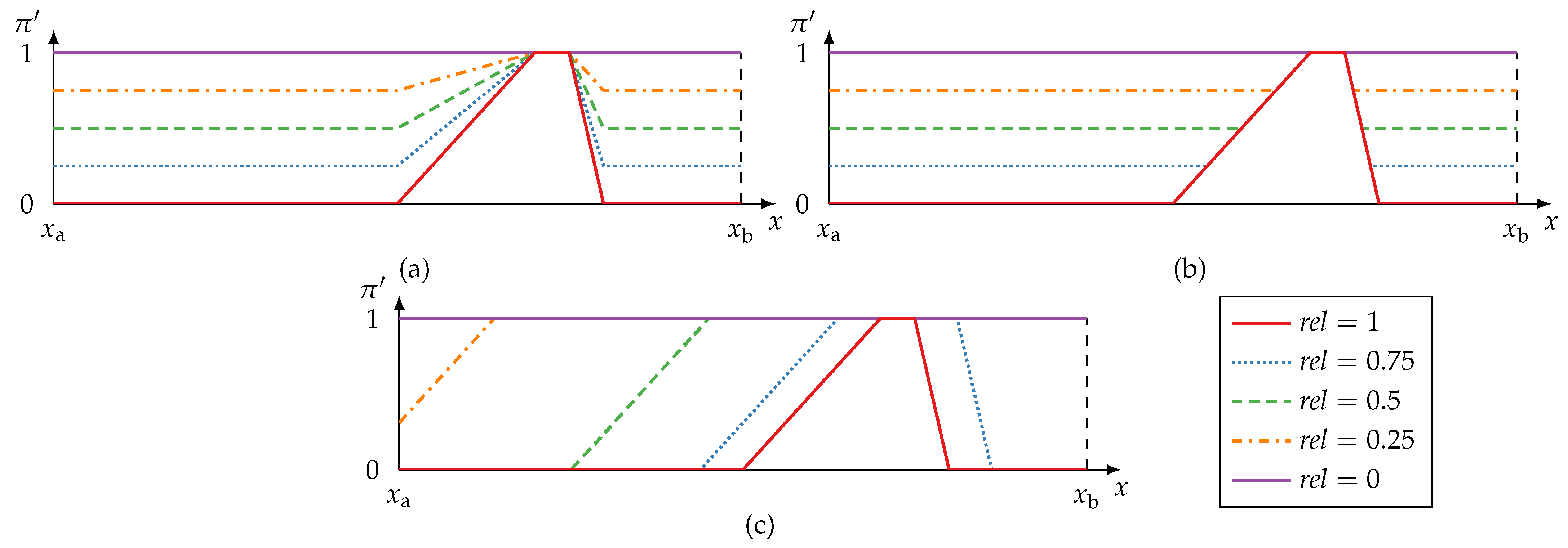
4.1.3. Reliability and Redundancy Metrics
- Information preservation: If , then the available information must not be changed but be preserved, i.e., .
- Specificity interaction: If , then the information needs to be modified to model total ignorance, i.e., . Information must not get more specific by the modification: for any .
4.2. Redundant Information Sources
- If information sources are redundant, then they provide redundant information items. Consequently, increases as the redundancy of information items belonging to the sources in increase.
- The reverse is not necessarily true. Redundant information items do no necessitate that their information sources are also redundant. Due to cases of incomplete information, redundant information items may support spurious redundancy (similar to spurious correlation which is depicted in Figure 1).
- Boundaries: A redundancy metric should be able to model complete redundancy and complete non-redundancy. It follows that ρ is minimally and maximally bounded. It is proposed that .
- Symmetry: The metric ρ is a symmetric function in all its arguments, i.e.,for any permutation p on .
4.2.1. Evidence Against Redundancy
- Absorbing element: for any , that is, if information sources in produce non-redundant items, then this is evidence that are not redundant as well.
4.2.2. Evidence Pro Redundancy
- Upper bound: If , then and .
- Lower bound: if , that is, all possibility distributions are identical.
- if ( models total ignorance), then ,
- if and only if and ( models complete knowledge at ), and
- if and only if and ( models complete knowledge at ).
- : The evidence (22) averages the redundancies of information items obtained by which is by definition in (see Definition 4).
- : The type II redundancy metric is symmetric per definition (Definition 4). The evidence (22) averages over all provided information items and is consequently also symmetric.
5. Evaluation
5.1. Implementation
- Imprecision is modelled with probability distributions or not at all rather than with possibility distributions. Precise information items given as singletons are often only allegedly so—modelling the imprecision is often neglected.
- Information comes from unreliable sources.
- Information comes from heterogeneous sensors meaning that information is provided regarding different frame of discernments.
- If information are provided as singletons or probability distributions, they are transformed into possibility distributions.
- The unreliability of information sources is taken into account by modifying (widening) the possibility distribution using (20) with parameters and selected appropriately for each dataset.
- All information are mapped to a common frame of discernment.
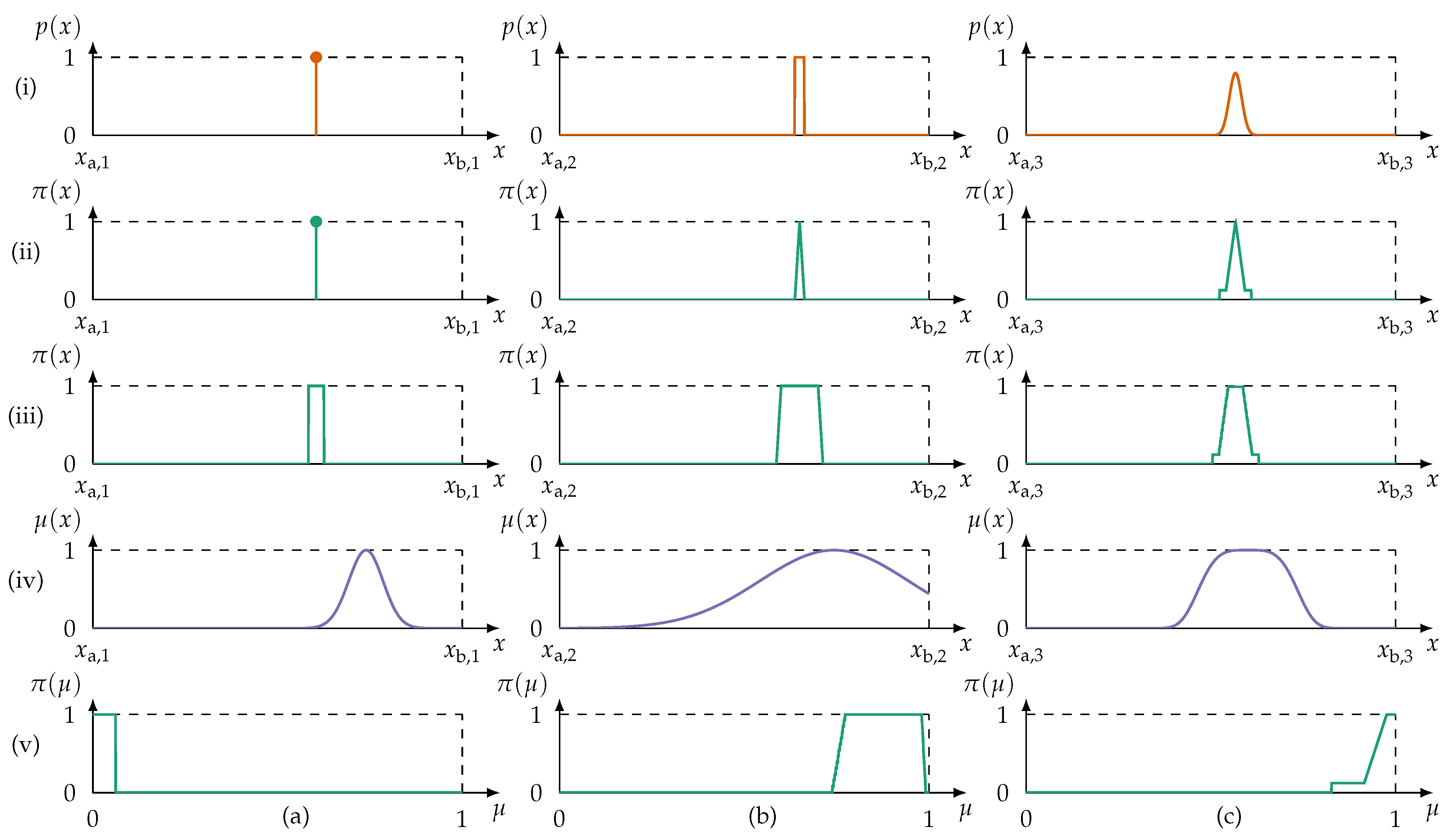
5.1.1. Probability Possibility Transform
- Normalization condition: The resulting possibility distribution is required to be normal ().
- Consistency principle: What is probable must preliminarily be possible, that is, the possibility of an event A is an upper bound for its probability ().
- Preference preservation: Given a probability distribution p, .
5.1.2. Unifying Heterogeneous Information
5.2. Results and Discussion
- Pearson’s correlation coefficient: Correlation coefficients are computed on the expected value of the original data because sources from the TSD dataset provide information associated with an imprecision interval modeled by a uniform PDF. Let be the expected value of the imprecise data provided by source at instance j and let be the arithmetic mean of the expected values of . Then, the correlation coefficient is computed by
- Inconsistency-based approach: In [5] the inconsistency of a possibility distribution is determined within a set of possibility distributions. The inconsistency is the distance between the distribution’s position and the position of the majority observation within the set: . The position is determined by (24). Since we compare only pairs of information sources, no majority observation can be found and the distance between the positions of both information items is taken. The approach in [5] is designed for streaming data and the inconsistency of information items is averaged with a moving average filter. Instead of this kind of filter, is averaged so that:Similar to our approach, a homogenous frame of discernment between information items is required. Therefore, the inconsistency is computed on the possibility distributions obtained by the preprocessing steps detailed previously. The measure determines the degree of non-redundancy between information sources.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPS | Cyber–Physical Systems |
| MI | Mutual Information |
| OWA | Ordered Weighted Averaging |
| Probability Density Function | |
| PosT | Possibility Theory |
| ProbT | Probability Theory |
| TTPPT | Truncated Triangular Probability-Possibility Transform |
| UPF | Unimodal Potential Function |
Appendix A. Additional Proofs
Appendix A.1. Proofs of Section 4.1.1
Appendix A.2. Proofs of Section 4.1.2
- Part (i)
- if . It follows that
- Part (ii)
- if . The same steps as carried out in part (i) can be applied. This leads to
Appendix A.3. Proofs of Section 4.1.3
Appendix A.4. Proofs of Section 4.2.2
References
- Elmenreich, W. An Introduction to Sensor Fusion; Technical Report; Vienna University of Technology: Vienna, Austria, 2002. [Google Scholar]
- Hall, D.L.; Llinas, J.; Liggins, M.E. (Eds.) Handbook of Multisensor Data Fusion: Theory and Practice, 2nd ed.; The Electrical Engineering and Applied Signal Processing Series; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Bloch, I.; Hunter, A.; Appriou, A.; Ayoun, A.; Benferhat, S.; Besnard, P.; Cholvy, L.; Cooke, R.; Cuppens, F.; Dubois, D.; et al. Fusion: General concepts and characteristics. Int. J. Intell. Syst. 2001, 16, 1107–1134. [Google Scholar] [CrossRef]
- Dubois, D.; Liu, W.; Ma, J.; Prade, H. The basic principles of uncertain information fusion. An organised review of merging rules in different representation frameworks. Inf. Fusion 2016, 32, 12–39. [Google Scholar] [CrossRef]
- Ehlenbröker, J.F.; Mönks, U.; Lohweg, V. Sensor defect detection in multisensor information fusion. J. Sens. Sens. Syst. 2016, 5, 337–353. [Google Scholar] [CrossRef]
- Holst, C.A.; Lohweg, V. Improving majority-guided fuzzy information fusion for Industry 4.0 condition monitoring. In Proceedings of the 2019 22nd International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, 2–5 July 2019. [Google Scholar] [CrossRef]
- Holst, C.A.; Lohweg, V. Feature fusion to increase the robustness of machine learners in industrial environments. at-Automatisierungstechnik 2019, 67, 853–865. [Google Scholar] [CrossRef]
- Berk, M.; Schubert, O.; Kroll, H.; Buschardt, B.; Straub, D. Exploiting redundancy for reliability analysis of sensor perception in automated driving vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 1–13. [Google Scholar] [CrossRef]
- Rogova, G.L. Information quality in fusion-driven human-machine environments. In Information Quality in Information Fusion and Decision Making; Bossé, É., Rogova, G.L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 3–29. [Google Scholar] [CrossRef]
- Mönks, U.; Lohweg, V.; Dörksen, H. Conflict measures and importance weighting for information fusion applied to Industry 4.0. In Information Quality in Information Fusion and Decision Making; Bossé, É., Rogova, G.L., Eds.; Information Fusion and Data Science; Springer International Publishing: Cham, Switzerland, 2019; pp. 539–561. [Google Scholar] [CrossRef]
- Fritze, A.; Mönks, U.; Holst, C.A.; Lohweg, V. An approach to automated fusion system design and adaptation. Sensors 2017, 17, 601. [Google Scholar] [CrossRef]
- Guyon, I.; Gunn, S.R.; Nikravesh, M.; Zadeh, L.A. Feature Extraction: Foundations and Applications; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2006; Volume 207. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility theory in information fusion. In Proceedings of the Third International Conference on Information Fusion, Paris, France, 10–13 July 2000; Volume 1. [Google Scholar] [CrossRef]
- Bocklisch, S.F. Prozeßanalyse mit Unscharfen Verfahren, 1st ed.; Verlag Technik: Berlin, Germany, 1987. [Google Scholar]
- Calude, C.; Longo, G. The deluge of spurious correlations in big data. Found. Sci. 2017, 22, 595–612. [Google Scholar] [CrossRef]
- Holst, C.A.; Lohweg, V. A redundancy metric based on the framework of possibility theory for technical systems. In Proceedings of the 2020 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020. [Google Scholar] [CrossRef]
- Luo, R.C.; Kay, M.G. Multisensor integration and fusion in intelligent systems. IEEE Trans. Syst. Man Cybern. 1989, 19, 901–931. [Google Scholar] [CrossRef]
- Ding, C.; Peng, H. Minimum redundancy feature selection from microarray gene expression data. J. Bioinform. Comput. Biol. 2005, 3, 185–205. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Reza, F.M. An Introduction to Information Theory; International Student Edition; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Lughofer, E.; Hüllermeier, E. On-line redundancy elimination in evolving fuzzy regression models using a fuzzy inclusion measure. In Proceedings of the 7th conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-11), Aix-les-Bains, France, 18–22 July 2011; pp. 380–387. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H.; Ughetto, L. Checking the coherence and redundancy of fuzzy knowledge bases. IEEE Trans. Fuzzy Syst. 1997, 5, 398–417. [Google Scholar] [CrossRef]
- Dvořák, A.; Štěpnička, M.; Štěpničková, L. On redundancies in systems of fuzzy/linguistic IF–THEN rules under perception-based logical deduction inference. Fuzzy Sets Syst. 2015, 277, 22–43. [Google Scholar] [CrossRef]
- Bastide, Y.; Pasquier, N.; Taouil, R.; Stumme, G.; Lakhal, L. Mining Minimal Non-Redundant Association Rules Using Frequent Closed Itemsets. In Computational Logic—CL 2000; Lloyd, J., Dahl, V., Furbach, U., Kerber, M., Lau, K.K., Palamidessi, C., Pereira, L.M., Sagiv, Y., Stuckey, P.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 972–986. [Google Scholar] [CrossRef]
- Díaz Vera, J.C.; Negrín Ortiz, G.M.; Molina, C.; Vila, M.A. Knowledge redundancy approach to reduce size in association rules. Informatica 2020, 44. [Google Scholar] [CrossRef]
- Zhang, Y.; Callan, J.; Minka, T. Novelty and redundancy detection in adaptive filtering. In Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR ’02), Tampere, Finland, 11–15 August 2002; Association for Computing Machinery: New York, NY, USA, 2002; pp. 81–88. [Google Scholar] [CrossRef]
- Mönks, U. Information Fusion Under Consideration of Conflicting Input Signals. In Technologies for Intelligent Automation; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Auffarth, B.; López, M.; Cerquides, J. Comparison of redundancy and relevance measures for feature selection in tissue classification of CT images. In Advances in Data Mining. Applications and Theoretical Aspects; Perner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 248–262. [Google Scholar] [CrossRef]
- Chakraborty, R.; Lin, C.T.; Pal, N.R. Sensor (group feature) selection with controlled redundancy in a connectionist framework. Int. J. Neural Syst. 2014, 24. [Google Scholar] [CrossRef] [PubMed]
- Pfannschmidt, L.; Jakob, J.; Hinder, F.; Biehl, M.; Tino, P.; Hammer, B. Feature relevance determination for ordinal regression in the context of feature redundancies and privileged information. Neurocomputing 2020, 416, 266–279. [Google Scholar] [CrossRef]
- Pfannschmidt, L.; Göpfert, C.; Neumann, U.; Heider, D.; Hammer, B. FRI-Feature relevance intervals for interpretable and interactive data exploration. In Proceedings of the 2019 IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Siena, Italy, 9–11 July 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Langley, P.; Sage, S. Induction of selective Bayesian classifiers. In Uncertainty Proceedings 1994; de Mantaras, R.L., Poole, D., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1994; pp. 399–406. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Nguyen, H.; Franke, K.; Petrovic, S. Improving effectiveness of intrusion detection by correlation feature selection. In Proceedings of the 2010 International Conference on Availability, Reliability and Security, Krakow, Poland, 15–18 February 2010; pp. 17–24. [Google Scholar] [CrossRef]
- Brown, K.E.; Talbert, D.A. Heuristically reducing the cost of correlation-based feature selection. In Proceedings of the 2019 ACM Southeast Conference on ZZZ-ACM SE ’19, Kennesaw, GA, USA, 18–20 April 2019; Lo, D., Ed.; ACM Press: New York, NY, USA, 2019; pp. 24–30. [Google Scholar] [CrossRef]
- Goswami, S.; Das, A.K.; Chakrabarti, A.; Chakraborty, B. A feature cluster taxonomy based feature selection technique. Expert Syst. Appl. 2017, 79, 76–89. [Google Scholar] [CrossRef]
- Mursalin, M.; Zhang, Y.; Chen, Y.; Chawla, N.V. Automated epileptic seizure detection using improved correlation-based feature selection with random forest classifier. Neurocomputing 2017, 241, 204–214. [Google Scholar] [CrossRef]
- Jain, I.; Jain, V.K.; Jain, R. Correlation feature selection based improved-Binary Particle Swarm Optimization for gene selection and cancer classification. Appl. Soft Comput. 2018, 62, 203–215. [Google Scholar] [CrossRef]
- Battiti, R. Using mutual information for selecting features in supervised neural net learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Bennasar, M.; Hicks, Y.; Setchi, R. Feature selection using Joint Mutual Information Maximisation. Expert Syst. Appl. 2015, 42, 8520–8532. [Google Scholar] [CrossRef]
- Li, F.; Miao, D.; Pedrycz, W. Granular multi-label feature selection based on mutual information. Pattern Recognit. 2017, 67, 410–423. [Google Scholar] [CrossRef]
- González-López, J.; Ventura, S.; Cano, A. Distributed multi-label feature selection using individual mutual information measures. Knowl. Based Syst. 2020, 188, 105052. [Google Scholar] [CrossRef]
- Che, J.; Yang, Y.; Li, L.; Bai, X.; Zhang, S.; Deng, C. Maximum relevance minimum common redundancy feature selection for nonlinear data. Inf. Sci. 2017, 409–410, 68–86. [Google Scholar] [CrossRef]
- Ricquebourg, V.; Delafosse, M.; Delahoche, L.; Marhic, B.; Jolly-Desodt, A.M.; Menga, D. Fault detection by combining redundant sensors : A conflict approach within the TBM framework. In Proceedings of the Cognitive Systems with Interactive Sensors (COGIS 2007), Paris, France, 15–17 March 2006. [Google Scholar]
- Ricquebourg, V.; Delahoche, L.; Marhic, B.; Delafosse, M.; Jolly-Desodt, A.M.; Menga, D. Anomalies recognition in a context aware architecture based on TBM approach. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8. [Google Scholar]
- Bakr, M.A.; Lee, S. Distributed multisensor data fusion under unknown correlation and data inconsistency. Sensors 2017, 17, 2472. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Denœux, T.; Dubois, D.; Prade, H. Representations of uncertainty in artificial intelligence: Probability and possibility. In A Guided Tour of Artificial Intelligence Research: Volume I: Knowledge Representation, Reasoning and Learning; Marquis, P., Papini, O., Prade, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 69–117. [Google Scholar] [CrossRef]
- Salicone, S.; Prioli, M. Measuring Uncertainty within the Theory of Evidence; Springer Series in Measurement Science and Technology; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility theory and its applications: A retrospective and prospective view. In Proceedings of the 12th International Fuzzy Systems Conference (FUZZ ’03), St. Louis, MO, USA, 25–28 May 2003; pp. 5–11. [Google Scholar] [CrossRef]
- Dubois, D.; Foulloy, L.; Mauris, G.; Prade, H. Probability-possibility transformations, triangular fuzzy sets, and probabilistic inequalities. Reliab. Comput. 2004, 10, 273–297. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Practical methods for constructing possibility distributions. Int. J. Intell. Syst. 2016, 31, 215–239. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. From possibilistic rule-based systems to machine learning—A discussion paper. In Scalable Uncertainty Management; Davis, J., Tabia, K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 35–51. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Yager, R.R. On the specificity of a possibility distribution. Fuzzy Sets Syst. 1992, 50, 279–292. [Google Scholar] [CrossRef]
- Yager, R.R. Measures of specificity. In Computational Intelligence: Soft Computing and Fuzzy-Neuro Integration with Applications; Kaynak, O., Zadeh, L.A., Türkşen, B., Rudas, I.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 94–113. [Google Scholar]
- Yager, R.R. On the instantiation of possibility distributions. Fuzzy Sets Syst. 2002, 128, 261–266. [Google Scholar] [CrossRef]
- Yager, R.R. Measures of specificity over continuous spaces under similarity relations. Fuzzy Sets Syst. 2008, 159, 2193–2210. [Google Scholar] [CrossRef]
- Solaiman, B.; Bossé, É. Possibility Theory for the Design of Information Fusion Systems; Information Fusion and Data Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Lohweg, V.; Voth, K.; Glock, S. A possibilistic framework for sensor fusion with monitoring of sensor reliability. In Sensor Fusion; Thomas, C., Ed.; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef]
- Dubois, D.; Everaere, P.; Konieczny, S.; Papini, O. Main issues in belief revision, belief merging and information fusion. In A Guided Tour of Artificial Intelligence Research: Volume I: Knowledge Representation, Reasoning and Learning; Marquis, P., Papini, O., Prade, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 441–485. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H.; Sandri, S. On possibility/probability transformations. In Fuzzy Logic: State of the Art; Lowen, R., Roubens, M., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 103–112. [Google Scholar] [CrossRef]
- Lasserre, V.; Mauris, G.; Foulloy, L. A simple possibilistic modelisation of measurement uncertainty. In Uncertainty in Intelligent and Information Systems; Bouchon-Meunier, B., Yager, R.R., Zadeh, L.A., Eds.; World Scientific: Toh Tuck Link, Singapore, 2000; Volume 20, pp. 58–69. [Google Scholar] [CrossRef]
- Mauris, G.; Lasserre, V.; Foulloy, L. Fuzzy modeling of measurement data acquired from physical sensors. IEEE Trans. Instrum. Meas. 2000, 49, 1201–1205. [Google Scholar] [CrossRef]
- Oussalah, M. On the probability/possibility transformations: A comparative analysis. Int. J. Gen. Syst. 2000, 29, 671–718. [Google Scholar] [CrossRef]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Dubois, D.; Prade, H. Possibility theory and data fusion in poorly informed environments. Control Eng. Pract. 1994, 2, 811–823. [Google Scholar] [CrossRef]
- Higashi, M.; Klir, G.J. Measures of uncertainty and information based on possibility distributions. Int. J. Gen. Syst. 1982, 9, 43–58. [Google Scholar] [CrossRef]
- Higashi, M.; Klir, G.J. On the notion of distance representing information closeness: Possibility and probability distributions. Int. J. Gen. Syst. 1983, 9, 103–115. [Google Scholar] [CrossRef]
- Jenhani, I.; Ben Amor, N.; Elouedi, Z.; Benferhat, S.; Mellouli, K. Information affinity: A new similarity measure for possibilistic uncertain information. In Symbolic and Quantitative Approaches to Reasoning with Uncertainty; Mellouli, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 840–852. [Google Scholar] [CrossRef]
- Charfi, A.; Bouhamed, S.A.; Bossé, É.; Kallel, I.K.; Bouchaala, W.; Solaiman, B.; Derbel, N. Possibilistic similarity measures for data science and machine learning applications. IEEE Access 2020, 8, 49198–49211. [Google Scholar] [CrossRef]
- Bloch, I. On fuzzy distances and their use in image processing under imprecision. Pattern Recognit. 1999, 32, 1873–1895. [Google Scholar] [CrossRef]
- Yager, R.R.; Kelman, A. Fusion of fuzzy information with considerations for compatibility, partial aggregation, and reinforcement. Int. J. Approx. Reason. 1996, 15, 93–122. [Google Scholar] [CrossRef]
- Yager, R.R. Nonmonotonic OWA operators. Soft Comput. 1999, 3, 187–196. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Klir, G.J. Uncertainty Modeling and Analysis in Engineering and the Sciences; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Anguita, D.; Ghio, A.; Oneto, L.; Parra, X.; Reyes-Ortiz, J.L. A public domain dataset for human activity recognition using smartphones. ESANN 2013, 3, 3. [Google Scholar]
- Paschke, F.; Bayer, C.; Bator, M.; Mönks, U.; Dicks, A.; Enge-Rosenblatt, O.; Lohweg, V. Sensorlose Zustandsüberwachung an Synchronmotoren. In 23. Workshop Computational Intelligence; Hoffmann, F., Hüllermeier, E., Mikut, R., Eds.; KIT Scientific Publishing: Karlsruhe, Germany, 2013; Volume 46, pp. 211–225. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2020; Available online: http://archive.ics.uci.edu/ml (accessed on 7 February 2021).
- Lohweg, V.; Diederichs, C.; Müller, D. Algorithms for hardware-based pattern recognition. EURASIP J. Appl. Signal Process. 2004, 2004, 1912–1920. [Google Scholar] [CrossRef]
- Aizerman, M.A.; Braverman, E.M.; Rozonoer, L.I. Theoretical foundations of the potential function method in pattern recognition learning. Autom. Remote. Control 1964, 25, 821–837. [Google Scholar]
- Voth, K.; Glock, S.; Mönks, U.; Lohweg, V.; Türke, T. Multi-sensory machine diagnosis on security printing machines with two-layer conflict solving. In Proceedings of the SENSOR+TEST Conference 2011, Nuremberg, Germany, 7–9 June 2011; pp. 686–691. [Google Scholar] [CrossRef]
- Mönks, U.; Petker, D.; Lohweg, V. Fuzzy-Pattern-Classifier training with small data sets. In Information Processing and Management of Uncertainty in Knowledge-Based Systems. Theory and Methods; Hüllermeier, E., Kruse, R., Hoffmann, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 426–435. [Google Scholar] [CrossRef]
- Bocklisch, F.; Hausmann, D. Multidimensional fuzzy pattern classifier sequences for medical diagnostic reasoning. Appl. Soft Comput. 2018, 66, 297–310. [Google Scholar] [CrossRef]

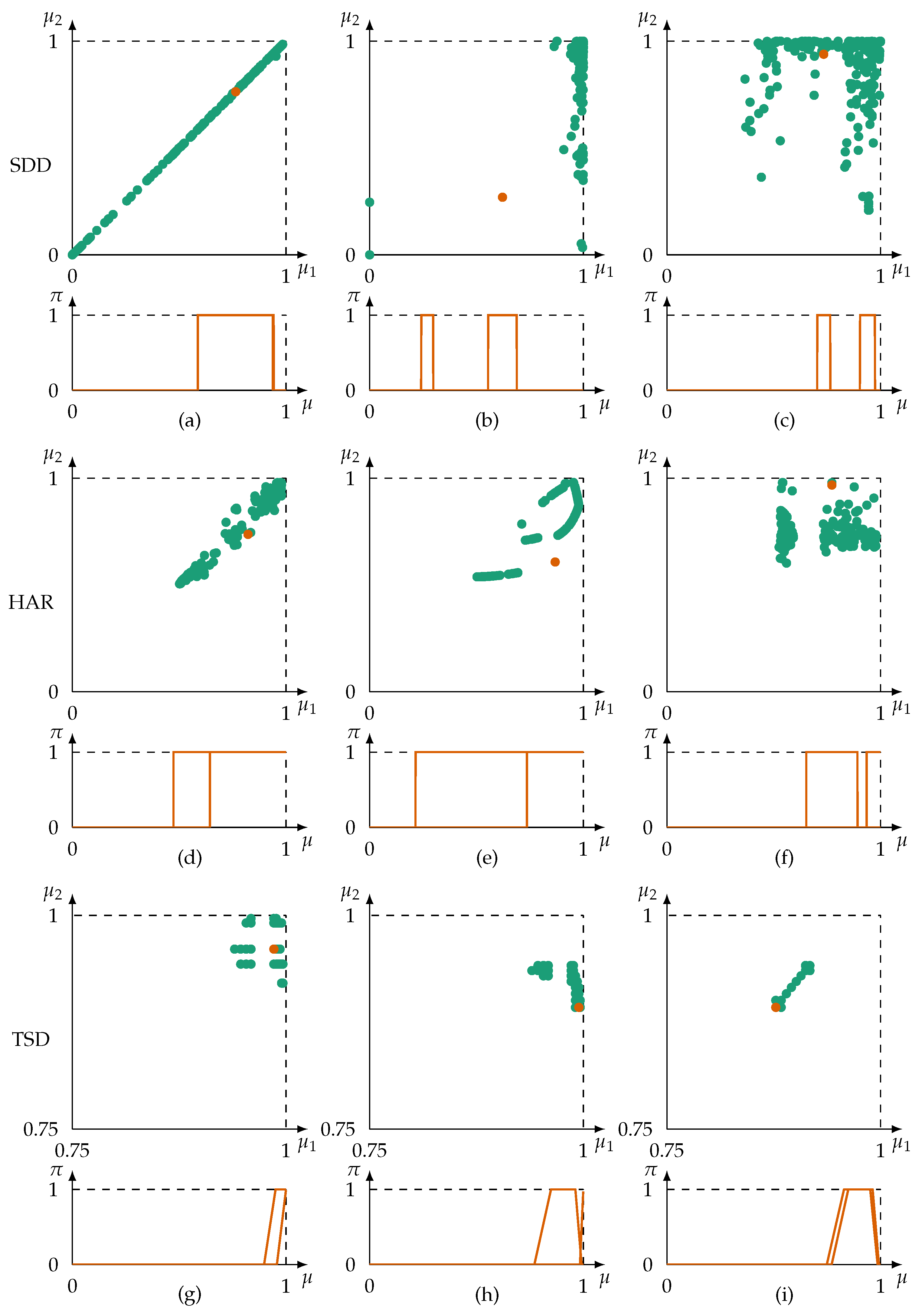
| Dataset | Information Sources (Columns) | Information Items (Rows) | Format | Imprecision | Noteworthy Characteristics |
|---|---|---|---|---|---|
| SDD | 48 | 58509 | real-valued, | precise, , | highly linearly correlated |
| HAR | 561 | 5744 | real-valued, | precise, , | noisy |
| TSD | 22 | 72500 | real-valued, binary-valued, | imprecise, uniform PDF | incomplete information |
| Gaussian | |||
| Laplace | |||
| Triangular | |||
| Uniform | 0 |
| Case | Dataset | |||||||
|---|---|---|---|---|---|---|---|---|
| (a) | SDD | 7 | 8 | 0 | 1 | 0 | ||
| (b) | SDD | 2 | 46 | 1 | 0 | |||
| (c) | SDD | 20 | 36 | 1 | 0 | |||
| (d) | HAR | 89 | 102 | 0 | ||||
| (e) | HAR | 86 | 99 | 0 | ||||
| (f) | HAR | 12 | 50 | 1 | 0 | |||
| (g) | TSD | 9 | 15 | 0 | ||||
| (h) | TSD | 9 | 18 | |||||
| (i) | TSD | 14 | 18 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holst, C.-A.; Lohweg, V. A Redundancy Metric Set within Possibility Theory for Multi-Sensor Systems. Sensors 2021, 21, 2508. https://doi.org/10.3390/s21072508
Holst C-A, Lohweg V. A Redundancy Metric Set within Possibility Theory for Multi-Sensor Systems. Sensors. 2021; 21(7):2508. https://doi.org/10.3390/s21072508
Chicago/Turabian StyleHolst, Christoph-Alexander, and Volker Lohweg. 2021. "A Redundancy Metric Set within Possibility Theory for Multi-Sensor Systems" Sensors 21, no. 7: 2508. https://doi.org/10.3390/s21072508
APA StyleHolst, C.-A., & Lohweg, V. (2021). A Redundancy Metric Set within Possibility Theory for Multi-Sensor Systems. Sensors, 21(7), 2508. https://doi.org/10.3390/s21072508







