Seepage Time Soft Sensor Model of Nonwoven Fabric Based on the Extreme Learning Machine Integrating Monte Carlo
Abstract
1. Introduction
2. Related Work
3. The Extreme Learning Machine (ELM) Combining the Monte Carlo (MC) Algorithm
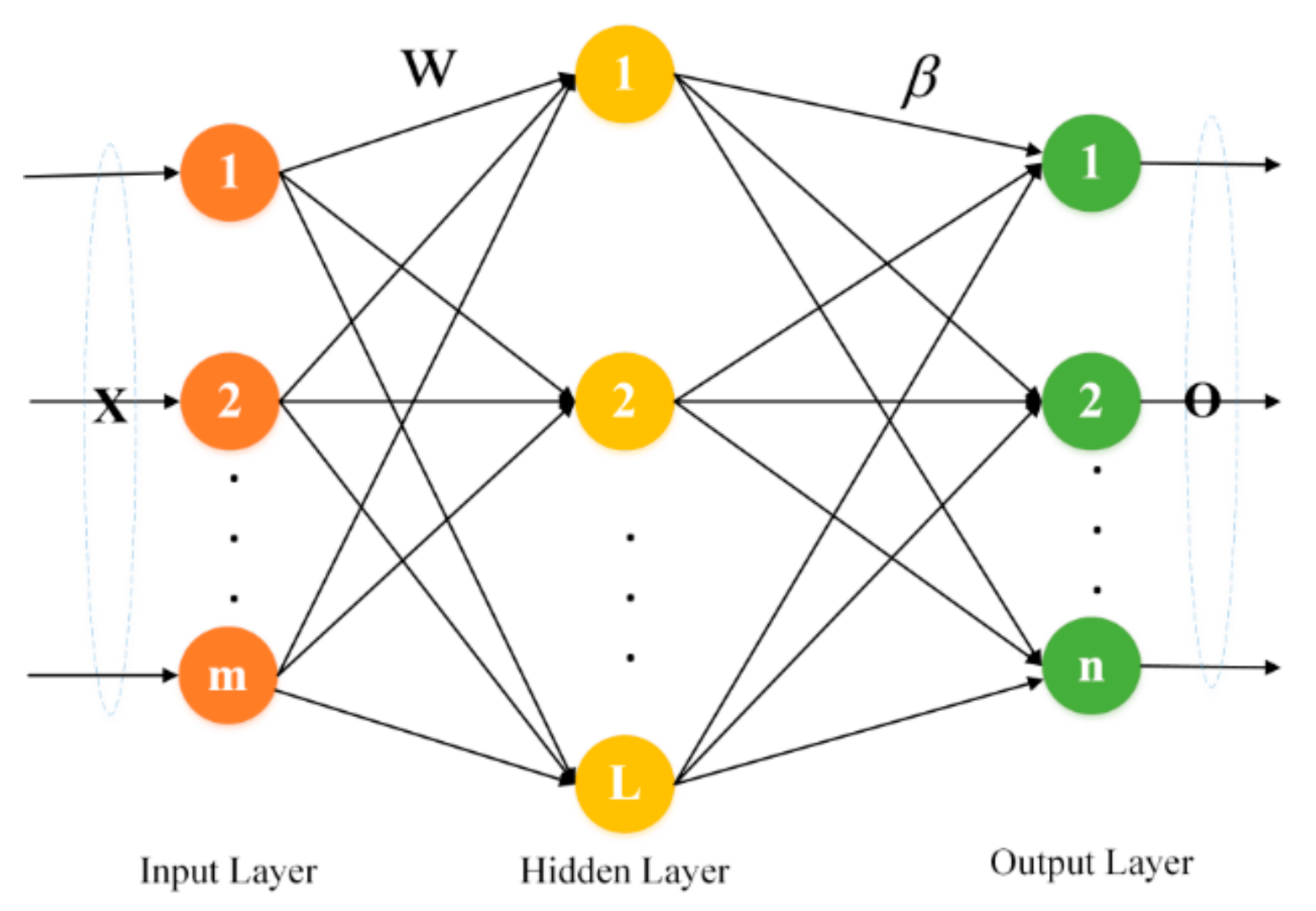
3.1. The ELM
- Step 1: Randomly generate the weight between the input and the hidden layer, as well as the hidden layer threshold, and determine the activation function.
- Step 2: Calculate the hidden layer output .
- Step 3: Get and obtain the output layer weight according to .
3.2. The MC Algorithm
- Step 1: Describe the probability process.
- Step 2: Sampling from a known probability distribution.
- Step 3: Establish an estimate.
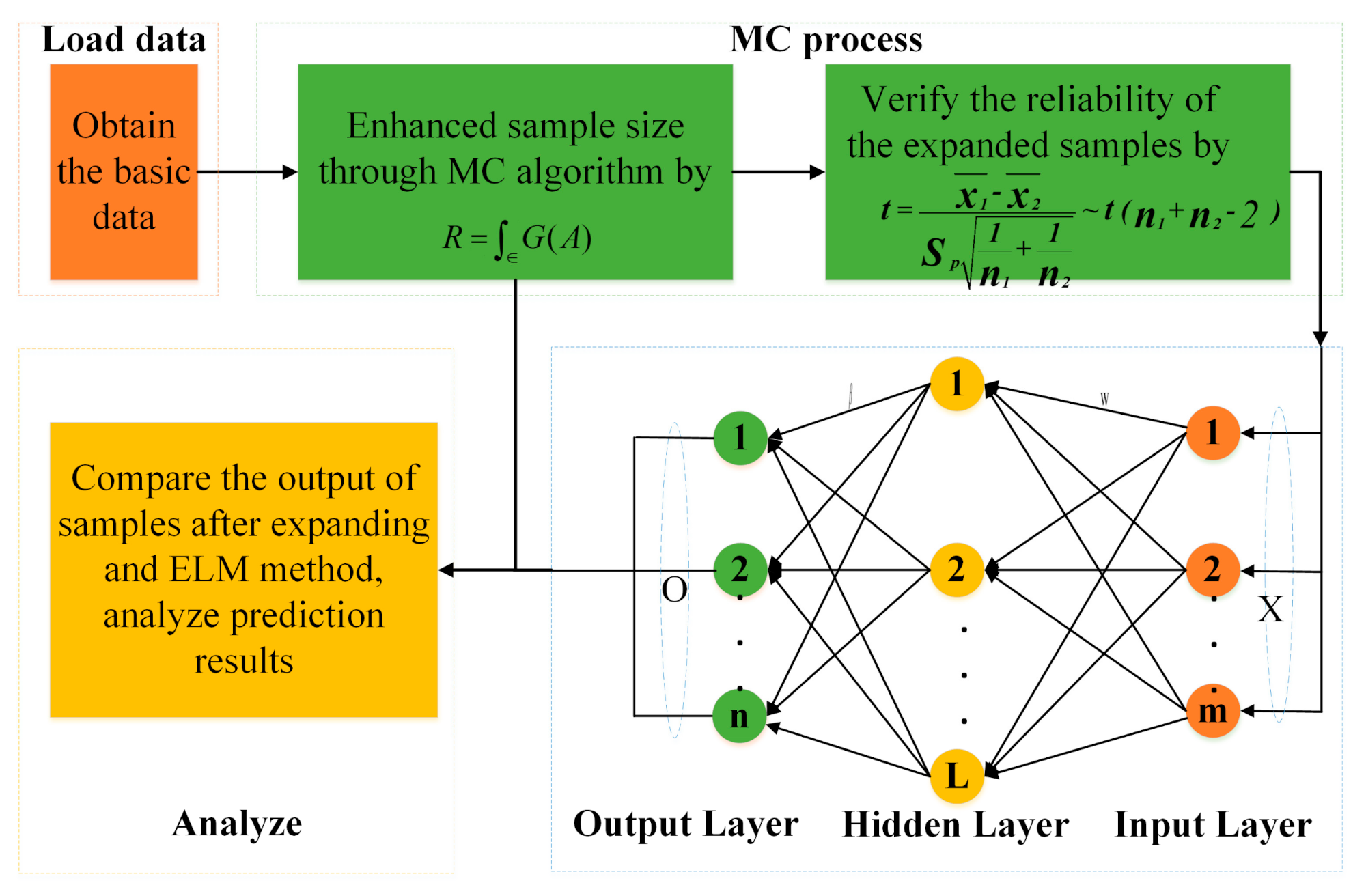
3.3. The Framework of ELM Combining the MC Algorithm
- Step 1: Obtain the basic dataset for the experiment with the help of simulation software.
- Step 2: Enhance sample size through the MC algorithm.
- Step 3: Verify that there is no significant difference between the original data and the extended data by the hypothesis test.
- Step 4: Use the samples obtained in Step2 to train the ELM and compare the output of the network with the real result.
- Step 5: Obtain the MCELM model and analyze the prediction result according to the different error values.
4. Case Study: Prediction of the Time Required of the Dyeing Process
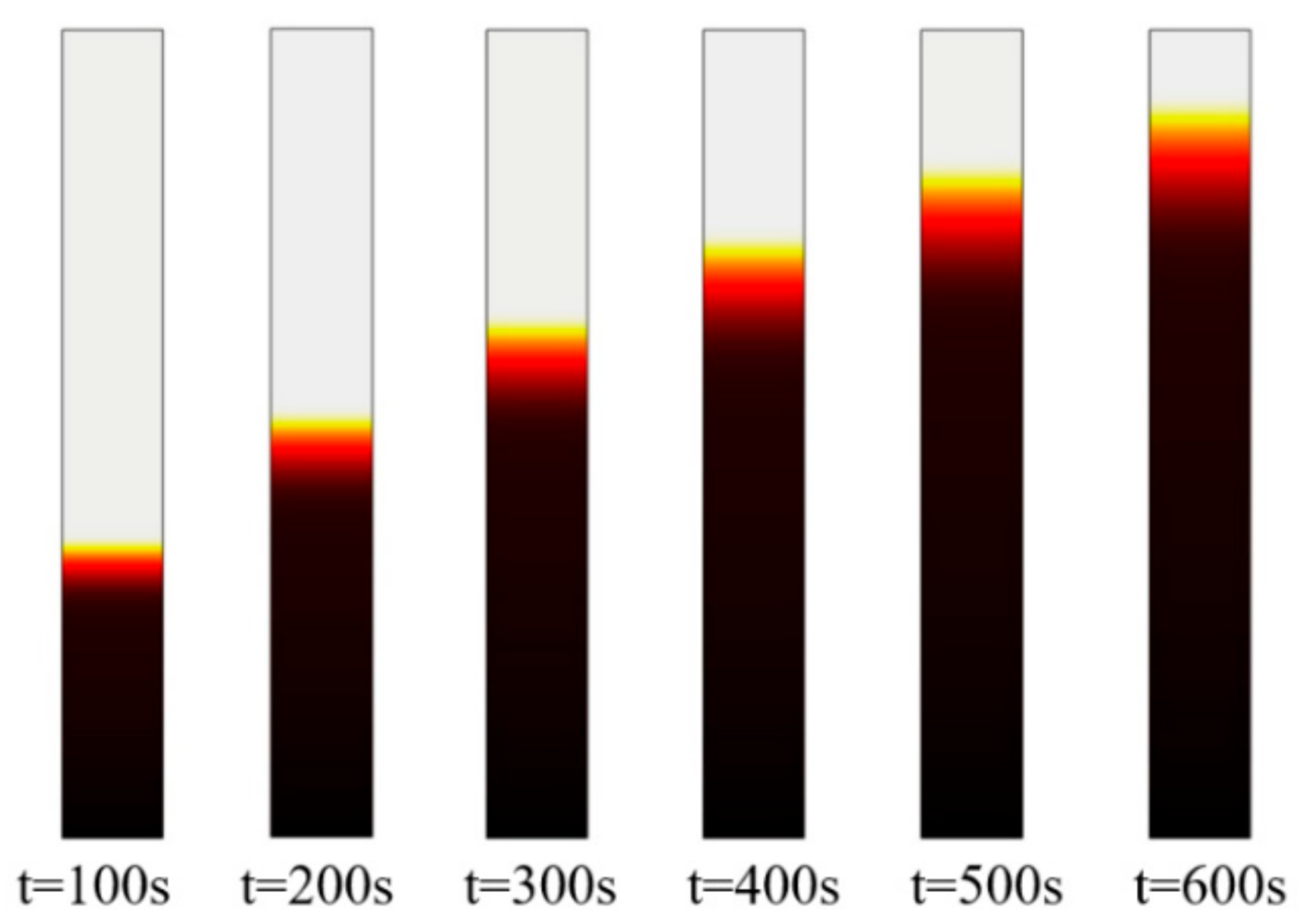
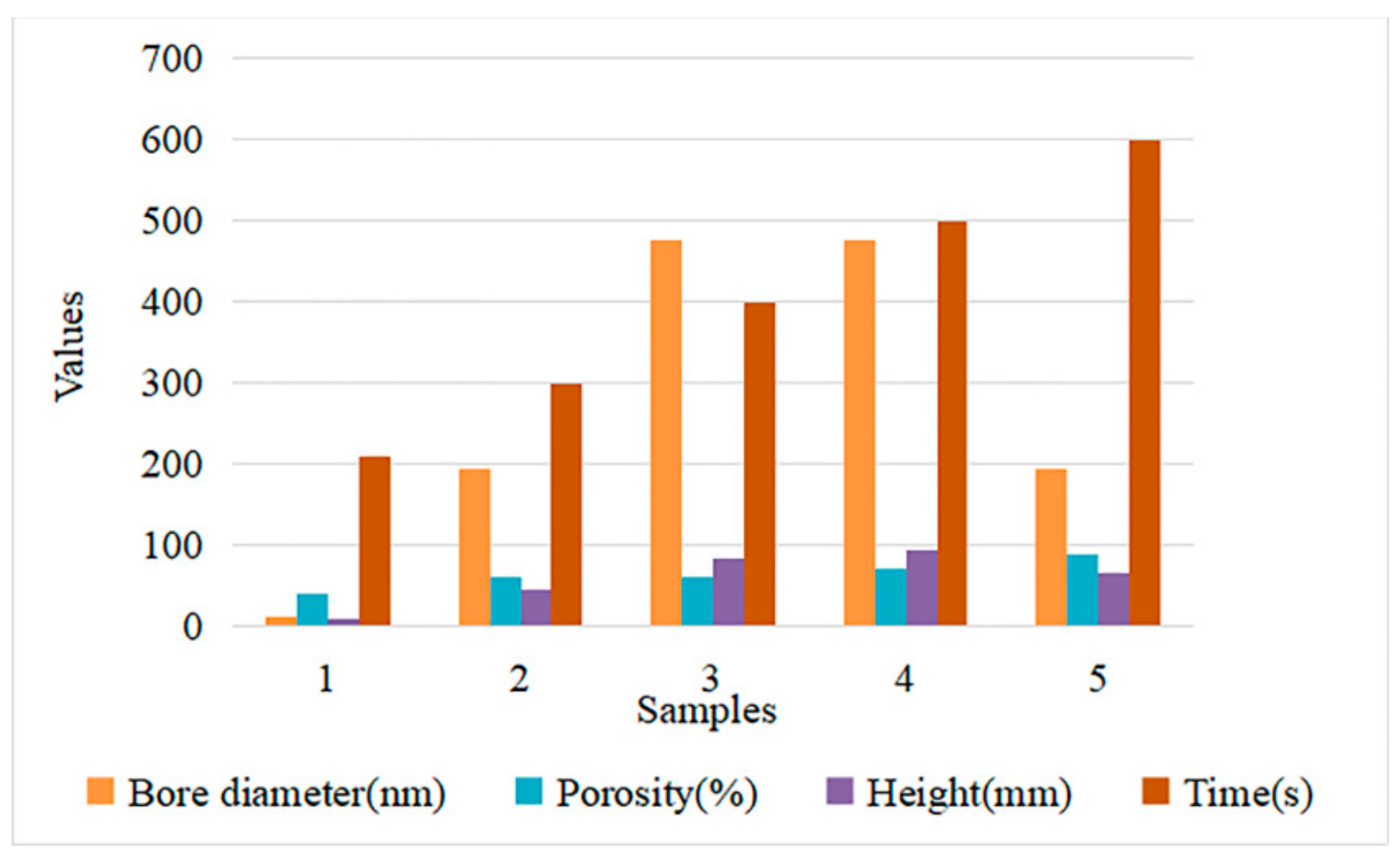
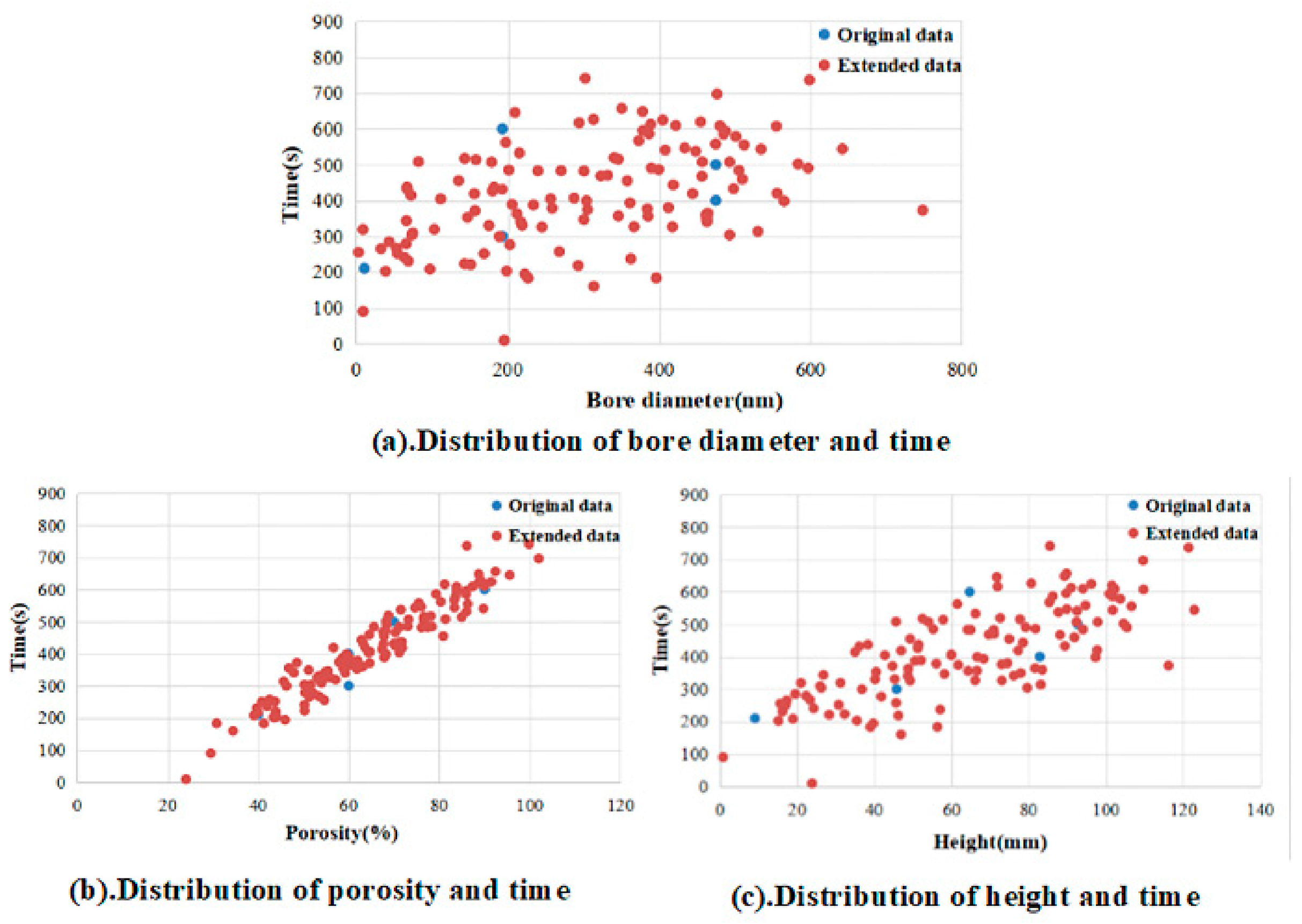
4.1. Data Analysis
4.2. Prediction of the Time Required of the Dyeing Process
4.2.1. Verification of Data Samples Obtained by the MC Method
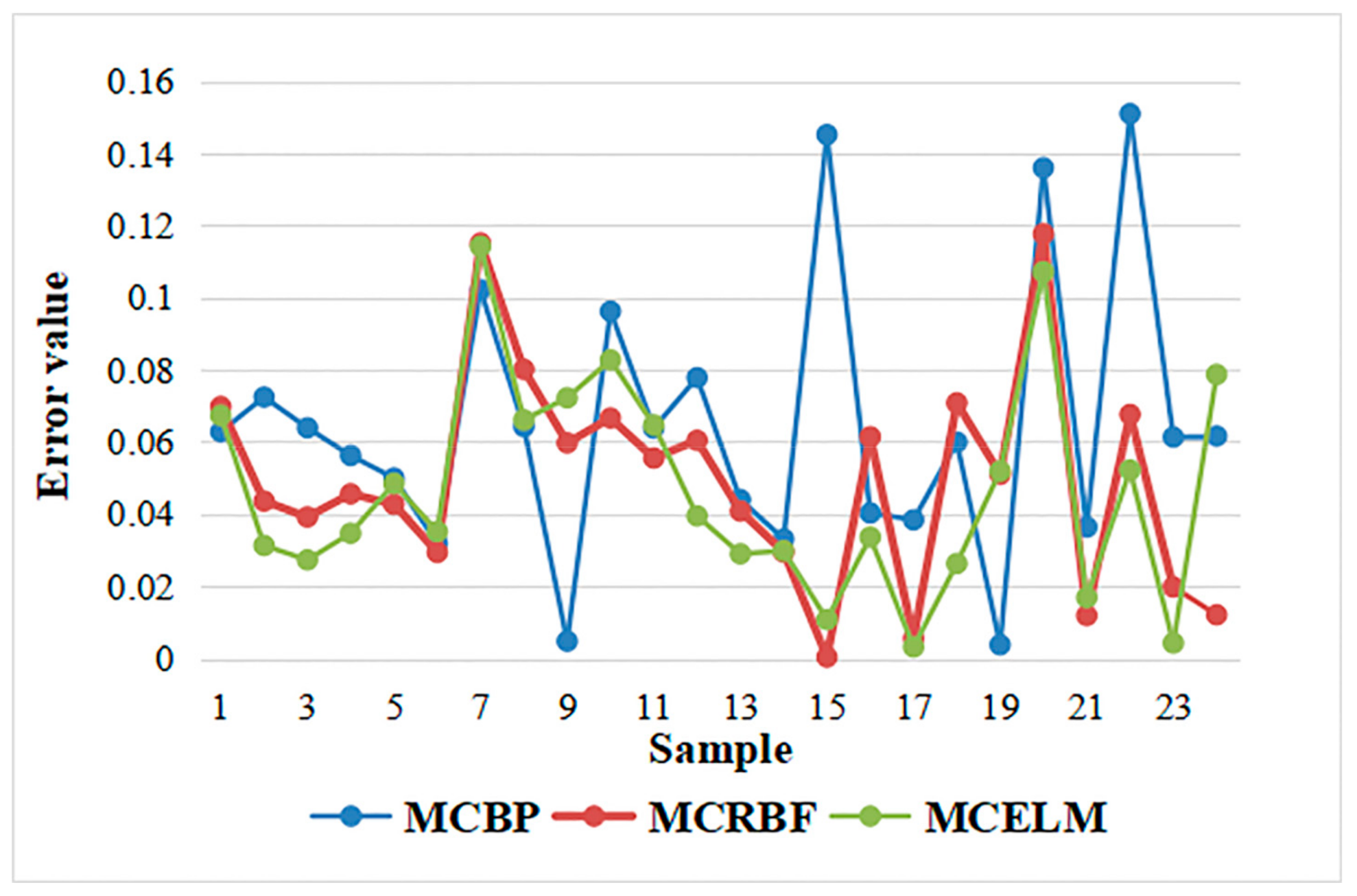
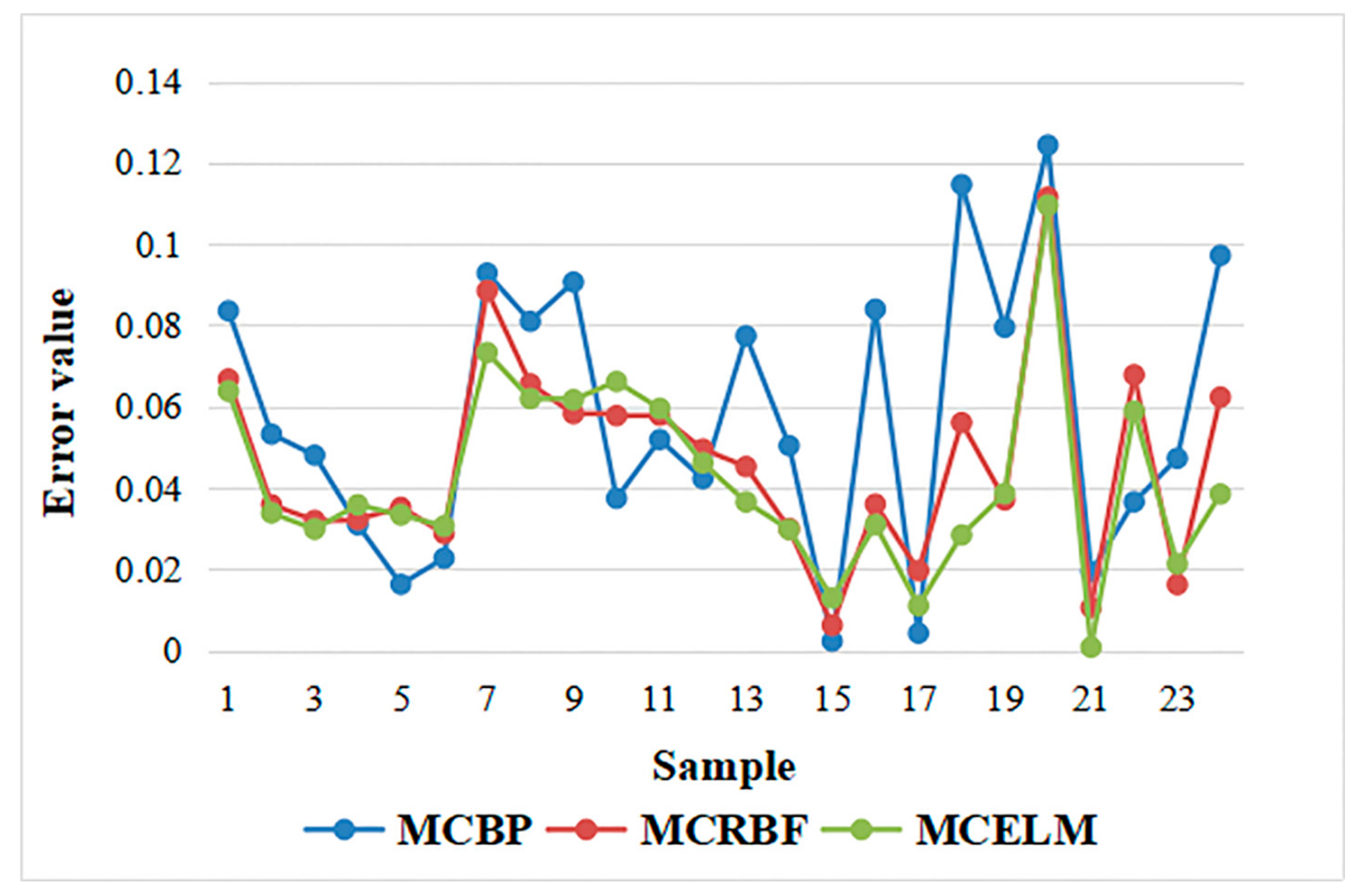
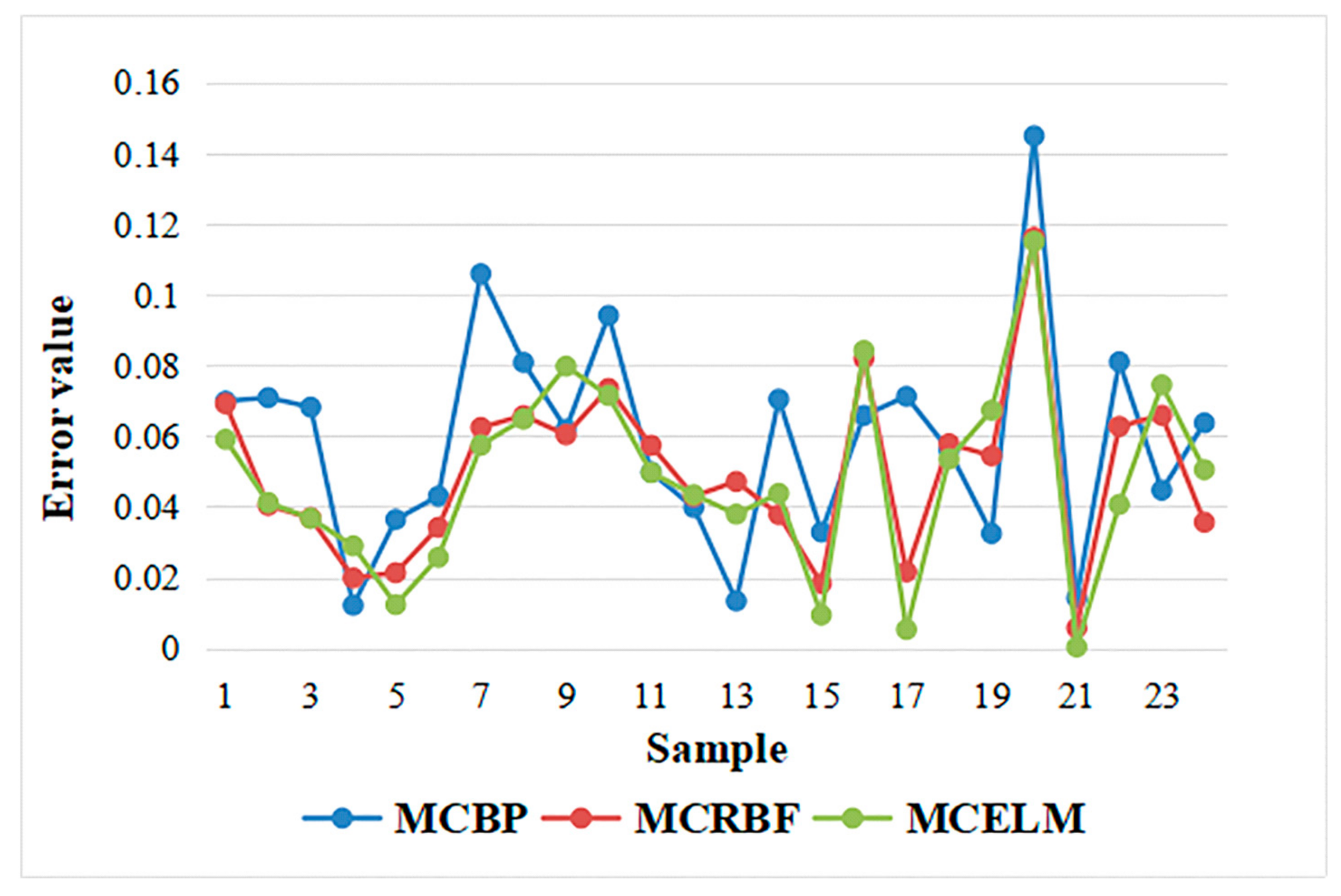
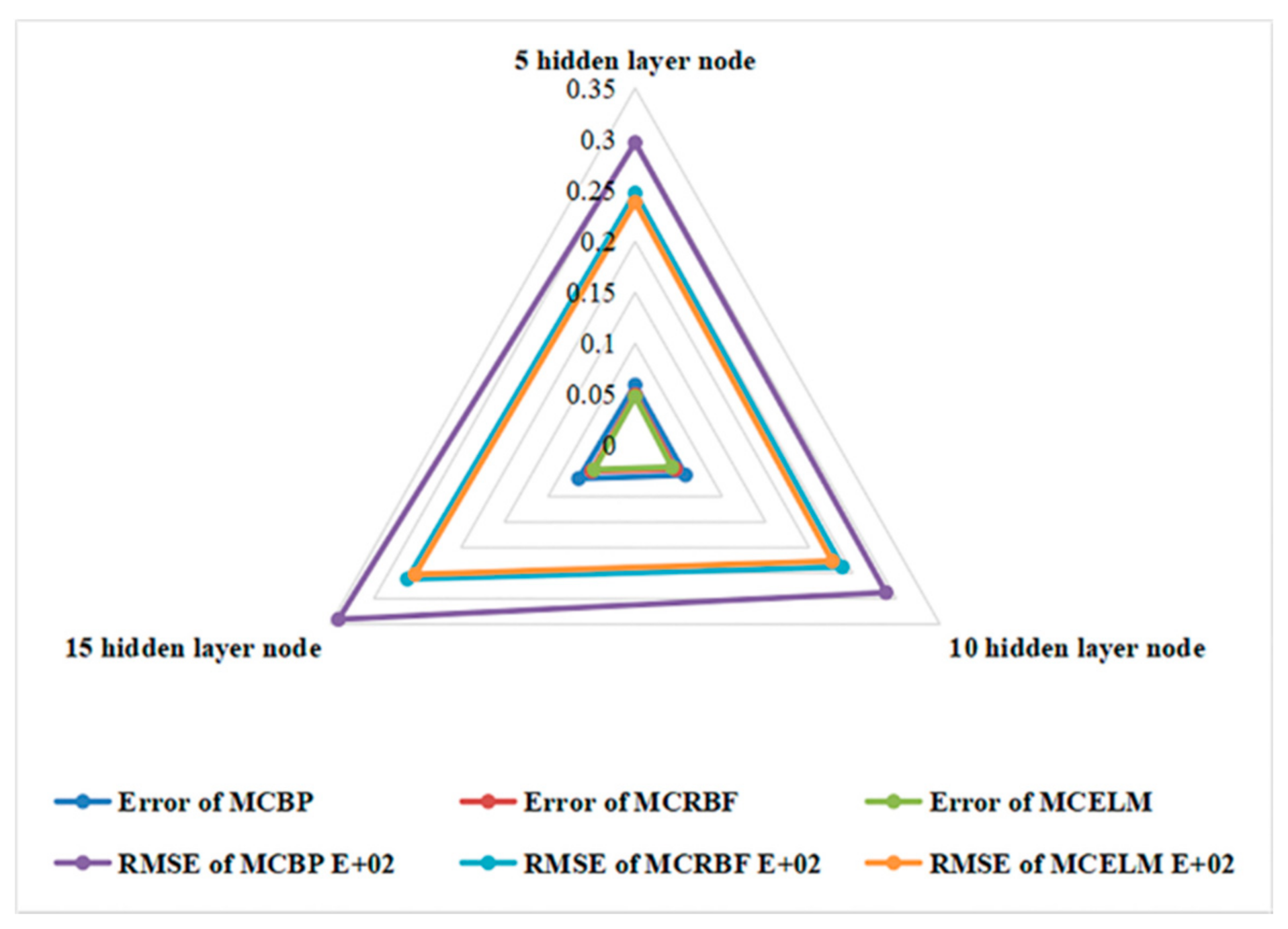
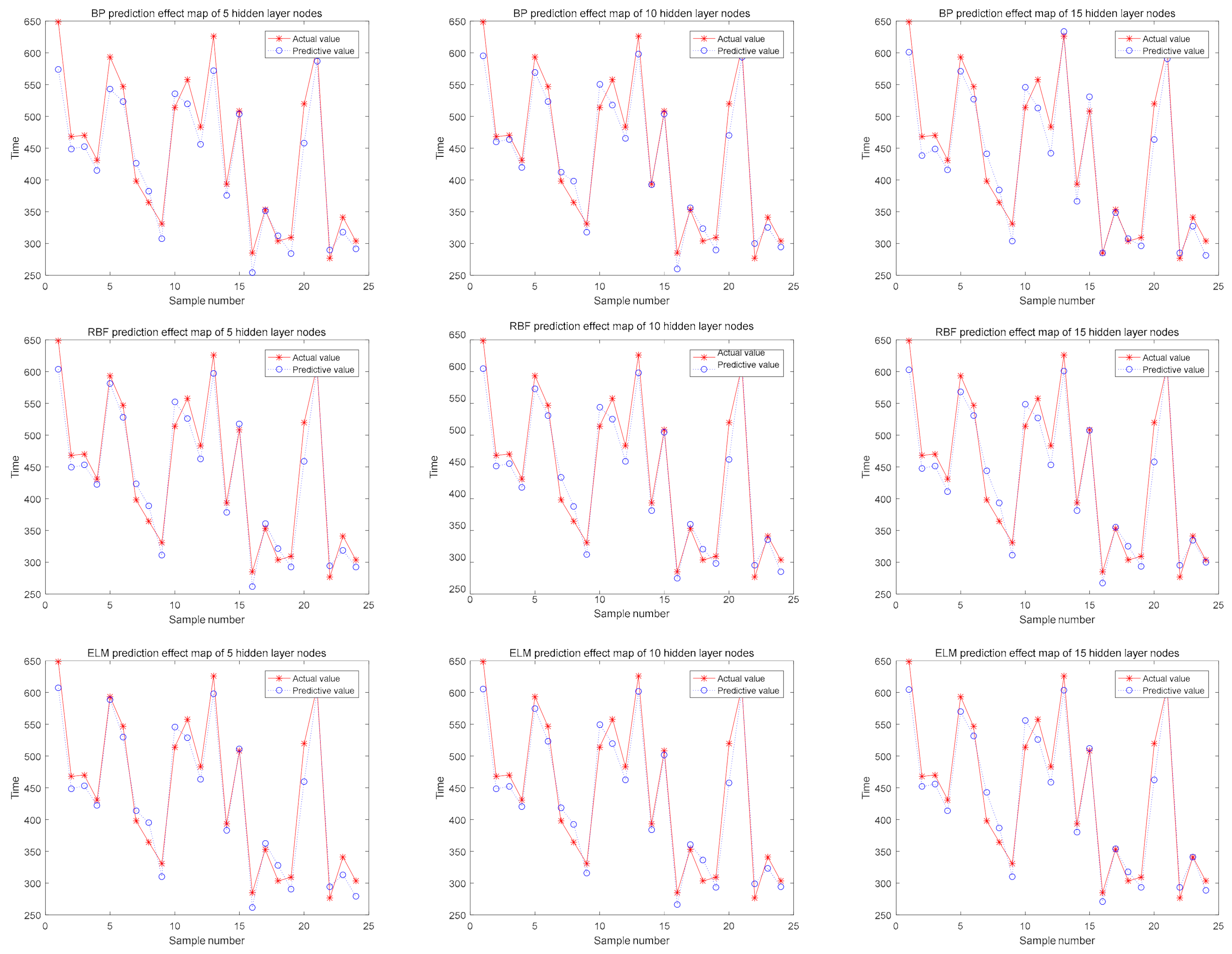
4.2.2. The Time Required Analysis and Prediction of the Dyeing Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ELM | Extreme learning machine |
| MC | Monte Carlo |
| MCELM | Extreme learning machine combing Monte Carlo |
| T-test | Student’s t test |
| BP | Back propagation |
| RBF | Radial basis function |
| GA | Genetic algorithm |
| PSO | Particle swarm optimization |
| DE | Differential evolution |
| WOA | Whale optimization algorithm |
| NIR | Near-infrared |
| VSG | Virtual sample generation |
| SLFNs | Single hidden layer feed-forward neural networks |
| The input of ELM | |
| The output attributes of samples | |
| L | Number of hidden layer nodes |
| h(x) | The activation function |
| The output of ELM | |
| Weight between the input layer node and the hidden layer node | |
| Weight between the hidden layer and the output layer | |
| Threshold of the hidden layer node | |
| H | Hidden layer output matrix |
| Moore-Penrose generalized inverse | |
| Dependable function | |
| nm | Nanometer |
| mm | Millimeter |
| s | Second |
| Eva | Equal variances assumed |
| Evna | Equal variances not assumed |
| MCBP | BP network combined with MC algorithm |
| MCRBF | RBF combined with MC algorithm |
| RMSE | Root mean squared error |
References
- Prospective Economists. The Status and Prospects of China’s Non-Woven Fabric Industry in 2020, the Market Size will Reach 157.2 Billion Yuan in 2025. Available online: https://baijiahao.baidu.com/s?id=1679329169537404479,20-10-01 (accessed on 28 January 2021).
- Li, J. Study on Wipes Used V-Type Melt-Blown Nonwomens and Products Development; Donghua University: Shanghai, China, 2016. [Google Scholar]
- Han, L. Study of Hydrophilic Finishing of ES Fiber Non-Wovens and Their Performances; Zhejiang Sci-Tech University: Hangzhou, Zhejiang, China, 2017. [Google Scholar]
- Zhu, L.; Perwuelz, A.; Lewandowski, M.; Campagne, C. Static and Dynamic Aspects of Liquid Capillary Flow in Thermally Bonded Polyester Nonwoven Fabrics; Taylor & Francis Group: London, UK, 2012; Volume 22. [Google Scholar]
- Viktor, K.; Horváth Stanley, H.E. Temporal Scaling of Interfaces Propagating in Porous Media. Phys. Rev. E 1995, 52, 5166. [Google Scholar]
- Bijeljic, B.; Markicevic, B.; Navaz, H.K. Capillary climb dynamics in the limits of prevailing capillary and gravity force. Phys. Rev. E Statal Nonlinear Soft Matter Phys. 2011, 83, 056310. [Google Scholar] [CrossRef] [PubMed]
- Wiklund, H.S.; Uesaka, T. Microfluidics of imbibition in random porous media. Phys. Rev. E Statal Nonlinear Soft Matter Phys. 2013, 87, 023006. [Google Scholar] [CrossRef] [PubMed]
- Nordlund, M. Numerical Study of the Local Permeability of Noncrimp Fabrics. J. Compos. Mater. 2005, 39, 929–947. [Google Scholar] [CrossRef]
- Chen, X.; Papathanasiou, T.D. The transverse permeability of disordered fiber arrays: A statistical correlation in terms of the mean nearest interfiber spacing. Transp. Porous Media 2008, 71, 233–251. [Google Scholar] [CrossRef]
- Srinidhi, D.P.; Vasantha, K.S.A. Artificial Neural Network (FFBP-ANN) Based Grey Relational Analysis for Modeling Dyestuff Solubility in Supercritical CO2 with Ethanol as the Co-Solvent; ChemRxiv. Preprint. 2020. Available online: https://chemrxiv.org/articles/preprint/Artificial_Neural_Network_FFBP-ANN_Based_Grey_s_Relational_Analysis_for_Modeling_Dyestuff_Solubility_in_Supercritical_CO2_with_Ethanol_as_the_Co-Solvent/11973273 (accessed on 28 January 2021).
- Laura, D.J.Z.O.; José, A.V.L.; Paloma, T.G.R.; Moisés, T.E. Generación de la formulación de color en un producto textil mediante redes neuronales artificiales. Nova Sci. 2018, 10, 78–96. [Google Scholar]
- Shen, J.J.; Zhou, X. Spectrophotometric colour matching algorithm for top-dyed mélange yarn, based on an artificial neural network. Coloration Technol. 2017, 133, 341–346. [Google Scholar] [CrossRef]
- Schubert, M.; Muffler, A.; Mourad, S. The use of a radial basis neural network and genetic algorithm for improving the efficiency of laccase-mediated dye decolorization. J. Biotechnol. 2012, 161, 429–436. [Google Scholar] [CrossRef] [PubMed]
- Li, H.T.; Shi, A.S.; Zhang, B.S.; Feng, W.Y.; Gao, F. A dyeing color matching method combining RBF neural networks with genetic algorithms. In Proceedings of the SNPD 2007: Eighth Acis International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing, Qingdao, China, 30 July 2007–1 August 2007; Volume 2, p. 701. [Google Scholar]
- Liu, Z.; Liang, Y. The spectral characterizing model based on optimized RBF neural network for digital textile printing. Lect. Notes Electr. Eng. 2018, 477, 55–60. [Google Scholar]
- Lu, H.Q.; Zhang, B.S. Application of Particle Swarm Optimization Algorithm Based on RBF Neural Network in Textile Dyeing Color Matching. J. Qingdao Univ. 2009, 24, 10–12. [Google Scholar]
- Zhu, Q.Y.; Qin, A.K.; Suganthan, P.N.; Huang, G.B. Evolutionary extreme learning machine. Pattern Recognit. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Wang, C.; Zhang, J.X.; Zhu, Z.F. Color difference classification of solid color printing and dyeing products based on optimization of the extreme learning machine of the improved whale optimization algorithm. Text. Res. J. 2020, 90, 135–155. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.Y.; Zhu, J.H.; Cheng, L.D.; Jiang, L. Study of the Automatic Knitting Defect Detection and Its Classification. Knitt. Ind. 2016, 17–20. [Google Scholar] [CrossRef]
- Chen, H.; Tan, C.; Lin, Z. Quantitative Determination of the Fiber Components in Textiles by Near-Infrared Spectroscopy and Extreme Learning Machine. Anal. Lett. 2020, 53, 844–857. [Google Scholar] [CrossRef]
- Li, D.C.; Wu, C.S.; Tsai, T.I. Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge. Comput. Oper. Res. 2007, 34, 966–982. [Google Scholar] [CrossRef]
- Chen, Z.S.; Zhu, B.; He, Y.L.; Yu, L.A.A. PSO based virtual sample generation method for small sample sets: Applications to regression datasets. Eng. Appl. Artif. Intell. 2017, 59, 236–243. [Google Scholar] [CrossRef]
- Yang, J.; Yu, X.; Xie, Z.Q.; Zhang, J.P. A novel virtual sample generation method based on Gaussian distribution. Knowl. Based Syst. 2011, 24, 740–748. [Google Scholar] [CrossRef]
- Otsuki, S. Symmetry relationships for multiple scattering of polarized light in turbid spherical samples: Theory and a Monte Carlo simulation. J. Opt. Soc. Am. A 2016, 33, 258–269. [Google Scholar] [CrossRef]
- Gong, H.F.; Chen, Z.S.; Zhu, Q.X.; He, Y.L. A Monte Carlo and PSO based virtual sample generation method for enhancing the energy prediction and energy optimization on small data problem: An empirical study of petrochemical industries. Appl. Energy 2017, 197, 405–415. [Google Scholar] [CrossRef]
- Jérôme, F.; Benjamin, Z.; Brian, E.; Jens, A.; Gürkan, S. Reverse Engineering of Working Fluid Selection for Industrial Heat Pump Based on Monte Carlo Sampling and Uncertainty Analysis. Ind. Eng. Chem. Res. 2018, 57, 13463–13477. [Google Scholar]
- Guo, Y.X.; Hou, Y.J.; Qi, P. Analysis of typhoon wind hazard in Shenzhen City by Monte-Carlo Simulation. J. Oceanol. Limnol. 2019, 37, 1994–2013. [Google Scholar] [CrossRef]
- Barth, A.; Schwab, C.; Sukys, J. Multilevel Monte Carlo Simulation of Statistical Solutions to the Navier-Stokes Equations. Monte Carlo Quasi-Monte Carlo Methods 2016, 163, 209–227. [Google Scholar]
- Masoodi, R.; Pillai, K.M. Darcy’s Law-Based Model for Wicking in Paper-Like Swelling Porous Media. AIChE J. 2010, 56, 2257–2267. [Google Scholar] [CrossRef]
| Physical Parameters | Expression | Value | Unit |
|---|---|---|---|
| Density of water | rho-water | 1 × 103 | kg/m3 |
| Water viscosity | mu-water | 2.98 × 10−3 | Pa·s |
| Surface Tension | gamma | 0.0723 | N/m |
| Density of air | rho-air | 1.293 | kg/m3 |
| Air viscosity | mu-air | 1.79 × 10−5 | Pa·s |
| Porosity | por | 0.6 | — |
| Bore diameter | Rc | 4.75 × 10−7 | m |
| Permeability | 1.69932 × 10−10 | m2 | |
| Contact angle | theta | 0 | ° |
| Inlet capillary pressure | 3.044 × 10−7 | Pa | |
| length | L0 | 12 | cm |
| width | W0 | 1.5 | cm |
| height | th | 1 | mm |
| Group | Mean | Standard Deviation | Standard Error Mean | |
|---|---|---|---|---|
| Bore diameter(nm) | Original data | 269.36 | 201.922 | 90.302 |
| Expanded data | 301.905 | 165.946 | 14.902 | |
| Porosity (%) | Original data | 64 | 18.166 | 8.124 |
| Expanded data | 65.011 | 16.316 | 1.465 | |
| Height(mm) | Original data | 59.008 | 33.187 | 14.842 |
| Expanded data | 64.211 | 27.894 | 2.505 | |
| Time(s) | Original data | 402 | 154.984 | 69.311 |
| Expanded data | 417.4 | 141.248 | 12.684 |
| Levene’s Test for Equality of Variances | T-Test for Equality of Means | |||||||
|---|---|---|---|---|---|---|---|---|
| F | Significance | t | Degrees of Freedom | Significance (Two-Tailed) | 95% Confidence Interval of the Difference | |||
| Lower | Upper | |||||||
| Bore diameter (nm) | Eva | 0.36 | 0.55 | −0.427 | 127 | 0.67 | −183.461 | 118.371 |
| Evna | −0.356 | 4.221 | 0.739 | −281.5 | 216.41 | |||
| Porosity (%) | Eva | 0.025 | 0.874 | −0.014 | 127 | 0.893 | −15.793 | 13.772 |
| Evna | −0.122 | 4.264 | 0.908 | −23.381 | 21.36 | |||
| Height (mm) | Eva | 0.063 | 0.802 | −0.406 | 127 | 0.685 | −30.544 | 20.139 |
| Evna | −0.346 | 4.231 | 0.746 | −46.108 | 35.703 | |||
| Time (s) | Eva | 0.007 | 0.934 | −0.238 | 127 | 0.812 | −143.303 | 112.502 |
| Evna | −0.219 | 4.272 | 0.837 | −206.214 | 175.413 | |||
| 5 Hidden Layer Node | 10 Hidden Layer Node | 15 Hidden Layer Node | ||||
|---|---|---|---|---|---|---|
| MRE | RMSE | MRE | RMSE | MRE | RMSE | |
| MCBP | 0.0593 | 29.657 | 0.0578 | 28.805 | 0.0649 | 34.069 |
| MCRBF | 0.0495 | 24.719 | 0.0461 | 23.793 | 0.0498 | 26.157 |
| MCELM | 0.048 | 23.802 | 0.0422 | 22.630 | 0.047 | 25.246 |
| BP | RBF | ELM | |
|---|---|---|---|
| 5 hidden layer node | 4.821386 s | 4.128717 s | 3.398797 s |
| 10 hidden layer node | 4.901459 s | 4.031216 s | 3.449390 s |
| 15 hidden layer node | 5.045841 s | 4.521651 s | 3.348385 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Fan, Y.; Zhang, L.; Xu, C.; Dong, X.; Liu, L.; Zhang, Z.; Qiu, X. Seepage Time Soft Sensor Model of Nonwoven Fabric Based on the Extreme Learning Machine Integrating Monte Carlo. Sensors 2021, 21, 2377. https://doi.org/10.3390/s21072377
Zhang J, Fan Y, Zhang L, Xu C, Dong X, Liu L, Zhang Z, Qiu X. Seepage Time Soft Sensor Model of Nonwoven Fabric Based on the Extreme Learning Machine Integrating Monte Carlo. Sensors. 2021; 21(7):2377. https://doi.org/10.3390/s21072377
Chicago/Turabian StyleZhang, Jing, Yiqiang Fan, Lulu Zhang, Chi Xu, Xiaobin Dong, Luyao Liu, Zhongping Zhang, and Xianbo Qiu. 2021. "Seepage Time Soft Sensor Model of Nonwoven Fabric Based on the Extreme Learning Machine Integrating Monte Carlo" Sensors 21, no. 7: 2377. https://doi.org/10.3390/s21072377
APA StyleZhang, J., Fan, Y., Zhang, L., Xu, C., Dong, X., Liu, L., Zhang, Z., & Qiu, X. (2021). Seepage Time Soft Sensor Model of Nonwoven Fabric Based on the Extreme Learning Machine Integrating Monte Carlo. Sensors, 21(7), 2377. https://doi.org/10.3390/s21072377







