EDISON: An Edge-Native Method and Architecture for Distributed Interpolation
Abstract
1. Introduction
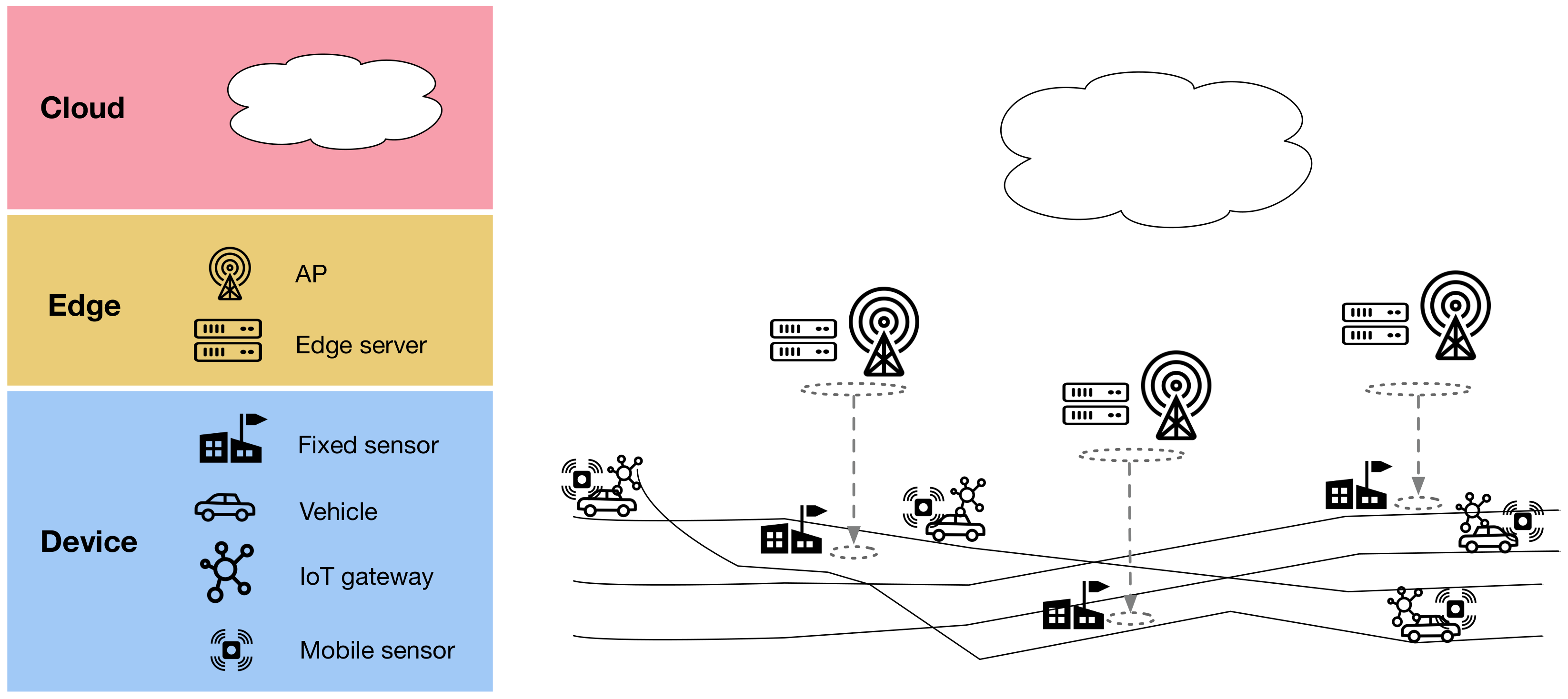
- We present an edge-native, distributed interpolation architecture for the smart city networking environment, characterized by spatio-temporal nature and large-scale communications.
- We present a distributed learning and inference method for our architecture, to make edge-native interpolations with spatio-temporally distributed data.
- We evaluate our solution with a controlled environment of simulations, enforcing the natural phenomena observed in our previous work [23].
2. Related Work
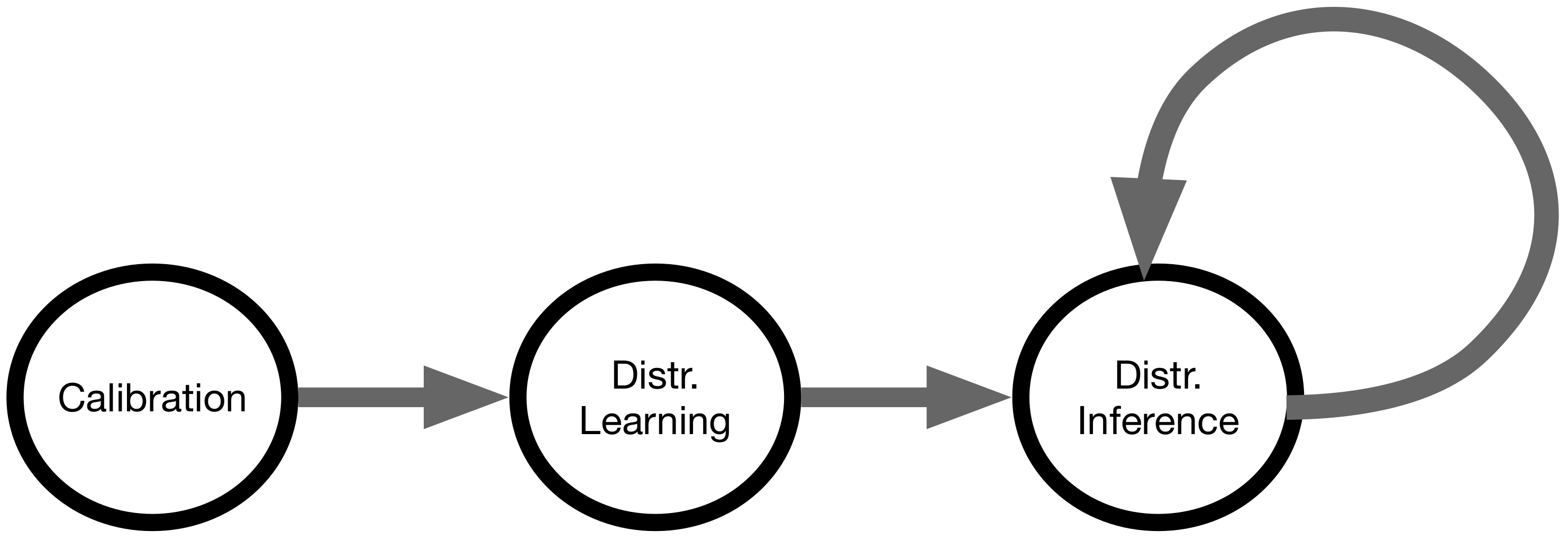
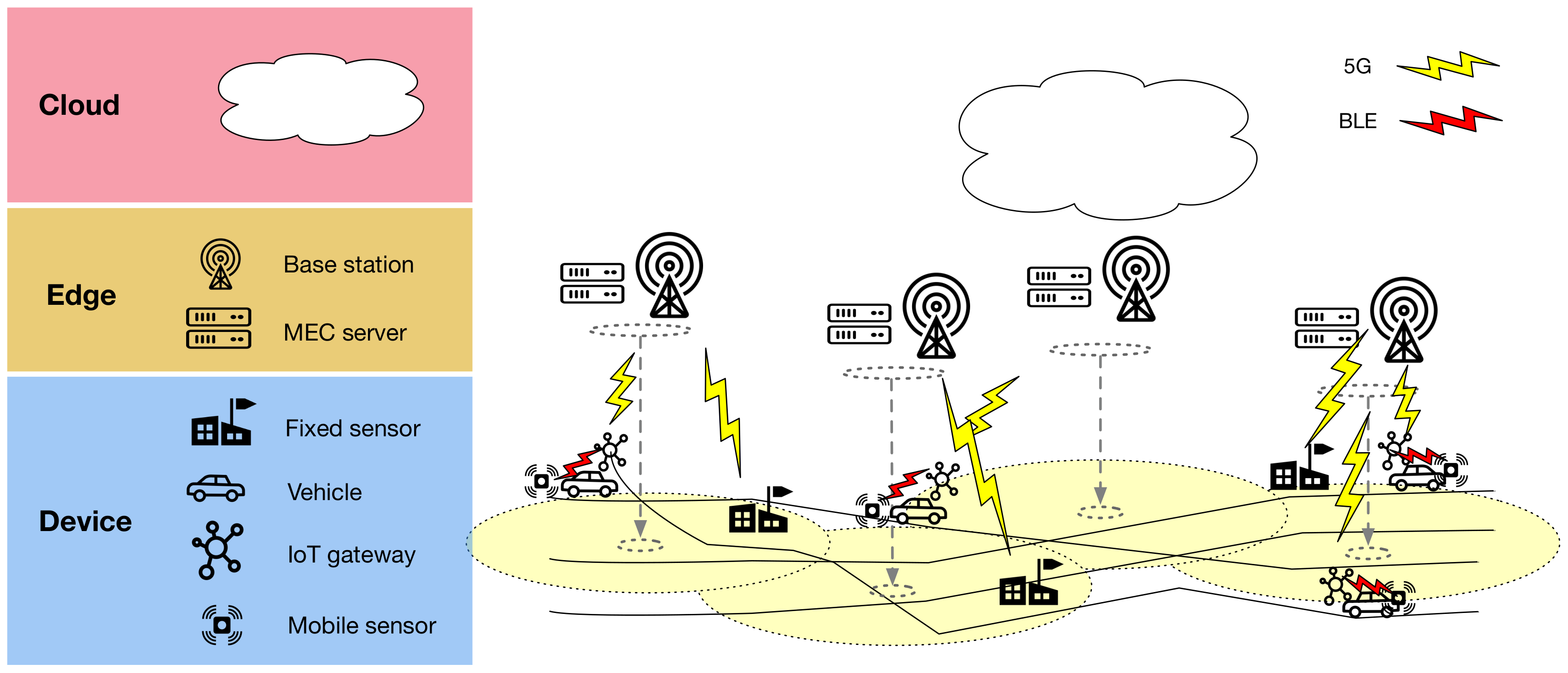
3. EDISON
- Calibration
- (a)
- CLOUD: Estimate calibration parameters for mobile sensors. Calibrate the collected sensor training set.
- (b)
- CLOUD: Transmit estimate calibration parameters to edge servers.
- (c)
- EDGE SERVERS: Transmit calibration parameters to IoT gateways passing by.
- (d)
- IOT GATEWAYS: Transmit calibration parameters to mobile sensors.
- (e)
- MOBILE SENSORS: Apply calibration.
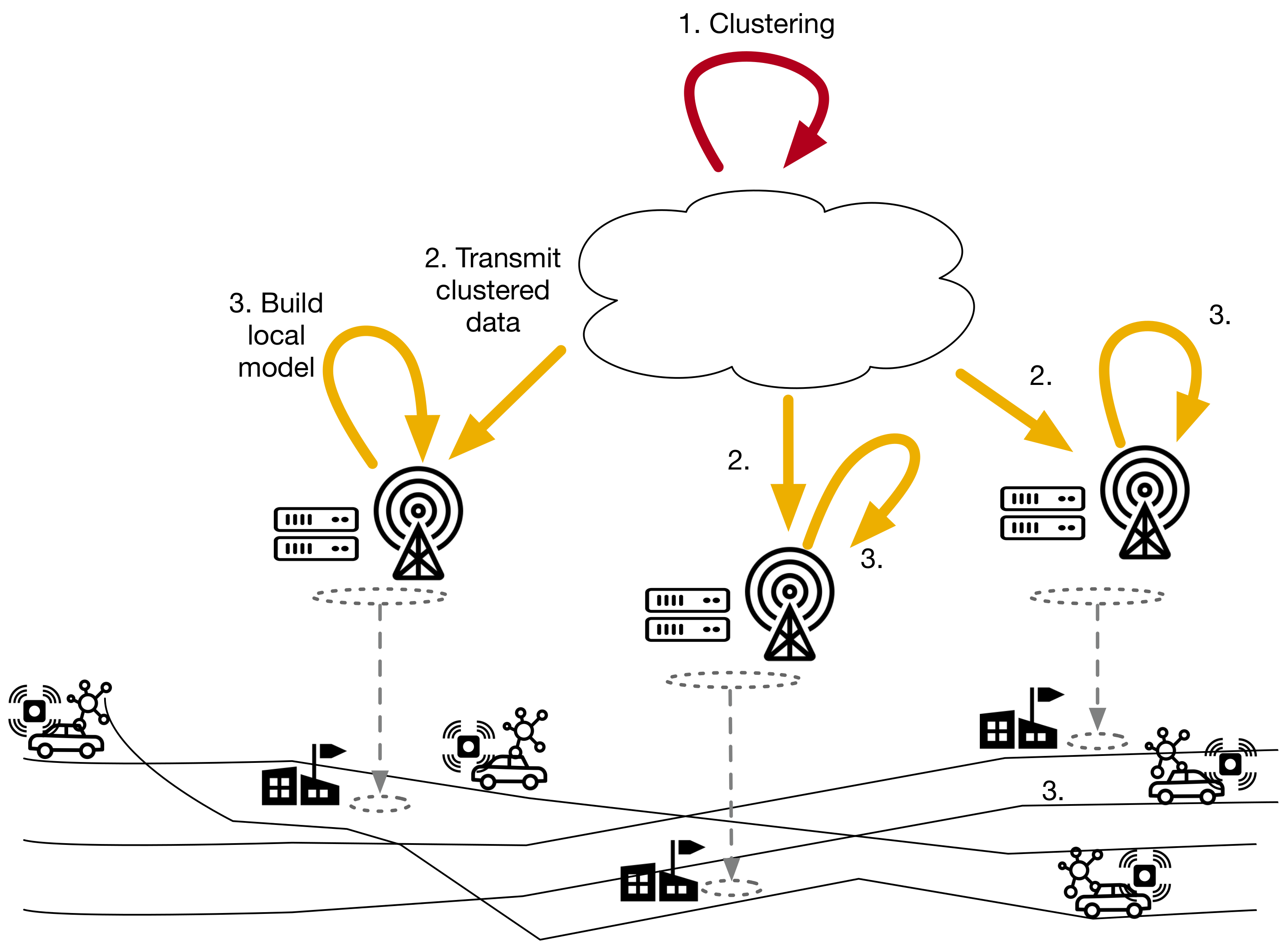
- Distributed learning
- (a)
- CLOUD: Partition the training set into subsets of observations around each edge server. Aim for subsets whose observations are maximally independent of the observations in other subsets.
- (b)
- CLOUD: Send the partitioned training set to all edge servers, rasterized to reduce transmission burden.
- (c)
- EDGE SERVERS: Fit a local, spatio-temporal interpolation model for the observations in the edge server’s subset of the training set.
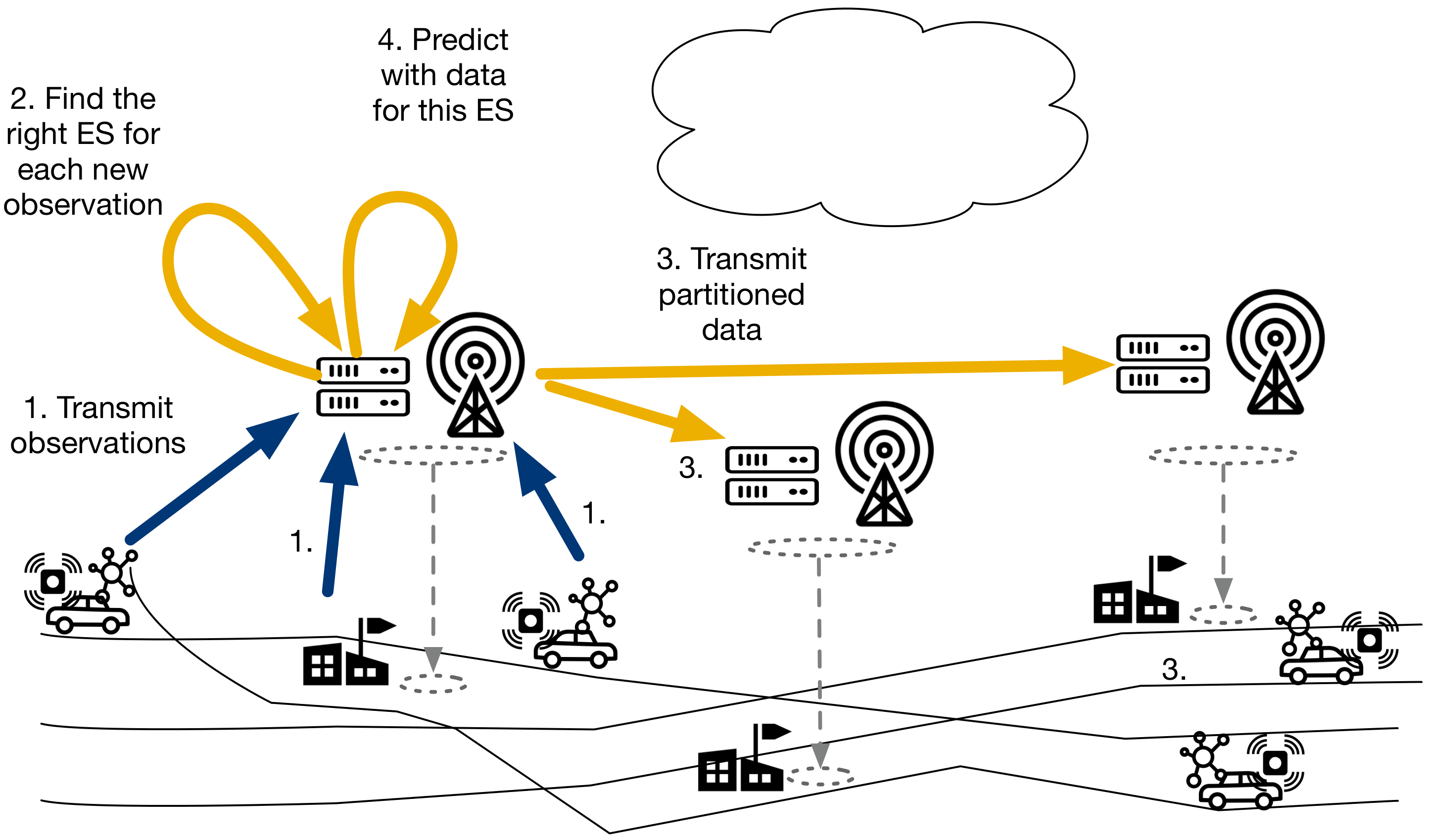
- Distributed inference
- (a)
- MOBILE SENSORS: Send all observations immediately to the IoT gateway in the vehicle.
- (b)
- IOT GATEWAY: Store observations. Send stored observations to an edge server when passing by.
- (c)
- FIXED SENSORS: Send all observations immediately to edge servers.
- (d)
- EDGE SERVERS: Every time interval, find the right edge server (i.e., the right cluster) for each new mobile observation from IoT gateways that have passed by.
- (e)
- EDGE SERVERS: Send new mobile observations to selected edge servers.
- (f)
- EDGE SERVERS: Every time interval, apply the local interpolation model with the data collected by the sensors.
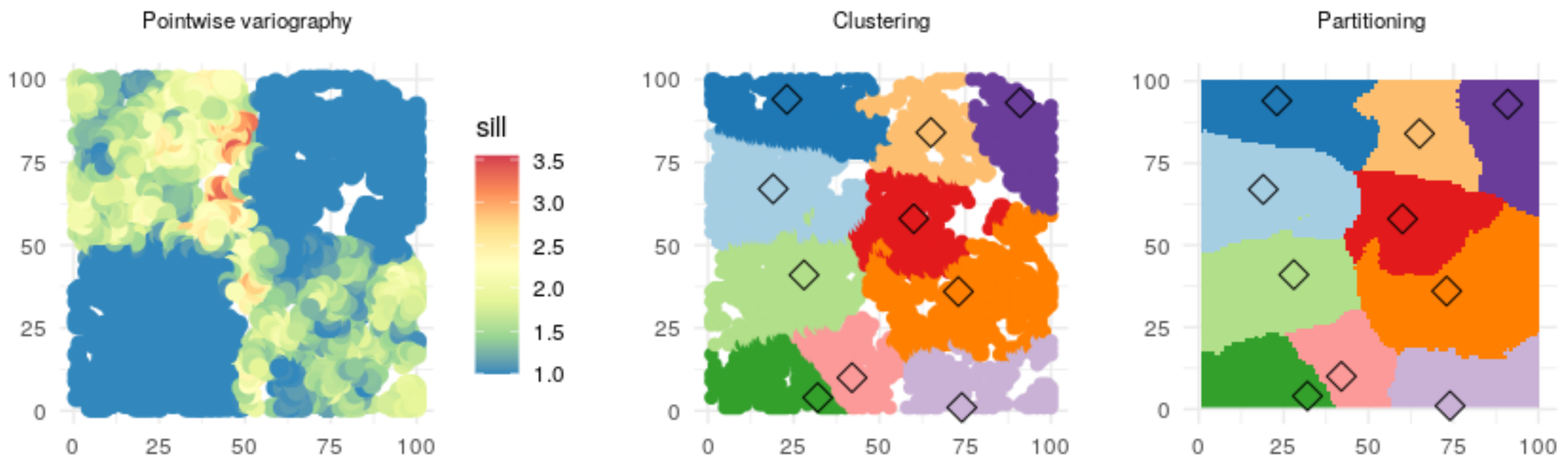
3.1. Distributed Learning
- Independence: each subset should be as independent as possible from the others.
- Spatial connectedness: each resulting subset should be a spatially connected set of points.
| Algorithm 1:Distributed learning |
 |
3.2. Clustering
3.3. Distributed Inference
| Algorithm 2:Distributed inference |
 |
4. Evaluation
- Generate artificial ground truth data comprising complex spatio-temporal dependency structures.
- Simulate sensor data.
- (a)
- Simulate static sensor locations.
- (b)
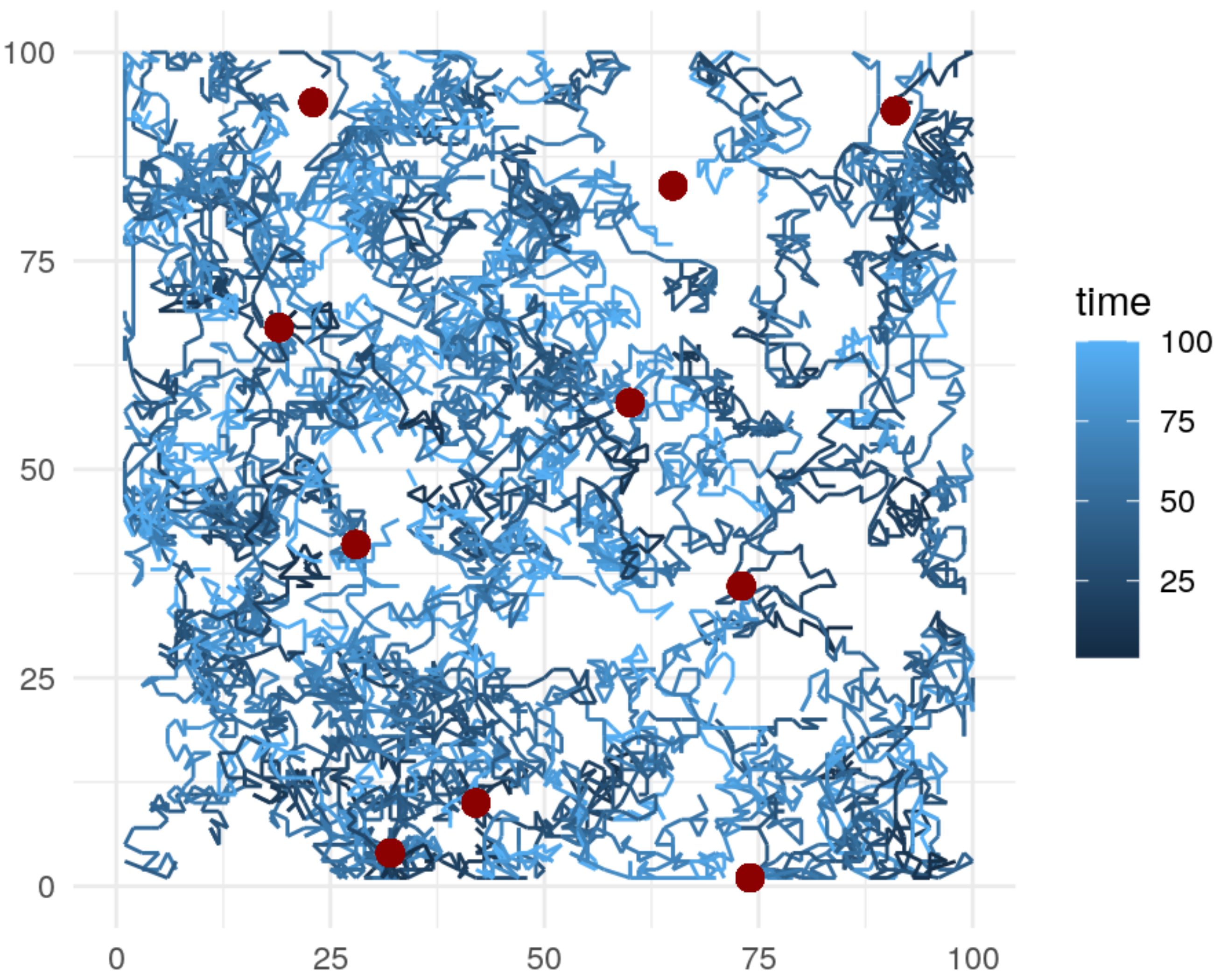
- Simulate mobile sensor trajectories.
- (c)
- Collect observations from the static sensor locations and along the mobile sensor trajectories.
- Run EDISON.
- (a)
- Split the observations into training and test sets.
- (b)
- Conduct EDISON distributed learning on the training set.
- (c)
- Conduct EDISON distributed inference on the test set.
- Calculate results.
- (a)
- Compare EDISON results to ground truth with RMSE.
- (b)
- Compare reference results to ground truth with RMSE.
4.1. Data Generation
4.2. Sensor Simulation
4.3. EDISON
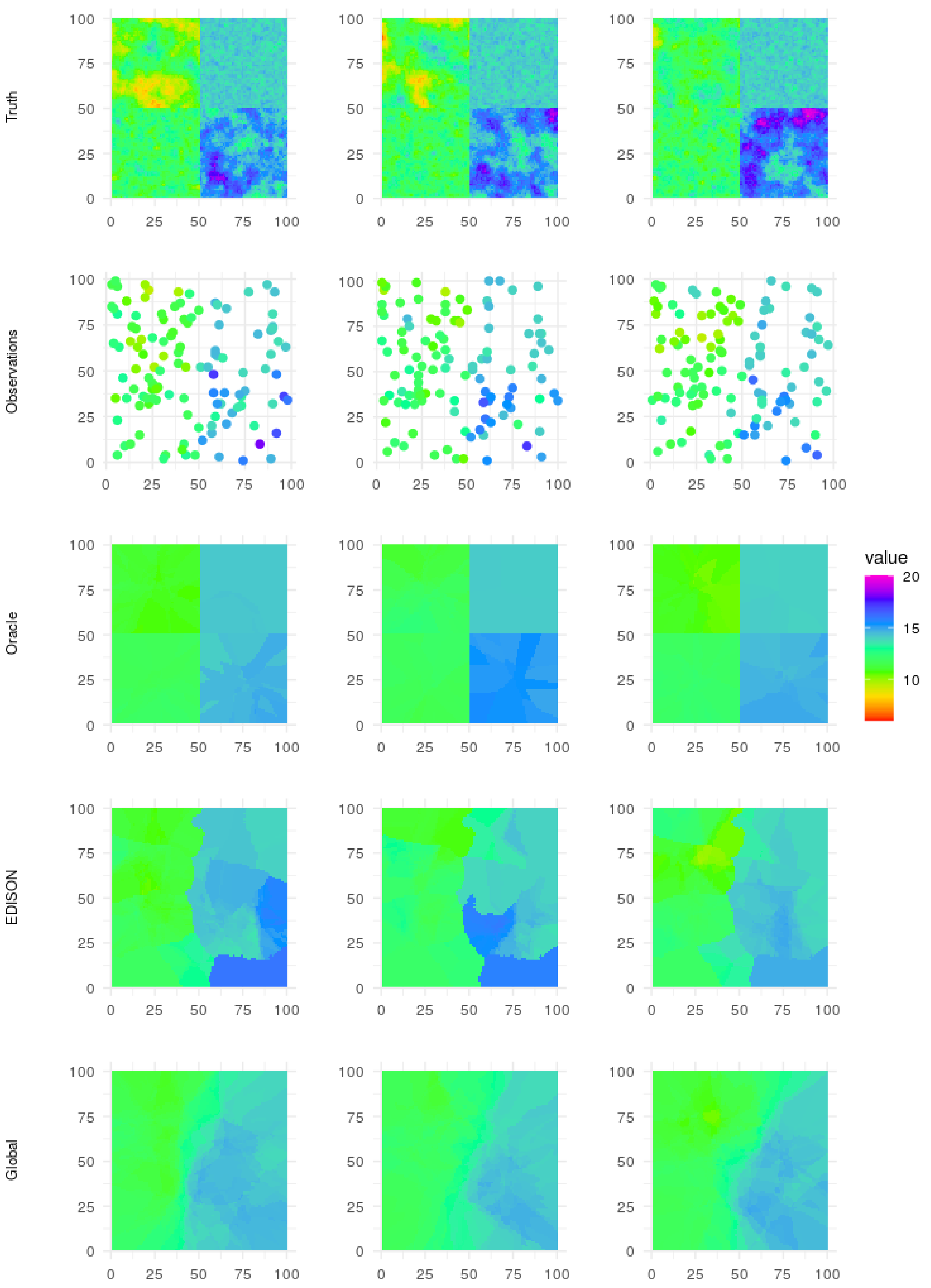
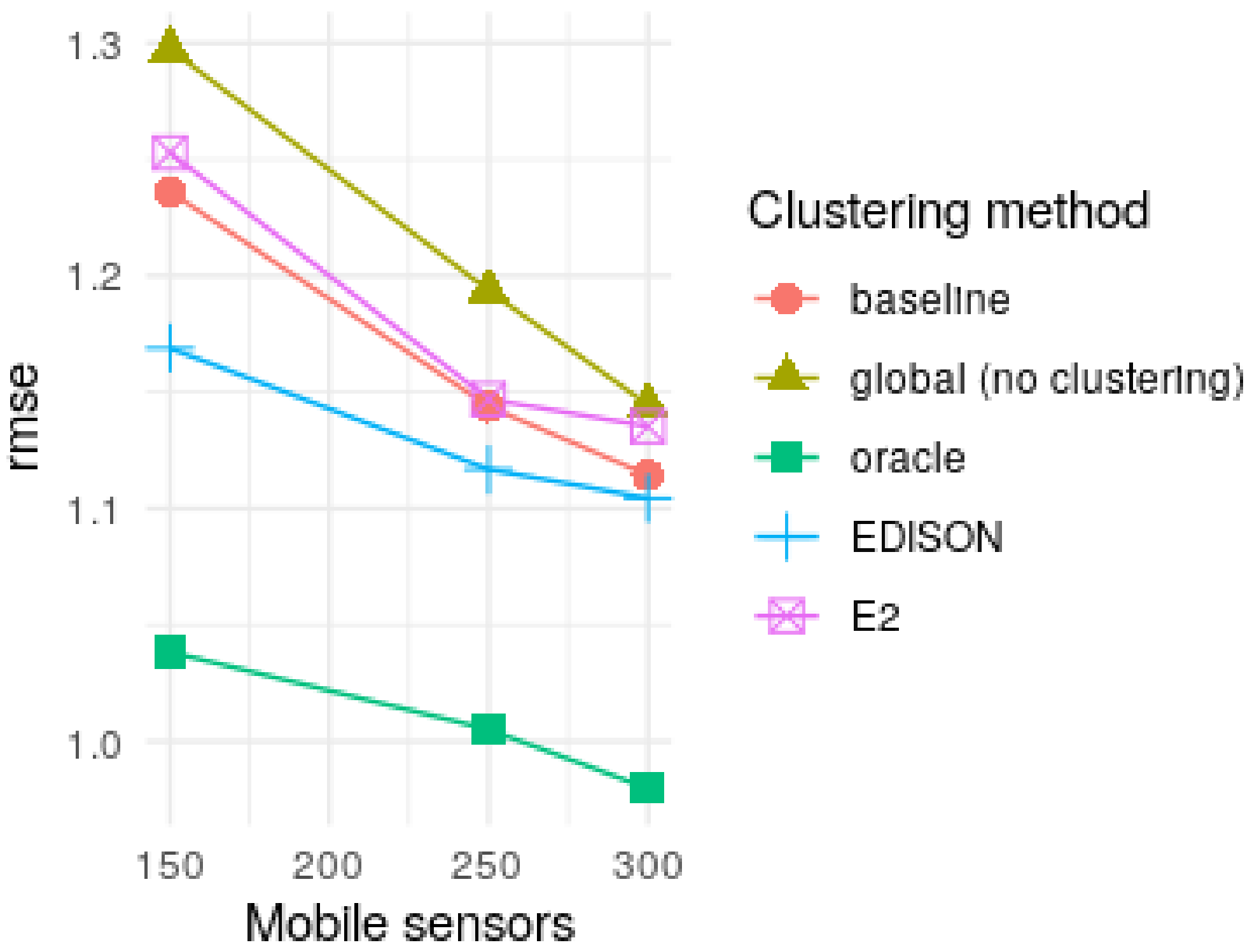
4.4. Results
- global: unclustered interpolation over the whole map
- oracle: interpolation with pre-knowledge of the borders between the four data-generating processes
- baseline: each observation is assigned to the closest edge server
- E2: EDISON algorithm whose proximity part of the distance function (i.e., the spatial distance part) is squared, instead of cubed (see Section 3.2)
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AP | Access point |
| EDISON | Edge-native distributed interpolation |
| ES | Edge server |
| GP | Gaussian process |
| MDPI | Multidisciplinary Digital Publishing Institute |
References
- United Nations, Department of Economic and Social Affairs, Population Division. World Urbanization Prospects: The 2018 Revision (ST/ESA/SER.A/420); United Nations: New York, NY, USA, 2019. [Google Scholar]
- Meijer, A.; Bolívar, M.P.R. Governing the smart city: A review of the literature on smart urban governance. Int. Rev. Adm. Sci. 2016, 82, 392–408. [Google Scholar]
- Gaur, A.; Scotney, B.; Parr, G.; McClean, S. Smart city architecture and its applications based on IoT. Procedia Comput. Sci. 2015, 52, 1089–1094. [Google Scholar] [CrossRef]
- Strohbach, M.; Ziekow, H.; Gazis, V.; Akiva, N. Towards a big data analytics framework for IoT and smart city applications. In Modeling and Processing for Next-Generation Big-Data Technologies; Springer: Berlin/Heidelberg, Germany, 2015; pp. 257–282. [Google Scholar]
- Angelidou, M.; Psaltoglou, A.; Komninos, N.; Kakderi, C.; Tsarchopoulos, P.; Panori, A. Enhancing sustainable urban development through smart city applications. J. Sci. Technol. Policy Manag. 2018, 9. [Google Scholar] [CrossRef]
- Naphade, M.; Banavar, G.; Harrison, C.; Paraszczak, J.; Morris, R. Smarter cities and their innovation challenges. Computer 2011, 44, 32–39. [Google Scholar] [CrossRef]
- Lau, B.P.L.; Marakkalage, S.H.; Zhou, Y.; Hassan, N.U.; Yuen, C.; Zhang, M.; Tan, U.X. A survey of data fusion in smart city applications. Inf. Fusion 2019, 52, 357–374. [Google Scholar] [CrossRef]
- Bokolo, A.J.; Majid, M.A.; Romli, A. A trivial approach for achieving Smart City: A way forward towards a sustainable society. In Proceedings of the 2018 21st Saudi Computer Society National Computer Conference (NCC), Riyadh, Saudi Arabia, 25–26 April 2018; pp. 1–6. [Google Scholar]
- Jararweh, Y.; Otoum, S.; Al Ridhawi, I. Trustworthy and sustainable smart city services at the edge. Sustain. Cities Soc. 2020, 62, 102394. [Google Scholar] [CrossRef]
- Barthélemy, J.; Verstaevel, N.; Forehead, H.; Perez, P. Edge-computing video analytics for real-time traffic monitoring in a smart city. Sensors 2019, 19, 2048. [Google Scholar] [CrossRef] [PubMed]
- Cicirelli, F.; Guerrieri, A.; Spezzano, G.; Vinci, A. An edge-based platform for dynamic Smart City applications. Future Gener. Comput. Syst. 2017, 76, 106–118. [Google Scholar] [CrossRef]
- Taleb, T.; Dutta, S.; Ksentini, A.; Iqbal, M.; Flinck, H. Mobile edge computing potential in making cities smarter. IEEE Commun. Mag. 2017, 55, 38–43. [Google Scholar] [CrossRef]
- Giordano, A.; Spezzano, G.; Vinci, A. Smart agents and fog computing for smart city applications. In Proceedings of the International Conference on Smart Cities, Malaga, Spain, 15–17 June 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 137–146. [Google Scholar]
- Deng, Y.; Chen, Z.; Yao, X.; Hassan, S.; Wu, J. Task scheduling for smart city applications based on multi-server mobile edge computing. IEEE Access 2019, 7, 14410–14421. [Google Scholar] [CrossRef]
- Chiang, M.; Shi, W. Grand Challenges in Edge Computing; Technical Report; National Science Foundation: Washington, DC, USA, 2017.
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge Computing: Vision and Challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Kitchin, R. Making sense of smart cities: Addressing present shortcomings. Camb. J. Reg. Econ. Soc. 2015, 8, 131–136. [Google Scholar] [CrossRef]
- He, Y.; Yu, F.R.; Zhao, N.; Leung, V.C.; Yin, H. Software-defined networks with mobile edge computing and caching for smart cities: A big data deep reinforcement learning approach. IEEE Commun. Mag. 2017, 55, 31–37. [Google Scholar] [CrossRef]
- Li, M.; Si, P.; Zhang, Y. Delay-tolerant data traffic to software-defined vehicular networks with mobile edge computing in smart city. IEEE Trans. Veh. Technol. 2018, 67, 9073–9086. [Google Scholar] [CrossRef]
- Lovén, L.; Leppänen, T.; Peltonen, E.; Partala, J.; Harjula, E.; Porambage, P.; Ylianttila, M.; Riekki, J. EdgeAI: A vision for distributed, edge-native artificial intelligence in future 6G networks. In Proceedings of the 1st 6G Wireless Summit, Levi, Finland, 24–26 March 2019; pp. 1–2. [Google Scholar]
- Partala, J.; Lovén, L.; Peltonen, E.; Porambage, P.; Ylianttila, M.; Seppänen, T. EdgeAI: A vision for privacy-preserving machine learning on the edge. In Proceedings of the 10th Nordic Workshop on System and Network Optimization for Wireless (SNOW), Ruka, Finland, 1–4 April 2019. [Google Scholar]
- Park, J.; Samarakoon, S.; Bennis, M.; Debbah, M.M. Wireless network intelligence at the edge. Proc. IEEE 2019, 107, 2204–2239. [Google Scholar] [CrossRef]
- Lovén, L.; Karsisto, V.; Järvinen, H.; Sillanpää, M.J.; Leppänen, T.; Peltonen, E.; Pirttikangas, S.; Riekki, J. Mobile road weather sensor calibration by sensor fusion and linear mixed models. PLoS ONE 2019, 14, 1–17. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Processes for Machine Learning; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Lovén, L.; Peltonen, E.; Pandya, A.; Leppänen, T.; Gilman, E.; Pirttikangas, S.; Riekki, J. Towards EDISON: An edge-native approach to distributed interpolation of environmental data. In Proceedings of the 28th International Conference on Computer Communications and Networks (ICCCN2019), 1st Edge of Things Workshop 2019 (EoT2019), Valencia, Spain, 29 July–1 August 2019. [Google Scholar]
- Iorga, M.; Feldman, L.; Barton, R.; Martin, M.J.; Goren, N.; Mahmoudi, C. Fog Computing Conceptual Model; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [CrossRef]
- Walravens, N. Mobile city applications for Brussels citizens: Smart City trends, challenges and a reality check. Telemat. Inform. 2015, 32, 282–299. [Google Scholar] [CrossRef]
- Santana, E.F.Z.; Chaves, A.P.; Gerosa, M.A.; Kon, F.; Milojicic, D. Software platforms for smart cities: Concepts, requirements, challenges, and a unified reference architecture. ACM Comput. Surv. 2016, 50, 1–37. [Google Scholar] [CrossRef]
- Mehmood, H.; Gilman, E.; Cortes, M. Implementing big data lake for heterogeneous data sources. In Proceedings of the 1st International Workshop on Data-Driven Smart Cities, in Conjunction with 35th IEEE International Conference on Data Engineering (ICDE 2019), Macao, China, 8–12 April 2019. [Google Scholar]
- Raza, U.; Camerra, A.; Murphy, A.L.; Palpanas, T.; Picco, G.P. What does model-driven data acquisition really achieve in wireless sensor networks? In Proceedings of the 2012 IEEE International Conference on Pervasive Computing and Communications, PerCom 2012, Lugano, Switzerland, 19–23 March 2012; pp. 85–94. [Google Scholar] [CrossRef]
- Peltonen, E.; Leppänen, T.; Lovén, L. EdgeAI: Edge-native distributed platform for artificial intelligence. In Proceedings of the 1st 6G Wireless Summit, Levi, Finland, 24–26 March 2019; pp. 1–2. [Google Scholar]
- Hossain, S.K.A.; Rahman, M.A.; Hossain, M.A. Edge computing framework for enabling situation awareness in IoT based smart city. J. Parallel Distrib. Comput. 2018, 122, 226–237. [Google Scholar] [CrossRef]
- Fortino, G.; Russo, W.; Savaglio, C.; Viroli, M.; Zhou, M. Modeling opportunistic IoT services in open IoT ecosystems. In Proceedings of the XVIII Workshop “From Objects to Agents”, Scilla, Italy, 15–17 June 2017; pp. 90–95. [Google Scholar]
- Baker, T.; Aldawsari, B.; Asim, M.; Tawfik, H.; Maamar, Z.; Buyya, R. Cloud-SEnergy: A bin-packing based multi-cloud service broker for energy efficient composition and execution of data-intensive applications. Sustain. Comput. Inform. Syst. 2018, 19, 242–252. [Google Scholar] [CrossRef]
- Lagerspetz, E.; Varjonen, S.; Concas, F.; Mineraud, J.; Tarkoma, S. Demo: MegaSense: Megacity-scale accurate air quality sensing with the edge. In Proceedings of the 24th Annual International Conference on Mobile Computing and Networking (MobiCom ’18), New Delhi, India, 29 October–2 November 2018; ACM: New York, NY, USA, 2018; pp. 843–845. [Google Scholar]
- Van Stein, B.; Wang, H.; Kowalczyk, W.; Emmerich, M.; Bäck, T. Cluster-based kriging approximation algorithms for complexity reduction. Appl. Intell. 2020, 50, 778–791. [Google Scholar] [CrossRef]
- Amato, F.; Guignard, F.; Robert, S.; Kanevski, M. A novel framework for spatio-temporal prediction of environmental data using deep learning. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Apley, D. Patchwork kriging for large-scale Gaussian process regression. J. Mach. Learn. Res. 2018, 19, 1–43. [Google Scholar]
- Yasojima, C.; Protázio, J.; Meiguins, B.; Neto, N.; Morais, J. A new methodology for automatic cluster-based kriging using K-nearest neighbor and genetic algorithms. Information 2019, 10, 357. [Google Scholar] [CrossRef]
- Hernández-Peñaloza, G.; Beferull-Lozano, B. Field estimation in wireless sensor networks using distributed kriging. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 724–729. [Google Scholar] [CrossRef]
- Chowdappa, V.P.; Botella, C.; Beferull-Lozano, B. Distributed clustering algorithm for spatial field reconstruction in wireless sensor networks. IEEE Veh. Technol. Conf. 2015, 2015. [Google Scholar] [CrossRef]
- Park, J.; Wang, S.; Elgabli, A.; Oh, S.; Jeong, E.; Cha, H.; Kim, H.; Kim, S.L.; Bennis, M. Distilling on-device intelligence at the network edge. arXiv 2019, arXiv:1908.05895v1. [Google Scholar]
- Deng, S.; Zhao, H.; Fang, W.; Yin, J.; Dustdar, S.; Zomaya, A.Y. Edge intelligence: The confluence of edge computing and artificial intelligence. IEEE Internet Things J. 2020, 7, 7457–7469. [Google Scholar] [CrossRef]
- Xu, D.; Li, T.; Li, Y.; Su, X.; Tarkoma, S.; Hui, P. A survey on edge intelligence. arXiv 2020, arXiv:2003.12172. [Google Scholar]
- Zhou, Z.; Chen, X.; Li, E.; Zeng, L.; Luo, K.; Zhang, J. Edge intelligence: Paving the last mile of artificial intelligence with edge computing. Proc. IEEE 2019, 107. [Google Scholar] [CrossRef]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S.L. Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data. arXiv 2018, arXiv:1811.11479. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Lähderanta, T.; Leppänen, T.; Ruha, L.; Lovén, L.; Harjula, E.; Ylianttila, M.; Riekki, J.; Sillanpää, M.J. Edge computing server placement with capacitated location allocation. J. Parallel Distrib. Comput. 2021, in press. [Google Scholar]
- Ruha, L.; Lähderanta, T.; Lovén, L.; Kuismin, M.; Leppänen, T.; Riekki, J.; Sillanpää, M.J. Capacitated spatial clustering with multiple constraints and attributes. arXiv 2020, arXiv:2010.06333. [Google Scholar]
- Lovén, L.; Lähderanta, T.; Ruha, L.; Leppänen, T.; Peltonen, E.; Riekki, J.; Sillanpää, M.J. Scaling up an Edge Server Deployment. In Proceedings of the 2020 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), online, 23–27 March 2020; pp. 1–7. [Google Scholar]
- Fix, E.; Hodges, J.L. Discriminatory Analysis. Nonparametric Discrimination: Consistency Properties; Technical Report; USAF School of Aviation Medicine: Randolph Field, TX, USA, 1951. [Google Scholar]
- Nychka, D.; Furrer, R.; Paige, J.; Sain, S. Fields: Tools for Spatial Data. R Package Version 11.6; CRAN. 2017. Available online: https://cran.r-project.org/web/packages/fields/index.html (accessed on 23 March 2021).
- Dimoudi, A.; Kantzioura, A.; Zoras, S.; Pallas, C.; Kosmopoulos, P. Investigation of urban microclimate parameters in an urban center. Energy Build. 2013, 64, 1–9. [Google Scholar] [CrossRef]
- McLean, D.J.; Volponi, M.A.S. trajr: An R package for characterisation of animal trajectories. Ethology 2018, 124. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. RFID J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Pebesma, E. Spacetime: Spatio-Temporal Data in R. J. Stat. Softw. 2012, 51, 1–30. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.; Gomez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ahmad, I.; Shahabuddin, S.; Malik, H.; Harjula, E.; Leppanen, T.; Lovén, L.; Anttonen, A.; Sodhro, A.H.; Mahtab Alam, M.; Juntti, M.; et al. Machine Learning Meets Communication Networks: Current Trends and Future Challenges. IEEE Access 2020, 8, 223418–223460. [Google Scholar] [CrossRef]
- Karsisto, V.; Lovén, L. Verification of road surface temperature forecasts assimilating data from mobile sensors. Weather Forecast. 2019, 34, 539–558. [Google Scholar] [CrossRef]
- Lovén, L.; Gilman, E.; Riekki, J.; Läärä, E.; Sukuvaara, T.; Mäenpää, K.; Sillanpää, M.J.; Pirttikangas, S. Pilot study: Road–tyre friction prediction by statistical methods and data fusion. In In Proceedings of the 2017 International Workshop on Smart Sensing System (IWSSS17), Oulu, Finland, 7–8 August 2017; University of Oulu: Oulu, Finland, 2017; pp. 1–2. [Google Scholar]
| Symbol | Range | Description | |
|---|---|---|---|
| N | the number of observations in the training set | ||
| L | the number of observations for inference | ||
| M | size of neighbourhood (i.e., n. of obs.) around each observation | ||
| K | number of fixed sensors/clusters | ||
| observations in the neighbourhood around observation i | |||
| O | the number of raster cells on the map | ||
| coordinates of the center of raster cell o | |||
| location of fixed sensor l | |||
| Q | ; | the dimension of the interpolation model parameters | |
| interpolation model parameters of the ngbh. around observation i | |||
| mean of the interpolation model parameters at raster cell o | |||
| mean of the interpolation model parameters at | |||
| membership of observation i to cluster j | |||
| tradeoff between proximity and similarity in clustering | |||
| d | size of neighbourhood for knn | ||
| z | the interpolation by the cluster model | ||
| distance between two locations | |||
| set |
| Region | Component | Cov. Funct. | Range | Smoothness | phi | |
|---|---|---|---|---|---|---|
| 1 | 12 | Spatial | Matern | 1 | 1.7 | 0.5 |
| 2 | 11 | Spatial | Matern | 9 | 0.7 | 2 |
| 3 | 15 | Spatial | Matern | 6 | 0.6 | 1.5 |
| 4 | 14 | Spatial | Matern | 0.5 | 1.7 | 0.1 |
| Approach | Mobile Sensors | ||
|---|---|---|---|
| 150 | 250 | 300 | |
| Global | 1.30 | 1.19 | 1.14 |
| Baseline | 1.24 | 1.14 | 1.11 |
| E2 | 1.25 | 1.15 | 1.14 |
| EDISON (this study) | 1.17 | 1.12 | 1.10 |
| Improvement over global | 10% | 6% | 4% |
| Improvement over baseline | 6% | 2% | 1% |
| Improvement over E2 | 6% | 3% | 4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovén, L.; Lähderanta, T.; Ruha, L.; Peltonen, E.; Launonen, I.; Sillanpää, M.J.; Riekki, J.; Pirttikangas, S. EDISON: An Edge-Native Method and Architecture for Distributed Interpolation. Sensors 2021, 21, 2279. https://doi.org/10.3390/s21072279
Lovén L, Lähderanta T, Ruha L, Peltonen E, Launonen I, Sillanpää MJ, Riekki J, Pirttikangas S. EDISON: An Edge-Native Method and Architecture for Distributed Interpolation. Sensors. 2021; 21(7):2279. https://doi.org/10.3390/s21072279
Chicago/Turabian StyleLovén, Lauri, Tero Lähderanta, Leena Ruha, Ella Peltonen, Ilkka Launonen, Mikko J. Sillanpää, Jukka Riekki, and Susanna Pirttikangas. 2021. "EDISON: An Edge-Native Method and Architecture for Distributed Interpolation" Sensors 21, no. 7: 2279. https://doi.org/10.3390/s21072279
APA StyleLovén, L., Lähderanta, T., Ruha, L., Peltonen, E., Launonen, I., Sillanpää, M. J., Riekki, J., & Pirttikangas, S. (2021). EDISON: An Edge-Native Method and Architecture for Distributed Interpolation. Sensors, 21(7), 2279. https://doi.org/10.3390/s21072279









