Rubber Material Property Prediction Using Electron Microscope Images of Internal Structures Taken under Multiple Conditions
Abstract
1. Introduction
- Our new robust material property prediction method considering different imaging conditions has a wide applicability not only to rubber materials but also to other materials.
- Only reliable prediction results are automatically selected and integrated based on the prediction interval and the DS evidence theory.
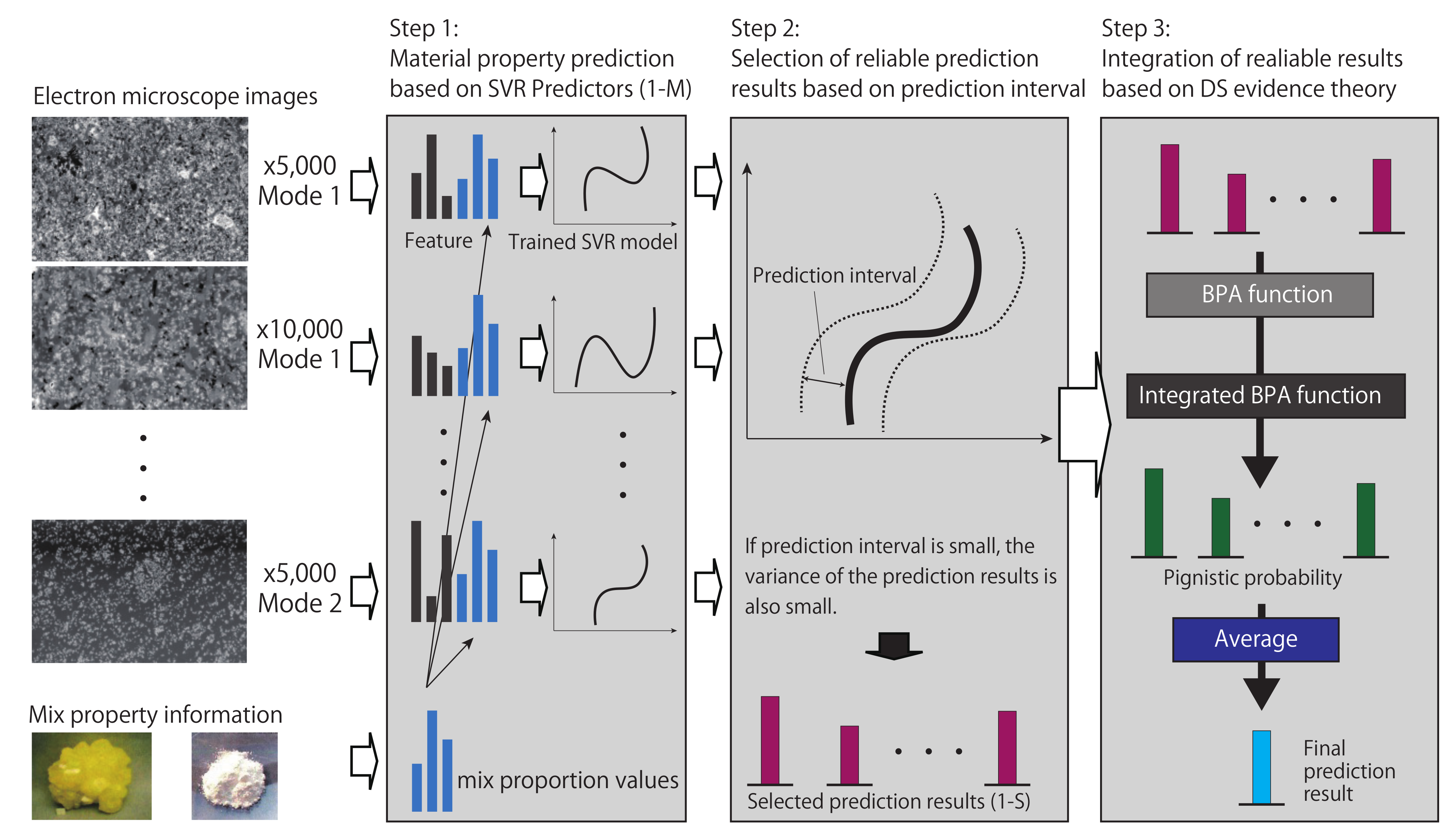
2. Method for Prediction of Rubber Material Properties
2.1. Step 1: Property Prediction for Each Imaging Condition
2.2. Step 2: Selection of Reliable Prediction Results
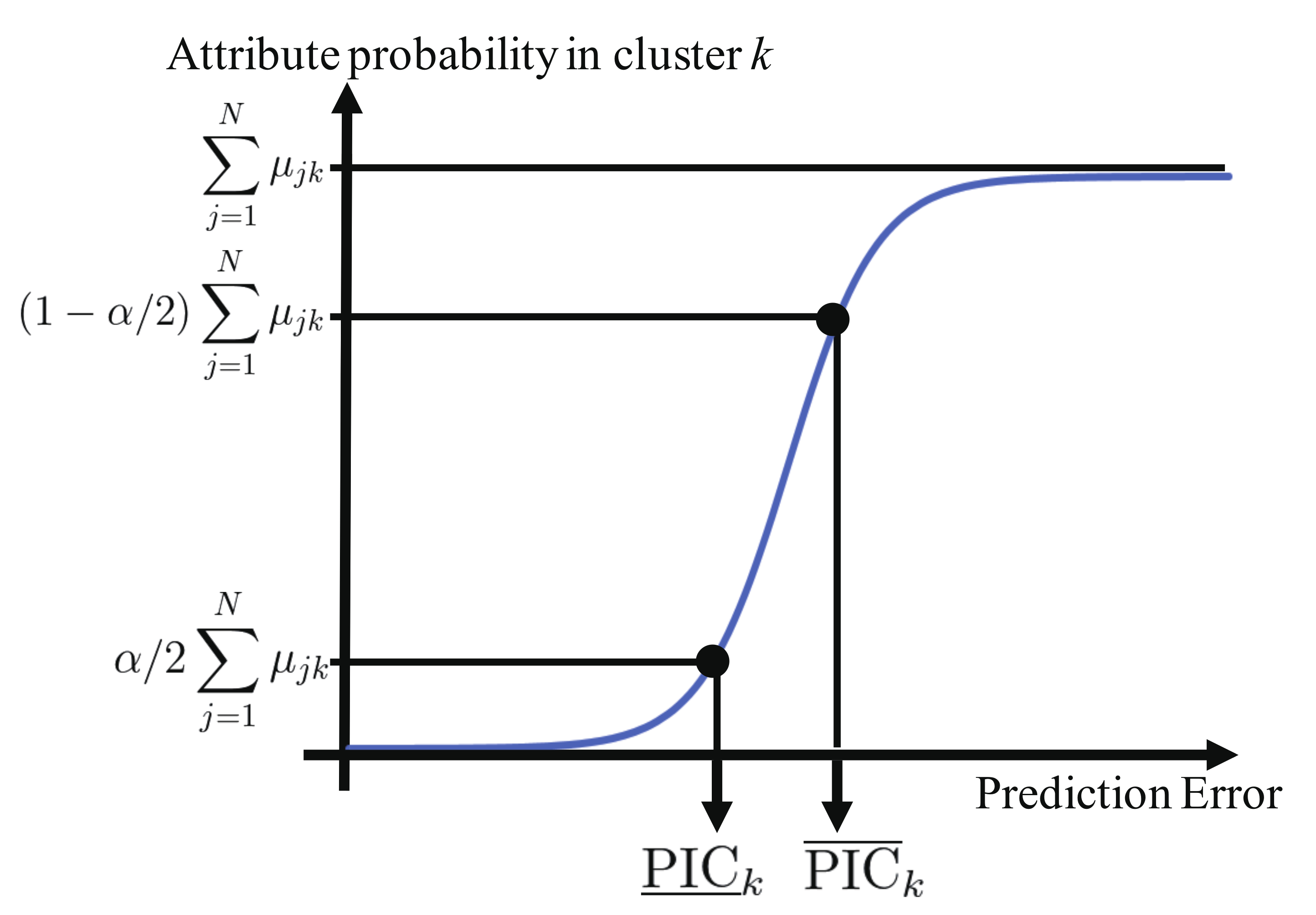
2.3. Step 3: Integration of Reliable Results Based on DS Evidence Theory
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Togo, R.; Saito, N.; Ogawa, T.; Haseyama, M. Estimating Regions of Deterioration in Electron Microscope Images of Rubber Materials via a Transfer Learning-Based Anomaly Detection Model. IEEE Access 2019, 7, 162395–162404. [Google Scholar] [CrossRef]
- Xiong, Z.; Cai, Q.; Liu, F.; Li, L.; Long, Y. Dynamic performance of RAC-filled double-skin tubular columns subjected to cyclic axial compression. Constr. Build. Mater. 2020, 248, 118665. [Google Scholar] [CrossRef]
- Rui, L.; Zappa, E.; Collina, A. Vision-based measurement of crack generation and evolution during static testing of concrete sleepers. Eng. Fract. Mech. 2020, 224, 106715. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, M.; Lin, Y.; Huang, X.; Huang, K.; He, Y.; Li, L. Vision-based three-dimensional reconstruction and monitoring of large-scale steel tubular structures. Adv. Civ. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Mars, W.; Fatemi, A. A literature survey on fatigue analysis approaches for rubber. Int. J. Fatigue 2002, 24, 949–961. [Google Scholar] [CrossRef]
- Kazmi, S.M.S.; Munir, M.J.; Wu, Y.F. Application of waste tire rubber and recycled aggregates in concrete products: A new compression casting approach. Resour. Conserv. Recycl. 2021, 167, 105353. [Google Scholar] [CrossRef]
- Cesar, M.B.; Borges, F.A.; Bilck, A.P.; Yamashita, F.; Paulino, C.G.; Herculano, R.D. Development and characterization of natural rubber latex and polylactic acid membranes for biomedical application. J. Polym. Environ. 2020, 28, 220–230. [Google Scholar] [CrossRef]
- Lo Presti, D.; Airey, G. Tyre rubber-modified bitumens development: The effect of varying processing conditions. Road Mater. Pavement Des. 2013, 14, 888–900. [Google Scholar] [CrossRef]
- Bernal, M.; Nenadic, I.; Urban, M.W.; Greenleaf, J.F. Material property estimation for tubes and arteries using ultrasound radiation force and analysis of propagating modes. J. Acoust. Soc. Am. 2011, 129, 1344–1354. [Google Scholar] [CrossRef] [PubMed]
- Vijayabaskar, V.; Gupta, R.; Chakrabarti, P.P.; Bhowmick, A.K. Prediction of properties of rubber by using artificial neural networks. J. Appl. Polym. Sci. 2006, 100, 2227–2237. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Z. Real-time property prediction for an industrial rubber-mixing process with probabilistic ensemble Gaussian process regression models. J. Appl. Polym. Sci. 2015, 132, 41432. [Google Scholar] [CrossRef]
- Jin, W.; Liu, Y.; Gao, Z. Fast property prediction in an industrial rubber mixing process with local ELM model. J. Appl. Polym. Sci. 2017, 134, 45391. [Google Scholar] [CrossRef]
- Yang, Y.S.; Chou, J.H.; Huang, W.; Fu, T.C.; Li, G.W. An artificial neural network for predicting the friction coefficient of deposited Cr 1- x Al x C films. Appl. Soft Comput. 2013, 13, 109–115. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, J.; Xu, W.; Zhang, Y.; Chen, H. Prediction of elastic compressibility of rock material with soft computing techniques. Appl. Soft Comput. 2014, 22, 118–125. [Google Scholar] [CrossRef]
- Guo, H.; Yin, J.; Zhao, J.; Yao, L.; Xia, X.; Luo, H. An ensemble learning for predicting breakdown field strength of polyimide nanocomposite films. J. Nanomater. 2015, 2015, 7. [Google Scholar] [CrossRef]
- Cang, R.; Li, H.; Yao, H.; Jiao, Y.; Ren, Y. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comput. Mater. Sci. 2018, 150, 212–221. [Google Scholar] [CrossRef]
- Paola, J.D.; Schowengerdt, R.A. A review and analysis of backpropagation neural networks for classification of remotely-sensed multi-spectral imagery. Int. J. Remote Sens. 1995, 16, 3033–3058. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Heskes, T. Practical confidence and prediction intervals. In Advances in Neural Information Processing Systems 9; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 176–182. [Google Scholar]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; Volume 1. [Google Scholar]
- Tian, J.; Zhao, W.; Du, R.; Zhang, Z. DS evidence theory and its data fusion application in intrusion detection. In Proceedings of the International Conference on Computational and Information Science, Atlanta, GA, USA, 22–25 May 2005; pp. 115–119. [Google Scholar]
- Zeng, D.; Xu, J.; Xu, G. Data fusion for traffic incident detection using DS evidence theory with probabilistic SVMs. J. Comput. 2008, 3, 36–43. [Google Scholar] [CrossRef]
- Sun, R.; Huang, H.Z.; Miao, Q. Improved information fusion approach based on DS evidence theory. J. Mech. Sci. Technol. 2008, 22, 2417–2425. [Google Scholar] [CrossRef]
- Ogawa, T.; Takahashi, A.; Haseyama, M. Classifying Insects from SEM Images Based on Optimal Classifier Selection and DS Evidence Theory. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, 99, 1971–1980. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Shrestha, D.L.; Solomatine, D.P. Machine learning approaches for estimation of prediction interval for the model output. Neural Netw. 2006, 19, 225–235. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Su, X.; Mahadevan, S.; Li, C.; Deng, Y. A non-parametric method to determine basic probability assignment for classification problems. Appl. Intell. 2014, 41, 681–693. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man, Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
- Ahmadian, A.; Mostafa, A. An efficient texture classification algorithm using Gabor wavelet. In Proceedings of the 25th Annual International Conference of Engineering in Medicine and Biology Society, Cancun, Mexico, 17–21 September 2003; pp. 930–933. [Google Scholar]
- Lin, C.H.; Liu, C.W.; Chen, H.Y. Image retrieval and classification using adaptive local binary patterns based on texture features. IET Image Process. 2012, 6, 822–830. [Google Scholar] [CrossRef]
- Donahue, J.; Jia, Y.; Vinyals, O.; Hoffman, J.; Zhang, N.; Tzeng, E.; Darrell, T. Decaf: A deep convolutional activation feature for generic visual recognition. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 647–655. [Google Scholar]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973. [Google Scholar] [CrossRef]
- Park, H.S.; Jun, C.H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in natural and artificial systems. In An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Williams, C.K. Prediction with Gaussian processes: From linear regression to linear prediction and beyond. In Learning in Graphical Models; Springer Science and Business Media: New York, NY, USA, 1998; pp. 599–621. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]

| Condition | Magnification & Mode | Number of Samples | Number of Images |
|---|---|---|---|
| Condition 1 | × 5000, Mode 1 | 71 | 71 |
| Condition 2 | × 10,000, Mode 1 | 72 | 152 |
| Condition 3 | × 20,000, Mode 1 | 72 | 156 |
| Condition 4 | × 40,000, Mode 1 | 56 | 118 |
| Condition 5 | × 2500, Mode 2 | 19 | 19 |
| Condition 6 | × 5000, Mode 2 | 19 | 38 |
| Condition 7 | × 10,000, Mode 2 | 19 | 52 |
| Condition 8 | × 20,000, Mode 2 | 19 | 57 |
| Method | Overview |
|---|---|
| CM1 | The final prediction result is obtained by integration of reliable results using the DS evidence theory. Reliable results are selected from prediction results obtained by an SVR predictor that do not consider different imaging conditions. |
| CM2 | The final prediction result is calculated by integration of reliable results using the DS evidence theory. Reliable results are selected from prediction results obtained by the predictor of each condition using only visual features. |
| CM3 | The final prediction result is obtained by the SVR predictor using only mix proportion features. Each rubber material sample is assumed to have a single mix proportion. Therefore, CM3 does not apply selection and integration of prediction results. |
| CM4 | The final prediction result is calculated by the average of the multiple prediction results. |
| CM5 | The final prediction result is obtained by weighted average of the prediction results. CM5 utilizes prediction interval as the weight. |
| CM6 | The final prediction result is obtained by selection of a reliable result from multiple prediction results using prediction intervals. |
| CM7 | The final prediction result is calculated by the average of reliable results selected from the prediction results obtained by the predictor of each condition using visual and mix proportions features. |
| CM8 | The final prediction result is calculated by integration of multiple prediction results based on the DS evidence theory. |
| CM9 | The final prediction result is calculated by selection and integration of prediction results obtained by a convolutional neural network (CNN) [37]. Specifically, CM9 utilizes Xception [39] that is fine-tuned for property prediction using electron microscope images. |
| PM | CM1 | CM2 | CM3 | CM4 | CM5 | CM6 | CM7 | CM8 | CM9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | 2.68 | 4.14 | 3.77 | 3.17 | 2.93 | 3.04 | 3.17 | 2.93 | 2.69 | 3.80 |
| MAPE | 9.64% | 15.4% | 12.3% | 11.7% | 11.2% | 11.5% | 11.7% | 11.2% | 10.4% | 13.7% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Togo, R.; Saito, N.; Maeda, K.; Ogawa, T.; Haseyama, M. Rubber Material Property Prediction Using Electron Microscope Images of Internal Structures Taken under Multiple Conditions. Sensors 2021, 21, 2088. https://doi.org/10.3390/s21062088
Togo R, Saito N, Maeda K, Ogawa T, Haseyama M. Rubber Material Property Prediction Using Electron Microscope Images of Internal Structures Taken under Multiple Conditions. Sensors. 2021; 21(6):2088. https://doi.org/10.3390/s21062088
Chicago/Turabian StyleTogo, Ren, Naoki Saito, Keisuke Maeda, Takahiro Ogawa, and Miki Haseyama. 2021. "Rubber Material Property Prediction Using Electron Microscope Images of Internal Structures Taken under Multiple Conditions" Sensors 21, no. 6: 2088. https://doi.org/10.3390/s21062088
APA StyleTogo, R., Saito, N., Maeda, K., Ogawa, T., & Haseyama, M. (2021). Rubber Material Property Prediction Using Electron Microscope Images of Internal Structures Taken under Multiple Conditions. Sensors, 21(6), 2088. https://doi.org/10.3390/s21062088






