Abstract
In wireless sensor networks, the reliability of communication can be greatly improved by applying low-density parity-check (LDPC) codes. Algorithms based on progressive-edge-growth (PEG) pattern and quasi-cyclic (QC) pattern are the mainstream approaches to constructing LDPC codes with good performance. However, these algorithms are not guaranteed to remove all short cycles to achieve the desired girth, and their excellent inputs are difficult to obtain. Herein, we propose an algorithm, which must be able to construct LDPC codes with the girth desired. In addition, the optimal input to the proposed algorithm is easy to find. Theoretical and experimental evidence of this study shows that the LDPC codes we construct have better decoding performance and less power consumption than the PEG-based and QC-based codes.
1. Introduction
The wireless sensor network (WSN) [1,2] is a distributed network, which consists of lots of small sensor nodes. Information from the environment is collected by the sensors and is delivered over the wireless channel to a central station where the desired data can be obtained by users. Due to the features such as scalability and self-organization, WSNs have a wide range of applications in the areas of medical care [3], target tracking [4], military [5], environmental monitoring [6] and so on [7,8,9]. Ensuring reliable communication is the most basic requirement of WSNs. However, since sensor nodes of WSNs are tiny in size and rely on lightweight batteries, they are heavily constrained by limited memory and processing power. In this case, using efficient block coding is needed. Low-density parity-check (LDPC) codes [10] have remarkable error-correcting performance, which can greatly improve the reliability of communication [11,12]. In addition, the low coding and decoding complexity of LDPC codes can reduce power consumption, thus extending the lifetimes of WSNs [13,14,15].
LDPC code was proposed by Gallager in 1962 [10]. It attracts an enormous amount of interest because of its capacity-approaching performance and low-complexity iterative decoding combined with the belief-propagation (BP) algorithm [16,17]. BP can provide optimum decoding when the LDPC code is cycle-free, so it is important to reduce the impact of cycles.
The girth is the low bound of the lengths of all cycles in an LDPC code, and a larger girth indicates that the code evades more short cycles. Algorithms based on progressive-edge-growth (PEG) pattern [18,19,20] and quasi-cyclic (QC) pattern [21,22] are the two main kinds of LDPC code construction algorithms used to create codes with large girth. In PEG-based algorithms, edges are greedily added into the LDPC code to maximize the length of the current shortest cycle such that the algorithms manage to make the girth larger. They are flexible and convenient to generate regular and irregular LDPC codes with short or medium code length. As for the QC-based algorithms, an LDPC code is divided into several parts and each part can be represented as either a zero matrix or a circulant permutation matrix. Eliminating short cycles to maximize the girth can be realized by changing the shift value [21] of every circulant permutation matrix. These algorithms are easy for hardware parallel implementation and the codes they constructed are space-saving. Despite these strengths, neither PEG-based nor QC-based algorithms can overcome some shortcomings which they consistently suffer from. Firstly, they just try to make the girth larger rather than decide the value of it, so the LDPC codes they constructed still suffer the loss of performance caused by short cycles. It would be unrealistic to raise the girth further beyond their capacity because of unbearable computational costs. Secondly, the quality of LDPC codes constructed via them has an over-reliance on their inputs, whereas excellent inputs are rarely available.
To solve these problems, we put forward an algorithm for constructing LDPC codes with arbitrary girth, and we call the algorithm the girth-cycle-embedding (GCE) algorithm. The algorithm requires the girth as the only input, and the code is constructed by embedding girth-member cycles into it. Our algorithm can overcome the above disadvantages through theoretical analysis, and produces LDPC codes with better performance than codes from PEG-based and QC-based algorithms in practice.
The rest of the paper is organized as follows: In Section 2, we introduce the representations of LDPC code, the concept of the cycle and its impact on LDPC code. In Section 3, PEG-based and QC-based algorithms are reviewed in detail. Section 4 depicts the GCE algorithm we proposed. Section 5 gives the performance evaluation of GCE, PEG-based and QC-based algorithms. The conclusion are presented in Section 6.
2. Preliminaries
In LDPC codes, a cycle is a path which alternately passes through check nodes and variable nodes [18] and ends at the same node it starts from. As an important factor, the cycle significantly influences the performance of an LDPC code. There is a large volume of published studies [23,24,25] indicating that shorter cycles are more harmful to the codes. When decoding, the circulation of information among different nodes is beneficial to error correction. However, the circulation of information is hindered by the existence of cycles, thus wrong information in cycles can not be updated by extrinsic information in time and makes errors difficult to correct. As the length of cycles gets shorter, the frequency of wrong information being recycled gets higher and the difficulty of error correction becomes greater. The length of the shortest cycles in an LDPC code is called the girth. An LDPC code with a large girth means that there are no cycles with lengths smaller than the girth, so numerous LDPC code construction algorithms have a very important goal, maximizing the girth. The hazard level of a cycle should be measured not only by its length but also by its connectivity [23,26,27] which measures the impact of extrinsic paths on the cycle. Currently, extrinsic message degree (EMD) [23], approximate cycle EMD (ACE) [26], etc., are used to quantify the connectivity. For two cycles of the same length, the cycle with higher connectivity receives more extrinsic information via the extrinsic paths, thereby breaking the information barrier faster. In other words, cycles with higher connectivity are relatively harmless.
In view of the harm of short cycles, many LDPC code construction algorithms are designed along the lines of maximizing the girth of LDPC codes, i.e., trying to avoid generating or to eliminate short cycles, and improving the connectivity of the short cycles when they cannot be avoided or removed. Next, we will introduce two main types of construction algorithms.
3. Construction Algorithms of LDPC Codes
There are many construction algorithms of LDPC codes, among which PEG-based and QC-based algorithms are the two main kinds of methods.
In the PEG-based algorithms, all the variable nodes are assigned targeted degrees by a variable-node degree distribution [18,28]. Then, for each variable node , edges are greedily added into the LDPC code to maximize the length of the shortest cycle which participates in such that the algorithms manage to make the girth larger. The primary improvement direction of PEG-based algorithms is to develop better selection criteria, with which a variable node can decide which check nodes to connect with edges. For instance, in the PEG algorithm [18] the check node with the minimum degree will be chosen; in the improved PEG algorithm [19], it selects the check node with the highest cycle connectivity from check nodes with the minimum degree; generalized PEG algorithm [20] has harsher criteria: highest cycle connectivity, shortest paths, minimum degree, etc. These PEG-based algorithms are flexible and convenient to construct short-length and medium-length LDPC codes. In addition, both regular and irregular LDPC codes can be generated. Moreover, the codes created by these algorithms with an excellent variable-node degree distribution perform very well, especially in the waterfall region [29] which is signal noise ratio (SNR) or bit error rate (BER) region near the code threshold.
As for the QC-based algorithms, a matrix (LDPC code) is divided into many square matrices of the same size. Each of these square matrices is either a zero matrix or a circulant permutation matrix, which is obtained by cyclically right-shifting an identity matrix by p positions and p is called the shift of this circulant permutation matrix. Eliminating short cycles can be realized by giving suitable shift p for every circulant permutation matrix. In [21], a Hill-Climbing algorithm was proposed to greedily adjust those shift values to create a QC-LDPC code. In [22], the Hill-Climbing algorithm was improved in computational cost and the quality of matrices. These QC-based algorithms can remove cycles and are easy for hardware parallel implementation. The QC-LDPC codes they constructed save storage space and perform well in the error-floor region [30] which is the region with high SNR or with low BER.
Through the reviews of the PEG-based and QC-based algorithms above, we know that they remain the mainstream approaches to constructing LDPC codes because of many advantages. Despite these strengths, they consistently suffer from several shortcomings which are difficult to overcome.
Firstly, we found that all the PEG-based algorithms have an over-reliance on variable-node degree distribution [18,28]. It is one of the inputs of these algorithms and is used to decide the degree of each variable node. When too many variable nodes are assigned small degrees in one variable-node degree distribution, LDPC codes constructed may not provide enough information to help with error correction. However, increasing the number of variable nodes with large degrees is fairly easy to cause lots of short cycles. Therefore, variable-node degree distribution balancing degrees of all the variable nodes directly affects the quality of LDPC codes generated by the PEG-based algorithms. Several methods, e.g., density evolution [31,32] and Gaussian approximation [33], exist currently for creating variable-node degree distribution, but a major problem of them is that finite-length codes applying these methods only achieve suboptimal or general performance, and the performance even worsens for short-length codes. Thus, it is challenging to obtain an excellent variable-node degree distribution which is suitable for the code length you need. Secondly, there is no way to remove short cycles efficiently, because LDPC codes created by PEG-based algorithms are not structured and computational cost is prohibitive if all short cycles are detected and eliminated.
For structured LDPC codes generated by the QC-based algorithms, removing short cycles can be realized via changing the shifts. However, the computational cost needed grows exponentially with the increase of cycle length. Intuitively speaking, it is hard enough to discover and eliminate all eight-member cycles. Next, constructing a superb base matrix after determining its size is also a high-complexity question. Specifically, a matrix (LDPC code) is divided into an base matrix, and each element of the base matrix is a zero matrix or a circulant permutation matrix, where . Therefore, there are possible combinations for the base matrix. At last, matrices from the QC-based algorithms suffer relatively poor performance compared with matrices from the PEG-based algorithms in the waterfall region.
Variants [34,35] of PEG-based and QC-based algorithms face similar drawbacks and have other disadvantages. For example, although the algorithm in [34] can construct LDPC codes with arbitrary girth, it reaches exponential complexity and can only generate regular LDPC codes [36,37].
4. Girth-Cycle-Embedding (GCE) Algorithm
As specified above, neither PEG-based nor QC-based algorithms can fully decide the girth so that the LDPC codes they constructed still suffer the loss of performance caused by short cycles. Furthermore, in these algorithms, the quality of LDPC codes is closely related to the inputs, i.e., variable-node degree distribution and base matrix, whereas excellent inputs are rarely available. In order to solve these problems, we put forward a new algorithm for LDPC code construction. In the algorithm, the expected girth is designed as the only input, and an LDPC code is constructed by way of embedding girth-member cycles into it. The algorithm overcomes the disadvantages mentioned above and produces LDPC codes with better performance than ones from PEG-based and QC-based algorithms. We call the algorithm we proposed GCE algorithm.
In the GCE algorithm, we denote the girth by g which can be expressed as because the length of any cycle must be an even number. To aid in managing all nodes, m check nodes are split into two sets, for check nodes with zero degree while for the others. In like manner, n variable nodes are divided into and . In addition, we have designed an operation called with as an input, where two nodes whose distance is are chosen and exported. In operation, support tree [18,23] spreading from one check node as the root is used. For ensuring that a support tree has finite layers, all the nodes only appear in the tree once. Pseudocode of operation is given in Algorithm 1.
| Algorithm 1. |
|
In operation, one of two nodes is a check node from , the other is also a check node from if is even or a variable node from if is odd. The detailed operation is as follows: sort all the check node in based on the degree in ascending order; get a check node in order and build a support tree spreading from which is denoted by ; if can grow to the layer, randomly select one node with the minimum degree on this layer, and output and ; if not, build the support tree of the next check node; the operation is considered a failure when all the support trees are less than layers.
After illustrating the operation, we will introduce the GCE algorithm in detail. GCE is divided into four steps, each of which is a process of embedding girth-member cycles into the LDPC code in different ways as below. The pseudocode and an example of the GCE algorithm are shown in Algorithm 2 and Appendix A, respectively.
- Initialize node sets and form the first cycle.Initialize the node sets: , , . Then fetch check nodes from and x variable nodes from , to form a girth-member cycle followed by putting these nodes into and , respectively.
- Exhaust check nodes inSet a constant h:If is greater than or equal to h, execute when x is even or when x is odd. If exports and , connect and to create some girth-member cycles with h check nodes from and variable nodes from , and put these h check nodes and variable nodes into and , respectively. Then repeat step 2.If is positive and less than h, execute . If exports and , connect and to create some girth-member cycles with check nodes from and variable nodes from , and put these check nodes and variable nodes into and , respectively. Then skip to step 3.If is zero, then skip to step 3.
- Exhaust variable nodes inIf is a positive number, then execute with input . If exports and , connect and with a variable node from to create some girth-member cycles, and put the variable node into . Then repeat step 3.If is zero, then skip to step 4.
- Increase the degrees of variable nodes.Execute . If exports and , connect and directly. Repeat step 4 until fails.
| Algorithm 2 Girth-cycle-embedding algorithm. |
|
Except for step 1, steps 2–4 are executed with the help of operation. Cycles with lengths less than g are avoided by setting the input of reasonably, hence no more operations are needed to remove these cycles. As for cycles with lengths greater than or equivalent to g, their harm is significantly reduced by improving their connectivity in steps 2–4. Moreover, the only uncertain input in the GCE algorithm is the girth g, which greatly lowers the external influence on the quality of LDPC codes. The advantages above are shown directly in the experiments. Of course, GCE remains some shortcomings, for example leading to too small average variable-node degree and weakening the performance if g is too large or too small. However, compared with obtaining an excellent variable-node degree distribution for the PEG-based algorithms and a superb base matrix for the QC-based algorithms, the complexity of selecting an optimal g in GCE algorithm is low enough.
For an algorithm, it needs to consider space complexity and time complexity. Generally, the -notation can be used to denote the asymptotic upper bound of space or time complexity [38]. We calculate the space and time complexity of GCE algorithm, some PEG-based and QC-based algorithms [18,19,20,21,22], and present the results in Table 1. It is observed that the GCE algorithm is not as good as the QC-based algorithms [21,22] in terms of space complexity, but it also remains linear. As for time complexity, the GCE algorithm has the lowest one compared to other algorithms. This indicates that the GCE algorithm has the least computational consumption when constructing an LDPC code in the asymptotic case.

Table 1.
Space and time complexity of different algorithms.
5. Simulation Results
In this section, we executed three experiments to verify the advantages of the GCE algorithm. Before the experiments, we have constructed six matrices (LDPC codes) with code rate (3072 check nodes and 6144 variable nodes) for the experiments. Three of them were created by using three PEG-based algorithms, i.e., PEG algorithm [18], improved PEG algorithm [19] and generalized PEG algorithm [20]. The variable-node degree distribution required was obtained by density evolution [31,32] and published in [32]. In QC-based algorithms, the Hill-Climbing algorithm [21] and the improved Hill-Climbing algorithm [22] were utilized to construct two matrices which both had base matrices initialized in a random manner. The last matrix was generated via the GCE algorithm we proposed in Section 4 and its girth g was set to 12.
5.1. Decoding Performance
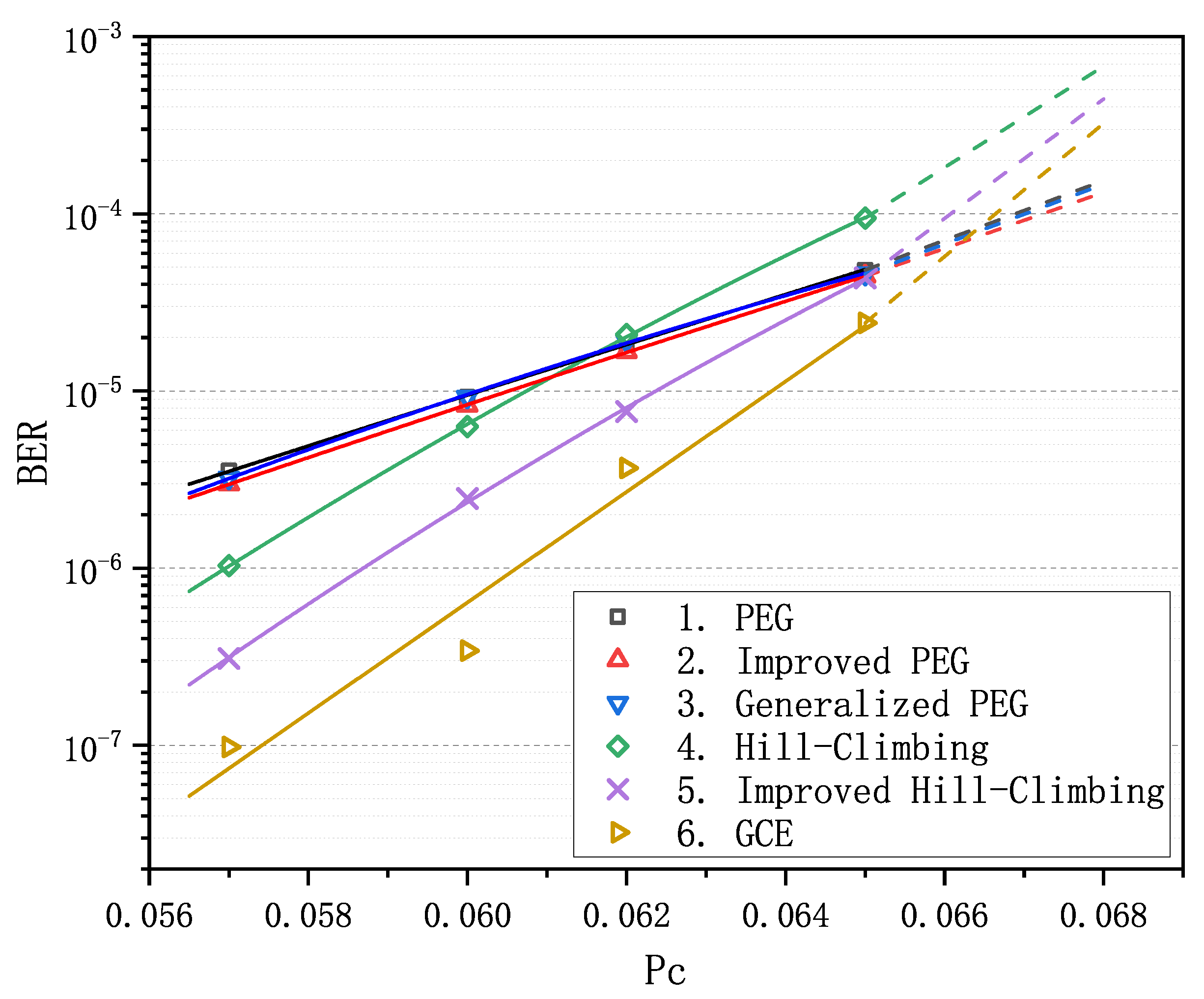
Decoding with LDPC codes can correct errors in messages and thus guarantee the communication reliability of WSNs. For the comparison of decoding performance of finite-length LDPC codes, we chose to perform decoding simulations instead of running some analysis algorithms [39,40] which are inapplicable to the GCE algorithm. We first evaluated the decoding performance of the above six finite-length matrices with BP decoder introduced in [16,17] on the binary symmetric channel (BSC). Figure 1 presents the results with BER as the function of crossover probability . For the convenience of reporting the results, all the matrices are numbered consecutively from 1 to 6: 1. PEG algorithm [18]; 2. improved PEG algorithm [19]; 3. generalized PEG algorithm [20]; 4. Hill-Climbing algorithm [21]; 5. improved Hill-Climbing algorithm [22]; and 6. GCE algorithm. It is apparent that there is not much difference in the performances of PEG-based matrices 1–3, while for two QC-based matrices, matrix 5 performs better than matrix 4.
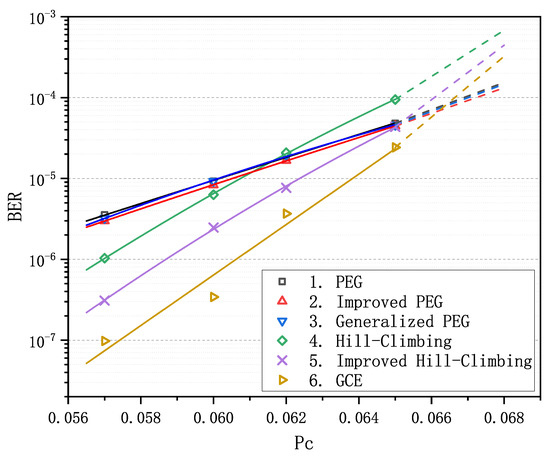
Figure 1.
Comparison of decoding performance of the progressive-edge-growth (PEG)-based codes, quasi-cyclic (QC)-based codes and the code from the girth-cycle-embedding (GCE) algorithm at different values over binary symmetric channel (BSC).
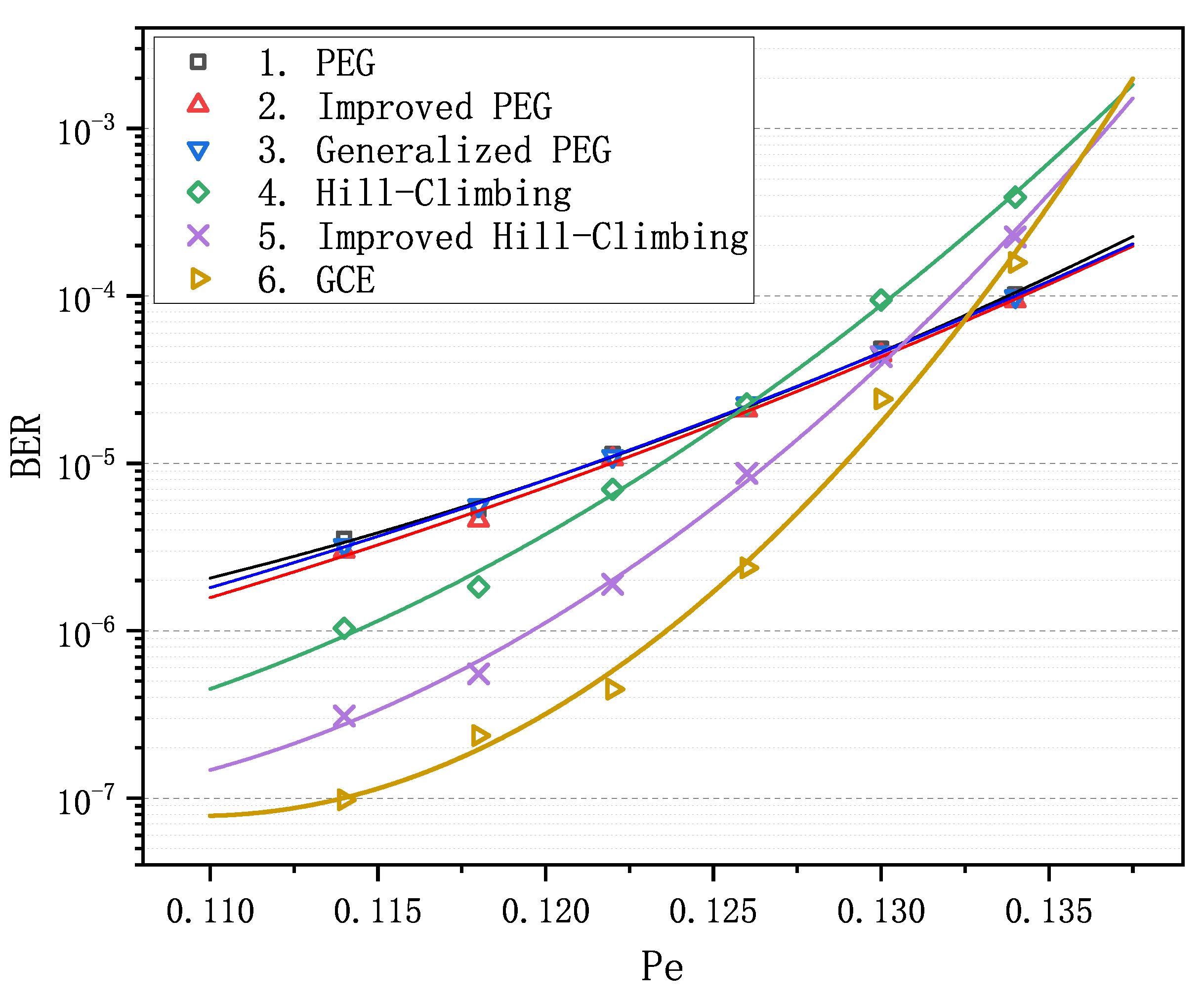
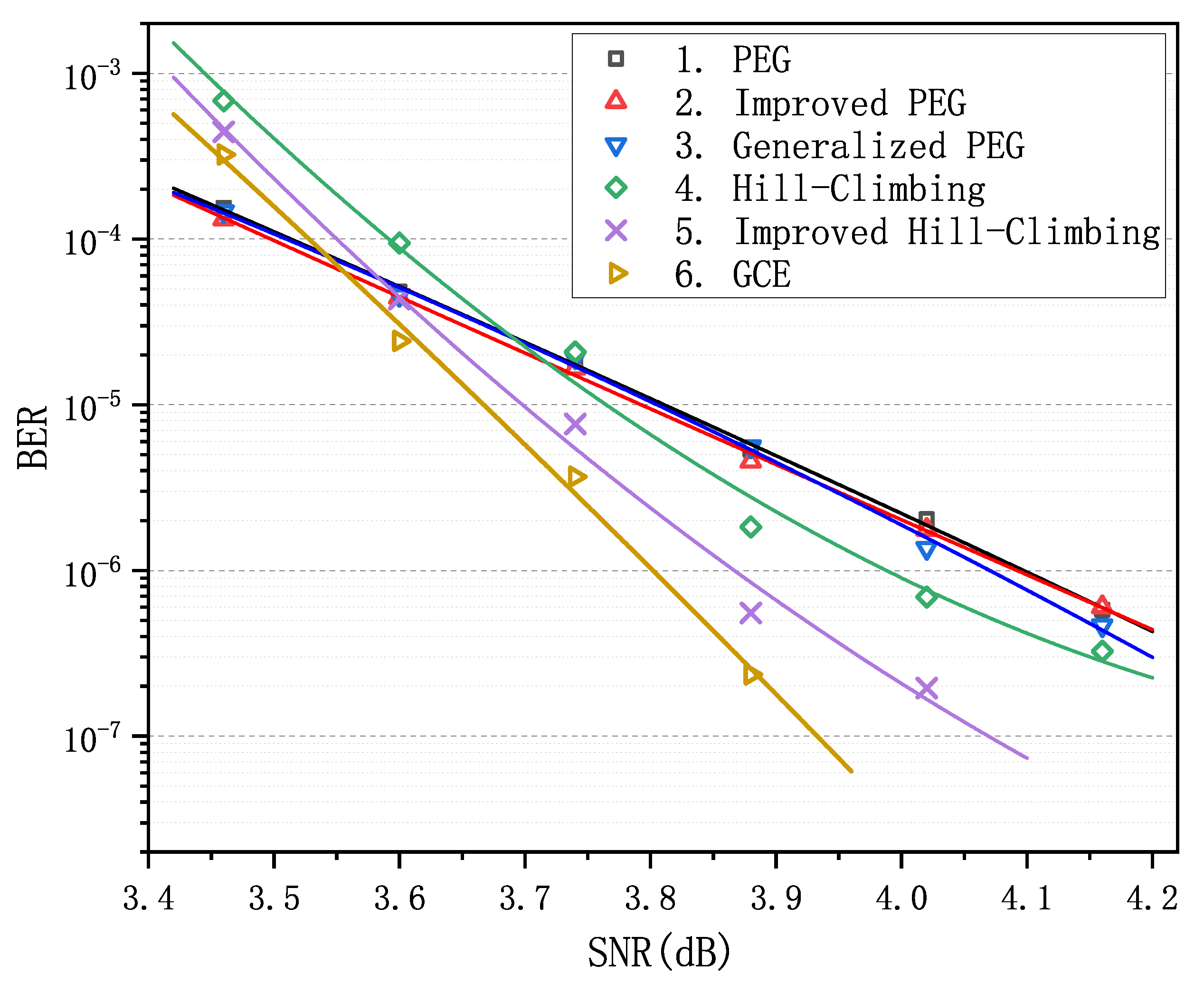
We observe that matrix 6 achieves the optimal performance when is less than . Particularly in the error-floor region, the gaps between the curve of matrix 6 and the others are rather striking. For example, when equals to , BER is for matrices 1–3 and is for matrix 6, which span more than an order of magnitude. Obviously, as increases and goes into the waterfall region, matrix 6 gradually loses its advantage in decoding performance compared with matrices 1–3, nevertheless it still remains absolutely dominant compared with matrices 4 and 5. In order to verify the LDPC codes constructed by GCE outperform the LDPC codes constructed by other algorithms on different channels, we carried out two more decoding experiments over the binary erasure channel (BEC) and the additive white Gaussian noise channel (AWGNC), which are presented in Figure 2 and Figure 3, respectively. It is apparent that GCE algorithm surpasses the other algorithms in the error-floor region over different channels, which suggests that LDPC codes from GCE algorithm can provide more reliable communication for WSNs. The reason for outstanding decoding performance of the GCE algorithm is analyzed in Appendix B.
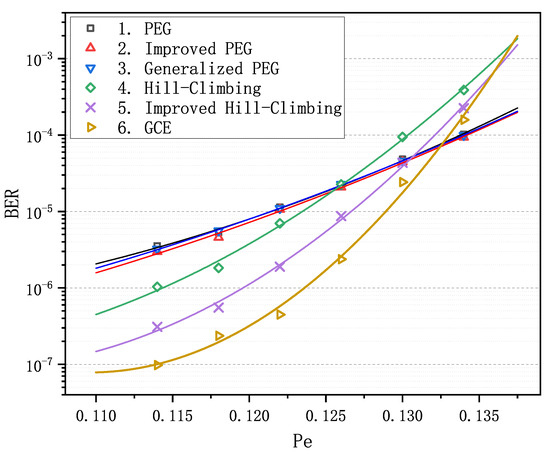
Figure 2.
Comparison of decoding performance of the PEG-based codes, QC-based codes and the code from the GCE algorithm at different erasure probability over binary erasure channel (BEC).
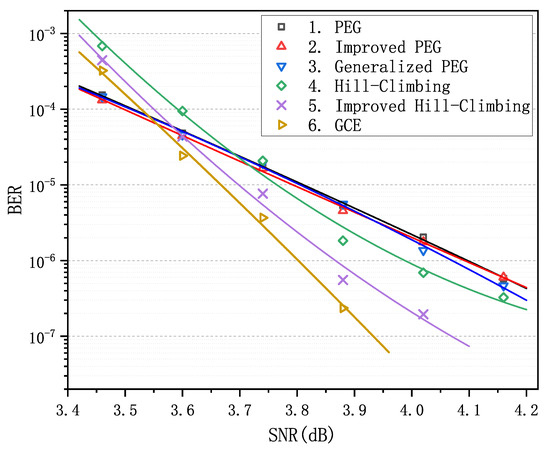
Figure 3.
Comparison of decoding performance of the PEG-based codes, QC-based codes and the code from the GCE algorithm at different SNR over additive white Gaussian noise channel (AWGNC).
5.2. Power Consumption
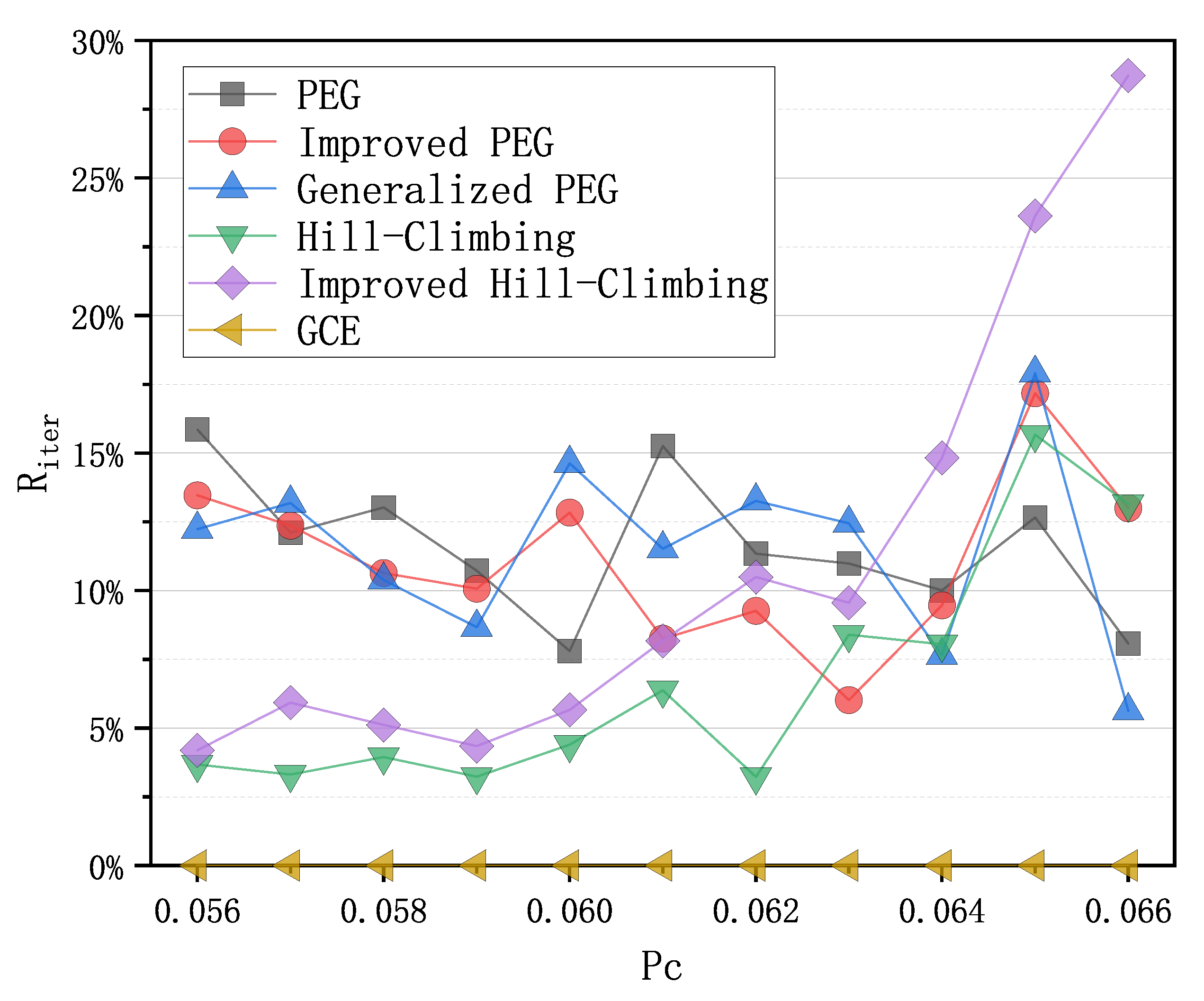
Since the power of sensor nodes is limited, LDPC codes that achieve the same decoding effect but consume less energy are needed. Power consumption for decoding can be measured by the iteration number of BP decoder. A good LDPC code can effectively reduce the iteration number of BP decoder and such save energy. Therefore, we performed an experiment to calculate the average iteration numbers corresponding to the PEG-based codes, QC-based codes and the code from GCE algorithm, and present the results in Figure 4 with Equation (2) below,
where is the average iteration number with an LDPC code from one construction algorithm of LDPC codes, and is the average iteration number with an LDPC code from the GCE algorithm. From Figure 4, it can be seen that the LDPC code from GCE has the lowest iteration numbers at different crossover probabilities . Assuming that the energy consumed per iteration is equal, the LDPC code from GCE can save to of energy compared to the LDPC codes obtained by other algorithms, which can effectively extend the lifetime of sensor nodes in WSNs.
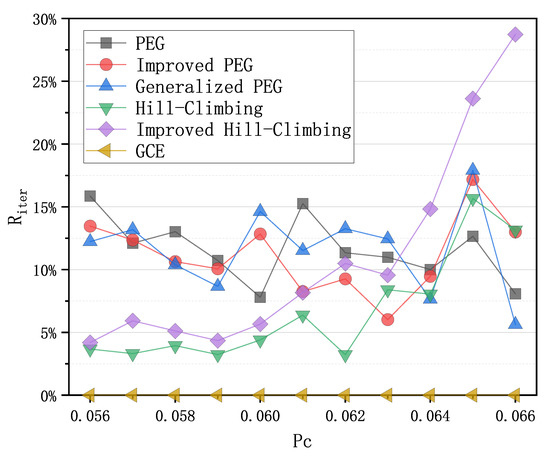
Figure 4.
Comparison of iteration numbers of the PEG-based codes, QC-based codes and the code from the GCE algorithm with from Equation (2) as the function of over binary symmetric channel (BSC).
5.3. Optimal Girth
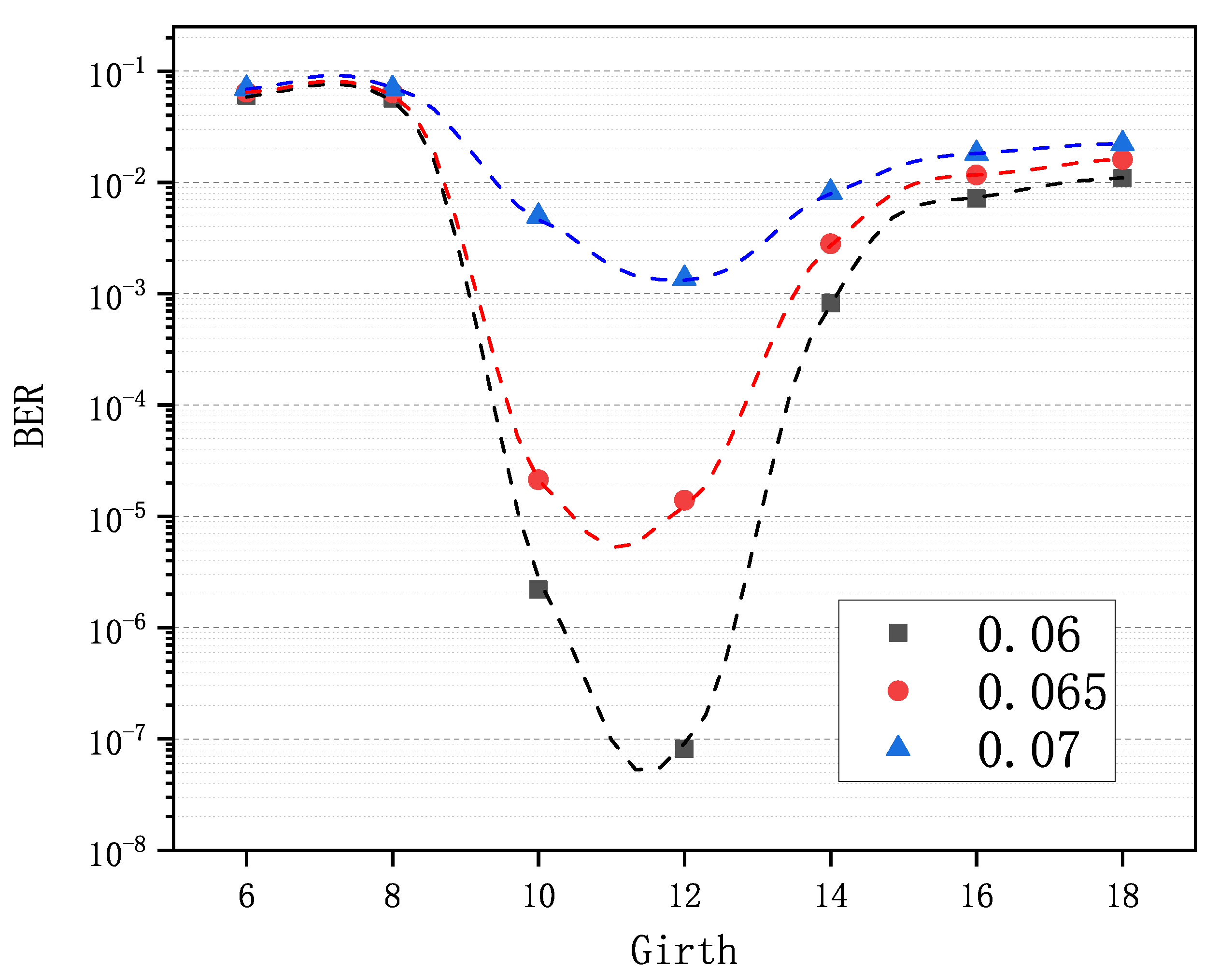
An LDPC code construction algorithm is easy to wield, meaning that the user can easily get the optimal input to the algorithm. In Section 4, we know that compared with obtaining an excellent variable-node degree distribution for the PEG-based algorithms and a superb base matrix for the QC-based algorithms, it is much easier to find the optimal girth for the GCE algorithm, which is illustrated in Figure 5. In the test, seven matrices were generated via the GCE algorithm with girths g 6∼18, and key pairs were simulated for each of three values. Then, BER was calculated for each matrix and each . As we can see in Figure 5, the optimal girths are the same, i.e., 12 for all of the values. The curves on both sides of the optimal girth are all monotonic. Therefore, by choosing one optionally and taking advantage of the monotonicity, we can approach and finally find the optimal girth for any code rate and any code length.
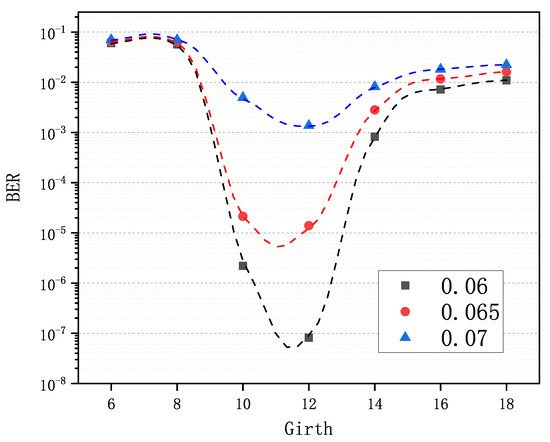
Figure 5.
Comparison of decoding performance of the LDPC codes from the GCE algorithm with different girths (6–18) at different values (, , ).
6. Conclusions
LDPC code is a good candidate for channel coding of WSN and can be constructed by PEG-based and QC-based algorithms. The aim of the present research was to discuss the ways to overcome the shortcomings of PEG-based and QC-based algorithms. We solve the problems by proposing GCE algorithm for constructing LDPC codes of any desired girth to avoid generating short cycles. The experimental result shows that the LDPC codes we construct have better decoding performance than the PEG-based and QC-based codes, especially in the error-floor region. LDPC codes constructed by GCE can effectively reduce the iteration number of decoding, thus reducing the power consumption of WSNs. In addition, the optimal input to GCE algorithm is easy to find.
Author Contributions
Conceptualization, C.G.; methodology, C.G. and S.L.; software, S.L.; validation, S.L.; formal analysis, C.G.; data curation, D.J.; writing—original draft preparation, C.G.; supervision, D.J. and L.C.; project administration, D.J. and L.C.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research is financially supported by the National Key Research and Development Program of China (Grant No. 2017YFA0303704), the Major Program of National Natural Science Foundation of China (Grants No. 11690030 and No. 11690032), the National Natural Science Foundation of China (Grant No. 61771236) and the Natural Science Foundation of Jiangsu Province (Grant No. BK20190297).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to subjects’ personal privacy and patents. The model of the subjects was public.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the writing of the manuscript or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| WSN | Wireless sensor network |
| PEG | Progressive-edge-growth |
| QC | Quasi-cyclic |
| LDPC | Low-density parity-check |
| BP | Belief-propagation |
| GCE | Girth-cycle-embedding |
| EMD | Extrinsic message degree |
| ACE | Approximate cycle extrinsic message degree |
| SNR | Signal noise ratio |
| BER | Bit error rate |
| BSC | Binary symmetric channel |
| BEC | Binary erasure channel |
| AWGNC | Additive white Gaussian noise channel |
Appendix A
In this section, we provide an example of constructing an LDPC code with 16 check nodes and 23 variable nodes by GCE algorithm. The input of the GCE algorithm, i.e., the girth of the code, is . For the convenience of presenting cycles, the LDPC code is represented by a non-standard Tanner graph [41] without restriction on the locations of nodes. In addition, all the nodes are numbered in the order in which they are used. The entire process of the example is shown in Figure A1. For each subgraph, black lines indicate the new part; gray lines represent the previous part; ten-member cycles containing the new part are displayed with red lines.
In the first step of GCE algorithm, we initialize the node sets , , , and form the first ten-member cycle as shown in Figure A1a with 5 check nodes and 5 variable nodes from and , respectively.
In the second step, we execute to find two check nodes, and whose distance is , and fetch 2 check nodes from and 3 variable nodes from to connect and , forming another ten-member cycle. Repeat the same action to find and connect four other check-node pairs: , , , , and obtain four other ten-member cycles as indicated in Figure A1b. So far, , and in order to exhaust the last check node we find and with distance 6 by and connect them with the last check node and 2 variable nodes from . As presented in Figure A1c, two ten-member cycles are newly generated. Up to this point, all the check nodes have participated in the construction of the LDPC code, i.e., .
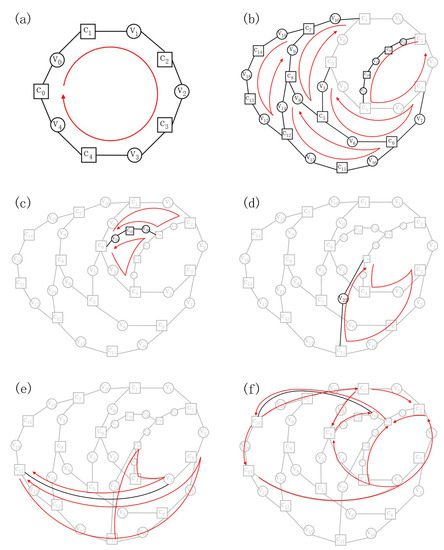
Figure A1.
An example of constructing a low-density parity-check (LDPC) code with girth 10 by GCE algorithm. (a) Initialize node sets and form the first cycle. (b,c) Exhaust check nodes in . (d) Exhaust variable nodes in . (e,f) Increase the degrees of variable nodes.
Figure A1.
An example of constructing a low-density parity-check (LDPC) code with girth 10 by GCE algorithm. (a) Initialize node sets and form the first cycle. (b,c) Exhaust check nodes in . (d) Exhaust variable nodes in . (e,f) Increase the degrees of variable nodes.
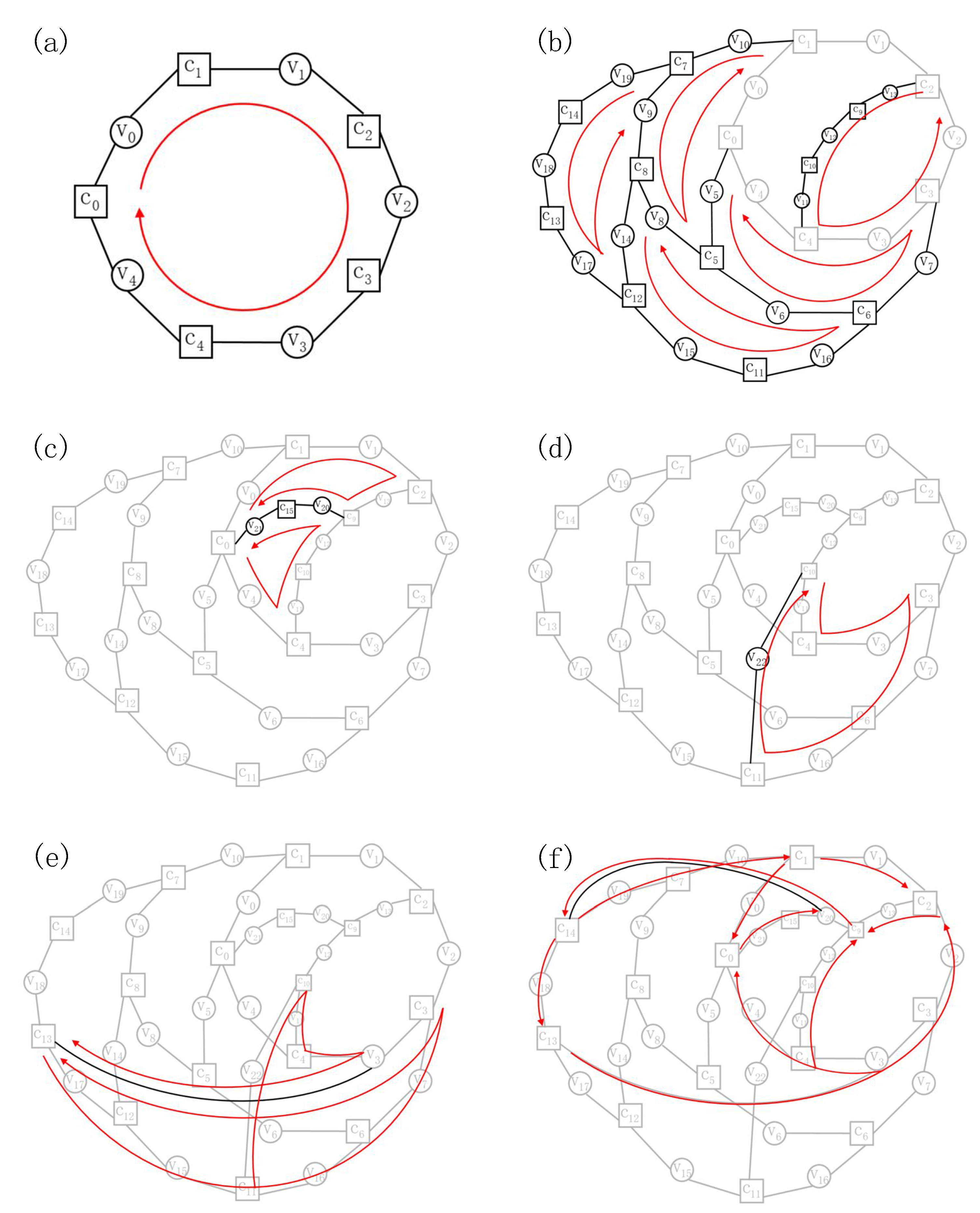
The result of the third step is plotted in Figure A1d. Two check nodes, and with distance 8, are exported by and connected with the last variable node from . Thus all the variable nodes have been exhausted, i.e., .
In the forth step, we generate two ten-member cycles as shown in Figure A1e by connecting and with distance 9 directly. In like manner, we connect and in Figure A1f. So far, the distance between any check and variable nodes is less than 9.
A LDPC code with girth 10 has been constructed after the steps above. We transform the Tanner graph in Figure A1f into a matrix provided in Figure A2.
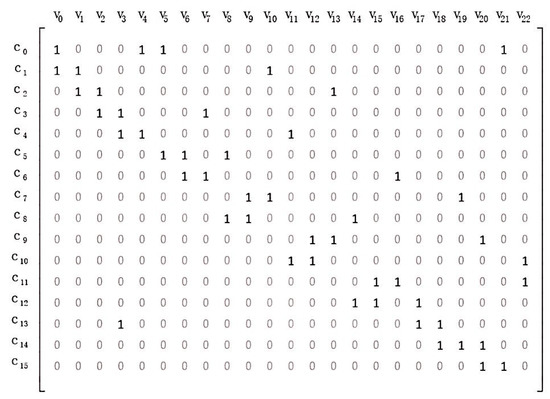
Figure A2.
A matrix transformed from the Tanner graph in Figure A1f.
Figure A2.
A matrix transformed from the Tanner graph in Figure A1f.

Appendix B
To find the reason for the outstanding decoding performance of GCE algorithm, for all the matrices in Section 5, we present their ACE spectra [26] associated with cycles of lengths 4–10 in Table A1 and their maximum degrees of variable nodes in Table A2. The ACE spectrum [26] of a matrix can be regarded as a vector where each element represents the minimum ACE of all the cycles with a certain cycle length. The minimum ACE of l-member cycles is positively related to the overall connectively of all the l-member cycles in the matrix. When there are no l-member cycles, the corresponding minimum ACE in the ACE spectrum is taken to be ∞.

Table A1.
Approximate cycle extrinsic message degree (ACE) spectra of all the matrices.
Table A1.
Approximate cycle extrinsic message degree (ACE) spectra of all the matrices.
| Length | 4 | 6 | 8 | 10 | |
|---|---|---|---|---|---|
| Matrix | |||||
| 1 | ∞ | 13 | 13 | 5 | |
| 2 | ∞ | 27 | 13 | 10 | |
| 3 | ∞ | 39 | 13 | 11 | |
| 4 | ∞ | ∞ | 4 | 5 | |
| 5 | ∞ | ∞ | 4 | 5 | |
| 6 | ∞ | ∞ | ∞ | ∞ | |

Table A2.
Maximum degrees of variable nodes for all the matrices.
Table A2.
Maximum degrees of variable nodes for all the matrices.
| Matrix | 1 | 2 | 3 | 4 | 5 | 6 |
| Degree | 15 | 15 | 15 | 3 | 3 | 7 |
As can be seen from Table A1, matrices 4 and 5 eliminate all six-member cycles while matrices 1–3 do not, which explains why matrices 4 and 5 outweigh matrices 1–3 when is less than . Moreover, it is noted that matrix 6 evades all four-member to ten-member cycles which can degrade the performance of any matrix, and thus outperforms the others. With the increase of , however, the matrices with high-degree variable nodes gradually have the advantages. Connectivity of short cycles can be improved by raising the degrees of variable nodes to increase extrinsic paths (see Table A1), such that the hazard of short cycles is weakened. The variable nodes with high degrees can provide more decoding information to correct errors. In this respect, it is theoretically explained that matrices 1–3 with maximum degree 15 gradually perform better than matrices 4 and 5 with maximum degree 3 as displayed in Table A2. In addition, though matrix 6 has no cycles of lengths 4–10, its maximum degree is relatively smaller than matrices 1–3. Therefore, when gets into the waterfall region, matrix 6 works worse than matrices 1–3. In summary, the analysis above suggests that the matrices from the GCE algorithm we proposed have better decoding performance than the matrices constructed by PEG-based algorithms and QC-based algorithms, especially in the error-floor region.
References
- Shih, E.; Cho, S.-H.; Ickes, N.; Min, R.; Sinha, A.; Wang, A.; Chandrakasan, A. Physical layer driven protocol and algorithm design for energy-efficient wireless sensor networks. In Proceedings of the 7th Annual International Conference on Mobile Computing and Networking, Rome, Italy, 16–21 July 2001; pp. 272–287. [Google Scholar]
- Sankarasubramaniam, Y.; Akyildiz, I.F.; McLaughlin, S.W. Energy efficiency based packet size optimization in wireless sensor networks. In Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 11 May 2003; pp. 1–8. [Google Scholar]
- Haque, S.A.; Rahman, M.; Aziz, S.M. Sensor anomaly detection in wireless sensor networks for healthcare. Sensors 2015, 15, 8764–8786. [Google Scholar] [CrossRef]
- Calafate, C.T.; Lino, C.; Diaz-Ramirez, A.; Cano, J.-C.; Manzoni, P. An integral model for target tracking based on the use of a WSN. Sensors 2013, 13, 7250–7278. [Google Scholar] [CrossRef] [PubMed]
- Winkler, M.; Tuchs, K.-D.; Hughes, K.; Barclay, G. Theoretical and practical aspects of military wireless sensor networks. J. Telecommun. Inf. Technol. 2008, 2, 37–45. [Google Scholar]
- Rosero-Montalvo, P.D.; Erazo-Chamorro, V.C.; Lopez-Batista, V.F.; Moreno-Garcia, M.N.; Peluffo-Ordonez, D.H. Environment monitoring of rose crops greenhouse based on autonomous vehicles with a WSN and data analysis. Sensors 2020, 20, 5905. [Google Scholar] [CrossRef]
- Santana, S.G.; Abril, J.S.; Sosa, J.; Montiel-Nelson, J.-A.; Bautista, T. Design of a practical underwater sensor network for offshore fish farm cages. Sensors 2020, 20, 4459. [Google Scholar] [CrossRef] [PubMed]
- Lihakanga, R.; Ding, Y.; Medero, G.M.; Chapman, S.; Goussetis, G. A high-resolution open source platform for building envelope thermal performance assessment using a wireless sensor network. Sensors 2020, 20, 1755. [Google Scholar] [CrossRef]
- Nkemeni, V.; Mieyeville, F.; Tsafack, P. A distributed computing solution based on distributed kalman filter for leak detection in WSN-based water pipeline monitoring. Sensors 2020, 20, 5204. [Google Scholar] [CrossRef] [PubMed]
- Gallager, R.G. Low-density parity-check codes. IEEE Trans. Inf. Theory 1962, 8, 21–28. [Google Scholar] [CrossRef]
- Biroli, A.D.G.; Martina, M.; Masera, G. An LDPC decoder architecture for wireless sensor network applications. Sensors 2012, 12, 1529–1543. [Google Scholar] [CrossRef]
- Meng, J.; Zhao, D.; Zhang, L. Design and analysis of non-binary LDPC-CPM system for hybrid check matrix construction algorithm of WSN. Sensors 2018, 18, 2418. [Google Scholar] [CrossRef] [PubMed]
- Sartipi, M.; Fekri, F. Source and channel coding in wireless sensor networks using LDPC codes. In Proceedings of the First Annual IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks, Santa Clara, CA, USA, 4–7 October 2004; pp. 309–316. [Google Scholar]
- McDonagh, J.; Sala, M.; O’hAllmhurain, A.; Katewa, V.; Popovici, E. Efficient construction and implementation of short LDPC codes for wireless sensor networks. In Proceedings of the 18th European Conference on Circuit Theory and Design, Sevilla, Spain, 27–30 August 2007; pp. 703–706. [Google Scholar]
- Qaisar, S.B.; Radha, H. Optimal progressive error recovery for wireless sensor networks using irregular LDPC codes. In Proceedings of the 41st Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 14–16 March 2007; pp. 232–237. [Google Scholar]
- McEliece, R.J.; MacKay, D.J.; Cheng, J.-F. Turbo decoding as an instance of Pearl’s “belief propagation” algorithm. IEEE J. Sel. Areas Commun. 1998, 16, 140–152. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.-A. Factor graphs and the sum-product algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Hu, X.-Y.; Eleftheriou, E.; Arnold, D.M. Regular and irregular progressive edge-growth tanner graphs. IEEE Trans. Inf. Theory 2005, 51, 386–398. [Google Scholar] [CrossRef]
- Xiao, H.; Banihashemi, A.H. Improved progressive-edge-growth (PEG) construction of irregular LDPC codes. IEEE Commun. Lett. 2004, 8, 715–717. [Google Scholar] [CrossRef]
- Vukobratovic, D.; Senk, V. Generalized ACE constrained progressive edge-growth LDPC code design. IEEE Commun. Lett. 2008, 12, 32–34. [Google Scholar] [CrossRef]
- Wang, Y.; Yedidia, J.S.; Draper, S.C. Construction of high-girth QC-LDPC codes. In Proceedings of the 5th International Symposium on Turbo Codes and Related Topics, Lausanne, Switzerland, 1–5 September 2008; pp. 180–185. [Google Scholar]
- Lau, F.C.; Tam, W.M. A fast searching method for the construction of QC-LDPC codes with large girth. In Proceedings of the IEEE Symposium on Computers and Communications, Cappadocia, Turkey, 1–4 July 2012; pp. 125–128. [Google Scholar]
- Tian, T.; Jones, C.R.; Villasenor, J.D.; Wesel, R.D. Selective avoidance of cycles in irregular LDPC code construction. IEEE Trans. Commun. 2004, 52, 1242–1247. [Google Scholar] [CrossRef]
- Fan, J.; Xiao, Y. A method of counting the number of cycles in LDPC codes. In Proceedings of the 8th International Conference on Signal Processing, Beijing, China, 16–20 November 2006. [Google Scholar]
- Tian, T.; Jones, C.; Villasenor, J.D.; Wesel, R.D. Construction of irregular LDPC codes with low error floors. In Proceedings of the IEEE International Conference on Communications, Anchorage, AK, USA, 11–15 May 2003; pp. 3125–3129. [Google Scholar]
- Vukobratovic, D.; Djurendic, A.; Senk, V. ACE spectrum of LDPC codes and generalized ACE design. In Proceedings of the IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 665–670. [Google Scholar]
- Healy, C.T.; de Lamare, R.C. Design of LDPC codes based on multipath EMD strategies for progressive edge growth. IEEE Trans. Commun. 2016, 64, 3208–3219. [Google Scholar] [CrossRef]
- Elkouss, D.; Leverrier, A.; Alléaume, R. Efficient reconciliation protocol for discrete-variable quantum key distribution. In Proceedings of the IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 1879–1883. [Google Scholar]
- Yazdani, R.; Ardakani, M. Waterfall performance analysis of finite-length LDPC codes on symmetric channels. IEEE Trans. Commun. 2009, 57, 3183–3187. [Google Scholar] [CrossRef]
- Richardson, T. Error floors of LDPC codes. In Proceedings of the Annual Allerton Conference on Communication Control and Computing, Monticello, IL, USA, 1–3 October 2003; pp. 1426–1435. [Google Scholar]
- Richardson, T.J.; Urbanke, R.L. The capacity of low-density parity-check codes under message-passing decoding. IEEE Trans. Inf. Theory 2001, 47, 599–618. [Google Scholar] [CrossRef]
- Richardson, T.J.; Shokrollahi, M.A.; Urbanke, R.L. Design of capacity-approaching irregular low-density parity-check codes. IEEE Trans. Inf. Theory 2001, 47, 619–637. [Google Scholar] [CrossRef]
- Chung, S.-Y.; Urbanke, R.; Richardson, T.J. Gaussian approximation for sum-product decoding of low-density parity-check codes. In Proceedings of the IEEE International Symposium on Information Theory, Sorrento, Italy, 25–30 June 2000; p. 318. [Google Scholar]
- Asamov, T.; Aydin, N. LDPC codes of arbitrary girth. In Proceedings of the Canadian Workshop on Information Theory, Edmonton, AB, Canada, 6–8 June 2007; pp. 69–72. [Google Scholar]
- Sarvaghad-Moghaddam, M.; Ullah, W.; Jayakody, D.; Affes, S. A new construction of high performance LDPC matrices for mobile networks. Sensors 2020, 20, 2300. [Google Scholar] [CrossRef]
- Luby, M.G.; Shokrollahi, M.A.; Mitzenmacher, M.; Spielman, D.A. Improved low-density parity-check codes using irregular graphs and belief propagation. In Proceedings of the IEEE International Symposium on Information Theory, Cambridge, MA, USA, 16–21 August 1998; p. 117. [Google Scholar]
- Luby, M.G.; Mitzenmacher, M.; Shokrollahi, M.A.; Spielman, D.A. Improved low-density parity-check codes using irregular graphs. IEEE Trans. Inf. Theory 2001, 47, 585–598. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009; pp. 43–64. [Google Scholar]
- Noor, M.; Nguyen, K.D.; Lechner, G. Finite length analysis of LDPC codes. In Proceedings of the IEEE Wireless Communications and Networking Conference, Istanbul, Turkey, 6–9 April 2014; pp. 206–211. [Google Scholar]
- Amraou, A.; Montanari, A.; Richardson, T.; Urbanke, R. Finite-length scaling for iteratively decoded LDPC ensembles. IEEE Trans. Inf. Theory 2009, 55, 473–498. [Google Scholar] [CrossRef]
- Tanner, R. A recursive approach to low complexity codes. IEEE Trans. Inf. Theory 1981, 27, 533–547. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).