MSDU-Net: A Multi-Scale Dilated U-Net for Blur Detection
Abstract
1. Introduction
- We proposed a group of extractors with dilated convolution to capture multi-scale texture information on purpose rather than using a fully convolutional network multiple times on the different scales of the image.
- We designed a new model with our extractors based on U-net, which can fuse the multi-scale texture and semantic features simultaneously to improve the accuracy.
- Most methods only can detect the defocus blur or the motion blur, but our method addressed the blur detection, ignoring the specific cause of the blur and thus could detect both defocus blur and motion blur. Compared with the state-of-the-art blur detection methods, the proposed model obtained F-measure scores of more than in all the three datasets.
2. Related Work
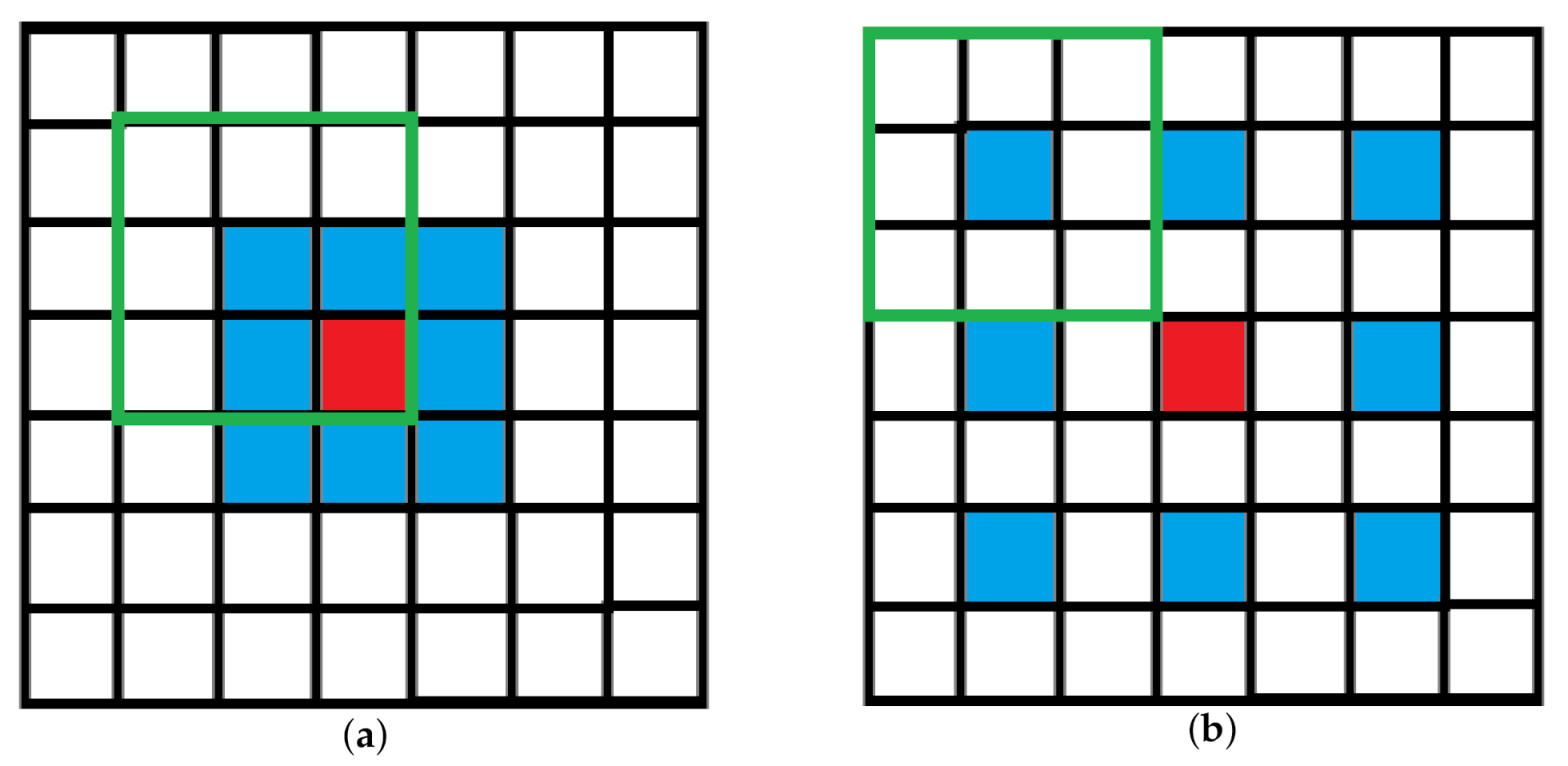
3. Proposed MSD-Unet
3.1. Basic Components
3.2. Model Details
4. Experiments
4.1. Datasets and Implementation
4.2. Evaluation Criteria and Comparison
4.3. Ablation Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, T.; Jin, W.; Zhang, C.; Wang, P.; Li, W. Salient Object Detection via Weighted Low Rank Matrix Recovery. IEEE Signal Process. Lett. 2017, 24, 490–494. [Google Scholar]
- Sun, X.; Zhang, X.; Zou, W.; Xu, C. Focus prior estimation for salient object detection. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 1532–1536. [Google Scholar]
- Chang, T.; Chunping, H.; Zhanjie, S. Defocus map estimation from a single image via spectrum contrast. Opt. Lett. 2013, 38, 1706–1708. [Google Scholar]
- Bae, S.; Durand, F. Defocus magnification. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2007; Volume 26, pp. 571–579. [Google Scholar]
- Tang, C.; Hou, C.; Hou, Y.; Wang, P.; Li, W. An effective edge-preserving smoothing method for image manipulation. Digit. Signal Process. 2017, 63, 10–24. [Google Scholar] [CrossRef]
- Wang, X.; Tian, B.; Liang, C.; Shi, D. Blind image quality assessment for measuring image blur. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, Hainan, 27–30 May 2008; pp. 467–470. [Google Scholar]
- Shi, J.; Xu, L.; Jia, J. Discriminative blur detection features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2965–2972. [Google Scholar]
- Zhang, W.; Cham, W.K. Single image focus editing. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 1947–1954. [Google Scholar]
- Zhang, W.; Cham, W.K. Single-image refocusing and defocusing. IEEE Trans. Image Process. 2011, 21, 873–882. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Tao, D.; Zhuo, S.; Xu, X.; Pu, S.; Song, M. AllFocus: Patch-based video out-of-focus blur reconstruction. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 1895–1908. [Google Scholar] [CrossRef]
- Munkberg, C.J.; Vaidyanathan, K.; Hasselgren, J.N.; Clarberg, F.P.; Akenine-Moller, T.G.; Salvi, M. Layered Reconstruction for Defocus and Motion Blur. U.S. Patent 9,483,869, 2016. [Google Scholar]
- Yi, X.; Eramian, M. LBP-based segmentation of defocus blur. IEEE Trans. Image Process. 2016, 25, 1626–1638. [Google Scholar] [CrossRef]
- Golestaneh, S.A.; Karam, L.J. Spatially-Varying Blur Detection Based on Multiscale Fused and Sorted Transform Coefficients of Gradient Magnitudes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 596–605. [Google Scholar]
- Karaali, A.; Jung, C.R. Edge-based defocus blur estimation with adaptive scale selection. IEEE Trans. Image Process. 2017, 27, 1126–1137. [Google Scholar] [CrossRef]
- Xu, G.; Quan, Y.; Ji, H. Estimating defocus blur via rank of local patches. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 5371–5379. [Google Scholar]
- Shi, J.; Xu, L.; Jia, J. Just noticeable defocus blur detection and estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 657–665. [Google Scholar]
- Tang, C.; Wu, J.; Hou, Y.; Wang, P.; Li, W. A spectral and spatial approach of coarse-to-fine blurred image region detection. IEEE Signal Process. Lett. 2016, 23, 1652–1656. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. arXiv 2015, arXiv:1506.01497. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Qi, Y.; Zhang, S.; Qin, L.; Yao, H.; Huang, Q.; Lim, J.; Yang, M.H. Hedged deep tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4303–4311. [Google Scholar]
- Li, P.; Wang, D.; Wang, L.; Lu, H. Deep visual tracking: Review and experimental comparison. Pattern Recognit. 2018, 76, 323–338. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Shao, W.; Shen, P.; Xiao, X.; Zhang, L.; Wang, M.; Li, Z.; Qin, C.; Zhang, X. Advanced edge-preserving pixel-level mesh data-dependent interpolation technique by triangulation. In Proceedings of the 2011 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 14–16 September 2011; pp. 1–6. [Google Scholar]
- Kim, J.; Kwon Lee, J.; Mu Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, Z.; Yao, Y. Defocus Blur Detection and Estimation from Imaging Sensors. Sensors 2018, 18, 1135. [Google Scholar]
- Zhao, W.; Zheng, B.; Lin, Q.; Lu, H. Enhancing Diversity of Defocus Blur Detectors via Cross-Ensemble Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 8905–8913. [Google Scholar]
- Ma, K.; Fu, H.; Liu, T.; Wang, Z.; Tao, D. Deep blur mapping: Exploiting high-level semantics by deep neural networks. IEEE Trans. Image Process. 2018, 27, 5155–5166. [Google Scholar] [CrossRef]
- Tang, C.; Zhu, X.; Liu, X.; Wang, L.; Zomaya, A. DeFusionNET: Defocus Blur Detection via Recurrently Fusing and Refining Multi-Scale Deep Features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 2700–2709. [Google Scholar]
- Huang, R.; Feng, W.; Fan, M.; Wan, L.; Sun, J. Multiscale blur detection by learning discriminative deep features. Neurocomputing 2018, 285, 154–166. [Google Scholar] [CrossRef]
- Park, J.; Tai, Y.W.; Cho, D.; So Kweon, I. A unified approach of multi-scale deep and hand-crafted features for defocus estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1736–1745. [Google Scholar]
- Chen, Y.; Fang, H.; Xu, B.; Yan, Z.; Kalantidis, Y.; Rohrbach, M.; Yan, S.; Feng, J. Drop an octave: Reducing spatial redundancy in convolutional neural networks with octave convolution. arXiv 2019, arXiv:1904.05049. [Google Scholar]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding convolution for semantic segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1451–1460. [Google Scholar]
- Su, B.; Lu, S.; Tan, C.L. Blurred image region detection and classification. In Proceedings of the 19th ACM International Conference on Multimedia, Scottsdale, AZ, USA, 28 November–1 December 2011; pp. 1397–1400. [Google Scholar]
- Zhao, W.; Zhao, F.; Wang, D.; Lu, H. Defocus blur detection via multi-stream bottom-top-bottom fully convolutional network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 15–23 June 2018; pp. 3080–3088. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer: New York, NY, USA, 2018; pp. 3–11. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. arXiv 2019, arXiv:1904.00592. [Google Scholar] [CrossRef]
- Iglovikov, V.; Shvets, A. Ternausnet: U-net with vgg11 encoder pre-trained on imagenet for image segmentation. arXiv 2018, arXiv:1801.05746. [Google Scholar]
- Zhang, J.; Jin, Y.; Xu, J.; Xu, X.; Zhang, Y. MDU-Net: Multi-scale Densely Connected U-Net for biomedical image segmentation. arXiv 2018, arXiv:1812.00352. [Google Scholar]
- Chaurasia, A.; Culurciello, E. Linknet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; pp. 1–4. [Google Scholar]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchamitchian, P. A real-time algorithm for signal analysis with the help of the wavelet transform. In Wavelets; Springer: New York, NY, USA, 1990; pp. 286–297. [Google Scholar]



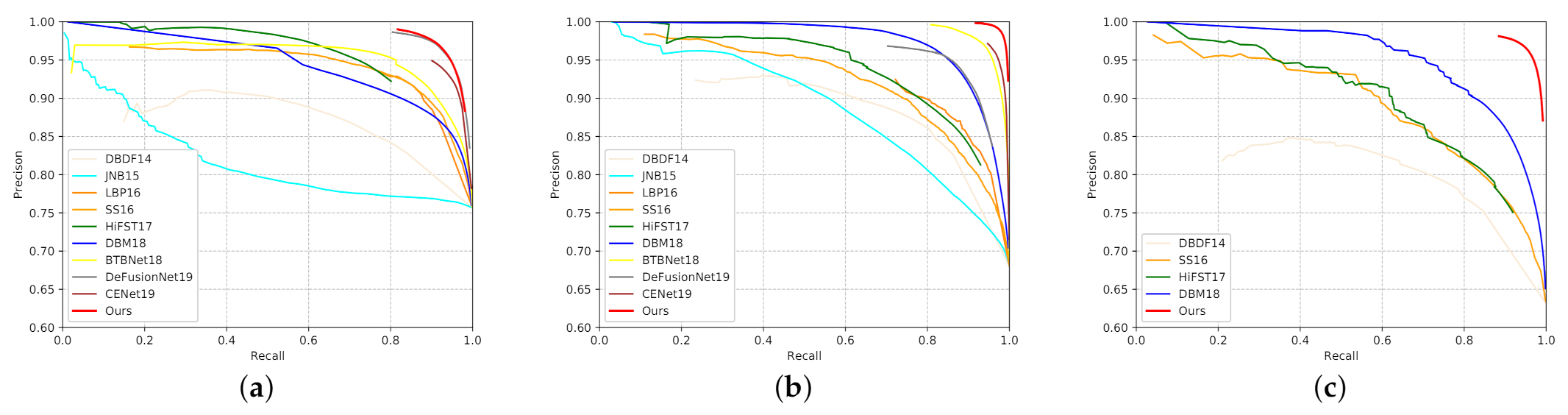
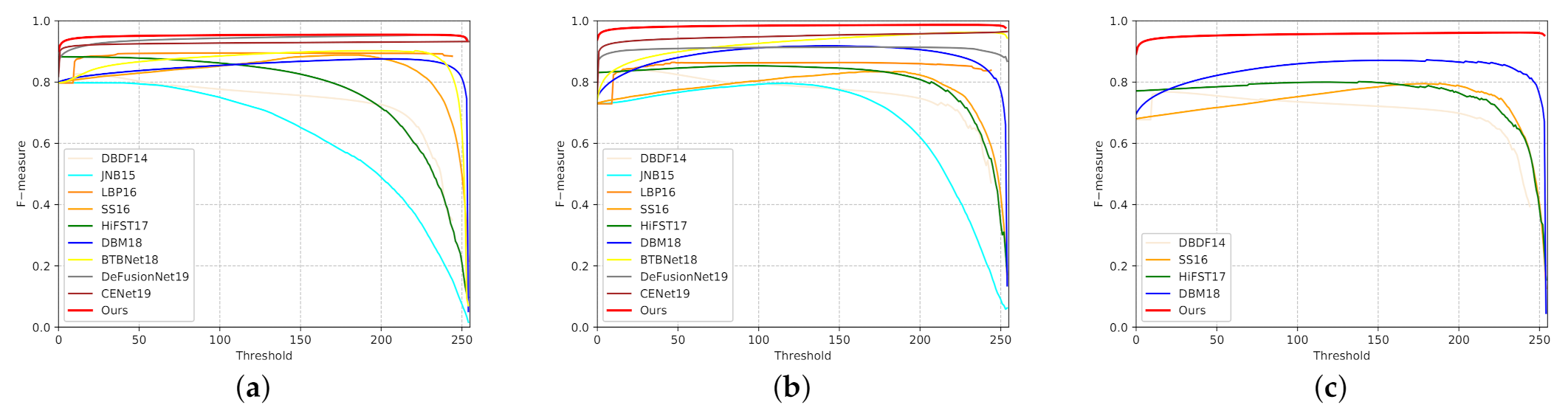


| Datasets | Metric | DBDF | JNB | LBP | SS | HiFST | DBM | BTB | DeF | CENet | MSDU-Net |
|---|---|---|---|---|---|---|---|---|---|---|---|
| DUT | F | 0.827 | 0.798 | 0.895 | 0.889 | 0.883 | 0.876 | 0.902 | 0.953 | 0.932 | 0.954 |
| MEA | 0.244 | 0.244 | 0.168 | 0.163 | 0.203 | 0.165 | 0.145 | 0.078 | 0.098 | 0.075 | |
| CUHK* | F | 0.841 | 0.796 | 0.864 | 0.834 | 0.853 | 0.918 | 0.963 | 0.914 | 0.965 | 0.976 |
| MEA | 0.208 | 0.260 | 0.174 | 0.215 | 0.179 | 0.114 | 0.057 | 0.103 | 0.049 | 0.032 | |
| CUHK | F | 0.768 | - | - | 0.795 | 0.799 | 0.871 | - | - | - | 0.953 |
| MEA | 0.257 | - | - | 0.248 | 0.207 | 0.123 | - | - | - | 0.042 |
| Network | No Skip | MSDU-Net |
|---|---|---|
| F-measure | 0.851 | 0.952 |
| MEA | 0.137 | 0.042 |
| Network | U-Net | No Dilated () | MSDU-Net |
|---|---|---|---|
| F-measure | 0.843 | 0.956 | 0.950 |
| MEA | 0.146 | 0.044 | 0.046 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Yang, F.; Sadovnik, A. MSDU-Net: A Multi-Scale Dilated U-Net for Blur Detection. Sensors 2021, 21, 1873. https://doi.org/10.3390/s21051873
Xiao X, Yang F, Sadovnik A. MSDU-Net: A Multi-Scale Dilated U-Net for Blur Detection. Sensors. 2021; 21(5):1873. https://doi.org/10.3390/s21051873
Chicago/Turabian StyleXiao, Xiao, Fan Yang, and Amir Sadovnik. 2021. "MSDU-Net: A Multi-Scale Dilated U-Net for Blur Detection" Sensors 21, no. 5: 1873. https://doi.org/10.3390/s21051873
APA StyleXiao, X., Yang, F., & Sadovnik, A. (2021). MSDU-Net: A Multi-Scale Dilated U-Net for Blur Detection. Sensors, 21(5), 1873. https://doi.org/10.3390/s21051873





