Direct Scaling of Measure on Vortex Shedding through a Flapping Flag Device in the Open Channel around a Cylinder at Re∼103: Taylor’s Law Approach
Abstract
1. Introduction
2. Materials and Methods
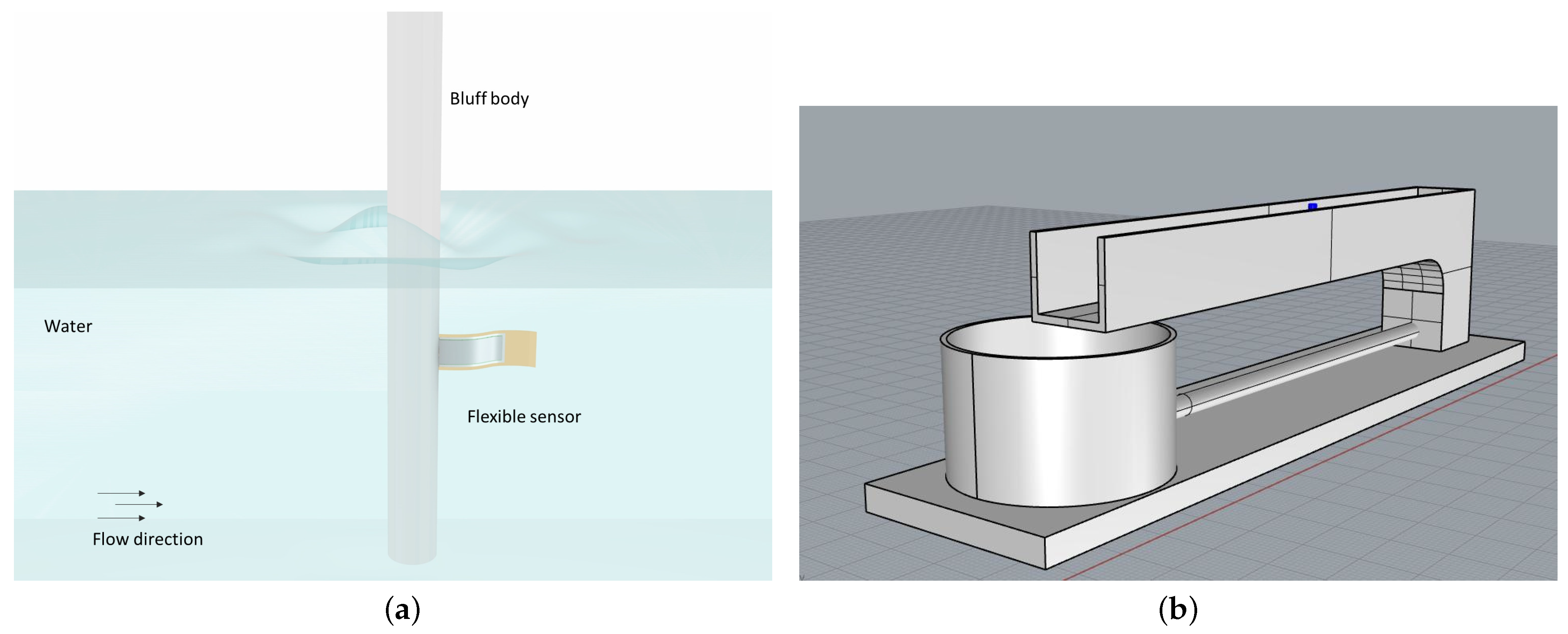
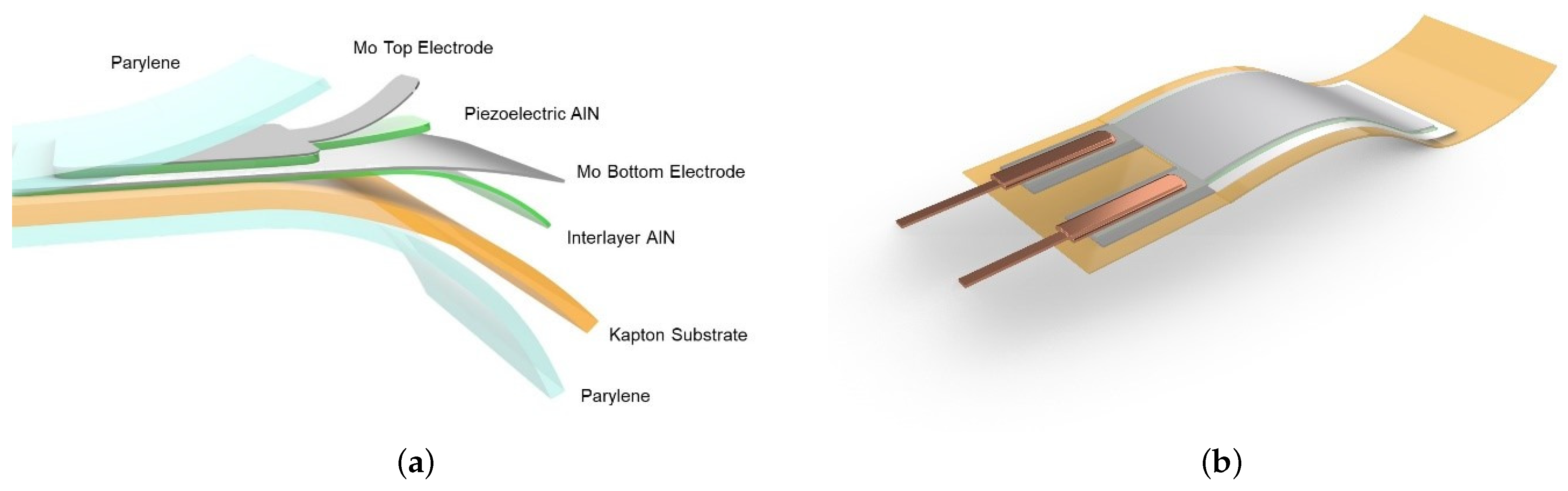
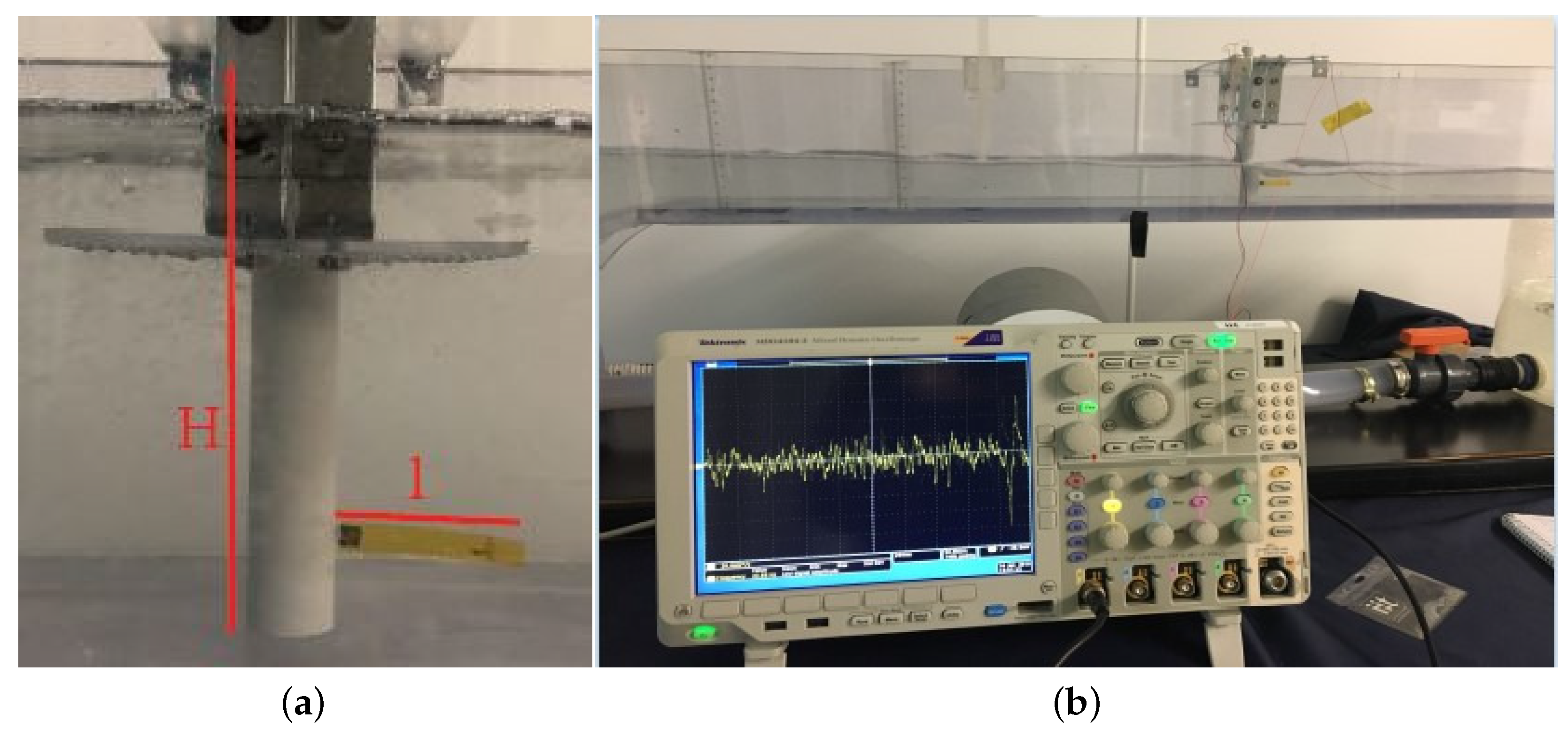
2.1. Thin Films-Based Device and Experimental Setup
2.2. Strohual and Reynolds Numbers Relationship
2.3. Direct Scaling Analysis on the Voltage Fluctuations: Taylor’s Law Approach
3. Experimental Results and Discussions
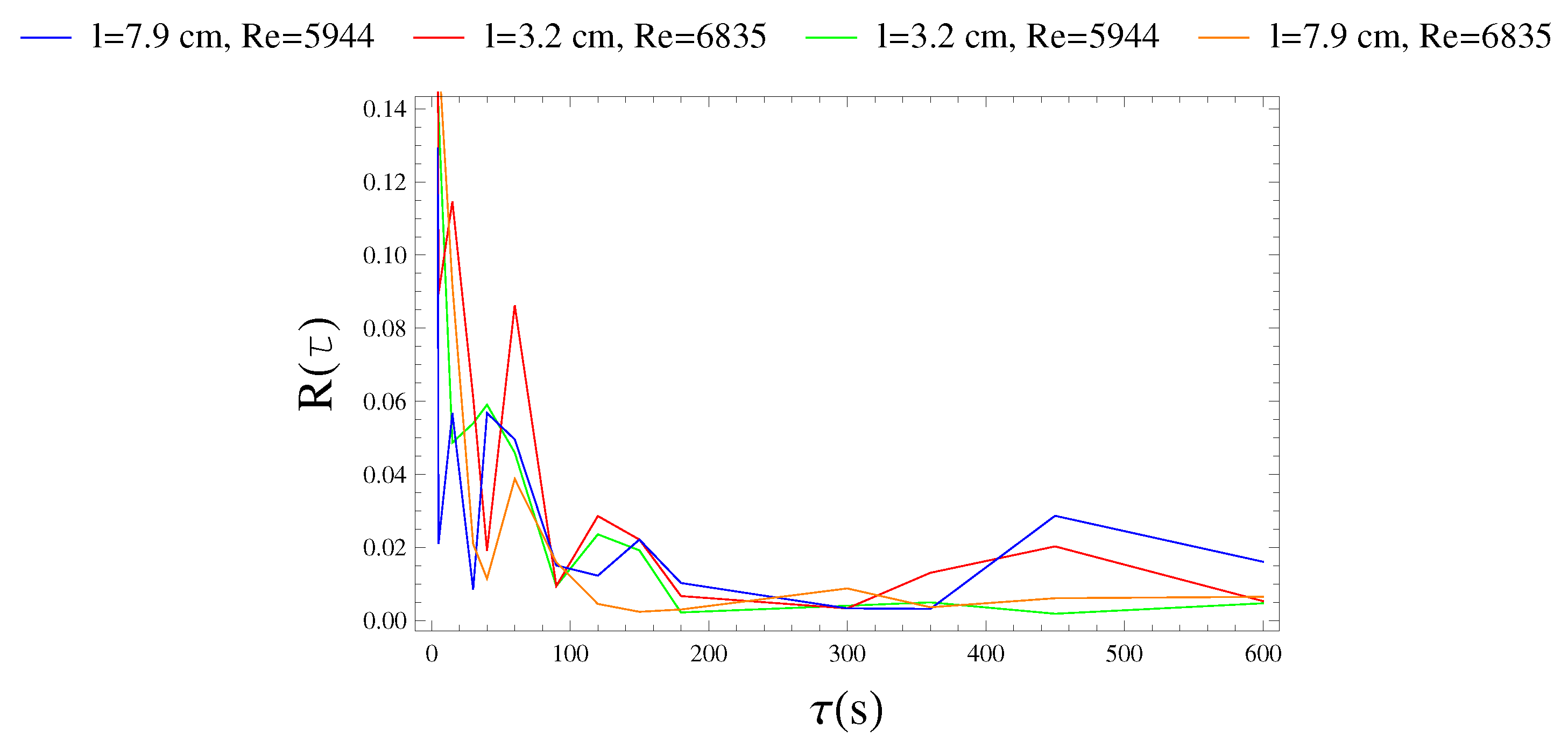
3.1. Correlation Time
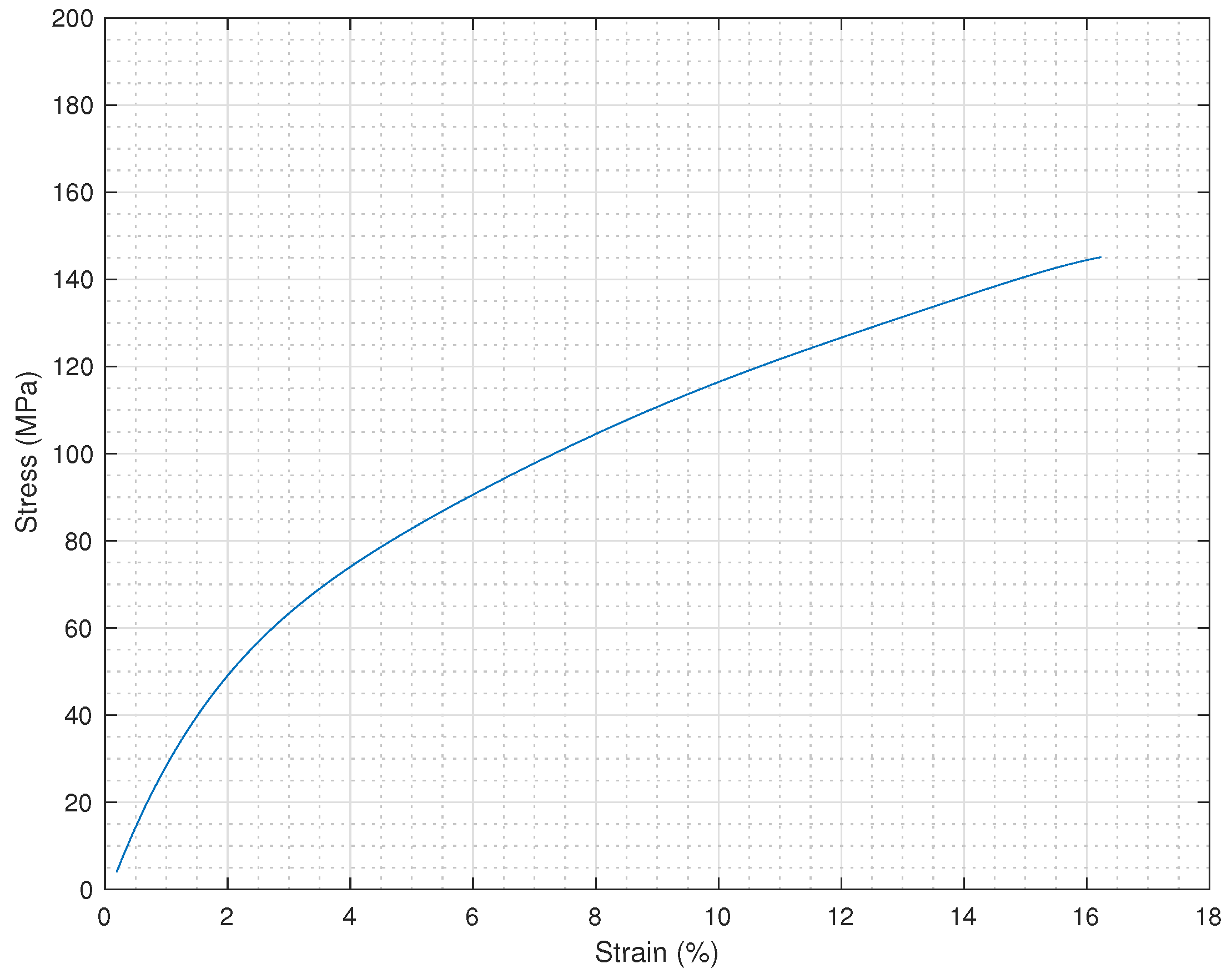
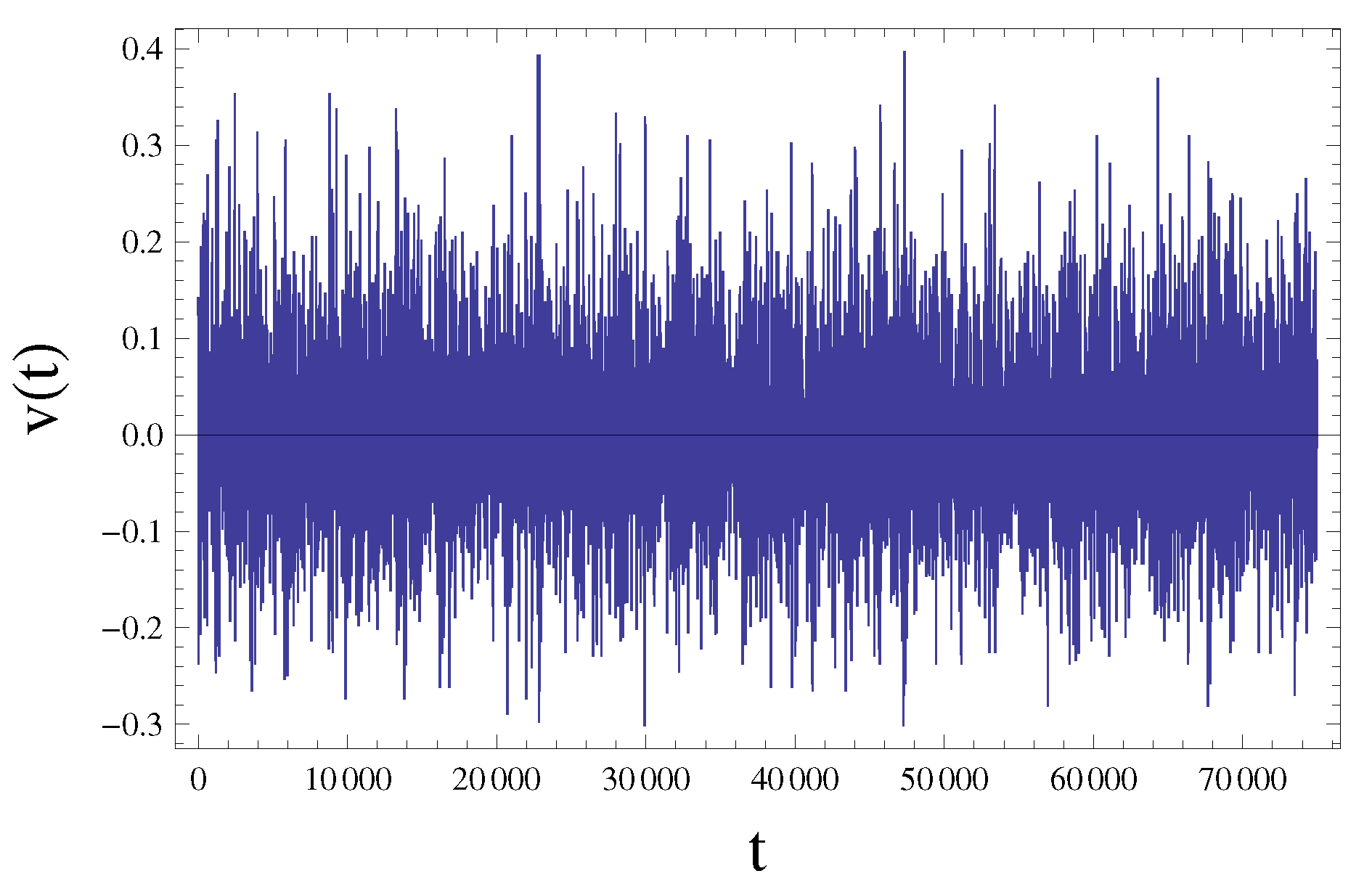
3.2. Vortex Shedding Measures and Relationship Voltage-Pressure
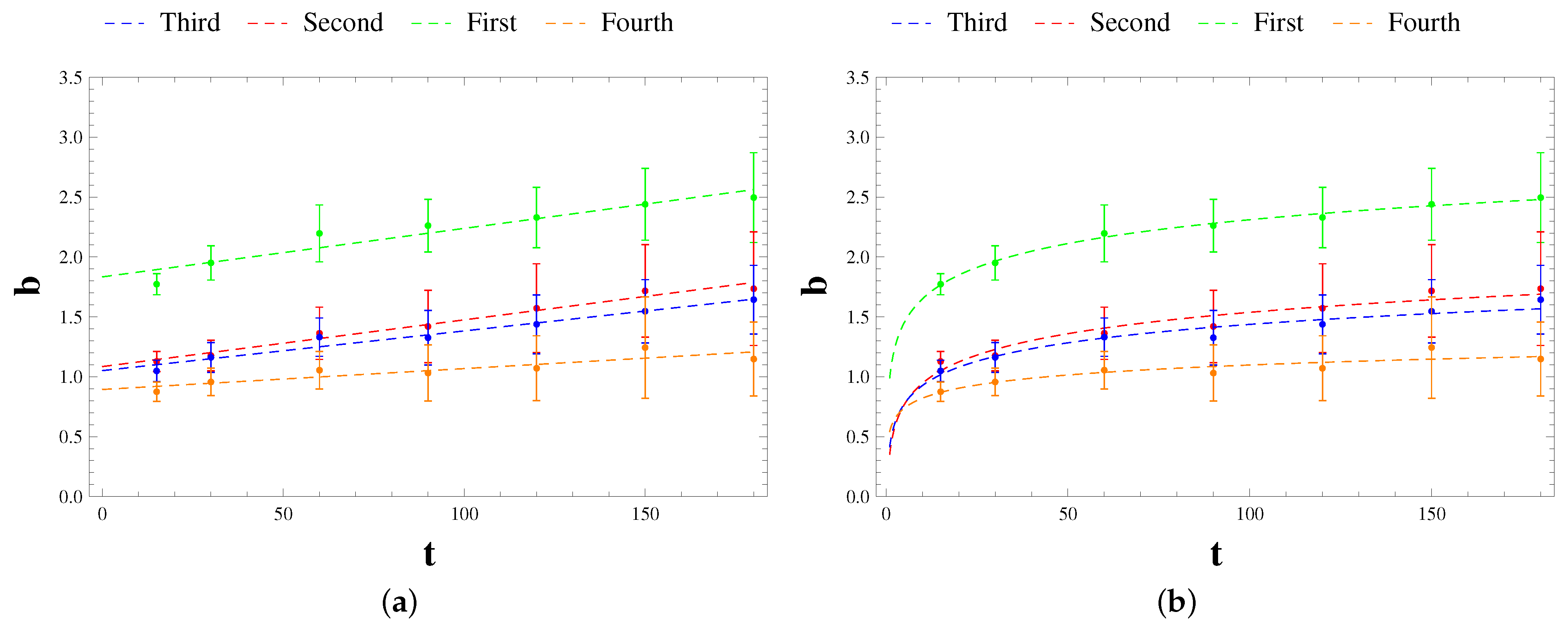
3.3. Taylor’s Law Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics: Fundamental and Applications; McGraw Hill Science Engineering Math: New York, NY, USA, 2004. [Google Scholar]
- Albrecht, H.-E.; Borys, M.; Damaschke, N.; Tropea, C. Laser Doppler and Phase Doppler Measurement Techniques; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Katopodes, D.N. Free Surface Flow: Environmental Fluid Mechanics; Elsevier Science and Technology: Cambridge/Oxford, UK, 2018. [Google Scholar]
- Roshko, A. Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 1961, 10, 345–356. [Google Scholar] [CrossRef]
- Bearman, P. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 1965, 21, 241–255. [Google Scholar] [CrossRef]
- Griffin, O.M. A universal Strouhal number for the ‘locking-on’ of vortex shedding to the vibrations of bluff cylinders. J. Fluid Mech. 1978, 85, 591–606. [Google Scholar] [CrossRef]
- Okajima, A. Strouhal numbers of rectangular cylinders. J. Fluid Mech. 1982, 123, 379–398. [Google Scholar] [CrossRef]
- Gonçalves, H.C.; Vieira, E.D.R. Strouhal Number Determination for Several Regular Polygon Cylinders for Reynolds Number up to 600. In Proceedings of the XV Congresso Brasileiro de Engenharia Mecânica, Aguas de Lindoia, Brazil, 22–26 November 1999; p. 10. [Google Scholar]
- Taylor, G.K.; Nudds, R.L.; Thomas, A.L.R. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 2003, 425, 707–711. [Google Scholar] [CrossRef] [PubMed]
- Eloy, C. Optimal Strouhal number for swimming animals. J. Fluids Struct. 2012, 30, 205–218. [Google Scholar] [CrossRef]
- Shi, L.; Yu, Z.; Jaworski, A.J. Investigation into the Strouhal numbers associated with vortex shedding from parallel-plate thermoacoustic stacks in oscillatory flow conditions. Eur. J. Mech. B/Fluids 2011, 30, 206–217. [Google Scholar] [CrossRef]
- Rodriguez, I.; Lehmkul, O.; Chiva, J.; Borrell, R.; Oliva, A. On the flow past a circular cylinder from critical to super-critical Reynolds numbers: Wake topology and vortex shedding. Int. J. Heat Fluid Flow 2015, 55, 91–103. [Google Scholar] [CrossRef]
- Mouro, J.; Pinto, R.; Paoletti, P.; Tiribilli, B. Microcantilever: Dynamical Response for Mass Sensing and Fluid Characterization. Sensors 2020, 21, 115. [Google Scholar] [CrossRef]
- Ma, R.-H.; Wang, D.-A.; Hsueh, T.-H.; Lee, C.-Y. A MEMS-Based Flow Rate and Flow Direction Sensing Platform with Integrated Temperature Compensation Scheme. Sensors 2009, 9, 5460–5476. [Google Scholar] [CrossRef]
- Algieri, L.; Todaro, M.T.; Guido, F.; Mastronardi, V.; Desmaële, D.; Qualtieri, A.; Giannini, C.; Sibillano, T.; De Vittorio, M. Flexible Piezoelectric Energy-Harvesting Exploiting Biocompatible AlN Thin Films Grown onto Spin-Coated Polyimide Layers. ACS Appl. Energy Mater. 2018, 1, 5203–5210. [Google Scholar] [CrossRef]
- Bischur, E.; Pobering, S.; Menacher, M.; Schwesinger, N. Piezoelectric energy harvester operating in flowing water. In Active and Passive Smart Structures and Integrated Systems; International Society for Optics and Photonics: San Diego, CA, USA, 2010; Volume 7643, p. 76432Z. [Google Scholar] [CrossRef]
- Kim, S.G.; Priya, S.; Kanno, I. Piezoelectric MEMS for Energy Harvesting. MRS Bull. 2012, 37, 1039–1050. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Daniel Deng, Z. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Madaro, F.; Mehdipour, I.; Caricato, A.; Guido, F.; Rizzi, F.; Carlucci, A.P.; De Vittorio, M. Available Energy in Cars’ Exhaust System for IoT Remote Exhaust Gas Sensor and Piezoelectric Harvesting. Energies 2020, 13, 4169. [Google Scholar] [CrossRef]
- Petroni, S.; Rizzi, F.; Guido, F.; Cannavale, A.; Donateo, T.; Ingrosso, F.; Mastronardi, V.; Cingolani, R.; De Vittorio, M. Flexible AlN flags for efficient wind energy harvesting at ultralow cut-in wind speed. RSC Adv. 2015, 5, 14047–14052. [Google Scholar] [CrossRef]
- Pobering, S.; Schwesinger, N. A Novel Hydropower Harvesting Device. In Proceedings of the International Conference on MEMS, NANO and Smart Systems (ICMENS’04), Banff, AB, Canada, 25–27 August 2004; pp. 480–485. [Google Scholar] [CrossRef]
- Pobering, S.; Ebermeyer, S.; Schwesinger, N. Generation of electrical energy using short piezoelectric cantilevers in flowing media. In Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring; International Society for Optics and Photonics: San Diego, CA, USA, 2009; Volume 7288, p. 728807. [Google Scholar]
- Vyas, A.; Staaf, H.; Rusu, C.; Ebefors, T.; Liljeholm, J.; Smith, A.D.; Lundgren, P.; Enoksson, P. A Micromachined Coupled-Cantilever for Piezoelectric Energy Harvesters. Micromachines 2018, 9, 252. [Google Scholar] [CrossRef]
- Kwon, S.D. A T-shaped piezoelectric cantilever for fluid energy harvesting. Appl. Phys. Lett. 2010, 97, 164102. [Google Scholar] [CrossRef]
- Lozoya-Santos, J.D.J.; Félix-Herrán, L.C.; Tudón-Martínez, J.C.; Vargas-Martinez, A.; Ramirez-Mendoza, R.A. Design and implementation of an IoT oriented strain smart sensor with exploratory capabilities on energy harvesting and MRE transducer. Appl. Sci. 2020, 10, 4387. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Z.; Jia, Y.; Kan, J.; Cheng, G. Piezoelectric Bimorph Cantilever for Vibration-Producing-Hydrogen. Sensors 2013, 13, 367–374. [Google Scholar] [CrossRef] [PubMed]
- Nieradka, K.; Kopiec, D.; Małozięć, G.; Kowalska, Z.; Grabiec, P.; Janus, P.; Sierakowski, A.; Domański, K.; Gotszalk, T. Fabrication and characterization of electromagnetically actuated microcantilevers for biochemical sensing, parallel AFM and nanomanipulation. Microelectron. Eng. 2012, 98, 676–679. [Google Scholar] [CrossRef]
- Jendzelovsky, N.; Antal, R. Fluid-Structure Interaction Analysis and the Detection of Wind Induced Vibration of Triangular Lamella. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 052009. [Google Scholar] [CrossRef]
- Manela, A.; Howe, M.S. The forced motion of a flag. J. Fluid Mech. 2008, 635, 439–454. [Google Scholar] [CrossRef]
- Michelin, S.; LLewellyn Smith, S.G.; Glover, B.J. Vortex shedding model of a flapping flag. J. Fluid Mech. 2008, 617, 1–10. [Google Scholar] [CrossRef]
- Akcabay, D.T.; Young, Y.L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Phys. Fluids 2012, 24, 054106. [Google Scholar] [CrossRef]
- Kiya, M.; Tamura, H.; Arie, M. Vortex shedding from a circular cylinder in moderate-Reynolds-number shear flow. Ecol. Model. 1980, 141, 721–735. [Google Scholar] [CrossRef]
- Blevins, R.D. Flow-Induced Vibration; Van Nostrand Reinhold: New York, NY, USA, 1990. [Google Scholar]
- Strouhal, V. Ueber eine besondere Art der Tonerregung. Ann. Phys. Chem. 1878, 241, 216–251. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, L. Strouhal–Reynolds number relationship for flow past a circular cylinder. J. Fluid Mech. 2017, 832, 170–188. [Google Scholar] [CrossRef]
- Fey, U.; König, M.; Eckelmann, H. A new Strouhal––Reynolds number relationship for the circular cylinder in the range 47 < Re < 2 × 105. Phys. Fluids 1998, 10, 1547–1549. [Google Scholar]
- Ponta, F.L. Effect of shear–layer thickness on the Strouhal––Reynolds number relationship for bluff–body wakes. J. Fluids Struct. 2006, 22, 1133–1138. [Google Scholar] [CrossRef]
- Ponta, F.L.; Aref, H. Strouhal—Reynolds number relationship for vortex Reynolds number relationship for vortex streets. Phys. Rev. Lett. 2004, 93, 084501. [Google Scholar] [CrossRef]
- Roshko, A. On the development of turbulent wakes from vortex streets. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1952. [Google Scholar]
- Roushan, P.; Wu, X.L. Structure–based interpretation of the Strouhal––Reynolds number relationship. Phys. Rev. Lett. 2005, 94, 054504. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.H.K.; Brown, G.L. A series in 1/ to represent the Strouhal-Reynolds number relationship of the cylinder wake. J. Fluids Struct. 1989, 12, 1073–1085. [Google Scholar] [CrossRef]
- Eisler, Z.; Bartos, I.; Kertesz, J. Fluctuation scaling in complex systems: Taylor’s Law and beyond. Adv. Phys. 2008, 57, 89–142. [Google Scholar] [CrossRef]
- Fronczak, A.; Fronczak, P. Origins of Taylor’s power law for fluctuation scaling in complex systems. Phys. Rev. E 2010, 81, 066112. [Google Scholar] [CrossRef]
- Kendal, W.S.; Jorgensen, B. Taylor’s power law and fluctuation scaling explained by a central-limit-like convergence. Phys. Rev. E 2011, 83, 066115. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L. Aggregation, Variance and the Mean. Nature 1961, 189, 732–735. [Google Scholar] [CrossRef]
- Giometto, A.; Formentin, M.; Rinaldo, A.; Cohen, J.E.; Maritan, A. Sample and population exponents of generalized Taylor’s law. Proc. Natl. Acad. Sci. USA 2015, 112, 7755–7760. [Google Scholar] [CrossRef]
- Anile, S.; Devillard, S. Spatial variance-mass allometry of population density in felids from camera-trapping studies worldwide. Sci. Rep. 2020, 10, 14814. [Google Scholar] [CrossRef]
- Morand, S.; Krasnov, B. Why apply ecological laws to epidemiology? Trends Parasitol. 2008, 24, 304–309. [Google Scholar] [CrossRef]
- Kendal, W.S. A probabilistic model for the variance to mean power law in ecology. Ecol. Model. 1995, 80, 293–297. [Google Scholar] [CrossRef]
- Cohen, J.E. Statistics of primes (and probably twin primes) satisfy Taylor’s Law from ecology. Am. Stat. 2016, 70, 399–404. [Google Scholar] [CrossRef]
- Neuman, S.P. Apparent/spurious multifractality of data sampled from fractional Brownian/Lévy motions. Hydrol. Process. 2010, 24, 2056–2067. [Google Scholar] [CrossRef]
- Tomasicchio, G.R.; Lusito, L.; D’Alessandro, F.; Frega, F.; Francone, A.; De Bartolo, S. A direct scaling analysis for the sea level rise. Stoch. Environ. Res. Risk Assess. 2018, 32, 3397–3408. [Google Scholar] [CrossRef]
- De Bartolo, S.; Fallico, C.; Severino, G. A fractal analysis of the water retention curve. Hydrol. Process. 2018, 32, 1401–1405. [Google Scholar] [CrossRef]
- Severino, G.; De Bartolo, S. A scale invariant property of the water retention curve in weakly heterogeneous vadose zone. Hydrol. Process. 2019, 33, 1032–1039. [Google Scholar] [CrossRef]
- De Silva, C.M.; Marusic, I.; Woodcock, J.D.; Meneveau, C. Scaling of second-and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 2015, 769, 654–686. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 1991, 224, 429–484. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cornell, NY, USA, 2003. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA; London, UK, 1972. [Google Scholar]
- Lienhard, J.H. Synopsis of Lift, Drag, and Vortex Frequency Data for Rigid Circular Cylinders; Technical Extension Service, Washington State University: Pullman, WA, USA, 1966. [Google Scholar]
- Maurer, B.A.; Taper, M.L. Connecting geographical distributions with population processes. Ecol. Lett. 2002, 5, 223–231. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Guo, L.; Zhou, W.-X. Endogenous and exogenous dynamics in the fluctuation of capital fluxe. Eur. Phys. J. 2007, 57, 347–355. [Google Scholar] [CrossRef]
- Mu, G.-H.; Zhou, W.-X.; Chen, W.; Kertész, J. Long-term correlations and multifractality in trading volumes for Chinese stocks. Phys. Procedia 2010, 3, 1631–1640. [Google Scholar] [CrossRef][Green Version]
- Durst, F.; Launder, B.E.; Lumley, J.L.; Schmidt, F.W.; Whitelaw, J.H. Turbulent Shear Flows, 5th ed.; Cornell University: Ithaca, NY, USA, 1985. [Google Scholar]
- Townsend, A.A. The Structure of Turbulent Shear Flow, 2nd ed.; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Yamamoto, K.; Kambe, T. Gaussian and near-exponential probability distributions of turbulence obtained from a numerical simulation. Fluid Dyn. Res. 1991, 8, 65–72. [Google Scholar] [CrossRef]





| l [cm] | 3.20 | 3.50 | 4.00 | 7.90 |
| [] | 8.40 | 7.38 | 5.40 | 1.10 |
| l | H | u | |||
|---|---|---|---|---|---|
| (cm) | (cm) | (m s | (-) | (s | (-) |
| 3.2 | 4.6 | 0.293 | 5859 | 2.50 | 0.17 |
| 3.2 | 4.0 | 0.337 | 6738 | 2.35 | 0.14 |
| 3.5 | 6.9 | 0.197 | 3934 | 2.09 | 0.21 |
| 3.5 | 6.8 | 0.198 | 3963 | 2.20 | 0.22 |
| 3.5 | 6.8 | 0.198 | 3934 | 1.93 | 0.19 |
| 3.5 | 6.7 | 0.201 | 4022 | 2.11 | 0.21 |
| 3.5 | 6.7 | 0.201 | 4022 | 2.12 | 0.21 |
| 3.5 | 6.6 | 0.204 | 4083 | 1.98 | 0.19 |
| 3.5 | 6.5 | 0.207 | 4146 | 2.05 | 0.20 |
| 3.5 | 6.5 | 0.207 | 4146 | 2.00 | 0.19 |
| 3.5 | 6.4 | 0.211 | 4211 | 2.13 | 0.20 |
| 3.5 | 6.3 | 0.214 | 4278 | 2.22 | 0.21 |
| 3.5 | 6.2 | 0.217 | 4347 | 2.45 | 0.23 |
| 3.5 | 6.2 | 0.217 | 4347 | 2.45 | 0.23 |
| 4.0 | 10.7 | 0.126 | 2519 | 1.45 | 0.23 |
| 4.0 | 6.8 | 0.198 | 3963 | 2.01 | 0.20 |
| 4.0 | 5.6 | 0.241 | 4813 | 2.54 | 0.21 |
| 4.0 | 5.4 | 0.250 | 4991 | 2.33 | 0.19 |
| 4.0 | 5.2 | 0.259 | 5183 | 2.86 | 0.22 |
| 4.0 | 5.1 | 0.264 | 5284 | 2.54 | 0.19 |
| 4.0 | 4.7 | 0.287 | 5734 | 2.72 | 0.19 |
| 4.0 | 4.5 | 0.299 | 5989 | 3.01 | 0.20 |
| 4.0 | 4.4 | 0.306 | 6125 | 3.50 | 0.23 |
| 4.0 | 4.3 | 0.313 | 6167 | 3.67 | 0.23 |
| 4.0 | 4.0 | 0.337 | 6738 | 3.90 | 0.23 |
| 4.0 | 3.4 | 0.396 | 7926 | 4.54 | 0.23 |
| 7.9 | 4.6 | 0.293 | 5859 | 2.71 | 0.19 |
| 7.9 | 4.0 | 0.337 | 6738 | 3.54 | 0.21 |
| b | ||||
|---|---|---|---|---|
| First | Second | Third | Fourth | |
| (s) | cm | cm | cm | cm |
| = 5944 | = 6835 | = 5944 | = 6835 | |
| 15 | 1.773 | 1.128 | 1.049 | 0.875 |
| 30 | 1.951 | 1.177 | 1.162 | 0.957 |
| 60 | 2.197 | 1.363 | 1.331 | 1.055 |
| 90 | 2.262 | 1.420 | 1.326 | 1.031 |
| 120 | 2.330 | 1.572 | 1.438 | 1.071 |
| 150 | 2.440 | 1,717 | 1.547 | 1.244 |
| 180 | 2.496 | 1.735 | 1.644 | 1.148 |
| First | Second | Third | Fourth | |
| (s) | = 3.2 cm | = 3.2 cm | = 7.9 cm | = 7.9 cm |
| 15 | 0.953 | 0.964 | 0.971 | 0.970 |
| 30 | 0.952 | 0.967 | 0.978 | 0.975 |
| 60 | 0.952 | 0.964 | 0.985 | 0.978 |
| 90 | 0.975 | 0.964 | 0.983 | 0.978 |
| 120 | 0.977 | 0.966 | 0.985 | 0.977 |
| 150 | 0.977 | 0.973 | 0.989 | 0.973 |
| 180 | 0.974 | 0.971 | 0.991 | 0.981 |
| First | Second | Third | Fourth | |
|---|---|---|---|---|
| 0.989 | 0.353 | 0.416 | 0.544 | |
| k | 0.287 | 0.257 | 0.222 | 0.120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Bartolo, S.; Vittorio, M.D.; Francone, A.; Guido, F.; Leone, E.; Mastronardi, V.M.; Notaro, A.; Tomasicchio, G.R. Direct Scaling of Measure on Vortex Shedding through a Flapping Flag Device in the Open Channel around a Cylinder at Re∼103: Taylor’s Law Approach. Sensors 2021, 21, 1871. https://doi.org/10.3390/s21051871
De Bartolo S, Vittorio MD, Francone A, Guido F, Leone E, Mastronardi VM, Notaro A, Tomasicchio GR. Direct Scaling of Measure on Vortex Shedding through a Flapping Flag Device in the Open Channel around a Cylinder at Re∼103: Taylor’s Law Approach. Sensors. 2021; 21(5):1871. https://doi.org/10.3390/s21051871
Chicago/Turabian StyleDe Bartolo, Samuele, Massimo De Vittorio, Antonio Francone, Francesco Guido, Elisa Leone, Vincenzo Mariano Mastronardi, Andrea Notaro, and Giuseppe Roberto Tomasicchio. 2021. "Direct Scaling of Measure on Vortex Shedding through a Flapping Flag Device in the Open Channel around a Cylinder at Re∼103: Taylor’s Law Approach" Sensors 21, no. 5: 1871. https://doi.org/10.3390/s21051871
APA StyleDe Bartolo, S., Vittorio, M. D., Francone, A., Guido, F., Leone, E., Mastronardi, V. M., Notaro, A., & Tomasicchio, G. R. (2021). Direct Scaling of Measure on Vortex Shedding through a Flapping Flag Device in the Open Channel around a Cylinder at Re∼103: Taylor’s Law Approach. Sensors, 21(5), 1871. https://doi.org/10.3390/s21051871









