Signal Identification of Gear Vibration in Engine-Gearbox Systems Based on Auto-Regression and Optimized Resonance-Based Signal Sparse Decomposition
Abstract
1. Introduction
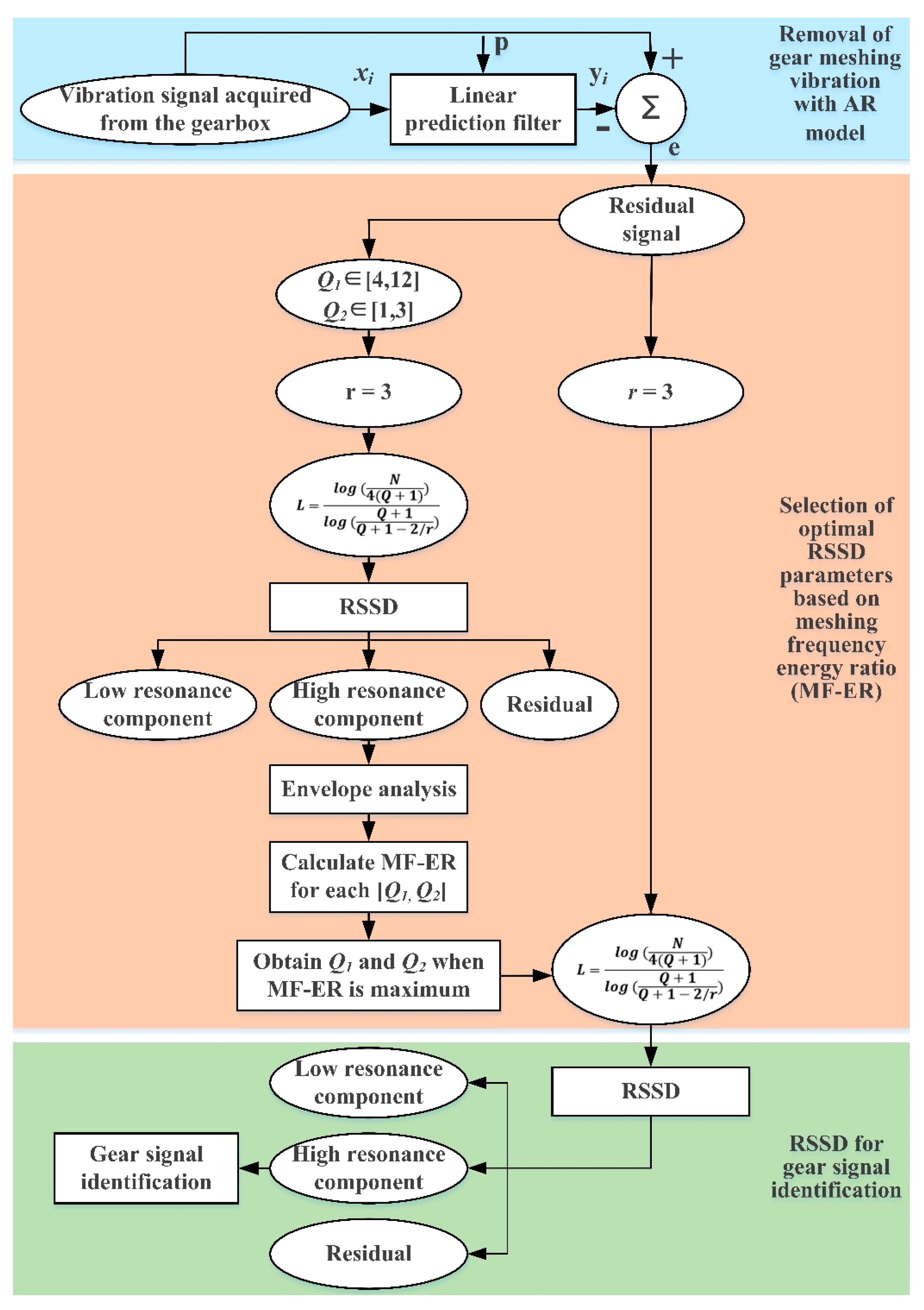
2. Methodology: Auto-Regression Model-Based Optimized Resonance-Based Signal Sparse Decomposition (AR-ORSSD)
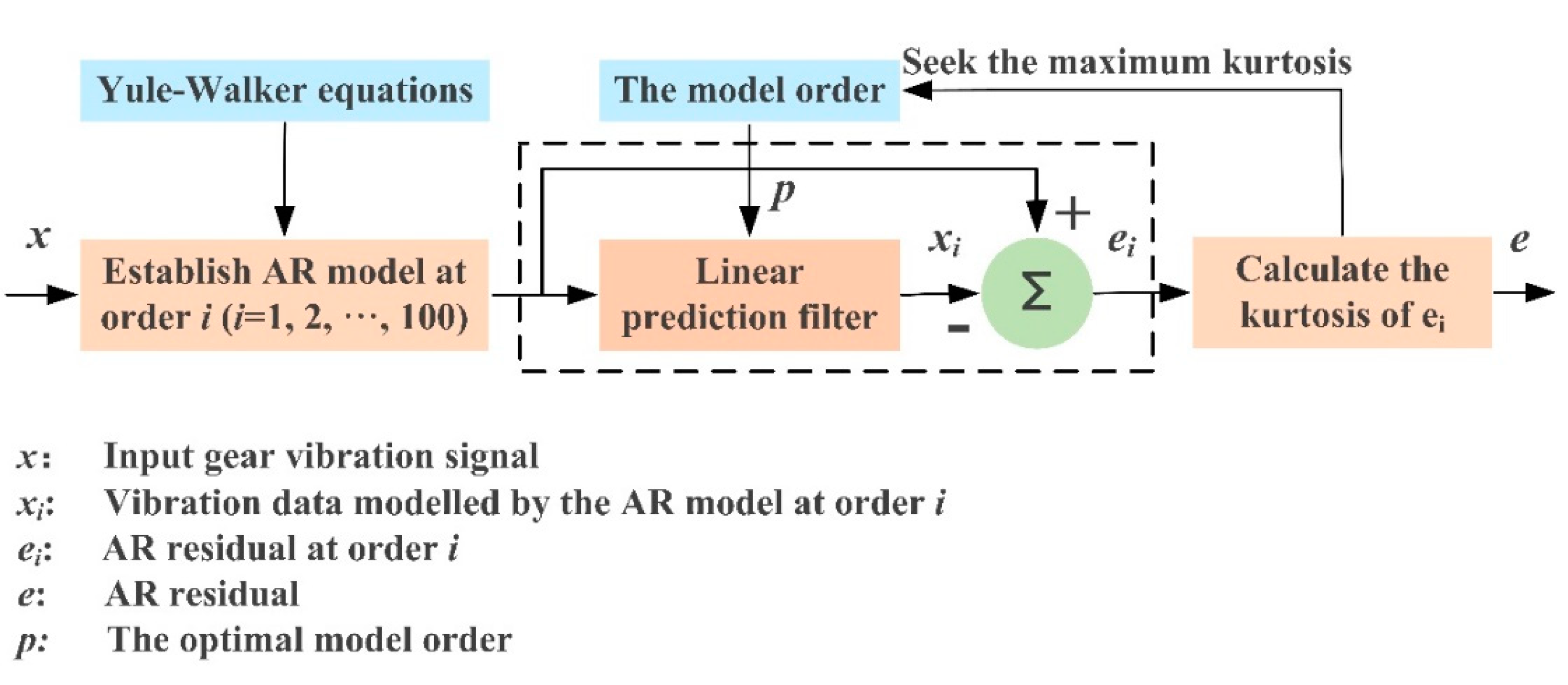
2.1. Pre-Whitening with the AR Model
2.2. Optimized Resonance-Based Signal Sparse Decomposition Based on Meshing Frequency Amplitude Ratio
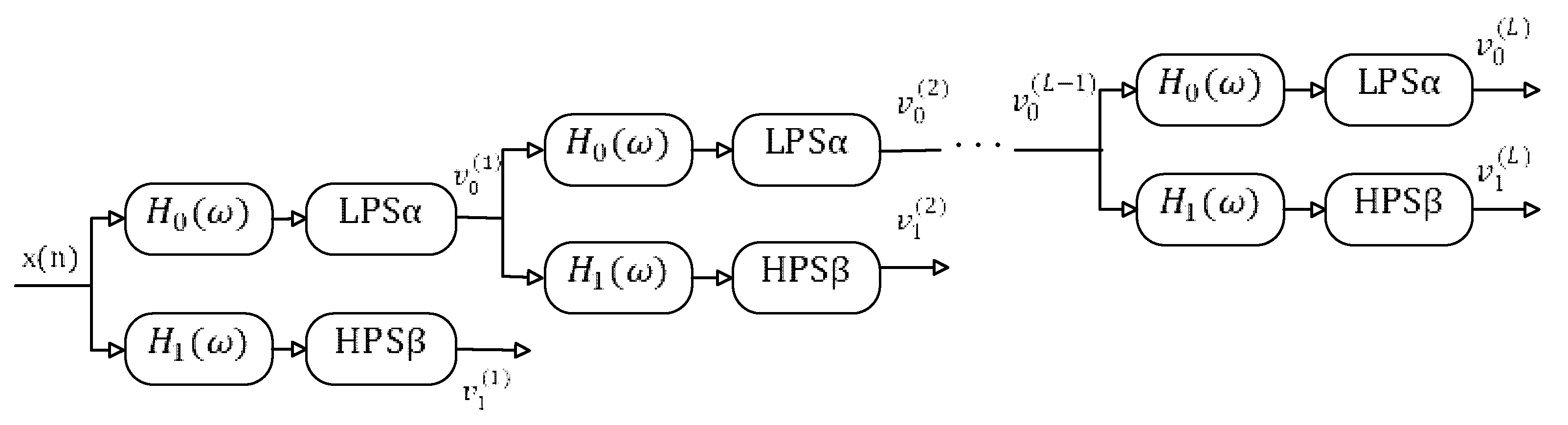
2.2.1. Resonance-Based Signal Sparse Decomposition
2.2.2. Parameter Selection Problem
2.2.3. Parameter Optimization Based on Meshing Frequency Energy Ratio
2.3. The Proposed AR-ORSSD Algorithm
- (1)
- Remove the normal gear meshing vibration using the AR model;
- (2)
- Determine the ranges of , , , , in steps of 0.5;
- (3)
- Perform the RSSD operation;
- (4)
- Calculate the MF–ER value for each combination of ;
- (5)
- Obtain the optimal -factors when MF–ER achieves the maximum;
- (6)
- Implement the RSSD with the optimal -factors;
- (7)
- Identify the gear vibration signal with the optimized RSSD method.
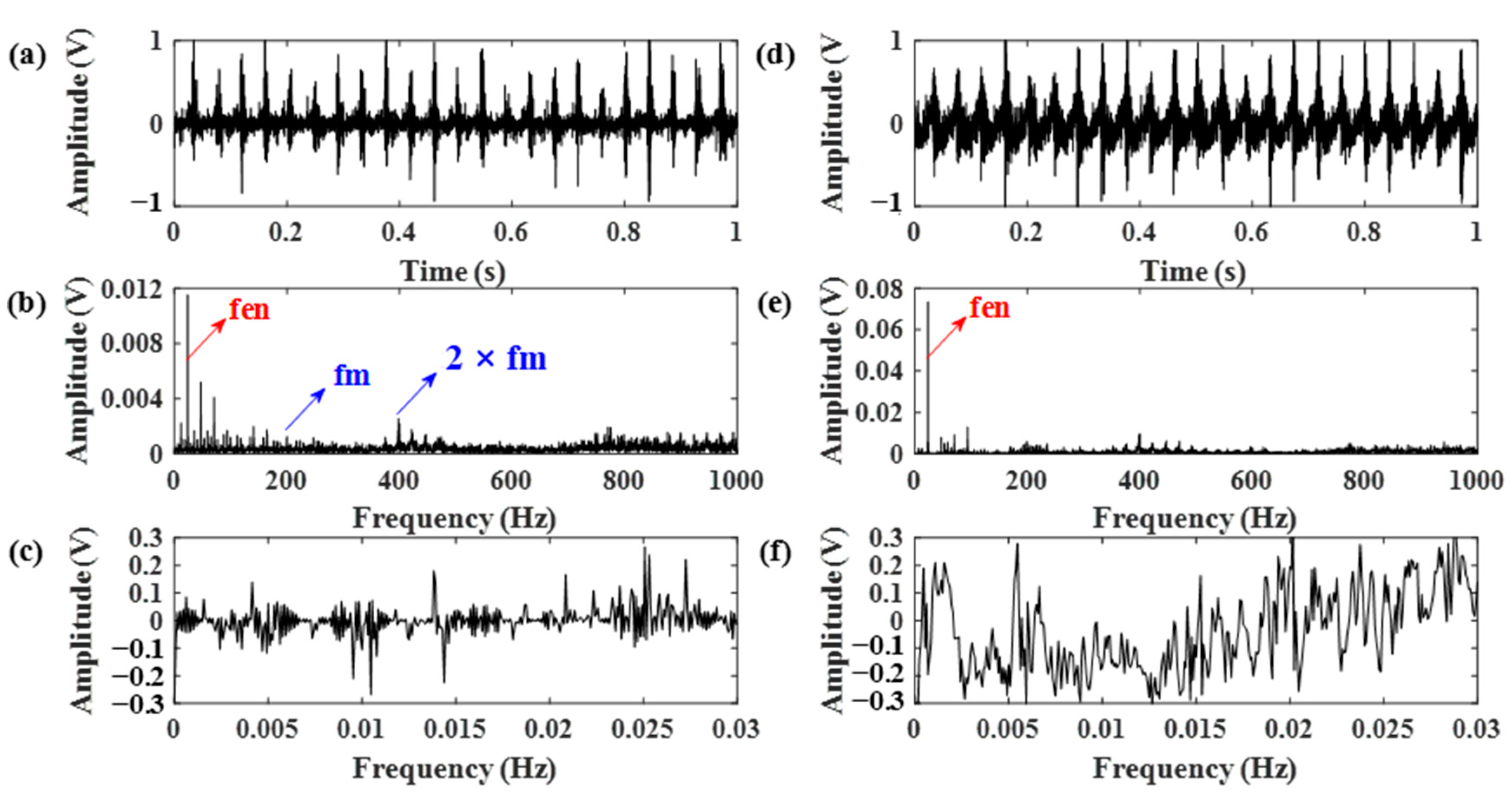
3. Simulated Signal Analysis
4. Experimental Verification
5. Conclusions
- (1)
- The main idea of this paper is that the gear meshing impact has better frequency aggregation than the engine ignition impact. Therefore, the RSSD algorithm is introduced.
- (2)
- The biggest innovation of this paper is that we define the MF–ER index and introduce it into the RSSD algorithm to adaptively choose the optimal Q-factors, which can improve the accuracy of the separation results.
- (3)
- Due to the interferences of the normal gear meshing vibration, the use of the RSSD algorithm alone cannot achieve perfect results. Therefore, the AR model is used as a pre-processing step to eliminate the normal gear meshing vibration.
- (4)
- Both simulated signals and experimental signals acquired from the engine-gearbox system in a forklift validate the effectiveness of the proposed algorithm.
- (5)
- Both simulated signals and experimental signals validate the necessity of adopting the AR model.
- (6)
- Through comparison with the GA-based RSSD method, it is indicated that the AR-ORSSD algorithm achieves superior performance in identifying gear vibration signals especially when under strong interferences.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Data points at time , respectively, V | |
| Model order | |
| The optimal model order | |
| th coefficient of the AR model | |
| Residual error at time , V | |
| Quality factor | |
| Center frequency, Hz | |
| Bandwidth, Hz | |
| High-pass scale | |
| Low-pass scale | |
| Redundancy | |
| Decomposition layer | |
| Sampling frequency, Hz | |
| High-pass and low-pass filters | |
| Angle, rad | |
| Function, | |
| Vibration signal, V | |
| High and low resonance components, V | |
| The overcomplete dictionaries for | |
| The wavelet coefficients of , | |
| The regularization parameters of , | |
| The wavelet coefficients of and when cost function achieves the minimum | |
| The optimal high and low resonance components, V | |
| Quality factors of and | |
| Decomposition layers of and | |
| Redundancies of and | |
| The data length | |
| The rounding operation | |
| MF–ER | Meshing frequency energy ratio |
| The Hilbert transform of , V | |
| The analytical signal of , V | |
| The envelop waveform of , V | |
| The envelop spectrum of , V | |
| Gear meshing frequency, Hz | |
| The number of meshing frequency harmonics | |
| The rotating frequencies of the pinion and gear, Hz | |
| The resonance frequency excited by gear meshing impact, Hz | |
| The magnitudes of the amplitude and phase modulations, V | |
| The amplitude of the impulses due to meshing impacts, V | |
| Damping characteristic frequency, Hz | |
| Ignition frequency, Hz | |
| The time of occurrence of the kth impulse, s | |
| The amplitude of the ignition impulses of the engine, V | |
| The structural damping characteristic frequency of the ignition impact, Hz | |
| The resonance frequency induced by the engine ignition impact, Hz | |
| The time of occurrence of the mth impulse, s | |
| The cylinder number | |
| The engine stroke constant | |
| Engine rotating speed, rpm |
References
- Zhou, P.; Peng, Z.; Chen, S.; Tian, Z.; Zuo, M.J. Sinusoidal FM patterns of fault-related vibration signals for planetary gearbox fault detection under non-stationary conditions. Mech. Syst. Signal Process. 2021, 155. [Google Scholar] [CrossRef]
- Brumercik, F.; Lukac, M.; Caban, J.; Krzysiak, Z.; Glowacz, A. Comparison of selected parameters of a planetary gearbox with involute and convex-concave teeth flank profiles. Appl. Sci. 2020, 10, 1417. [Google Scholar] [CrossRef]
- Tong, S.; Huang, Y.; Jiang, Y.; Weng, Y.; Tong, Z.; Tang, N.; Cong, F. The identification of gearbox vibration using the meshing impacts based demodulation technique. J. Sound Vib. 2019, 461, 114879. [Google Scholar] [CrossRef]
- Tong, S.; Huang, Y.; Tong, Z.; Cong, F. A novel short-frequency slip fault energy distribution-based demodulation technique for gear diagnosis and prognosis. Int. J. Adv. Robot. Syst. 2020, 17, 172988142091503. [Google Scholar] [CrossRef]
- Peeters, C.; Antoni, J.; Helsen, J. Blind filters based on envelope spectrum sparsity indicators for bearing and gear vibration-based condition monitoring. Mech. Syst. Signal Process. 2020, 138. [Google Scholar] [CrossRef]
- Laval, X.; Mailhes, C.; Martin, N.; Bellemain, P.; Pachaud, C. Amplitude and phase interaction in Hilbert demodulation of vibration signals: Natural gear wear modeling and time tracking for condition monitoring. Mech. Syst. Signal Process. 2021, 150. [Google Scholar] [CrossRef]
- Antoni, J. The spectral kurtosis: A useful tool for characterising non-stationary signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, X.; Zhu, Y. Feature extraction of the hydraulic pump fault based on improved Autogram. Meas. J. Int. Meas. Confed. 2020, 163. [Google Scholar] [CrossRef]
- Wang, L.; Xiang, J.; Liu, Y. A time-frequency-based maximum correlated kurtosis deconvolution approach for detecting bearing faults under variable speed conditions. Meas. Sci. Technol. 2019, 30. [Google Scholar] [CrossRef]
- Du, W.T.; Zeng, Q.; Shao, Y.M.; Wang, L.M.; Ding, X.X. Multi-scale demodulation for fault diagnosis based on a weighted-EMD de-noising technique and time–frequency envelope analysis. Appl. Sci. 2020, 10, 7796. [Google Scholar] [CrossRef]
- Chen, X.H.; Cheng, G.; Shan, X.L.; Hu, X.; Guo, Q.; Liu, H.G. Research of weak fault feature information extraction of planetary gear based on ensemble empirical mode decomposition and adaptive stochastic resonance. Meas. J. Int. Meas. Confed. 2015, 73, 55–67. [Google Scholar] [CrossRef]
- Cheng, Z.; Tong, S.; Tong, Z. Bi-directional nozzle control of multistage radial-inflow turbine for optimal part-load operation of compressed air energy storage. Energy Convers. Manag. 2019, 181, 485–500. [Google Scholar] [CrossRef]
- Sun, S.; Przystupa, K.; Wei, M.; Yu, H.; Ye, Z.; Kochan, O. Fast bearing fault diagnosis of rolling element using lévy moth-flame optimization algorithm and naive bayes. Eksploat. Niezawodn. Maint. Reliab. 2020, 22, 730–740. [Google Scholar] [CrossRef]
- Sheng, Z.; Xu, Y.; Zhang, K. Applications in bearing fault diagnosis of an improved Kurtogram algorithm based on flexible frequency slice wavelet transform filter bank. Meas. J. Int. Meas. Confed. 2021, 174. [Google Scholar] [CrossRef]
- Chen, Y.; Schmidt, S.; Heyns, P.S.; Zuo, M.J. A time series model-based method for gear tooth crack detection and severity assessment under random speed variation. Mech. Syst. Signal Process. 2021, 156. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, Y.; Tong, Z.; Tong, S. Residual stress distribution design for gear surfaces based on genetic algorithm optimization. Materials 2021, 14, 366. [Google Scholar] [CrossRef]
- Nguyen, C.D.; Prosvirin, A.E.; Kim, C.H.; Kim, J.M. Construction of a sensitive and speed invariant gearbox fault diagnosis model using an incorporated utilizing adaptive noise control and a stacked sparse autoencoder-based deep neural network. Sensors 2021, 21, 18. [Google Scholar] [CrossRef]
- Chen, P.; Li, Y.; Wang, K.; Zuo, M.J. An automatic speed adaption neural network model for planetary gearbox fault diagnosis. Meas. J. Int. Meas. Confed. 2021, 171. [Google Scholar] [CrossRef]
- Tong, Z.M.; Xin, J.G.; Tong, S.G.; Yang, Z.Q.; Zhao, J.Y.; Mao, J.H. Internal flow structure, fault detection, and performance optimization of centrifugal pumps. J. Zhejiang Univ. Sci. A 2020, 21, 85–117. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Selesnick, I.W. Wavelet transform with tunable Q-factor. IEEE Trans. Signal Process. 2011, 59, 3560–3575. [Google Scholar] [CrossRef]
- Selesnick, I.W. Resonance-based signal decomposition: A new sparsity-enabled signal analysis method. Signal Process. 2011, 91, 2793–2809. [Google Scholar] [CrossRef]
- Luo, J.; Yu, D.; Liang, M. A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform. Meas. Sci. Technol. 2013, 24. [Google Scholar] [CrossRef]
- Chen, X.M.; Yu, D.J.; Luo, J.S. Envelope demodulation method based on resonance-based sparse signal decomposition and its application in roller bearing fault diagnosis. Zhendong Gongcheng Xuebao J. Vib. Eng. 2012, 25, 628–636. [Google Scholar]
- Wang, H.; Chen, J.; Dong, G. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2014, 48, 103–119. [Google Scholar] [CrossRef]
- Cai, G.; Chen, X.; He, Z. Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox. Mech. Syst. Signal Process. 2013, 41, 34–53. [Google Scholar] [CrossRef]
- Yan, J.; Sun, H.; Chen, H.; Junejo, N.U.R.; Cheng, E. Resonance-based time-frequency manifold for feature extraction of ship-radiated noise. Sensors 2018, 18, 936. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Ghaffar, E.A. Effect of tuning TQWT parameters on epileptic seizure detection from EEG signals. In Proceedings of the ICCES 2017 12th International Conference on Computer Engineering and Systems, Cairo, Egypt, 19–20 December 2017; pp. 47–51. [Google Scholar]
- Huang, W.; Sun, H.; Wang, W. Resonance-based sparse signal decomposition and its application in mechanical fault diagnosis: A review. Sensors 2017, 17, 1279. [Google Scholar] [CrossRef]
- Huang, W.; Fu, Q.; Dou, H.; Dong, Z. Resonance-based sparse signal decomposition based on genetic optimization and its application to composite fault diagnosis of rolling bearings. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Proceedings (IMECE), Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Zhang, D.; Yu, D.; Zhang, W. Energy operator demodulating of optimal resonance components for the compound faults diagnosis of gearboxes. Meas. Sci. Technol. 2015, 26. [Google Scholar] [CrossRef]
- Zhang, D.; Entezami, M.; Stewart, E.; Roberts, C.; Yu, D. Adaptive fault feature extraction from wayside acoustic signals from train bearings. J. Sound Vib. 2018, 425, 221–238. [Google Scholar] [CrossRef]
- Chen, B.; Shen, B.; Chen, F.; Tian, H.; Xiao, W.; Zhang, F.; Zhao, C. Fault diagnosis method based on integration of RSSD and wavelet transform to rolling bearing. Meas. J. Int. Meas. Confed. 2019, 131, 400–411. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, D.; Li, X. Optimal resonance-based signal sparse decomposition and its application to fault diagnosis of rotating machinery. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4670–4683. [Google Scholar] [CrossRef]
- Chai, N.; Yang, M.; Ni, Q.; Xu, D. Gear fault diagnosis based on dual parameter optimized resonance-based sparse signal decomposition of motor current. IEEE Trans. Ind. Appl. 2018, 54, 3782–3792. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, D. Multi-fault diagnosis of gearbox based on resonance-based signal sparse decomposition and comb filter. Measurement 2017, 103, 361–369. [Google Scholar] [CrossRef]
- Wang, C.; Li, H.; Ou, J.; Hu, R.; Hu, S.; Liu, A. Identification of planetary gearbox weak compound fault based on parallel dual-parameter optimized resonance sparse decomposition and improved MOMEDA. Meas. J. Int. Meas. Confed. 2020, 165. [Google Scholar] [CrossRef]
- Wang, W.; Wong, A.K. Autoregressive model-based gear fault diagnosis. J. Vib. Acoust. Trans. ASME 2002, 124, 172–179. [Google Scholar] [CrossRef]
- Rantala, S.; Suoranta, R. Enhanced vibration monitoring using parametric modelling technique. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference, Atlanta, GA, USA, 14–16 May 1991; pp. 2–5. [Google Scholar]
- Junsheng, C.; Dejie, Y.; Yu, Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mech. Syst. Signal Process. 2006, 20, 350–362. [Google Scholar] [CrossRef]
- Endo, H.; Randall, R.B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter. Mech. Syst. Signal Process. 2007, 21, 906–919. [Google Scholar] [CrossRef]
- Li, Z.; Yan, X.; Yuan, C.; Peng, Z.; Li, L. Virtual prototype and experimental research on gear multi-fault diagnosis using wavelet-autoregressive model and principal component analysis method. Mech. Syst. Signal Process. 2011, 25, 2589–2607. [Google Scholar] [CrossRef]
- Zhan, Y.; Makis, V. A robust diagnostic model for gearboxes subject to vibration monitoring. J. Sound Vib. 2006, 290, 928–955. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G. Spectral kurtosis based on AR model for fault diagnosis and condition monitoring of rolling bearing. J. Mech. Sci. Technol. 2012, 26, 301–306. [Google Scholar] [CrossRef]
- Huang, W.; Jiang, Y.; Sun, H.; Wang, W. Automatic quantitative diagnosis for rolling bearing compound faults via adapted dictionary free orthogonal matching pursuit. Meas. J. Int. Meas. Confed. 2020, 154. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Han, Q.; Kong, Y. Compound faults detection in gearbox via meshing resonance and spectral kurtosis methods. J. Sound Vib. 2017, 392, 367–381. [Google Scholar] [CrossRef]
- Tong, S.; Huang, Y.; Tong, Z.; Tang, N.; Yu, Y.; Zhou, Y.; Cong, F. Gear vibration signal extraction based on meshing impact under heavy load condition. Smart Innov. Syst. Technol. 2020, 166, 1205–1214. [Google Scholar]
- Sawalhi, N.; Randall, R.B.; Endo, H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis. Mech. Syst. Signal Process. 2007, 21, 2616–2633. [Google Scholar] [CrossRef]
- Bobin, J.; Starck, J.L.; Fadili, J.M.; Moudden, Y.; Donoho, D.L. Morphological component analysis: An adaptive thresholding strategy. IEEE Trans. Image Process. 2007, 16, 2675–2681. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. Fast image recovery using variable splitting and constrained optimization. IEEE Trans. Image Process. 2010, 19, 2345–2356. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Xu, M.; Huang, W. Early fault feature extraction of rolling bearing based on ICD and tunable Q-factor wavelet transform. Mech. Syst. Signal Process. 2017, 86, 204–223. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Feng, Z. Meshing frequency modulation (MFM) index-based kurtogram for planet bearing fault detection. J. Sound Vib. 2018, 432, 437–453. [Google Scholar] [CrossRef]
- Wang, T.; Chu, F.; Han, Q. Fault diagnosis for wind turbine planetary ring gear via a meshing resonance based filtering algorithm. ISA Trans. 2017, 67, 173–182. [Google Scholar] [CrossRef]
- He, W.; Zi, Y.; Chen, B.; Wu, F.; He, Z. Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform. Mech. Syst. Signal Process. 2015, 54–55, 457–480. [Google Scholar] [CrossRef]
- Wang, W. Early detection of gear tooth cracking using the resonance demodulation technique. Mech. Syst. Signal Process. 2001, 15, 887–903. [Google Scholar] [CrossRef]
- Mu, Y.; Fang, Z.; Zhang, X. Theoretical analysis on meshing impact of spiral bevel gears. Huazhong Keji Daxue Xuebao Ziran Kexue Ban J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2018, 46, 7–11. [Google Scholar] [CrossRef]
- Wu, B.L.; Yang, S.J.; Yao, J.H. Theoretical analysis on meshing impact of involute gears. Jixie Kexue Yu Jishu Mech. Sci. Technol. 2003, 22, 55. [Google Scholar]
- Hoy, J.; Mubarak, N.; Nelson, S.; de Landas, M.S.; Magnusson, M.; Okunribido, O.; Pope, M. Whole body vibration and posture as risk factors for low back pain among forklift truck drivers. J. Sound Vib. 2005, 284, 933–946. [Google Scholar] [CrossRef]

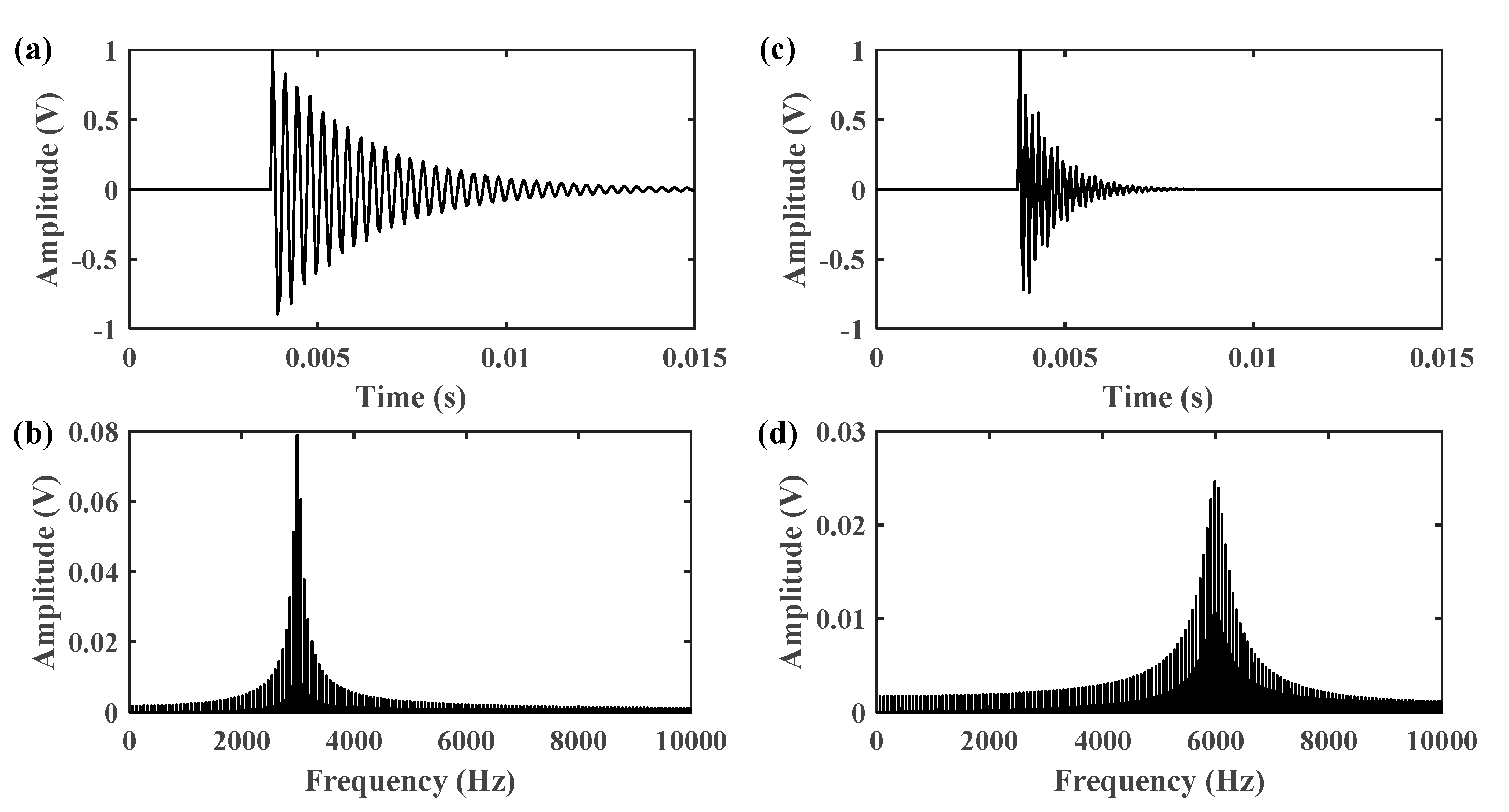
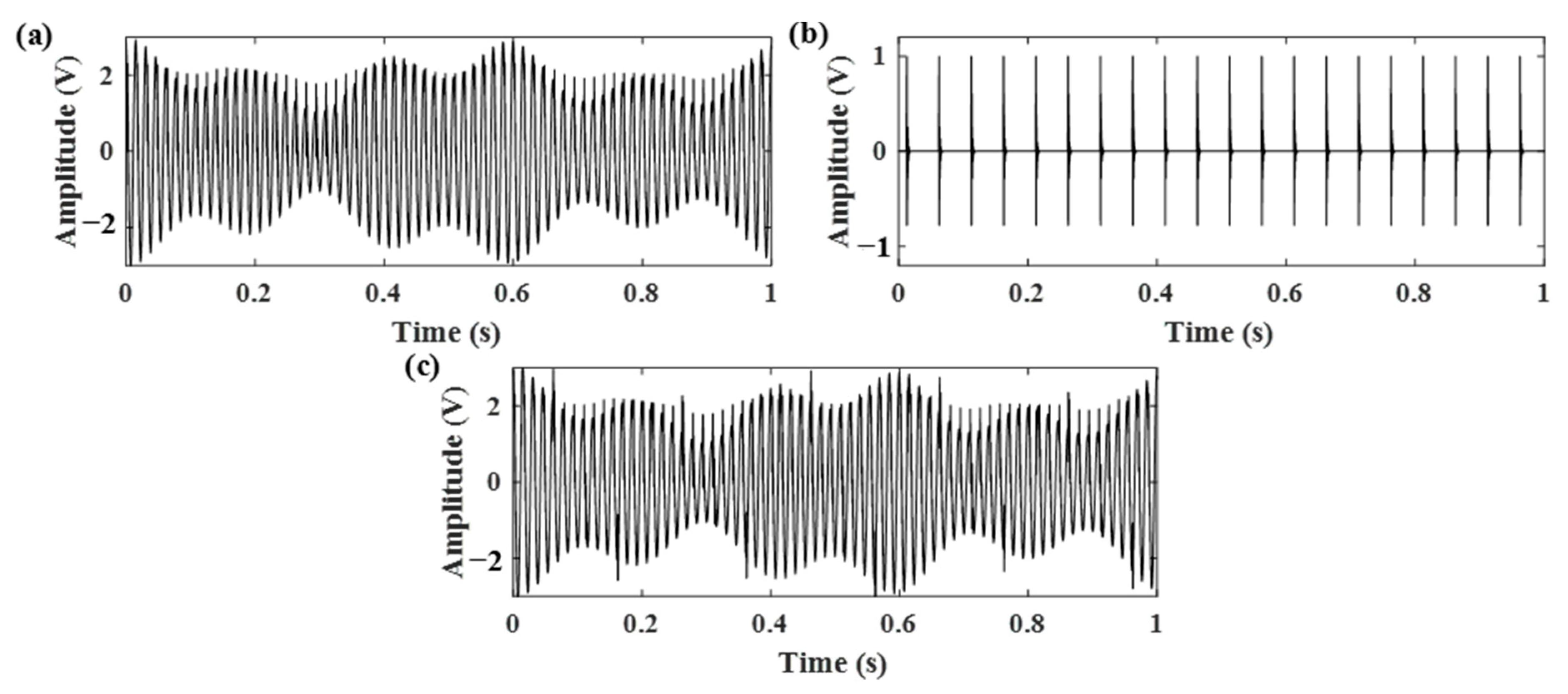
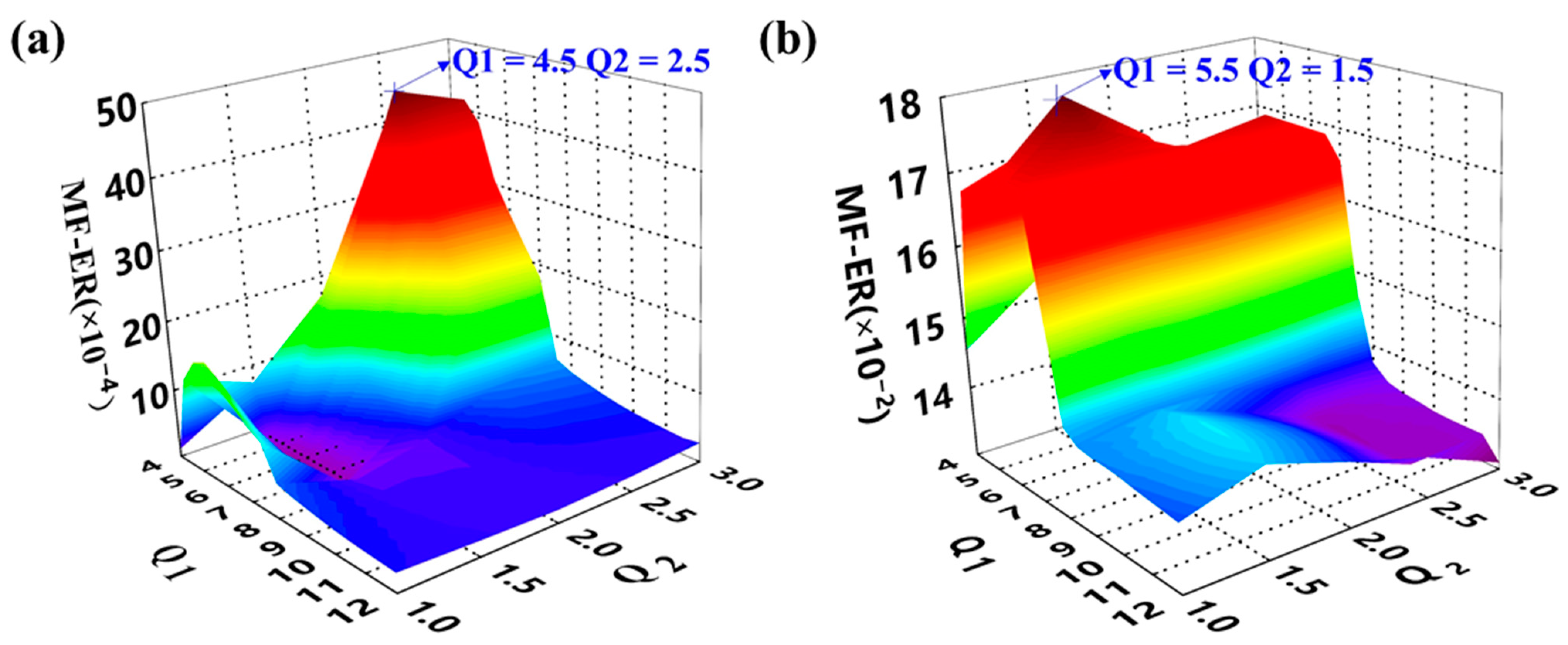

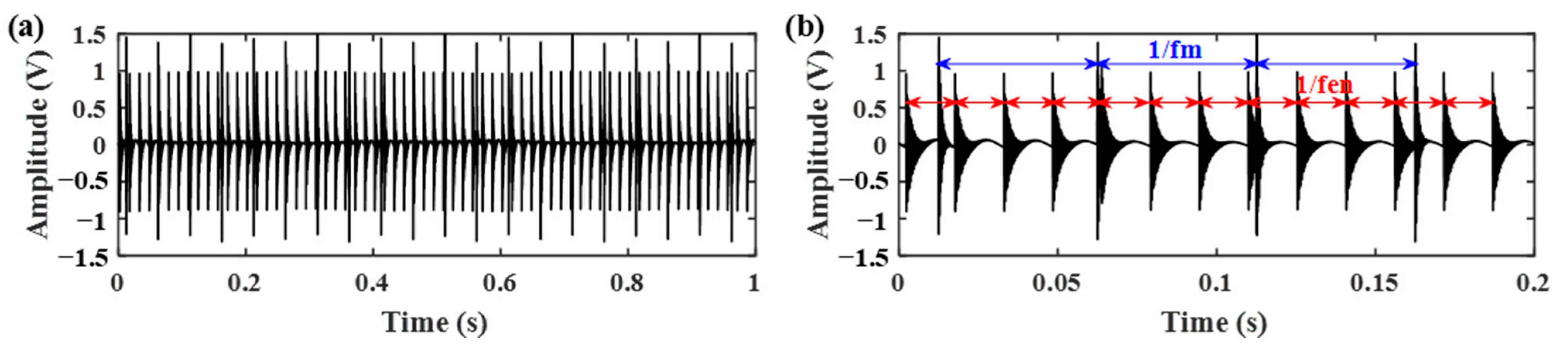
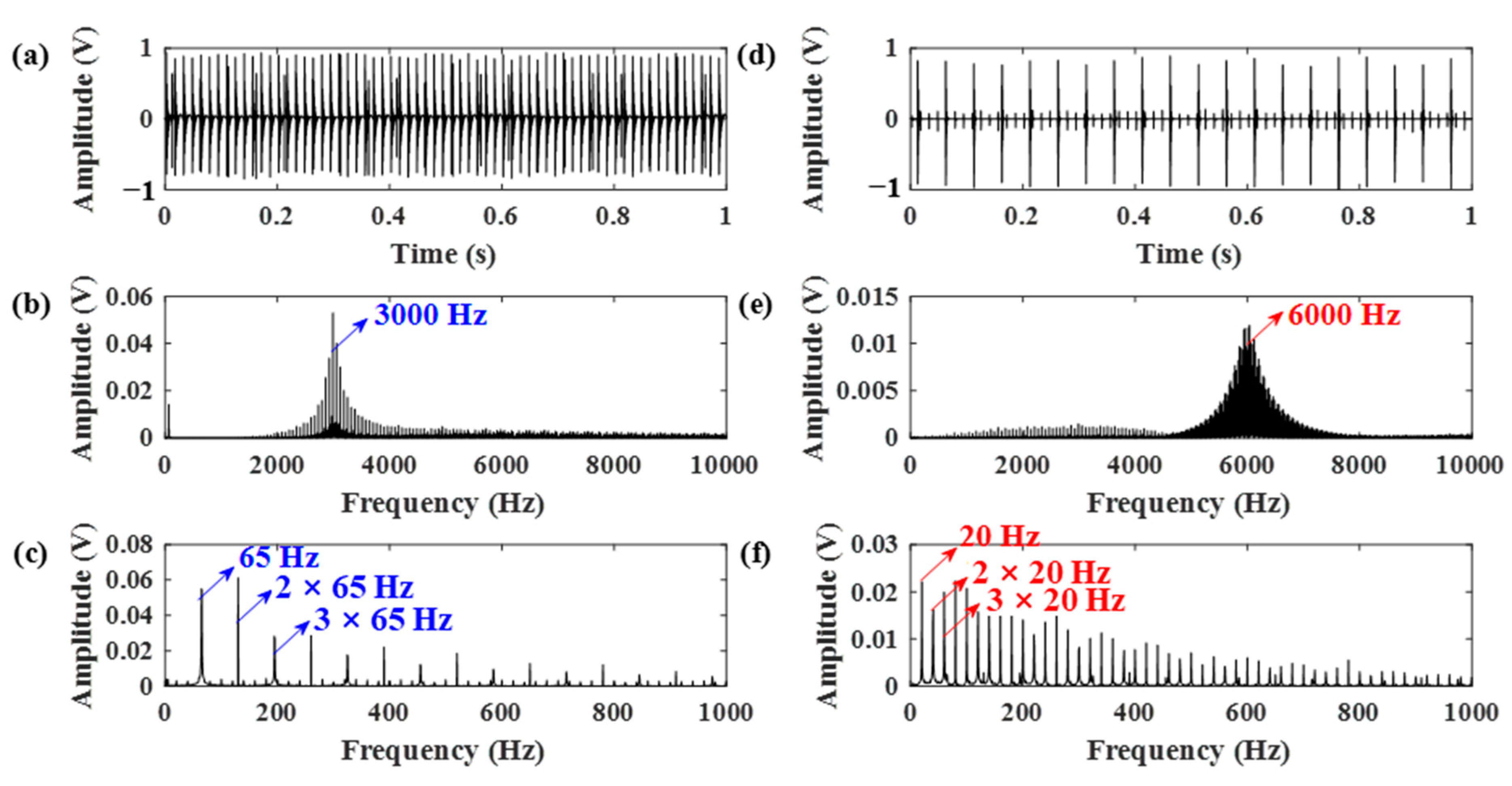
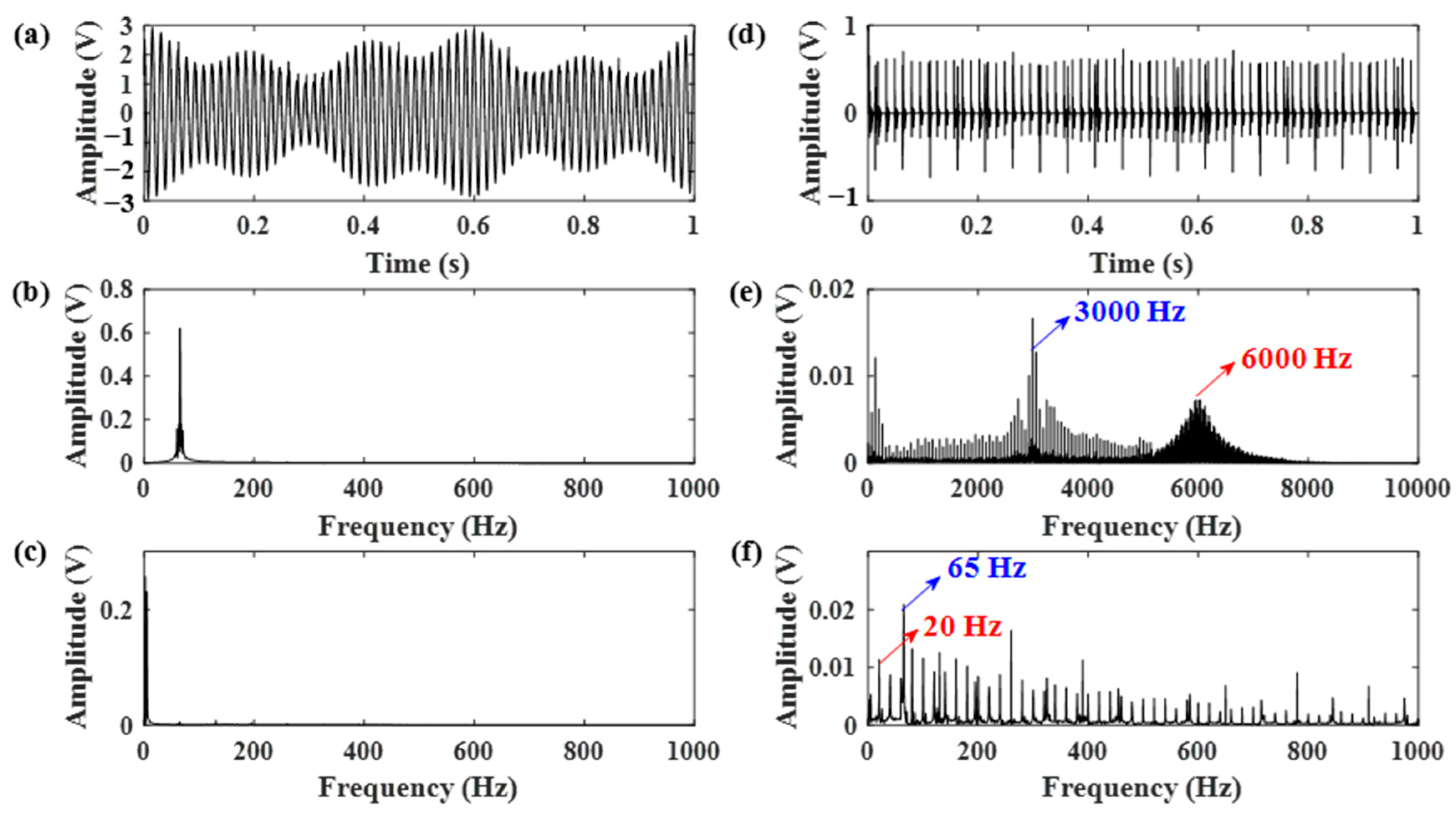

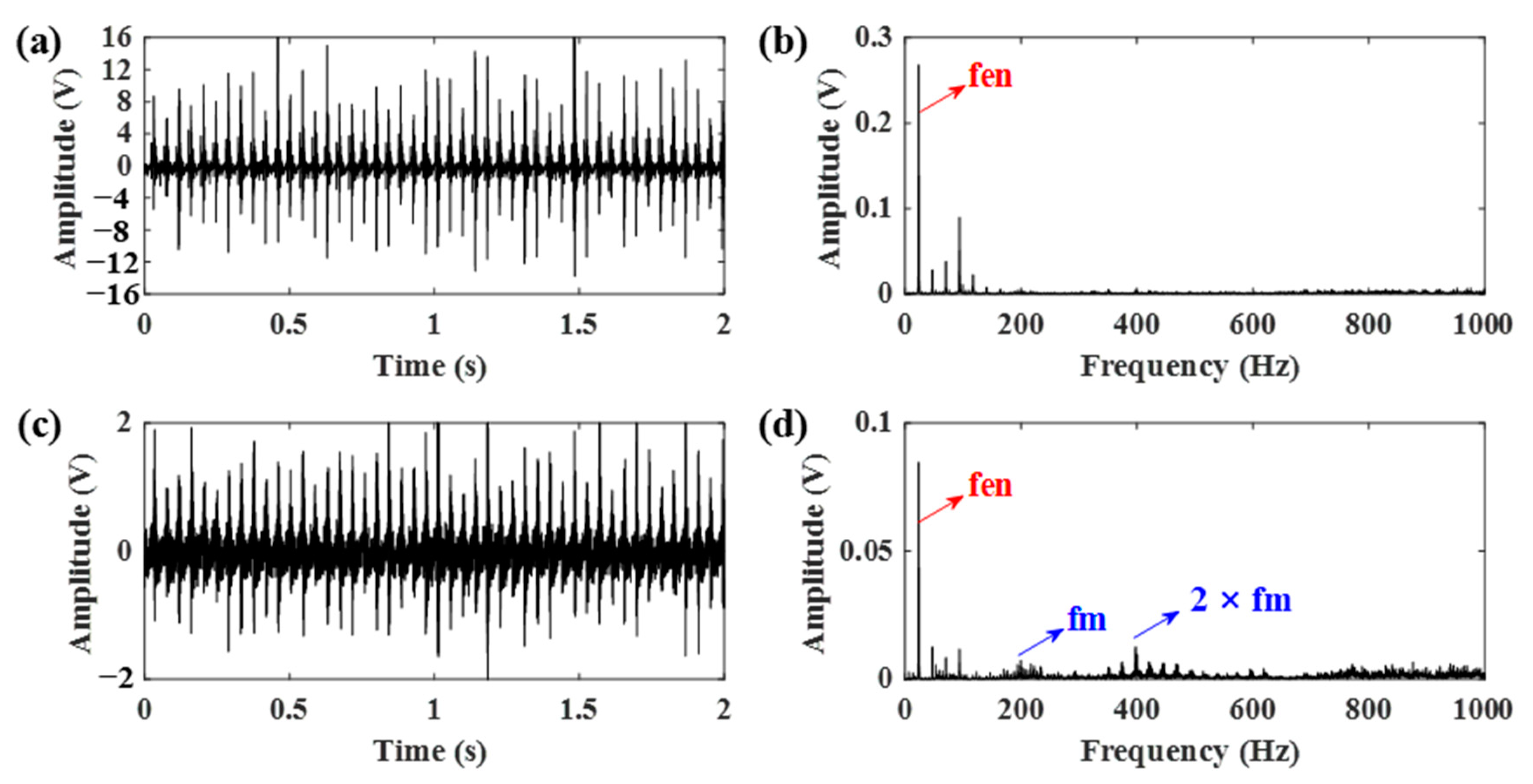
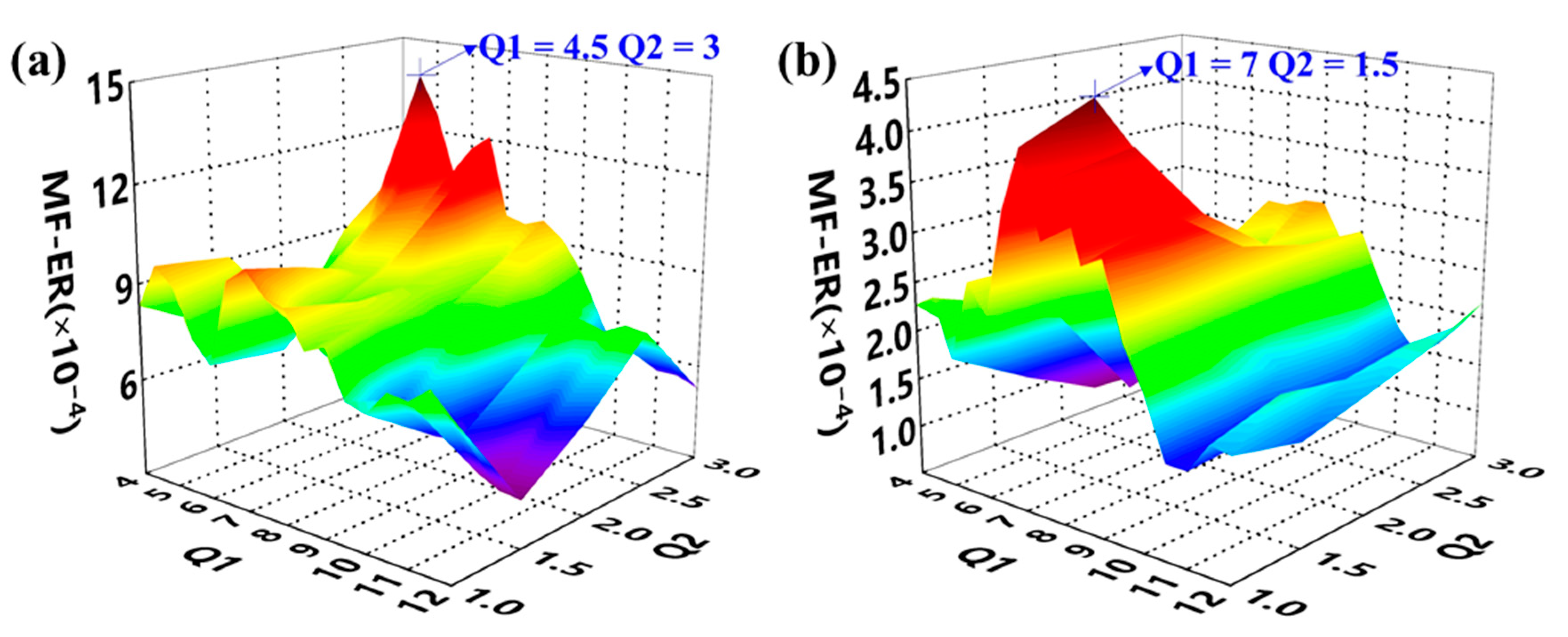

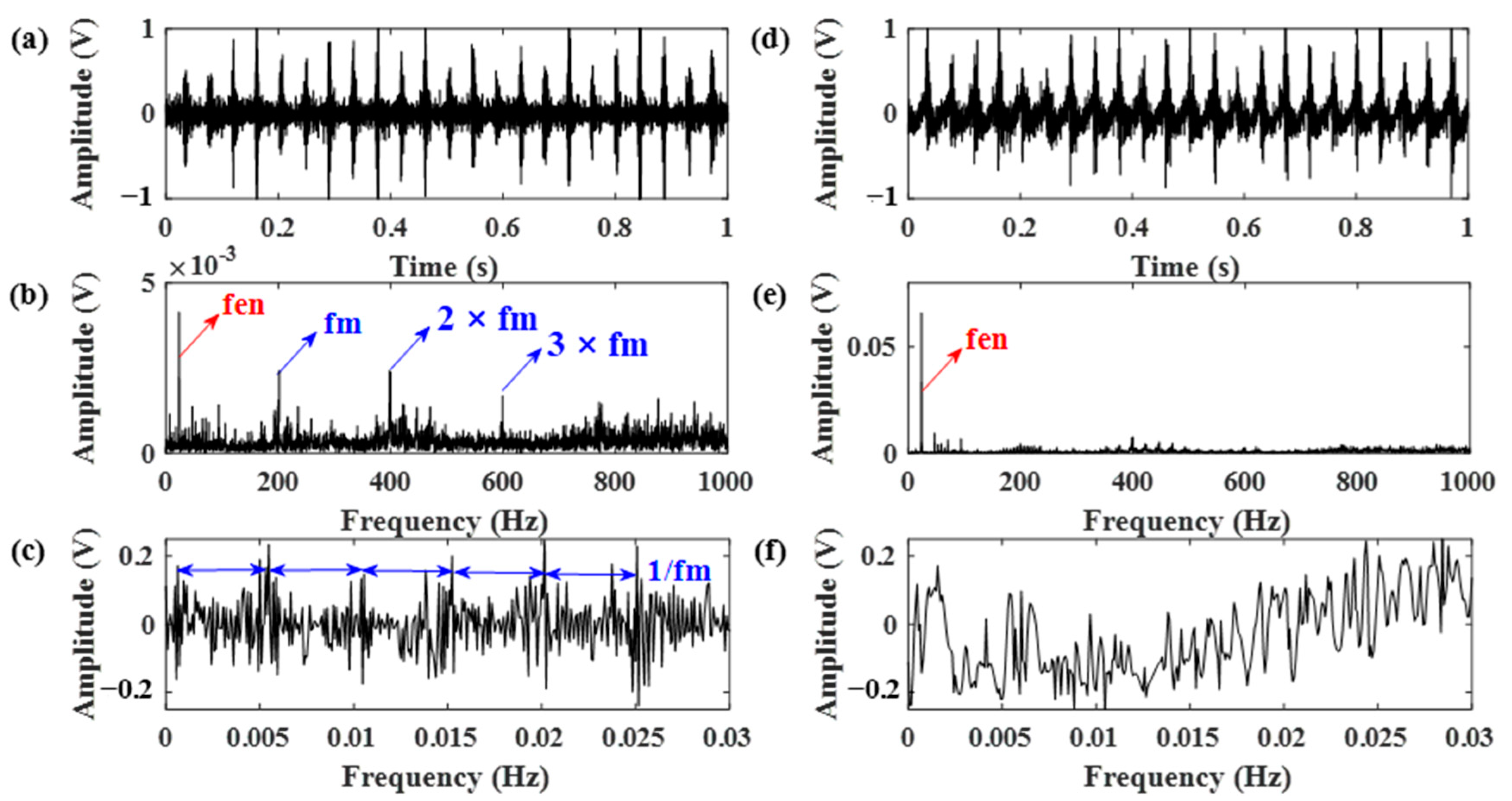
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 0.5 | 1000 | ||
| 0.2 | 600 | ||
| 1 | 20 | ||
| 5 | 3000 | ||
| 2 | 6000 | ||
| 65 | 0.015 | ||
| 1 | 0.05 |
| 4.65 | 1 | 5.05 | 6.44 |
| 9.21 | 1.74 | 9.83 | 3.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Tong, S.; Tong, Z.; Cong, F. Signal Identification of Gear Vibration in Engine-Gearbox Systems Based on Auto-Regression and Optimized Resonance-Based Signal Sparse Decomposition. Sensors 2021, 21, 1868. https://doi.org/10.3390/s21051868
Huang Y, Tong S, Tong Z, Cong F. Signal Identification of Gear Vibration in Engine-Gearbox Systems Based on Auto-Regression and Optimized Resonance-Based Signal Sparse Decomposition. Sensors. 2021; 21(5):1868. https://doi.org/10.3390/s21051868
Chicago/Turabian StyleHuang, Yuanyuan, Shuiguang Tong, Zheming Tong, and Feiyun Cong. 2021. "Signal Identification of Gear Vibration in Engine-Gearbox Systems Based on Auto-Regression and Optimized Resonance-Based Signal Sparse Decomposition" Sensors 21, no. 5: 1868. https://doi.org/10.3390/s21051868
APA StyleHuang, Y., Tong, S., Tong, Z., & Cong, F. (2021). Signal Identification of Gear Vibration in Engine-Gearbox Systems Based on Auto-Regression and Optimized Resonance-Based Signal Sparse Decomposition. Sensors, 21(5), 1868. https://doi.org/10.3390/s21051868







