Validation of Walking Speed Estimation from Trunk Mounted Accelerometers for a Range of Walking Speeds
Abstract
1. Introduction
2. Materials and Methods
2.1. Studies
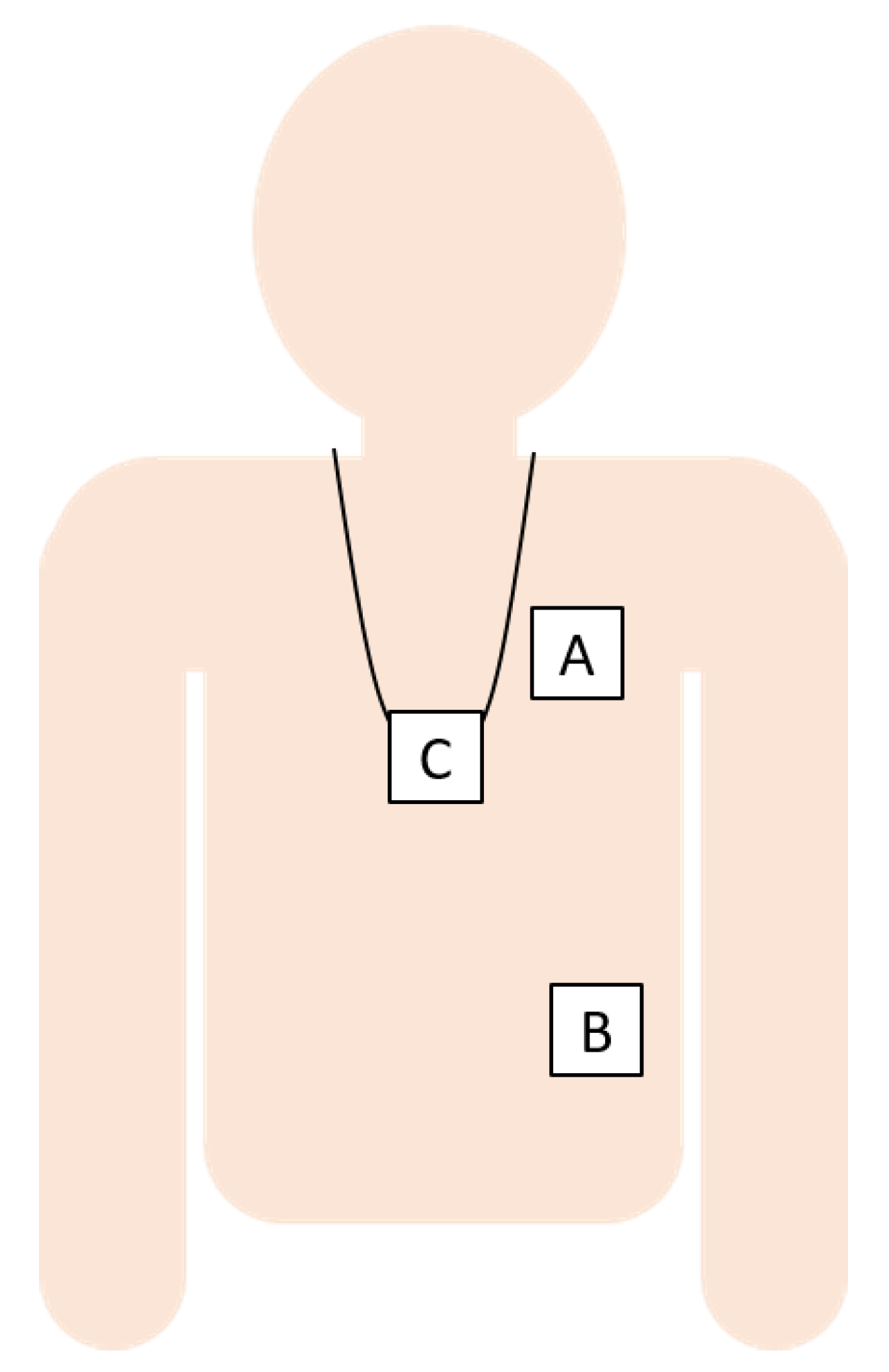
2.2. Walk Data Selection
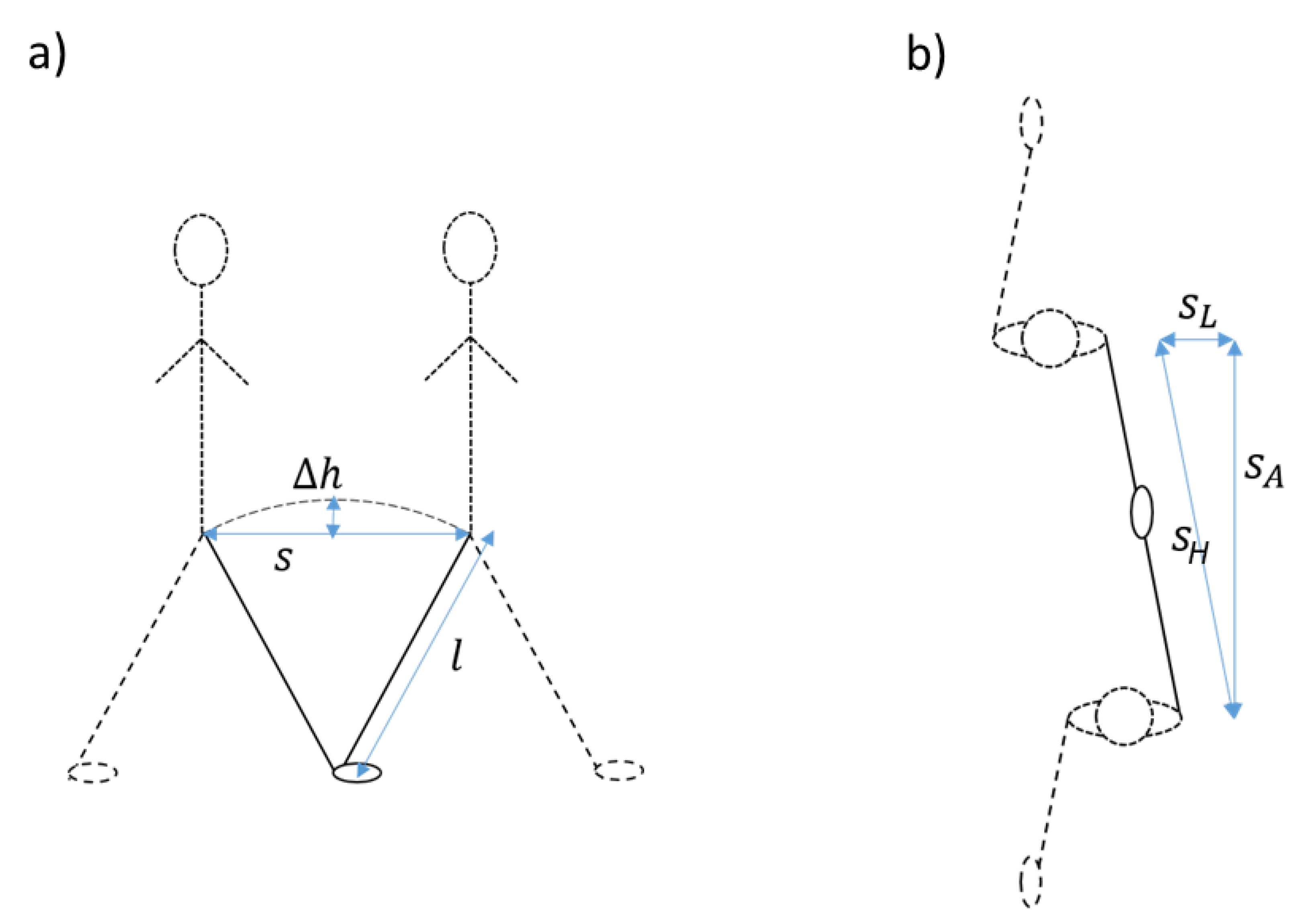
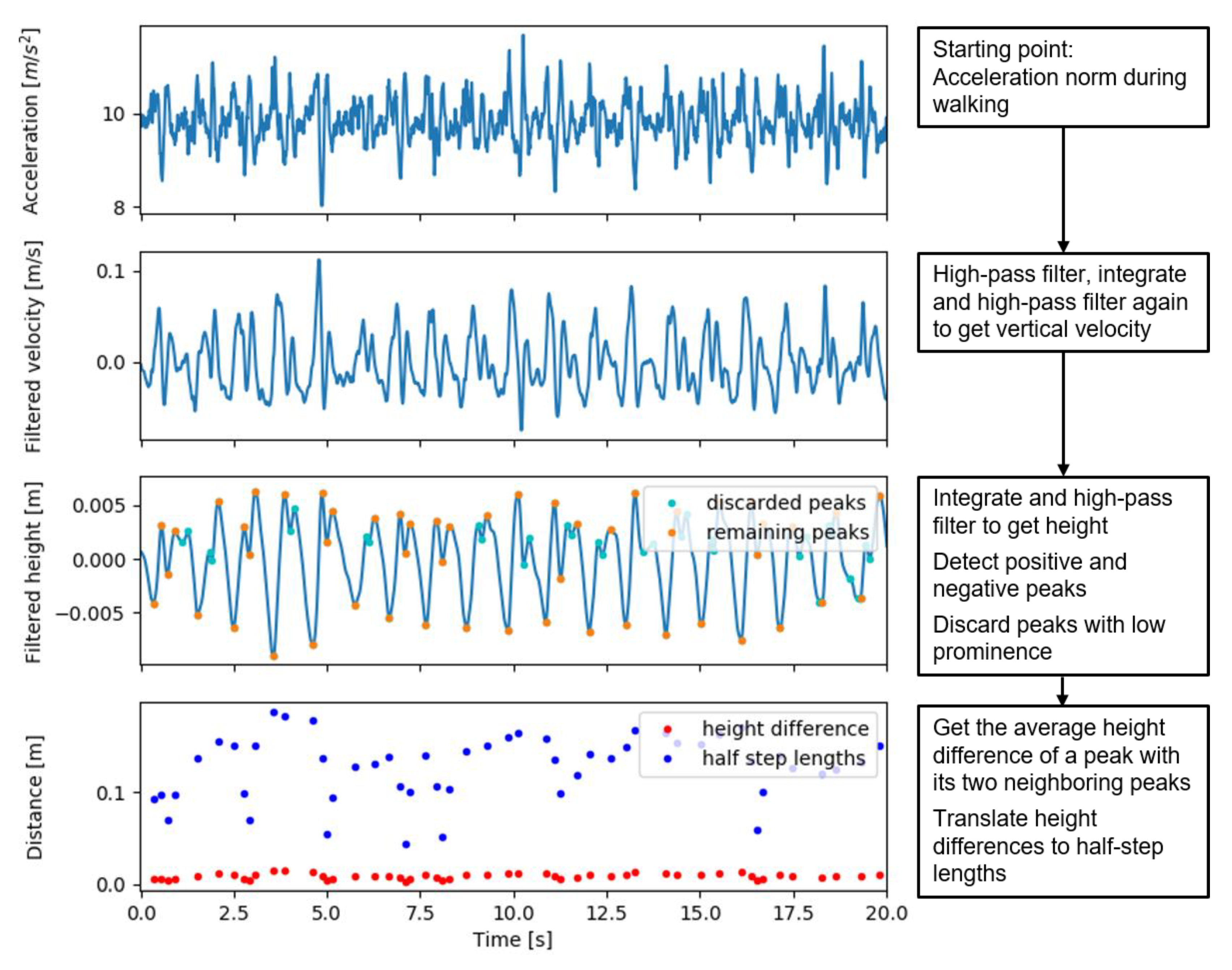
2.3. Estimation of Walking Speed
2.4. Analyses
3. Results
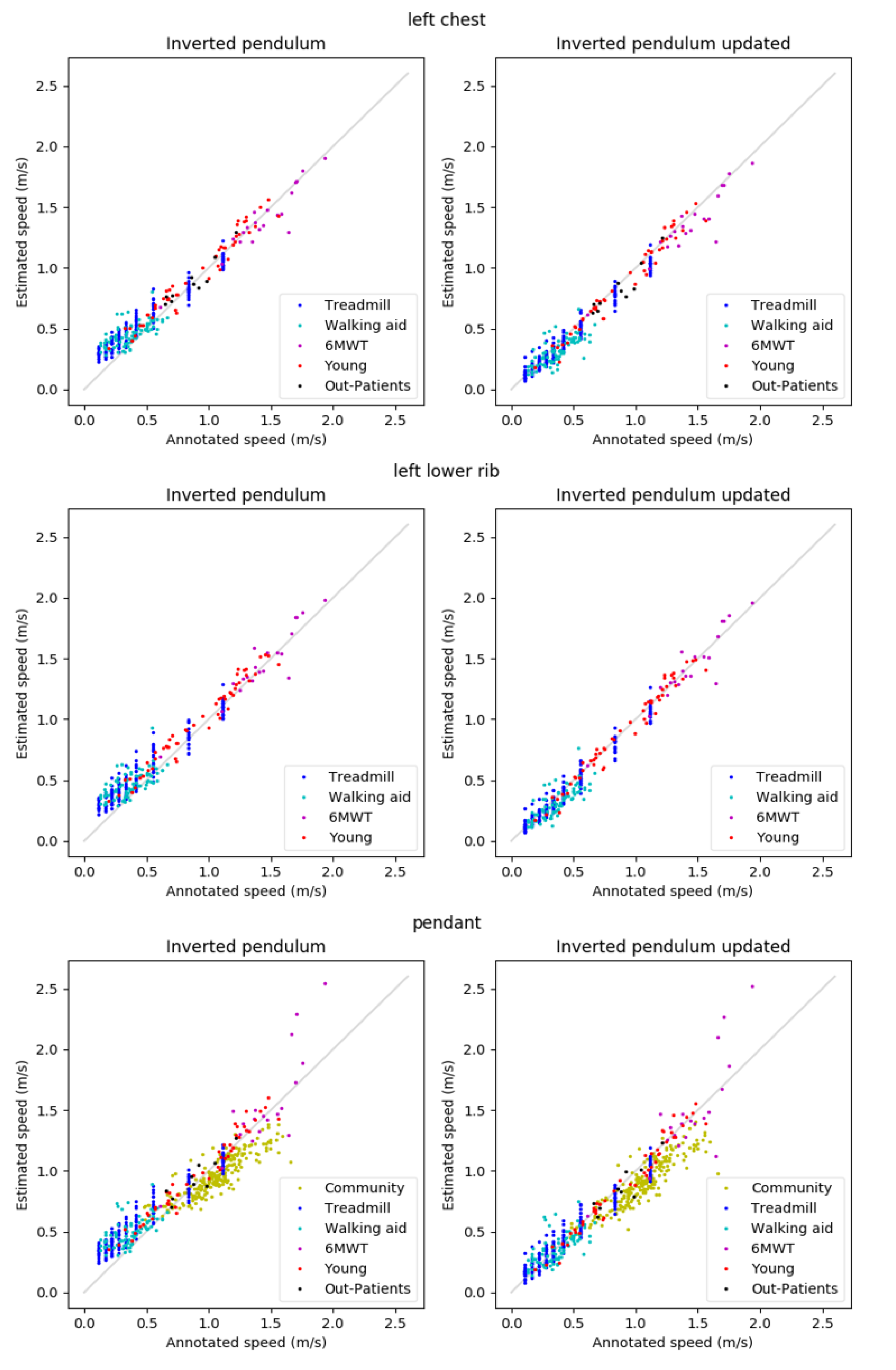
3.1. Results for Both Algorithms, Per Activity
3.2. Comparisons between Wearing Positions
4. Discussion
4.1. Findings
4.2. Context
4.3. Implications
4.4. Limitations
4.5. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Studenski, S.; Perera, S.; Patel, K.; Rosano, C.; Faulkner, K.; Inzitari, M.; Brach, J.; Chandler, J.; Cawthon, P.; Connor, E.B.; et al. Gait speed and survival in older adults. JAMA 2011, 305, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Kyrdalen, I.L.; Thingstad, P.; Sandvik, L.; Ormstad, H. Associations between gait speed and well-known fall risk factors among community-dwelling older adults. Physiother. Res. Int. 2019, 24, e1743. [Google Scholar] [CrossRef] [PubMed]
- Montero-Odasso, M.; Schapira, M.; Soriano, E.R.; Varela, M.; Kaplan, R.; Camera, L.A.; Mayorga, L.M. Gait Velocity as a Single Predictor of Adverse Events in Healthy Seniors Aged 75 Years and Older. J. Gerontol. Ser. A 2005, 60, 1304–1309. [Google Scholar] [CrossRef] [PubMed]
- Abellan van Kan, G.; Rolland, Y.; Andrieu, S.; Bauer, J.; Beauchet, O.; Bonnefoy, M.; Cesari, M.; Donini, L.M.; Gillette-Guyonnet, S.; Inzitari, M.; et al. Gait speed at usual pace as a predictor of adverse outcomes in community-dwelling older people an International Academy on Nutrition and Aging (IANA) Task Force. J. Nutr. Health Aging. 2010, 13, 881–889. [Google Scholar] [CrossRef] [PubMed]
- Purser, J.L.; Weinberger, M.; Cohen, H.J.; Pieper, C.F.; Morey, M.C.; Li, T.; Williams, G.R.; Lapuerta, P. Walking speed predicts health status and hospital costs for frail elderly male veterans. J. Rehabil. Res. Dev. 2005, 42, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Agarwala, P.; Salzman, S.H. Six-Minute Walk Test: Clinical Role, Technique, Coding and Reimbursement. Chest 2020, 157, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Zijlstra, W.; Hof, A.L. Assessment of spatio-temporal gait parameters from trunk accelerations during human walking. Gait Posture 2003, 18, 1–10. [Google Scholar] [CrossRef]
- Yang, S.; Li, Q. Inertial Sensor-Based Methods in Walking Speed Estimation: A Systematic Review. Sensors 2012, 12, 6102–6116. [Google Scholar] [CrossRef] [PubMed]
- Alfredsson, J.; Stebbins, A.; Brennan, J.M.; Matsouaka, R.; Afilalo, J.; Peterson, E.D.; Vemulapalli, S.; Rumsfeld, J.S.; Shahian, D.; Mack, M.J.; et al. Gait Speed Predicts 30-Day Mortality After Transcatheter Aortic Valve Replacement: Results From the Society of Thoracic Surgeons/American College of Cardiology Transcatheter Valve Therapy Registry. Circulation 2016, 133, 1351–1359. [Google Scholar] [CrossRef] [PubMed]
- Saporito, S.; Brodie, M.A.; Delbaere, K.; Hoogland, J.; Nijboer, H.; Rispens, S.M.; Spina, G.; Stevens, M.; Annegarn, J. Remote Timed Up and Go Evaluation from Activities of Daily Living Reveals Changing Mobility after Surgery. Physiol. Meas. 2019, 40. [Google Scholar] [CrossRef] [PubMed]
- Fridriksdottir, E.; Bonomi, A.G. Accelerometer-based human activity recognition for patient monitoring using a deep neural network. Sens. Basel. 2020, 20, 6424. [Google Scholar] [CrossRef] [PubMed]
- Gschwind, Y.J.; Eichberg, S.; Marston, H.R.; Ejupi, A.; De Rosario, H.; Kroll, M.; Drobics, M.; Annegarn, J.; Wieching, R.; Lord, S.R.; et al. ICT-based system to predict and prevent falls (iStoppFalls): Study protocol for an international multicenter randomized controlled trial. BMC Geriatr. 2014, 14, 91. [Google Scholar] [CrossRef] [PubMed]
- Rispens, S.M.; Van Schooten, K.S.; Pijnappels, M.; Daffertshofer, A.; Beek, P.J.; Van Dieën, J.H. Identification of Fall Risk Predictors in Daily Life Measurements: Gait Characteristics’ Reliability and Association With Self-reported Fall History. Neurorehabilit. Neural Repair 2014, 29, 54–61. [Google Scholar] [CrossRef] [PubMed]
- Morio, Y.; Izawa, K.P.; Omori, Y.; Katata, H.; Ishiyama, D.; Koyama, S.; Yamano, Y. The Relationship between Walking Speed and Step Length in Older Aged Patients. Diseases 2019, 7, 17. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Verghese, J.; Holtzer, R.; Mahoney, J.R.; Oh-Park, M. Trunk sway during walking among older adults: Norms and correlation with gait velocity. Gait Posture 2014, 40, 676–681. [Google Scholar] [CrossRef] [PubMed]
- Byun, S.; Lee, H.J.; Han, J.W.; Kim, J.S.; Choi, E.; Kim, W.K. Walking-speed estimation using a single inertial measurement unit for the older adults. PloS ONE 2019. [Google Scholar] [CrossRef] [PubMed]
- Ostir, G.D.; Berges, I.M.; Kuo, Y.F.; Goodwin, J.S.; Fisher, S.R.; Guralnik, J.M. Mobility Activity and its Value as a Prognostic Indicator of Survival in Hospitalized Older Patients. J. Am. Geriatr. Soc. 2013, 61, 551–557. [Google Scholar] [CrossRef] [PubMed]
| N | Female/Male | Age (y) | Height (m) | Weight (kg) | |
|---|---|---|---|---|---|
| Young | 9 | 1/8 | 35.0 ± 4.6 | 1.83 ± 0.06 | 73.9 ± 7.5 |
| Out-Patients | 10 | 5/5 | 73.0 ± 4.7 | 1.71 ± 0.09 | 89.2 ± 20.2 |
| Simulated Hospital | 20 | 10/10 | 43.3 ± 13.4 | 1.75 ± 0.11 | 78.4 ± 14.8 |
| Community | 120 | 82/38 | 80.4 ± 6.7 | 1.63 ± 0.09 | 71.1 ± 14.8 |
| Chest | Rib | Pendant | |||||
|---|---|---|---|---|---|---|---|
| IP | Updated IP | IP | Updated IP | IP | Updated IP | ||
| Community | R | - | - | - | - | 0.86 | 0.88 |
| RMSE [m/s] | - | - | - | - | 0.15 * | 0.18 | |
| MAE [m/s] | - | - | - | - | 0.13 * | 0.16 | |
| Treadmill | R | 0.97 | 0.98 | 0.96 | 0.98 | 0.96 | 0.97 |
| RMSE [m/s] | 0.13 | 0.06 * | 0.14 | 0.06 * | 0.17 | 0.08 * | |
| MAE [m/s] | 0.12 | 0.05 * | 0.12 | 0.05 * | 0.15 | 0.06 * | |
| Walking aid | R | 0.66 | 0.75 | 0.64 | 0.78 | 0.60 | 0.64 |
| RMSE [m/s] | 0.14 | 0.10 | 0.15 | 0.10 * | 0.18 | 0.11 * | |
| MAE [m/s] | 0.11 | 0.08 | 0.12 | 0.08 * | 0.14 | 0.09 * | |
| 6MWT | R | 0.94 | 0.93 | 0.94 | 0.94 | 0.84 | 0.82 |
| RMSE [m/s] | 0.10 | 0.13 | 0.11 | 0.11 | 0.25 | 0.26 | |
| MAE [m/s] | 0.07 | 0.08 | 0.08 | 0.08 | 0.17 | 0.17 | |
| Young | R | 0.98 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 |
| RMSE [m/s] | 0.09 | 0.07 * | 0.10 | 0.06 * | 0.10 | 0.07 * | |
| MAE [m/s] | 0.08 | 0.05 * | 0.09 | 0.05 * | 0.09 | 0.05 * | |
| Out-Patients | R | 0.93 | 0.93 | - | - | 0.90 | 0.90 |
| RMSE [m/s] | 0.07 | 0.08 | - | - | 0.09 | 0.08 | |
| MAE [m/s] | 0.06 | 0.05 | - | - | 0.08 | 0.05 | |
| <0.5 m/s | R | 0.72 | 0.81 | 0.70 | 0.82 | 0.67 | 0.73 |
| RMSE [m/s] | 0.15 | 0.07 * | 0.16 | 0.06 * | 0.19 | 0.09 * | |
| MAE [m/s] | 0.13 | 0.05 * | 0.14 | 0.05 * | 0.17 | 0.06 * | |
| ≥ 0.5 m/s | R | 0.97 | 0.97 | 0.96 | 0.98 | 0.87 | 0.90 |
| RMSE [m/s] | 0.09 | 0.10 | 0.10 | 0.09 | 0.15 * | 0.16 | |
| MAE [m/s] | 0.07 | 0.07 | 0.08 | 0.07 | 0.11 * | 0.13 | |
| All | R | 0.98 | 0.98 | 0.97 | 0.98 | 0.94 | 0.95 |
| RMSE [m/s] | 0.13 | 0.08 * | 0.14 | 0.08 * | 0.16 | 0.14 * | |
| MAE [m/s] | 0.10 | 0.06 * | 0.11 | 0.06 * | 0.13 | 0.10 * | |
| IP | Updated IP | ||||||
|---|---|---|---|---|---|---|---|
| Chest | Rib | Pendant | Chest | Rib | Pendant | ||
| <0.5 m/s | R | 0.72 | 0.70 | 0.65 | 0.81 | 0.82 | 0.72 |
| RMSE [m/s] | 0.15 a,b | 0.16 b | 0.19 | 0.07 | 0.07 | 0.09 | |
| MAE [m/s] | 0.13 a,b | 0.14 b | 0.17 | 0.05 | 0.05 | 0.06 | |
| ≥0.5 m/s | R | 0.97 | 0.96 | 0.94 | 0.97 | 0.98 | 0.95 |
| RMSE [m/s] | 0.09 | 0.10 | 0.14 | 0.10 | 0.09 c | 0.13 | |
| MAE [m/s] | 0.07 | 0.08 | 0.10 | 0.08 | 0.07 c | 0.09 | |
| all | R | 0.98 | 0.97 | 0.96 | 0.98 | 0.98 | 0.96 |
| RMSE [m/s] | 0.13 a,b | 0.14 b | 0.17 | 0.08 | 0.08 c | 0.11 | |
| MAE [m/s] | 0.11 a,b | 0.11 b | 0.14 | 0.06 | 0.06 c | 0.07 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rispens, S.M.; Cox, L.G.E.; Ejupi, A.; Delbaere, K.; Annegarn, J.; Bonomi, A.G. Validation of Walking Speed Estimation from Trunk Mounted Accelerometers for a Range of Walking Speeds. Sensors 2021, 21, 1854. https://doi.org/10.3390/s21051854
Rispens SM, Cox LGE, Ejupi A, Delbaere K, Annegarn J, Bonomi AG. Validation of Walking Speed Estimation from Trunk Mounted Accelerometers for a Range of Walking Speeds. Sensors. 2021; 21(5):1854. https://doi.org/10.3390/s21051854
Chicago/Turabian StyleRispens, Sietse M., Lieke G. E. Cox, Andreas Ejupi, Kim Delbaere, Janneke Annegarn, and Alberto G. Bonomi. 2021. "Validation of Walking Speed Estimation from Trunk Mounted Accelerometers for a Range of Walking Speeds" Sensors 21, no. 5: 1854. https://doi.org/10.3390/s21051854
APA StyleRispens, S. M., Cox, L. G. E., Ejupi, A., Delbaere, K., Annegarn, J., & Bonomi, A. G. (2021). Validation of Walking Speed Estimation from Trunk Mounted Accelerometers for a Range of Walking Speeds. Sensors, 21(5), 1854. https://doi.org/10.3390/s21051854





