Hierarchical Mission Planning with a GA-Optimizer for Unmanned High Altitude Pseudo-Satellites
Abstract
:1. Introduction
- Cumulonimbus clouds: Although clouds are rare in the stratosphere where HAPSs operate, the anvil of Cumulonimbus clouds can reach high altitudes and is extremely dangerous. Hence, it must be avoided with substantial distance (∼37 km laterally and 1.5 km vertically) to prevent structural impairment to the platforms [6].
- Turbulences and Precipitation: These weather phenomena can be caused by strong winds and wind shear [7]. Although rare and harmless to bigger aircraft (e.g., airliners), turbulences and precipitations can cause extreme difficulties to HAPSs navigation and damage their structures.
- Wind field: Given the low airspeed of the HAPS, even mild wind (with wind speed up to 5 m/s) must be considered in planning for wind drift correction.
2. Problem Description
2.1. Monitoring Scenarios
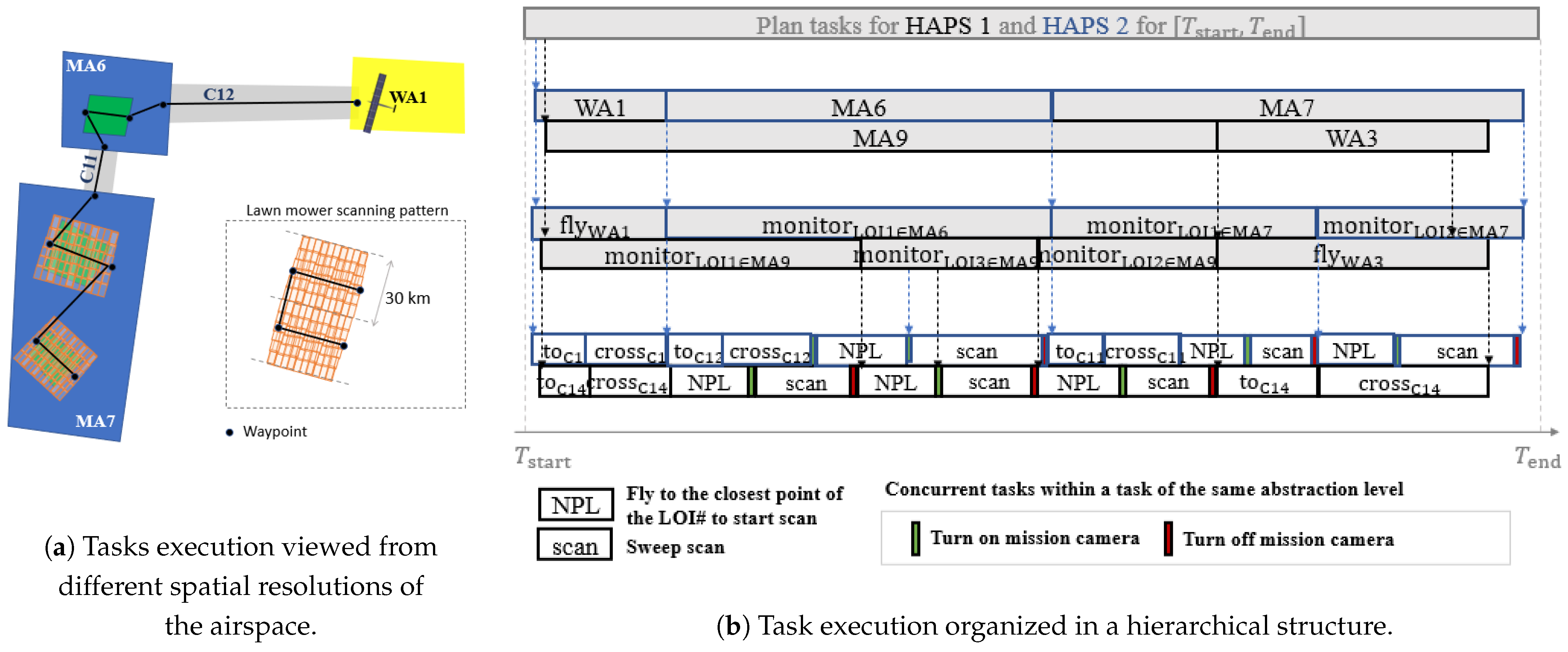
2.2. Hierarchical Task Plan
- MA level, where the plans are the sequences of mission areas (MA#) and waiting areas (WA#) that each HAPS operates.
- LOI level, where the plans are sequences of tasks to be performed in the mission elements expressed at one higher abstraction level (i.e., MA# and WA#). Examples of these tasks are flying through a WA (fly) and monitoring a LOI in a given MA (monitor).
- Waypoint (WP) level, where the plans consist of either executing a scan pattern (scan) over a LOI or flying to sequences of waypoint, which are: fly to the closest entrance of a given corridor (to), cross and fly to the end location of the given corridor (cross), and fly to the closest vertex of the LOI that has to be monitored (NPL).
2.3. Mission Payload
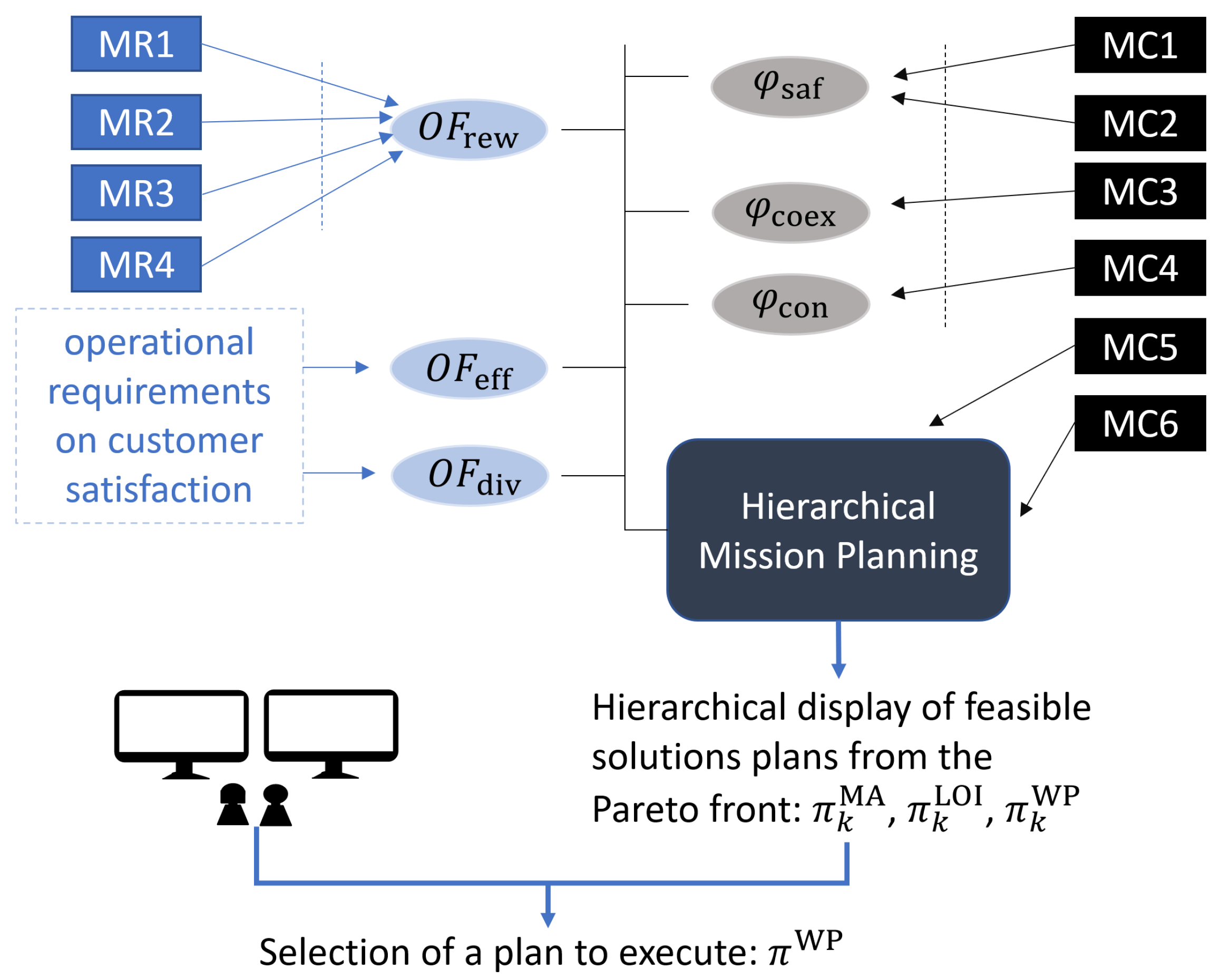
2.4. Mission Requirements
- MR1: The recorded image of each LOI has a coverage of the LOI that is bigger than the minimum required coverage for its corresponding MA.
- MR2: The captured images of each LOI are within the time windows requested by the client for each MA.
- MR3: The time-lapse between two consecutive successful visits to the MA is larger than the imposed minimum inter-visit time-lapse for the MA.
- MR4: The MA has not been visited more frequently per day than required by the client.
2.5. Mission Constraints
- MC1: any mission element that the HAPS is operating in has a wind field with a wind magnitude smaller than 5 m/s.
- MC2: the MA or WA that the HAPS is operating in (e.g., a MA, a WA, or a C) has an obstacle occlusion (related with zones of adverse weather) smaller than 30%.
- MC3: Only one HAPS can operate in a MA (i.e., the simultaneous coexisting of HAPSs in a MA is forbidden).
- MC4: Consecutive MAs or WAs have to be connected according to the mission scenario.
- MC5: LOIs are monitored exactly once at each visit to the MA.
- MC6: A MA cannot be used as a corridor, i.e., HAPS cannot pass the MA without monitoring all its encompassed LOIs.
2.6. Weather Conditions
3. Formal Problem Statement
3.1. Formal Definition of the Hierarchical Plan
- At the MA level, the plan can be represented as the ordered list of tasks displayed in Equation (1), where is the i-th mission task (i.e., a MA# or WA# of the mission scenario) on the list that will be performed by HAPS h, and and are the start time and the duration of the task of HAPS h.Under this formulation, the high level mission plan of the first HAPS displayed in Figure 2b will be represented as =< WA1(, ), MA6(, ), MA7(, )>.
- At the LOI-level, the plan can be represented with Equation (2), where is the i-th mission task (i.e., fly or monitor) that will be performed by HAPS h, and and are the start time and duration of the task of HAPS h.Under this formulation, the middle level mission plan of the first HAPS displayed in Figure 2b will be represented as <(, ), (, ), (, ), (, )>. Moreover, we can relate the time variables of the MA and LOI level (e.g., , , , or ) to signify the decomposition of the higher level task into lower-level tasks.
- A similar representation, where are the actions that can be performed at the lower mission level, and and are its corresponding start time and duration, applies to the WP-level.
- Finally, we extend the previous notations as follows:
- –
- , and represent the plans of the set of H HAPSs (i.e., , where * stands either for MA, LOI, or WP).
- –
- , and represent the partial plans between the i-th and j-th task (i.e., , where * stands either for MA, LOI, or WP.
3.2. Objectives
3.2.1. Expected Cumulative Rewards per Hour
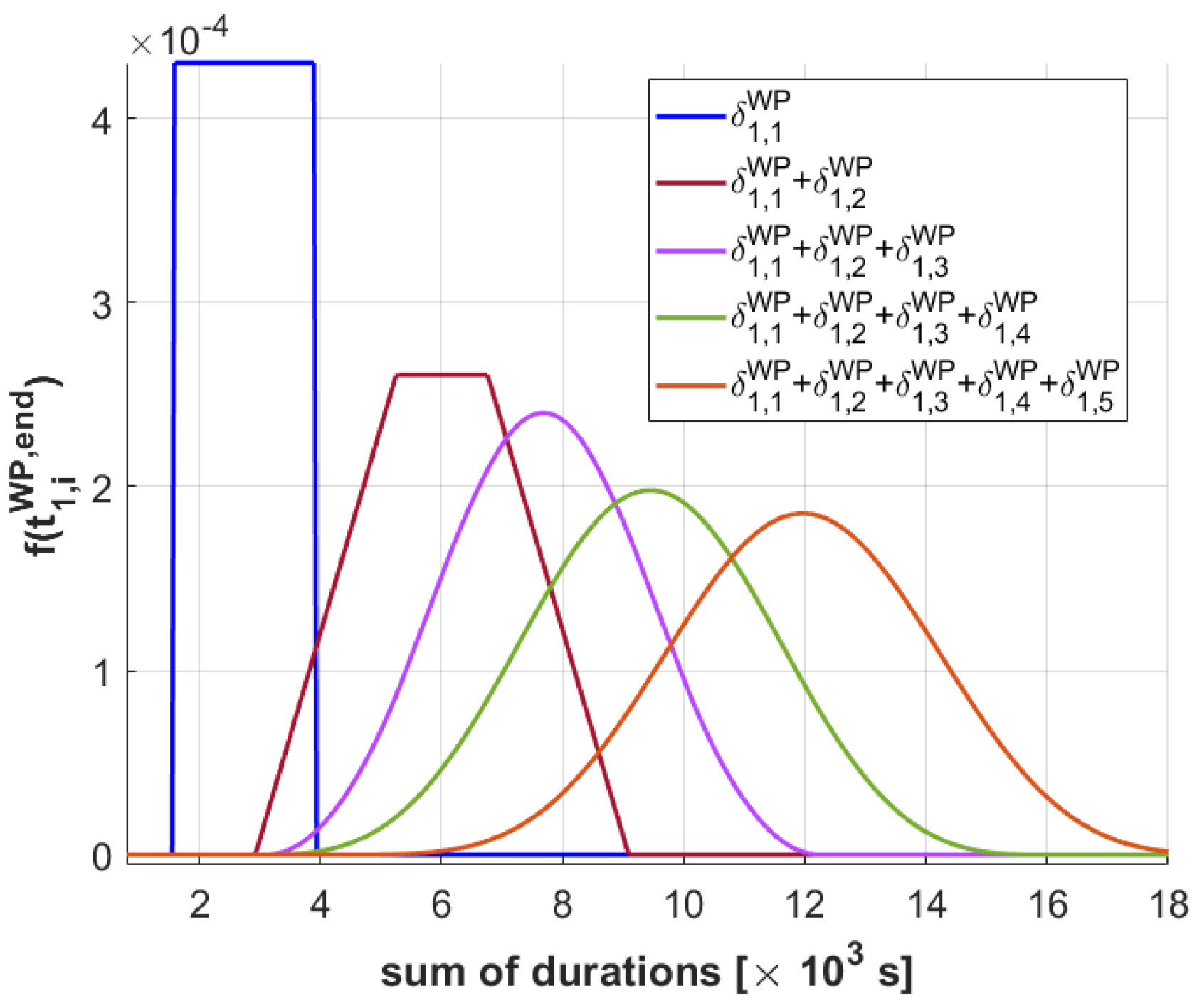
- It takes into account the immediate reward obtained after monitoring the selected mission area at end time , as well as the reward of the remaining action plan .
- It considers the likelihood of performing the task successfully and unsuccessfully, depending on the weather conditions, or more specifically, on the cloud coverage, which is related to the mission requirements (i.e., MR1) listed in Section 2.4.
- It exploits the weighting imposed by at the given times . This is helpful since the weather forecast is constantly updated and a replanning can occur in the future. Therefore, while it is important to “look forward” in the plan to optimize it for a longer time horizon, we allocate more weighting according to immediacy, since a replanning could be triggered to improve the plan quality in the future.
3.2.2. Effort
3.2.3. Diversity
3.3. Constraints
3.3.1. Safety
3.3.2. Coexistence
3.3.3. Connection
3.3.4. Overall Constraint Violation
4. Implementation of a GA-Guided Hierarchical Task Planner
4.1. Plan Codification
4.2. Temporal Hierarchical Task Decomposition
| Algorithm 1: Temporal hierarchical task decomposition |
 |
4.3. GA-Guided Search of the Best Plans
| Algorithm 2: NSGA-II-guided search of nondominated solutions of hierarchical plans |
 |
5. Results and Analysis
5.1. Scenarios
5.2. Planner Configurations
- Planner Configuration 1 (PC1). The constraint-handling technique proposed by [19] is used for select the pair of parents in the k-tournament selection (at Line 17 of Algorithm 2) and for recombining the old and new populations (at Line 26). In other words, solutions that fulfill or are closer to fulfilling the constraints are preferred to solutions that do not fulfill or are further to fulfilling them, and among solutions that are equally good regarding the constraints, solutions that Pareto dominate the others regarding the objective functions are preferred to solutions that are Pareto dominated. As this configuration implements the standard constraint-handling techniques of NSGA-II [19], it is also the one described in Section 4.
- Planner Configuration 2 (PC2). The constraint-handling criteria are only applied to select the pair of parents in the k-tournament selection in Line 17 of Algorithm 2 and ignored during the recombination of old and new populations. That is, during the recombination step in Line 26 of Algorithm 2, the solutions are sorted by only taking into account the ordering imposed by the Pareto comparison of the objective functions. The motivation of this variation is to have a planner configuration that is less “stringent” with the hierarchical plans that violate the constraints (i.e., that have ), and to give them more chances to be selected for the next generation (or even be selected as parents for the generation of children solutions of the next iteration).
- Planner Configuration 3 (PC3). The diversity objective function () is ignored both during the parents selection and recombination steps. This configuration has been set up to put forth the benefit of considering the diversity (and not only the expected reward or the effort) for planning.
5.3. Results Representation
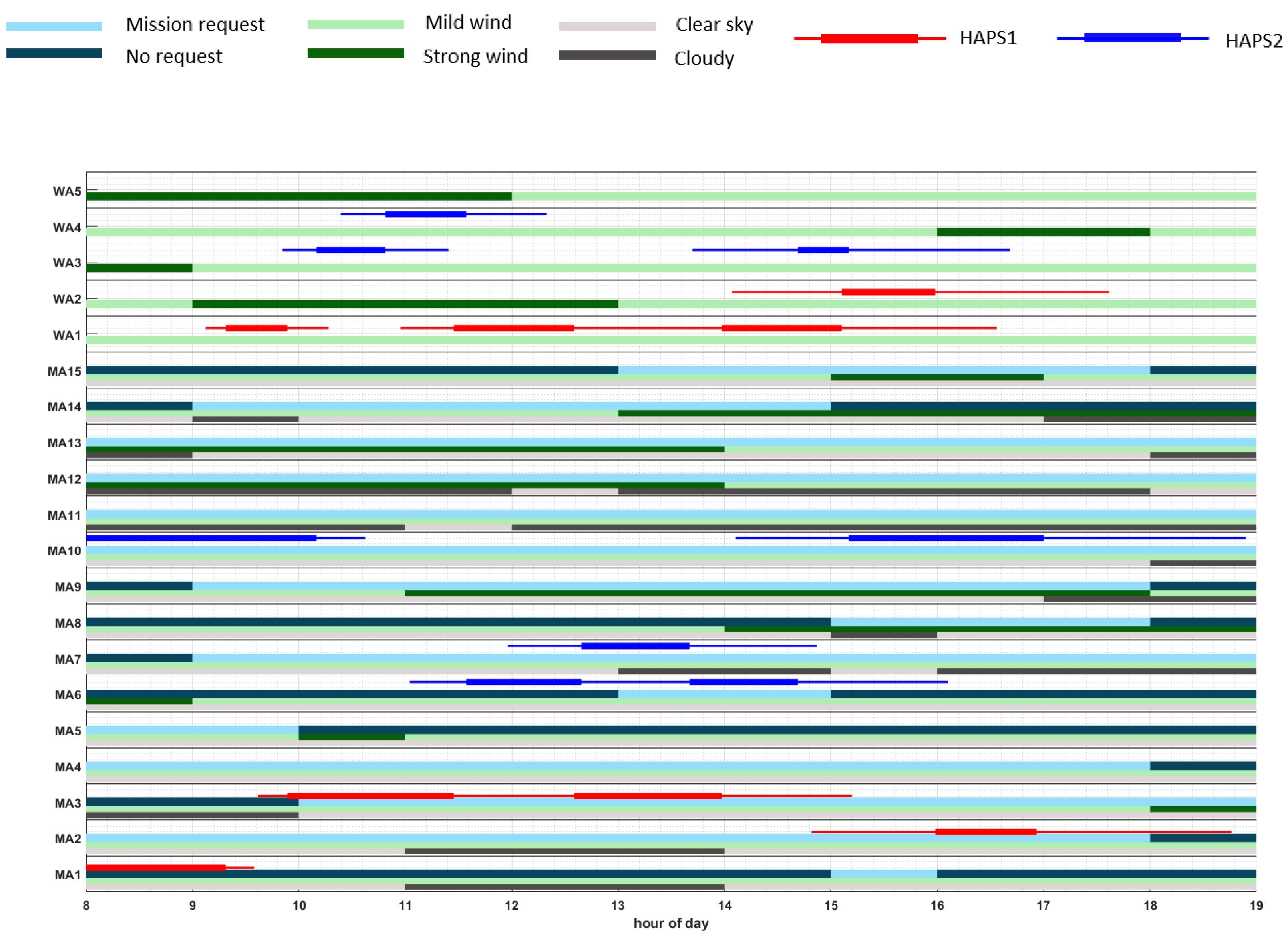
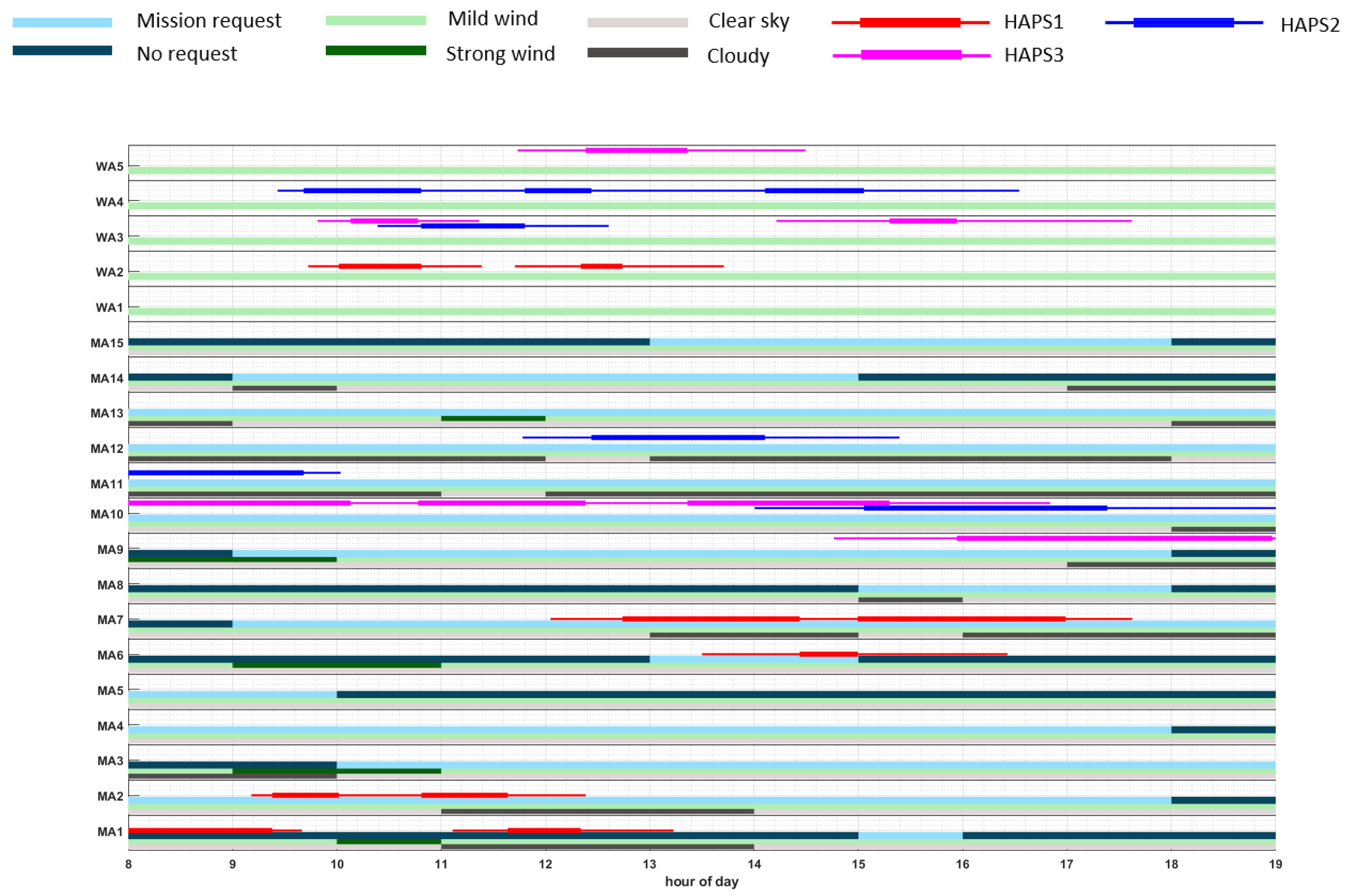
- The light-grey bars represent the time windows with clear sky, while the dark-grey bars signify high cloud coverage above the corresponding MA.
- The light-green bars represent the time windows for the absence of critical weather conditions at the MA or WA, while the dark-green bars signify critical weather conditions for the corresponding MA or WA, e.g., strong wind.
- The light-blue bars represent the time windows where monitoring missions at the corresponding MA are requested (and therefore rewarded), while the dark-blue bars signify the absence of mission request for the corresponding MA.
- Red lines represent the monitoring/fly-by tasks of HAPS1 to be performed on the corresponding MA/WA, according to the representative plan . Moreover, the thicker line in the middle marks the median start and end time, while the thinner lines mark the time range from the minimum starting time to the maximum end time of each task.
- Similarly, blue lines represent the tasks at MA-level to be performed by HAPS2 and magenta lines represent tasks at MA-level to be performed by HAPS3.
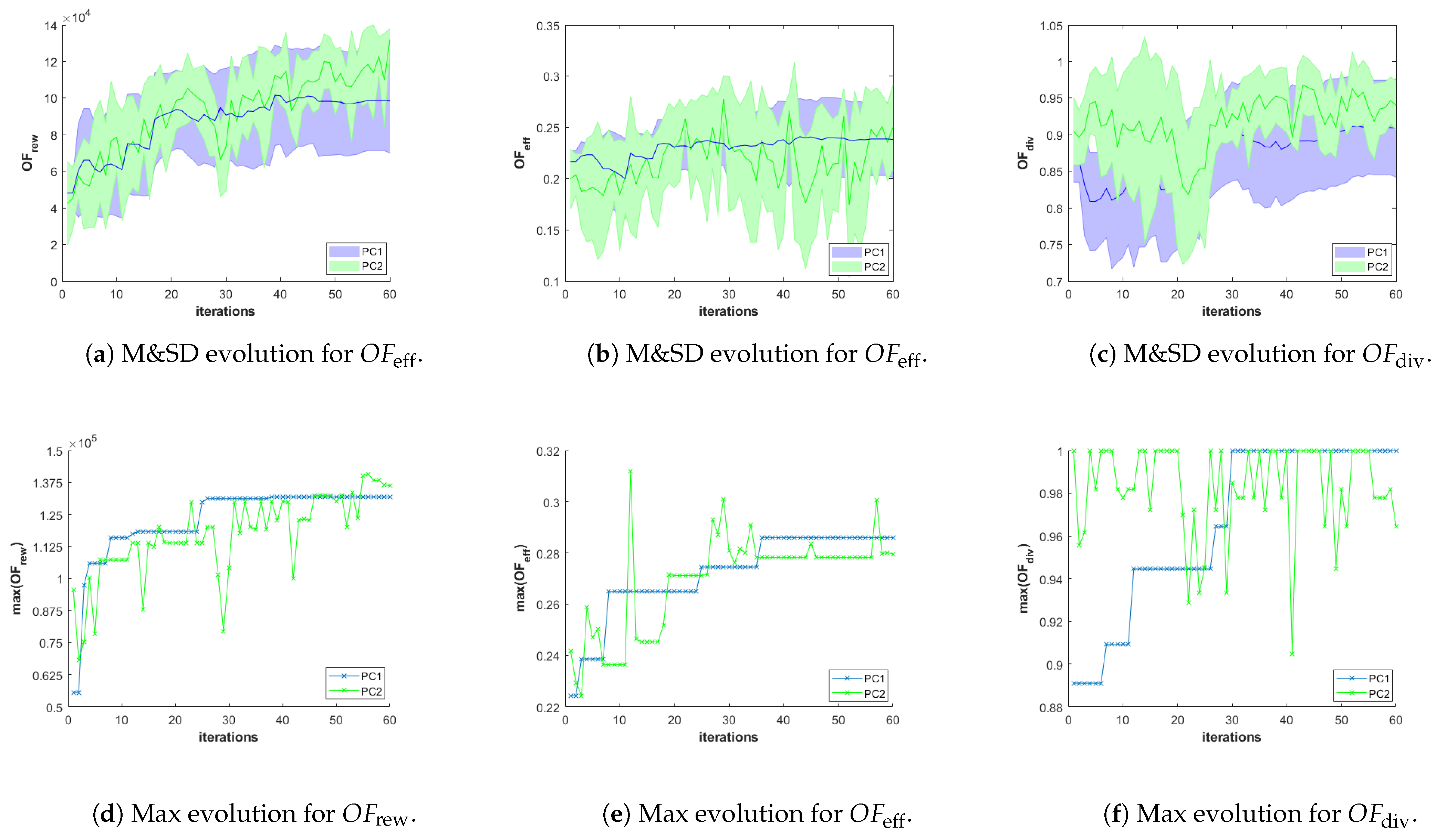
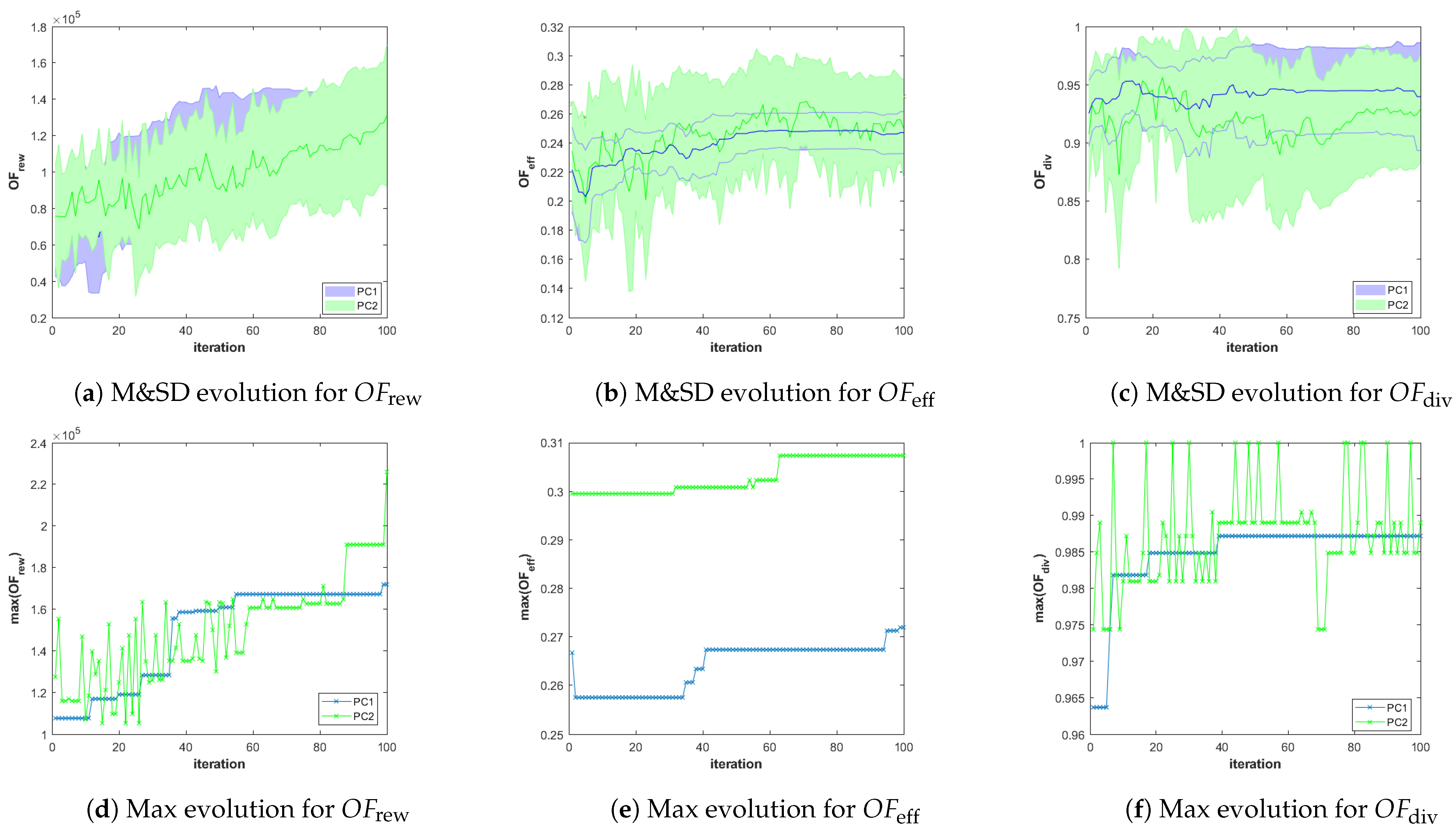
- The evolution over iterations of the Mean and Standard Deviation (M&SD) of the values of each objective function of the feasible solutions that belong to the best front. Considering only feasible solutions of the best front is initially necessary for the three planner configuration, since it is possible that the first Pareto fronts are initially infeasible. Besides, it is always necessary in PC2, since the fronts are obtained by ignoring the constraints, and therefore, the best front obtained using PC2 can contain infeasible solutions. Moreover, this is meaningful since only the final feasible solution plans of the best Pareto front will be presented to the HAPS operator. The M&SD evolution graphs for each objective function are presented in the first row of Figures 8–13 for Scenario 1, 2, and 3, respectively. The mean and standard deviation values of each objective function are represented in different columns of the figures (left column , middle column , and right column ). Besides, while the mean is depicted over iterations with a bold line, the shadowed area around it represents the standard deviation, using a different color for each planner configuration (blue for PC1, green for PC2, and red for PC3).
- The evolution of the Maximum (Max) value of each objective function obtained among the solutions of the first Pareto front that also fulfill the constraints are plotted in the lower row of graphs of Figures 8–13. These graphs, organized as the previous and using only a line for the Max value, complement the M&SD evolution graphs as they show the objective values of the best solutions with respect to each objective in the Pareto front.
- A 3D representation of the values of the three objective functions of all the solutions of the population versus the values of the objective functions of the solutions of the best Pareto front, at selected iterations of the planner (and a 2D representation of versus ). This information, represented in Figure 7, marking in red the points associated to the solutions of the best Pareto front and in black the remaining solutions of the population, is used to graphically demonstrate the effectiveness of the planner in evolving and finding solutions of the Pareto front.
- The number of infeasible solutions within the population at each iteration. This information, represented in Figure 9, is used to put forth the advantage of enabling/disabling the constraint handling during the recombination step of PC1 and PC2.
5.4. Comparative Analysis
5.4.1. Analysis for Scenario 1 (SC1)
5.4.2. Analysis for Scenario 2 (SC2)
5.4.3. Analysis for Scenario 3 (SC3)
6. Related Works
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| C | Corridor |
| EA | Evolutionary Algorithm |
| EO | Electro-Optical |
| FL | Flight Level |
| GA | Genetic Algorithm |
| GCS | Ground Control Station |
| HALE | High Altitude Long Endurance |
| HAPS | High Altitude Pseudo-Satellite |
| HFR | High-level Flight Rules |
| LOI | Location Of Interest |
| MA | Mission Area |
| MC | Mission Constraint |
| MOEA | Multi-Objective Evolutionary Algorithm |
| MR | Mission Requirement |
| NSGA | Nondominated Sorting Genetic Algorithm |
| PC | Planner Configuration |
| TDMVRP | Time Dependent Multi-Vehicle Routing Problem |
| UAV | Unmanned Aerial Vehicle |
| WA | Waiting Area |
| WP | Waypoint |
Appendix A. Numerical Details on the HAPS Model and on the Mission Parameters
| Build/Fight Performance/Payload | Parameter Values |
|---|---|
| Weight | 100 kg |
| Wingspan | 30 m |
| Payload | 5–10 kg |
| Battery capacity | 15 kWh |
| Electro-motor maximum propulsive power | 1700 W |
| Operating altitude | 18 km |
| Cruise airspeed at the operating altitude | 30 m/s |
| Endurance | 3 months |
| Ground sampling distance at 18 km | 30 cm |
| of an image | 360 × 3000 m |
| C | Longest Diagonal [km] | MA/WA | Longest Diagonal [km] | LoI 1 | LoI 2 | LoI 3 |
|---|---|---|---|---|---|---|
| C1 | 60.78 | MA1 | 27.58 | 17.10 | ||
| C2 | 37.83 | MA2 | 69.49 | 19.83 | ||
| C3 | 33.67 | MA3 | 103.11 | 20.07 | 44.27 | |
| C4 | 58.88 | MA4 | 25.32 | 15.56 | ||
| C5 | 34.22 | MA5 | 52.90 | 13.25 | ||
| C6 | 17.64 | MA6 | 46.51 | 21.61 | ||
| C7 | 70.41 | MA7 | 84.03 | 21.42 | 25.88 | |
| C8 | 40.27 | MA8 | 36.62 | 10.84 | ||
| C9 | 66.19 | MA9 | 133.30 | 34.36 | 21.24 | 38.13 |
| C10 | 72.10 | MA10 | 123.35 | 39.96 | 44.74 | |
| C11 | 20.52 | MA11 | 74.98 | 31.62 | 24.53 | |
| C12 | 73.35 | MA12 | 73.49 | 18.28 | 26.38 | |
| C13 | 39.34 | MA13 | 56.87 | 18.62 | ||
| C14 | 88.46 | MA14 | 36.28 | 14.31 | ||
| C15 | 63.04 | MA15 | 104.92 | 23.66 | 36.46 | |
| C16 | 70.70 | WA1 | 47.90 | |||
| C17 | 71.98 | WA2 | 34.44 | |||
| C18 | 71.38 | WA3 | 46.41 | |||
| C19 | 61.77 | WA4 | 47.96 | |||
| C20 | 42.75 | WA5 | 26.44 | |||
| C21 | 46.67 | |||||
| C22 | 39.80 | |||||
| C23 | 74.26 | |||||
| C24 | 38.15 | |||||
| C25 | 106.86 | |||||
| C26 | 63.86 |
| Mission Area | Coverage (%) | Reward (€) | Mission Area | Coverage (%) | Reward (€) |
|---|---|---|---|---|---|
| MA1 | 80 | 4 | MA9 | 60 | 13 |
| MA2 | 80 | 50 | MA10 | 60 | 18 |
| MA3 | 60 | 100 | MA11 | 70 | 20 |
| MA4 | 80 | 20 | MA12 | 70 | 10 |
| MA5 | 80 | 3 | MA13 | 60 | 8 |
| MA6 | 70 | 5 | MA14 | 90 | 18 |
| MA7 | 70 | 15 | MA15 | 50 | 9 |
| MA8 | 80 | 3 |
References
- Klöckner, A. Behavior Trees for Mission Management of High-Altitude Pseudo-Satellites; Verlag Dr. Hut: Munich, Germany, 2016. [Google Scholar]
- Airbus. Zephyr Press Release. Available online: https://www.airbus.com/newsroom/press-releases/en/2018/08/Airbus-Zephyr-Solar-High-Altitude-Pseudo-Satellite-flies-for-longer-than-any-other-aircraft.html (accessed on 19 February 2021).
- Hunter, S. Safe Operations above FL600. In Proceedings of the 2015 Space Traffic Management Conference, Daytona Beach, FL, USA, 12–13 November 2015. [Google Scholar]
- Kiam, J.J. Al-Based Mission Planning for High-Altitude Pseudo-Satellites in Time-Varying Environments. Ph.D. Thesis, University der Bundeswehr Munich, Munich, Germany, 2019. [Google Scholar]
- Finnegan, P. World Civil Unmanned Aerial Systems: Teal Market Profile and Forecast; TEAL CROUP: Fairfax, VA, USA, 2017. [Google Scholar]
- Airbus. Adverse Weather Operations: Optimum Use of the Weather Radar; Technical Report; Flight Operations Briefing Notes; Airbus: Blagnac, France, 2007. [Google Scholar]
- Leena, P.; Ratnam, M.V.; Murthy, B.K.; Rao, S. Detection of High Frequency Gravity Waves Using High Resolution Radiosonde Observations. J. Atmos. Sol. Terr. Phys. 2012, 77, 254–259. [Google Scholar] [CrossRef]
- EUROCONTROL; EASA. UAS ATM Integration: Integration Operational Concept. EUROCONTROL, November 2018. Available online: https://www.eurocontrol.int/publication/unmanned-aircraft-systems-uas-atm-integration (accessed on 19 February 2021).
- EUROCONTROL. Advance Flexible Use of Airspace (FUA) Concept. EUROCONTROL, 24 July 2015. Available online: https://www.eurocontrol.int/publication/advanced-flexible-use-airspace-afua-concept (accessed on 19 February 2021).
- Kiam, J.; Besada-Portas, E.; Hehtke, V.; Schulte, A. GA-guided task planning for multiple-HAPS in realistic time-varying operation environments. In Proceedings of the 2019 Genetic and Evolutionary Computation Conference, Prague, Czech Republic, 13–17 July 2019. [Google Scholar]
- Müller, R.; Kiam, J.; Mothes, F. Multiphysical simulation of a semi-autonomous solar powered high altitude pseudo-satellite. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2018. [Google Scholar]
- Delauré, B.; Michiels, D.; Lewyckyj, N.; van Achteren, T. The development of a family of lightweight and wide swath UAV camera systems around an innovative dual-sensor on-single-chip detector. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2013, XL-1/W2, 101–106. [Google Scholar]
- Baldauf, M.; Gebhardt, C.; Theis, S.; Ritter, B.; Schraff, C. Beschreibung des Operationellen Kürzestfristvorhersagemodells COSMO-D2 und COSMO-D2-EPS und Seiner Ausgabe in die Datenbanken des DWD; Technical Report; Deutscher Wetterdienst, DWD: Offenbach, Germany, 2018. [Google Scholar]
- National Centres for Environmental Information (NOAA). Global Forecast System Weather Download. Available online: https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs (accessed on 19 February 2021).
- European Centre for Medium-Range Weather Forecasts. IFS Documentation—Cy45r1: Operational Implementation 5 June 2018; ECMWF: Reading, UK, 2018. [Google Scholar]
- Bradley, D.; Gupta, R. On the Distribution of the Sum of n Non-Identically Distributed Uniform Random Variables. Ann. Inst. Stat. Math. 2002, 54, 689–700. [Google Scholar] [CrossRef] [Green Version]
- Boyan, J.; Littman, M. Exact solutions to time-dependent MDPs. In Proceedings of the 13th International Conference on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 3–8 December 2000. [Google Scholar]
- Simpsons, E. Measurement of Diversity. Nature 1949, 163, 688. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Runarsson, T.P.; Yao, X. Stochastic Ranking for Constrained Evolutionary Optimization. IEEE Trans. Evol. Comput. 2000, 4, 284–294. [Google Scholar] [CrossRef] [Green Version]
- Linchant, J.; Lisein, J.; Semeki, J.; Lejeune, P.; Vermeulen, C. Are Unmanned Aircraft Systems (UASs) the Future of Wildlife Monitoring? A Review of Accomplishments and Challenges. Mammal Rev. 2015, 45, 239–252. [Google Scholar] [CrossRef]
- Remondino, F.; Barazzetti, L.; Nex, F.; Scaioni, M.; Sarazzi, D. UAV Photogrammetry for Mapping and 3D Modeling—Current Status and Future Perspectives. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, C22. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Kirubarajan, T.; Tharmarasa, R.; Jassemi-Zargani, R.; Kashyap, N. Multiperiod Coverage Path Planning and Scheduling for Airborne Surveillance. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2257–2273. [Google Scholar] [CrossRef]
- Aurora. Odysseus Press Realase. Available online: https://www.aurora.aero/odysseus-high-altitude-pseudo-satellite-haps/ (accessed on 19 February 2021).
- Spangelo, S.; Gilbert, E. Power Optimization of Solar-powered Aircraft with Specified Closed Ground Tracks. J. Aircr. 2012, 50, 232–238. [Google Scholar] [CrossRef]
- Hosseini, S.; Dai, R.; Mesbahi, M. Optimal path planning and power allocation for a long endurance solar-powered UAV. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Gao, X.; Hou, Z.; Guo, Z.; Chen, X.; Chen, X. Joint Optimization of Battery Mass and Flight Trajectory for High-Altitude Solar-powered Aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2439–2451. [Google Scholar] [CrossRef]
- Lee, J.; Yu, K. Optimal Path Planning of Solar-powered UAV Using Gravitational Potential Energy. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1442–1451. [Google Scholar] [CrossRef]
- Bolandhemmat, H.; Thomsen, B.; Marriott, J. Energy-optimized trajectory planning for High Altitude Long Endurance (HALE) aircraft. In Proceedings of the 18th European Control Conference, Naples, Italy, 25–28 June 2019. [Google Scholar]
- Guerra-Padilla, G.; Kim, K.; Yu, K. Flight Path Planning and Signal Behavior Analysis of a LALE Solar-Powered UAV for Communication Relay; Asia Pacific International Symposium on Aerospace Technology: Gold Coast, Australia, 2019. [Google Scholar]
- Guerra-Padilla, G.; Kim, K.; Park, S.; Yu, K. Flight Path Planning of Solar-powered UAV for Sustainable Communication Relay. IEEE Robot. Autom. Lett. 2020, 5, 6772–6779. [Google Scholar] [CrossRef]
- Huang, H.; Savkin, A.V.; Ni, W. Energy-efficient 3D Navigation of a Solar-powered UAV for Secure Communication in the Presence of Eavesdroppers and No-fly Zones. Energies 2020, 13, 1445. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wang, H.; Li, N.; Yao, P.; Huang, Y.; Su, Z.; Yu, Y. Distributed Trajectory Optimization for Multiple Solar-powered UAVs Target Tracking in Urban Environment by Adaptive Grasshopper Optimization Algorithm. Aerosp. Sci. Technol. 2017, 70, 497–510. [Google Scholar] [CrossRef]
- Kiam, J.; Schulte, A. Multilateral quality mission planning for solar-powered long-endurance UAV. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- Kiam, J.J.; Schulte, A. Multilateral mission planning in a time-varying vector field with dynamic constraints. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018. [Google Scholar]
- Fonseca, C.; Fleming, P. Genetic Algorithms for multiobjective optimization: Formulation, discussion and generalization. In Proceedings of the Fifth International Conference on Genetic Algorithms, Urbana-Champaign, IL, USA, 17–21 June 1993. [Google Scholar]
- Liu, W.; Li-Gang, L. Mission Planning of Space Astronomical Satellite Based on Improved Genetic Algorithm. Comput. Simul. 2014, 31, 54–58. [Google Scholar]
- Chen, H.; Du, C.; Li, J.; Jing, N.; Wang, L. An approach of satellite periodic continuous observation task scheduling based on evolutionary computation. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO), Berlin, Germany, 15–19 July 2017. [Google Scholar]
- Long, J.; Li, C.; Zhu, L.; Chen, S.; Liu, J. An Efficient Task Autonomous Planning Method for Small Satellites. Information 2018, 9, 181. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Atienza, C.; Ser, J.; Camacho, D. Weighted Strategies to Guide a Multi-objective Evolutionary Algorithm for Multi-UAV Mission Planning. Swarm Evol. Comput. 2019, 44, 480–495. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Long, T.; Wen, Y. Multi-UAV Reconnaissance Task Allocation for Heterogeneous Targets Using an Opposition-based Genetic Algorithm with Double-chromosome Encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Li, X.; Wang, T.; Bai1, S.; Wang, Y. Solving a Multi-objective Mission Planning Problem for UAV Swarms with an Improved NSGA-III Algorithm. Int. J. Comput. Intell. Syst. 2018, 11, 1067–1081. [Google Scholar] [CrossRef] [Green Version]
- Wilhelm, J.; Rojas, J.; Eberhart, G.; Perhinschi, M. Heterogeneous Aerial Platform Adaptive Mission Planning Using Genetic Algorithms. Unmanned Syst. 2017, 5, 19–30. [Google Scholar] [CrossRef]
- Zhang, B.; Tang, L.; Roemer, M. Probabilistic Weather Forecasting Analysis for Unmanned Aerial Vehicle Path Planning. J. Guid. Control Dyn. 2014, 37, 309–312. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Bocewicz, G.; Radzki, G.; Nielsen, P.; Banaszak, Z. UAV Mission Planning Resistant to Weather Uncertainty. Sensors 2020, 20, 515. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Liang, Z.; Zhu, M.; Hu, X.; Wang, G. Integrated Optimization of Unmanned Aerial Vehicle Task Allocation and Path Planning under Steady Wind. PLoS ONE 2018, 13, e0194690. [Google Scholar] [CrossRef] [Green Version]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.; de la Cruz, J. A real world multi-UAV evolutionary planner for minimum time target detection. In Proceedings of the 18th Conference on Genetic and Evolutionary Computation, Denver, CO, USA, 20–24 July 2016. [Google Scholar]
- Perez-Carabaza, S.; Besada-Portas, E.; Lopez-Orozco, J.; Pajares, G. Minimum Time Search in Real-World Scenarios Using Multiple UAVs with Onboard Orientable Cameras. J. Sens. 2019, 2019, 7673859. [Google Scholar] [CrossRef]
- Besada-Portas, E.; de la Torre, L.; de la Cruz, J.; Andres-Toro, B. Evolutionary Trajectory Planner for Multiple UAVs in Realistic Scenarios. IEEE Trans. Robot. 2010, 26, 619–634. [Google Scholar] [CrossRef]
- Yang, P.; Tang, K.; Lozano, J.A.; Cao, X. Path Planning for Single Unmanned Aerial Vehicle by Separately Evolving Waypoints. IEEE Trans. Robot. 2015, 31, 1130–1146. [Google Scholar] [CrossRef] [Green Version]
- Fdez-Olivares, J.; Castillo, L.; Garcıa-Pérez, O.; Palao, F. Bringing users and planning technology together. Experiences in SIADEX. In Proceedings of the 2006 International Conference on Autonomous Planning and Scheduling (ICAPS), Cumbria, UK, 6–10 June 2006. [Google Scholar]
- Dvorak, F.; Bit-Monnot, A.; Ingrand, F.; Ghallab, M. A flexible ANML actor and planner in robotics. In Proceedings of the 2nd ICAPS Workshop on Planning and Robotics (ICAPS-PlanRob), Portsmouth, NH, USA, 22 June 2014. [Google Scholar]
- Hehtke, V.; Kiam, J.; Schulte, A. An Autonomous Mission Management System to Assist Decision Making of a HALE Operator; Deutscher Luft- und Raumfahrtkongress: Munich, Germany, 2017. [Google Scholar]
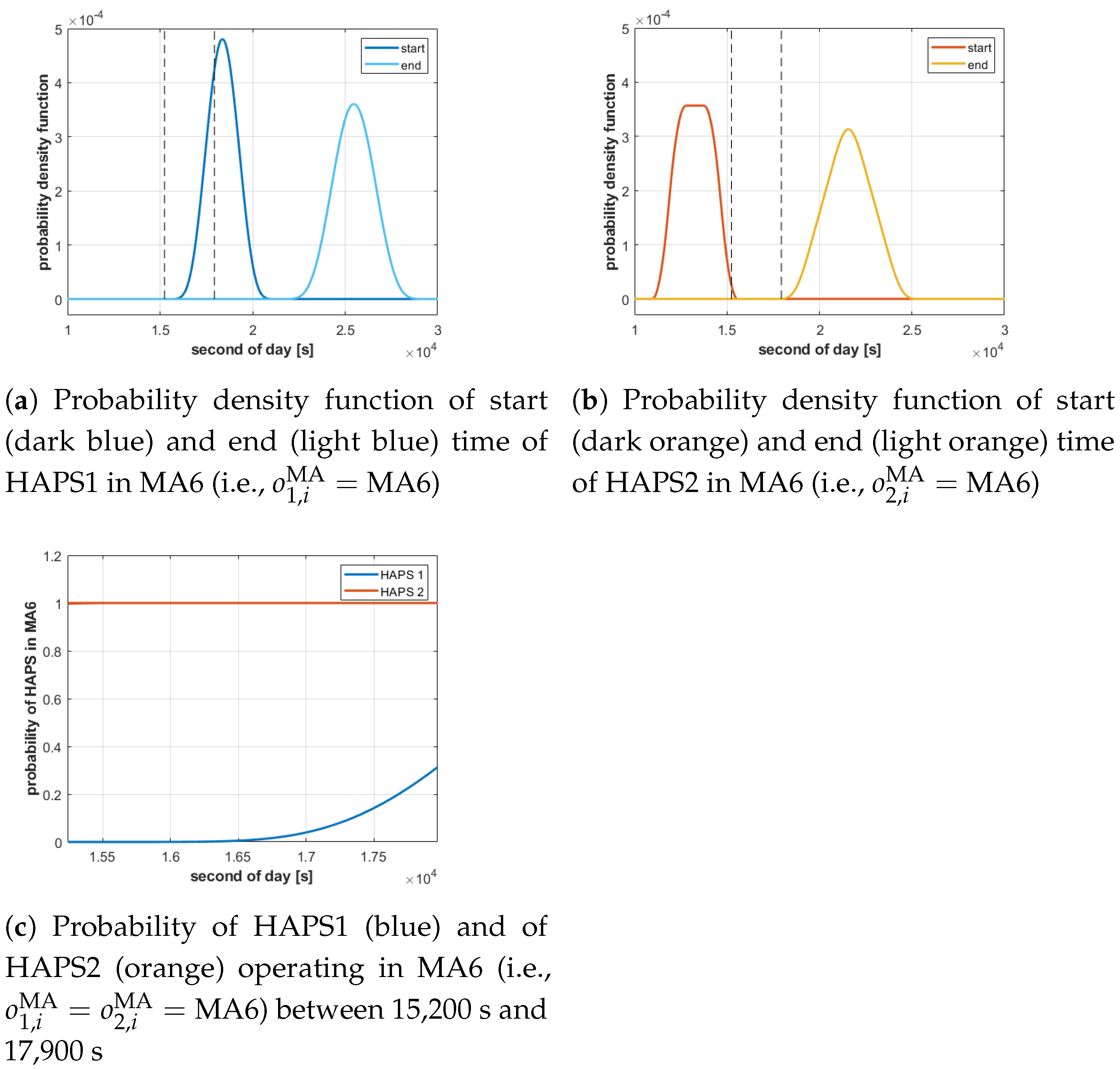
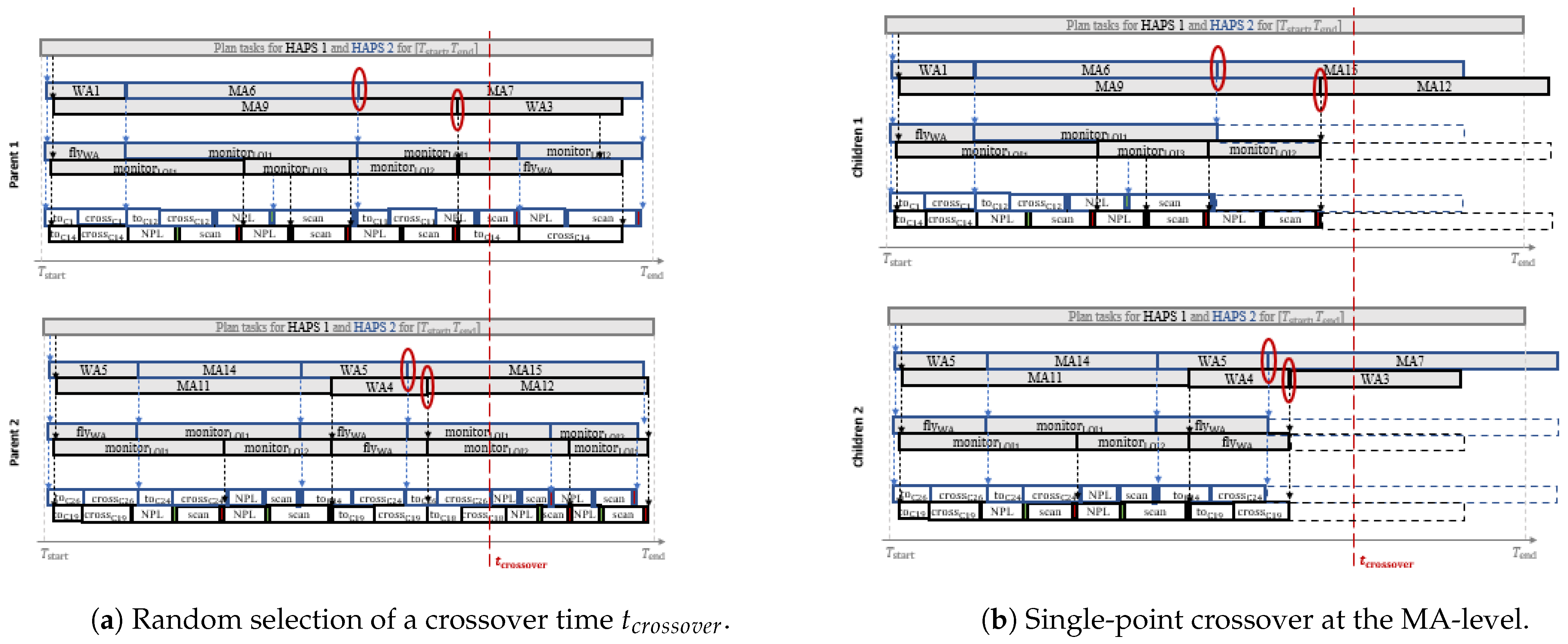
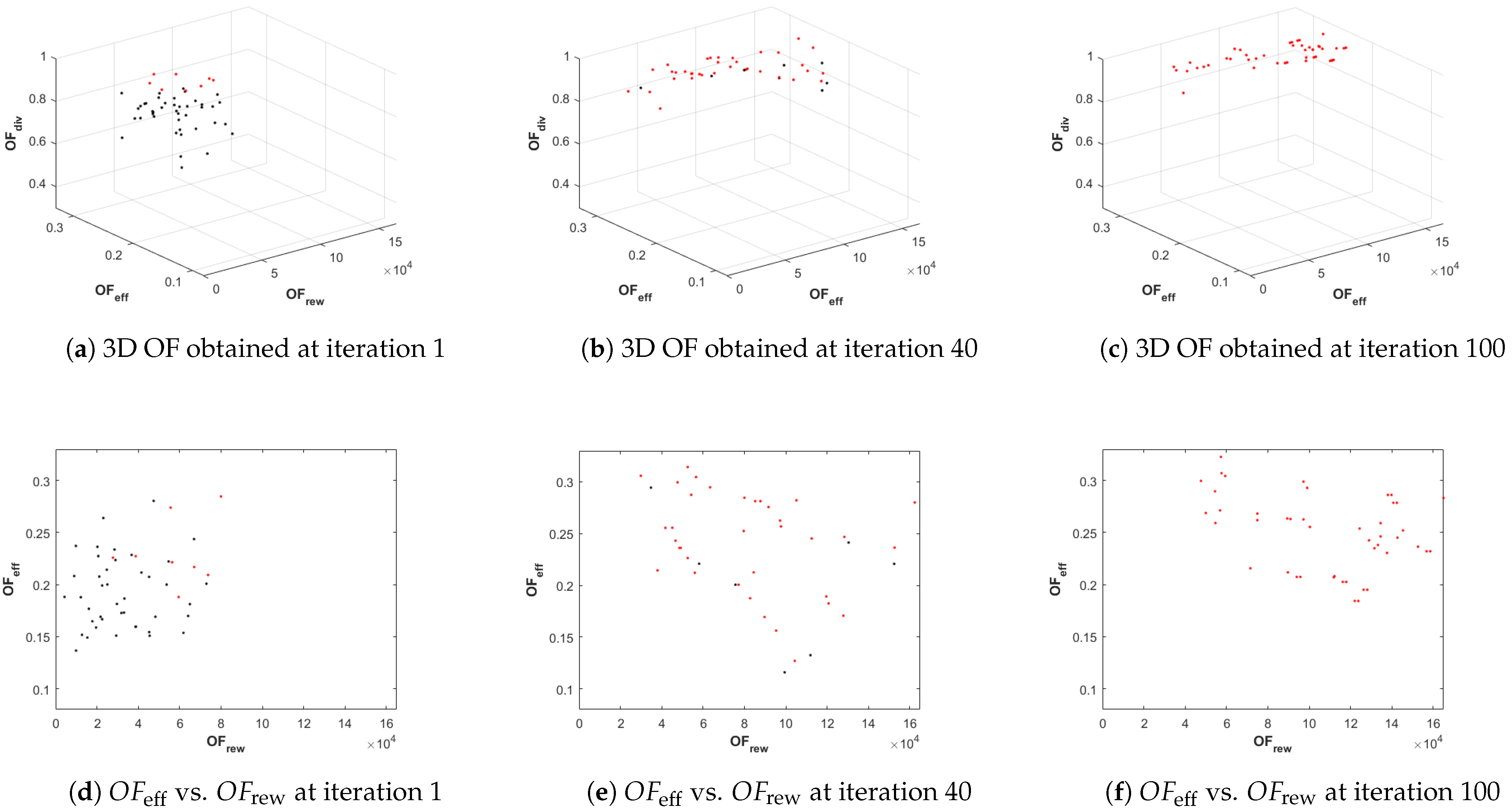

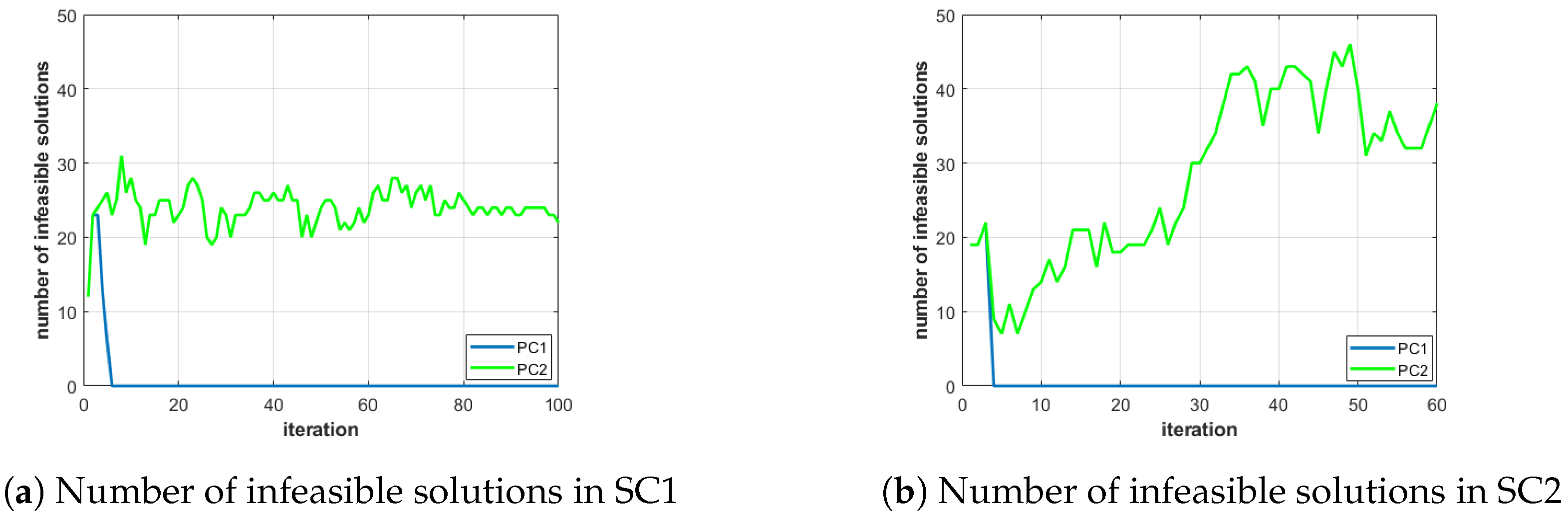

| Properties | Benefits and Challenges during Operation |
|---|---|
| Light-weight material | (+) Energy efficient (−) Fragile and vulnerable to adverse weather |
| Limited payload | (+) Energy efficient (−) Limited onboard computation power |
| Fixed-wing, large wingspan | (+) More surface for harvesting solar power (−) Limited maneuverability with respect to turn rate and mid-air still-stop |
| High flight altitude | (+) Calmer weather (−) Takeoff and landing are time consuming |
| Extreme long endurance | (+) Suitable for longer missions (+) No frequent takeoff and landing necessary (−) High operating cost |
| Low-power electro-motor, low airspeed | (+) Energy efficient (−) Wind effect cannot be neglected |
| Scenarios | Weather Data | Number of HAPSs |
|---|---|---|
| SC1 (Nominal scenario) | Historical (April 2018) | 2 |
| SC2 (Challenging weather scenario) | With synthetically increased wind magnitude | 2 |
| SC3 (Three HAPSs scenario) | Historical (April 2018) | 3 |
| Planner Parameters | Parameter Values |
|---|---|
| Crossover probability, | 0.9 |
| Mutation probability, | 0.1 |
| Population size, | 50 |
| Tournament size, | 3 |
| Number of generations, | 100 (in SC1 and SC3), 60 (in SC2) |
| Constraint Thresholds | Threshold Values |
| 0.1 | |
| 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiam, J.J.; Besada-Portas, E.; Schulte, A. Hierarchical Mission Planning with a GA-Optimizer for Unmanned High Altitude Pseudo-Satellites. Sensors 2021, 21, 1630. https://doi.org/10.3390/s21051630
Kiam JJ, Besada-Portas E, Schulte A. Hierarchical Mission Planning with a GA-Optimizer for Unmanned High Altitude Pseudo-Satellites. Sensors. 2021; 21(5):1630. https://doi.org/10.3390/s21051630
Chicago/Turabian StyleKiam, Jane Jean, Eva Besada-Portas, and Axel Schulte. 2021. "Hierarchical Mission Planning with a GA-Optimizer for Unmanned High Altitude Pseudo-Satellites" Sensors 21, no. 5: 1630. https://doi.org/10.3390/s21051630
APA StyleKiam, J. J., Besada-Portas, E., & Schulte, A. (2021). Hierarchical Mission Planning with a GA-Optimizer for Unmanned High Altitude Pseudo-Satellites. Sensors, 21(5), 1630. https://doi.org/10.3390/s21051630







