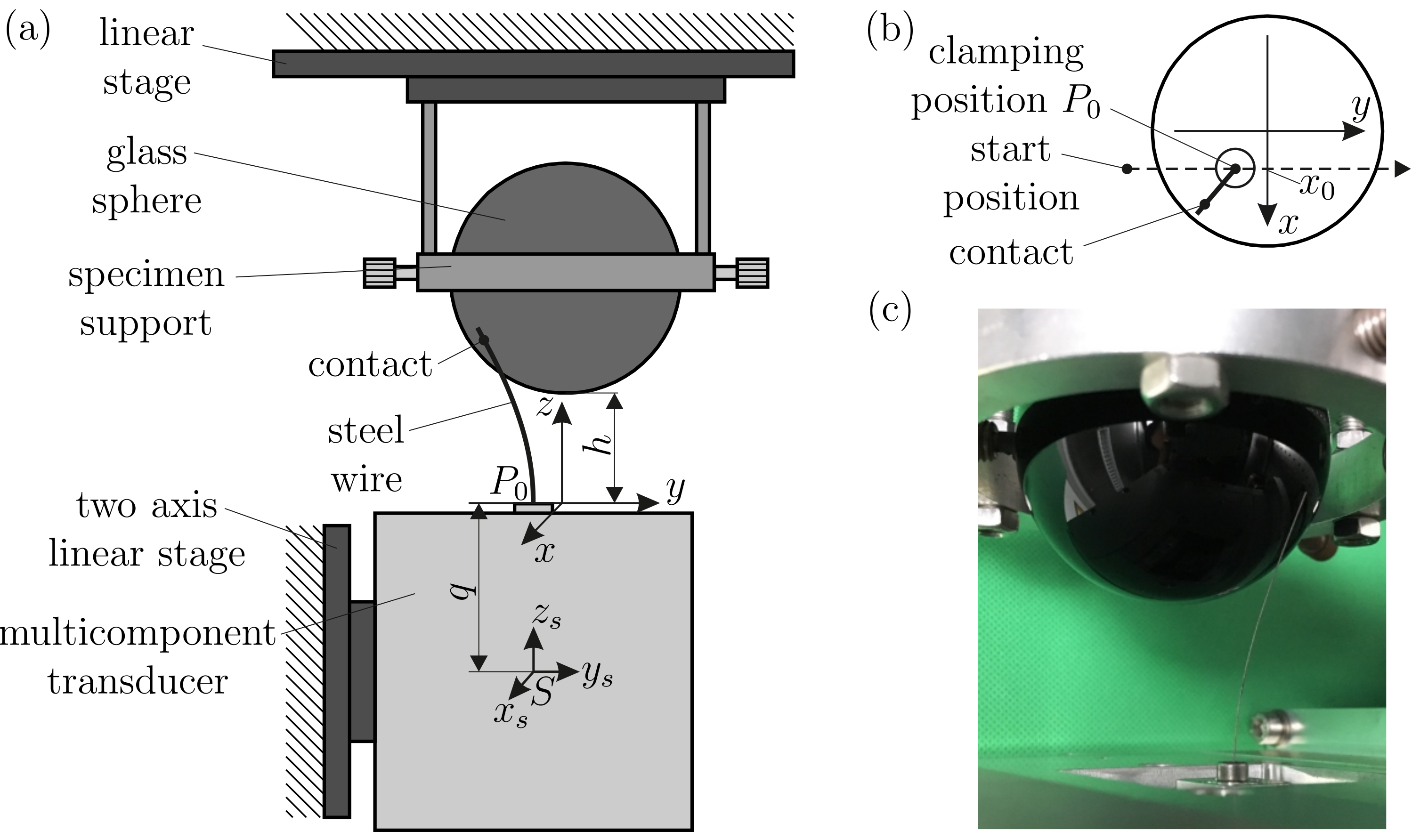
3.1. Measured Signals during Object Scanning
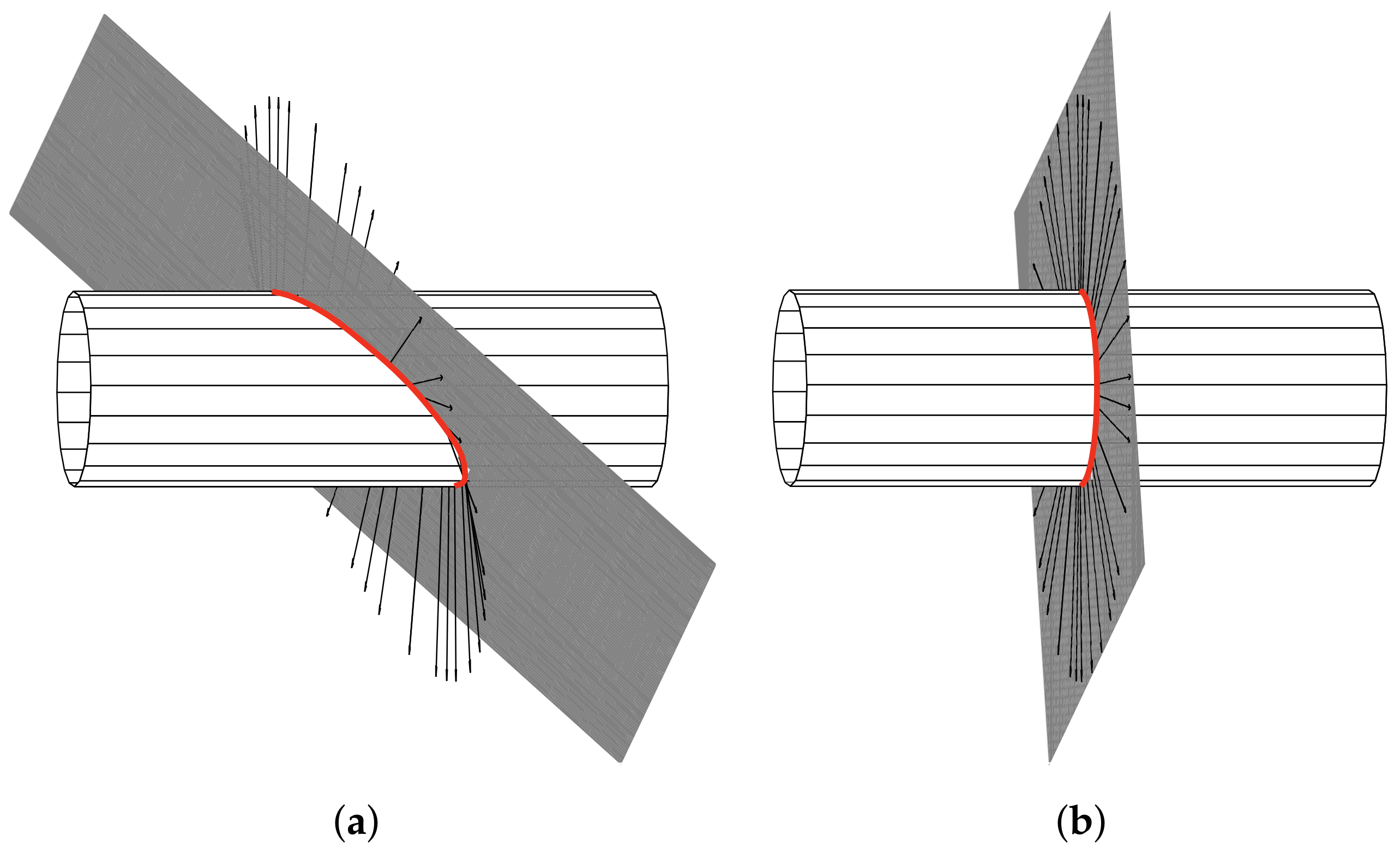
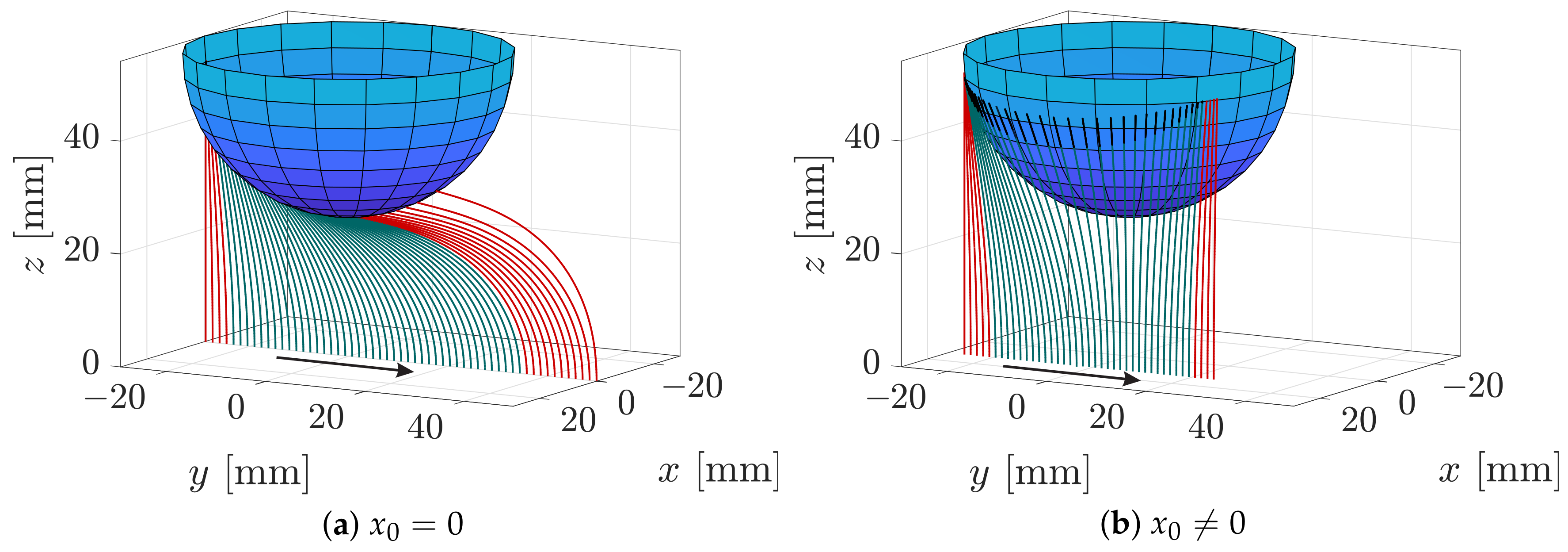
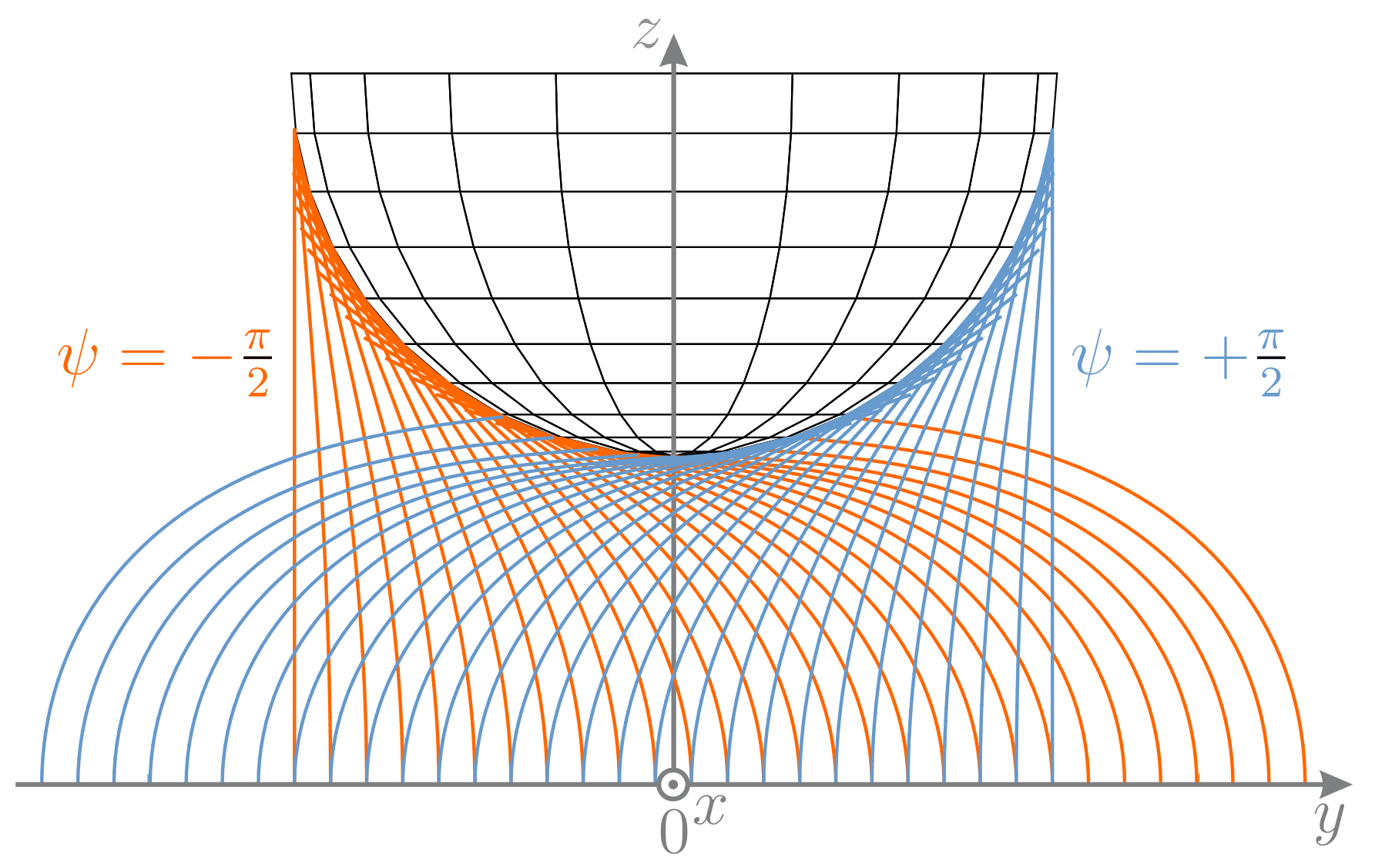
From a theoretical point of view, there are two distinct ways in which the rod can slide along the sphere, depending on the scanning trail The scanning trail defines the scanning plane, which is the plane defined by the base point
as well as the trail and clamping directions. If
, the trail runs exactly below the center of the sphere. For this particular case, the normal vectors of the sphere at each point on the intersection curve between the scanning plane and the sphere lie within the scanning plane, compare
Figure 3b. Thus, scanning the sphere on a trail with
is a special case, where the entire scanning sweep takes place in a plane and, thus, no lateral but only longitudinal slip occurs [
22]. Such a scanning sweep, ending with a terminating snap-off of the wire from the sphere is shown in
Figure 7a. However, another characteristic way that the rod sweeps along the sphere, which is more likely to occur results when the scanning trail is laterally shifted from the coordinate origin
. Then, the normal vectors of the sphere at each point on the intersection curve between the scanning plane and the sphere do
not lie within the scanning plane—compare to
Figure 3a. Such a sweep includes lateral slip in a way that the rod symmetrically bends around the sphere and finally smoothly detaches from the object without any snap-off, see
Figure 7b. In
Figure 7 tip contacts are colored in red, tangential contacts in green and the straight end of the rod (
) in black. Both sweeps start with a sequence of tip contacts, continued with a tangential contact phase and finally end with another sequence of tip contacts. For scanning sweeps with a larger object distance, only tip contacts occur (not shown).
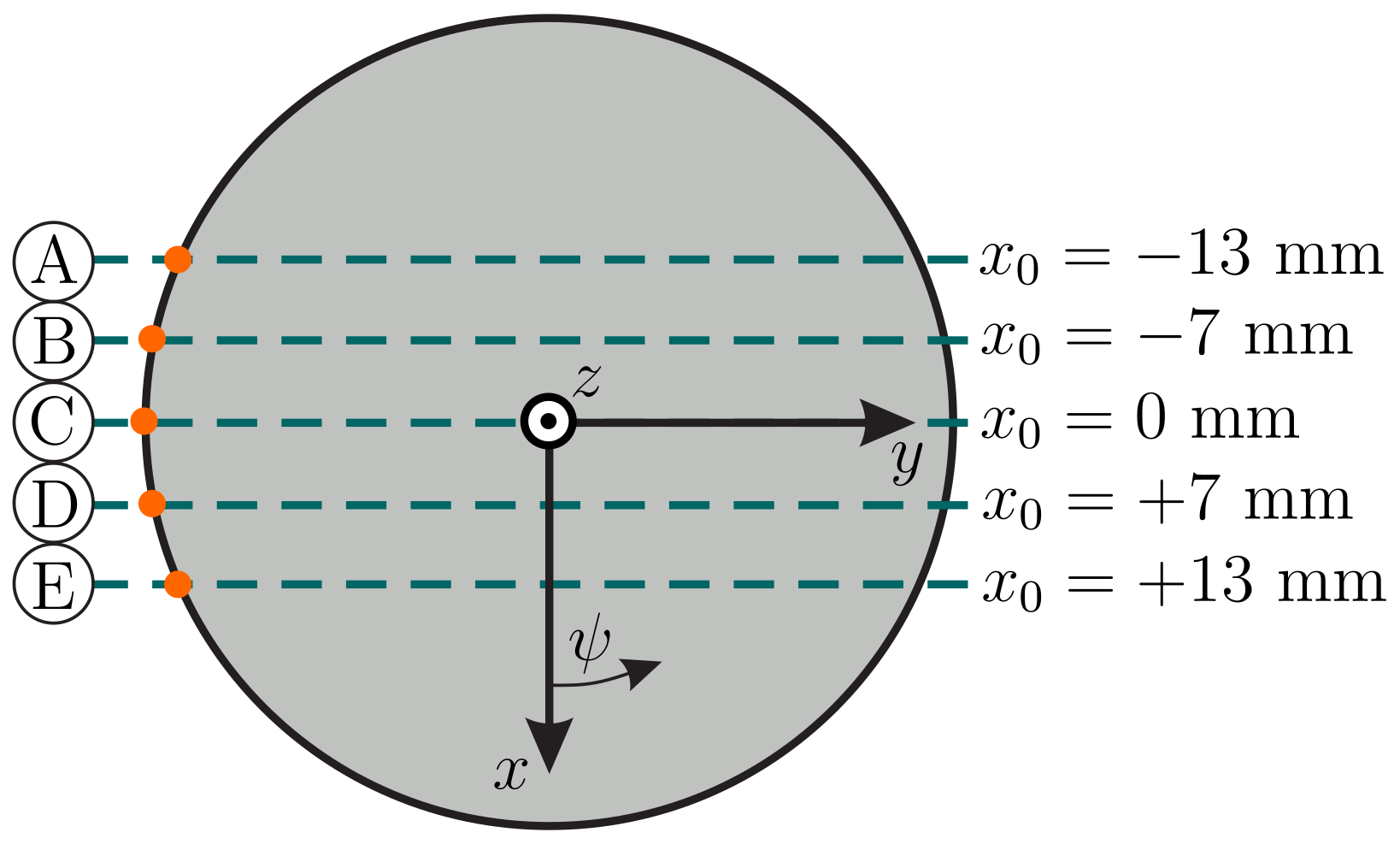
Figure 8 is a schematic representation of five exemplary scanning trails (dashed lines) A–E. It is intended to assist in interpreting the results in
Figure 9. The orange dots indicate the position of the first contact between the tip of the undeformed rod and the sphere. Sweep C (
mm) corresponds to
Figure 7a and sweep E (
mm) to
Figure 7b.
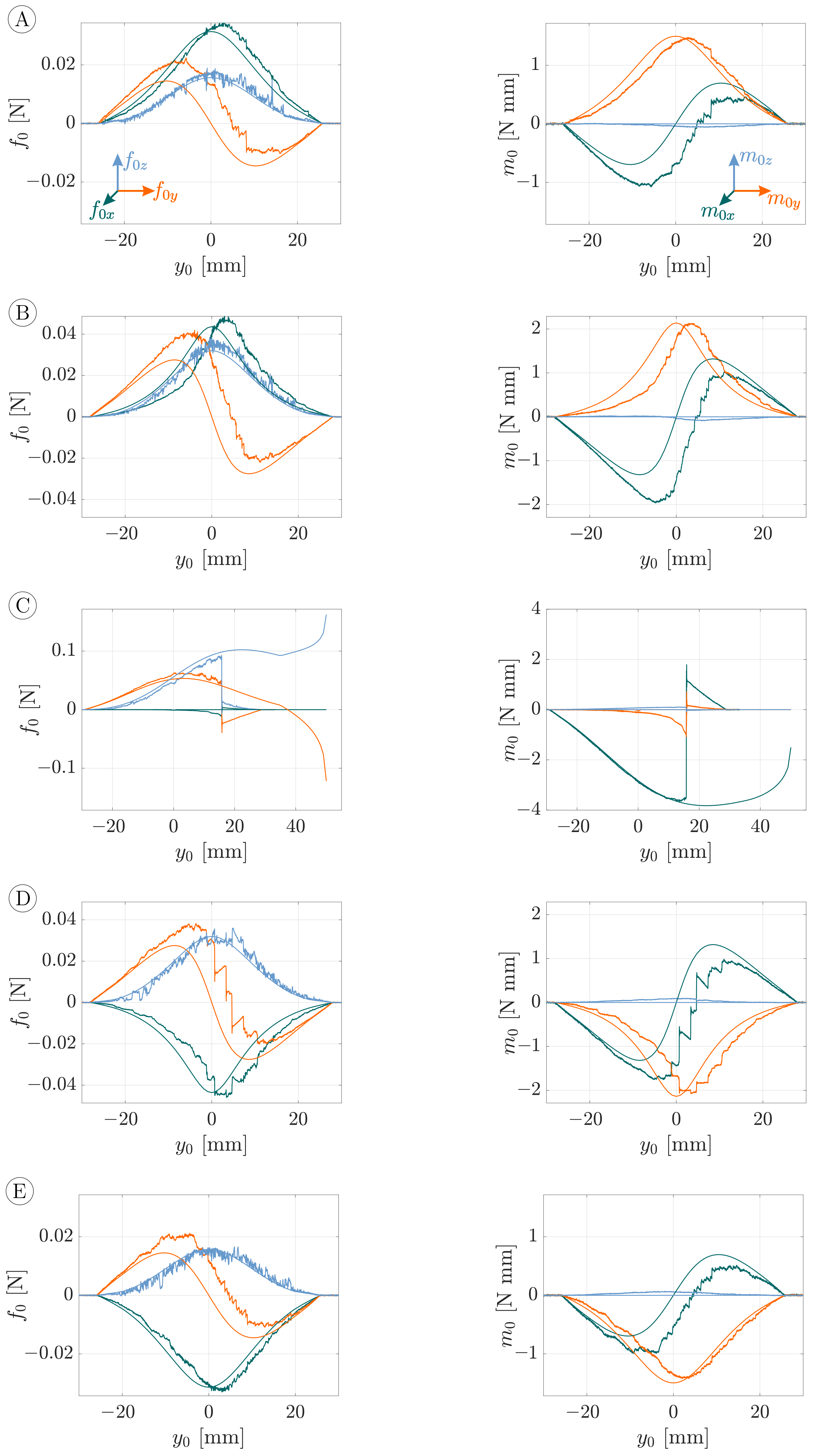
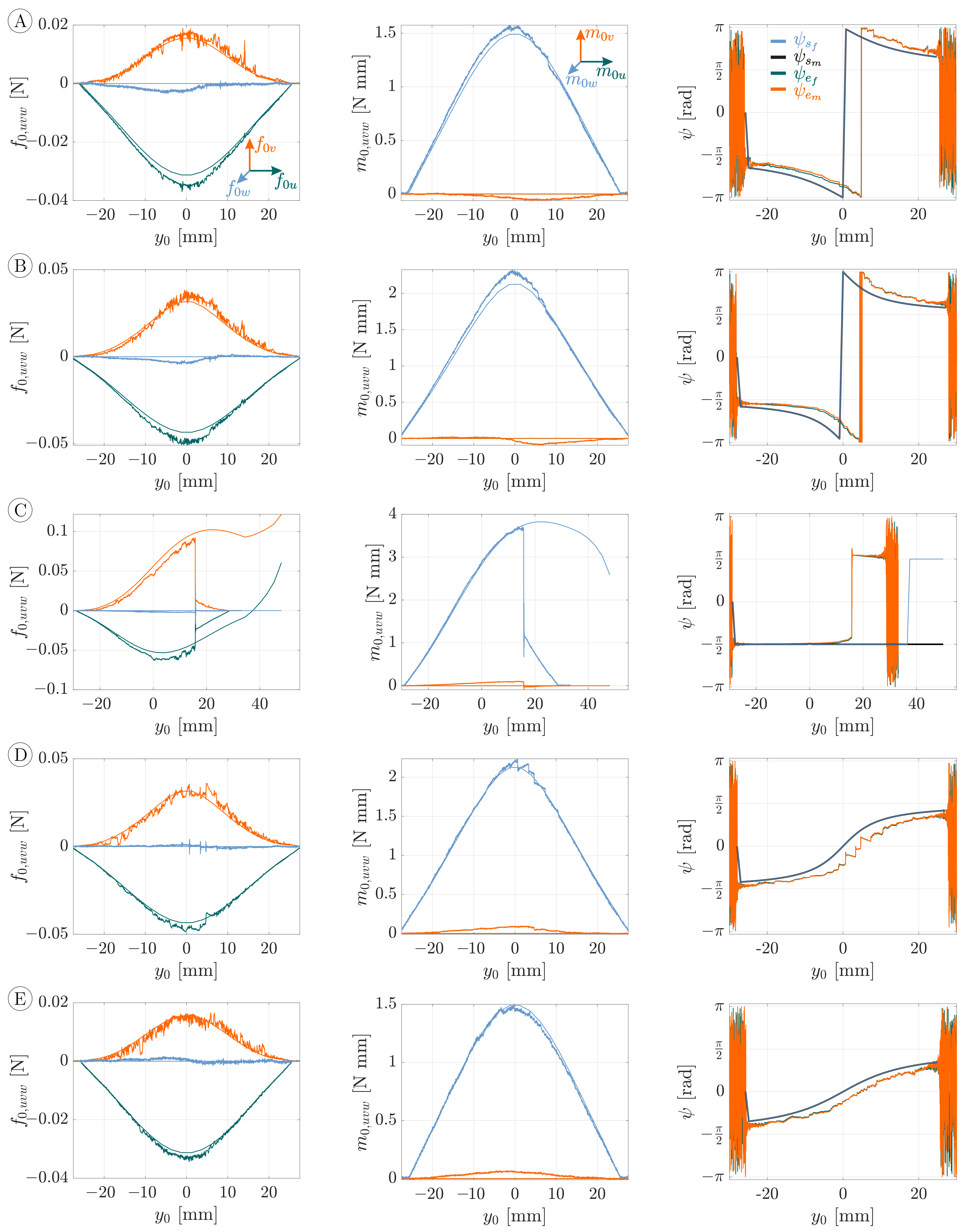
A comparison between the simulated and experimental support reactions (observables) during object scanning with an object distance of
25 mm is shown in
Figure 9 (
-coordinate system). The rows A–E correspond to the scanning trails A–E in
Figure 8. Appearing as smooth curves, the simulated data in
Figure 9 can be clearly distinguished from the noisy measured signals.
Figure 9 contains the reaction forces
(green),
(orange) and
(blue) on the left as well as the reaction moments
(green),
(orange) and
(blue) on the right. Let us firstly discuss these results from a theoretical point of view and, thus, focus on the simulated data (smooth curves). For all scanning sweeps, except the special case C (see
Figure 7a), the support reactions are vertical or point symmetric, as a consequence of the symmetric bending of the rod around the sphere, see
Figure 7b. It is obvious that the maximum values of all support reactions increase with decreasing
, i.e., the closer the scanning trail is to the coordinate origin. Negative values
(trail A and B) lead to positive reaction forces
while positive values
(trail D and E) cause negative forces
. The component
always changes in sign from plus to minus, due to the scanning direction. The reaction force
must accept positive values to counteract the contact force. Due to the symmetry of those scanning trails with the same
, i.e., A and E as well as B and D (see
Figure 8), the components
and
of the corresponding sweeps are identical while
is mirrored with respect to the
-axis. The components
and
of the clamping moment are positive for negative values
(trail A and B) and vice versa (trail D and E). Again, this leads to a symmetry in the reaction moments of the sweeps A and E and B and D, respectively. According to Equation (
21) the reaction moment
must always be zero in the absence of friction (in theory).
Considering the measured data, there is a good qualitative overall accordance with the simulated data. While the maximum values of the support reactions , , and match well with the simulated data, the maximum values of the components and differ slightly from the simulation. In addition, it is striking that, compared to the simulated data, all measured support reactions, except the reaction force , are distorted in the -direction. Both the deviation of the maximum values and the distortion of the signals are probably caused by frictional effects during the experiment. Another observation, which is likely to be friction-related, is the deviation of the measured component from the theoretically expected value of zero. This is due to the fact that the wire has some radial dimension and, thus, the frictional force induced a twisting moment during lateral slip. In addition, the experiments were influenced by stick-slip effects, which lead to saw-tooth patterns in the support reactions, in particular during scanning sweep D. It was empirically observed that stick-slip effects particularly occurred during lateral slip. Moreover, stick-slip effects were reinforced the closer the trail was to the coordinate origin, . For longitudinal slip during scanning sweep C, however, stick-slip effects were barely noticeable with the naked eye. It is interesting that the support reactions of the symmetric scanning sweeps B and D differ in a way that scanning sweep D seems to be more affected by stick-slip effects. This indicates that minor external factors, such as soiling or the microscopic surface structure of the wire or the glass sphere strongly affect the stick-slip behavior.
One scanning sweep, particularly standing out of
Figure 9 and requiring closer consideration, is the special scanning sweep C. At the beginning of this sweep, the measured support reactions coincide well with the simulated data. However, at some point
mm, all support reactions jump from a high to a lower level. This discontinuity of the experimental data was caused by a lateral jump of the rod from one side to the opposite side of the sphere. In order to understand this behavior, Equations (
14) and (
16) are adapted for the special case of a spherical object:
Both arguments of Equation (
28) have the same sign, if
and differ in sign if
. Depending on
, the term
can accept positive or negative values. Therefore, according to the definition of
atan2, there are two solutions
and
for each clamping position except for
, where the second argument of Equation (
28) is not defined. This indicates that, except for
, there might be two possible equilibrium states of the rod. For the entire scanning sweep C
the second argument of Equation (
28) is zero, resulting in two possible orientation angles
and
of
, according to the definition of
atan2. Due to the principle of minimum energy, it can be expected that the lower potential energy state has a preferential appearance in reality. However, the simulation algorithm proceeds by using the parameters of the previous deformation state as initial values for determining the subsequent deformation state. Therefore, the numerical algorithm always finds that solution, which is the most similar to the previous one and not necessarily that one that minimizes the potential energy. For that reason, the orientation
does not change during simulation. It can be expected, that, in an ideal world without any disturbance, sweep would occur without a jump, just as observed in the simulation. In practice, however,
has never the exact value of zero due to minimal deviations. These deviations, however minor, might cause the rod to snap from one to the opposite side of the sphere, jumping from a higher to a lower energy state. In
Figure 10, an ideal scanning sweep C (orange:
) is outlined and overlaid with the alternative solutions (blue:
).
Since the arrangement of deformation states is symmetric, the blue configurations might also be interpreted as an ideal backward sweep in negative direction of
y. It can be seen that for most clamping positions, except for those exceeding the area below the sphere, there are two configurations (orange and blue) as already observed analyzing Equation (
28). However, from a physical point of view, it is impossible that, e.g., scanning sweep C starts with a blue configuration due to the scanning direction from left to right. This raises the question, at which point of a real-world scanning sweep, the rod might snap from an orange to a blue configuration. Therefore, the elastic deformation energy
of each deformation state of the rod was calculated. For the scanning sweep in positive
y-direction, the blue configuration is in a higher energy state than the corresponding orange configuration until the clamping reaches the position
. At
, the second argument of Equation (
28) is not defined. Practically, there is an infinite number of possible deformation planes
with
due to the rotational symmetry of the object. For this particular case, all possible deformation states have the same states of energy and are, therefore, indifferent equilibria. As
further increases, the blue configurations are in a lower energy state than the orange ones. Therefore, the rod tends to snap to the opposite side of the sphere when
crosses zero. However, as can be seen in the support reactions of scanning sweep C, the jump occurs long after
was crossing zero. This is presumably due to the fact that friction has a stabilizing effect in a way that the frictional forces counteract with lateral slip of the rod.
Figure 11 shows the support reactions from
Figure 9, which were transformed to the
-coordinate system in the following way:
In doing so, the angle
was calculated using the support reactions
and
exploiting Equation (
23). The reaction forces
(green),
(orange) and
(blue) during the scanning sweeps A–E are shown on the left side, the reaction moments
(green),
(orange) and
(blue) in the middle and the orientation angle
of the deformation plane
on the right side of
Figure 11. Theoretically, the components
,
and
are zero due to the plane bending assumption. The experimental data of these components show only a slight deviation from the theoretical values.
The overall accordance of the remaining simulation and experimental data (
,
and
), which is related to the plane bending problem, is even better than in
Figure 9. On the one hand, this is apparent from the maximum values of the support reactions. On the other hand, the distortion in the
-direction of the support reactions in
Figure 9 is less pronounced in
Figure 11. The support reactions are approximately symmetrical with respect to a vertical axis at
. The components
and
are always positive while
is always negative. Again, scanning sweep C stands out of
Figure 11 due to the jump of the wire from one to the opposite side of the sphere, which was discussed above. In contrast to
Figure 9, the support reactions of sweeps A and E, as well as B and D, are approximately the same. This observation indicates that measuring only components
,
and
with respect to the deformation plane would not be sufficient to uniquely identify the corresponding scanning sweep. Instead, the angular information on the right side of
Figure 11 must be taken into account in order to distinguish sweeps A and E and B and D, based on the support reactions for reliable reconstructions in
Section 3.2.
The orientation angle
in
Figure 11 is determined from the measured and simulated support reactions using Equation (
23). In doing so, both the reaction forces
and
as well as the reaction moments
and
are evaluated. The green curves (based on the measured forces) are almost perfectly aligned (obscured) with the orange curves (based on the measured moments). At the beginning and the end, both curves are characterized by strong noise due to the noise of the support reactions before and after contact, which reappear in
. Glancing at angle
during scanning sweep C, it can be seen that, as the wire jumps from one to the opposite side of the sphere, the angle
jumps from
to
—compare to
Figure 10. For the sweeps A, B, D and E, the blue curves, which are based on the reaction forces resulting from simulations, are identical with the black curves, resulting from evaluating the simulated reaction moments. For scanning sweep C, the blue curve deviates from the black curve in a way that it jumps from
to
while the black curve remains at
. Although this jump seems to resemble the experimental result, it occurs for a different reason: the simulated scanning sweep does not include any jump of the rod—see
Figure 7a. Instead, the jump in
occurs as a result of a change in sign of
as the contact point crosses the lowest point (south pole) of the sphere. For scanning sweep C, this results in an error when determining
based on the reaction forces (blue curve). In contrast, using the reaction moments (black curve), the change in the sign of
does not inhibit a correct determination of
. Even though exploiting the forces and moments might lead to different results for
, the experimental data (orange and green curves) coincides well. This is due to the fact that the rod snaps around the sphere before the contact point crosses its south pole (before a change in the sign of
). However, a change in the sign of
occurred in experimental scanning sweeps along 2D object contours (no lateral curvature). Therefore, in general, the evaluation of the clamping moment is more reliable to determine the orientation angle
. Finally, it can be seen that, for each scanning sweep, the angle based on the measured data lags behind that based on the simulation. This offset presumably results from frictional effects, which are already apparent in the support reactions in
Figure 9. The lag in the experimental data of
seems to have a corrective effect when transforming the support reactions from the (
) to the (
)-coordinate system using Equation (
29)—compare
Figure 9 and
Figure 11.
3.2. Object Shape Reconstruction
Obviously,
Figure 9 and
Figure 11 do not directly provide any information regarding the scanned object. Therefore, the simulation and experimental quantities are used for object shape reconstruction, as described in
Section 2.1. Within the present paper, we use the data in the (
)-coordinate system from
Figure 9, as provided by the used sensor.
Remark 5. In general, the data from Figure 11 is equally suitable for object reconstruction and might be chosen as observable but only if the orientation angle ψ defining the ()-coordinate system is measured as well. Thus, only four observables, namely , , and ψ, are sufficient for object reconstruction. Initially, we evaluated only those 27 scanning sweeps with smallest object distance
mm. The experiments showed that, for this object distance, the size of the scanned part of the object was the largest and the support reactions had the best signal to noise ratio. In this way, we aimed to investigate, whether a single object distance is sufficient for object reconstruction. In the first row of
Figure 12, the reconstructed sequences of contact points based on 27 simulated scanning sweeps with an object distance of
mm are outlined, where
Figure 12a is an isometric and
Figure 12b is a top view.
Each reconstructed sequence of contact points resulting from a single simulated sweep is connected with a line. The colors of the points are arbitrarily chosen and are solely aimed for an easy distinction between adjacent contact point sequences. As the theoretical results indicate, object scanning using a single object distance is sufficient to provide a variety of contact points, approximating the shape of the sphere. However, there is a large gap in the reconstructed area. It is crossed by the reconstructed sequence of contact points resulting from the special scanning sweep C (
). The theoretical reconstruction errors of all points are negligible (within the numerical boundaries). The symmetry of the support reactions (see
Figure 9) reappears in the reconstructed sequences of contact points, which are axially symmetric with respect to the
x-axis (except that resulting from scanning sweep C ending with a snap-off). In addition, those contact sequences resulting from scanning sweeps with the same distance
from the coordinate origin are symmetrical in pairs, with respect to the
y-axis. Having in mind that the step-size
for the displacement of the clamping position
is constant for all simulations, it is important to note that the reconstructed points are not equidistantly distributed. Instead, the distances between the points increase in the middle of each sequence—see, e.g.,
Figure 12a (blue). This effect is reinforced the closer the scanning trail is to the coordinate origin, i.e., the smaller
. In particular, this is evident in the innermost sequences, which narrows the reconstruction gap. Even though the presented mechanical model is a quasi-static one, this fact may be a hint at the contact point velocity during scanning. It can be expected that the ratio between the displacement of the contact point and the displacement of the clamping position might be the same as that between the contact point velocity and the clamping velocity. Thus, greater distances between the reconstructed points might be interpreted as higher contact point velocities. This is consistent with our observations during the experiments: the contact point starts moving slowly and gets increasingly fast in the middle of the scanning sweep until it finally slows down again.
Figure 12c,d show the reconstructed points based on the measured data of 27 scanning sweeps (
mm) superimposed with the original object surface. The color of each point denotes the reconstruction error in mm, which is defined as the closest distance between the point and the object surface. The error is directly evident from the color bar in
Figure 12d. It can be seen that the maximum reconstruction error after expunging the outliers is 1.58 mm or approximately 3.2% of the wire length. A positive sign of the reconstruction error indicates that a contact point is outside and a negative sign that it is inside of the original object. Having the scanning direction in mind (positive
y-direction), it is obvious that positive errors occur, especially at the beginning and the end of the scanning sweep, when the deformation of the wire is small. These errors are not surprising, since small wire deformation results in a bad signal to noise ratio. Negative errors increasingly occur as the wire bends in the
x-direction. In
Figure 12d the outer reconstructed sequences seem fairly axial symmetric with respect to the
x-axis. In addition, the pairwise arrangement of sweeps with the same lateral displacement
are symmetrical to some extent. However, it is striking that the reconstruction error seems asymmetric in the sense that negative errors are greater for
.
Figure 9 has already shown that the support reactions resulting from scanning sweeps with
(sweep D and E) were more affected by stick-slip effects, which probably cause the asymmetry of the reconstruction error. The jump of the rod from one side to the opposite side of the sphere during scanning sweep C is apparent, looking at the innermost sequence of reconstructed contact points, which start at
. At the beginning of the scanning sweep, all contact points approximately lie in the x-z-plane, which indicates that only longitudinal slip occurred. Subsequently, the contact point begins to move slightly laterally in a
x-direction. Finally, the sequence of contact points breaks off due to the jump of the rod to the opposite side of the sphere. It is interesting that this behavior is not only apparent for the innermost scanning sweep but also for some sweeps with a small lateral displacement
. This could be related to the large distances between the reconstructed points when simulating scanning sweeps with a small lateral displacement
.
Perhaps surprisingly, the distortion in the
-direction between the simulated and measured data in
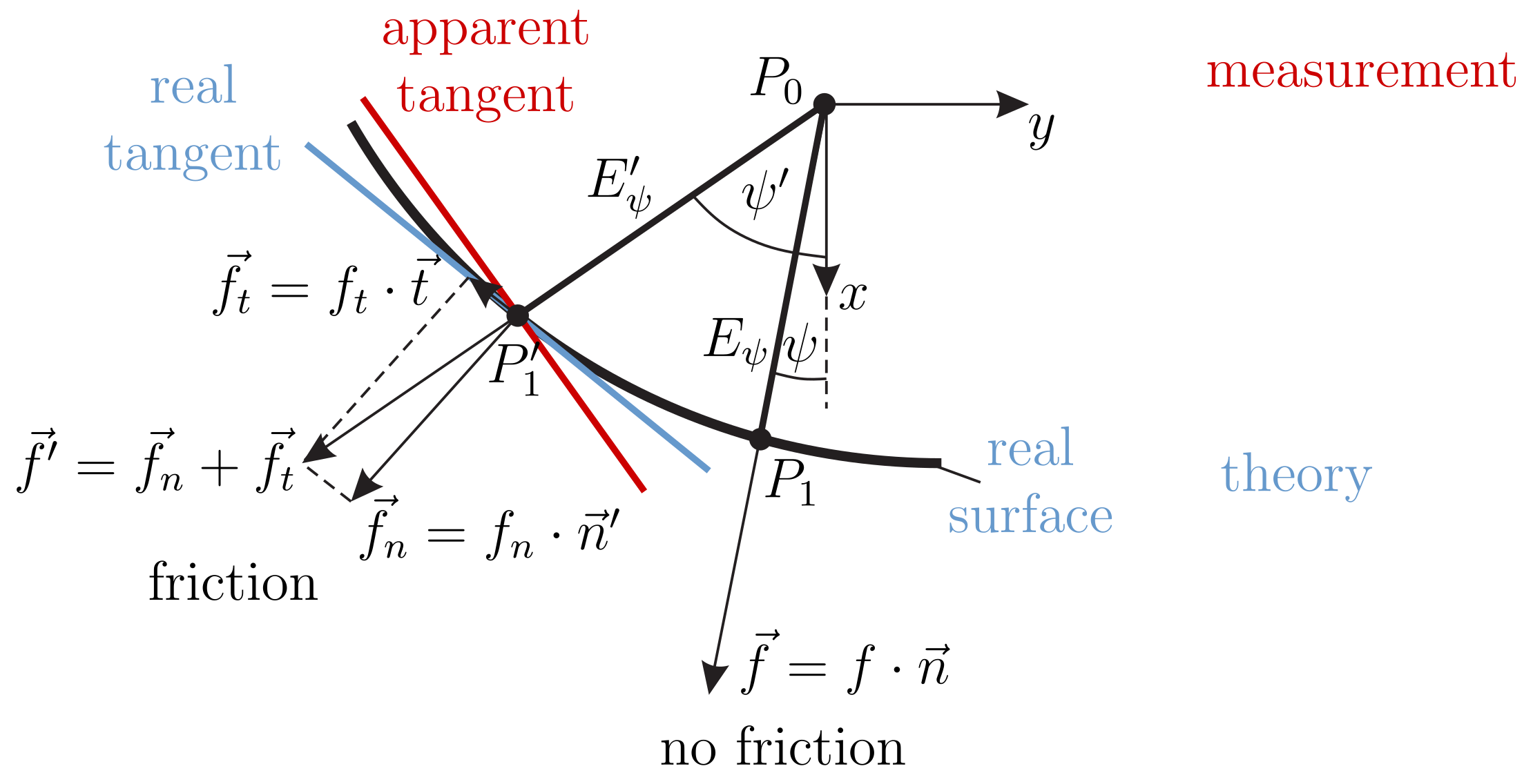
Figure 9, which is presumably friction-induced, does not appear to affect the outcome of the object reconstruction. As the color bar shows, there is no significant distortion between the reconstructed points and the original object. In order to understand this result, the effect of friction during object scanning is analyzed in more detail. One key assumption of the mechanical model is that the scanning sweep takes place in the absence of friction. Therefore, in theory, the contact force is always orientated in direction of the outward-pointing normal vector of the object surface—see
Figure 13.
However, in a real-world scanning sweep, friction causes an additional tangential force component opposed to the direction of contact point movement. Therefore, the resulting contact force vector no longer coincides with the surface normal. For a given clamping position
, this leads to a different deformation plane
(and consequently to another contact point
), than that, which would have been achieved in the absence of friction. This explains the deviations between the simulated and experimental data in
Figure 9 as well as the distortions of the orientation angle
in
Figure 11. If the measured support reactions are used for contact point localization, the resulting contact force
can be determined, but not decomposed into its normal and tangential components
and
. Therefore, the normal vector
of the surface remains unknown. However, as the single force assumption is not violated, the rod still bends in a plane. Using Equation (
23) exploiting the measured, friction effected support reactions, the orientation
of the friction-affected deformation plane can be determined. Thus, even in the presence of friction, the object reconstruction problem reduces to the plane once, discussed in
Section 2.1. It is important to understand that, even though a point
which is reconstructed in the presence of friction (experiment) is different from the point
, which would have been reconstructed in the absence of friction (simulation), both points
and
lie on the original object surface.
This observation indicates that the object reconstruction is less sensitive to frictional effects than perhaps expected, which highlights an important characteristic of the measuring principle. However, stick-slip effects might cause reconstruction errors due to the fact that they induce dynamical effects.
In
Figure 12e,f the reconstruction algorithm presented in [
27] was applied to the data in
Figure 12c,d. Using implicit B-splines, the algorithm fits a surface to a 3D cloud of points accompanied by normal vectors. In general, the involvement of the surface normals improves the reconstruction result as they contain additional information about the local surface orientation. However, as discussed above, the reconstructed force vector no longer coincides with the normal vector of the surface in the presence of friction. Therefore, considering the reconstructed contact force vector as a normal vector is only a rough approximation and only appropriate in the case of little friction. This raises the question of how friction might be estimated during object scanning, which is discussed in
Section 4. In
Figure 12e,f the point clouds are overlaid with the reconstructed tactile image of the scanned object (gridded surface). It is obvious that the algorithm interpolates between and extrapolates beyond the reconstructed points. In our experiment, 27 scanning sweeps with a single object distance are sufficient to reconstruct a significant part of the object. Visually comparing the tactile image from
Figure 12e with the original object surface in
Figure 12c, it can be seen that, despite frictional effects during the experiment, the evaluation of the force vectors for generating the tactile image does not result in significant reconstruction errors.
Even though a large part of the object is reconstructed in
Figure 12f there remains a reconstruction gap. Evaluating all 135 scanning sweeps with different object distances, this reconstruction gap can be filled to a large extent as shown in
Figure 14. Even though there still remains an area with a lack of information due to the limited reachability of the rod, the extent of the reconstruction is probably sufficient for many cases of application. Otherwise, the reachability of the rod might be improved by either changing the scanning direction or changing from a sweeping to a tapping scanning strategy. Returning to the biological paragon, this reflects the behavior that can be observed in rats during environmental exploration [
29].