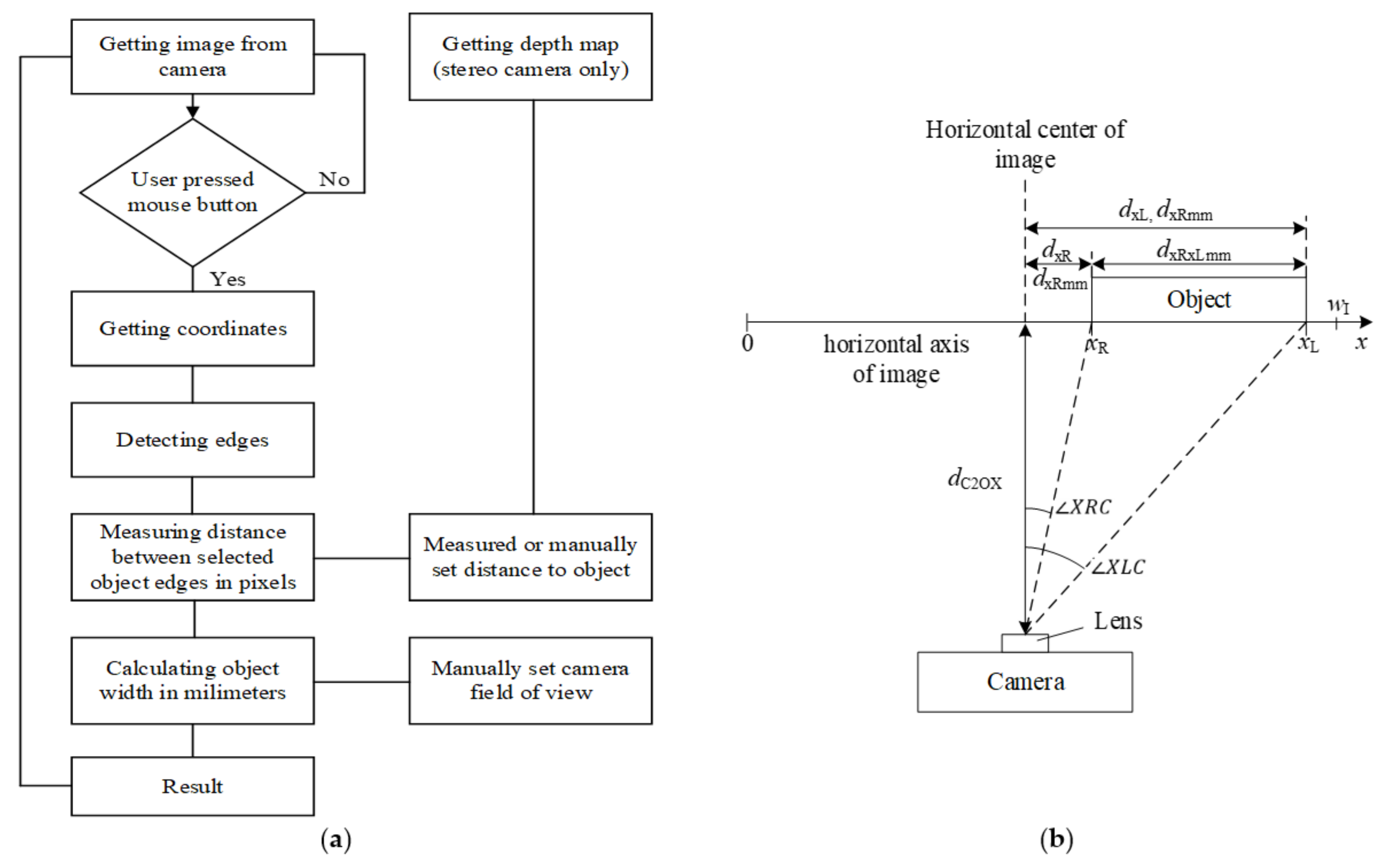
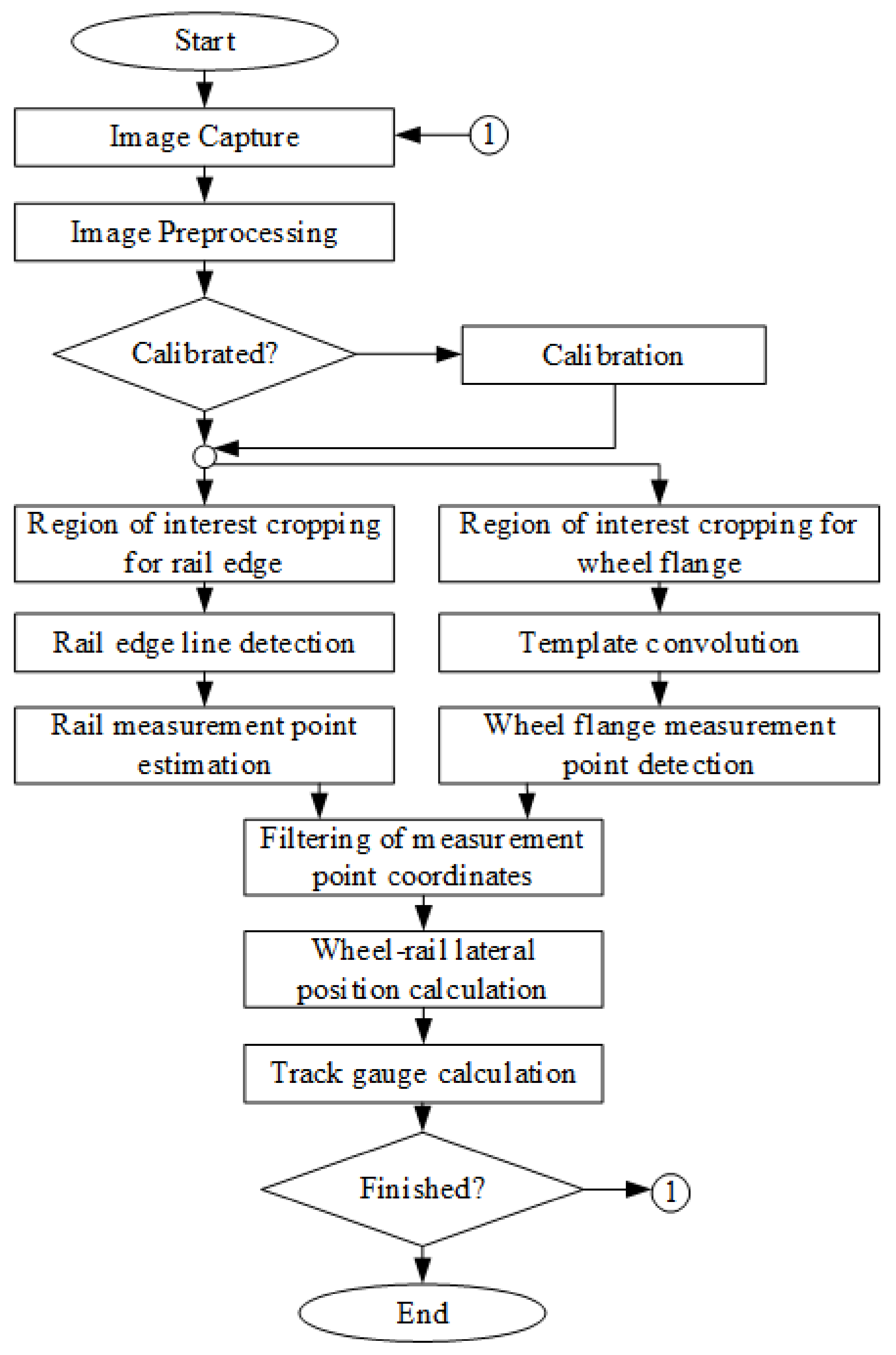
1. Introduction
The transport sector is a vital sector of the economy in European Union countries. However, there are many challenges, such as congestion in urban areas, oil dependency, emissions, and unevenly developed infrastructure, that need to be solved. In tackling these challenges, the railway sector needs to take on a larger share of transport demand in the next few decades.
For both passenger and freight railway transport, safety is of great importance. Rolling stock and railway infrastructure must meet safety requirements concerning their construction and operation. A part of the safety requirements refers to the rules for the technical conditions of railway assets during exploitation. As the assets are subject to degradation, they are regularly inspected and maintained to ensure that their conditions are within the safety limits [
1]. For instance, track geometry (TG) maintenance is one of the most important activities for railway infrastructure. The track is inspected by specific track recording coaches (TRC) at set time intervals. More frequent inspection can generate more information on TG degradation over time, leading to more reasonable maintenance decisions. This finally results in a higher level of safety and reliability for railway infrastructure. However, in practice, the frequency of inspection is mainly limited by the availability of TRC and track, considering that the inspection should not affect the regular traffic. Therefore, it is desirable to conduct condition monitoring for TG on in-service vehicles. This research work aimed to develop a wheel–rail lateral position monitoring method that would improve the inertial system used for TG.
This investigation was aimed at testing the accuracy of the visual measurement and proving the possibility of its usage for track gauge evaluation. The achieved results and contribution to the field of science are as follows: (i) the accuracy of the visual measurement of the distance between image points using calibrated test samples is high enough to implement it for TG measurement tasks; (ii) the field test results show that the image point selection method developed for selecting the wheel and rail points for measuring distance is stable enough for TG measurement; (iii) recommendations for the further improvement of the developed system are presented. This proves the adaptability of a low-cost visual measurement system for wheel–rail lateral position evaluation and provides further research directions for improving its performance.
This paper is organised as follows: In
Section 2, the latest TG monitoring techniques are reviewed; the gaps are identified. In
Section 3, methods developed for wheel–rail lateral position monitoring employing stereo imaging are presented. In
Section 4, the results of the experimental investigation are presented. In
Section 5, the discussion is presented, and further steps for technology development are presented.
2. Related Work
In 2019, the TG measurement system market was valued at USD 2.8 billion and was proliferating; it is likely to reach USD 3.7 billion by 2024 [
2]. Major system manufacturers are AVANTE International Technology (Princeton Junction, NJ, USA), DMA (Turin, Italy), Balfour Beatty (London, UK), R. Bance & Co. (Long Ditton, UK), MER MEC (Monopoli, Italy), Fugro (Leidschendam, Netherlands), MRX Technologies/Siemens Mobility Solutions (Munich, Germany), KLD Labs (Hauppauge, NY, USA), ENSCO (Springfield, VA, USA), TVEMA (Moscow, Russia), Plasser & Theurer (Vienna, Austria), Graw/Goldschmidt Group (Gliwice, Poland/Leipzig, Germany), and others. These companies have three types of solutions: (i) for train control systems (TCS), (ii) for in-service vehicles, and (iii) manual measurement systems. The solutions used on TCS are expensive and require continuous maintenance. The measurement periodicity using a track geometry car (TGC) is low (from one month to twice per year) due to the high operational costs and track possession [
3]. TG measurement using in-service vehicles is not widespread yet; however, this may allow the continuous monitoring of track conditions in a cost-efficient way [
4]. The usage of in-service vehicles for TG measurement in urban areas brings many advantages as well [
5]. The performance of manual measurement systems is low; they may be used for specific tasks.
To ensure the safety of railway operations, TG parameters, including the track gauge, longitudinal level, cross-level, alignment, and twist, are usually inspected using TRC. The measurement requirements are provided in standard EN13848-1:2019 [
6]. Many researchers have analysed the TG measurement task. Chen [
7] proposed the integration of an inertial navigation system with geodetic surveying apparatus to set up a modular TG measuring trolley system. Kampczyk [
8] analysed and evaluated the turnout geometry conditions, thereby presenting the irregularities that cause turnout deformations. Madejski proposed an autonomous TG diagnostics system in 2004 [
9]. Analysis of the railway track’s safe and reliable operation from the perspective of TG quality was analysed by Ižvolta and Šmalo in 2015 [
10]. Different statistical methods can be used to evaluate the TG condition and make a prediction model for its degradation. Vale and Lurdes presented a stochastic model for the prognosis of a TG’s degradation process in 2013 [
11]. Markov and Bayesian models were used for the same task by Bai et al. and Andrade and Teixeira in 2015 [
12,
13]. Chiachío et al. proposed a paradigm shift to the rail by forecasting the future condition instead of using empirical modelling approaches based on historical data, in 2019 [
14].
Different methods to estimate TG parameters from vehicle dynamics and direct measurements have been proposed. The first type of system is an inertia-based compact and lightweight no-contact measuring system that allows an accurate evaluation of railway TG in various operational conditions. The acceleration sensor may be placed on the axle box, bogie frame, or car body. Bogie displacement can be estimated by the double integration and filtering of the measured accelerations. It is an indirect measurement; such a system has some drawbacks. For example, it requires the consideration of vehicle weight, which may change in a wide range of in-service vehicles, and the acceleration depends on it. Additionally, the absolute value of acceleration may exceed almost 100
g, which occurs due to short-wavelength railway track components and, simultaneously, accelerations caused by long-wavelength irregularities due to the wheelset oscillation phenomena often being below 1
g, which makes the estimating of long-wavelength components challenging and requires high-accuracy accelerometers that support a wide-enough range of measured accelerations [
4]. The method works reasonably well in the vertical direction. The results of the lateral measurements made with different vehicles are so widely scattered that it is virtually impossible to draw any conclusions [
15]. The most challenging is the estimation of lateral TG due to the relative wheel–rail motion in the lateral direction, which occurs on account of the peculiar geometry of wheel–rail contact [
4]. During measurements of the track gauge, the flanges of both wheelset wheels are not in contact at the same time. A few cases are possible: (i) the left wheel flange is contacting the left rail of the track; (ii) the right wheel flange is contacting another rail of the track; (iii) the wheels’ flanges are not in contact with any rail of the track (the “centred” position of the wheelset on the track). This means that the wheel’s displacement is not directly representative of the track’s alignment as happens with the estimation of the vertical irregularity components. The lateral alignment is hard to measure accurately without optical sensors using only an inertial system [
16]. To solve this issue, the displacement achieved from the lateral acceleration at the vehicle and lateral wheel–rail position is needed.
The second type is multiple-sensor systems that can be mounted on a suitable vehicle to implement TG measurement. Using the latest noncontact optical technology that provides direct measurement, such as laser-based or light detection and ranging (LIDAR)-based, accurate results can be achieved. An example of a multiple-sensor system is a mobile track inspection system—the Rail Infrastructure aLignment Acquisition system (RILA), developed by Fugro. This system uses several sensors combining both direct and indirect measurements [
3]: a global navigation satellite system (GNSS); an inertial measurement unit (IMU); LIDAR; two laser vision systems; three video cameras. It can be mounted on in-service vehicles, and the axle load issue is also solved; however, the price of such a system is high due to the number of sensors used.
The third type is the model-based methods proposed by Alfi and Bruni in 2008, and Rosa et al. in 2019 [
4,
17]. The acceleration measured at different positions (the axle boxes, bogie frame, or car body) is used to identify the system’s inputs. This can be done using a pseudoinversion of the frequency response function matrix derived from a vehicle mathematical model; however, lateral measurement uncertainty remains.
Different sensors were reviewed, searching for new techniques for TG measurement in the lateral direction. There is a list of requirements for such sensors: particular dimensions and weight, energy consumption, lifecycle costs, system robustness, measurement accuracy, technical compatibility, output data format, and measurement repeatability. The importance of these requirements is not equal. In 2017, Xiong et al. used a three-dimensional laser profiling system, which fused the outputs of a laser scanner, odometer, IMU, and global positioning system (GPS) for rail surface measurement [
18]. The authors used such a system to detect surface defects such as abrasions, scratches, and peeling. Laser-based systems have high measurement accuracy and a high sampling rate. However, the price of the system was not suitable for broad application on in-service trains. In 2011, Burstow et al. used thermal images to investigate wheel–rail contact [
19]; the authors found that such technology can be used to monitor the condition of assets such as switches and crossings and understand the behaviour of wheelsets through them. In 2019, Yamamoto extended the idea of Burstow et al. [
19] and proposed using a thermographic camera for tests for rail climb derailment [
20]. It is possible to extend such a system for gauge measurement. However, the resolution of the thermographic camera is low. Therefore, the geometry calculated from the pixels will have a relatively high error. Visual detection systems (VDSs) are used for detecting various defects in railways.
Marino and Stella used a VDS for infrastructure inspection in real time in 2017 [
21]. The proposed system autonomously detected the bolts that secure the rail to the sleepers and monitored the rail condition at high speeds, up to 460 km/h. VDSs are widely used for rail surface defect detection [
22,
23,
24,
25]. There are studies where the detection of defects of the railway plugs and fasteners using VDSs is analysed [
26,
27]. In 2019, Singh et al. developed a vision-based system for rail gauge measurement from a drone [
28]. Such a method allows measuring track gauges with errors ranging from 34 to 105 mm; the solution is more appropriate as an additional source of information for inspection. Karakose et al. used a camera for the fault diagnosis of the rail track, as well, in 2017 [
29]. The camera was placed on the front of the train. Following this procedure, the distance between the rails was calculated from the pixels. The camera was placed relatively far away from the track; therefore, the pixel count per measured distance decreased and affected the accuracy negatively. To maximize the track gauge measurement accuracy, the camera should be placed as close as possible to the measured area and have as narrow a field of view (FOV) as possible while including the full measurement area. A solution can be the use of a separate camera for each rail, and using the known distance between the cameras for estimation.
Summarising, current TG measurement systems are complex and combine different types of sensors; thus, their high cost precludes wide deployment in in-service trains. Inertia-based noncontact measuring systems allow an accurate evaluation of railway TG in a vertical direction, but the lateral measurement results are not reliable enough. A new robust and low-cost solution for lateral wheel–rail position measurement is needed.
5. Discussion
The investigation was intended to focus on developing and testing a low-cost system that allows the detection of the wheelset–track lateral position to extend the functionality of existing inertial TG measurement systems. To find a suitable solution, it is necessary to understand the specific characteristics of the measured object, which is a wheelset running on a track during rail vehicle operation. Due to the wheelset lateral oscillation phenomenon, the wheelset rotates about axis Y, moves linearly, and rotates about the track longitudinal axis X and vertical axis Z, as well on the tangent, resulting in a sinusoidal motion on the track. The wheelset movement trajectory becomes even more complex and difficult to describe when the rail vehicle runs on track curves and along track superelevation (inclined track).
The achieved results show that the proposed visual wheel–rail lateral position measurement system principle is suitable for track gauge measurement. During the investigation, it was found that it is possible to measure the geometrical parameters with an accuracy that meets the standard EN13848-1:2019 requirements in laboratory facilities [
6]; the error was less than ±1 mm for all the measurements.
It was found that the majority of the known algorithms used for geometry evaluation from an image are not suitable for wheel–rail lateral position measurement. The original algorithm was developed; it was validated on the image data obtained in the field measurements. The image processing methods used in the proposed algorithm require finetuning parameter settings, such as parameters for the filters and the line detector. The measurement results rely on the camera specifications, illumination conditions, camera fixation, and train parameters.
During the field test, a ZED stereo camera was used. The camera was oriented so that it could film both the rail edge and wheel flange surface. The camera’s horizontal FOV of 74.37°, covered by 1920 horizontal points, resulted in a ±0.338 mm theoretical accuracy and ±1 mm accuracy based on the presented laboratory test results. At a distance of 1000 mm, not only was the wheel–rail contact filmed but so were a lot of additional objects; they were redundant information for this task. For data processing, only part of the picture was used. It is better to use a camera with the smallest FOV; it increases accuracy. It was found that the relative displacement of the camera installed on the vehicle bogie was relatively small, and the distance between the camera and wheelset could be considered constant. There is no need to use a stereo camera in this case. If the device will be installed on the vehicle body, a stereo camera is the best solution. The IMU sensor inside the ZED camera showed that the acceleration in the vertical direction did not exceed 20 m/s2 during the field test. The designed damping system worked satisfactorily; with an increase in train velocity, the vibrations will increase, and this system should be revised.
The rail vehicle mass (loaded/unloaded) should be considered, as it is desired to conduct monitoring for TG on in-service vehicles. As the masses of in-service trains may vary, they may lead to different deformations of the wheelset, and measurement error may appear. Mass measurement/estimation is essential for the TG measurement system as a whole. Before integrating the proposed system into a TG system, the axle load needs to be defined. Our proposal is estimating the axle load considering the longitudinal vehicle dynamics, implementing a recursive least-squares algorithm.
The field tests showed that sunlight orientation might reduce the measurement quality; therefore, an artificial light source is required. During the experiment, two LED alternating-current (AC) light sources for each camera were used with a total luminous flux of 3400 lm. When filming, AC lighting introduces flickering that is seen when using exposure times less than the period of the AC. To decrease this effect, the exposure of the camera can be increased, but this leads to motion blur that decreases the video quality and does not allow using high-framerate cameras taking more than 60 FPS. A constant-current light source should be used to avoid flickering.
The proposed visual measurement system should work in a real-time manner. EN 13848-2:2006 requires all measurements to be sampled at constant distance-based intervals not larger than 0.5 m [
32]. The camera used in this study was set to sample at 30 FPS to ensure the high resolution of 1920 × 1080. That allows measurement for a vehicle running at 54 km/h. Therefore, a camera supporting a higher sample rate is desired for installation on in-service vehicles, considering that a regional train’s average speed is usually between 70 and 90 km/h. A higher sample rate will require processing hardware with higher processing speed or efficiency improvements in the data processing algorithm. It is worth noting that the traditional TG standards of the EN 13848 series are applicable for TG inspection, which is carried out at relatively large time intervals, such as every six months. Therefore, this standard series has strict requirements for inspection devices. The proposed visual measurement system was designed as a monitoring device installed on in-service vehicles, delivering a much larger amount of condition data and allowing statistical processing. This may compensate for some drawbacks of monitoring devices such as a low sample rate.
Weather variation may cause the performance degradation of the proposed system. In particular, in a harsh outdoor railway environment, variance in conditions is quite common, and the vehicles with the monitoring devices are deployed in different locations during different seasons. This raises high requirements for the robustness and the ability for easy adaptation of the algorithm. A detection and tracking algorithm based on a deep neural network may be a good candidate for meeting such requirements.
In conclusion, the developed system’s main advantage is its easy integration, low cost, and energy efficiency. The developed algorithm was validated and provided results comparable to those for a reference measurement system at lower speeds. This proves the suitability and applicability of the principles used in the proposed visual measurement system for wheel–rail lateral positioning, track gauge evaluation, and lateral alignment estimation after combining it with the inertial system output.