Pulsed Optically Pumped Magnetometers: Addressing Dead Time and Bandwidth for the Unshielded Magnetorelaxometry of Magnetic Nanoparticles
Abstract
1. Introduction
2. Materials and Methods
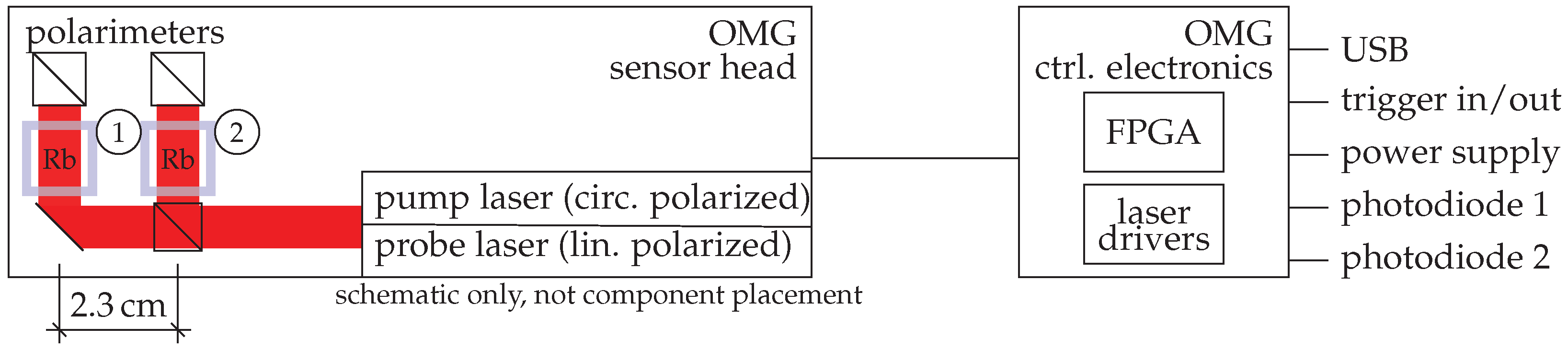
2.1. Setup Overview
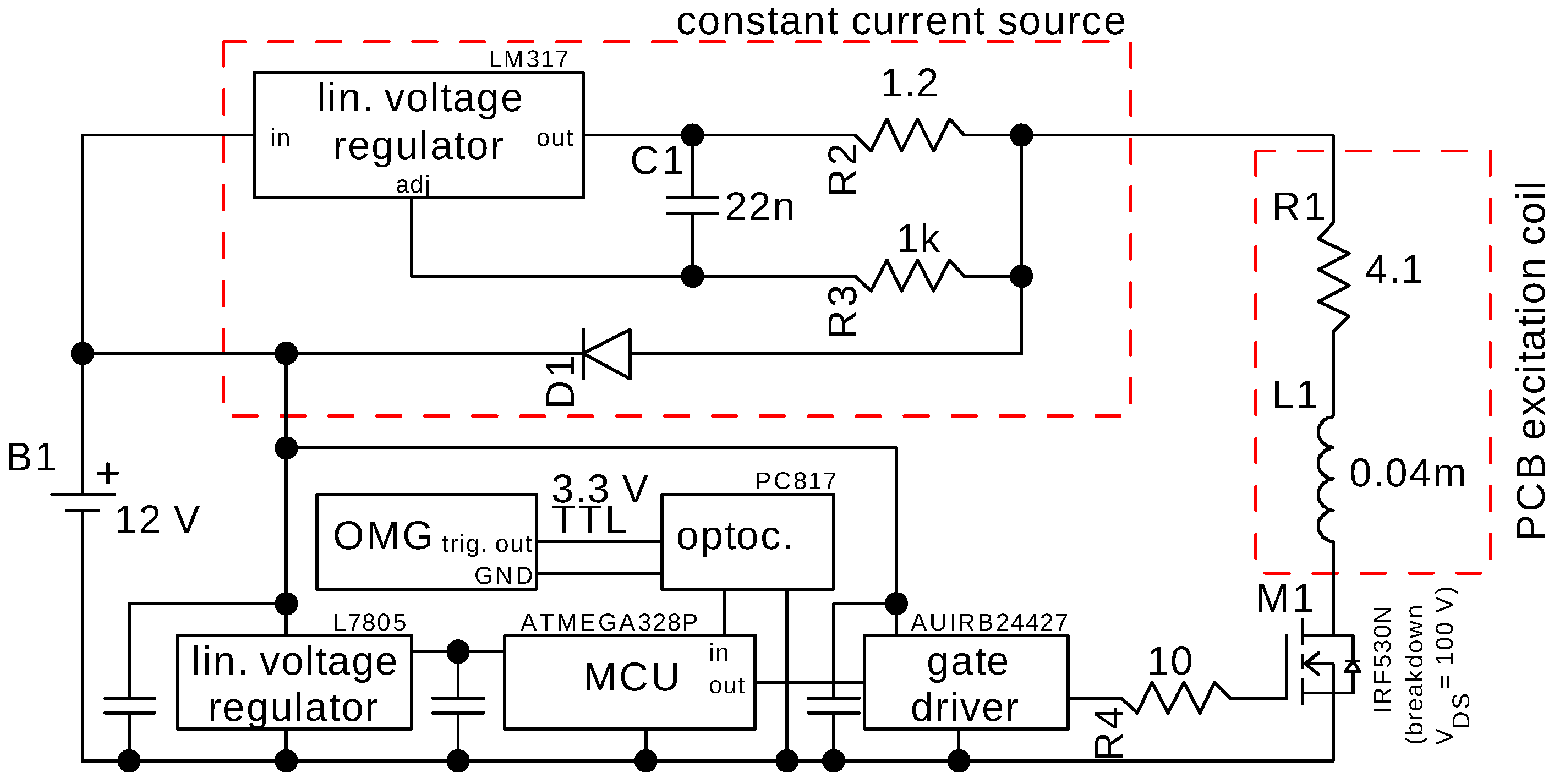
2.2. MNP Excitation Circuit
2.3. MNP
2.4. OPM: Optical Magnetic Gradiometer (OMG)
2.5. Data Acquisition, System Synchronization and Mains Synchronization
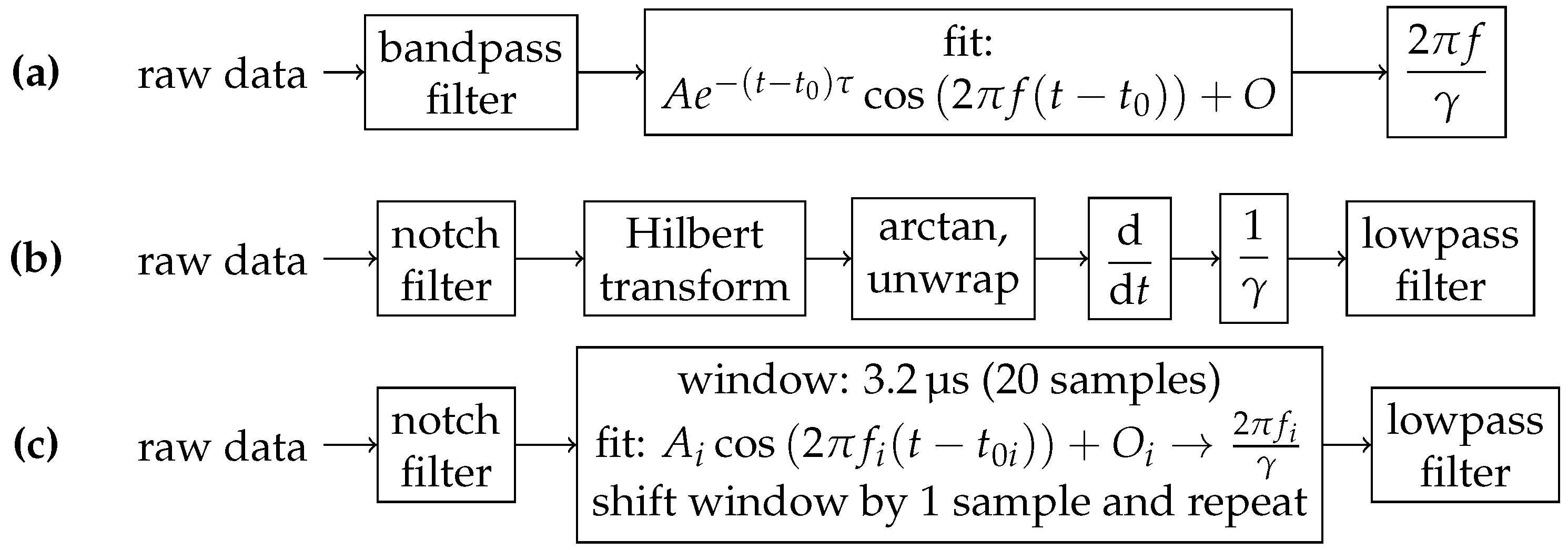
2.6. Data Processing: Raw Photodiode Data
2.7. Data Processing: FPGA Data
2.8. Data Processing: MRX Data
2.9. Proof of Principle Unshielded OPM-MRX with 100 mT Pulsed Fields
3. Results and Discussion
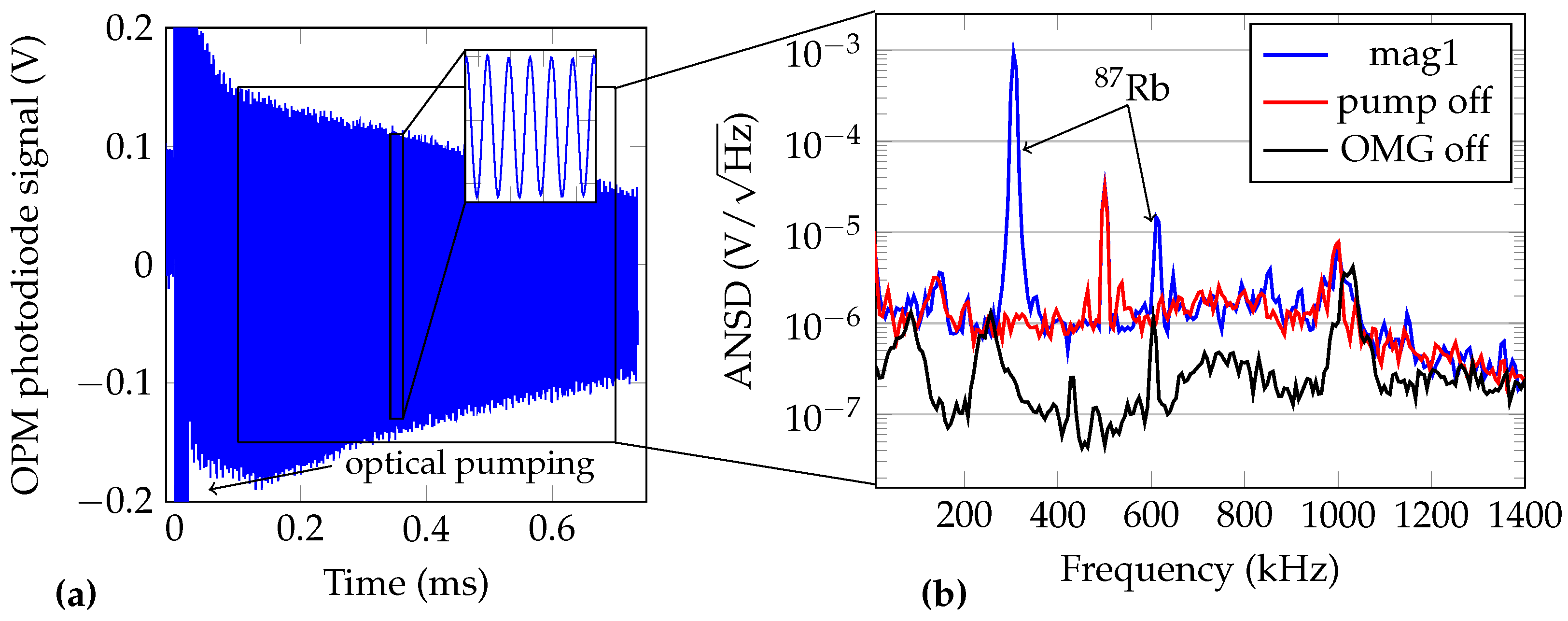
3.1. OMG Characterization and Performance
3.2. Unshielded MRX with OMG
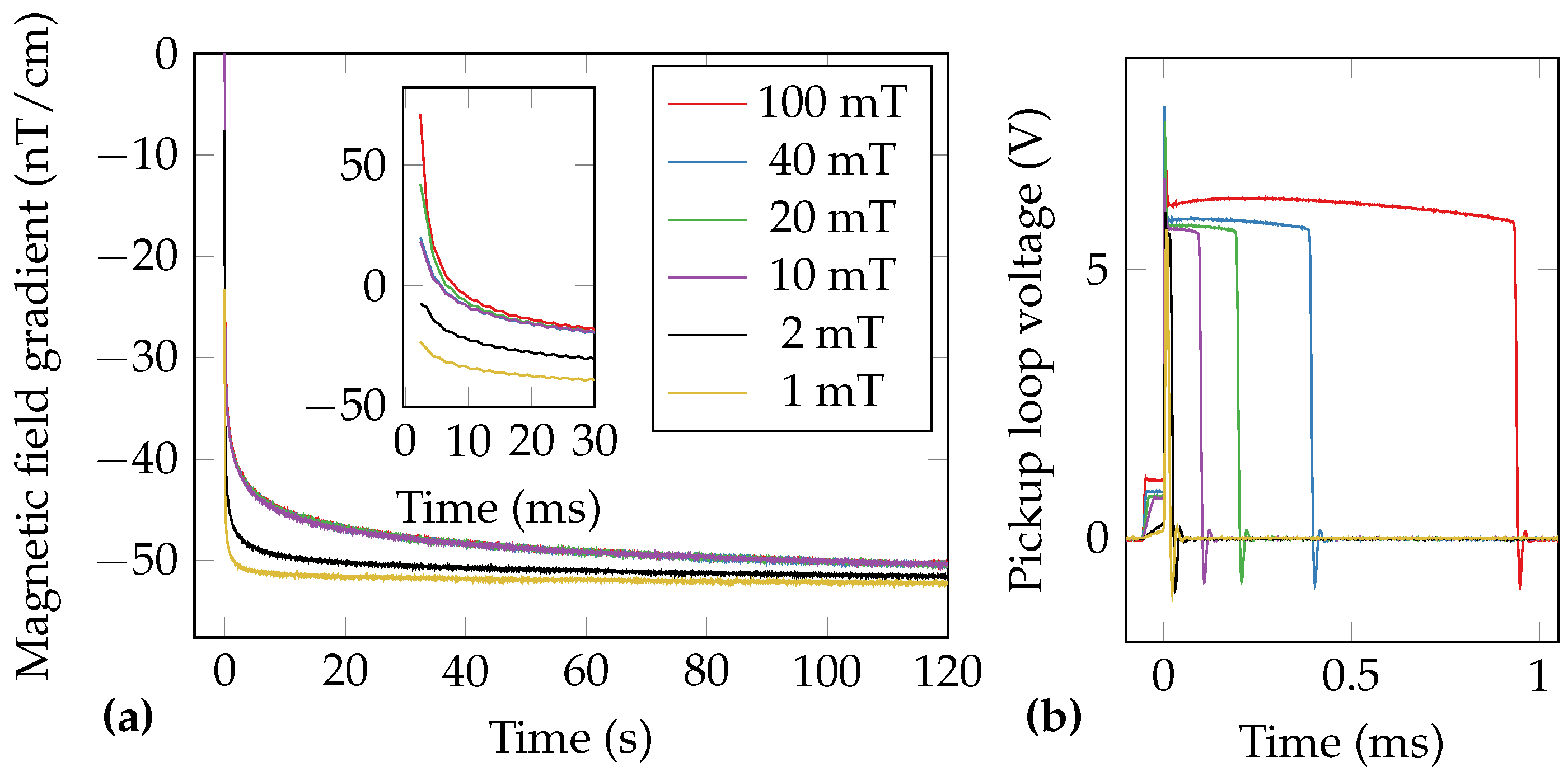
3.3. Proof of Principle Unshielded OPM-MRX with 100 mT Pulsed Fields
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Richter, H.; Kettering, M.; Wiekhorst, F.; Steinhoff, U.; Hilger, I.; Trahms, L. Magnetorelaxometry for localization and quantification of magnetic nanoparticles for thermal ablation studies. Phys. Med. Biol. 2010, 55, 623. [Google Scholar] [CrossRef]
- Usov, N.; Liubimov, B. Dynamics of magnetic nanoparticle in a viscous liquid: Application to magnetic nanoparticle hyperthermia. J. Appl. Phys. 2012, 112, 023901. [Google Scholar] [CrossRef]
- Wiekhorst, F.; Steinhoff, U.; Eberbeck, D.; Trahms, L. Magnetorelaxometry assisting biomedical applications of magnetic nanoparticles. Pharm. Res. 2011, 29, 1189–1202. [Google Scholar] [CrossRef]
- Liebl, M.; Wiekhorst, F.; Eberbeck, D.; Radon, P.; Gutkelch, D.; Baumgarten, D.; Steinhoff, U.; Trahms, L. Magnetorelaxometry procedures for quantitative imaging and characterization of magnetic nanoparticles in biomedical applications. Biomed. Eng. Tech. 2015, 60, 427–443. [Google Scholar] [CrossRef] [PubMed]
- Néel, L. Théorie du traînage magnétique des ferromagnétiques en grains fins avec applications aux terres cuites. Ann. Géophys. 1949, 5, 99–136. [Google Scholar]
- Brown, W.F., Jr. Thermal fluctuations of a single-domain particle. Phys. Rev. 1963, 130, 1677. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Shliomis, M.I. The effective field method in the orientational kinetics of magnetic fluids and liquid crystals. Adv. Chem. Phys. 1994, 87, 595–752. [Google Scholar]
- Chantrell, R.; Hoon, S.; Tanner, B. Time-dependent magnetization in fine-particle ferromagnetic systems. J. Magn. Magn. Mater. 1983, 38, 133–141. [Google Scholar] [CrossRef]
- Eberbeck, D.; Wiekhorst, F.; Steinhoff, U.; Trahms, L. Aggregation behaviour of magnetic nanoparticle suspensions investigated by magnetorelaxometry. J. Phys. Condens. Matter 2006, 18, S2829. [Google Scholar] [CrossRef]
- Ludwig, F.; Heim, E.; Eberbeck, D.; Schwarz, K.; Trahms, L.; Schilling, M. Comparison and Calibration of Fluxgate and SQUID Magnetorelaxometry Techniques for the Characterization of Magnetic Core-Shell Nanoparticles. IEEE Trans. Magn. 2009, 45, 4857–4860. [Google Scholar] [CrossRef]
- Denoual, M.; Saez, S.; Kauffman, F.; Dolabdjian, C. Magnetorelaxometry using Improved Giant MagnetoResistance Magnetometer. Sens. Actuators A Phys. 2010, 159, 184–188. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, C.C.; Hall, D.A. Giant magnetoresistive biosensor array for detecting magnetorelaxation. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 755–764. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, F.; Heim, E.; Mäuselein, S.; Eberbeck, D.; Schilling, M. Magnetorelaxometry of magnetic nanoparticles with fluxgate magnetometers for the analysis of biological targets. J. Magn. Magn. Mater. 2005, 293, 690–695. [Google Scholar] [CrossRef]
- Shen, H.M.; Hu, L.; Fu, X. Integrated Giant Magnetoresistance Technology for Approachable Weak Biomagnetic Signal Detections. Sensors 2018, 18, 148. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Skucha, K.; Megens, M.; Boser, B. A CMOS Hall-effect sensor for the characterization and detection of magnetic nanoparticles for biomedical applications. IEEE Trans. Magn. 2011, 47, 3449–3451. [Google Scholar] [CrossRef] [PubMed]
- Schmid-Lorch, D.; Häberle, T.; Reinhard, F.; Zappe, A.; Slota, M.; Bogani, L.; Finkler, A.; Wrachtrup, J. Relaxometry and dephasing imaging of superparamagnetic magnetite nanoparticles using a single qubit. Nano Lett. 2015, 15, 4942–4947. [Google Scholar] [CrossRef]
- Kuwahata, A.; Kitaizumi, T.; Saichi, K.; Sato, T.; Igarashi, R.; Ohshima, T.; Masuyama, Y.; Iwasaki, T.; Hatano, M.; Jelezko, F.; et al. Magnetometer with nitrogen-vacancy center in a bulk diamond for detecting magnetic nanoparticles in biomedical applications. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef]
- Dehmelt, H. Modulation of a light beam by precessing absorbing atoms. Phys. Rev. 1957, 105, 1924. [Google Scholar] [CrossRef]
- Bell, W.E.; Bloom, A.L. Optical detection of magnetic resonance in alkali metal vapor. Phys. Rev. 1957, 107, 1559. [Google Scholar] [CrossRef]
- Dupont-Roc, J.; Haroche, S.; Cohen-Tannoudji, C. Detection of very weak magnetic fields (10−9gauss) by 87Rb zero-field level crossing resonances. Phys. Lett. A 1969, 28, 638–639. [Google Scholar] [CrossRef]
- Happer, W.; Tang, H. Spin-exchange shift and narrowing of magnetic resonance lines in optically pumped alkali vapors. Phys. Rev. Lett. 1973, 31, 273. [Google Scholar] [CrossRef]
- Kominis, I.; Kornack, T.; Allred, J.; Romalis, M. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
- Allred, J.C.; Lyman, R.N.; Kornack, T.W.; Romalis, M.V. High-Sensitivity Atomic Magnetometer Unaffected by Spin-Exchange Relaxation. Phys. Rev. Lett. 2002, 89, 130801. [Google Scholar] [CrossRef]
- Johnson, C.; Adolphi, N.L.; Butler, K.L.; Lovato, D.M.; Larson, R.; Schwindt, P.D.; Flynn, E.R. Magnetic relaxometry with an atomic magnetometer and SQUID sensors on targeted cancer cells. J. Magn. Magn. Mater. 2012, 324, 2613–2619. [Google Scholar] [CrossRef]
- Dolgovskiy, V.; Lebedev, V.; Colombo, S.; Weis, A.; Michen, B.; Ackermann-Hirschi, L.; Petri-Fink, A. A quantitative study of particle size effects in the magnetorelaxometry of magnetic nanoparticles using atomic magnetometry. J. Magn. Magn. Mater. 2015, 379, 137–150. [Google Scholar] [CrossRef]
- Jaufenthaler, A.; Schier, P.; Middelmann, T.; Liebl, M.; Wiekhorst, F.; Baumgarten, D. Quantitative 2D magnetorelaxometry imaging of magnetic nanoparticles using optically pumped magnetometers. Sensors 2020, 20, 753. [Google Scholar] [CrossRef] [PubMed]
- Baffa, O.; Matsuda, R.; Arsalani, S.; Prospero, A.; Miranda, J.; Wakai, R. Development of an Optical Pumped Gradiometric System to Detect Magnetic Relaxation of Magnetic Nanoparticles. J. Magn. Magn. Mater. 2018, 475, 533–538. [Google Scholar] [CrossRef]
- Belfi, J.; Bevilacqua, G.; Biancalana, V.; Cartaleva, S.; Dancheva, Y.; Khanbekyan, K.; Moi, L. Dual channel self-oscillating optical magnetometer. JOSA B 2009, 26, 910–916. [Google Scholar] [CrossRef]
- Gemmel, C.; Heil, W.; Karpuk, S.; Lenz, K.; Ludwig, C.; Sobolev, Y.; Tullney, K.; Burghoff, M.; Kilian, W.; Knappe-Grüneberg, S.; et al. Ultra-sensitive magnetometry based on free precession of nuclear spins. Eur. Phys. J. D 2010, 57, 303–320. [Google Scholar] [CrossRef]
- Lenci, L.; Barreiro, S.; Valente, P.; Failache, H.; Lezama, A. A magnetometer suitable for measurement of the Earth’s field based on transient atomic response. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215401. [Google Scholar] [CrossRef]
- Grujić, Z.D.; Koss, P.A.; Bison, G.; Weis, A. A sensitive and accurate atomic magnetometer based on free spin precession. Eur. Phys. J. D 2015, 69, 135. [Google Scholar] [CrossRef]
- Hunter, D.; Piccolomo, S.; Pritchard, J.; Brockie, N.; Dyer, T.; Riis, E. Free-induction-decay magnetometer based on a microfabricated Cs vapor cell. Phys. Rev. Appl. 2018, 10, 014002. [Google Scholar] [CrossRef]
- Borna, A.; Carter, T.R.; DeRego, P.; James, C.D.; Schwindt, P.D. Magnetic source imaging using a pulsed optically pumped magnetometer array. IEEE Trans. Instrum. Meas. 2018, 68, 493–501. [Google Scholar] [CrossRef]
- Gerginov, V.; Pomponio, M.; Knappe, S. Scalar Magnetometry Below 100 fT/Hz 1/2 in a Microfabricated Cell. IEEE Sens. J. 2020, 20, 12684–12690. [Google Scholar] [CrossRef]
- Wilson, N.; Perrella, C.; Anderson, R.; Luiten, A.; Light, P. Wide-bandwidth atomic magnetometry via instantaneous-phase retrieval. Phys. Rev. Res. 2020, 2, 013213. [Google Scholar] [CrossRef]
- Li, S.; Vachaspati, P.; Sheng, D.; Dural, N.; Romalis, M.V. Optical rotation in excess of 100 rad generated by Rb vapor in a multipass cell. Phys. Rev. A 2011, 84, 061403. [Google Scholar] [CrossRef]
- Haller, A.; Matz, H.; Hartwig, S.; Kerberger, T.; Atzpadin, H.; Trahms, L. Low Tc SQUID measurement system for magnetic relaxation immunoassays in unshielded environment. IEEE Trans. Appl. Supercond. 2001, 11, 1371–1374. [Google Scholar] [CrossRef]
- Ludwig, F.; Mäuselein, S.; Heim, E.; Schilling, M. Magnetorelaxometry of magnetic nanoparticles in magnetically unshielded environment utilizing a differential fluxgate arrangement. Rev. Sci. Instrum. 2005, 76, 106102. [Google Scholar] [CrossRef]
- Lebedev, V.; Hartwig, S.; Middelmann, T. Fast and robust optically pumped cesium magnetometer. Adv. Opt. Technol. 2020, 9, 275–286. [Google Scholar] [CrossRef]
- Oelsner, G.; IJsselsteijn, R.; Scholtes, T.; Krüger, A.; Schultze, V.; Seyffert, G.; Werner, G.; Jäger, M.; Chwala, A.; Stolz, R. Integrated optically pumped magnetometer for measurements within Earth’s magnetic field. arXiv 2020, arXiv:2008.01570. [Google Scholar]
- Zhang, R.; Mhaskar, R.; Smith, K.; Prouty, M. Portable intrinsic gradiometer for ultra-sensitive detection of magnetic gradient in unshielded environment. Appl. Phys. Lett. 2020, 116, 143501. [Google Scholar] [CrossRef]
- Limes, M.; Foley, E.; Kornack, T.; Caliga, S.; McBride, S.; Braun, A.; Lee, W.; Lucivero, V.; Romalis, M. Portable magnetometry for detection of biomagnetism in ambient environments. Phys. Rev. Appl. 2020, 14, 011002. [Google Scholar] [CrossRef]
- Dedman, C.; Baldwin, K.; Colla, M. Fast switching of magnetic fields in a magneto-optic trap. Rev. Sci. Instrum. 2001, 72, 4055–4058. [Google Scholar] [CrossRef]
- Crevecoeur, G.; Baumgarten, D.; Steinhoff, U.; Haueisen, J.; Trahms, L.; Dupré, L. Advancements in magnetic nanoparticle reconstruction using sequential activation of excitation coil arrays using magnetorelaxometry. IEEE Trans. Magn. 2012, 48, 1313–1316. [Google Scholar] [CrossRef]
- Dennis, C.; Jackson, A.; Borchers, J.; Hoopes, P.; Strawbridge, R.; Foreman, A.; Van Lierop, J.; Grüttner, C.; Ivkov, R. Nearly complete regression of tumors via collective behavior of magnetic nanoparticles in hyperthermia. Nanotechnology 2009, 20, 395103. [Google Scholar] [CrossRef]
- Attaluri, A.; Kandala, S.K.; Wabler, M.; Zhou, H.; Cornejo, C.; Armour, M.; Hedayati, M.; Zhang, Y.; DeWeese, T.L.; Herman, C.; et al. Magnetic nanoparticle hyperthermia enhances radiation therapy: A study in mouse models of human prostate cancer. Int. J. Hyperth. 2015, 31, 359–374. [Google Scholar] [CrossRef]
- Eberbeck, D.; Dennis, C.; Huls, N.; Krycka, K.; Grüttner, C.; Westphal, F. Multicore Magnetic Nanoparticles for Magnetic Particle Imaging. Magn. IEEE Trans. 2013, 49, 269–274. [Google Scholar] [CrossRef]
- Schultze, V.; IJsselsteijn, R.; Meyer, H.G. Noise reduction in optically pumped magnetometer assemblies. Appl. Phys. B 2010, 100, 717–724. [Google Scholar] [CrossRef]
- Borkowski, J.; Kania, D.; Mroczka, J. Comparison of sine-wave frequency estimation methods in respect of speed and accuracy for a few observed cycles distorted by noise and harmonics. Metrol. Meas. Syst. 2018, 25. [Google Scholar]
- Harcombe, D.M.; Ruppert, M.G.; Fleming, A.J. A review of demodulation techniques for multifrequency atomic force microscopy. Beilstein J. Nanotechnol. 2020, 11, 76–91. [Google Scholar] [CrossRef]
- Liu, J.L.; Zheng, J.Y.; Wei, X.J.; Liao, F.Y.; Luo, Y.P. A new instantaneous frequency extraction method for nonstationary response signals in civil engineering structures. J. Low Freq. Noise Vib. Act. Control 2018, 37, 834–848. [Google Scholar] [CrossRef]
- Cramér, H. Mathematical Methods of Statistics; Princeton University Press: Princeton, NJ, USA, 1946. [Google Scholar]
- Rao, C.R. Information and the accuracy attainable in the estimation of statistical parameters. In Breakthroughs in Statistics; Springer: Berlin, Germany, 1992; pp. 235–247. [Google Scholar]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Rochester, S.; Ledbetter, M.; Zigdon, T.; Wilson-Gordon, A.; Budker, D. Orientation-to-alignment conversion and spin squeezing. Phys. Rev. A 2012, 85, 022125. [Google Scholar] [CrossRef]
- Lenci, L.; Auyuanet, A.; Barreiro, S.; Valente, P.; Lezama, A.; Failache, H. Vectorial atomic magnetometer based on coherent transients of laser absorption in Rb vapor. Phys. Rev. A 2014, 89, 043836. [Google Scholar] [CrossRef]
- Vershovskii, A.; Pazgalev, A.; Petrenko, M. All-Optical Magnetometric Sensor for Magnetoencephalography and Ultralow Field Tomography. Tech. Phys. Lett. 2020, 46, 877–880. [Google Scholar] [CrossRef]
- Li, R.; Baynes, F.N.; Luiten, A.N.; Perrella, C. Continuous High-Sensitivity and High-Bandwidth Atomic Magnetometer. Phys. Rev. Appl. 2020, 14, 064067. [Google Scholar] [CrossRef]
- Baumgarten, D.; Liehr, M.; Wiekhorst, F.; Steinhoff, U.; Münster, P.; Miethe, P.; Trahms, L.; Haueisen, J. Magnetic nanoparticle imaging by means of minimum norm estimates from remanence measurements. Med. Biol. Eng. Comput. 2008, 46, 1177. [Google Scholar] [CrossRef]
- Remmer, H.; Dieckhoff, J.; Schilling, M.; Ludwig, F. Suitability of magnetic single-and multi-core nanoparticles to detect protein binding with dynamic magnetic measurement techniques. J. Magn. Magn. Mater. 2015, 380, 236–240. [Google Scholar] [CrossRef]
- Sarangi, S.; Tan, I.; Brazdeikis, A. Brownian relaxation of interacting magnetic nanoparticles in a colloid subjected to a pulsatile magnetic field. J. Nanosci. Nanotechnol. 2011, 11, 4136–4141. [Google Scholar] [CrossRef]
- Bao, G.; Schild, D. Fast and accurate fitting and filtering of noisy exponentials in Legendre space. PLoS ONE 2014, 9, e90500. [Google Scholar] [CrossRef]
- Rusakov, V.; Raikher, Y. Magnetorelaxometry in the Presence of a DC Bias Field of Ferromagnetic Nanoparticles Bearing a Viscoelastic Corona. Sensors 2018, 18, 1661. [Google Scholar] [CrossRef] [PubMed]
- Jaufenthaler, A.; Schultze, V.; Scholtes, T.; Schmidt, C.B.; Handler, M.; Stolz, R.; Baumgarten, D. OPM magnetorelaxometry in the presence of a DC bias field. EPJ Quantum Technol. 2020, 7, 1–14. [Google Scholar] [CrossRef]




| Data | MNP | Dilution | Fe | O | R | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| from | Type | Factor | () | () | () | () | () | ) | () | () | |
| FPGA | BNF | 1:1 | 1370 | 321.23 | 1.35 | 72.57 | 5.20 | 389.62 | 1.10 | 26.98 | 1.00 |
| FPGA | BNF | 1:2 | 685 | 189.21 | 0.84 | 45.51 | 3.51 | 290.86 | 0.70 | 10.71 | 1.00 |
| FPGA | BNF | 1:10 | 137 | 44.89 | 0.64 | 9.58 | 3.25 | 84.19 | 0.56 | 2.30 | 1.00 |
| FPGA | BNF | 1:20 | 68.5 | 14.44 | 0.62 | 3.19 | 3.05 | 27.90 | 0.54 | 1.23 | 1.00 |
| FPGA | BNF | 1:100 | 13.7 | 2.73 | 0.64 | 0.74 | 3.09 | 4.98 | 0.54 | 0.30 | 1.00 |
| FPGA | BNF | 1:200 | 6.85 | 1.40 | 0.72 | 0.23 | 4.39 | 2.48 | 0.64 | 0.12 | 1.00 |
| FPGA | BNF | 1:1000 | 1.37 | 0.28 | 0.75 | 0.05 | 8.62 | 0.49 | 0.65 | 0.01 | 1.00 |
| HT | BNF | 1:1 | 1370 | 265.18 | 0.18 | 298.19 | 1.94 | 1214.60 | 0.13 | 33.42 | 0.99 |
| HT | BNF | 1:2 | 685 | 164.52 | 0.35 | 120.89 | 1.86 | 457.98 | 0.25 | 12.00 | 1.00 |
| HT | BNF | 1:10 | 137 | 39.68 | 0.42 | 21.98 | 1.81 | 95.46 | 0.32 | 2.64 | 1.00 |
| HT | BNF | 1:20 | 68.5 | 12.77 | 0.42 | 7.00 | 1.78 | 31.17 | 0.32 | 1.41 | 0.99 |
| HT | BNF | 1:100 | 13.7 | 2.43 | 0.42 | 1.52 | 1.76 | 5.68 | 0.31 | 0.28 | 0.61 |
| HT | BNF | 1:200 | 6.85 | 1.25 | 0.42 | 0.65 | 1.92 | 3.05 | 0.33 | 0.10 | 0.31 |
| FPGA | Perimag | 1:1 | 850 | 132.99 | 1.43 | 66.40 | 4.88 | 128.91 | 0.81 | 30.72 | 1.00 |
| FPGA | Perimag | 1:10 | 85 | 16.07 | 1.08 | 6.86 | 4.74 | 19.18 | 0.70 | 3.28 | 1.00 |
| HT | Perimag | 1:1 | 850 | 124.23 | 0.73 | 54.94 | 4.97 | 191.99 | 0.49 | 30.78 | 1.00 |
| HT | Perimag | 1:10 | 85 | 14.96 | 0.69 | 9.06 | 3.56 | 22.24 | 0.40 | 3.44 | 0.99 |
| O | |||
|---|---|---|---|
| () | () | () | ) |
| 100 | 120.98 | 6 | −50.01 |
| 40 | 69.98 | 48 | −50.09 |
| 20 | 92.34 | 16 | −50.14 |
| 10 | 68.30 | 58 | −50.07 |
| 2 | 43.66 | 58 | −51.24 |
| 1 | 28.65 | 40 | −51.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaufenthaler, A.; Kornack, T.; Lebedev, V.; Limes, M.E.; Körber, R.; Liebl, M.; Baumgarten, D. Pulsed Optically Pumped Magnetometers: Addressing Dead Time and Bandwidth for the Unshielded Magnetorelaxometry of Magnetic Nanoparticles. Sensors 2021, 21, 1212. https://doi.org/10.3390/s21041212
Jaufenthaler A, Kornack T, Lebedev V, Limes ME, Körber R, Liebl M, Baumgarten D. Pulsed Optically Pumped Magnetometers: Addressing Dead Time and Bandwidth for the Unshielded Magnetorelaxometry of Magnetic Nanoparticles. Sensors. 2021; 21(4):1212. https://doi.org/10.3390/s21041212
Chicago/Turabian StyleJaufenthaler, Aaron, Thomas Kornack, Victor Lebedev, Mark E. Limes, Rainer Körber, Maik Liebl, and Daniel Baumgarten. 2021. "Pulsed Optically Pumped Magnetometers: Addressing Dead Time and Bandwidth for the Unshielded Magnetorelaxometry of Magnetic Nanoparticles" Sensors 21, no. 4: 1212. https://doi.org/10.3390/s21041212
APA StyleJaufenthaler, A., Kornack, T., Lebedev, V., Limes, M. E., Körber, R., Liebl, M., & Baumgarten, D. (2021). Pulsed Optically Pumped Magnetometers: Addressing Dead Time and Bandwidth for the Unshielded Magnetorelaxometry of Magnetic Nanoparticles. Sensors, 21(4), 1212. https://doi.org/10.3390/s21041212






