Acoustic Emission Signal Entropy as a Means to Estimate Loads in Fiber Reinforced Polymer Rods
Abstract
1. Introduction
1.1. Motivation
1.2. Related Work
1.3. Contributions
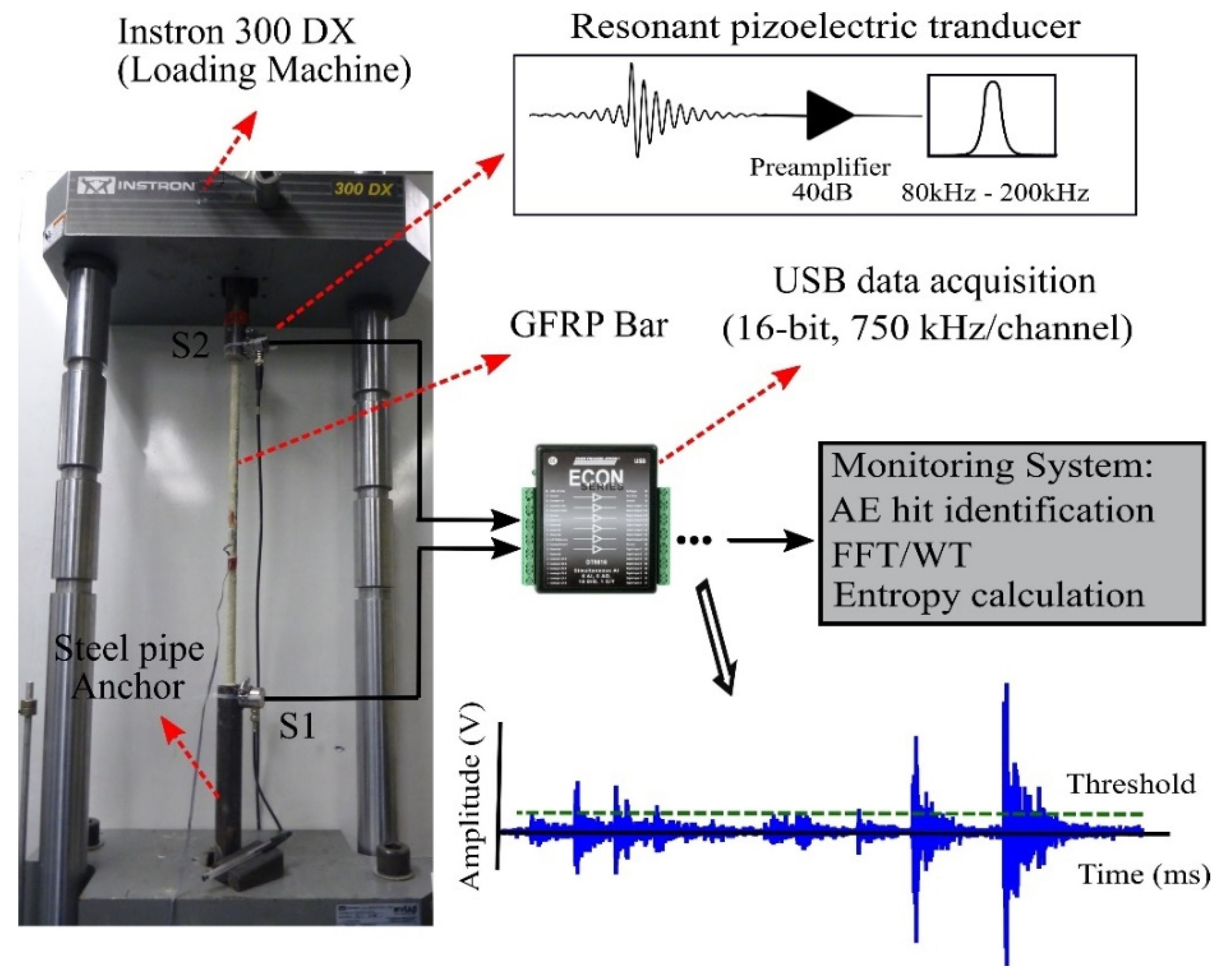
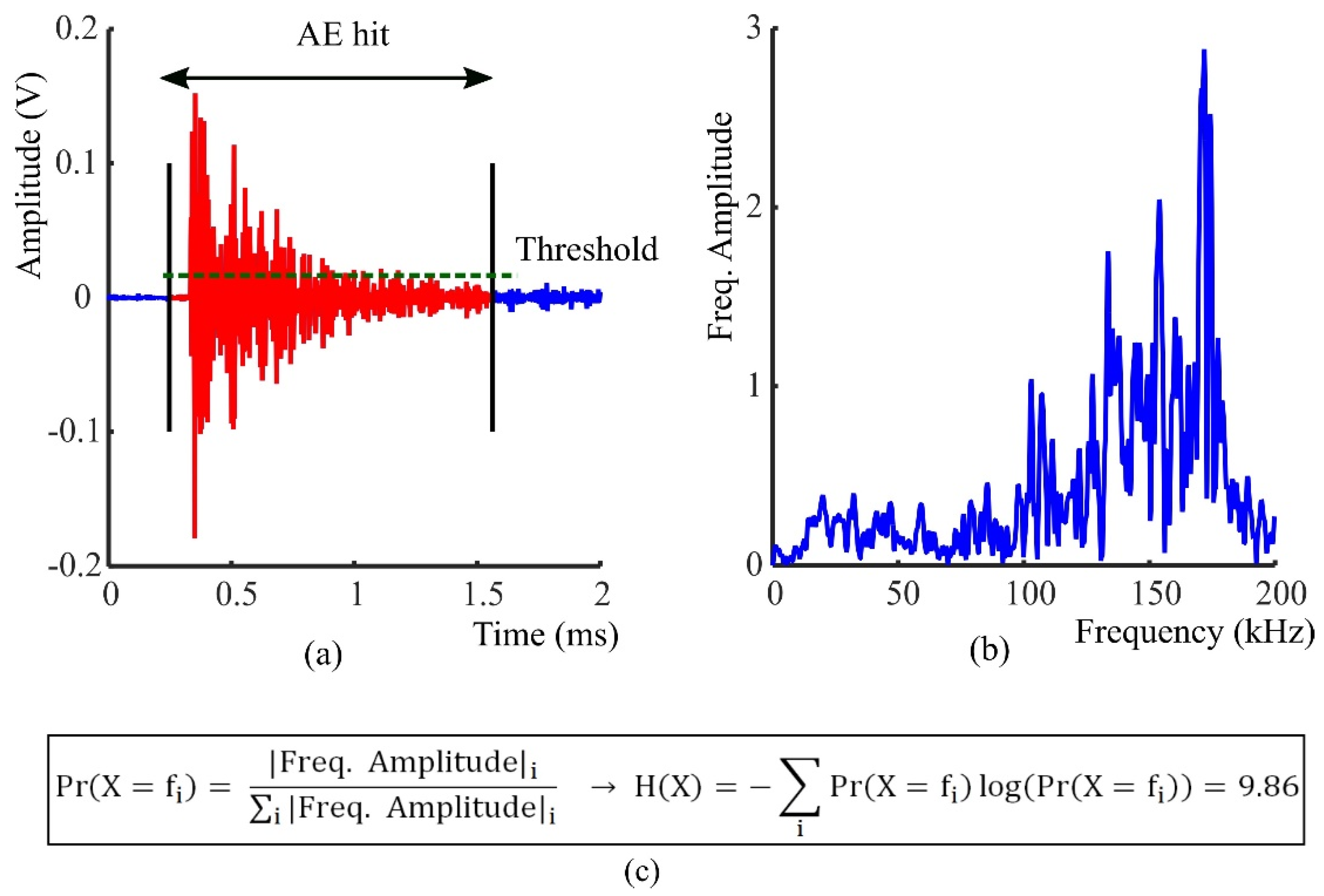
2. Materials and Methods
3. Results and Discussion
4. Conclusions
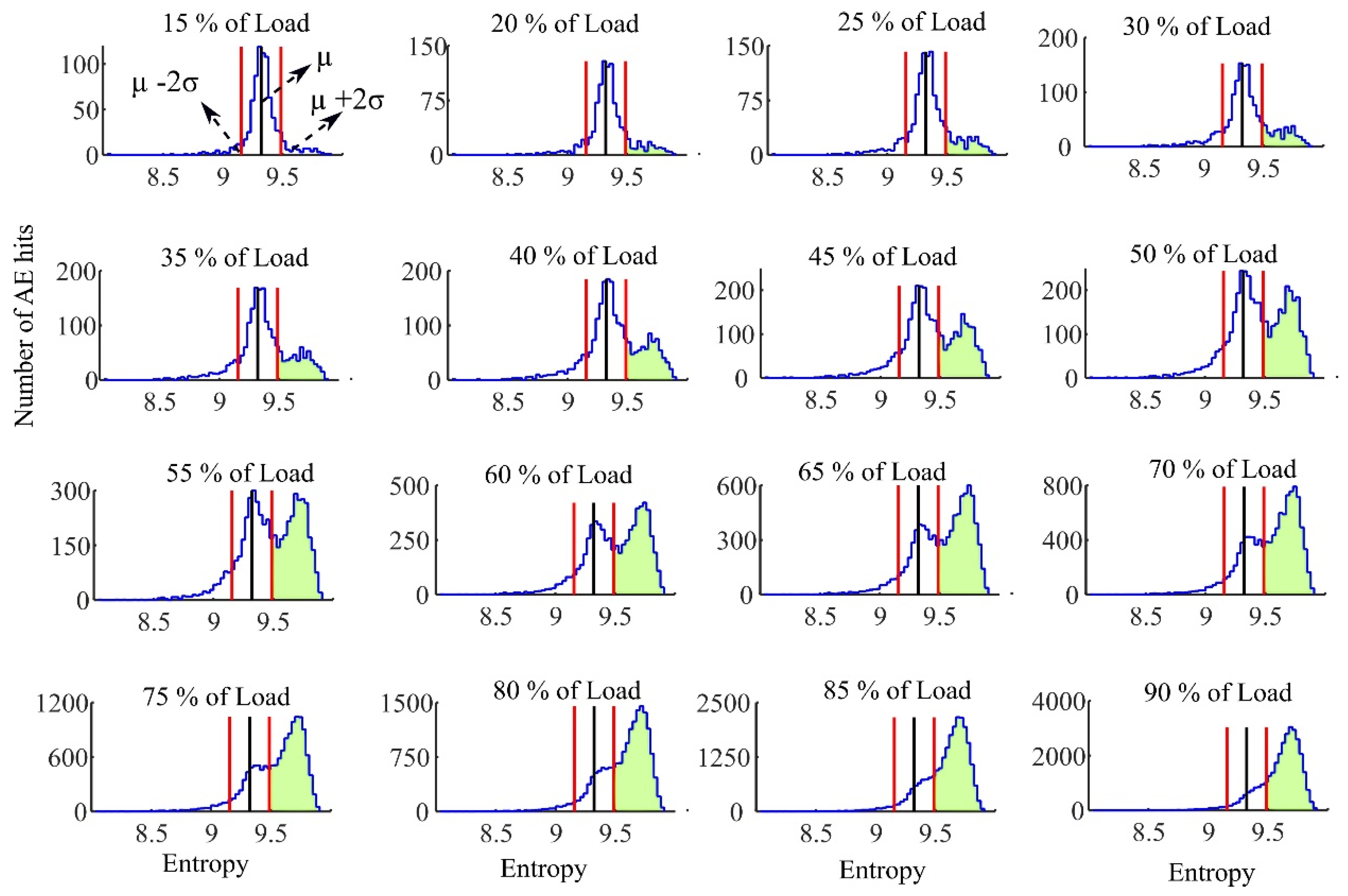
- When the load was less than 10–15% of the ultimate load, the AE entropy had approximately a normal distribution.
- When loads exceeded 10–15% of the ultimate load, AE hits with higher entropies were observed where the one-sided Chebyshev’s inequality (generated with the histogram of AE entropy at 10–15% of ultimate load) showed to be useful in detecting the emergence of a new entropy distribution.
- The emergence of a new distribution with high AE entropy events was correlated with loads exceeding the recommended service load limits for FRP rods. This occurred between 32–42% and 45–65% of ultimate load for GFRP and CFRP, respectively. These values correlated with the recommended maximum stress levels of 20–25% and 55–65% of the ultimate strength provided by standard codes for FRP bars such as ACI440.1R and CAN/CSA-S806-12.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uddin, N. (Ed.) Developments in Fiber-Reinforced Polymer (FRP) Composites for Civil Engineering; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Teng, J.G.; Yu, T.; Fernando, D. Strengthening of steel structures with fiber-reinforced polymer composites. J. Constr. Steel Res. 2012, 78, 131–143. [Google Scholar] [CrossRef]
- Busel, J.P. Fiber Reinforced Polymer (FRP) Composites Rebar; American Composites Manufacturers Association: Arlington, VA, USA, 2012. [Google Scholar]
- Greco, A.; Tsallis, C.; Rapisarda, A.; Pluchino, A.; Fichera, G.; Contrafatto, L. Acoustic emissions in compression of building materials: Q-statistics enables the anticipation of the breakdown point. Eur. Phys. J. Spec. Top. 2020, 229, 841–849. [Google Scholar] [CrossRef]
- Loukidis, A.; Triantis, D.; Stavrakas, I. Non-Extensive Statistical Analysis of Acoustic Emissions Recorded in Marble and Cement Mortar Specimens under Mechanical Load until Fracture. Entropy 2020, 22, 1115. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behaviour of fracture in triaxially deformed Etna basalt using acoustic emissions. Europhys. Lett. 2012, 97, 58002. [Google Scholar] [CrossRef]
- Kundu, A.; Eaton, M.J.; Al-Jumali, S.; Sikdar, S.; Pullin, R. Acoustic emission based damage localization in composites structures using Bayesian identification. In Proceedings of the 12th International Conference on Damage Assessment of Structures (DAMAS), Kitakyushu, Japan, 12 July 2017; pp. 10–12. [Google Scholar]
- Sikdar, S.; Ostachowicz, W.; Pal, J. Damage-induced acoustic emission source identification in an advanced sandwich composite structure. Compos. Struct. 2018, 202, 860–866. [Google Scholar] [CrossRef]
- Barre, S.; Benzeggagh, M.L. On the use of acoustic emission to investigate damage mechanisms in glass-fibre-reinforced polypropylene. Compos. Sci. Technol. 1994, 52, 369–376. [Google Scholar] [CrossRef]
- Ghaib, M.; Shateri, M.; Thomson, D.; Svecova, D. Study of FRP bars under tension using acoustic emission detection technique. J. Civ. Struct. Health Monit. 2018, 8, 285–300. [Google Scholar] [CrossRef]
- Tsamtsakis, D.; Wevers, M.; Demesster, P. Acoustic emission from CFRP laminates during fatigue loading. J. Reinf. Plast. Compos. 1998, 17, 1185–1201. [Google Scholar] [CrossRef]
- Valentin, D.; Bonniau, P.; Bunsell, A. Failure mechanism discrimination in carbon fiber-reinforced epoxy composites. Composites 1983, 14, 345–351. [Google Scholar] [CrossRef]
- Shateri, M.; Ghaib, M.; Svecova, D.; Thomson, D. On acoustic emission for damage detection and failure prediction in fiber reinforced polymer rods using pattern recognition analysis. J. Smart Mater. Struct. 2017, 26, 065023. [Google Scholar] [CrossRef]
- Godin, N.; Huguet, S.; Gaertner, R.; Salmon, L. Clustering of the acoustic emission signals collected during tensile tests on unidirectional glass/polyester composite using supervised and unsupervised classifiers. NDT E Int. 2004, 37, 253–264. [Google Scholar]
- De Oliveira, R.; Marques, A.T. Health monitoring of FRP using acoustic emission and artificial neural networks. Comput. Struct. 2008, 86, 367–373. [Google Scholar] [CrossRef]
- Ni, Q.; Iwamoto, M. Wavelet transform of acoustic emission signals in failure of model composites. Eng. Fract. Mech. 2002, 69, 717–728. [Google Scholar] [CrossRef]
- De Groot, P.J.; Wijnen, P.A.; Janssen, R.B. Real-time frequency determination of acoustic emission for different fracture mechanisms in carbon/epoxy composites. Compos. Sci. Technol. 1995, 55, 405–412. [Google Scholar] [CrossRef]
- Ramirez-Jimenez, C.R.; Papadakis, N.; Reynolds, N.; Gan, T.H.; Purnell, P.; Pharaoh, M. Identification of failure modes in glass/polypropylene composites by means of the primary frequency content of the acoustic emission event. Compos. Sci. Technol. 2004, 64, 1819–1827. [Google Scholar] [CrossRef]
- Bussiba, A.; Kupiec, M.; Piat, R.; Böhlke, T. Fracture characterization of C/C composites under various stress modes by monitoring both mechanical and acoustic responses. Carbon 2008, 46, 618–630. [Google Scholar] [CrossRef]
- Qi, G. Wavelet-based AE characterization of composite materials. NDT E Int. 2000, 33, 133–144. [Google Scholar]
- Loutas, T.H.; Kostopoulos, V.; Ramirez-Jimenez, C.; Pharaoh, M. Damage evolution in center-holed glass/polyester composites under quasi-static loading using time/frequency analysis of acoustic emission monitored waveforms. Compos. Sci. Technol. 2006, 66, 1366–1375. [Google Scholar] [CrossRef]
- Unnthorsson, R.; Runarsson, T.; Jonsson, M. AE entropy for the condition monitoring of CFRP subjected to cyclic fatigue. J. Acoust. Emiss. 2009, 26, 262–269. [Google Scholar]
- Carpinteri, A.; Lacidogna, G.; Accornero, F.; Mpalaskas, A.C.; Matikas, T.F.; Aggelis, D.G. Influence of damage in the acoustic emission parameters. Cem. Concr. Compos. 2013, 44, 9–16. [Google Scholar] [CrossRef]
- Sagar, R.V.; Prasad, B.R. An experimental study on acoustic emission energy as a quantitative measure of size independent specific fracture energy of concrete beams. Constr. Build. Mater. 2011, 25, 2349–2357. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Gallego, A.; Vico, J.M. An acoustic emission energy index for damage evaluation of reinforced concrete slabs under seismic loads. Struct. Health Monit. 2012, 11, 69–81. [Google Scholar] [CrossRef]
- Gutkin, R.; Green, C.; Vangrattanachai, S.; Pinho, S.; Robinson, P.; Curtis, P. On acoustic emission for failure investigation in CFRP: Pattern recognition and peak frequency analyses. Mech. Syst. Signal Process. 2011, 25, 1393–1407. [Google Scholar] [CrossRef]
- Savage, I.R. Probability inequalities of the tchebychefftype, Journal of Research 350 of the National Bureau of Standards-B. Math. Math. Phys. B 1961, 65, 211–222. [Google Scholar]
- Hsu, N.; Breckenridge, F. Characterization of acoustic emission sensors. Mater. Eval. 1981, 39, 60–68. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Grossmann, A.; Morlet, J. Decomposition of Hardy functions into square integrable wavelets of constant shape. SIAM J. Math. Anal. 1984, 15, 723–736. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1992. [Google Scholar]
- Marec, A.; Thomas, J.; El Guerjouma, R. Damage characterization of polymer-based composite materials: Multivariable analysis and wavelet transform for clustering acoustic emission data. Mech. Syst. Signal Process. 2008, 22, 1441–1464. [Google Scholar] [CrossRef]
- Bienaymé, I.J. Considérations à l’appui de la découverte de Laplace sur la loi de probabilité dans la méthode des moindres carrés. Compte Rendu des Siances de 1 ’Acadimie des Sciences Paris 1853, 37, 309–324. [Google Scholar]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not usestandard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]





| Bar Type | Diameter (mm) | Gauge Length (mm) | Surface Coating |
|---|---|---|---|
| CFRP size 2 | 6 | 240 | Sand coated |
| CFRP size 4 | 13 | 520 | Sand coated |
| GFRP size 4 | 13 | 520 | Undulation and sand coated |
| GFRP size 6 | 19 | 760 | Undulation and sand coated |
| Bar Type | No. Specimens | Displacement Rate | Ultimate Load (kN) |
|---|---|---|---|
| CFRP size 2 | 3 | 0.8 | 78 |
| CFRP size 4 | 2 | 1.8 | 250 |
| GFRP size 4 | 2 | 4 | 117 |
| GFRP size 6 | 2 | 6 | 240 |
| FRP Bar Type | Chebyshev’s t = Threshold Crossing (Percent of Ultimate Load %) | ||
|---|---|---|---|
| FFT Entropy | WT Entropy | ||
| CFRP size 2 | Specimen1 | 65 | 65 |
| Specimen2 | 45 | 45 | |
| Specimen3 | 55 | 55 | |
| Average | 53.33 | ||
| CFRP size 2 | Specimen1 | 57 | 48 |
| Specimen2 | 50 | 49 | |
| Average | 51 | ||
| GFRP size 4 | Specimen1 | 34 | 32 |
| Specimen2 | 37 | 35 | |
| Average | 34.5 | ||
| GFRP size 6 | Specimen1 | 42 | 32 |
| Specimen2 | 38 | 36 | |
| Average | 37 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shateri, M.; Ghaib, M.; Svecova, D.; Thomson, D. Acoustic Emission Signal Entropy as a Means to Estimate Loads in Fiber Reinforced Polymer Rods. Sensors 2021, 21, 1089. https://doi.org/10.3390/s21041089
Shateri M, Ghaib M, Svecova D, Thomson D. Acoustic Emission Signal Entropy as a Means to Estimate Loads in Fiber Reinforced Polymer Rods. Sensors. 2021; 21(4):1089. https://doi.org/10.3390/s21041089
Chicago/Turabian StyleShateri, Mohammadhadi, Maha Ghaib, Dagmar Svecova, and Douglas Thomson. 2021. "Acoustic Emission Signal Entropy as a Means to Estimate Loads in Fiber Reinforced Polymer Rods" Sensors 21, no. 4: 1089. https://doi.org/10.3390/s21041089
APA StyleShateri, M., Ghaib, M., Svecova, D., & Thomson, D. (2021). Acoustic Emission Signal Entropy as a Means to Estimate Loads in Fiber Reinforced Polymer Rods. Sensors, 21(4), 1089. https://doi.org/10.3390/s21041089






