Diagnosis of Bone Mineral Density Based on Backscattering Resonance Phenomenon Using Coregistered Functional Laser Photoacoustic and Ultrasonic Probes
Abstract
:1. Introduction
2. Materials and Methods
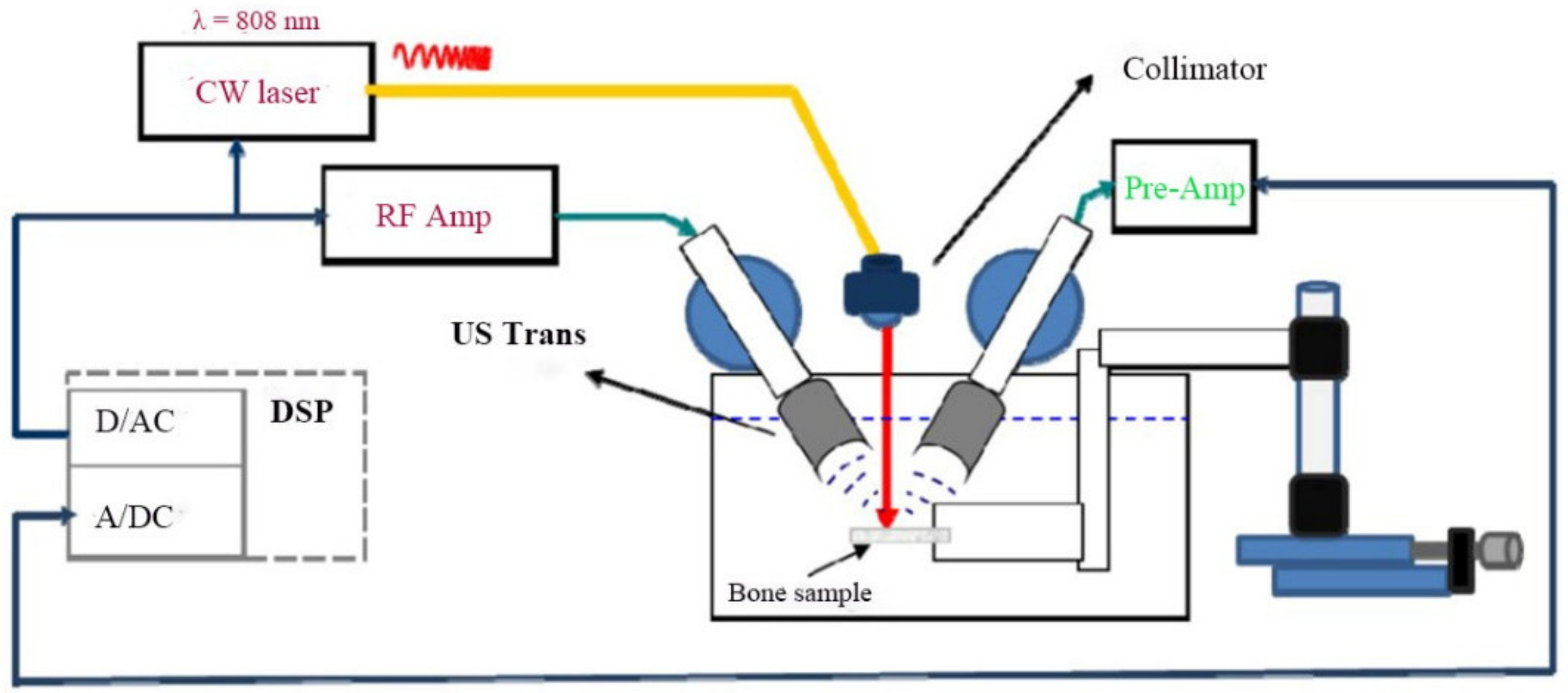
2.1. Experimental Setup
2.2. Bone Specimens
2.3. µCT Scanning
2.4. Photoacoustic Backscattering
2.5. Quantitative Ultrasound (QUS) and Photoacoustic (PA) Measurements
3. Results
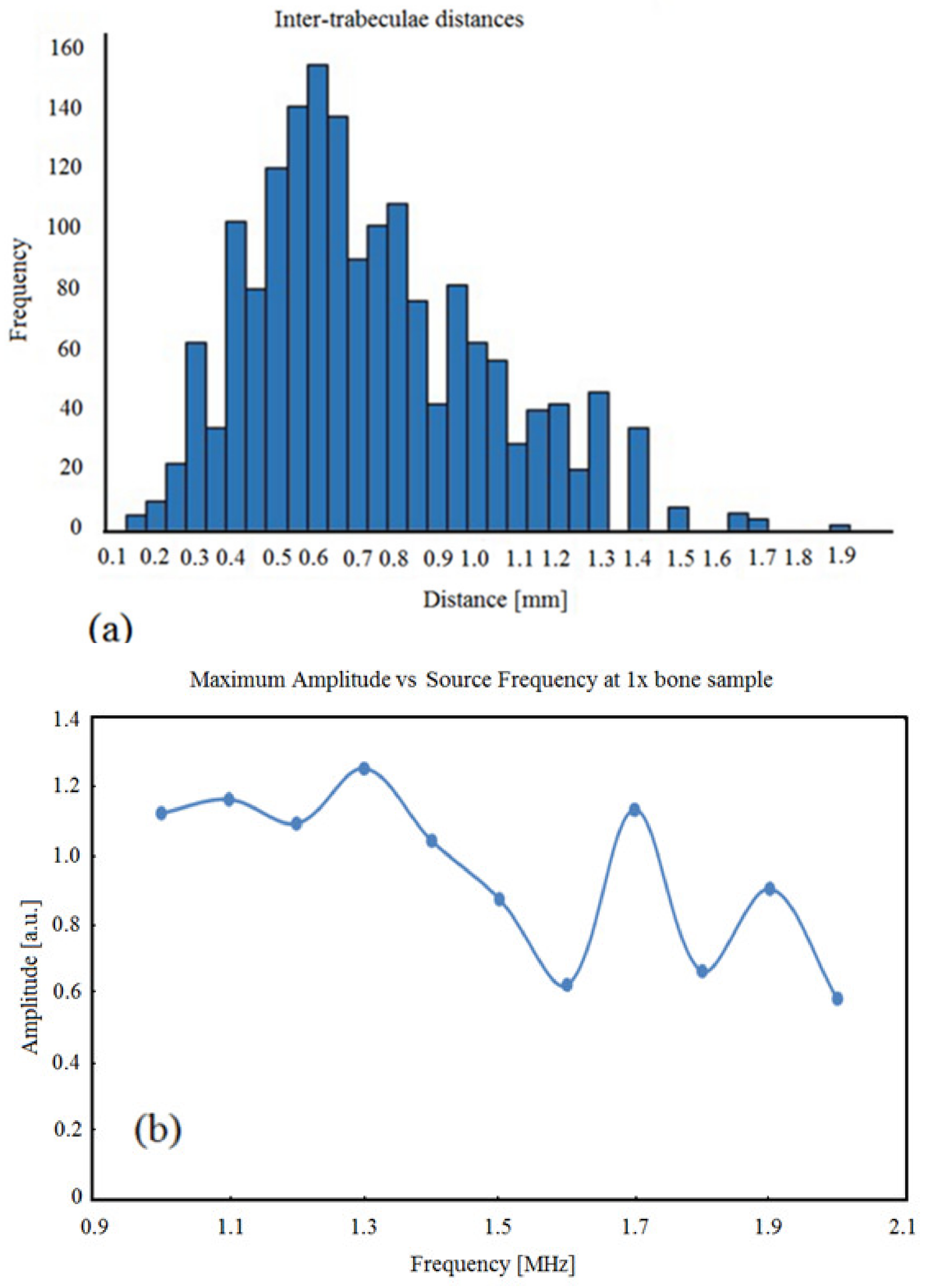
3.1. BoneSamples and µCT Scanning
3.2. Simulation Results
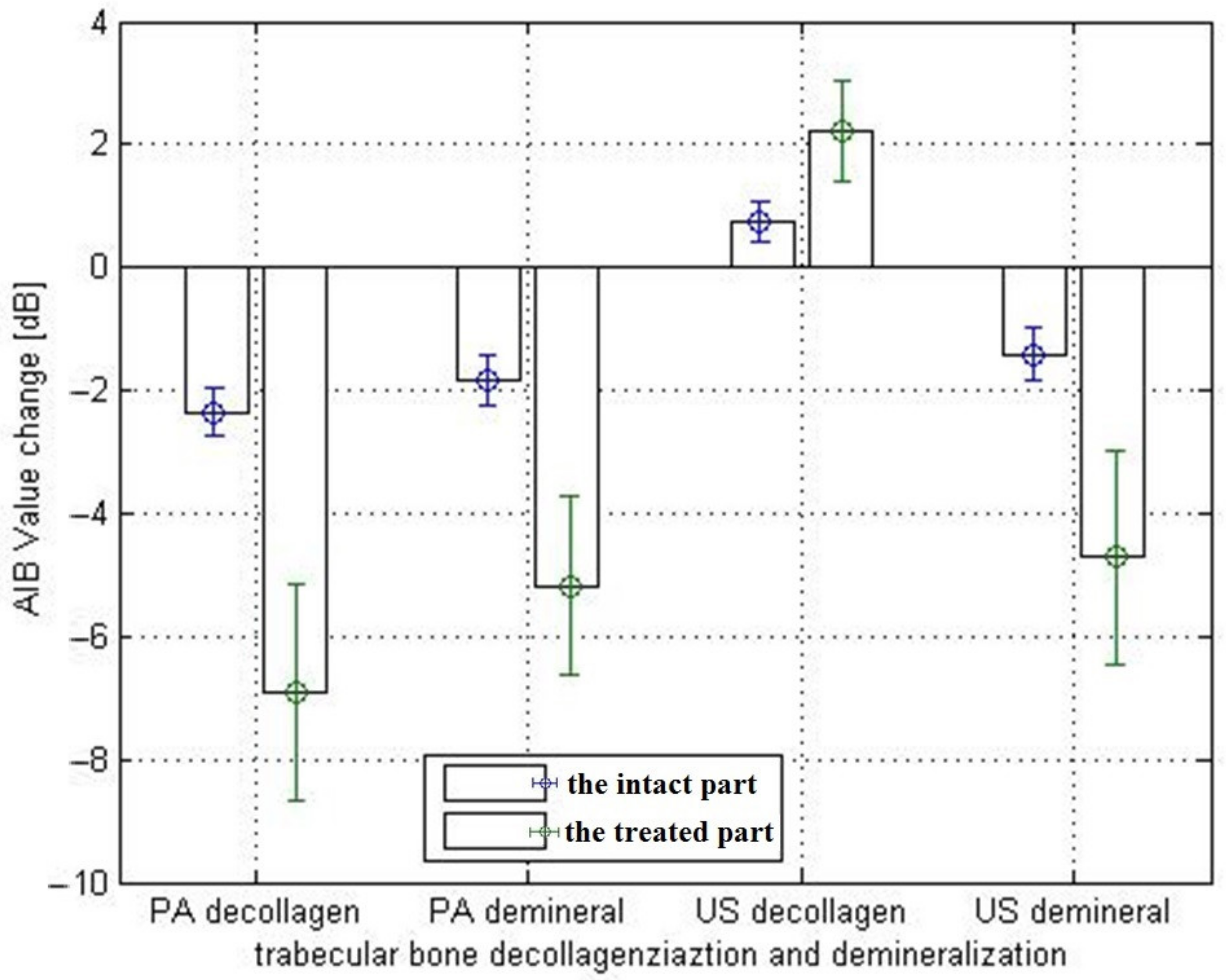
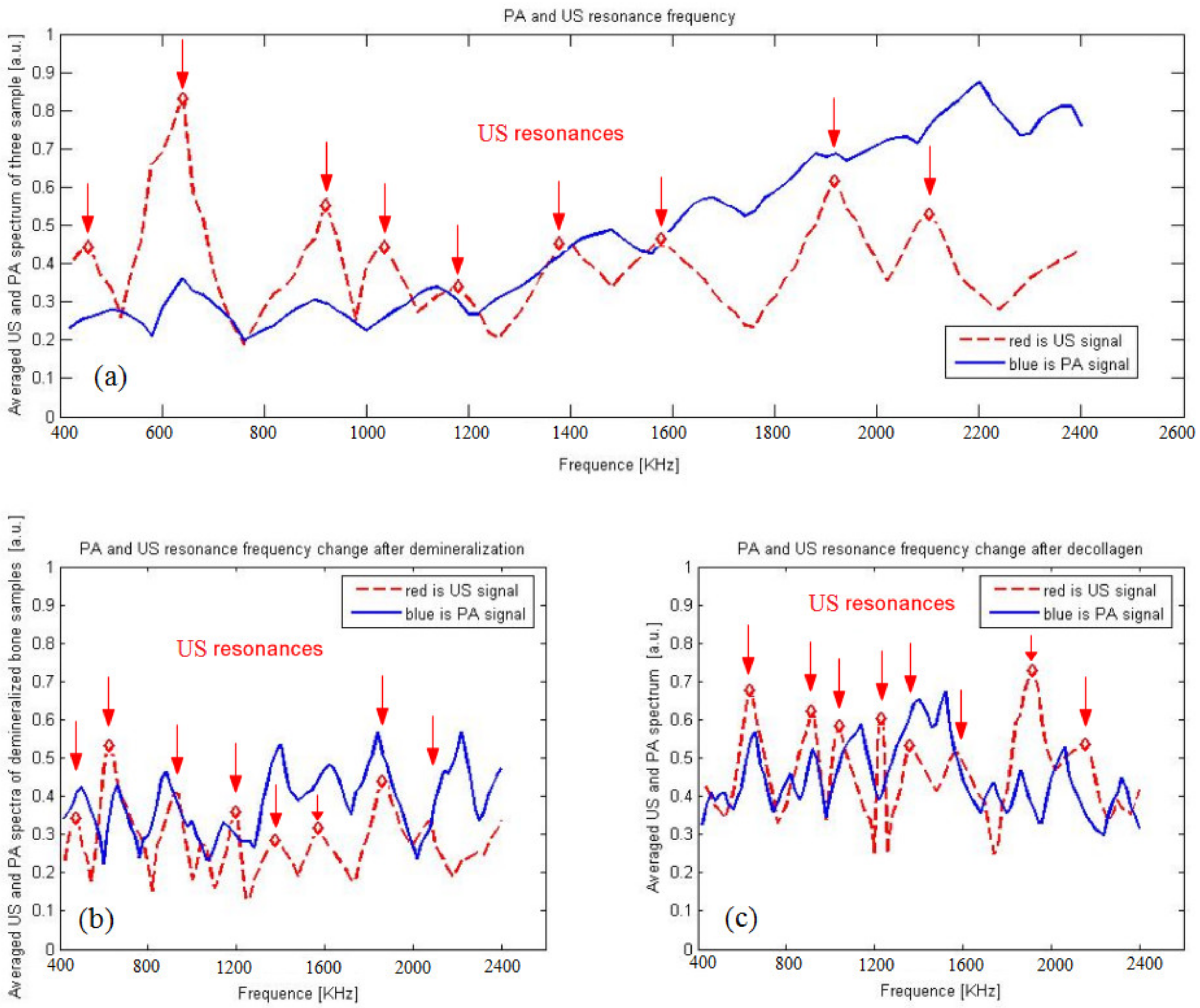
3.3. Photoacoustic and Ultrasound AIB Comparison
3.4. Actual Experiment Results
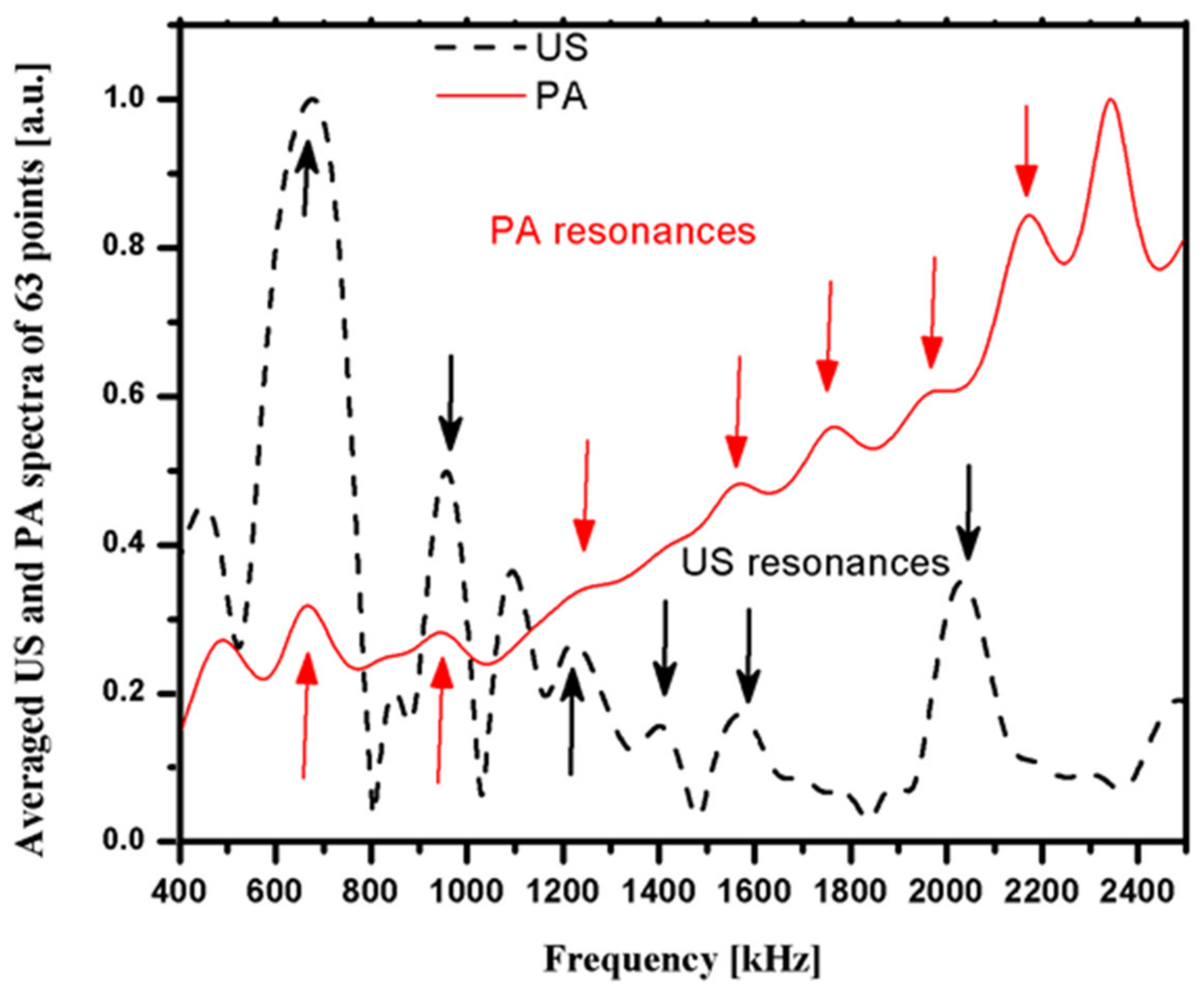
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- NIH Consensus Development Panel on Osteoporosis Prevention, Diagnosis, and Therapy. Osteoporosis prevention, diagnosis, and therapy. JAMA 2001, 285, 785–795. [Google Scholar] [CrossRef] [PubMed]
- Choksi, P.; Jepsen, K.J.; Clines, G.A. The challenges of diagnosing osteoporosis and the limitations of currently available tools. Clin. Diabetes Endocrinol. 2018, 4, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geusens, P.; Geel, T.V.; Huntjens, K.; van Helden, S.; Bours, S.; Bergh, J.V.D. Clinical fractures beyond low BMD. Int. J. Clin. Rheumatol. 2011, 6, 411–421. [Google Scholar] [CrossRef]
- Noale, M.; Maqqi, S.; Gonnelli, S.; Limonqi, F.; Zanoni, S.; Rozzini, R.; Crepaldi, G. Quantitative ultrasound criteria for risk stratification in clinical practice: A comparative assessment. Ultrasound Med. Biol. 2012, 38, 1138–1144. [Google Scholar] [CrossRef]
- Wang, X.D.; Ruud, A.B.; Johan, M.K.; Agrawal, C.M. The role of collagen in determining bone mechanical properties. J. Ortho. Res. 2001, 19, 1021–1026. [Google Scholar] [CrossRef]
- Carrin, S.V.; Garnero, P.; Delmas, P.D. The role of collagen in bone strength. Osteoporos. Int. 2006, 17, 319–336. [Google Scholar] [CrossRef]
- Bréban, S.; Briot, K.; Kolta, S.; Paternotte, S.; Ghazi, M.; Fechtenbaum, J.; Roux, C. Identification of rheumatoid arthritis patients with vertebral fractures using bone mineral density and trabecular bone score. J. Clin. Densitom. 2012, 15, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Krueger, D.; Fidler, E.; Libber, J.; Aubry-Rozier, B.; Hans, D.; Binkley, N. Spine Trabecular Bone Score Subsequent to Bone Mineral Density Improves Fracture Discrimination in Women. J. Clin. Densitom. 2013, 15, 482–487. [Google Scholar] [CrossRef]
- Chaffai, S.; Peyrin, F.; Nuzzo, S.; Porcher, R.; Berger, G.; Laugier, P. Ultrasonic characterization of human cancellous bone using transmission and backscatter measurements: Relationships to density and microstructure. Bone 2002, 30, 229–237. [Google Scholar] [CrossRef]
- Charles, H.T. Bone Strength: Current Concepts. Ann. N. Y. Acad. Sci. 2006, 1068, 429–446. [Google Scholar]
- Paschalis, E.P.; Shane, E.; Lyritis, G.; Skarantavos, G.; Mendelsohn, R.; Boskey, A.L. Bone fragility and collagen cross-links. J. Bone Miner. Res. 2004, 19, 2000–2004. [Google Scholar] [CrossRef]
- Wynnyckyj, C.; Willett, T.L.; Omelon, S.; Wang, J.; Wang, Z.; Grynpas, M.D. Changes in bone fatigue resistance due to collagen degradation. J. Orthop. Res. 2011, 29, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Willett, T.L.; Sutty, S.; Gaspar, A.; Avery, N.; Grynpas, M. In vitro non-enzymatic ribation reduces post-yield strain accommodation in cortical bone. Bone 2013, 52, 611–622. [Google Scholar] [CrossRef] [PubMed]
- Launey, M.E.; Buehler, M.J.; Ritchie, R.O. On the mechanistic origins of toughness in bone. Annu. Rev. Mater. Res. 2010, 40, 25–53. [Google Scholar] [CrossRef] [Green Version]
- Georg, E.F.H.; Johannes, H.K.; Hassenkama, T.; James, C.W. Influence of the degradation of the organic matrix on the microscopic fracture behavior of trabecular bone. Bone 2004, 35, 1013–1022. [Google Scholar]
- Qin, Y.X.; Lin, W.; Mittra, E.; Xia, Y.; Cheng, J.; Judex, S.; Rubin, C.; Muller, R. Prediction of trabecular bone qualitative properties using scanning quantitative ultrasound. Acta Astronaut. 2013, 92, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Karjalainen, J.P.; Toyras, J.; Riekkinen, O.; Hakulinen, M.; Jurvelin, J.S. Ultrasound backscatter imaging provides frequency-dependent information on structure, composition and mechanical properties of human trabecular bone. Ultrasound Med. Biol. 2009, 35, 1376–1384. [Google Scholar] [CrossRef]
- Rauma, P.H.; Pasco, J.A.; Berk, M.; Stuart, A.L.; Honkanen, H.K.; Honkanen, R.J.; Hodge, J.M.; Williams, L.J. The association between use of antidepressants and bone quality using quantitative heel ultrasound. Aust. N. Z. J. Psychiatry 2015, 49, 437–443. [Google Scholar] [CrossRef]
- Hakulinen, M.A.; Day, J.S.; Toyras, J.; Timonen, M.; Kroger, H.; Weinans, H.; Kiviranta, I.; Jurvelin, J.S. Prediction of density and mechanical properties of human trabecular bone in vitro by using ultrasound transmission and backscattering measurements at 0.2–6.7 MHz frequency range. Phys. Med. Biol. 2005, 50, 1629–1642. [Google Scholar] [CrossRef]
- Hakulinen, M.A.; Day, J.S.; Toyras, J.; Weinans, H.; Jurvelin, J.S. Ultrasonic characterization of human trabecular bone microstructure. Phys. Med. Biol. 2006, 51, 1633–1648. [Google Scholar] [CrossRef]
- Lashkari, B.; Mandelis, A. Coregistered photoacoustic and ultrasonic signatures of early bone density variations. J. Biomed. Opt. 2014, 19, 36015. [Google Scholar] [CrossRef] [PubMed]
- Lashkari, B.; Yang, L.; Mandelis, A. The application of backscattered ultrasound and photoacoustic signals for assessment of bone collagen and mineral contents. Quant. Imaging Med. Surg. 2015, 5, 46–56. [Google Scholar]
- Lashkari, B.; Mandelis, A. Linear frequency modulation photoacoustic radar: Optimal bandwidth for frequency-domain imaging of turbid media. J. Acoust. Soc. Am. 2011, 130, 1313–1324. [Google Scholar] [CrossRef]
- Lee, K., II; Choi, M.J. Frequency-dependent attenuation and backscatter coefficients in bovine trabecular bone from 0.2 to 1.2 MHz. J. Acoust. Soc. Am. 2012, 131, EL67–EL73. [Google Scholar]
- Ehrlich, H.; Koutsoukos, P.G.; Demadis, K.D.; Pokrovsky, O.S. Principles of demineralization Modern strategies for the isolation of organic frameworks, Part Ⅱ. Decalcification. Micron 2009, 40, 169–193. [Google Scholar] [CrossRef]
- Hoffmeister, B.K.; Whitten, S.A.; Kaste, S.C.; Rho, J.Y. Effect of collagen content and Mineral Content on the High-frequency Ultrasonic Properties of Human Cancellous Bone. Osteoporos Int. 2002, 13, 26–32. [Google Scholar] [CrossRef] [PubMed]
- Rajapakse, C.S.; Magland, J.F.; Wald, M.J.; Liu, X.S.; Zhang, X.H.; Guo, X.E.; Wehrli, F.W. Computational biomechanics of the distal tibia from high resolution MR and micro-CT images. Bone 2010, 47, 556–563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keyak, J.H.; Sigurdsson, S.; Karlsdottir, G.S.; Oskarsdottir, D.; Sigmarsdottir, A.; Kornak, J.; Harris, T.B.; Sigurdsson, G.; Jonsson, B.Y.; Siggeirsdottir, K.; et al. Effect of finite element model loading condition on fracture risk assessment in men and women: The AGES-Reykjavik study. Bone 2013, 57, 18–29. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Wang, Z.; Wang, L.; Li, T.; He, S.; Li, L.; Li, X.; Liu, S.; Li, J.; Li, S.; et al. A dual-mode nanoparticle based on natural biomaterials for photoacoustic and magnetic resonance imaging of bone mesenchymal stem cells in vivo. RSC Adv. 2019, 9, 35003–35010. [Google Scholar] [CrossRef] [Green Version]
- Nishiyama, K.K.; Ito, M.; Harada, A.; Boyd, S.K. Classification of women with and without hip fracture based on quantitative computed tomography and finite element analysis. Osteoporos. Int. 2014, 25, 619–626. [Google Scholar] [CrossRef]
- Yang, L.; Lashkari, B.; Tan, J.W.Y.; Mandelis, A. Photoacoustic and ultrasound imaging of cancellous bone tissue. J. Biomed. Opt. 2015, 20, 076016. [Google Scholar] [CrossRef] [PubMed]
- Vayron, R.; Nguyen, V.-H.; Lecuelle, B.; Lomami, H.; Meningaud, J.-P.; Bosc, R.; Haiat, G. Comparison of Resonance Frequency Analysis and of Quantitative Ultrasound to Assess Dental Implant Osseointegration. Sensors 2018, 18, 1397. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Samples | Intact Part | Treated Part | |||
|---|---|---|---|---|---|
| US/μCT | PA/μCT | US/μCT | PA/μCT | ||
| Demineralized | 1# | 0.632 | 0.327 | 0.375 | 0.052 |
| 2# | 0.579 | 0.213 | 0.252 | −0.323 | |
| 3# | 0.536 | −0.107 | 0.113 | −0.357 | |
| Average | 0.582 | 0.144 | 0.247 | −0.209 | |
| Decollagenized | 1# | 0.511 | 0.233 | 0.394 | −0.078 |
| 2# | 0.529 | 0.324 | 0.287 | −0.116 | |
| 3# | 0.468 | 0.156 | −0.132 | −0.096 | |
| Average | 0.503 | 0.238 | 0.183 | −0.097 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Chen, C.; Zhang, Z.; Wei, X. Diagnosis of Bone Mineral Density Based on Backscattering Resonance Phenomenon Using Coregistered Functional Laser Photoacoustic and Ultrasonic Probes. Sensors 2021, 21, 8243. https://doi.org/10.3390/s21248243
Yang L, Chen C, Zhang Z, Wei X. Diagnosis of Bone Mineral Density Based on Backscattering Resonance Phenomenon Using Coregistered Functional Laser Photoacoustic and Ultrasonic Probes. Sensors. 2021; 21(24):8243. https://doi.org/10.3390/s21248243
Chicago/Turabian StyleYang, Lifeng, Chulin Chen, Zhaojiang Zhang, and Xin Wei. 2021. "Diagnosis of Bone Mineral Density Based on Backscattering Resonance Phenomenon Using Coregistered Functional Laser Photoacoustic and Ultrasonic Probes" Sensors 21, no. 24: 8243. https://doi.org/10.3390/s21248243
APA StyleYang, L., Chen, C., Zhang, Z., & Wei, X. (2021). Diagnosis of Bone Mineral Density Based on Backscattering Resonance Phenomenon Using Coregistered Functional Laser Photoacoustic and Ultrasonic Probes. Sensors, 21(24), 8243. https://doi.org/10.3390/s21248243






