Using a Development Platform with an STM32 Processor to Prototype an Inexpensive 4-DoF Delta Parallel Robot
Abstract
:1. Introduction
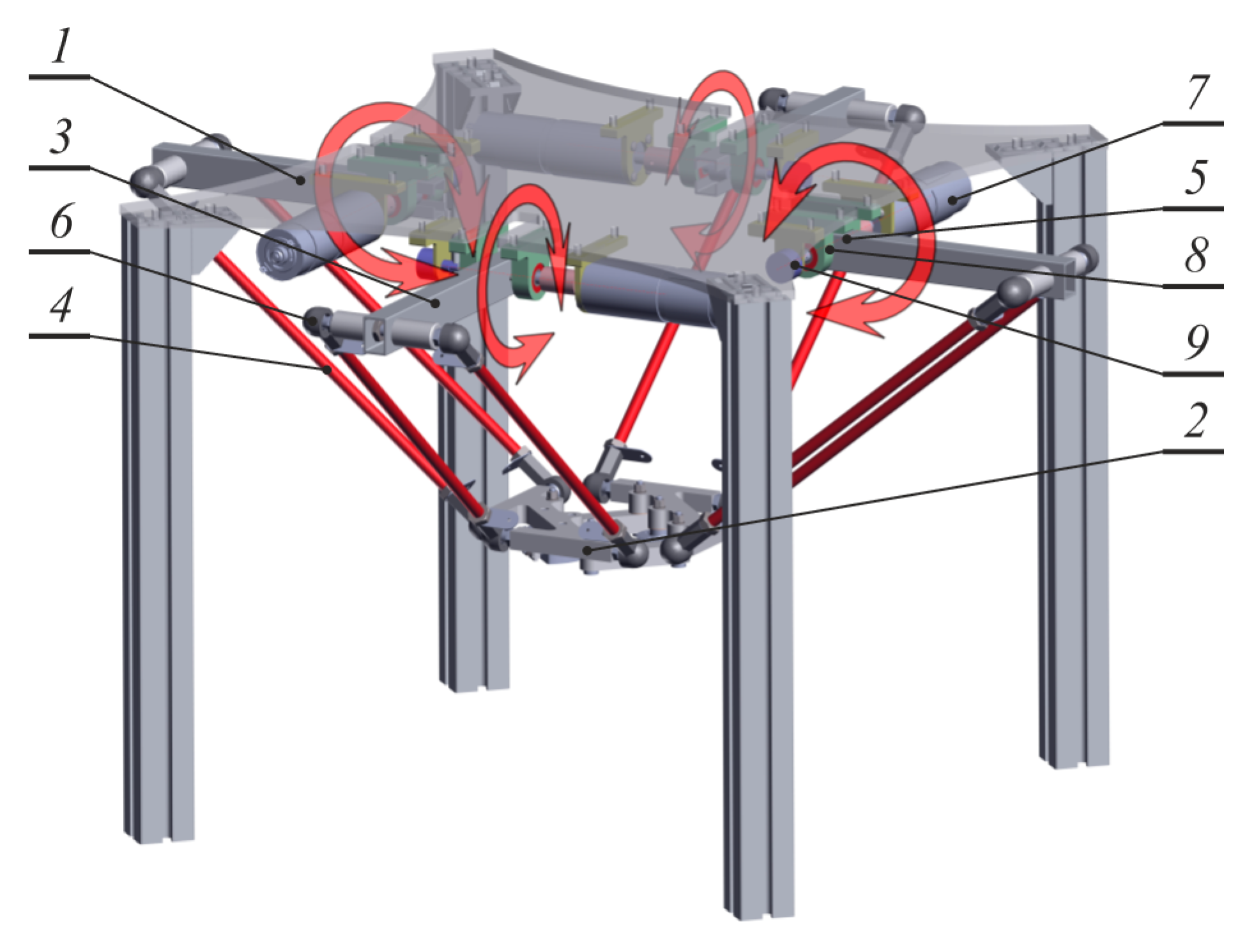
2. Solid Model of Delta 4-Dof Manipulator
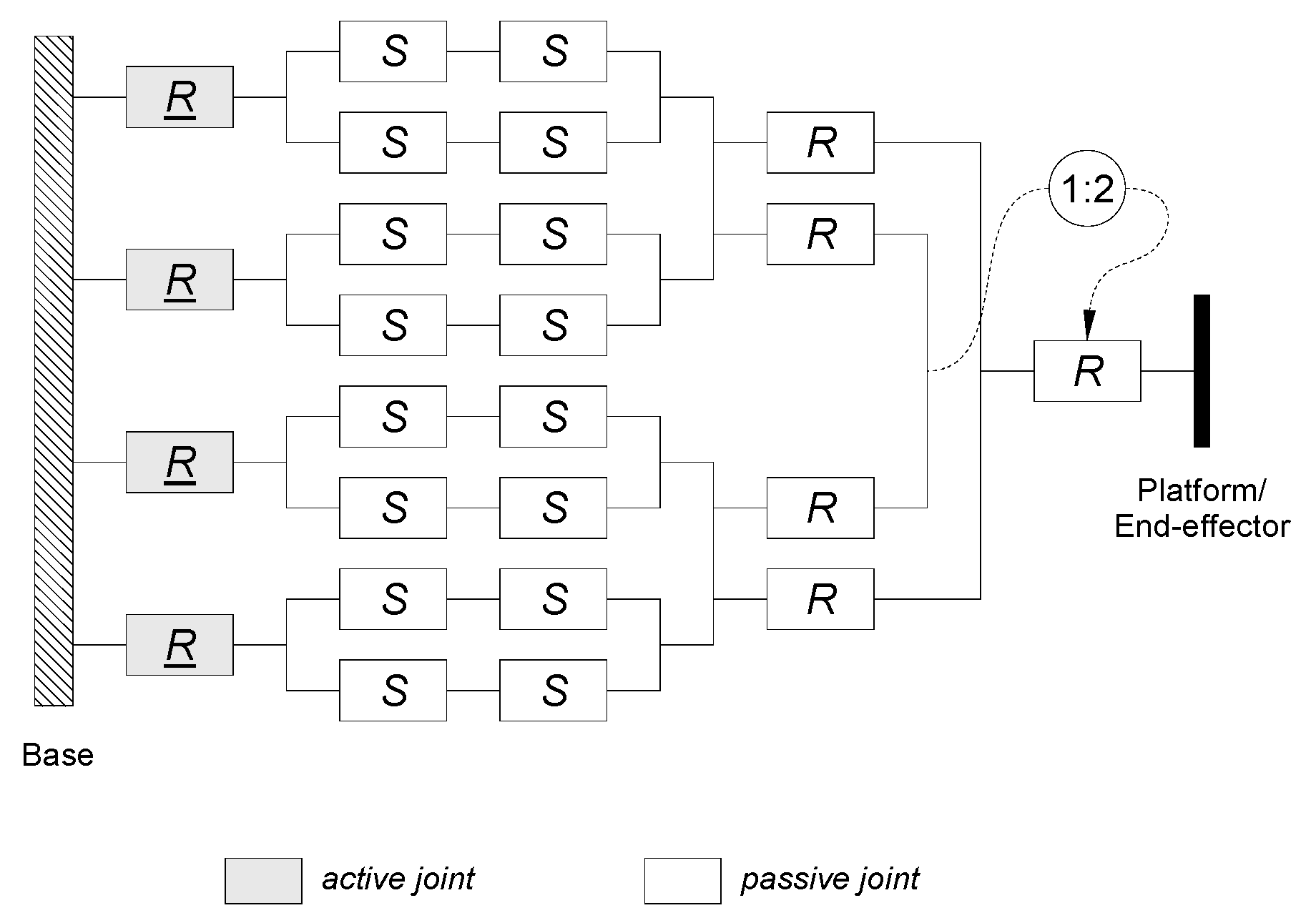
3. Kinematic Analysis of Delta 4-DoF Manipulator
3.1. Description of Kinematics of Delta 4-DoF Manipulator
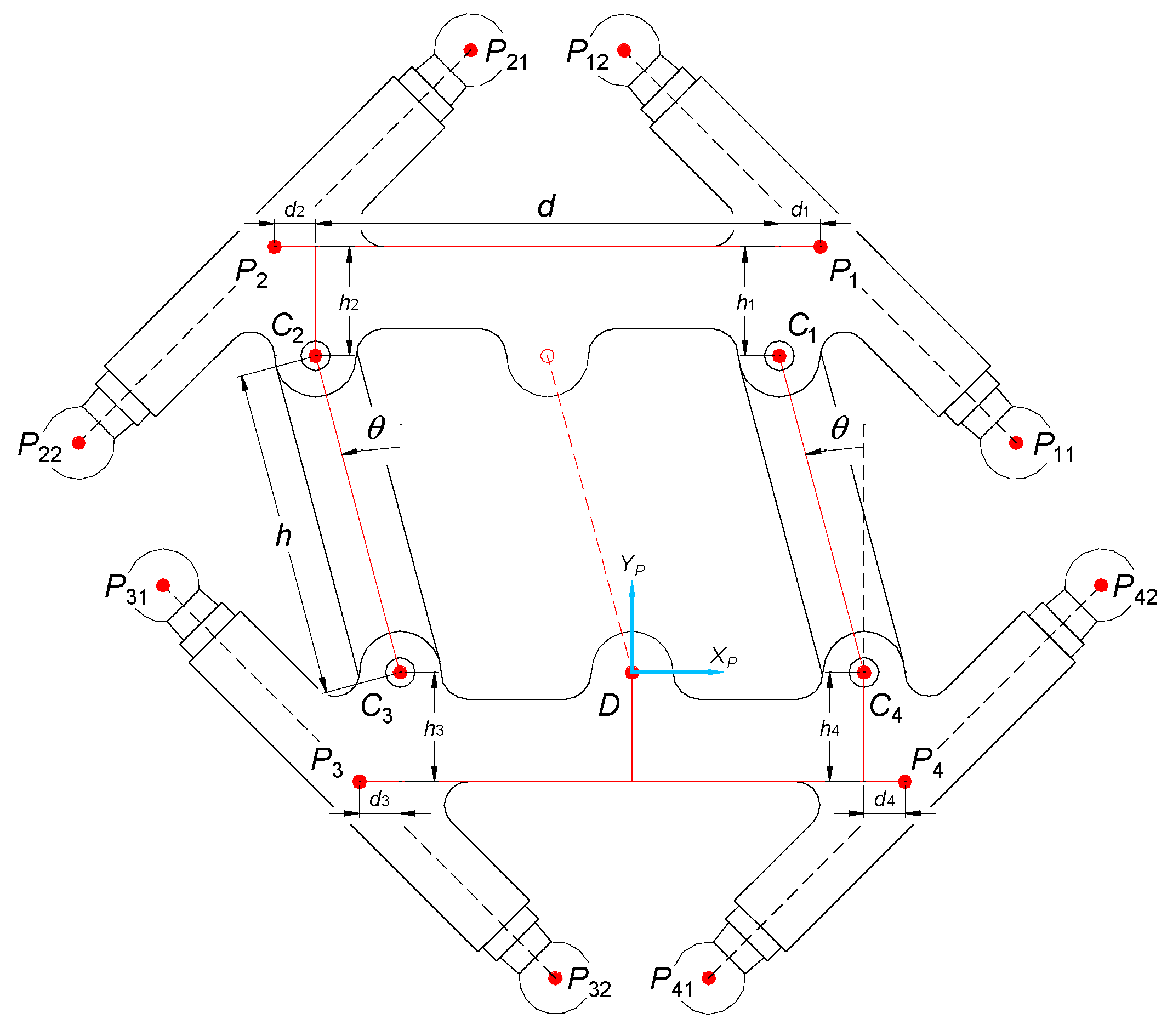
3.2. Inverse Kinematics of Delta 4-DoF Manipulator
- d—length of the main element of the moveable platform (along the axis x),
- h—length of the connectors of the articulated quadrangle of the moveable platform (measured between points C1 and C4 and C2 and C3),
- di and hi—distances between points Ci and Pi (along the axes x and y, respectively),
- θ—rotary angle of the articulated quadrangle of the moveable platform that results from its constructional limitations (±45°, without the mechanism increasing the range of movement).
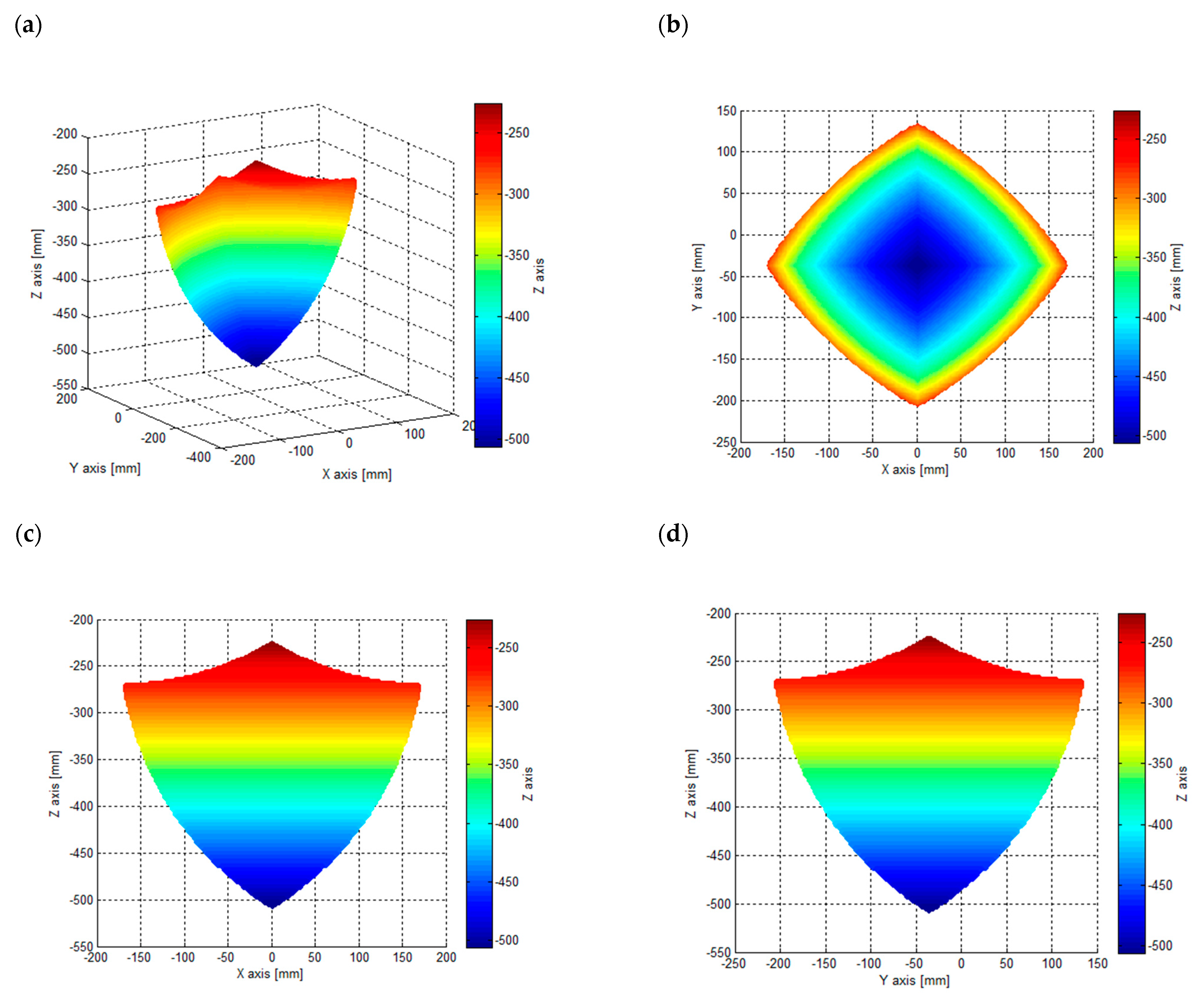
3.3. Manipulator Operating Space
4. Design of the Control System of Delta 4-Dof Manipulator
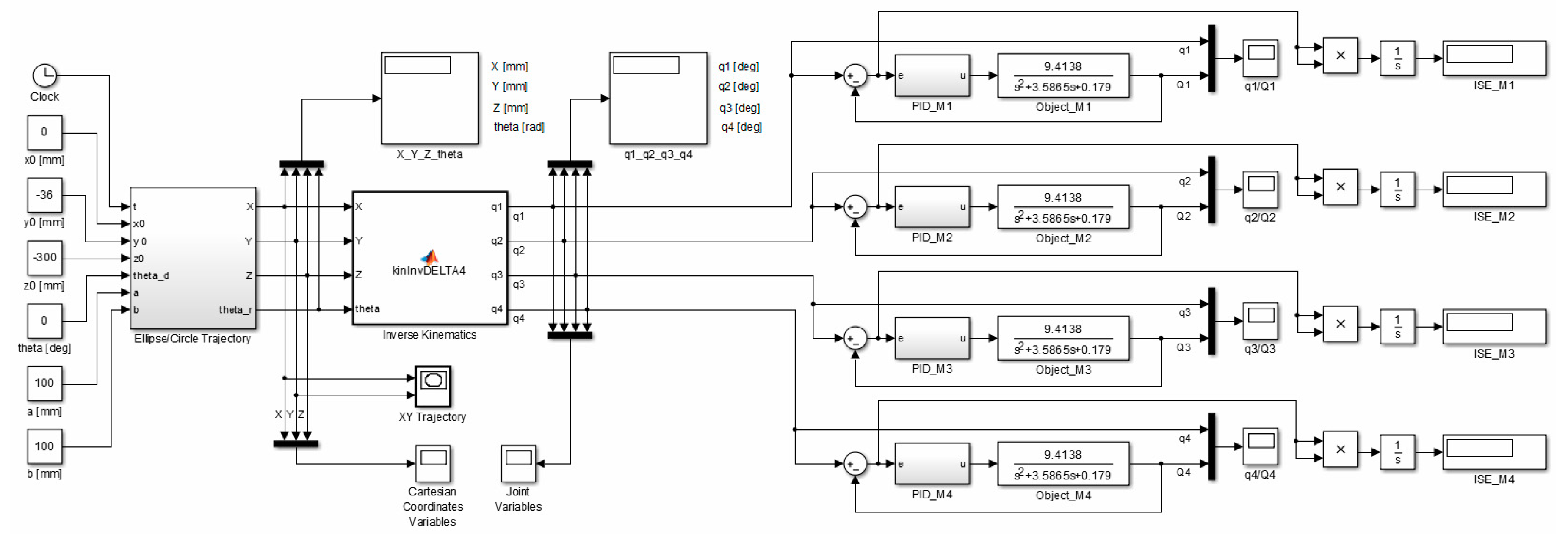
4.1. Robot Control System
4.2. Structure of Robot Control System
4.3. Identification of the Mathematical Model of DC Motor with a Gearbox
4.4. Choice of Type and Settings of the Controller
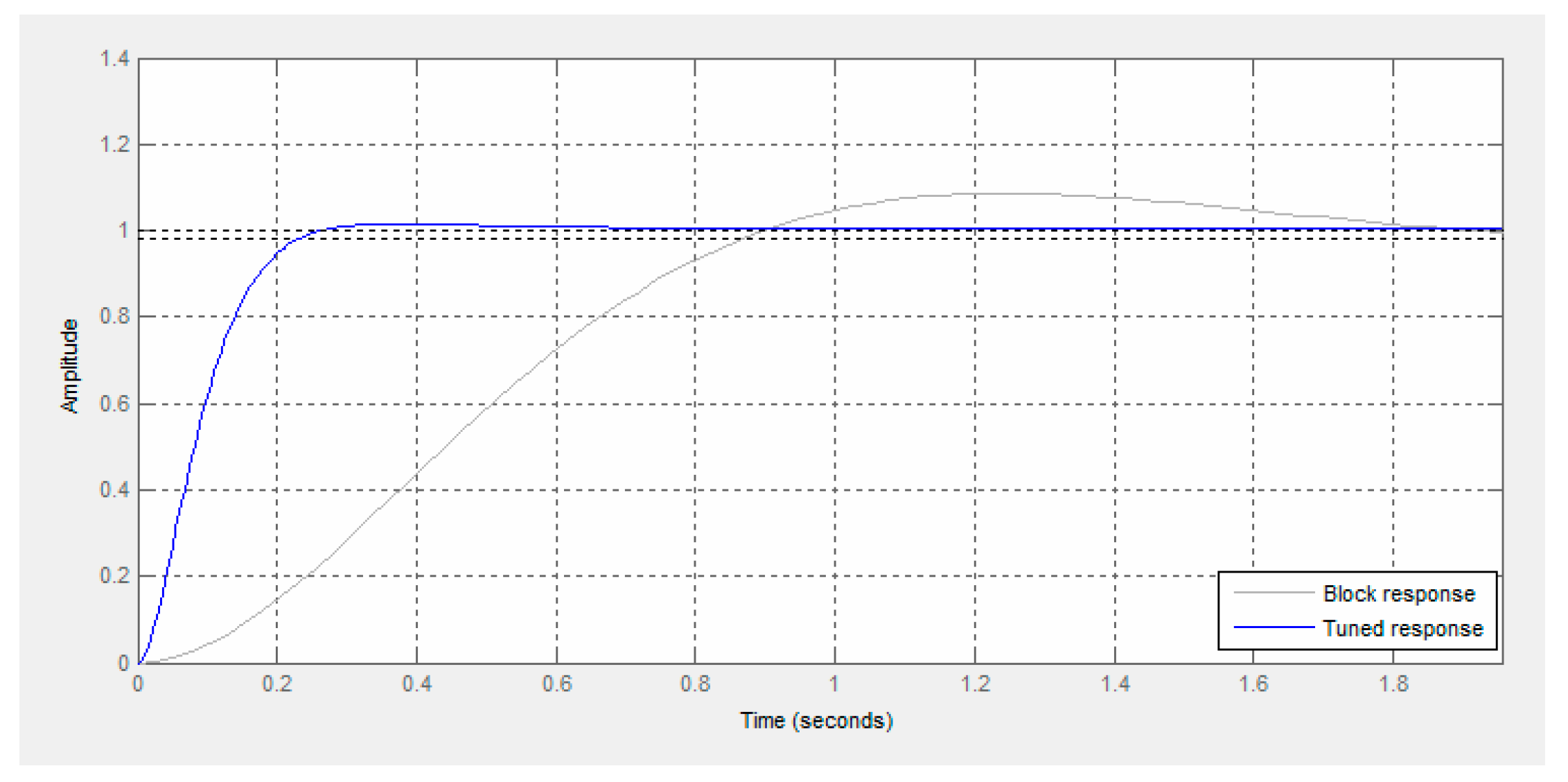
4.4.1. Choice of Settings of the Controller with the Use of Self-Tuning Method in Matlab/Simulink
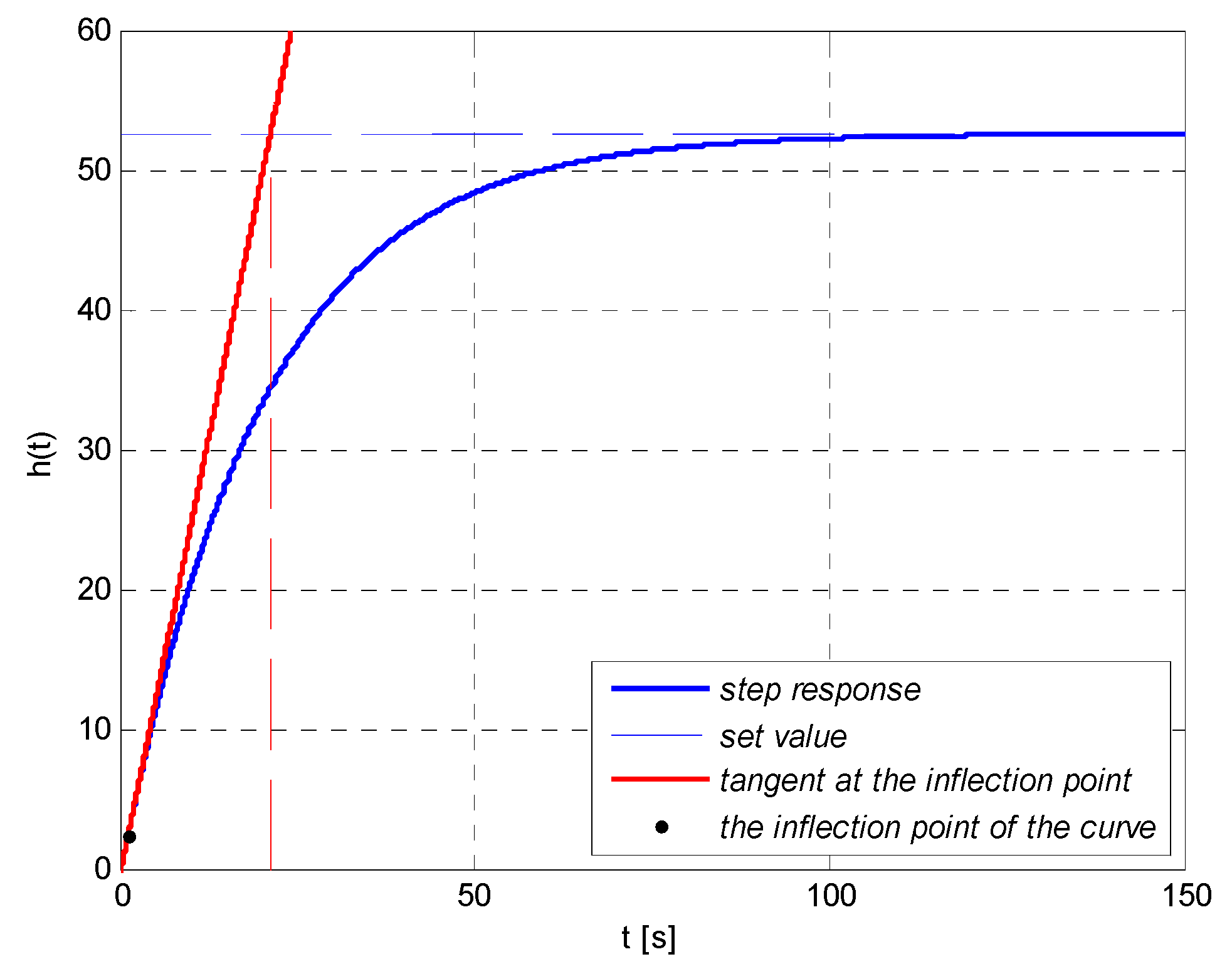
4.4.2. Choice of Settings of the Controller with the Method Based on the Approximation of the Parameters of the Fluctuating Response
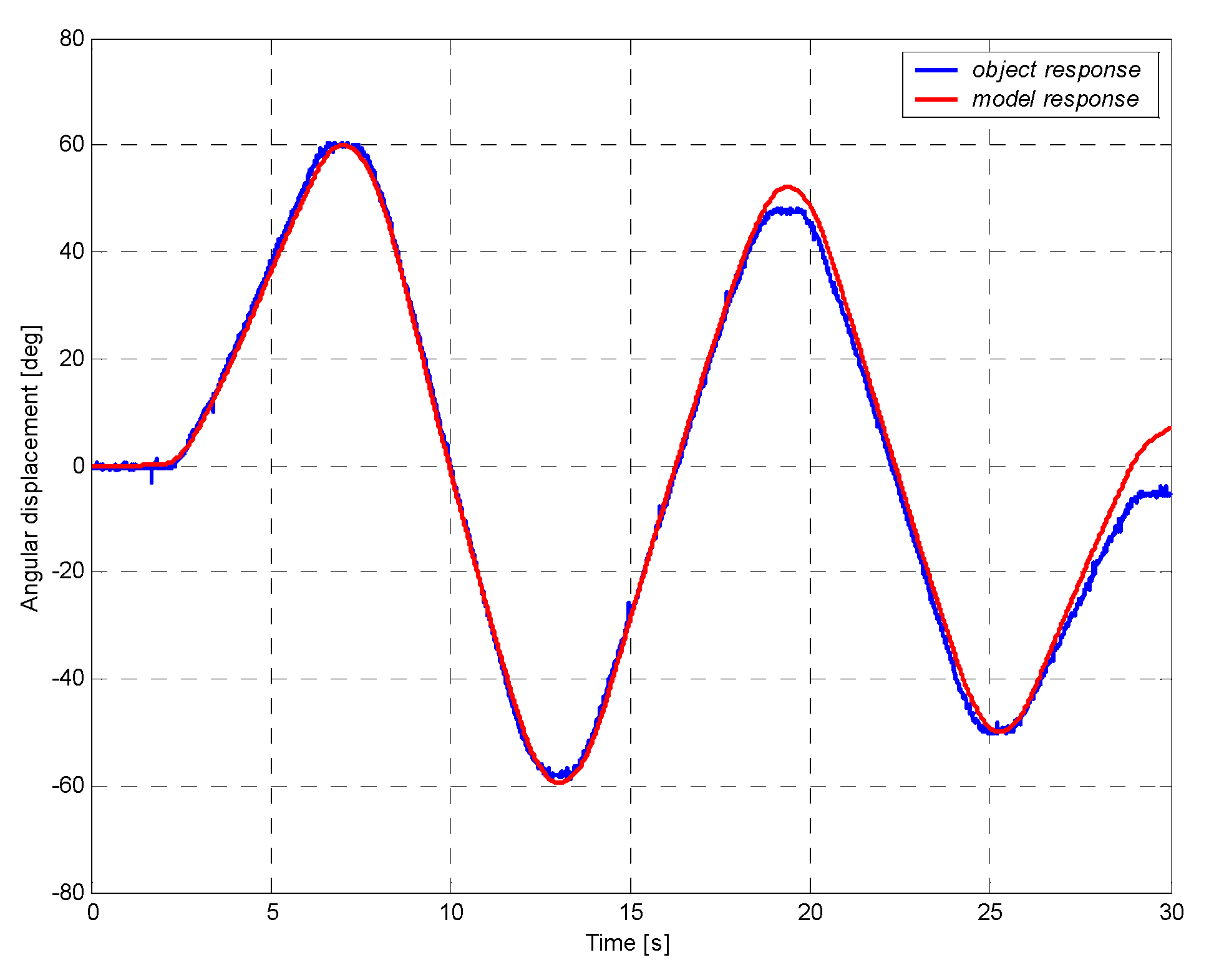
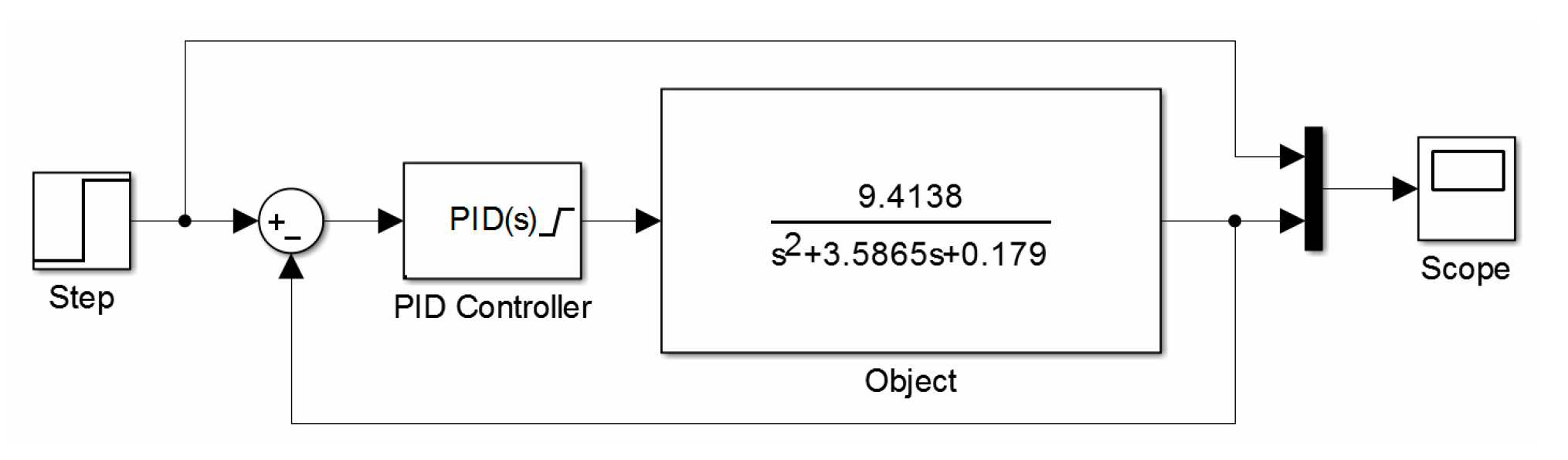
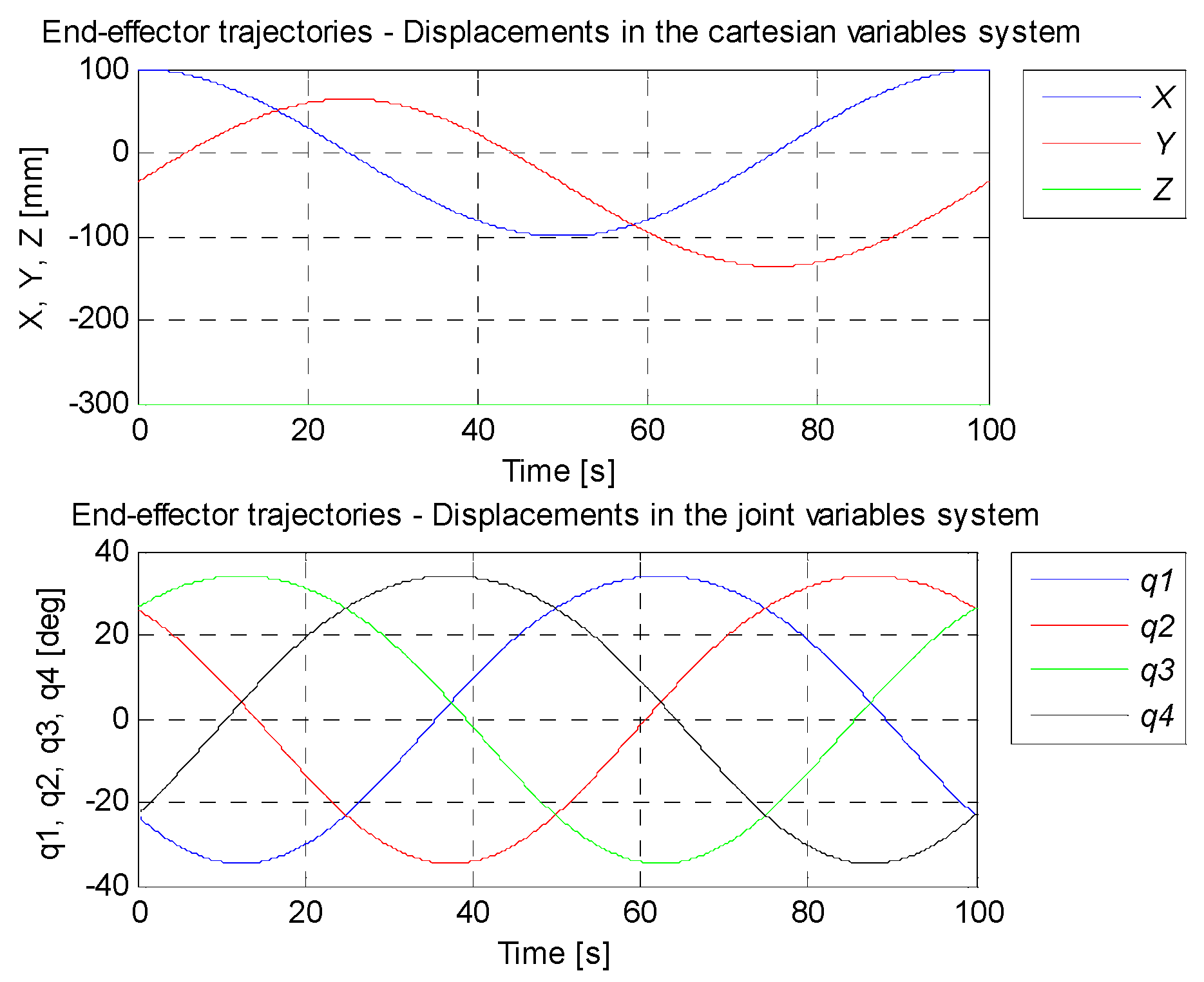
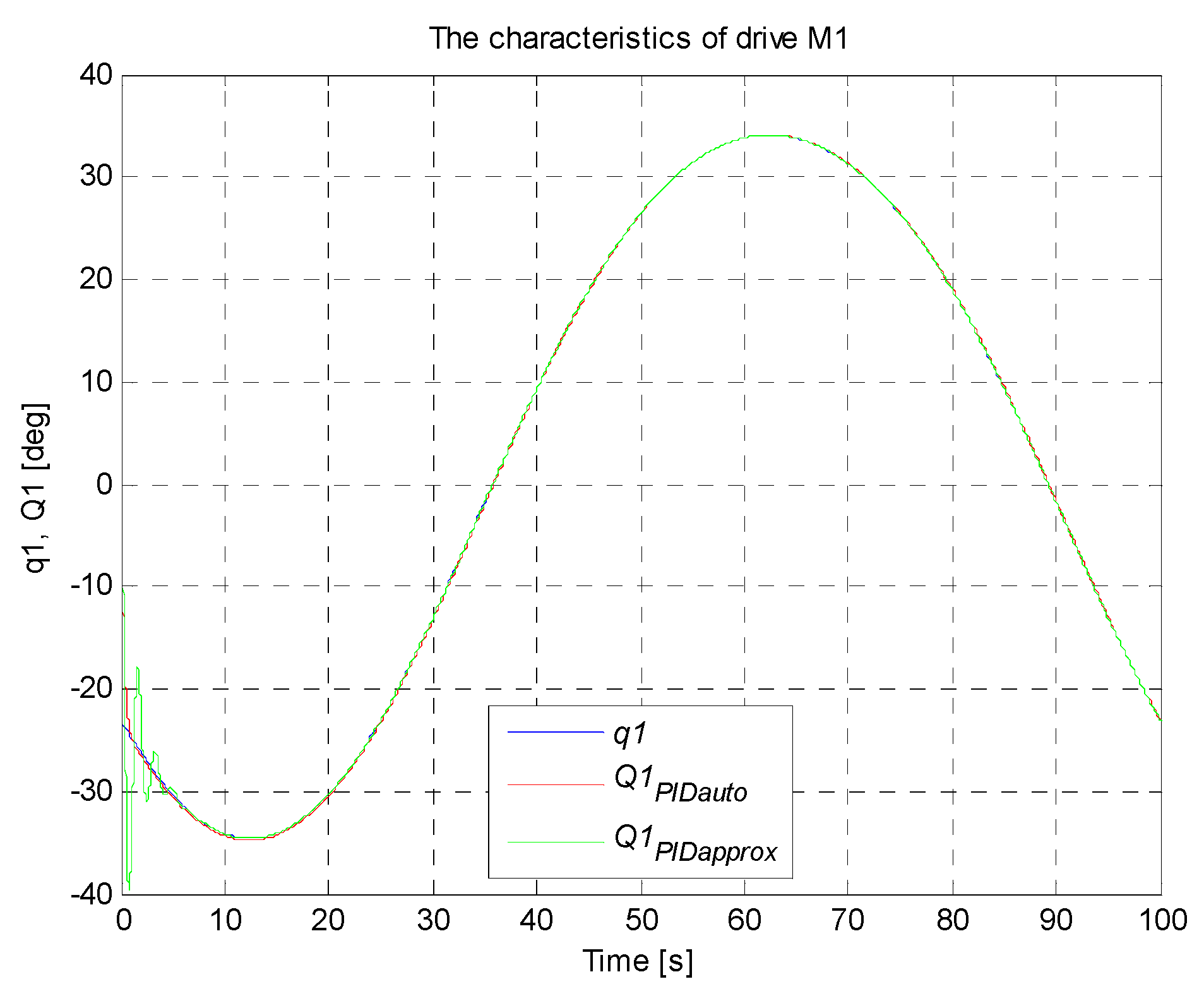
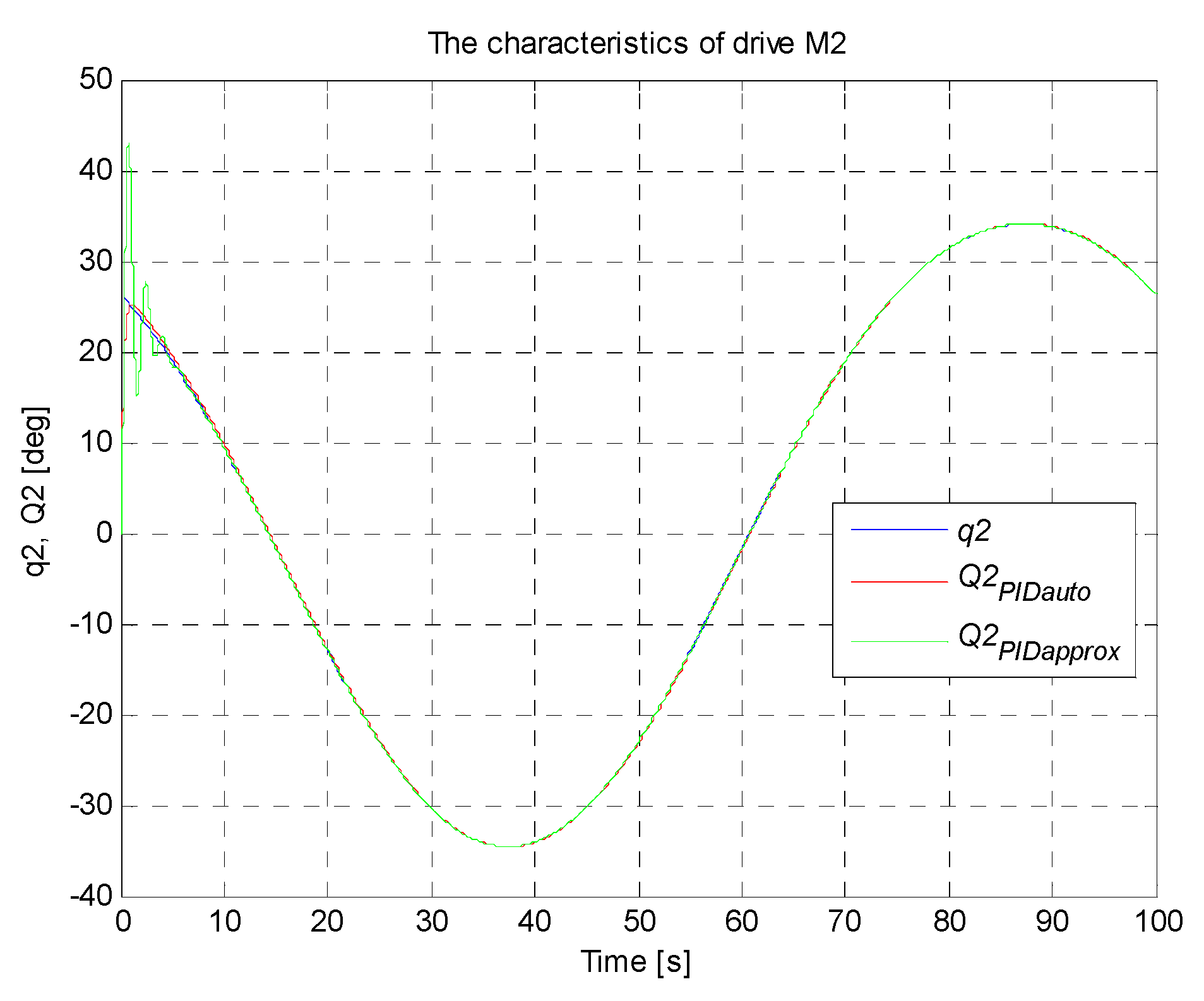
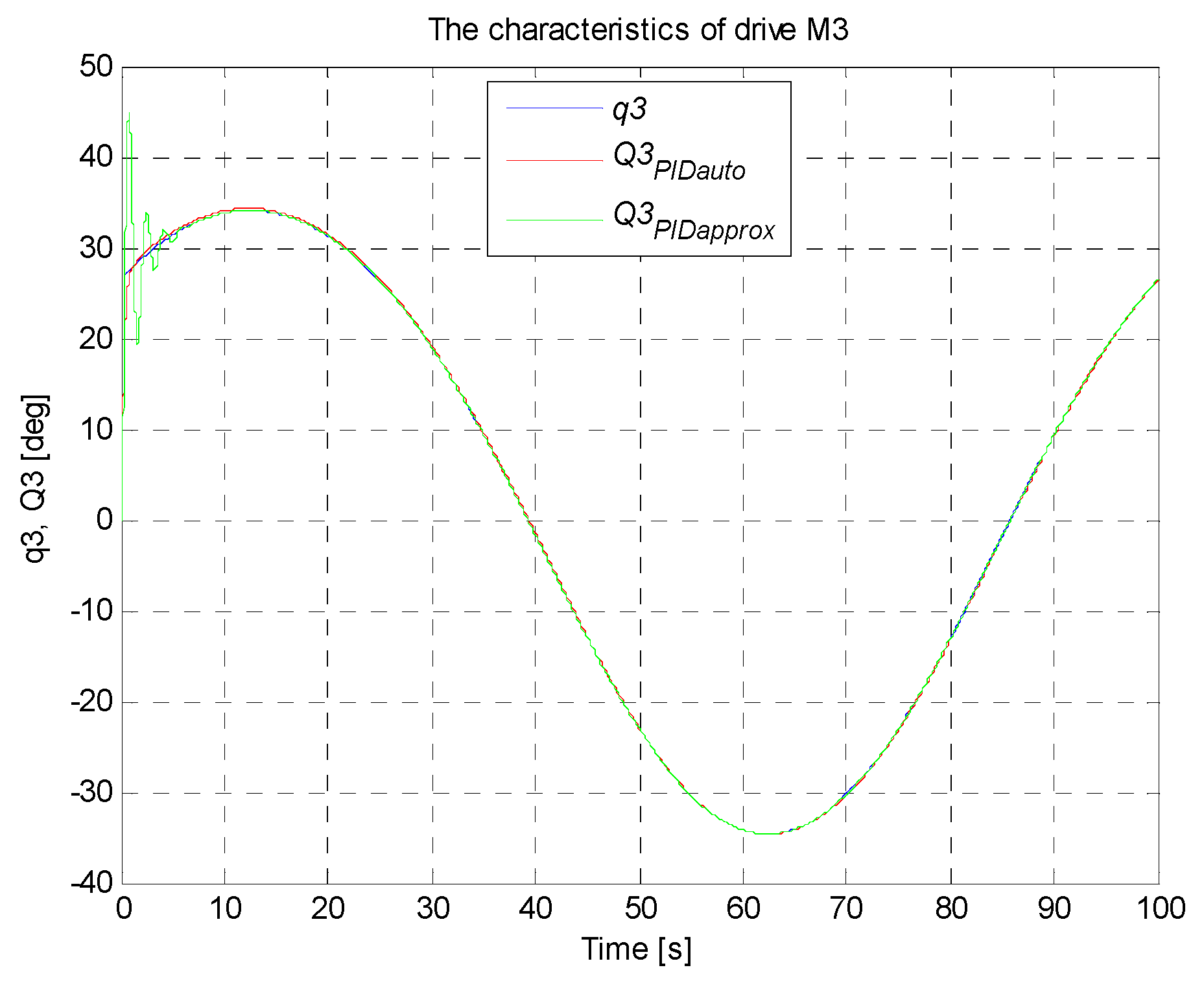
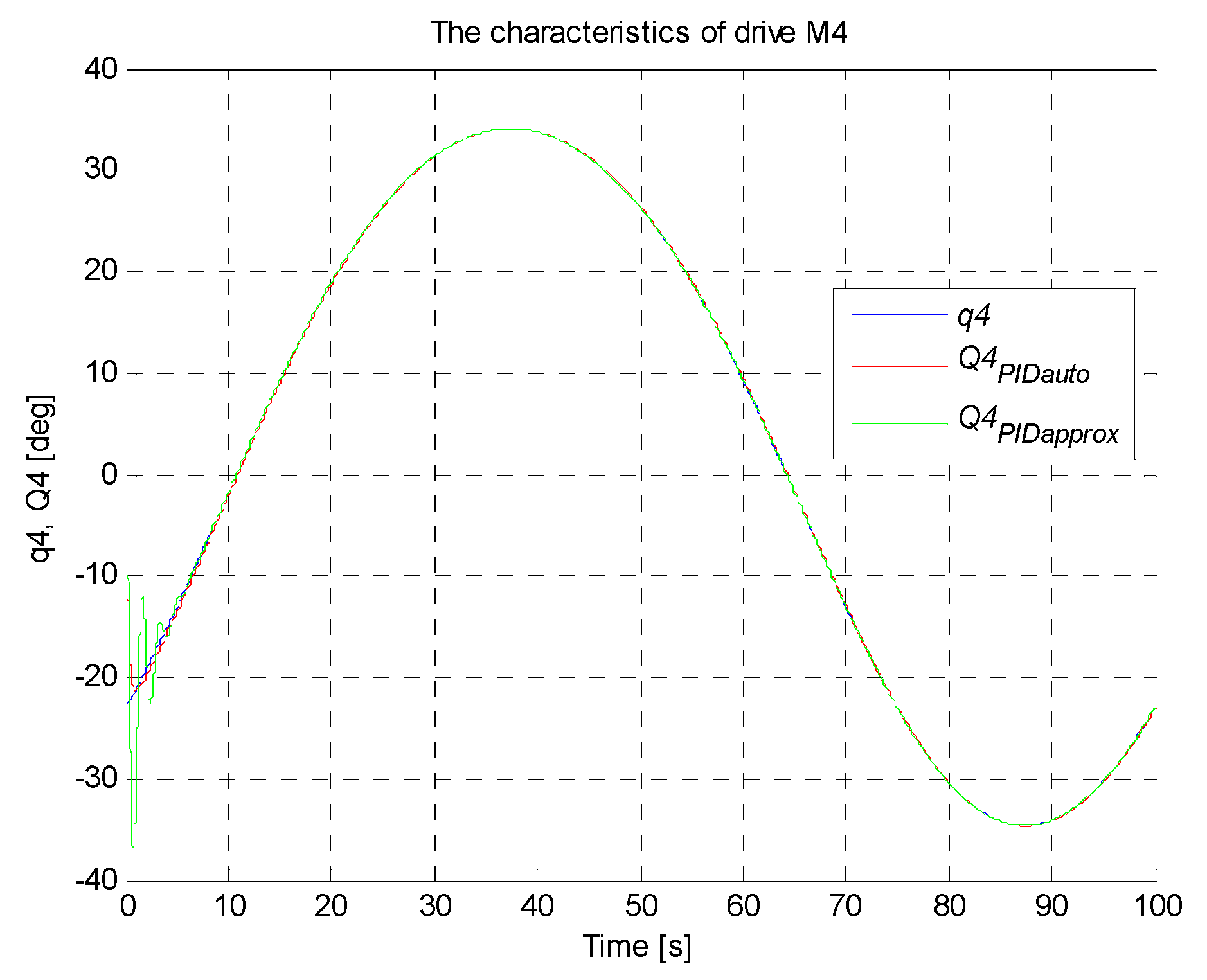
4.5. Simulation Research of the Manipulator Control System
4.6. Structures of the Complied Programmes on the Runtime Set STM32F4 Discovery
4.6.1. Programme Target_DELTA4.slx
4.6.2. Host_DELTA4.slx Programme
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, S.; Kang, H.; Tang, H.; Cui, Z.; Liu, Z.; Ouyang, P. Trajectory Optimization Algorithm for a 4-DOF Redundant Parallel Robot Based on 12-Phase Sine Jerk Motion Profile. Actuators 2021, 10, 80. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, R.; Li, Y.; Chen, Y.-H. Optimal Design of Adaptive Robust Control for the Delta Robot with Uncertainty: Fuzzy Set-Based Approach. Appl. Sci. 2020, 10, 3472. [Google Scholar] [CrossRef]
- Schappler, M.; Tappe, S.; Ortmaier, T. Modeling Parallel Robot Kinematics for 3T2R and 3T3R Tasks Using Reciprocal Sets of Euler Angles. Robotics 2019, 8, 68. [Google Scholar] [CrossRef] [Green Version]
- Doan, Q.V.; Le, T.D.; Vo, A.T. Synchronization Full-Order Terminal Sliding Mode Control for an Uncertain 3-DOF Planar Parallel Robotic Manipulator. Appl. Sci. 2019, 9, 1756. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Meng, H.; Bai, S.; Yao, Y.; Zhang, J. Stability and Gait Planning of 3-UPU Hexapod Walking Robot. Robotics 2018, 7, 48. [Google Scholar] [CrossRef] [Green Version]
- Sheng, L.; Li, W. Optimization Design by Genetic Algorithm Controller for Trajectory Control of a 3-RRR Parallel Robot. Algorithms 2018, 11, 7. [Google Scholar] [CrossRef] [Green Version]
- Garcia, L.; Campos, A. Maximal Singularity-Free Orientation Subregions Associated with Initial Parallel Manipulator Configuration. Robotics 2018, 7, 57. [Google Scholar] [CrossRef] [Green Version]
- Schulz, S. Performance Evaluation of a Sensor Concept for Solving the Direct Kinematics Problem of General Planar 3-RPR Parallel Mechanisms by Using Solely the Linear Actuators’ Orientations. Robotics 2019, 8, 72. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-J.; Chen, C.-T. Reconfiguration for the Maximum Dynamic Wrench Capability of a Parallel Robot. Appl. Sci. 2016, 6, 80. [Google Scholar] [CrossRef] [Green Version]
- Pisla, D.; Tarnita, D.; Tucan, P.; Tohanean, N.; Vaida, C.; Geonea, I.D.; Bogdan, G.; Abrudan, C.; Carbone, G.; Plitea, N. A Parallel Robot with Torque Monitoring for Brachial Monoparesis Rehabilitation Tasks. Appl. Sci. 2021, 11, 9932. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, Y.; Zhang, C.; Zhang, D.; Zhang, J. Error Modeling and Experimental Study of a Flexible Joint 6-UPUR Parallel Six-Axis Force Sensor. Sensors 2017, 17, 2238. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhang, C.; Zhang, D.; Shi, Z.; Zhao, T. Mathematical Model and Calibration Experiment of a Large Measurement Range Flexible Joints 6-UPUR Six-Axis Force Sensor. Sensors 2016, 16, 1271. [Google Scholar] [CrossRef] [Green Version]
- Chiang, M.-H.; Lin, H.-T. Development of a 3D Parallel Mechanism Robot Arm with Three Vertical-Axial Pneumatic Actuators Combined with a Stereo Vision System. Sensors 2011, 11, 11476–11494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tucan, P.; Gherman, B.; Major, K.; Vaida, C.; Major, Z.; Plitea, N.; Carbone, G.; Pisla, D. Fuzzy Logic-Based Risk Assessment of a Parallel Robot for Elbow and Wrist Rehabilitation. Int. J. Environ. Res. Public Health 2020, 17, 654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiang, M.-H.; Lin, H.-T.; Hou, C.-L. Development of a Stereo Vision Measurement System for a 3D Three-Axial Pneumatic Parallel Mechanism Robot Arm. Sensors 2011, 11, 2257–2281. [Google Scholar] [CrossRef] [Green Version]
- Huynh, B.-P.; Su, S.-F.; Kuo, Y.-L. Vision/Position Hybrid Control for a Hexa Robot Using Bacterial Foraging Optimization in Real-time Pose Adjustment. Symmetry 2020, 12, 564. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Li, T.; Wang, L.; Chen, F. Systematic Design Method and Experimental Validation of a 2-DOF Compliant Parallel Mechanism with Excellent Input and Output Decoupling Performances. Appl. Sci. 2017, 7, 591. [Google Scholar] [CrossRef] [Green Version]
- Annusewicz, A.M.; Laski, P.A. Design and Kinematic Analysis of the Parallel Robot 4-DoF SCARA; Springer International Publishing AG: Berlin/Heidelberg, Germany, 2018; Volume 743, ISBN 9783319771786. [Google Scholar]
- Laski, P.A. Kinematics and workspace analysis for a 6-DoF parallel manipulator with coaxial ctuated arms. In Proceedings of the 23rd International Conference Engineering Mechanics 2017, Prague, Czech Republic, 15–18 May 2017; pp. 586–589. [Google Scholar]
- Laski, P.A.; Takosoglu, J.E.; Blasiak, S. A delta type closed kinematics chain with pneumatic muscle actuator manipulator. In Proceedings of the 20th International Conference Engineering Mechanics 2014, Prague, Czech Republic, 12–15 May 2014; pp. 360–363. [Google Scholar]
- Laski, P.A.; Zwierzchowski, J.; Pietrala, D.S. Development of delta-type parallel robot using pneumatic artificial muscles in application for rehabilitation. In Proceedings of the 24th International Conference Engineering Mechanics 2018, Prague, Czech Republic, 14–17 May 2018; Volume 24, pp. 489–492. [Google Scholar]
- Laski Pawel, A.; Takosoglu Jakub, E.; Blasiak, S. Design of a 3-DOF tripod electro-pneumatic parallel manipulator. Rob. Auton. Syst. 2015, 72, 59–70. [Google Scholar] [CrossRef]
- Nabat, V.; de la O Rodriguez, M.; Company, O.; Krut, S.; Pierrot, F. Par4: Very high speed parallel robot for pick-and-place. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 553–558. [Google Scholar]
- Nabat, V.; Company, O.; Pierrot, F.; Poignet, P. Dynamic Modeling and Identification of Par4, A Very High Speed Parallel Manipulator. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 496–501. [Google Scholar]
- Scalera, L.; Boscariol, P.; Carabin, G.; Vidoni, R.; Gasparetto, A. Enhancing Energy Efficiency of a 4-DOF Parallel Robot Through Task-Related Analysis. Machines 2020, 8, 10. [Google Scholar] [CrossRef] [Green Version]
- Pulloquinga, J.L.; Escarabajal, R.J.; Ferrándiz, J.; Vallés, M.; Mata, V.; Urízar, M. Vision-Based Hybrid Controller to Release a 4-DOF Parallel Robot from a Type II Singularity. Sensors 2021, 21, 4080. [Google Scholar] [CrossRef]
- Zhang, X.; Ming, Z. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Appl. Sci. 2019, 9, 2770. [Google Scholar] [CrossRef] [Green Version]
- Company, O.; Krut, S.; Pierrot, F. Internal singularity analysis of a class of lower mobility parallel manipulators with articulated traveling plate. IEEE Trans. Robot. 2006, 22, 1–11. [Google Scholar] [CrossRef]
- Pierrot, F.; Nabat, V.; Company, O.; Krut, S. From Par4 to Adept Quattro. In Proceedings of the Robotic Systems for Handling and Assembly—3rd International Colloquium of the Collaborative Research Center SFB 562, Braunschweig, Germany, 28–29 April 2008; Shaker Verlag: Braunschweig, Germany, 2008; pp. 207–220. [Google Scholar]
- San Martin, Y.; Giménez, M.N.V. Máquinas de Cinemática Paralela: Implementación Industrialy Futuras Tendencias. Available online: https://www.interempresas.net/MetalMecanica/Articulos/26569-Maquinas-de-cinematica-paralela-implementacion-industrial-y-futuras-tendencias.html (accessed on 28 October 2021).
- Corbel, D.; Nabat, V.; Maurine, P. Geometrical Calibration of the High Speed Robot Par4 Using a Laser Tracker. In Proceedings of the MMAR’06: 12th International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 28–31 August 2006; pp. 687–692. [Google Scholar]
- Pierrot, F.; Nabat, V.; Company, O.; Krut, S.; Poignet, P. Optimal design of a 4-DOF parallel manipulator: From academia to industry. IEEE Trans. Robot. 2009, 25, 213–224. [Google Scholar] [CrossRef]
- User’s Guide. Adept Quattro User’s Guide; Omron Adept Technologies: Pleasanton, CA, USA, 2013; Available online: https://www.omron.com (accessed on 28 October 2021).
- Adept Quattro s650. User’s Guide; Omron Adept Technologies: Pleasanton, CA, USA, 2018; Available online: http://products.omron.us/Asset/Omron-Adept-Quattro-s650HS-Parallel-Robot_UG_EN_201602_R76IE01.pdf (accessed on 28 October 2021).
- Datasheet Robot Datasheet Adept Quattro s800H and s650H; Omron Adept Technologies: Pleasanton, CA, USA, 2014; Available online: https://industrial.omron.eu/ (accessed on 28 October 2021).




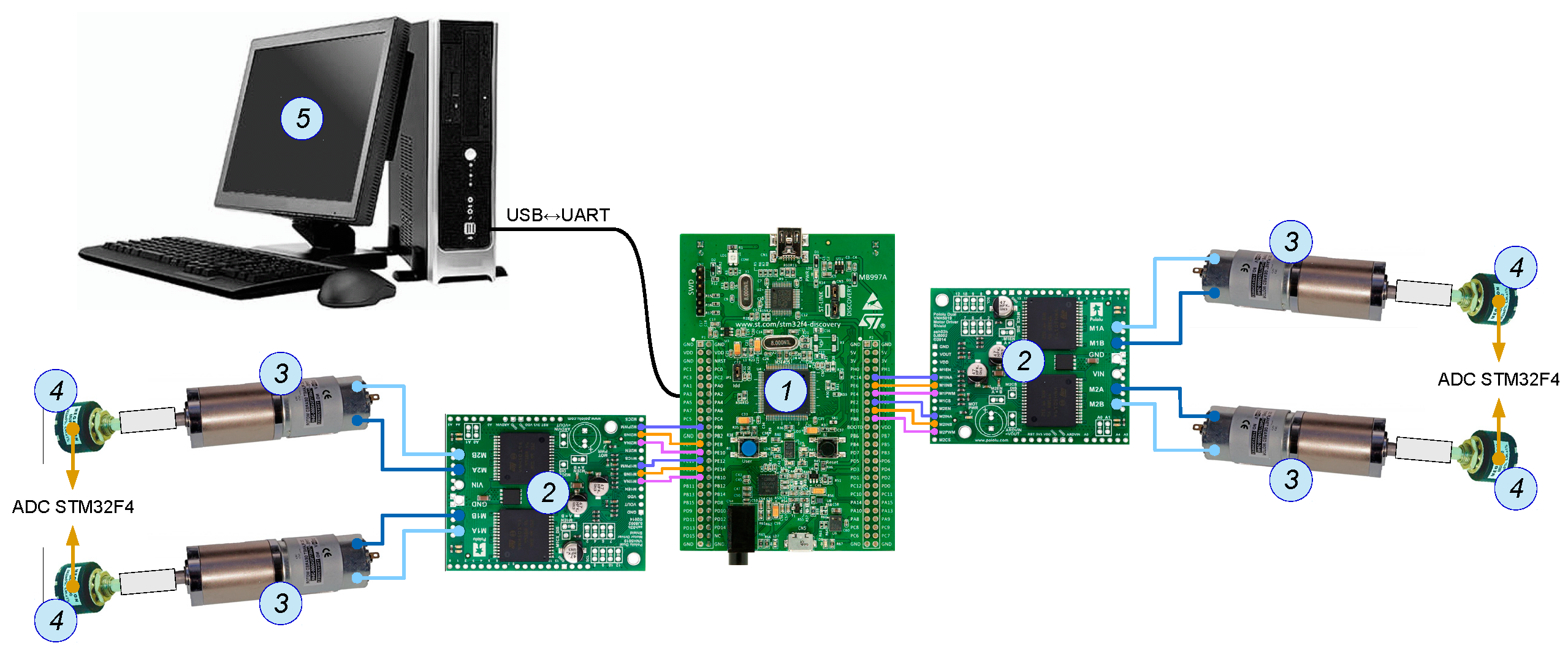
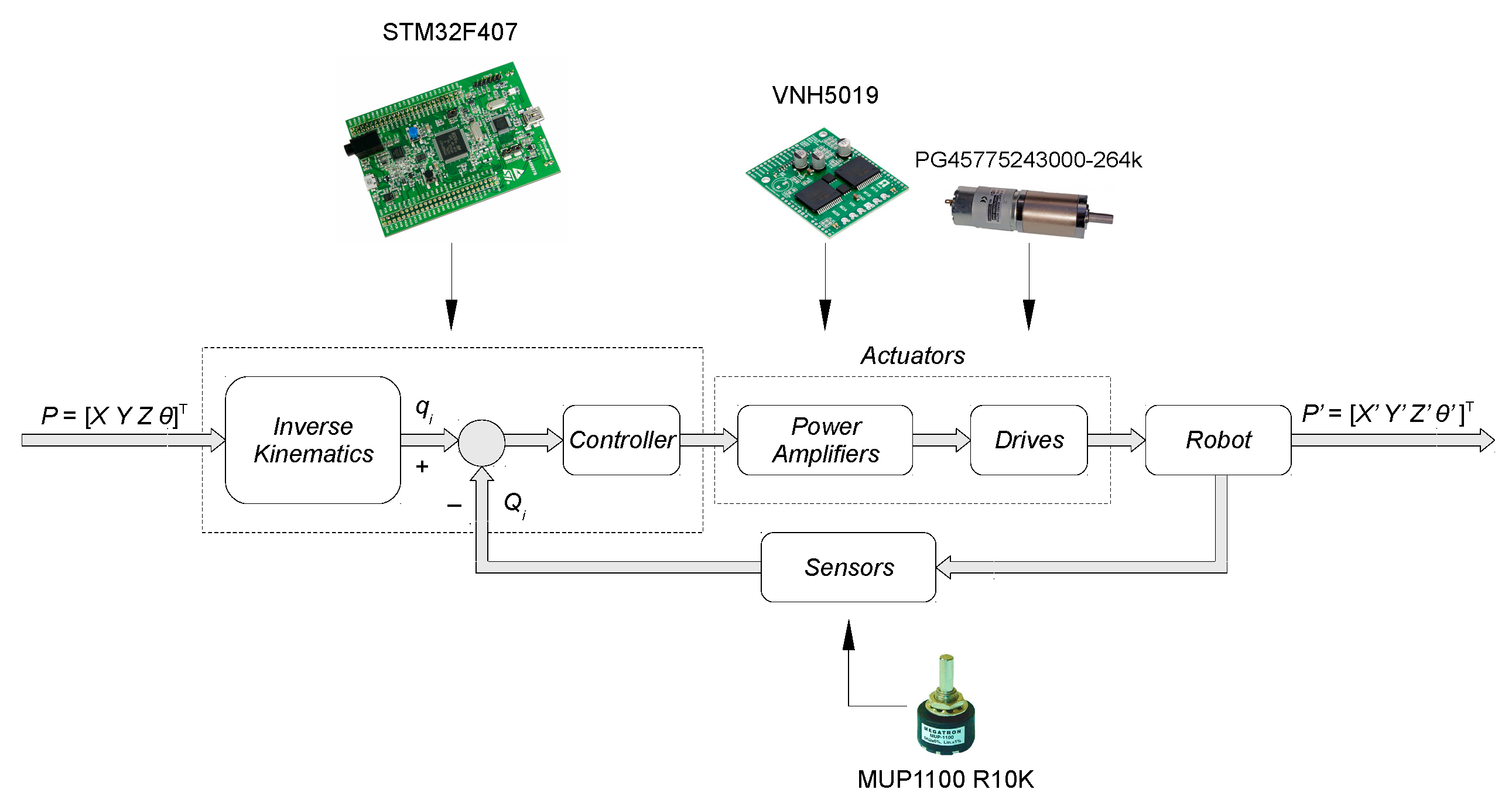



| Marking | Description | Value (mm) |
|---|---|---|
| R | Distance between the beginning of the reference system O and the driven axis of the active arm | 185 |
| L | Length of the active arm | 386 |
| l | Length of the passive arm | 200 |
| d | Length of the main element of the moveable platform (along the axis x) | 102 |
| di (i = 1, 2, 3, 4) | Distance between points Ci and Pi of the moveable platform (along the axis x) | 9 |
| h | Length of the connectors of the articulated quadrangle of the moveable platform | 72 |
| hi (i = 1, 2, 3, 4) | Distance between points Ci and Pi of the moveable platform (along the axis y) | 24 |
| PID Regulator Settings | |
|---|---|
| Pauto | 4.36210 |
| Iauto | 0.38231 |
| Dauto | 0.99919 |
| Nauto | 37.2929 |
| The Pareamters of the Object | |
|---|---|
| Object Proportionality Factor k | 52.5561 |
| Delay T0 [s] | 0.2445 |
| Time constant T [s] | 20.9963 |
| PID controller settings | |
| kp | 2.2880 |
| Ti [s] | 0.3178 |
| Td [s] | 0.1222 |
| PID Controller Settings | ISE Indicator | |||
|---|---|---|---|---|
| Drive I | Drive II | Drive III | Drive IV | |
| PIDauto | 91.45 | 124 | 126 | 88.85 |
| PIDapprox | 234.8 | 305.4 | 307.9 | 231.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laski, P.A.; Smykowski, M. Using a Development Platform with an STM32 Processor to Prototype an Inexpensive 4-DoF Delta Parallel Robot. Sensors 2021, 21, 7962. https://doi.org/10.3390/s21237962
Laski PA, Smykowski M. Using a Development Platform with an STM32 Processor to Prototype an Inexpensive 4-DoF Delta Parallel Robot. Sensors. 2021; 21(23):7962. https://doi.org/10.3390/s21237962
Chicago/Turabian StyleLaski, Pawel Andrzej, and Mateusz Smykowski. 2021. "Using a Development Platform with an STM32 Processor to Prototype an Inexpensive 4-DoF Delta Parallel Robot" Sensors 21, no. 23: 7962. https://doi.org/10.3390/s21237962
APA StyleLaski, P. A., & Smykowski, M. (2021). Using a Development Platform with an STM32 Processor to Prototype an Inexpensive 4-DoF Delta Parallel Robot. Sensors, 21(23), 7962. https://doi.org/10.3390/s21237962






