Random Fourier Features-Based Deep Learning Improvement with Class Activation Interpretability for Nerve Structure Segmentation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Deep-Learning-Based Semantic Segmentation Fundamentals
- –
- Fully convolutional network (FCN) [12]: It is known as the fundamental semantic segmentation architecture that avoids computational redundancy and replaces fully connected layers with convolutional ones. FCN is based on the well-known “very deep convolutional network for large-scale image recognition model” (also known as the VGG-16 algorithm) [46].
- –
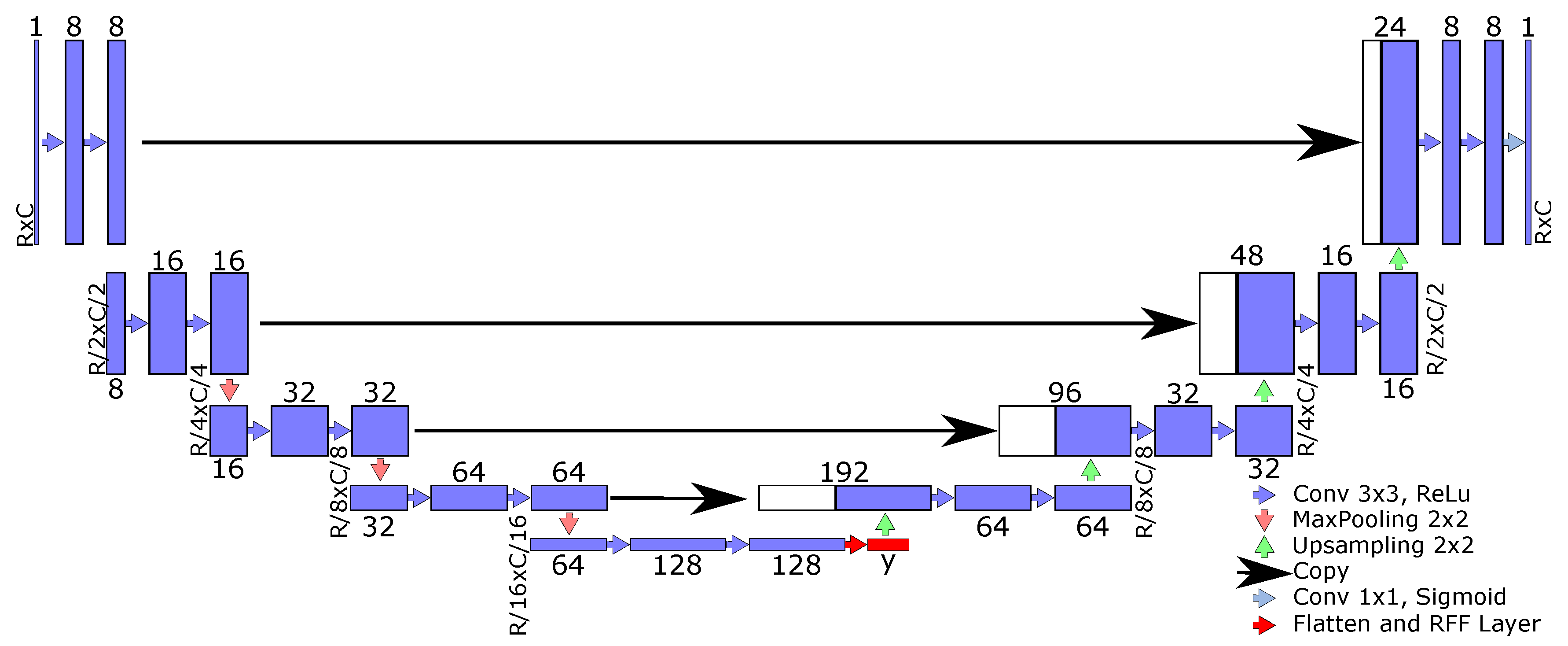
- U-net [14]: This approach aims to extract low-level features while preserving high-level semantic information. Moreover, the U-net algorithm pretends to relieve training problems related to a limited number of samples [47]. Remarkably, the U-net’s architecture includes an encoder and decoder stage, and is a U-shaped network.
- –
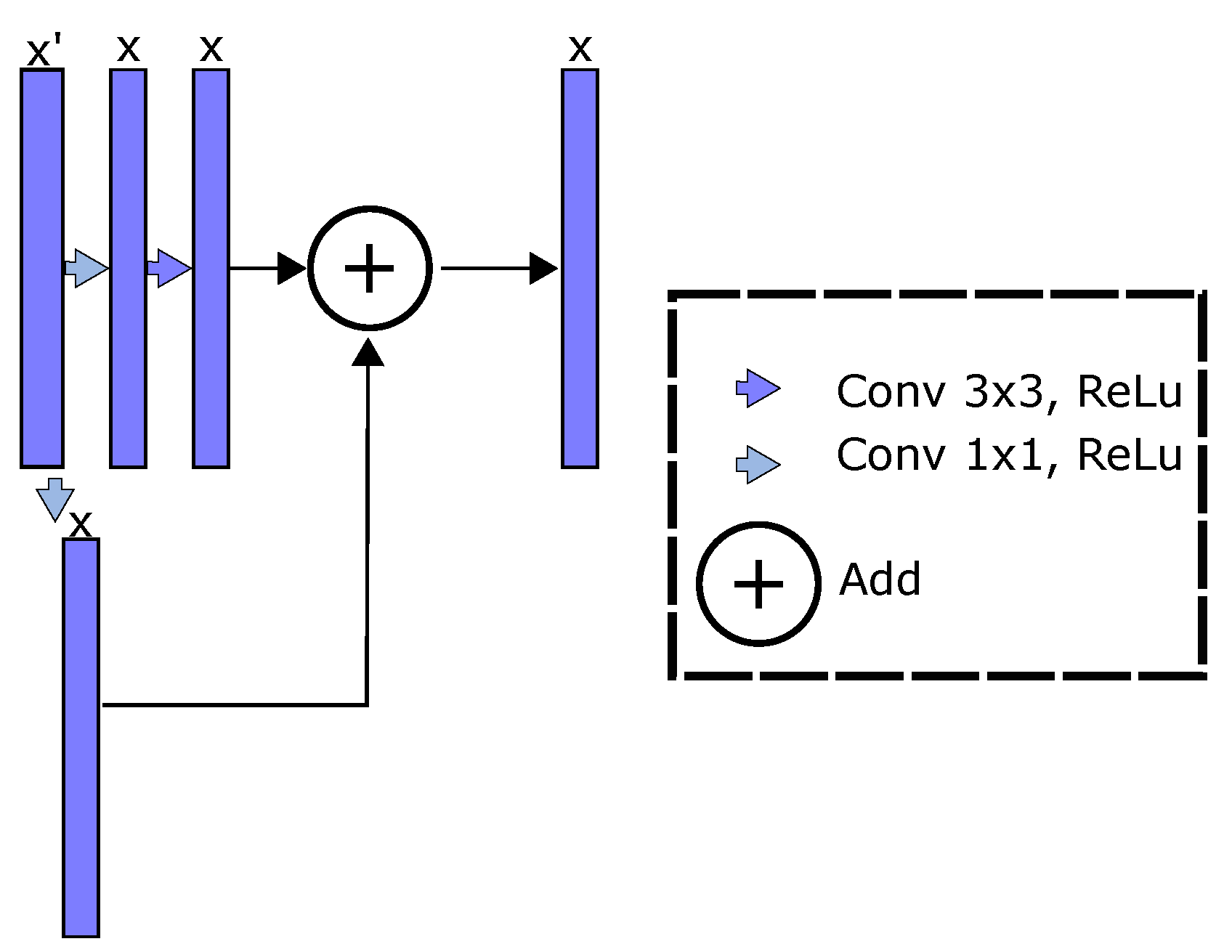
- Residual network and U-net (ResUnet) [16]: This approach enhances the U-net algorithm including residual blocks. Thereby, residual learning is employed to boost the model layers as residual functions referenced to the inputs, instead of learning unreferenced mappings; that is, the enhanced feature maps can be rewritten as [48]. Then, the ResUnet combines low and high-level features, favors the network optimization, and includes a deeper representation learning stage than U-net and FCN approaches.
2.2. Random Fourier Features Approximating Kernel Mappings
2.3. Relevance Analysis Based on Class Activation Mapping for Semantic Segmentation
2.4. RFF-Based Semantic Segmentation Pipeline and Main Contributions
3. Experimental Setup
3.1. Ultrasound Image Datasets for Nerve Structure Segmentation
- –
- Nerve-UTP: This dataset was acquired by the Universidad Tecnológica de Pereira (https://www.utp.edu.co, accessed on 17 November 2021) and the Santa Mónica Hospital, Dosquebradas, Colombia. It contains 691 images of the following nerve structures: the sciatic nerve (287 instances), the ulnar nerve (221 instances), the median nerve (41 instances), and the femoral nerve (70 instances). A SONOSITE Nano-Maxx device was used, fixing a pixel resolution. Each image was labeled by an anesthesiologist from the Santa Mónica Hospital. As prepossessing, morphological operations such as dilation and erosion were applied. Next, we defined a region of interest by computing the bounding box around each nerve structure. As a result, we obtained images holding a maximum resolution of pixels. Lastly, we applied a data augmentation scheme to obtain the following samples: 861 sciatic nerve images, 663 ulnar nerve images, 123 median nerve images, and 210 femoral nerve images (1857 input samples).
- –
- Nerve segment dataset (NSD): This dataset belongs to the Kaggle Competition repository [42]. It holds labeled ultrasound images of the neck concerning the brachial plexus (BP). In particular, 47 different subjects were studied, recording 119 to 580 images per subject (5635 as a whole) at pixel resolution. For concrete testing, we performed a pruning procedure to remove images with inconsistent annotations as suggested by authors in [18,19,20], yielding to 2323 samples.
3.2. Method Comparison, Performance Measures, and Implementation Details
4. Results and Discussion
4.1. Semantic Segmentation Results
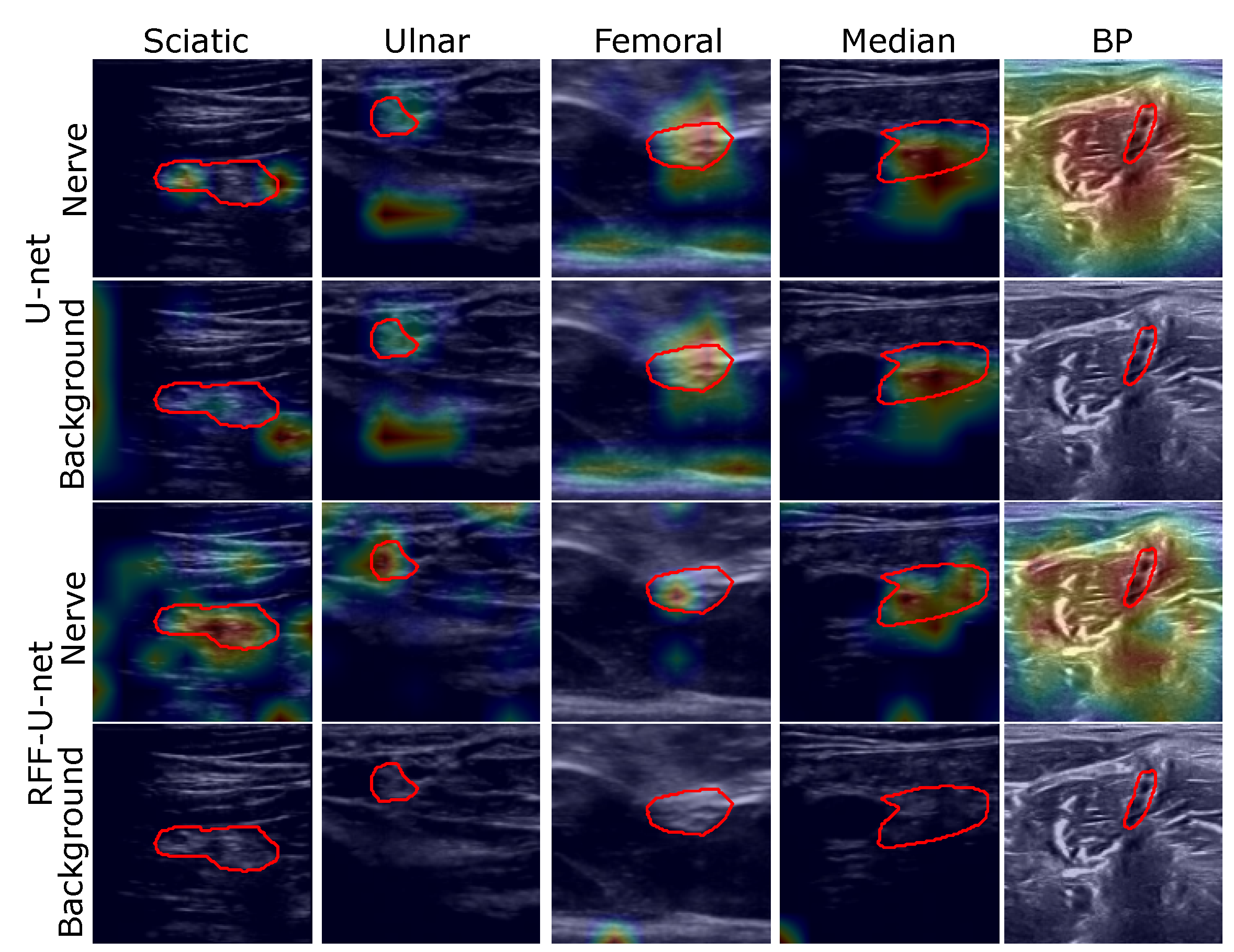
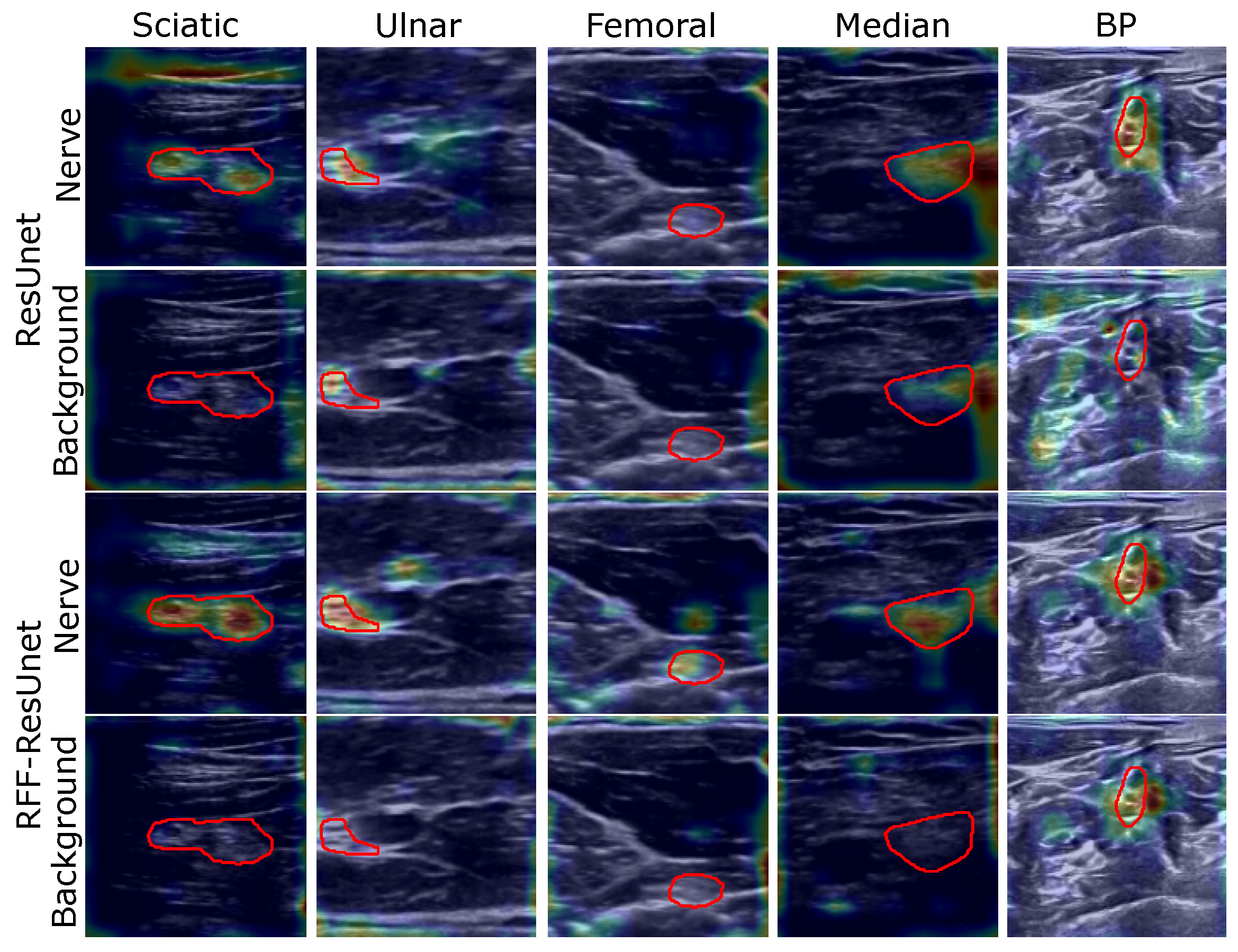
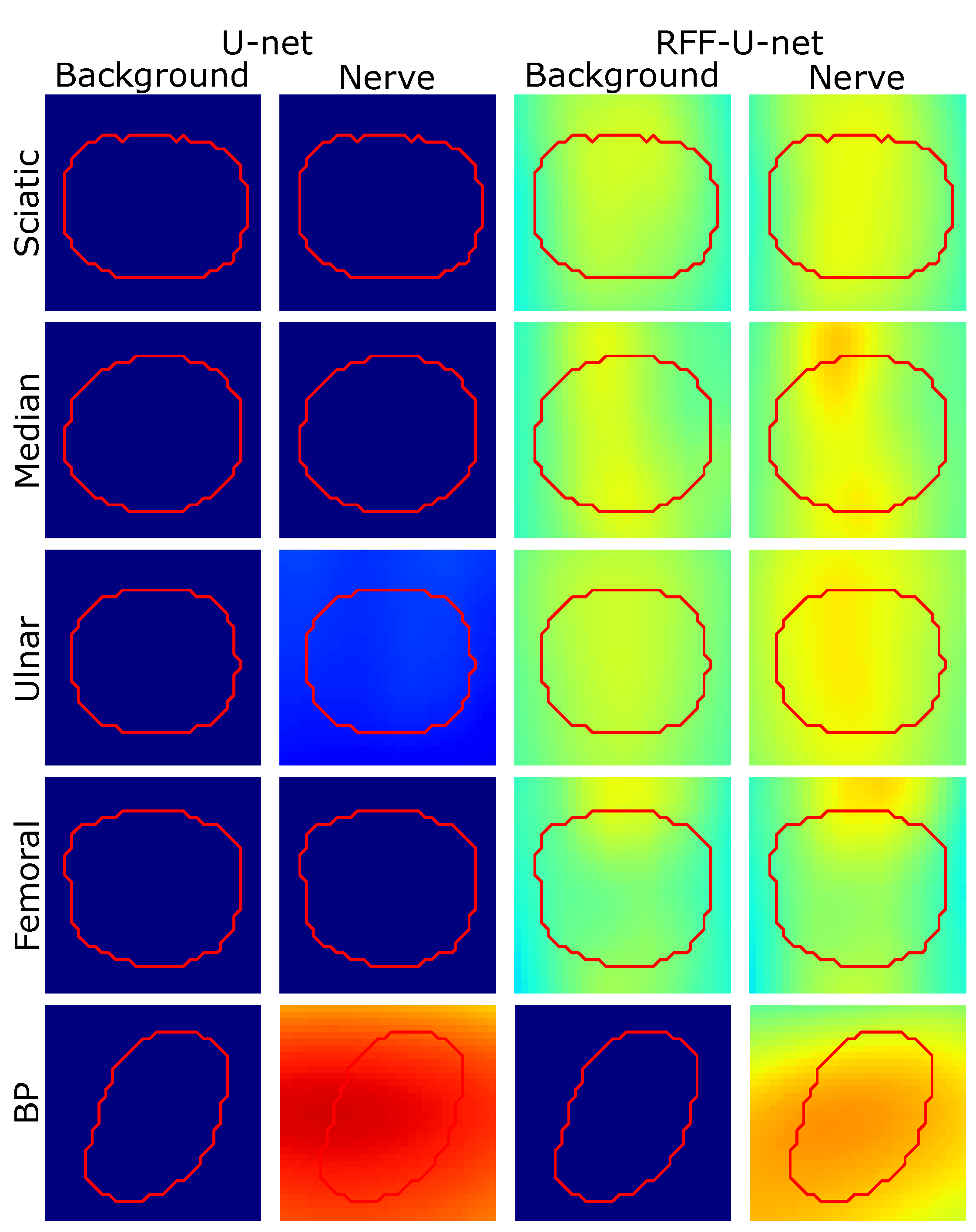
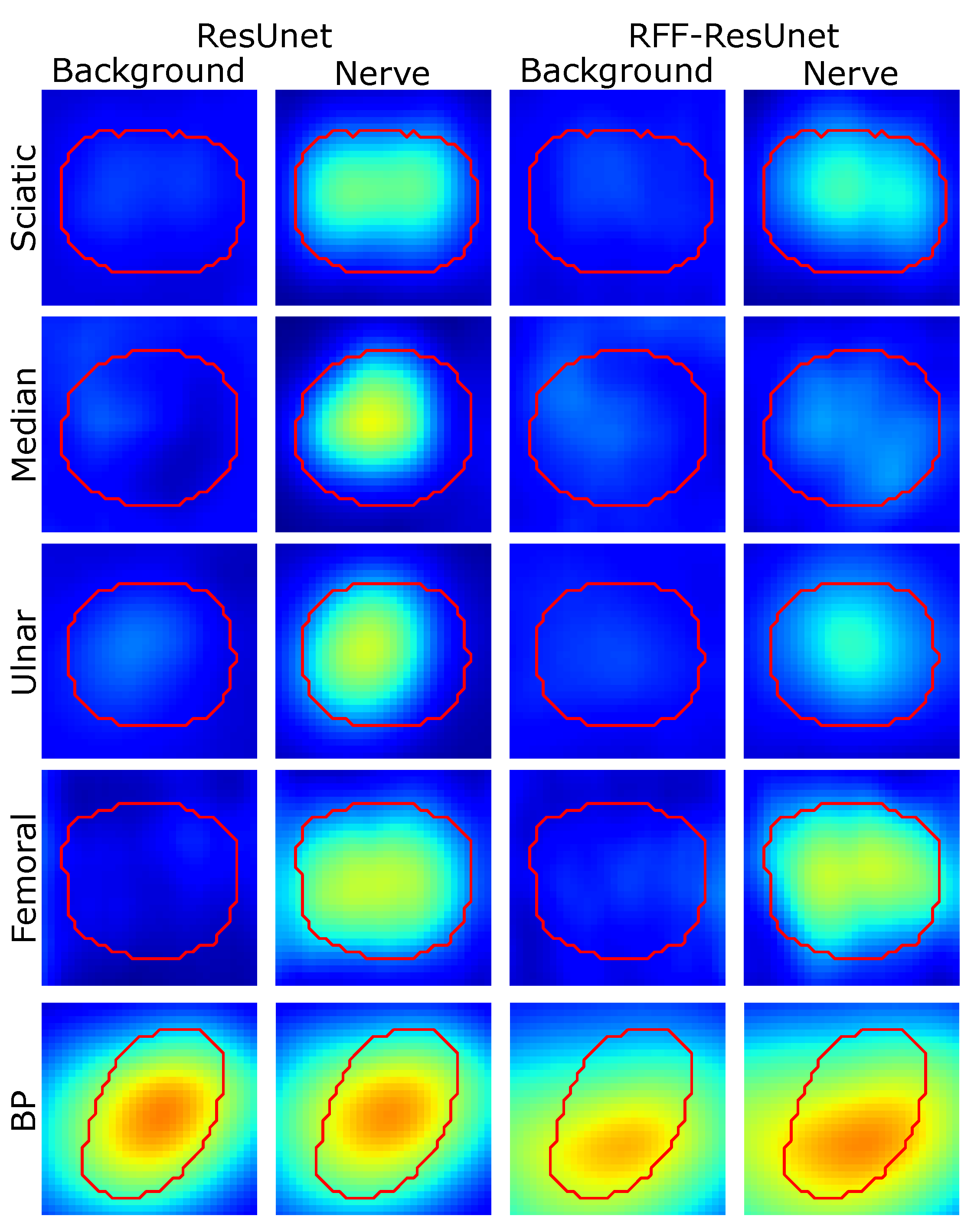
4.2. Relevance Analysis Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gil González, J.; Álvarez, A.; Valencia, A.; Orozco, A. Automatic peripheral nerve segmentation in presence of multiple annotators. In Iberoamerican Congress on Pattern Recognition; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2018; pp. 246–254. [Google Scholar] [CrossRef]
- Abraham, N.; Illanko, K.; Khan, N.; Androutsos, D. Deep Learning for Semantic Segmentation of Brachial Plexus Nervesin Ultrasound Images Using U-Net and M-Net. In Proceedings of the 2019 3rd International Conference on Imaging, Signal Processing and Communication (ICISPC), Singapore, 27–29 July 2019; pp. 85–89. [Google Scholar] [CrossRef]
- Scholten, H.J.; Pourtaherian, A.; Mihajlovic, N.; Korsten, H.H.M.; Bouwman, R.A. Improving needle tip identification during ultrasound-guided procedures in anaesthetic practice. Anaesthesia 2017, 72, 889–904. [Google Scholar] [CrossRef] [PubMed]
- Mwikirize, C.; Nosher, J.; Hacihaliloglu, I. Convolution neural networks for real-time needle detection and localization in 2D ultrasound. Int. J. Comput. Assist. Radiol. Surg. 2018, 13, 647–657. [Google Scholar] [CrossRef] [PubMed]
- Pesteie, M.; Lessoway, V.; Abolmaesumi, P.; Rohling, R. Automatic Localization of the Needle Target for Ultrasound-Guided Epidural Injections. IEEE Trans. Med. Imaging 2017, 37, 81–92. [Google Scholar] [CrossRef]
- Horng, M.H.; Yang, C.W.; Sun, Y.N.; Yang, T.H. DeepNerve: A New Convolutional Neural Network for the Localization and Segmentation of the Median Nerve in Ultrasound Image Sequences. Ultrasound Med. Biol. 2020, 46, 2439–2452. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, C.; Diaz, D.; Salazar, D.; Alvarez, A.M.; Orozco, A.; Henao, O. Nerve Structure Segmentation from Ultrasound Images Using Random Under-Sampling and an SVM Classifier. In Image Analysis and Recognition; Campilho, A., Karray, F., ter Haar Romeny, B., Eds.; Springer: Cham, Switzerland, 2018; pp. 571–578. [Google Scholar]
- GonzÁlez, J.G.; Álvarez, M.A.; Orozco, A.A. A probabilistic framework based on SLIC-superpixel and Gaussian processes for segmenting nerves in ultrasound images. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4133–4136. [Google Scholar] [CrossRef]
- Hernández-Muriel, J.A.; Mejía-Hernández, J.C.; Echeverry-Correa, J.D.; Orozco, A.A.; Cárdenas-Peña, D. HAPAN: Support Tool for Practicing Regional Anesthesia in Peripheral Nerves. In Understanding the Brain Function and Emotions; Ferrández Vicente, J.M., Álvarez-Sánchez, J.R., de la Paz López, F., Toledo Moreo, J., Adeli, H., Eds.; Springer: Cham, Switzerland, 2019; pp. 130–137. [Google Scholar]
- Giraldo, J.J.; Álvarez, M.A.; Orozco, A.A. Peripheral nerve segmentation using Nonparametric Bayesian Hierarchical Clustering. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 3101–3104. [Google Scholar] [CrossRef]
- Rubasinghe, I.; Meedeniya, D. Ultrasound nerve segmentation using deep probabilistic programming. J. ICT Res. Appl. 2019, 13, 241–256. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. arXiv 2015, arXiv:1411.4038. [Google Scholar]
- Du, G.; Cao, X.; Liang, J.; Chen, X.; Zhan, Y. Medical Image Segmentation based on U-Net: A Review. J. Imaging Sci. Technol. 2020, 64, 20508-1–20508-12. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Kumar, V.; Webb, J.M.; Gregory, A.; Denis, M.; Meixner, D.D.; Bayat, M.; Whaley, D.H.; Fatemi, M.; Alizad, A. Automated and real-time segmentation of suspicious breast masses using convolutional neural network. PLoS ONE 2018, 13, e0195816. [Google Scholar] [CrossRef] [PubMed]
- Anas, E.M.A.; Nouranian, S.; Mahdavi, S.S.; Spadinger, I.; Morris, W.J.; Salcudean, S.E.; Mousavi, P.; Abolmaesumi, P. Clinical Target-Volume Delineation in Prostate Brachytherapy Using Residual Neural Networks. In Medical Image Computing and Computer Assisted Intervention—MICCAI 2017; Descoteaux, M., Maier-Hein, L., Franz, A., Jannin, P., Collins, D.L., Duchesne, S., Eds.; Springer: Cham, Switzerland, 2017; pp. 365–373. [Google Scholar]
- Khan, M.Z.; Gajendran, M.K.; Lee, Y.; Khan, M.A. Deep Neural Architectures for Medical Image Semantic Segmentation: Review. IEEE Access 2021, 9, 83002–83024. [Google Scholar] [CrossRef]
- Baby, M.; Jereesh, A. Automatic nerve segmentation of ultrasound images. In Proceedings of the 2017 International conference of Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 20–22 April 2017; Volume 1, pp. 107–112. [Google Scholar] [CrossRef]
- Kakade, A.; Dumbali, J. Identification of nerve in ultrasound images using U-net architecture. In Proceedings of the 2018 International Conference on Communication information and Computing Technology (ICCICT), Mumbai, India, 2–3 February 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, R.; Shen, H.; Zhou, M. Ultrasound Nerve Segmentation of Brachial Plexus Based on Optimized ResU-Net. In Proceedings of the 2019 IEEE International Conference on Imaging Systems and Techniques (IST), Abu Dhabi, United Arab Emirates, 9–10 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Elhassan, M.A.; Huang, C.; Yang, C.; Munea, T.L. DSANet: Dilated spatial attention for real-time semantic segmentation in urban street scenes. Expert Syst. Appl. 2021, 183, 115090. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Cheng, H.; Xing, P.; Zhang, B. Semantic segmentation of breast ultrasound image with fuzzy deep learning network and breast anatomy constraints. Neurocomputing 2021, 450, 319–335. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Bengio, Y.; LeCun, Y. Scaling learning algorithms towards AI. Large-Scale Kernel Mach. 2017, 34, 1–41. [Google Scholar]
- Mohammadnia-Qaraei, M.R.; Monsefi, R.; Ghiasi-Shirazi, K. Convolutional kernel networks based on a convex combination of cosine kernels. Pattern Recognit. Lett. 2018, 116, 127–134. [Google Scholar] [CrossRef]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Deep Kernel Learning. arXiv 2015, arXiv:1511.02222. [Google Scholar]
- Lee, H.; Grosse, R.; Ranganath, R.; Ng, A.Y. Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations. In Proceedings of the 26th Annual International Conference on Machine Learning (ICML ’09), Montreal, QC, Canada, 14–18 June 2009; Association for Computing Machinery: New York, NY, USA, 2009; pp. 609–616. [Google Scholar] [CrossRef]
- Bu, S.; Liu, Z.; Han, J.; Wu, J.; Ji, R. Learning High-Level Feature by Deep Belief Networks for 3-D Model Retrieval and Recognition. IEEE Trans. Multimed. 2014, 16, 2154–2167. [Google Scholar] [CrossRef]
- Mairal, J.; Koniusz, P.; Harchaoui, Z.; Schmid, C. Convolutional kernel networks. Adv. Neural Inf. Process. Syst. 2014, 27, 2627–2635. [Google Scholar]
- Poria, S.; Cambria, E.; Gelbukh, A. Deep convolutional neural network textual features and multiple kernel learning for utterance-level multimodal sentiment analysis. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 2539–2544. [Google Scholar]
- Wang, T.; Xu, L.; Li, J. SDCRKL-GP: Scalable deep convolutional random kernel learning in gaussian process for image recognition. Neurocomputing 2021, 456, 288–298. [Google Scholar] [CrossRef]
- Le, L.; Hao, J.; Xie, Y.; Priestley, J. Deep Kernel: Learning Kernel Function from Data Using Deep Neural Network. In Proceedings of the 2016 IEEE/ACM 3rd International Conference on Big Data Computing Applications and Technologies (BDCAT), Shanghai, China, 6–9 December 2016; pp. 1–7. [Google Scholar]
- Ober, S.W.; Rasmussen, C.E.; van der Wilk, M. The Promises and Pitfalls of Deep Kernel Learning. arXiv 2021, arXiv:2102.12108. [Google Scholar]
- Rahimi, A.; Recht, B. Random Features for Large-Scale Kernel Machines. NIPS 2007, 3, 5. [Google Scholar]
- Rudin, W. Fourier Analysis on Groups; Courier Dover Publications: Mineola, NY, USA, 2017. [Google Scholar]
- Francis, D.P.; Raimond, K. A fast and accurate explicit kernel map. Appl. Intell. 2020, 50, 647–662. [Google Scholar] [CrossRef]
- Le, Q.; Sarlós, T.; Smola, A. Fastfood—Approximating kernel expansions in loglinear time. arXiv 2013, arXiv:1408.3060. [Google Scholar]
- Yu, F.; Suresh, A.; Choromanski, K.; Holtmann-Rice, D.; Kumar, S. Orthogonal random features. Adv. Neural Inf. Process. Syst. 2016, 29, 1975–1983. [Google Scholar]
- Munkhoeva, M.; Kapushev, Y.; Burnaev, E.; Oseledets, I. Quadrature-based features for kernel approximation. arXiv 2018, arXiv:1802.03832. [Google Scholar]
- Francis, D.; Raimond, K. Major advancements in kernel function approximation. Artif. Intell. Rev. 2021, 54, 843–876. [Google Scholar] [CrossRef]
- Lafci, B.; Merčep, E.; Morscher, S.; DeÁn-Ben, X.L.; Razansky, D. Deep Learning for Automatic Segmentation of Hybrid Optoacoustic Ultrasound (OPUS) Images. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2021, 68, 688–696. [Google Scholar] [CrossRef]
- Kaggle. Ultrasound Nerve Segmentation. 2016. Available online: https://www.kaggle.com/c/ultrasound-nerve-segmentation/data (accessed on 5 October 2021).
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018. [Google Scholar] [CrossRef] [Green Version]
- Vinogradova, K.; Dibrov, A.; Myers, G. Towards Interpretable Semantic Segmentation via Gradient-Weighted Class Activation Mapping (Student Abstract). In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 13943–13944. [Google Scholar] [CrossRef]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 437–478. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, P.S.; Deng, L.; Hasegawa-Johnson, M.; He, X. Random features for Kernel Deep Convex Network. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3143–3147. [Google Scholar] [CrossRef]
- Álvarez-Meza, A.M.; Cárdenas-Peña, D.; Castellanos-Dominguez, G. Unsupervised kernel function building using maximization of information potential variability. In Proceedings of the Iberoamerican Congress on Pattern Recognition; Springer: Cham, Switzerland, 2014; pp. 335–342. [Google Scholar]
- Zhou, B.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning deep features for discriminative localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2921–2929. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Gil-GonzÁlez, J.; Valencia-Duque, A.; Álvarez Meza, A.; Orozco-Gutiérrez, A.; García-Moreno, A. Regularized Chained Deep Neural Network Classifier for Multiple Annotators. Appl. Sci. 2021, 11, 5409. [Google Scholar] [CrossRef]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- Maji, D.; Sigedar, P.; Singh, M. Attention Res-UNet with Guided Decoder for semantic segmentation of brain tumors. Biomed. Signal Process. Control. 2022, 71, 103077. [Google Scholar] [CrossRef]
- Yamazaki, K.; Rathour, V.S.; Le, T. Invertible Residual Network with Regularization for Effective Medical Image Segmentation. arXiv 2021, arXiv:2103.09042. [Google Scholar]
- Banerjee, S.; Ling, S.H.; Lyu, J.; Su, S.; Zheng, Y.P. Automatic segmentation of 3d ultrasound spine curvature using convolutional neural network. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 2039–2042. [Google Scholar]



| Model | Measure | Sciatic | Ulnar | Femoral | Median | BP | Ranking |
|---|---|---|---|---|---|---|---|
| FCN [12] | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] | |||||||
| U-net [14,41] | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] | |||||||
| ResUnet [16] | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] | |||||||
| RFF-FCN | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] | |||||||
| RFF-U-net | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] | |||||||
| RFF-ResUnet | Sen [%] | ||||||
| Spe [%] | |||||||
| AUC [%] | |||||||
| GM [%] | |||||||
| Dice [%] | |||||||
| IOU [%] |
| Method | FCN [12] | Unet [14,41] | ResUnet [16] | RFF-FCN | RFF-U-net | RFF-ResUnet |
|---|---|---|---|---|---|---|
| FCN [12] | − | |||||
| U-net [14,41] | − | |||||
| ResUnet [16] | − | |||||
| RFF-FCN | − | |||||
| RFF-U-net | − | |||||
| RFF-ResUnet | − |
| Method | Dice [%] |
|---|---|
| Baby and Jereesh [18] | |
| Kakade and Dumbali [19] | |
| Wang et al. [20] | |
| FCN [12] | |
| U-net [14,41] | |
| ResUnet [16] | |
| RFF-FCN | |
| RFF-U-net | |
| RFF-ResUnet |
| Method | Relevance Measure | Sciatic | Ulnar | Median | Femoral | BP |
|---|---|---|---|---|---|---|
| FCN [12] | Increase Confidence [%] | 0.0 | 6.8 | 4.0 | 2.4 | 100.0 |
| Win(FCN, RFF-FCN) [%] | 43.6 | 53.4 | 32.0 | 42.9 | 51.0 | |
| U-net [14,41] | Increase Confidence [%] | 1.7 | 30.8 | 4.0 | 2.4 | 0.0 |
| Win(U-net, RFF-Unet) [%] | 0.0 | 6.0 | 0.0 | 0.0 | 95.7 | |
| ResUnet [16] | Increase Confidence [%] | 0.0 | 8.3 | 8.0 | 0.0 | 3.4 |
| Win(ResUnet, RFF-ResUnet) [%] | 39.5 | 32.3 | 48.0 | 21.4 | 51.0 | |
| RFF-FCN | Increase Confidence [%] | 4.7 | 10.5 | 4.0 | 2.4 | 100.0 |
| Win(RFF-FCN, FCN) [%] | 56.4 | 46.6 | 68.0 | 57.1 | 49.0 | |
| RFF-Unet | Increase Confidence [%] | 0.0 | 3.0 | 0.0 | 3.0 | 4.3 |
| Win(RFF-Unet, U-net) [%] | 100.0 | 94.0 | 100.0 | 100.0 | 4.3 | |
| RFF-ResUnet | Increase Confidence [%] | 0.0 | 7.5 | 0.0 | 0.0 | 4.9 |
| Win(RFF-ResUnet, ResUnet) [%] | 60.5 | 67.7 | 52.0 | 78.6 | 49.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jimenez-Castaño, C.A.; Álvarez-Meza, A.M.; Aguirre-Ospina, O.D.; Cárdenas-Peña, D.A.; Orozco-Gutiérrez, Á.A. Random Fourier Features-Based Deep Learning Improvement with Class Activation Interpretability for Nerve Structure Segmentation. Sensors 2021, 21, 7741. https://doi.org/10.3390/s21227741
Jimenez-Castaño CA, Álvarez-Meza AM, Aguirre-Ospina OD, Cárdenas-Peña DA, Orozco-Gutiérrez ÁA. Random Fourier Features-Based Deep Learning Improvement with Class Activation Interpretability for Nerve Structure Segmentation. Sensors. 2021; 21(22):7741. https://doi.org/10.3390/s21227741
Chicago/Turabian StyleJimenez-Castaño, Cristian Alfonso, Andrés Marino Álvarez-Meza, Oscar David Aguirre-Ospina, David Augusto Cárdenas-Peña, and Álvaro Angel Orozco-Gutiérrez. 2021. "Random Fourier Features-Based Deep Learning Improvement with Class Activation Interpretability for Nerve Structure Segmentation" Sensors 21, no. 22: 7741. https://doi.org/10.3390/s21227741
APA StyleJimenez-Castaño, C. A., Álvarez-Meza, A. M., Aguirre-Ospina, O. D., Cárdenas-Peña, D. A., & Orozco-Gutiérrez, Á. A. (2021). Random Fourier Features-Based Deep Learning Improvement with Class Activation Interpretability for Nerve Structure Segmentation. Sensors, 21(22), 7741. https://doi.org/10.3390/s21227741






