Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method
Abstract
:1. Introduction
2. Preliminaries
2.1. Fractional Integrodifferential Operators
2.2. Variable Structure Control
2.3. Fractional-Order Sensor
2.4. The Multidimensional Scaling Technique
3. Multidimensional Analysis and Visualization of Variable Structure Control
3.1. Integer Variable Structure Control and Fractional Sliding Mode
3.2. Fractional Variable Structure Control and Integer Sliding Mode
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Utkin, V.I. Variable Structure Systems with Sliding Modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding-mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Shi, J.; Liu, H.; Bajçinca, N. Robust control of robotic manipulators based on integral sliding mode. Int. J. Control 2008, 81, 1537–1548. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar]
- Veselỳ, V. Decentralized variable structure control of complex systems. Int. J. Syst. Sci. 1998, 29, 311–321. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, C.; Pan, L.; Yu, H. Integral sliding-mode control: Performance, modification, and improvement. IEEE Trans. Ind. Inform. 2017, 14, 3087–3096. [Google Scholar] [CrossRef]
- Young, K.K.D. Controller Design for a Manipulator Using Theory of Variable Structure System. IEEE Trans. Syst. Man Cybern. 1978, 8, 101–109. [Google Scholar] [CrossRef]
- Morgan, R.G.; Özgüner, U. A Decentralized Variable Structure Control Algorithm for Robotic Manipulators. J. Robot. Autom. 1985, 1, 57–65. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. A backstepping global fast terminal sliding-mode control for trajectory tracking control of industrial robotic manipulators. IEEE Access 2021, 9, 31921–31931. [Google Scholar] [CrossRef]
- Su, Y.; Zheng, C. A new nonsingular integral terminal sliding-mode control for robot manipulators. Int. J. Syst. Sci. 2020, 51, 1418–1428. [Google Scholar] [CrossRef]
- Slotine, J.J.E. The Robust Control of Robot Mattipulators. Int. J. Robot. Res. 1985, 4, 49–64. [Google Scholar] [CrossRef]
- Norsahperi, N.; Danapalasingam, K. An improved optimal integral sliding-mode control for uncertain robotic manipulators with reduced tracking error, chattering, and energy consumption. Mech. Syst. Signal Process. 2020, 142, 106747. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Zaare, S.; Haghgoo, M.; Moattari, M. Free-chattering fuzzy sliding-mode control of robot manipulators with joints flexibility in presence of matched and mismatched uncertainties in model dynamic and actuators. J. Intell. Robot. Syst. 2020, 100, 47–69. [Google Scholar] [CrossRef]
- Machado, J.A.T.; de Carvalho, J.L.M. A New Variable Structure Controller for Robot Manipulators. In Proceedings of the Third IEEE International Symposium on Intelligent Control, Arlington VA, USA, 24–26 August 1988. [Google Scholar]
- Huang, J.; Zhang, M.; Ri, S.; Xiong, C.; Li, Z.; Kang, Y. High-order disturbance-observer-based sliding-mode control for mobile wheeled inverted pendulum systems. IEEE Trans. Ind. Electron. 2019, 67, 2030–2041. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016; Volume 5. [Google Scholar]
- Kenneth, M.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Luo, Y.; Chen, Y. Fractional Order Motion Controls; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ionescu, C.M. The Human Respiratory System: An Analysis of the Interplay between Anatomy, Structure, Breathing and Fractal Dynamics; Springer: London, UK, 2013. [Google Scholar]
- Ionescu, C.M.; Dulf, E.H.; Ghita, M.; Muresan, C.I. Robust controller design: Recent emerging concepts for control of mechatronic systems. J. Frankl. Inst. 2020, 357, 7818–7844. [Google Scholar] [CrossRef]
- Chen, L.; Pan, W.; Wu, R.; Tenreiro Machado, J.A.; Lopes, A.M. Design and implementation of grid multi-scroll fractional-order chaotic attractors. Chaos 2016, 26, 084303. [Google Scholar] [CrossRef] [Green Version]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M. Shifted Jacobi–Gauss-collocation with convergence analysis for fractional integro-differential equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 342–359. [Google Scholar] [CrossRef]
- Ghita, M.; Neckebroek, M.; Juchem, J.; Copot, D.; Muresan, C.I.; Ionescu, C.M. Bioimpedance sensor and methodology for acute pain monitoring. Sensors 2020, 20, 6765. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.A.T. Modeling vegetable fractals by means of fractional-order equations. J. Vib. Control 2016, 22, 2100–2108. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Azenha, A. Fractional-Order Hybrid Control of Robot Manipulators. In Proceedings of the 1998 IEEE International Conference on Systems, Man and Cybernetics, San Diego, CA, USA, 11–14 October 1998. [Google Scholar]
- Önder Efe, M. Fractional Order Sliding Mode Controller Design for Fractional Order Dynamic Systems. In New Trends in Nanotechnology and Fractional Calculus Applications; Baleanu, D., Guvenc, Z.B., Tenreiro Machado, J.A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 463–470. [Google Scholar]
- Delavari, H.; Lanusse, P.; Sabatier, J. Fractional order controller design for a flexible link manipulator robot. Asian J. Control 2013, 15, 783–795. [Google Scholar] [CrossRef]
- Delavari, H.; Heydarinejad, H. Fractional-order backstepping sliding-mode control based on fractional-order nonlinear disturbance observer. J. Comput. Nonlinear Dyn. 2018, 13, 111009. [Google Scholar] [CrossRef]
- Fei, J.; Wang, H.; Fang, Y. Novel neural network fractional-order sliding-mode control with application to active power filter. IEEE Trans. Syst. Man Cybern. Syst. 2021. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Z.; Huang, P. Fractional-order control for uncertain teleoperated cyber-physical system with actuator fault. IEEE/ASME Trans. Mechatron. 2020, 26, 2472–2482. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, X.; Meng, W.; Zheng, S.; Jiang, L.; Meng, J.; Wang, S. Coupled fractional-order sliding-mode control and obstacle avoidance of a four-wheeled steerable mobile robot. ISA Trans. 2021, 108, 282–294. [Google Scholar] [CrossRef]
- Delavari, H.; Jokar, R. Intelligent Fractional-Order Active Fault-Tolerant Sliding Mode Controller for a Knee Joint Orthosis. J. Intell. Robot. Syst. 2021, 102, 1–18. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Yan, F.; Chen, B. Practical adaptive fractional-order nonsingular terminal sliding mode control for a cable-driven manipulator. Int. J. Robust Nonlinear Control 2019, 29, 1396–1417. [Google Scholar] [CrossRef]
- Zhou, M.; Feng, Y.; Xue, C.; Han, F. Deep convolutional neural network based fractional-order terminal sliding-mode control for robotic manipulators. Neurocomputing 2020, 416, 143–151. [Google Scholar] [CrossRef]
- Kumar, J.; Kumar, V.; Rana, K. Design of robust fractional order fuzzy sliding mode PID controller for two link robotic manipulator system. J. Intell. Fuzzy Syst. 2018, 35, 5301–5315. [Google Scholar] [CrossRef]
- Ahmed, S.; Wang, H.; Tian, Y. Adaptive fractional high-order terminal sliding-mode control for nonlinear robotic manipulator under alternating loads. Asian J. Control 2021, 23, 1900–1910. [Google Scholar] [CrossRef]
- Alipour, M.; Malekzadeh, M.; Ariaei, A. Practical fractional-order nonsingular terminal sliding-mode control of spacecraft. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Machado, J.T.; Galhano, A. Approximating fractional derivatives in the perspective of system control. Nonlinear Dyn. 2009, 56, 401–407. [Google Scholar] [CrossRef] [Green Version]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. An efficient algorithm for low-order direct discrete-time implementation of fractional order transfer functions. ISA Trans. 2018, 74, 229–238. [Google Scholar] [CrossRef] [PubMed]
- Oustaloup, A. La Commande CRONE: Commande Robuste D’Ordre Non Entier; Hermes: Paris, France, 1991. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Pan, I.; Das, S. Frequency domain design of fractional order PID controller for AVR system using chaotic multi-objective optimization. Int. J. Electr. Power Energy Syst. 2013, 51, 106–118. [Google Scholar] [CrossRef] [Green Version]
- Lopes, A.M.; Tenreiro Machado, J.; Galhano, A.M. Towards fractional sensors. J. Vib. Control 2019, 25, 52–60. [Google Scholar] [CrossRef]
- Muresan, C.I.; Birs, I.R.; Dulf, E.H.; Copot, D.; Miclea, L. A Review of Recent Advances in Fractional-Order Sensing and Filtering Techniques. Sensors 2021, 21, 5920. [Google Scholar] [CrossRef]
- Ware, C. Information Visualization: Perception for Design; Elsevier: Waltham, MA, USA, 2012. [Google Scholar]
- Spence, R. Information Visualization: An Introduction; Springer: Cham, Switzerland, 2001; Volume 1. [Google Scholar]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn. Res. 2009, 10, 66–71. [Google Scholar]
- Tenreiro Machado, J.; Lopes, A.M.; Galhano, A.M. Multidimensional scaling visualization using parametric similarity indices. Entropy 2015, 17, 1775–1794. [Google Scholar] [CrossRef] [Green Version]
- Dunteman, G.H. Principal Components Analysis; Number 69; Sage: London, UK, 1989. [Google Scholar]
- Thompson, B. Canonical correlation analysis. In Encyclopedia of Statistics in Behavioral Science; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A.E. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef] [Green Version]
- Child, D. The Essentials of Factor Analysis; Cassell Educational: London, UK, 1990. [Google Scholar]
- France, S.L.; Carroll, J.D. Two-way multidimensional scaling: A review. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2010, 41, 644–661. [Google Scholar] [CrossRef]
- Lee, J.A.; Lendasse, A.; Verleysen, M. Nonlinear projection with curvilinear distances: Isomap versus curvilinear distance analysis. Neurocomputing 2004, 57, 49–76. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Coifman, R.R.; Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 2006, 21, 5–30. [Google Scholar] [CrossRef] [Green Version]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- De Oliveira, E.C.; Machado, J. A review of definitions for fractional derivatives and integrals. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef] [Green Version]
- Dorčák, V. Numerical models for the simulation of the fractional-order control systems. arXiv 2002, arXiv:math/0204108. [Google Scholar]
- Podlubny, I. Functional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Al-Alaoui, M.A. Al-Alaoui operator and the new transformation polynomials for discretization of analogue systems. Electr. Eng. 2008, 90, 455–467. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Multidimensional scaling analysis of generalized mean discrete-time fractional order controllers. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105657. [Google Scholar] [CrossRef]
- Machado, J.A.T. Variable Structure Control of Manipulators with Joints having Flexibility and Backlash. Syst. Anal. Model. Simul. 1996, 23, 93–101. [Google Scholar]
- Azenha, A.; Machado, J.A.T. Dynamic Analysis in Variable Structure Position/Force Hybrid Control of Manipulators. In Proceedings of the 1997 IEEE International Conference on Systems, Man and Cybernetics, Orlando, FL, USA, 12–15 October 1997. [Google Scholar]
- Machado, J.T. The effect of fractional order in variable structure control. Comput. Math. Appl. 2012, 64, 3340–3350. [Google Scholar] [CrossRef] [Green Version]
- Machado, J.A.T.; de Carvalho, J.M.; Galhano, A. Analysis of Robot Dynamics and Compensation Using Classical and Computed Torque Techniques. IEEE Trans. Educ. 1993, 36, 372–379. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F.; Afshar, M.; Karimi-Ghartemani, M. Extension of the root-locus method to a certain class of fractional-order systems. ISA Trans. 2009, 48, 48–53. [Google Scholar] [CrossRef]
- Lopes, A.M.; Tenreiro Machado, J. Root locus practical sketching rules for fractional-order systems. Abstr. Appl. Anal. 2013, 2013, 102068. [Google Scholar] [CrossRef] [Green Version]
- Biswas, K.; Bohannan, G.; Caponetto, R.; Lopes, A.; Machado, T. Fractional Order Devices; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Petráš, I. Fractional-order feedback control of a DC motor. J. Electr. Eng. 2009, 60, 117–128. [Google Scholar]
- Ionescu, C.M.; Muntean, I.; Tenreiro-Machado, J.; De Keyser, R.; Abrudean, M. A theoretical study on modeling the respiratory tract with ladder networks by means of intrinsic fractal geometry. IEEE Trans. Biomed. Eng. 2010, 57, 246–253. [Google Scholar] [CrossRef]
- Daou, R.A.Z.; Francis, C.; Moreau, X. Synthesis and implementation of noninteger integrators using RLC devices. Int. J. Electron. 2009, 96, 1207–1223. [Google Scholar] [CrossRef]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]



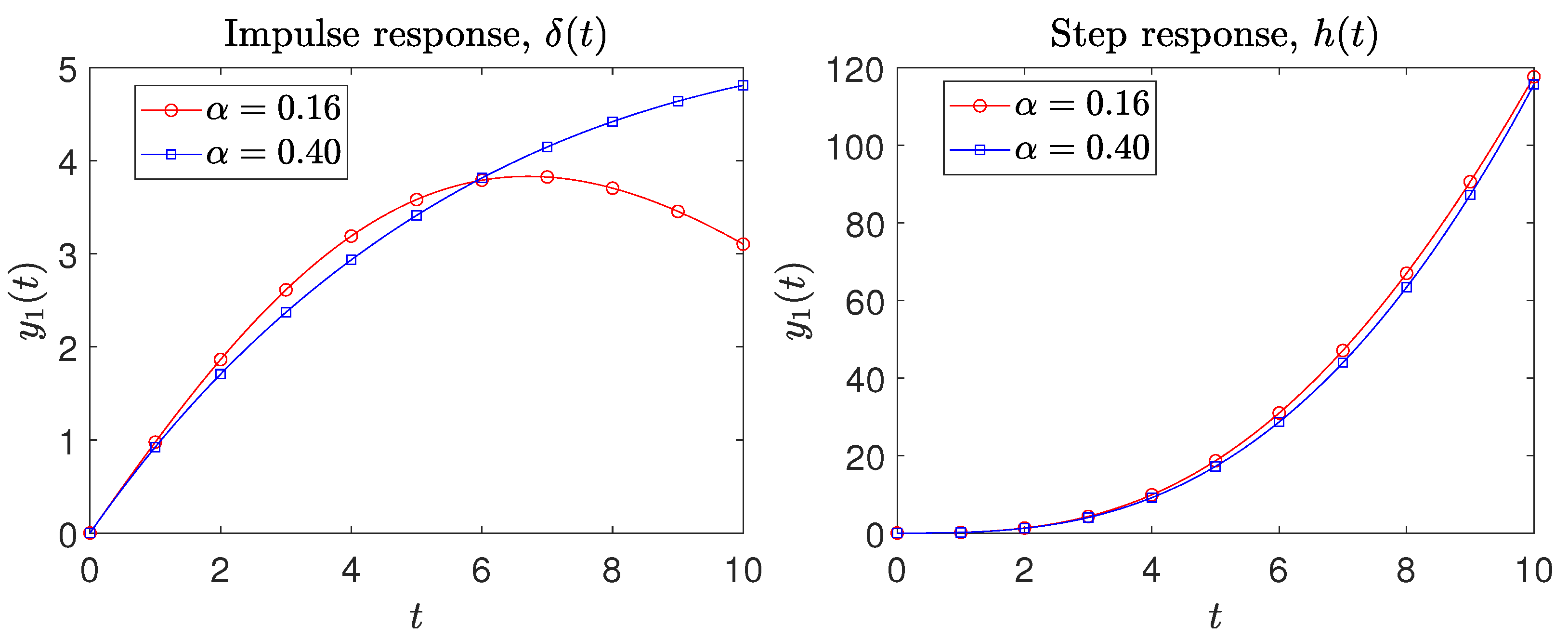
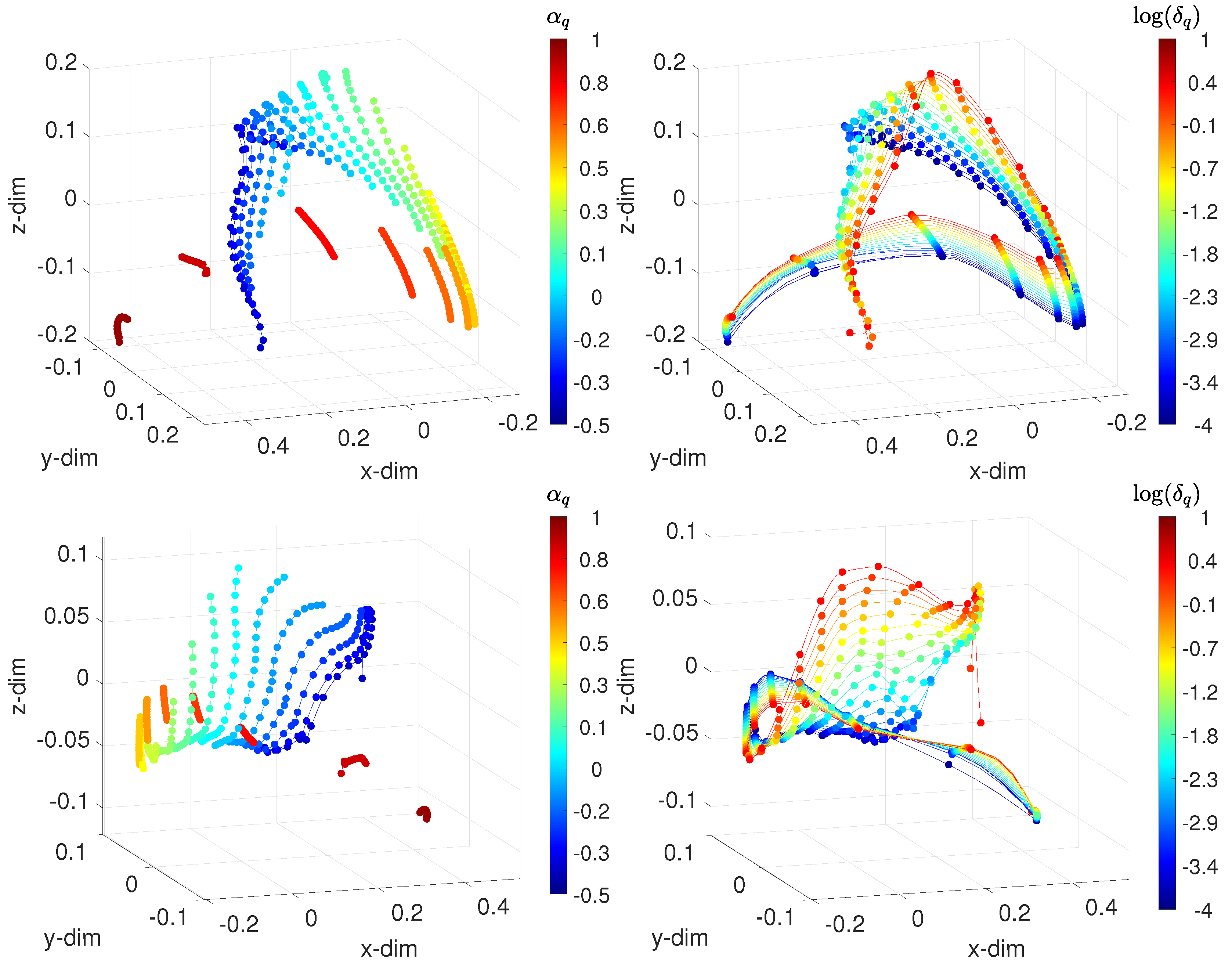
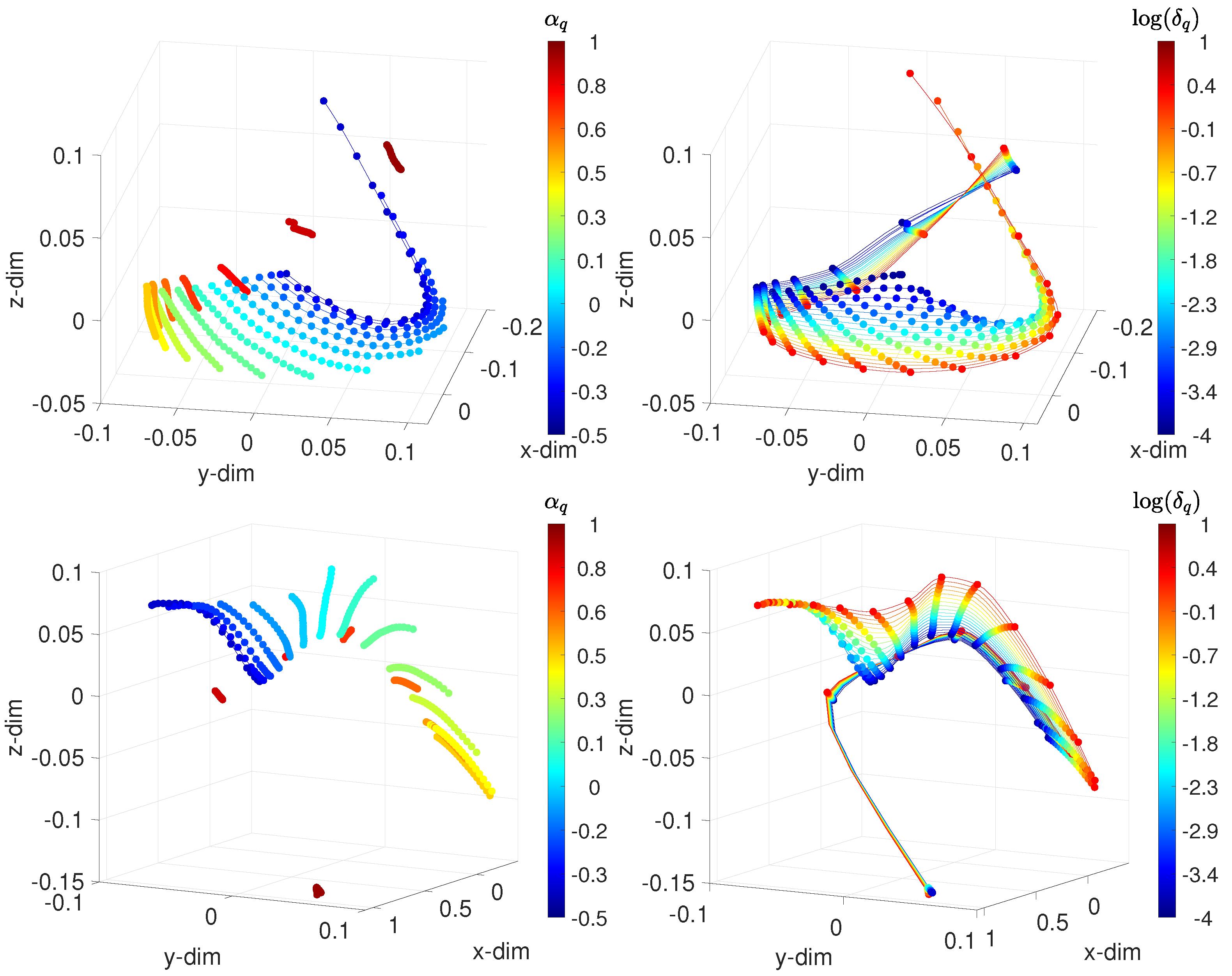


| Order | Stage Elements | Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| {,,}, | I | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 0.16 | 0.30, 0.09, 0.34 | 0.63, 0.33, 0.59 | 0.87, 0.22, 0.38 | 0.22, 0.98, 1.38 | 0.17, 0.44, 0.49 | 0.76, 0.77, 0.15 | 1.08 | 6.89 | 4.25 |
| 0.40 | 0.12, 0.78, 0.93 | 0.57, 0.22, 0.58 | 0.84, 0.75, 0.12 | 0.54, 0.08, 0.84 | 0.67, 0.36, 0.85 | 1.12, 1.15, 1.61 | 0.97 | 9.29 | 4.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, A.M.; Tenreiro Machado, J.A. Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method. Sensors 2021, 21, 7736. https://doi.org/10.3390/s21227736
Lopes AM, Tenreiro Machado JA. Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method. Sensors. 2021; 21(22):7736. https://doi.org/10.3390/s21227736
Chicago/Turabian StyleLopes, António M., and José A. Tenreiro Machado. 2021. "Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method" Sensors 21, no. 22: 7736. https://doi.org/10.3390/s21227736
APA StyleLopes, A. M., & Tenreiro Machado, J. A. (2021). Fractional-Order Sensing and Control: Embedding the Nonlinear Dynamics of Robot Manipulators into the Multidimensional Scaling Method. Sensors, 21(22), 7736. https://doi.org/10.3390/s21227736







