An Efficient and Robust Star Identification Algorithm Based on Neural Networks
Abstract
:1. Introduction
- A modified Log-Polar transform is used for star pattern construction. With the help of modified LPT, the training time of the network is reduced and the robustness of the network is improved.
- A 1D CNN is introduced for star pattern classification. The designed network could deal with position noise, magnitude noise, false stars and angular velocities.
- The global average pooling is introduced into the 1D CNN network to reduce the size of the network. Consequently, the designed network can be implemented on on-board processors.
2. Algorithm Description
2.1. Star Pattern Construction
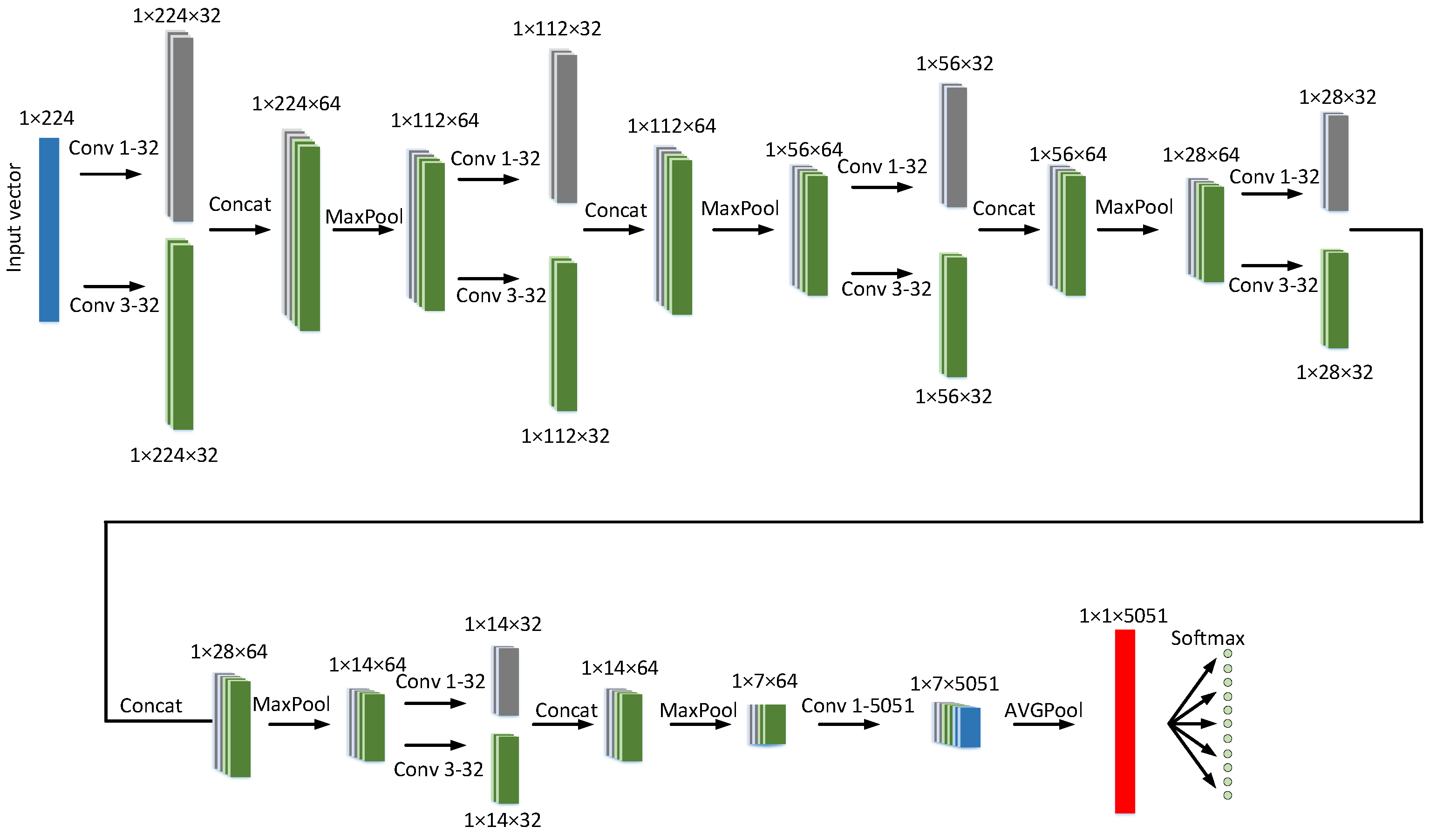
2.2. Neural Network Architecture
2.3. Construction of the Training Dataset
- The magnitude of the guide star should be less than 6.0 Mv.
- Double stars or binary stars are labelled as a single star.
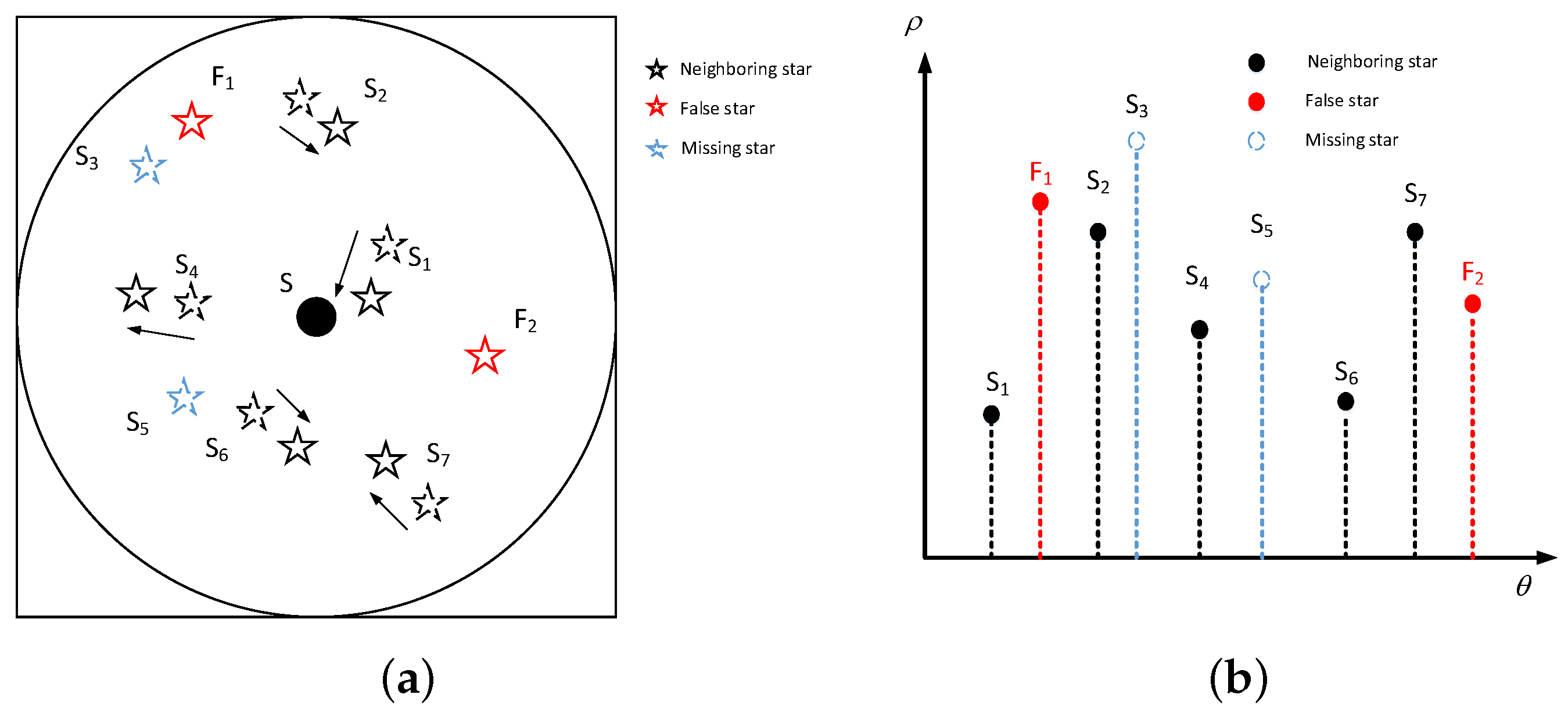
- Step1: Select a guide star as the reference star . Set the optic axis of the star tracker to point at S, which means the projection of lies at the center of the image. Then the neighboring stars appearing in the field of view are also projected from celestial coordinate system into the image coordinate system as shown in Figure 2a.
- Step2: The modified LPT transform is performed for every neighboring stars. A set of logarithmic distances and relative angles is obtained. Then same to the vector construction procedure, the log-polar coordinates of the neighboring stars are discreted and a vector is constructed, as shown in Figure 2b. is considered as the basic pattern of the reference star .
- Step3: Data augmentation is performed to reduce overfitting and enhance the generalization power of the network, which is also the major way to enhance the robustness of the algorithm. The details of data augmentation are described as follows:
- Random position deviations varying from pixels to 5 pixels were added to each star’s coordinates. As shown in Figure 2a, the curves with arrow denotes the direction of translation of each star.
- A random magnitude deviation varying from Mv to 0.5 Mv were added to each star. Therefore, some stars might appear or disappear due to the magnitude noise. As shown in Figure 2, and are the missing stars, and the corresponding elements of is set as 0.
- One to five false stars with random positions and magnitudes are added. As shown in Figure 2, and are the false stars added in the scene.
- In order to improve the rotation invariance of the algorithm, the basic pattern is shifted from to by step.
- Dynamic condition would decrease the magnitude limit of the star tracker and lead to missing stars. In order to make the network robust to dynamic condition, the magnitude limit is set from 4 Mv to 6 Mv, and the stars with a magnitude beyond the limit will be dropped.
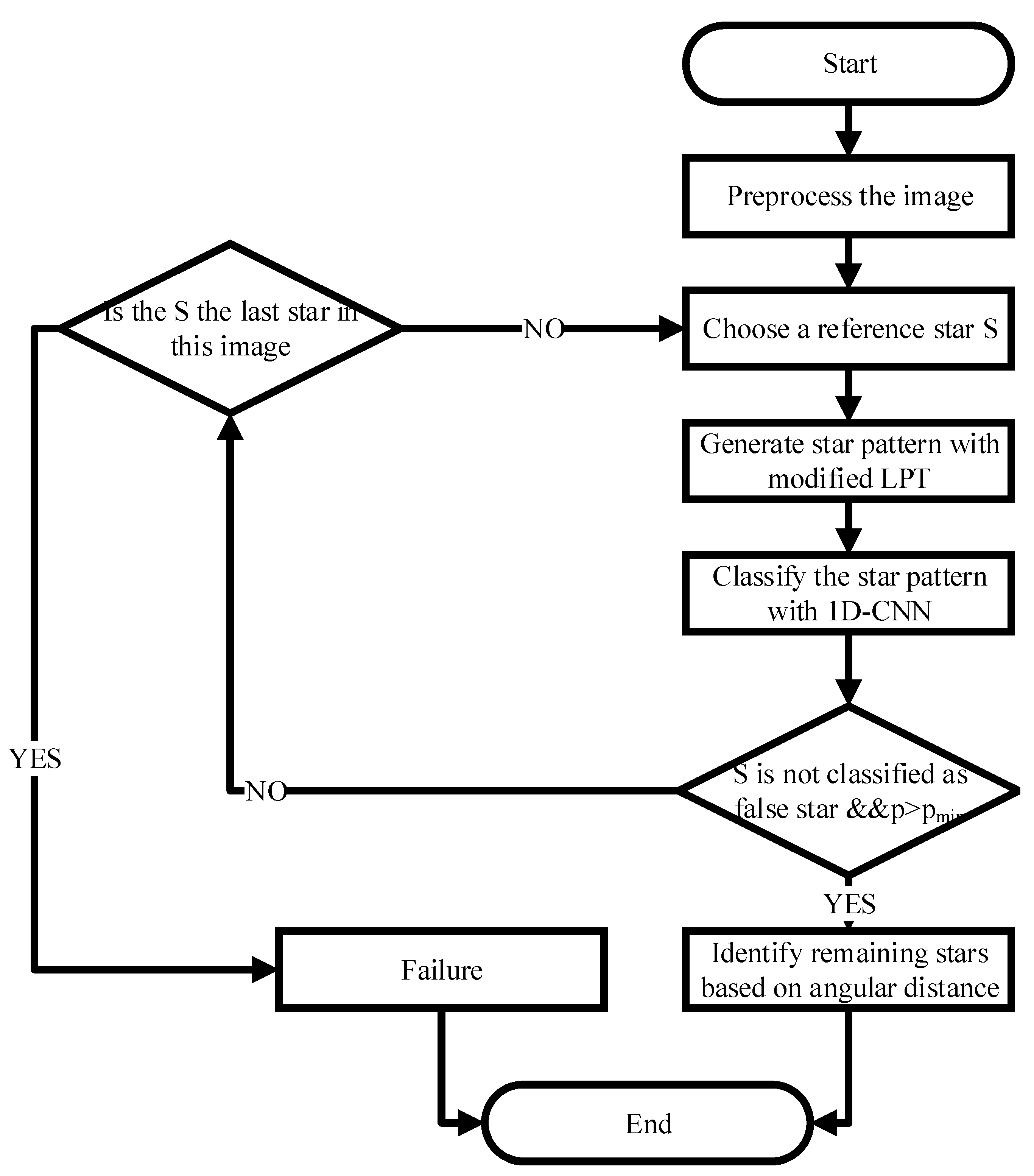
2.4. Star Identification Algorithm
- Image Preprocessing. Star points are extracted via centroid extraction algorithm.
- Reference Star Determination. The nearest star to the center of the image is taken as the reference star S.
- Star Pattern Construction. The star pattern is generated by modified LPT.
- Star Pattern Classification. Input the star pattern to the proposed network, then the ID of the reference star and the corresponding probability are obtained.
- Validation. Unless the reference star is not classified as a false star and , this identification is considered as a success. Otherwise, the reference star may be a false star or the ID is wrong. Then a new reference star will be selected, which means to go back to step 2.
- Remaining Stars Identification. Identify the remaining stars in the image by the angular distances between them and the reference star.
3. Experiments and Results
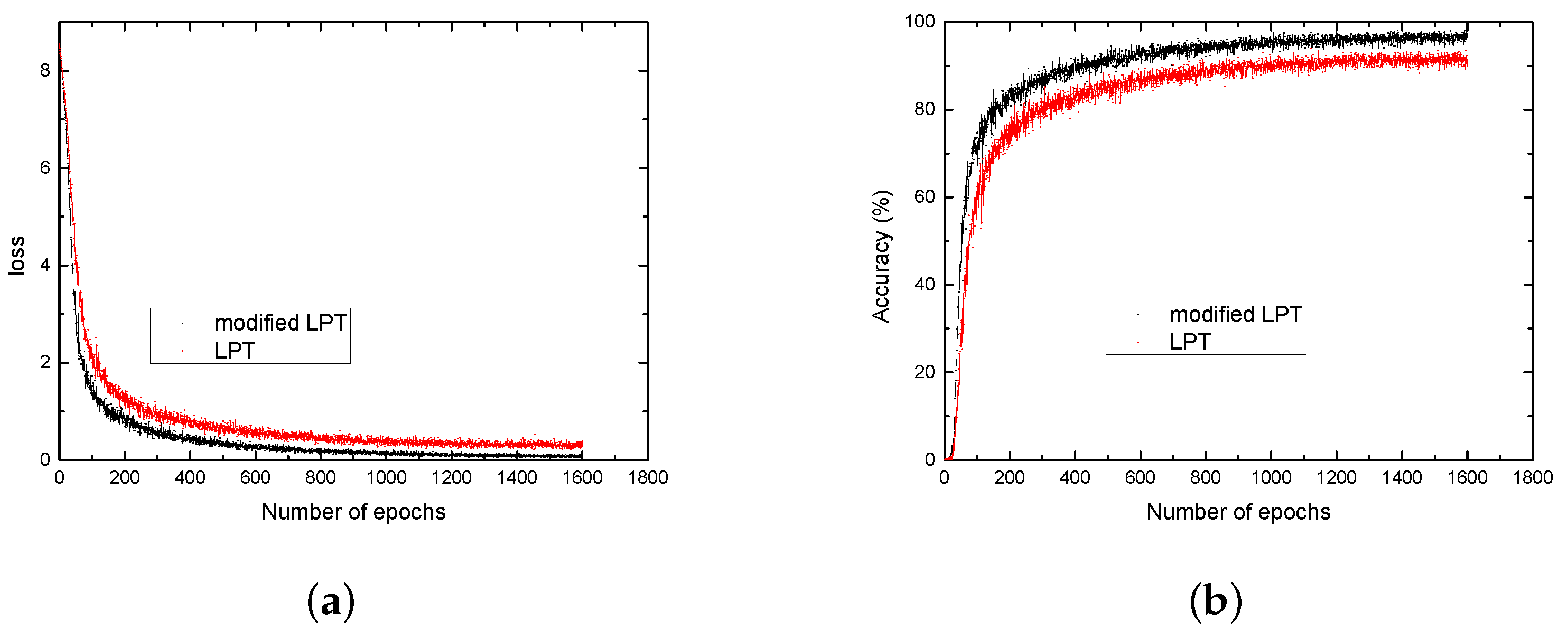
3.1. Training of the Network
3.2. Comparison and Analysis
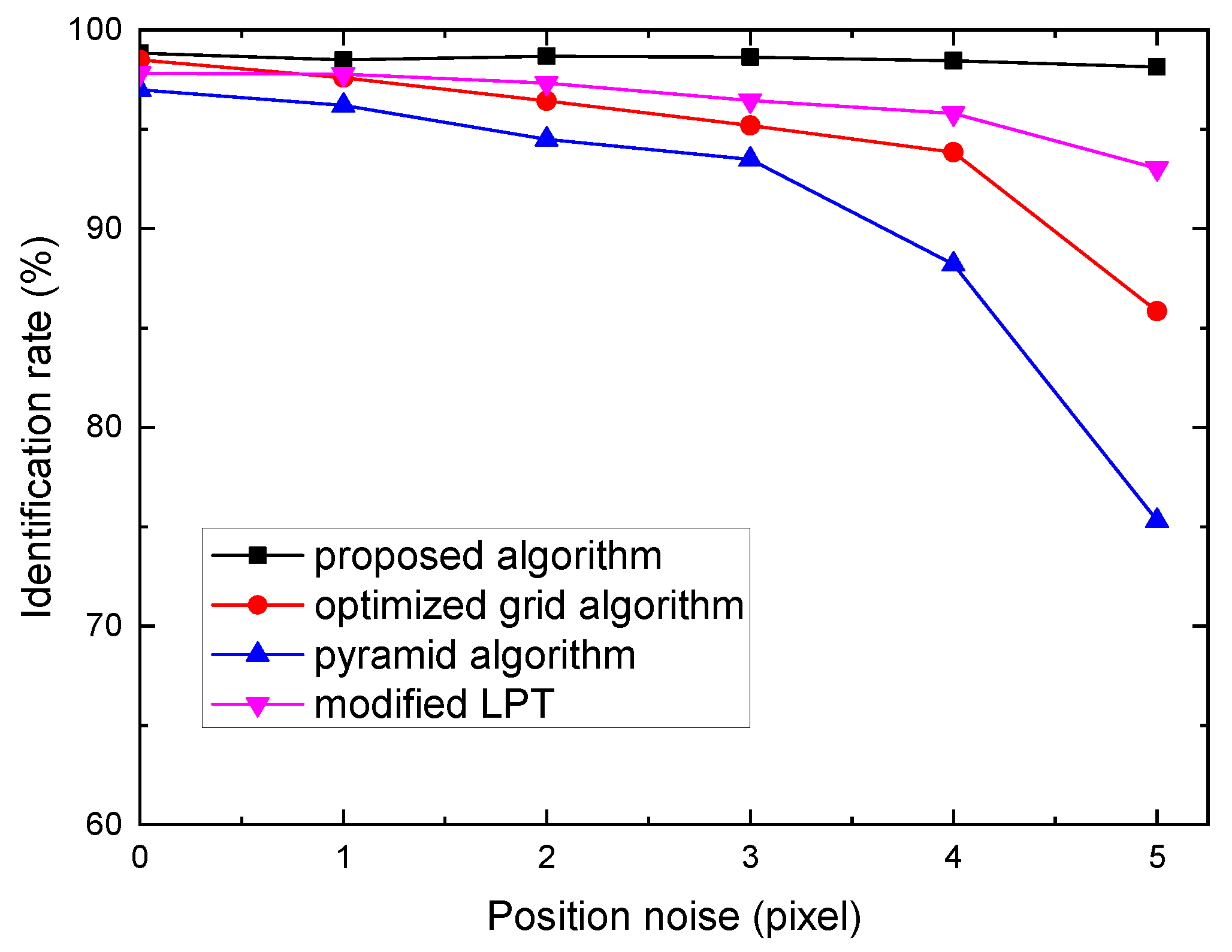
3.2.1. Robustness to Star Positional Noise
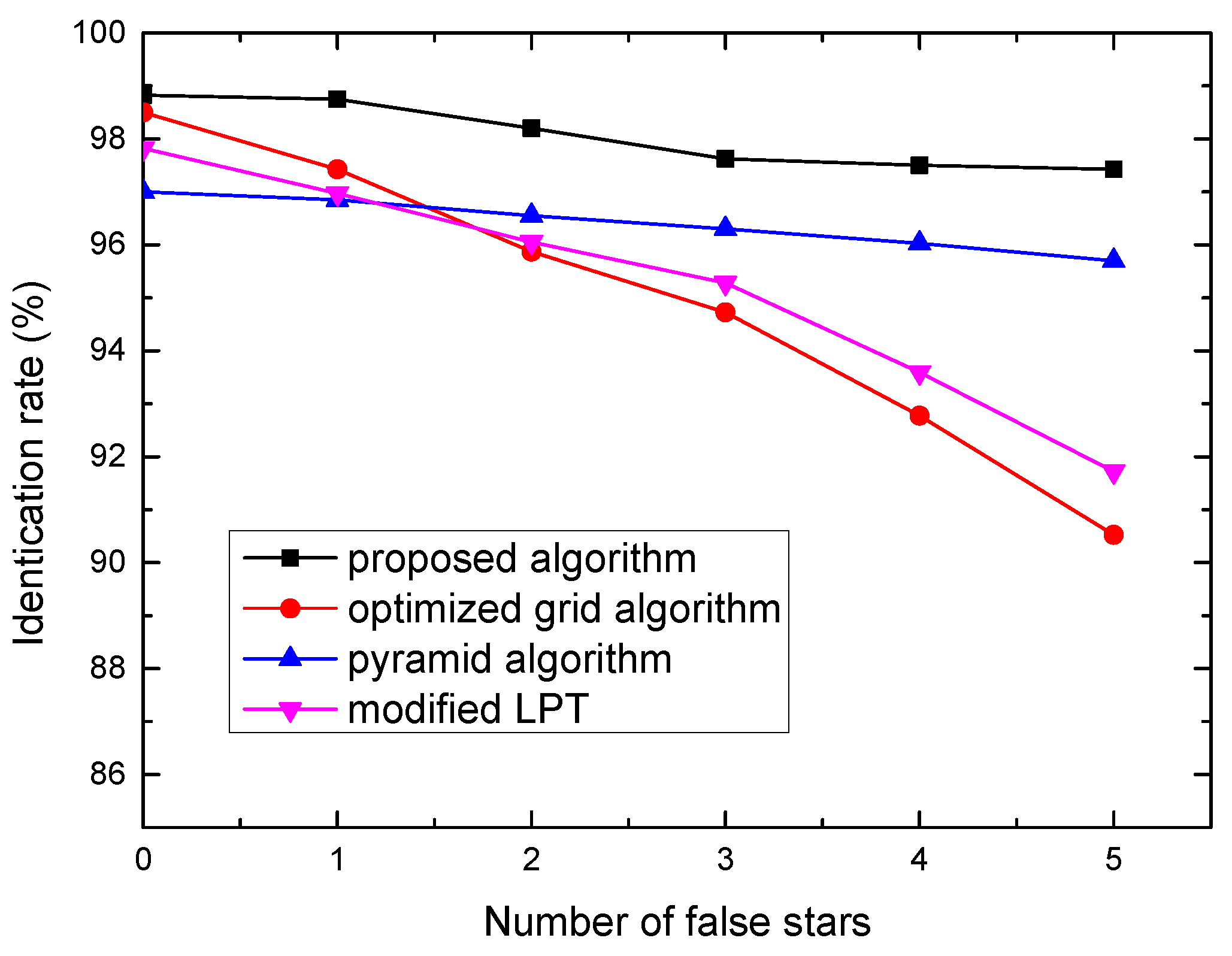
3.2.2. Robustness to False Stars
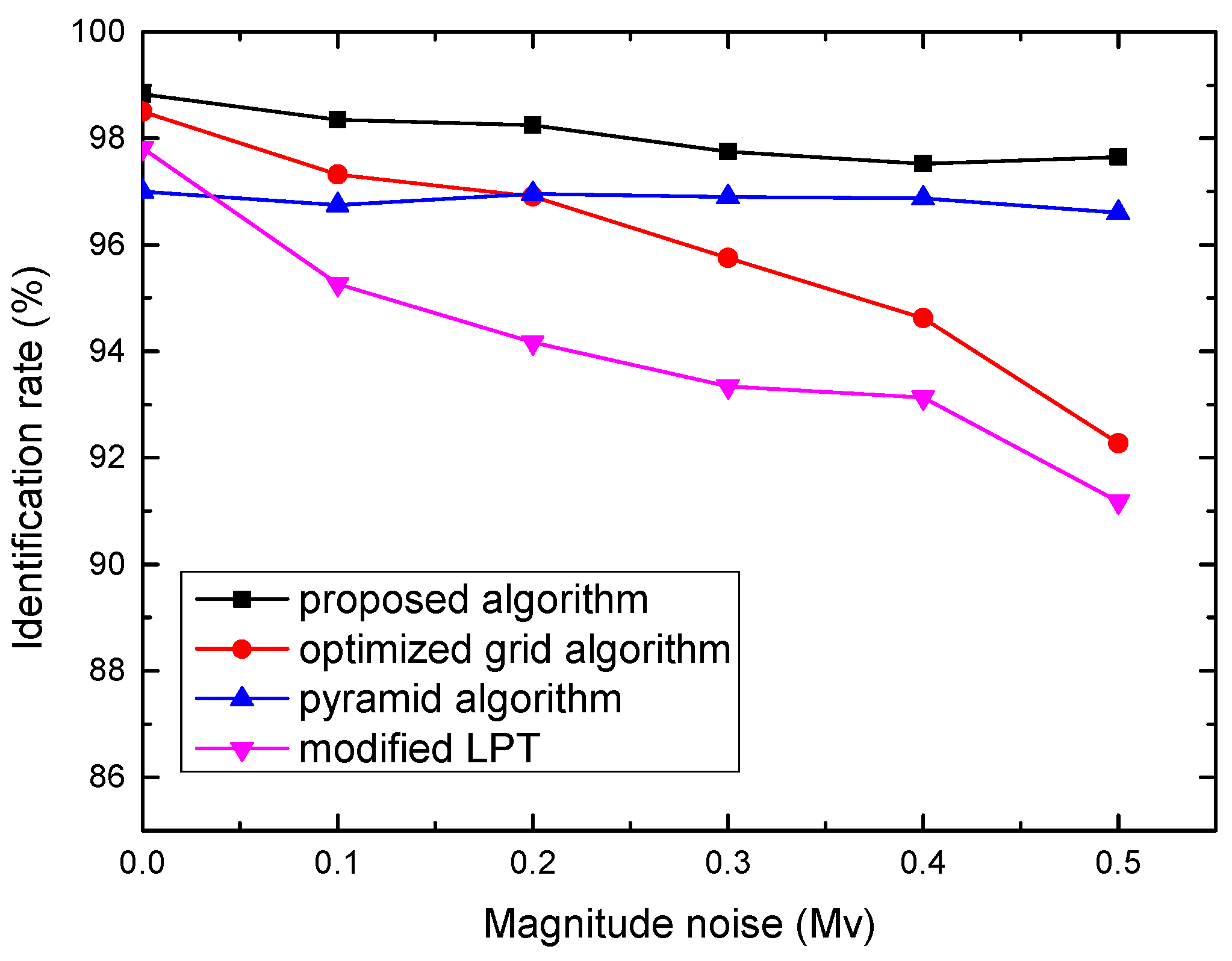
3.2.3. Robustness to Magnitude Noise
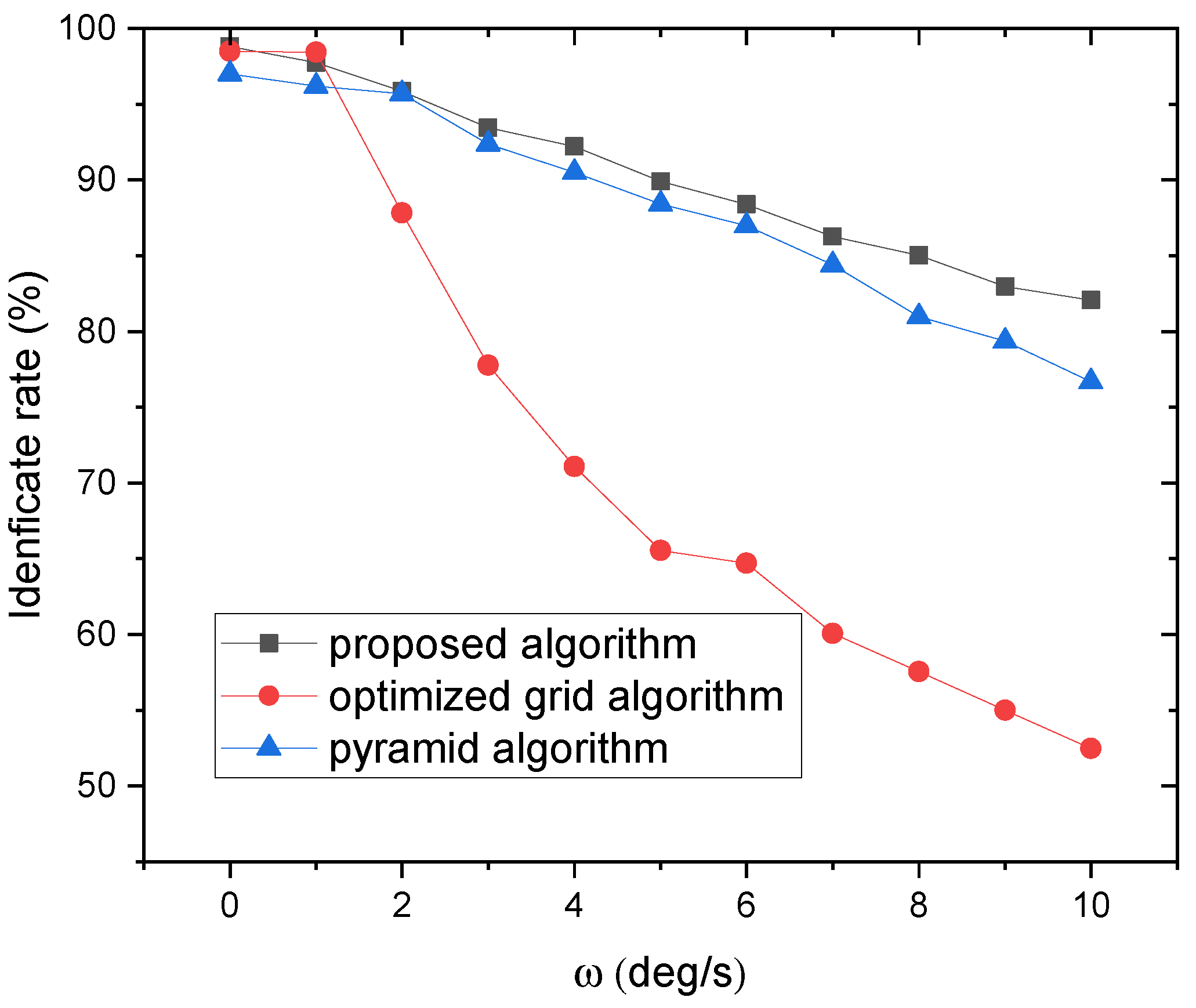
3.2.4. Robustness to Rotation Velocity of the Star Tracker
3.2.5. Performance of the Proposed Idea on Real Images
3.2.6. Time and Memory Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Padgett, C.; Kreutz-Delgado, K. A grid algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 202–213. [Google Scholar] [CrossRef]
- Liebe, C.C. Pattern recognition of star constellations for spacecraft applications. IEEE Aerosp. Electron. Syst. Mag. 1992, 7, 10–16. [Google Scholar] [CrossRef] [Green Version]
- Mortari, D.; Bruccoleri, C.; Junkins, J.L. The pyramid star identication technique. ION Navig. 2004, 51, 171–183. [Google Scholar] [CrossRef]
- Kumar, M.; Mortari, D.; Junkins, J.L. An analytical approach to star identification reliability. Acta Astronaut. 2010, 66, 508–515. [Google Scholar] [CrossRef]
- Kolomenkin, M.; Pollak, S.; Shimshoni, I.; Lindenbaum, M. Geometric voting algorithm for star trackers. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 441–456. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. A novel star identication technique robust to high presence of false objects: The multi-poles algorithm. Adv. Space Res. 2017, 59, 2133–2147. [Google Scholar] [CrossRef]
- Schiattarella, V.; Spiller, D.; Curti, F. Star identification robust to angular rates and false objects with rolling shutter compensation. Acta Astronaut. 2020, 166, 243–259. [Google Scholar] [CrossRef]
- Na, M.; Zheng, D.; Jia, P. Modified Grid Algorithm for Noisy All-Sky Autonomous Star Identification. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 516–522. [Google Scholar] [CrossRef]
- Aghaei, M.; Moghaddam, H.A. Grid star identification improvement using optimization approaches. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2082–2090. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Jiang, J. Full-sky autonomous star identication based on radial and cyclic features of star pattern. Image Vis. Comput. 2008, 26, 891–897. [Google Scholar] [CrossRef]
- Wei, X.; Wen, D.; Song, Z.; Xi, J.; Zhang, W.; Liu, G.; Li, Z. A star identification algorithm based on radial and dynamic cyclic features of star pattern. Adv. Space Res. 2019, 63, 2245–2259. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, G.; Jiang, J. Star identification algorithm based on Log-Polar transform. J. Aerosp. Comput. Inf. Commun. 2009, 6, 483–490. [Google Scholar] [CrossRef]
- Juang, J.N.; Kim, H.Y.; Junkins, J.L. An efficient and robust singular value method for star pattern recognition and attitude determination. J. Astronaut. Sci. 2019, 115, 211–220. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. A survey of lost-in-space star identification algorithms since 2009. Sensors 2020, 20, 2579. [Google Scholar] [CrossRef]
- Luo, L.; Xu, L.; Zhang, H.; Sun, J. Improved autonomous star identification algorithm. Chin. Phys. B 2015, 24, 064202. [Google Scholar] [CrossRef]
- Sun, Z.; Qi, X.; Jin, G.; Wang, T. Ellipticity pivot star method for autonomous star identification. Optik 2017, 137, 1–5. [Google Scholar] [CrossRef]
- Kim, K.; Bang, H. Algorithm with Patterned Singular Value Approach for Highly Reliable Autonomous Star Identification. Sensors 2020, 20, 374. [Google Scholar] [CrossRef] [Green Version]
- Alvelda, P.; Martin, M.A.S. Neural network star pattern recognition for spacecraft attitude determination and control. In Advances in Neural Information Processing Systems; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1989; pp. 314–322. [Google Scholar]
- Hong, J.; Dickerson, J.A. Neural-network-based autonomous star identification algorithm. J. Guid. Control Dyn. 2000, 28, 728–735. [Google Scholar] [CrossRef]
- Jing, Y.; Liang, W. An improved star identification method based on neural network. In Proceedings of the IEEE 10th International Conference on Industrial Informatics, Beijing, China, 25–27 July 2012. [Google Scholar]
- Xu, L.; Jiang, J.; Liu, L. RPNet: A Representation Learning-Based Star Identification Algorithm. IEEE Access 2019, 7, 92193–92202. [Google Scholar] [CrossRef]
- Rijlaarsdam, D.; Yous, H.; Byrne, J.; Oddenino, D.; Furano, G.; Moloney, D. Efficient Star Identification Using a Neural Network. Sensors 2020, 20, 3684. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Wang, B.; Yu, Z.; Jin, Z.; Crassidis, J.L. An artificial intelligence enhanced star identification algorithm. Front. Inform. Technol. Electron. Eng. 2020, 21, 1661–1670. [Google Scholar] [CrossRef]
- Wolberg, G.; Zokai, S. Robust image registration using log-polar transform. In Proceedings of the 2000 International Conference on Image Processing, Vancouver, BC, Canada, 10–13 September 2000. [Google Scholar]
- Amorim, M.; Bortoloti, F.; Ciarelli, P.M.; de Oliveira, E.; de Souza, A.F. Analysing rotation-invariance of a log-polar transformation in convolutional neural networks. In Proceedings of the 2018 International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the ACM Multimedia, Orlando, FL, USA, 7 November 2014. [Google Scholar]
- Zhang, G. Star Image Simulation. In Star Identification; Springer: Berlin, Germany, 2017; pp. 48–55. [Google Scholar]
- Hancock, B.R.; Stirbl, R.C.; Cunningham, T.J.; Pain, B.; Ringold, P.G. Cmos active pixel sensor specific performance effects on star tracker/imager position accuracy. In Proceedings of the Functional Integration of Opto-Electro-Mechanical Devices and Systems, San Jose, CA, USA, 15 May 2001. [Google Scholar]
- Kazemi, L.; Enright, J. Enabling technologies for high slew rate star trackers. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]

| Parameter | Value |
|---|---|
| Resolution of CMOS | |
| Size of One Pixel | |
| FOV | |
| Highest Visual Magnitude | Mv |
| Full Well Charge | 13,500 |
| Temporal Noise | 13 |
| Dark current signal | 125 |
| Fixed Pattern Noise | <1 LSB |
| Photon non-uniformity response noise | <1% RMS of signal |
| Astronomical Background | 10 Mv |
| Exposure time | 16 ms |
| Algorithm | Identification Time | Memory Consumption |
|---|---|---|
| Proposed algorithm | 32.7 ms | 1920.6 KB |
| Pyramid algorithm | 341.2 ms | 2282.3 KB |
| Optimized Grid algorithm | 178.7 ms | 348.1 KB |
| Modified LPT algorithm | 65.4 ms | 313.5 KB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wang, H.; Jin, Z. An Efficient and Robust Star Identification Algorithm Based on Neural Networks. Sensors 2021, 21, 7686. https://doi.org/10.3390/s21227686
Wang B, Wang H, Jin Z. An Efficient and Robust Star Identification Algorithm Based on Neural Networks. Sensors. 2021; 21(22):7686. https://doi.org/10.3390/s21227686
Chicago/Turabian StyleWang, Bendong, Hao Wang, and Zhonghe Jin. 2021. "An Efficient and Robust Star Identification Algorithm Based on Neural Networks" Sensors 21, no. 22: 7686. https://doi.org/10.3390/s21227686
APA StyleWang, B., Wang, H., & Jin, Z. (2021). An Efficient and Robust Star Identification Algorithm Based on Neural Networks. Sensors, 21(22), 7686. https://doi.org/10.3390/s21227686






