1. Introduction
Hospital readmissions are associated with high mortality rate and suffering for both patients and family members, and they cost the US health system billions of dollars. Unplanned patient readmissions following surgery are common in many treatments, with nearly a third of patients being readmitted within 30 days of discharge from the hospital [
1]. According to Zafar et al. (2018) [
2], up to 80% of readmsissions after cancer surgeries can be prevented if the readmission risk is accurately estimated and predicted. However, predicting who will be readmitted following a surgery is often challenging. Current approaches to readmission risk estimation use patients’ demographics, medical history, and hospital administrative information to estimate a singular risk of readmission in patients at the time of discharge and often categorize most patients as high-risk [
3,
4]. In addition, traditional measures use static information at the time of discharge and do not take into account other factors in patients’ daily life that may contribute to the increase or decrease of their readmission risk. These factors among others include a patient’s daily behavioral activities that affect their recovery after treatment. Currently, there is no mechanism to objectively measure readmission risk nor is there a method by which readmission risk can be updated over time based on changes in patients’ daily activity and behavior. Such a mechanism would help identify risk acuity ahead of time and provide the opportunity for healthcare providers to act accordingly.
Mobile and wearable devices made it possible to track daily activity and behavior of people seamlessly and unobtrusively [
5]. Through the analysis of signals collected from different sensing channels (e.g., GPS for location tracking and pedometer for activity tracking) and data sources (e.g., call and SMS logs), patterns of behavior can be analyzed and used for different purposes such as health promotion [
6] and medical diagnosis [
7]. A few studies leveraged patients’ activity data collected on Fitbit devices during hospitalization to predict whether or not the patient would be readmitted after discharge [
8,
9,
10]. These studies, in addition to their small scope and duration, only focus on prediction of the readmission status rather than continuous monitoring and prediction of the daily risk.
Our research addresses the challenge of daily readmission risk prediction after the hospital discharge through leveraging the abilities of mobile devices and deep learning models. Recurrent Neural Network strategies such as LSTMs (Long-Short Term Memory) are particularly appropriate for processing sequential data (like daily behavioral data) and have the ability to accurately predict the next states in a model [
11,
12]. We leverage these capabilities in a probabilistic framework to predict daily progression of readmission risk in the patient population. Our evaluation of the framework using data from mobile phones and Fitbit devices from 49 patients collected over 60 days after discharge from the hospital demonstrate the ability of our framework to closely predict daily readmission risk progressions in cancer patients, minimizing the error between the predicted and actual readmission risk and outperforming classical regression approaches. Our contributions are as follows:
We develop a new method that incorporates the static medical administration risk assessment value currently used in hospitals as the initial risk probability in an LSTM structure to infer the readmission risk progression trajectory of each patient from their processed behavioral mobile data.
We develop a new ranking method to evaluate the performance of the generated models. This method particularly contributes to selecting models that more accurately estimate the levels of risk in early days after discharge where patients are at a higher risk of readmission.
To our knowledge, this is the first approach for prediction of daily readmission risk progression through leveraging mobile data and deep learning frameworks. This framework can contribute to the continuous monitoring of patients outside of hospitals and help clinical professionals to identify patients at risk and act accordingly.
In the following, we first present the related work in readmission prediction and discuss the application of some machine learning and deep learning methods to predict readmission. We then introduce our framework to measure the daily risk probability in an LSTM structure. We describe our designed functions to simulate the daily risk of readmission probabilities and present the evaluation results of the framework on a real-world dataset.
2. Background and Related Work
Unplanned readmissions following cancer surgery are common—22–35% of pancreatic surgery patients readmitted within 30 to 90 days of discharge from the hospital [
1]. Although some readmissions are unavoidable, an estimated 82% of readmissions after cancer surgery are judged to be potentially preventable [
2]. The most common causes for readmission after cancer surgery include infections, gastrointestinal problems, and nutritional deficiency or dehydration [
2,
13], all of which could be managed on an outpatient basis if detected earlier. Existing risk calculators are based on administrative data available at time of discharge, but surgical recovery continues after hospital discharge. Continuous remote patient monitoring across the transition from hospital to home could allow clinicians to detect subtle changes in patient behavior and physiology that signal increasing readmission risk and to intervene earlier, before complications escalate.
While the period of monitoring after hospital discharge is important, a specific monitoring time window was not yet identified. Douglas et al. [
14] found that, while not statistically significant, the probability of readmission decreases over time with the greatest risk of readmission being within the first 30 days after the hospital discharge date. After 30 days, the hazard function curves flatten out; after 60 days, there is a negligible change in the probability of readmission. Carrol et al. [
15] demonstrated that there is a significant decrease of mortality for pancreatic adenocarcinoma in the first 60 days, and the risk of death does not change significantly between 60 days and 2 years, which indicates that 60 days may be an important endpoint.
When we followed up with the hospital administration about our studied patient population, they confirmed that none of the patients in our study were hospitalized after 60 days of discharge for complications related to their surgery. As such, the above mentioned studies and observations from our patient population suggest a 60-day period as a solid monitoring time window for patients after hospital discharge.
Significant past work has explored the potential of using machine learning models in readmission prediction [
16,
17]. For example, an analysis of machine learning techniques for heart failure readmissions by Mortazavi et al. [
18] compared three popular machine learning methods—random forest, boosting, and support vector machine—to identify comprehensive factors that contribute to heart failure readmission compared to a baseline of logistic regression. Frizzell et al. [
19] also examined readmission prediction in heart failure patients, comparing three machine learning models—tree-augmented naive bayesian network, random forest, and gradient boosting—with traditional statistical methods. The result showed a similar discrimination ability over all methods applied to the same dataset.
The artificial neural network model was used in early readmission prediction for several medical conditions. Aswathi et al. [
20] compared the performance of Multilayer Perceptron (MLP) to Logistic Regression for the early prediction of readmission of diabetic patients. They used features derived from patient health records from clinical encounters, including the index admission, discharge details, time in the hospital, diagnosis, and lab results. Maragatham et al. [
21] also utilized the electronic health record for early prediction of heart failure using LSTM. This work reported improved performance of LSTM over traditional machine learning methods, including K-Nearest Neighbors, Logistic Regression, Support Vector Machine, and Multi-layer Perceptron. Another study by Reddy et al. [
22] also implemented an LSTM structure to predict readmissions in patients with lupus. The results demonstrated improvement in prediction using the LSTM over neural network and logistic regression architecture on longitudinal records.
The previously mentioned studies attempted to predict whether or not the patient would be readmitted during a specific time period (classification). However, these analyses did not capture time until the readmission occurred. Vinzamuri et al. [
23] described the development of survival regression, which analyzes the expected duration of time until one or more events of interest occur, for censored data on electronic health records of aggregated lab values for 30-day heart failure readmission, and calculated the hazard probability of readmission for 30, 60, and 90 days readmission as a feature of the prediction. Bussy et al. [
24] proposed the use of the time-to-event outcome framework by combining survival analysis together with classification methodology. The work utilized data from sickle-cell disease patients and compared five machine learning classification models and three other survival analysis methods. The study concluded that using survival regression analysis on the problem of early-readmission could yield better performance compared to directly using classification methodology. However, none of these previous studies pursued the use of LSTM to predict readmission based on day-to-day behavioral data from smartphone and personal wearable sensors. Our contributions include developing a new deep learning framework for sequential prediction of readmission risk from behavioral data streams collected from smartphones and wearable devices. In our studies, we derived readmission probability from risk stratification metrics, including HOSPITAL and LACE scores, and then design an LSTM model to predict the daily probability of readmissions.
Only a few studies used data from sources other than patient health records and demographics for readmission prediction. Bae et al. [
9] explored the potential of Fitbit data to predict readmission status among cancer patients during hospitalization. The analysis demonstrated that more sedentary behavior during in-hospital recovery contributes to early readmission. Doryab et al. [
8] explored the prediction of readmission risk from disruptions in patients’ biobehavioral rhythms in three stages of treatment, namely before surgery, during hospitalization, and after discharge and showed circadian disruptions are predictive of readmission status after discharge. While we leverage the same type of data as this past work, we explore daily readmission risk prediction rather than only readmission status. To our knowledge this is the first deep learning framework for prediction of daily readmission risk from smartphone and wearable data streams. The following sections describe our framework followed by an evaluation using a real-world patient dataset.
3. Deep Learning Framework for Prediction of Daily Readmission Risk
Our framework for measuring daily readmission risk is composed of three main components. The first component calculates the daily probability risk from existing hospital administrative information. The second component utilizes the LSTM structure to process sensor data streams as input for readmission prediction, and the third component leverages ranking and statistical methods to measure the performance of the LSTM models in predicting daily risk probability. The following describes each component in details.
3.1. Calculating Probabilities of Readmission Risk
Given that the readmission status of the patients is unknown at the time of discharge, calculating daily readmission risk is a challenging task. We address the challenge by utilizing two validated measures called HOSPITAL score and LACE index that are widely used in hospitals to estimate risk of readmission at time of patient discharge [
25]. LACE derives its score from
Length of stay at the hospital,
Acuity of the admission,
Comorbidities, and
Emergency department visits during the previous 6 months, while HOSPITAL relies on low
Hemoglobin level at discharge, discharge from an
Oncology service, low
Sodium level at discharge,
Procedure during hospital stay,
Index admission
Type, number of hospital
Admissions during the previous year, and
Length of stay. We use these measures to calculate an initial risk probability at the time of hospital discharge. The initial probability is then used in other functions we develop to measure a daily readmission risk.
LACE estimates risk of readmission or death of a patient within 30 days of discharge. The index ranges from 0 to 19, with scores greater than 10 classified as high-risk. HOSPITAL identifies patients at a high risk of potentially avoidable hospital readmission within 30 days of discharge. The HOSPITAL index ranges from 0 to 15, with scores greater than 7 classified as high risk. HOSPITAL and LACE have exhibited good performance in the prediction of readmission risk in several studies [
25,
26,
27]. However, these studies also show that these tools had only moderate discriminative ability, hence additional information is required to improve accuracy [
26,
27]. These two measures are also static by nature and do not predict the progression of readmission risk over time. However, they can be used as initial risk probabilities for our model.
3.1.1. Initial Risk of Readmission
The initial risk of readmission (the risk on the day after discharge) is generated directly from the LACE and HOSPITAL indices. For example, if a patient receives a LACE score of 0 (i.e., unlikely to be readmitted), their initial probability of readmission is 0. If the patient receives a LACE score of 19 (highest score), their initial probability of readmission is 1. The probability of different scores are calculated linearly. For instance, the readmission probability for a score of 10 is .
3.1.2. Final Risk of Readmission
As mentioned in the background section, both existing studies and observations of our patient population suggest that the risk of surgery-related readmission is almost 0 after 60 days of discharge. As such, for nonreadmitted patients, we set the final risk of readmission for surgery to 0 on the 60th day after discharge. For readmitted patients, the risk is set to 1 on the day they were readmitted and dropped to 0 on the 60th day.
3.1.3. Daily Risk of Readmission
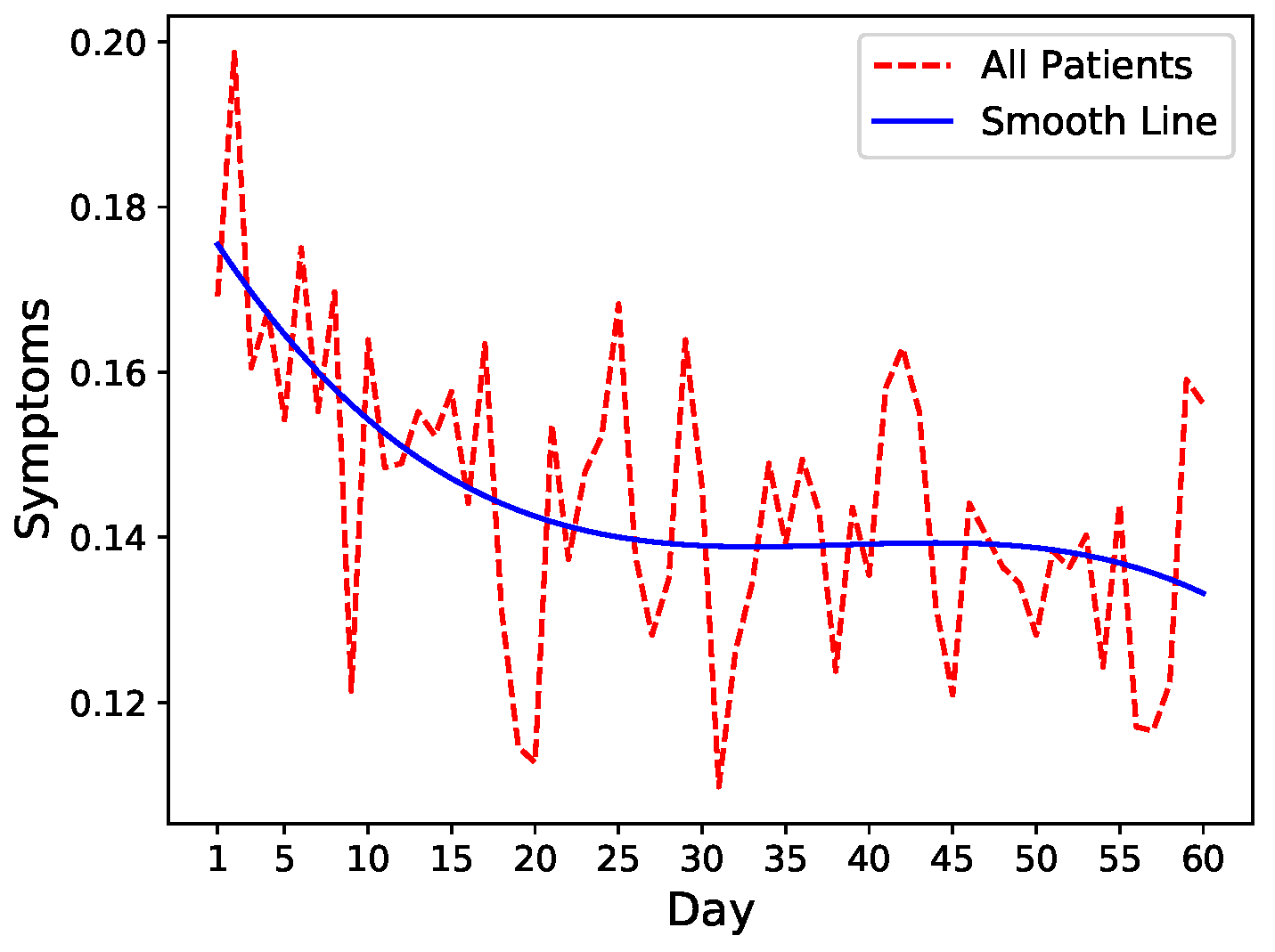
To get an intuition of the readmission risk trends, we leverage fluctuations in symptom levels as a proxy of increase or decrease in readmission risk. We, therefore, run an exploratory analysis on common symptoms including pain, fatigue, nausea, and diarrhea that closely mimic the severity of the patient’s condition after discharge. We calculate the mean of these four symptoms after normalization and visualize the trends combined with spline interpolation for smoothing. As shown in
Figure 1, there is a general decrease in symptoms severity in all patients after hospital discharge indicating slow recovery.
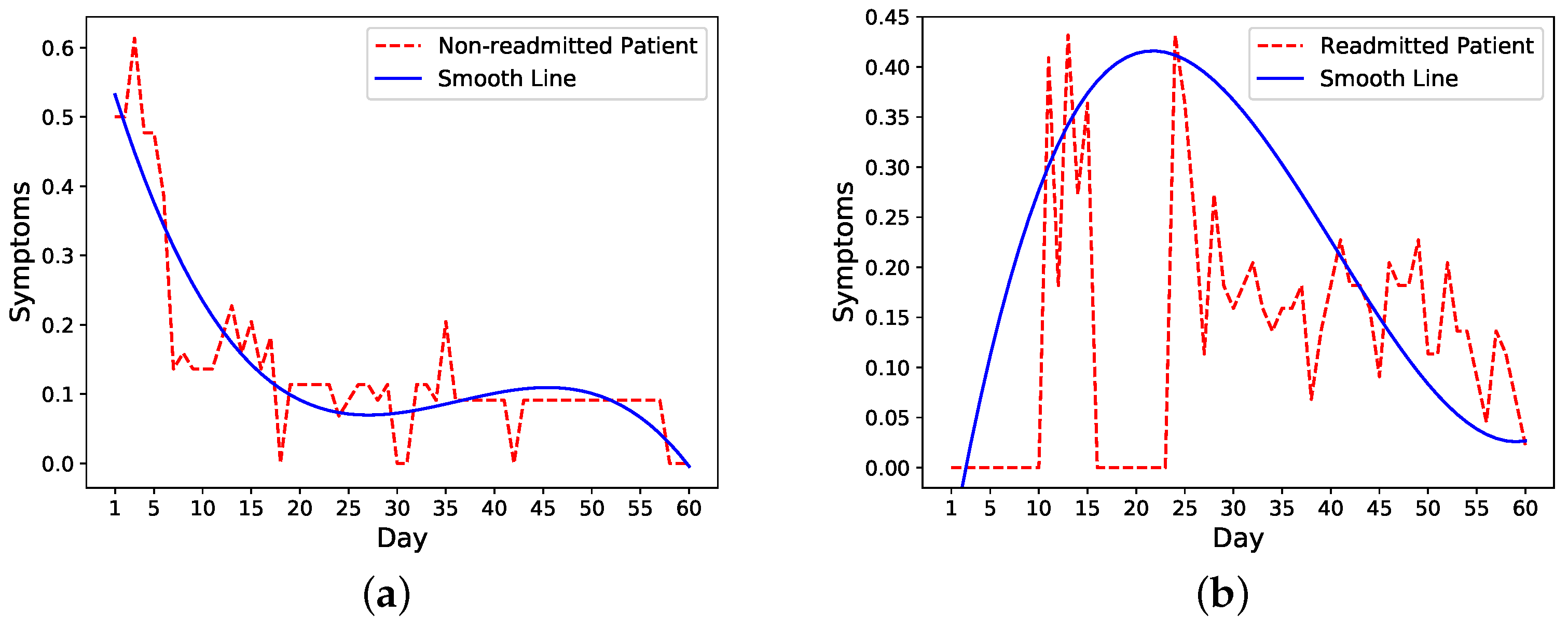
We then look more closely into symptoms trends in readmitted and nonreadmitted patients. The trends of one nonreadmitted patient and one readmitted patient in
Figure 2a,b show that for the nonreadmitted patient, the symptoms score decreases from a relatively large value to a small value on the 60th day. For the readmitted patient, on the other hand, the symptoms level peaks around the readmission (day 16) and starts to decrease a few days after the second discharge on day 21.
Based on these observations, we make an assumption that the trend of daily risk probability is similar to the trend of the symptoms score, which means for nonreadmitted patients, the probability would decrease from an initial probability to 0; for readmitted patients, the probability would increase to maximum of 1 on the readmission day and decrease to 0 after the second discharge. We test two cases for readmitted patients. In the first case, we reset the risk probability after the second discharge to the initial probability and decrease it to 0 on day 60. In the second case, we continue with the probability of 1 as the time of second discharge and decrease it to 0 on day 60 following our probability functions. We compare the performance of these two methods to determine the model that more closely follows a patient’s condition after the second discharge.
We then generate daily risk probability from the initial and final probability values. The probability simulates the risk of readmission on a particular day for each patient. The readmission status within
K days (
if patient is readmitted on day
k, otherwise
). We utilize three functions (linear, exponential, logarithmic) to simulate this trend as follows:
where
n is the index of day,
is the probability at day
n after discharge,
a and
b are two parameters that could be calculated based on probability values of initial and final day.
We also develop the following improved function based on a linear function called weighted linear function:
where
n is the day index,
is the probability of readmissions
n days after discharge,
is the probability of readmission at day
n calculated by Equation (
1),
represent start day index, and
represents the end day index. The range of the weight,
w, is between 0 and 1. When
w equals 1, the probability is fully determined by the linear value. When
w equals 0, the probability is fully determined by the previous day’s value.
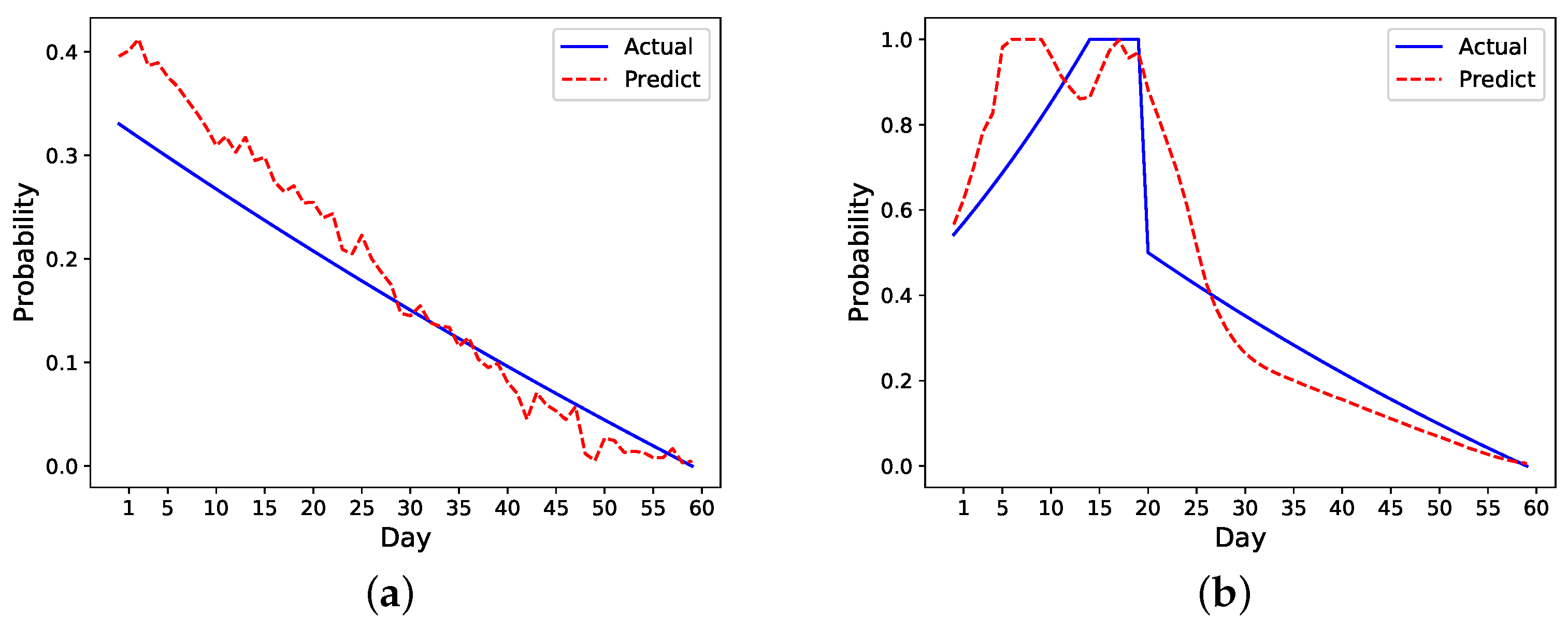
Take the previous nonreadmitted and readmitted patients in
Figure 2 as an example. For the nonreadmitted patient, the calculated initial risk of readmission based on HOSPITAL or LACE is 0.34 and the final risk is 0 on day 60. Thus, this patient’s daily probability decreases from 0.34 to 0 (see
Figure 3a). For the readmitted patient, the readmission occurs on day 16 and the discharge on day 21. Thus, the probability increases from 0.52 on day one to 1 on day 16. Depending on the setting, the risk probability while the patient is in the hospital (i.e., from days 16 to 21) is either set as 1 or decreases from 1 to the initial risk of readmission (i.e., 0.52). After the second discharge, which occurs on day 21, the probability decreases to 0 on day 60. In
Figure 3b, the probability is decreased from 1 to 0.
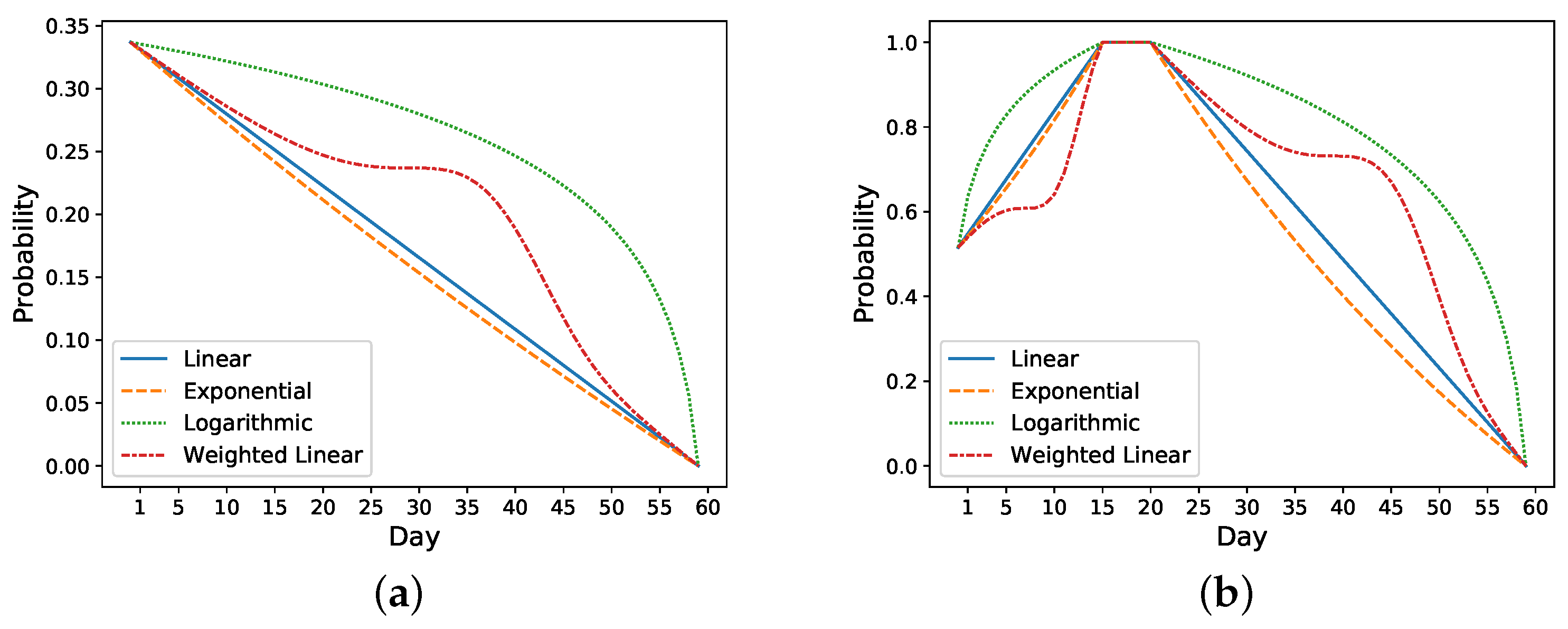
Figure 3 shows different approaches for increasing and decreasing the risk: linear, exponential, logarithmic, and weighted linear.
3.2. Modeling Approach
We build a two-layer LSTM with a single feed-forward output layer that uses Sigmoid as the activation function to produce the final risk probability. Adam [
28] is used as the optimizer during back propagation to adjust the weight of the model to minimize the loss with learning rate 0.01. We use mean-absolute error (see Equation (
6)) as the loss function and activate early stopping [
29] to avoid overfitting. Based on empirical evidence from experimentation, training ceased when the training loss did not decrease after 50 epochs.
where
Y is the actual probability label,
is the prediction, and
n is the total number of days on which we perform the analysis.
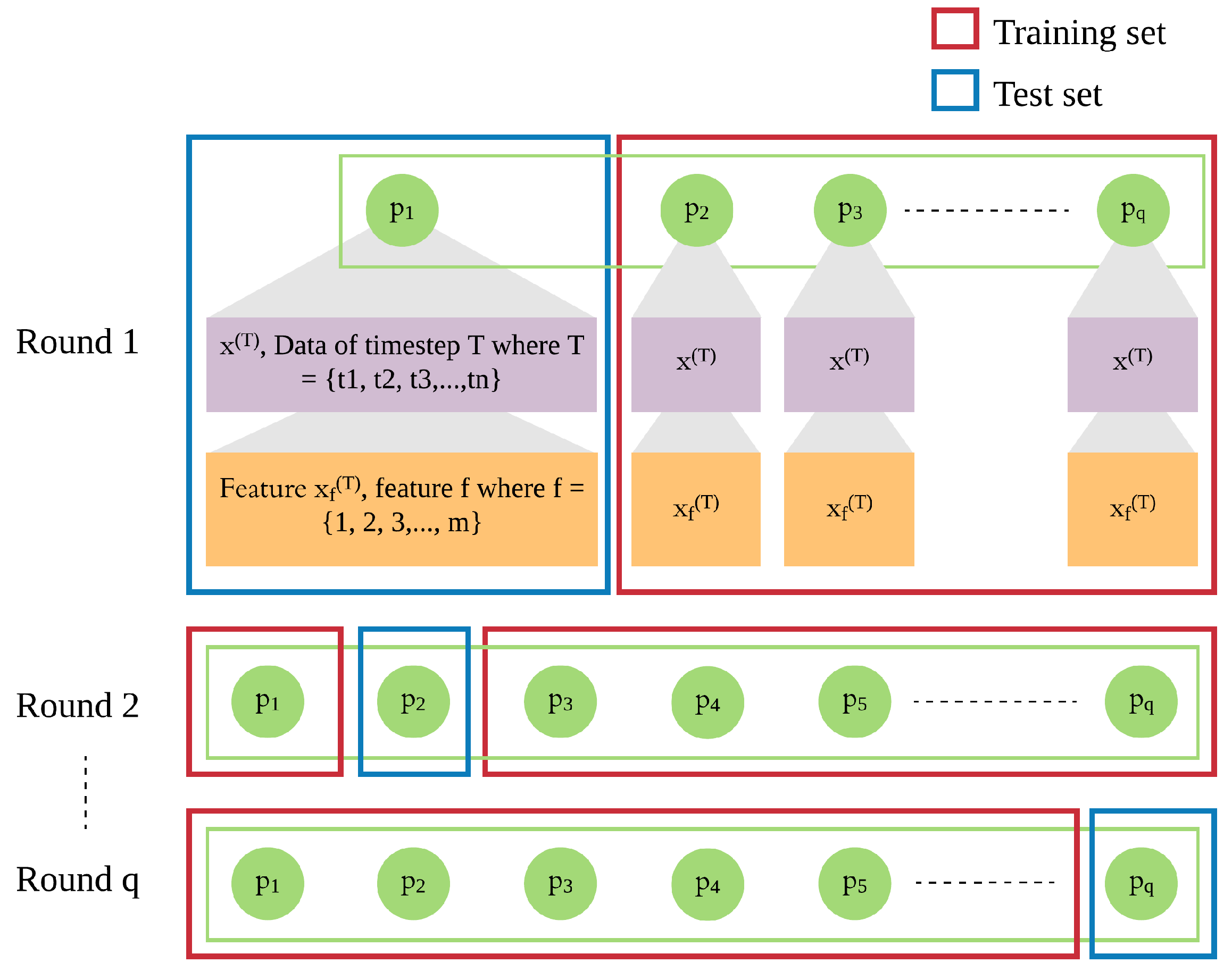
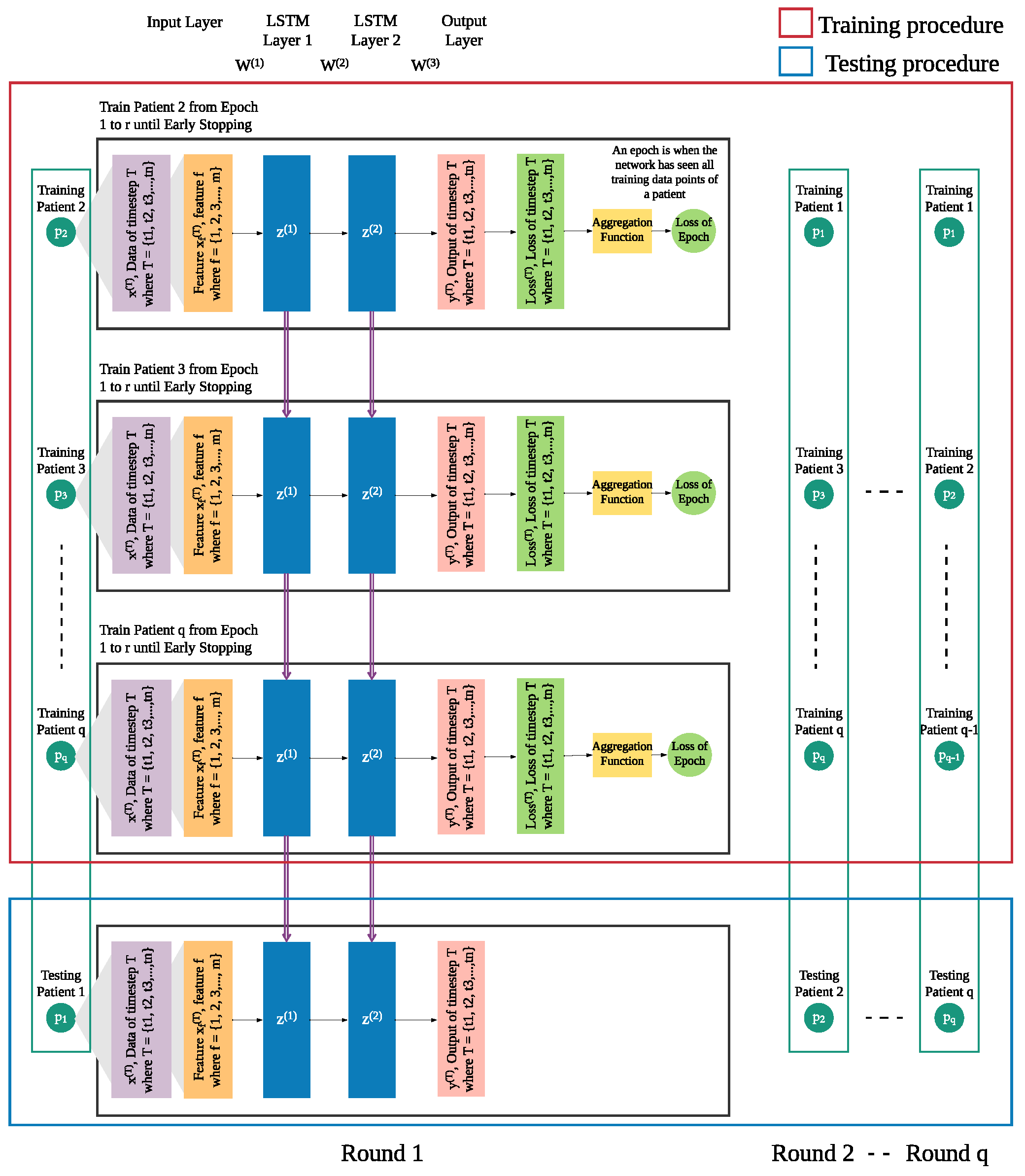
In addition to the patient’s own data from previous days, we integrate leave-one-patient-out iteration (as shown in
Figure 4) into the modeling process to leverage other patients’ data to improve the prediction of daily risk for an individual patient (as shown in
Figure 5). We adapt this process in training and testing procedures to build models of patients’ time series data. We then use those models for prediction of risk in the rest of the population, e.g., a new patient. For each patient, one model is trained for multiple rounds.
Each patient p has his own sequence of data represented by , where . Each consists of f features from 1 to m. This sequence of data of patient needs to be treated separately from of other patients ( to ), since the sequences of different patients are different. Hence, in each iteration, we leave out the sequence of one patient and use of the other patients as the training set, until all patients were left out once.
In each round, the trained model is used to produce the risk of readmission prediction against sequence of a patient p, where where is the prediction of input of that will be compared with the actual risk where and is the actual risk at timestep T.
3.3. Using Actual vs. Predicted Probability of Previous Day
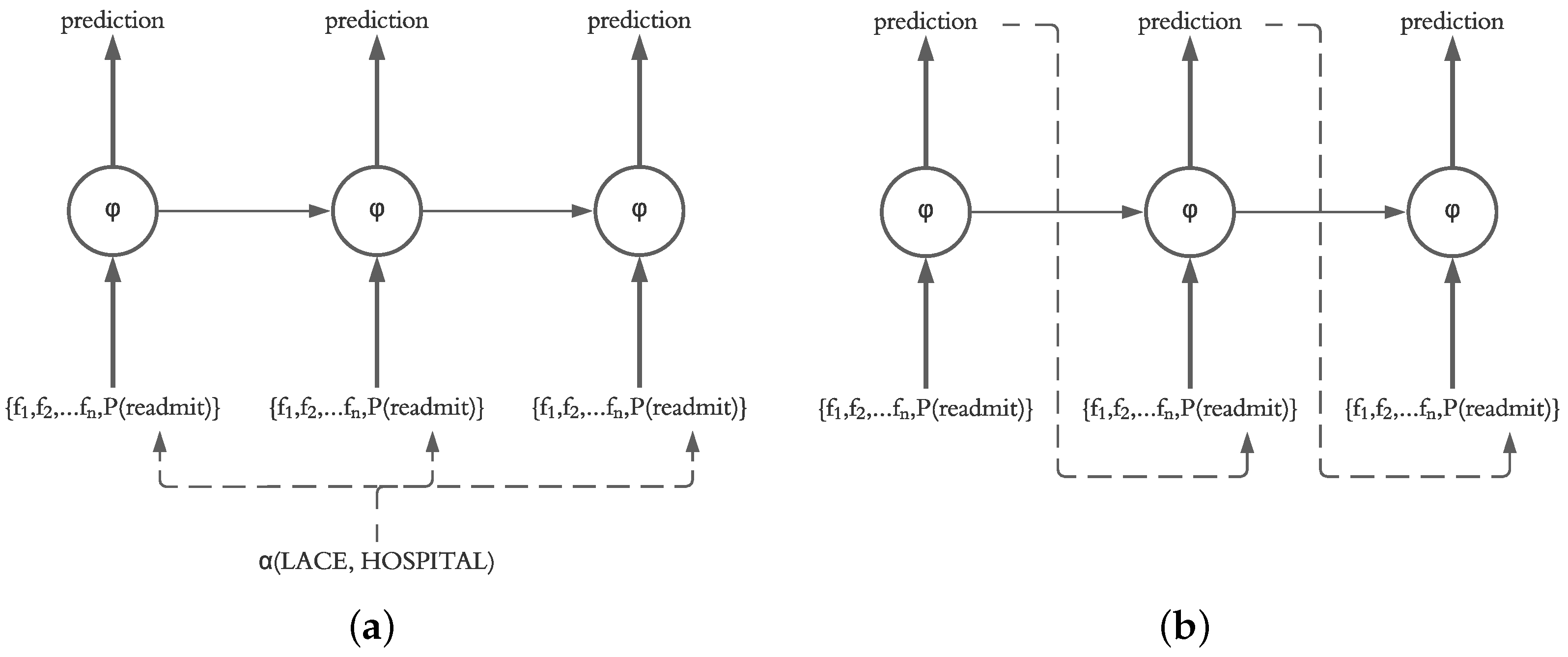
Our motivation for using an LSTM for prediction of daily readmission risk was based on the ability of LSTM models to sequentially predict the next states in the model. This decision is supported by the fact that the final readmission risk in patients after discharge is unknown, and therefore, a system for prediction of daily readmission risk utilizing our framework should operate based on the predicted probability calculated on a daily basis. However, it is also possible for the system to recalculate the readmission risk of the current and future days based on the known probabilities from previous days. Therefore, in our evaluation, we investigate the impact of injecting the actual probability (calculated using LACE and HOSPITAL) as well as the predicted probability of the previous day (calculated by the LSTM independent of LACE and HOSPITAL scores) into the current state in the LSTM structure, as shown in
Figure 6.
3.4. Measuring Performance
3.4.1. Ranking Metrics
The performance evaluation of each model is defined by several metrics, including mean squared error (
MSE) [
30] and covariance [
31]:
where
Y is the actual risk of readmission,
is the predicted risk of readmission, and
n is the total number of days for which we have data across all selected patients.
where
x and
y are the independent and dependent variables,
is the mean of the independent variable,
is the mean of the dependent variable, and
n is the number of data points in the sample. In our analysis, actual risk of readmission (
Y) is the independent variable, predicted risk of readmission (
) is the dependent variable, and the total number of days for which we have data across all selected patients (
n) is the number of data points.
Each metric is separated into six submetrics — all patients first k (e.g., 20) days, all patients all K (e.g., 60) days, readmitted patients first k days, readmitted patients all K days, nonreadmitted patients first k days, and nonreadmitted patients all K days. This allowed us to evaluate overall performance, performance for readmitted patients, and performance for nonreadmitted patients separately. The performance matrix will consist of , , and n (the number of patients) for readmitted patients. The calculation for nonreadmitted patients is similar to readmitted patients.
3.4.2. Ranking Process
We define a ranking process to determine which model parameters perform best. To leverage several metrics (MSE and Covariance), we need to accumulate these metrics into one ranking system which can output the top few models. The ranking process is described as follows:
where
are the metrics that are ranked by the ranking order described in
Table 1,
n is the number of metrics, and
is the number of models that need to be compared. After each metric
is ranked, the result of the ranking order is denoted by
. The better performance on that metric will result in a lower
. All
are summed using Equation (
9) to calculate the total points, which will be ranked again from largest to smallest to generate the final ranking (i.e., with Equation (
10)).
is used to decide which parameter settings result in the best performance.
3.5. Classic Models as Baselines
Given daily readmission risk prediction can be thought of as a regression problem, we compare several classic methods, including Multiple Linear Regression (MLR) [
32], Regression Tree (RTF) [
33], and Support Vector Regression (SVR) [
34], with our LSTM models. Each of these methods uses the same data as inputs, and each method outputs the predicted daily risk probability. Default parameters in the scikit-learn package are used for these algorithms to build baseline models.
3.5.1. Multiple Linear Regression (MLR)
MLR is one of the most common models in predictive modeling. In multiple linear regression, a dependent variable is determined by multiple independent variables and can be written as [
32]:
where
is the output of the model,
is the independent input variables, and
are different regression coefficients.
3.5.2. Regression Tree (RT)
RT is an application of decision trees, which is utilized when the predicted outcome is a continuous value or a real number. RT divides the feature space into units, each of which has a specific output. The test data are assigned to different units depending on the features to obtain the corresponding output values. In this study, we employ the Classification and Regression Tree (CART) algorithm [
33] to predict daily risk probabilities.
3.5.3. Support Vector Regression (SVR)
SVR is a two-class classification model whose basic model is defined as a linear classifier with the largest spacing in the feature space [
34]. The learning strategy of SVR is to maximize the spacing, which ultimately translates into the solution of a convex quadratic planning problem. SVR proved to be an effective tool in real-value function estimation [
35].
5. Discussion
We designed a deep learning framework based on LSTM to predict the daily risk of readmission in patients after hospital discharge. By using a dataset of smartphone sensors and Fitbit logs, we extracted different features from sensors and symptoms and also calculated the deviation of those features from previous days. Our results showed that all of these features are helpful in predicting the risk of readmission.
Most existing studies predict the readmission status as a classification problem and only a few predict the daily status of patients. By utilizing different functions including linear, exponential, logarithmic and weighted linear function, we designed a method to simulate the daily risk of readmission on patients; our results demonstrated the feasibility of this approach. Compared with classic models, the LSTM could better extract useful information and make full use of the predicted values of previous days, which improves performance.
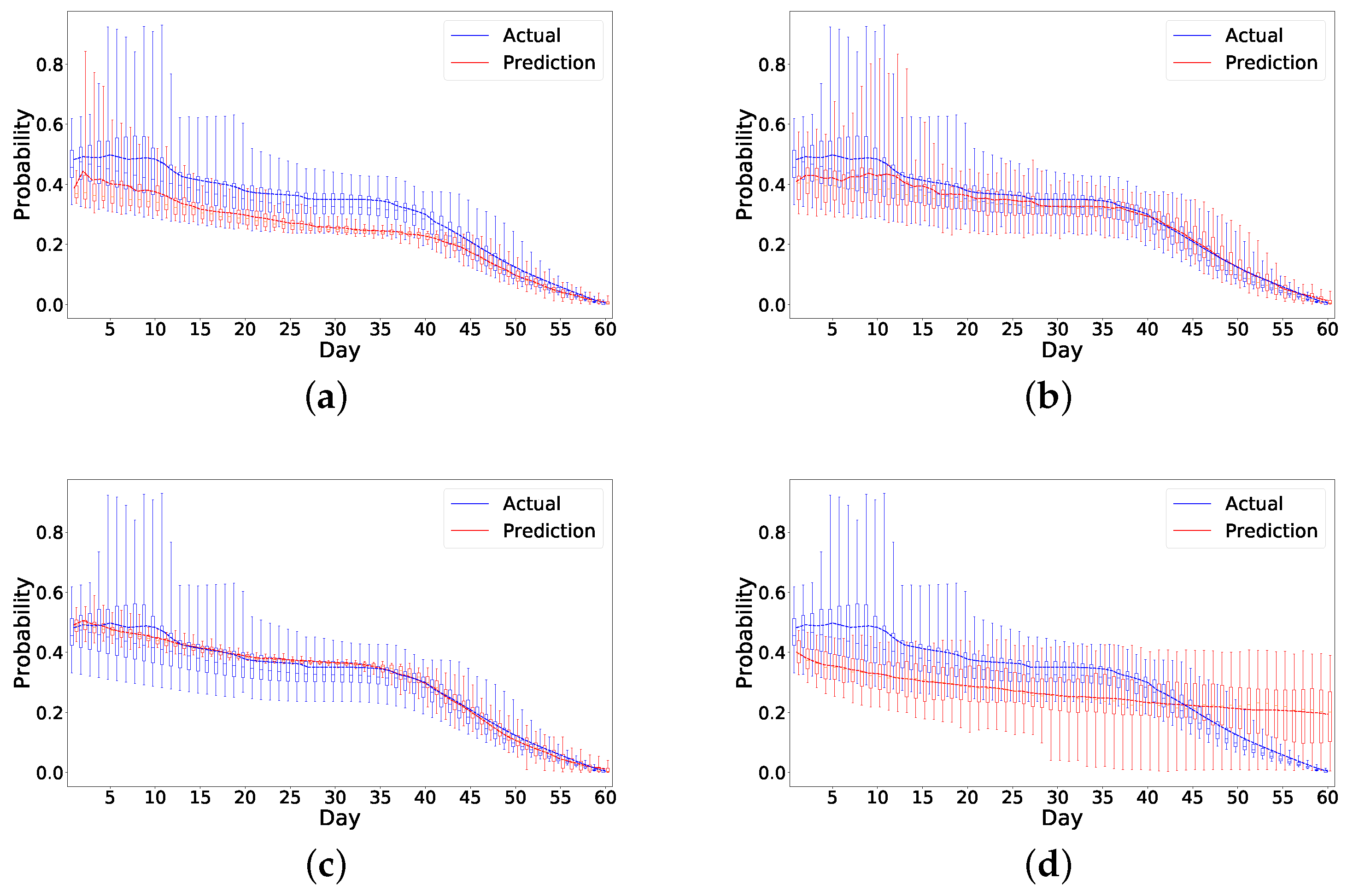
We also develop a ranking algorithm as part of the framework to evaluate the performance of different models. As there are metrics evaluating the first few days’ performance, this ranking mechanism in particular helps identify models that more accurately predict the early risk of readmission in patients within the first few days of hospital discharge. As the number of readmissions are higher within the first seven days after discharge, the ability to identify patients at risk is of utmost importance. The model chosen by this ranking mechanism shows a good performance on prediction as shown in
Figure 8. Specifically, it overestimates the risk in the readmitted patient a few days before the readmission happens, which is ideal as it can raise alarm to clinicians or caregivers to act ahead of time. Although the risk is also overestimated for the nonreadmitted patient, the error margin is small compared to the readmitted patient. In
Figure 7 and
Figure 8, it also appears that all the models have higher errors in the first few days than in later days. We believe this could be due to a lack of data in the beginning as we only have 49 patients for analysis. This problem is similar to the cold start problem [
38] and could be solved if we collect enough data in the future.
While our initial evaluation showed the feasibility of our deep learning framework to predict the daily risk of readmission for patients after cancer surgery, more evaluations on different datasets are needed to determine its practical use in the real world. Such a system could capture the status of the patient outside of the hospital by processing and analyzing data from personal devices without disturbing their life, determine their readmission risk on a daily basis and notify medical professionals about patients at potential risk of readmission (e.g., risk above a particular threshold) while there are still opportunities to intervene.
A large part of our framework addresses the challenge of measuring the actual daily risk to evaluate the performance of the models and has less focus on optimizing the LSTM settings that greatly impact the performance results. Also, as our LSTM models may slightly overestimate or underestimate the risk of readmission, our future work will focus on improving the structure of LSTM network to address this issue. Finally, our work used a real-world dataset from patients after cancer surgery and obtained a good performance. Future steps should explore whether this framework is as generalizable to other readmission problems due to diseases such as heart failure.
Although we develop and evaluate this framework in the context of readmission risk assessment, we believe our methods can be generalized and used in similar applications for risk assessment. Our future plans involve further evaluations on larger patient datasets as well as adjustments and refinements of our framework to be evaluated on datasets in other application domains including climate change, weather forecast, and operation research.