A Bidirectional Interpolation Method for Post-Processing in Sampling-Based Robot Path Planning
Abstract
:1. Introduction
2. Related Works
2.1. Classical Path Planning
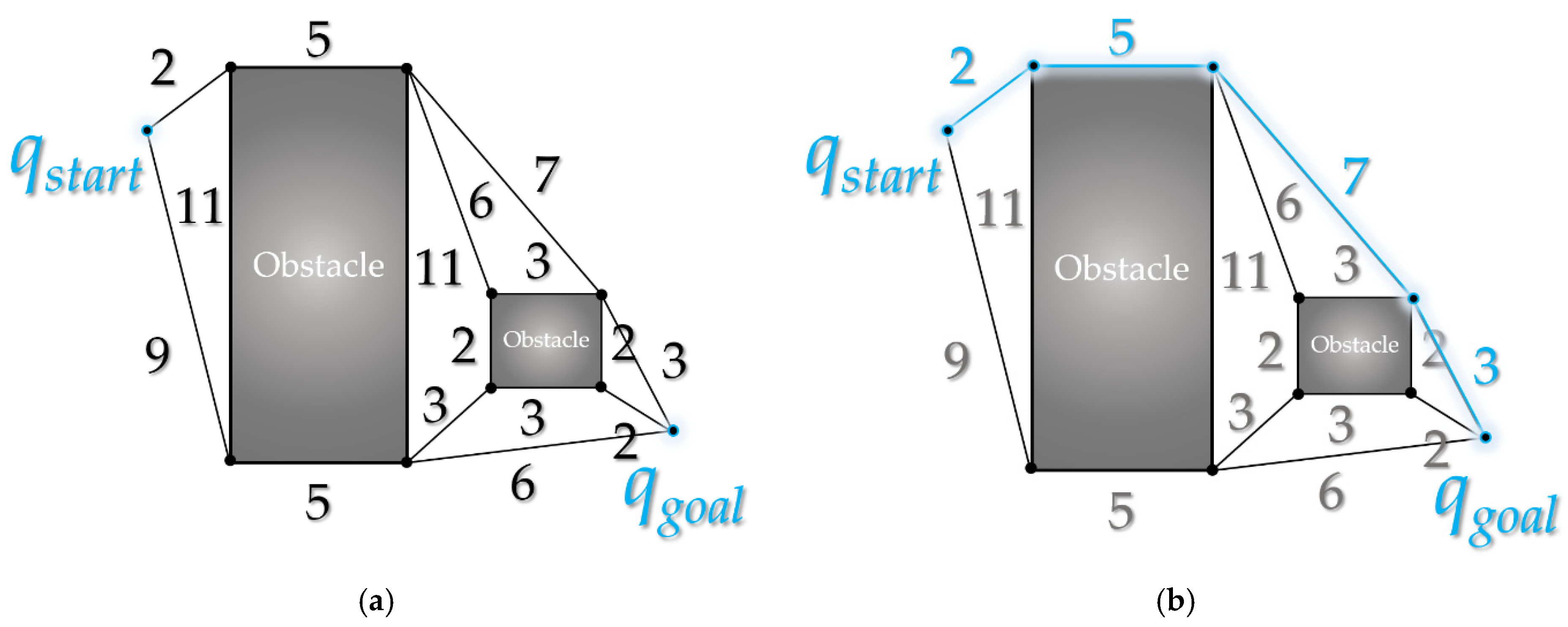
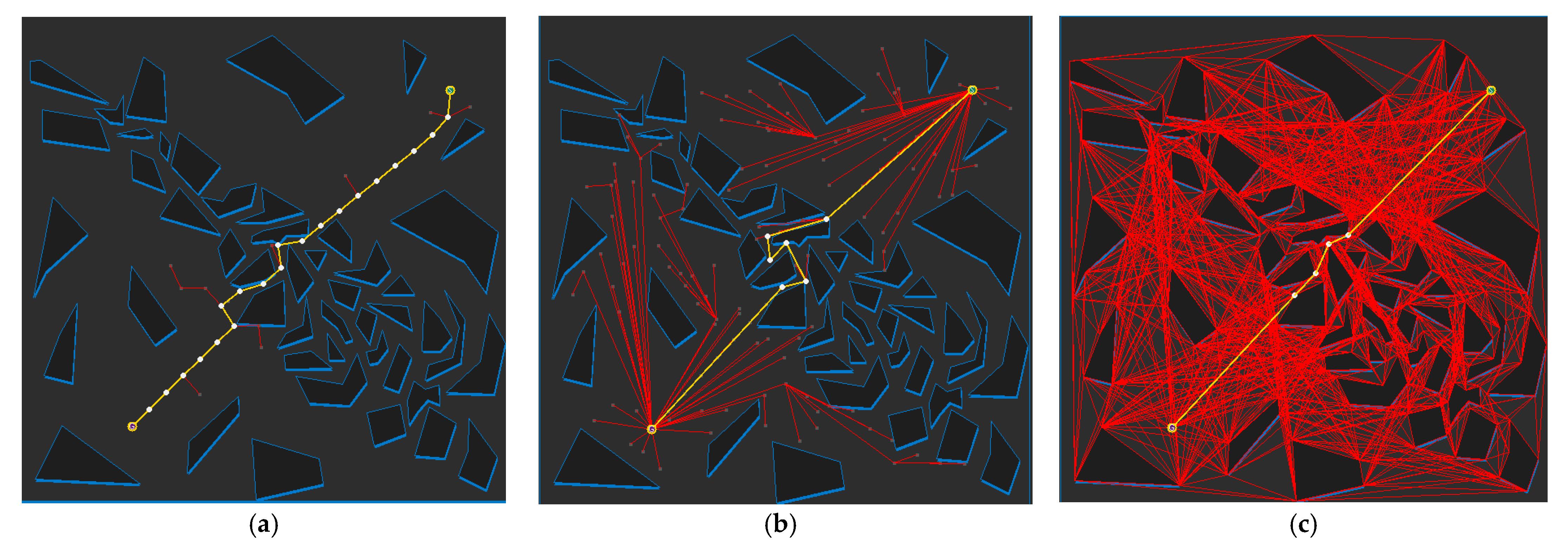
2.1.1. Visibility Graph
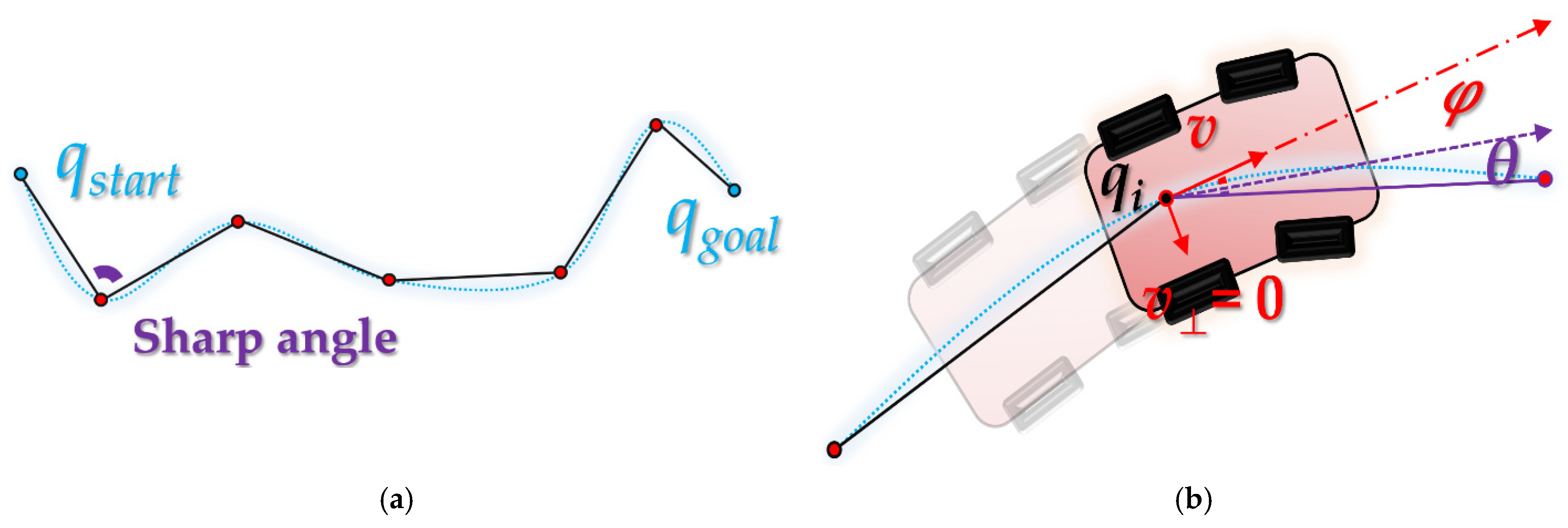
2.1.2. Limitation of Classical Path Planning
2.2. Sampling-Based Path Planning Algorithms
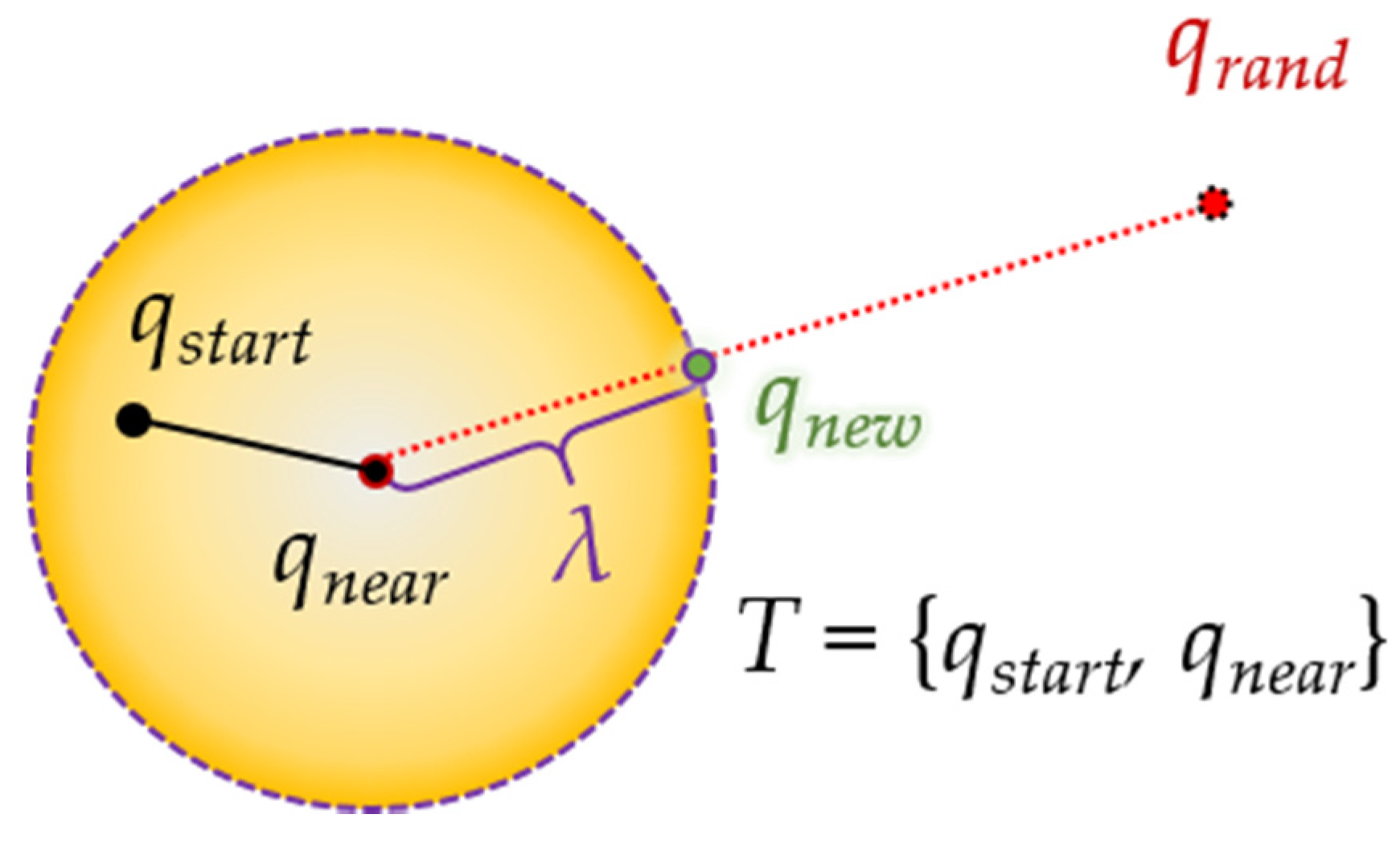
2.2.1. Rapidly Exploring Random Tree (RRT)
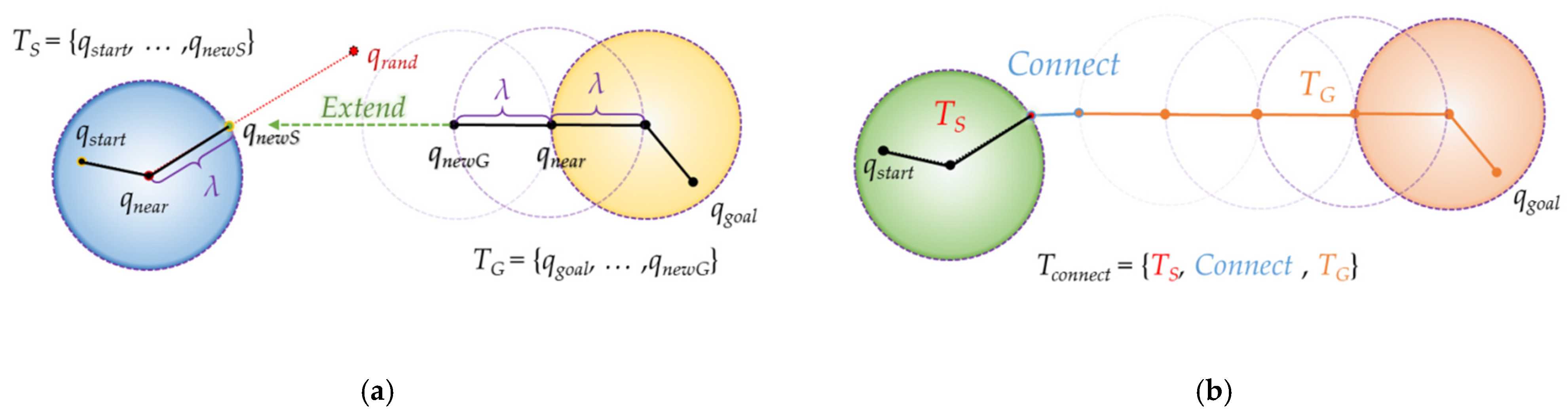
2.2.2. RRT-Connect
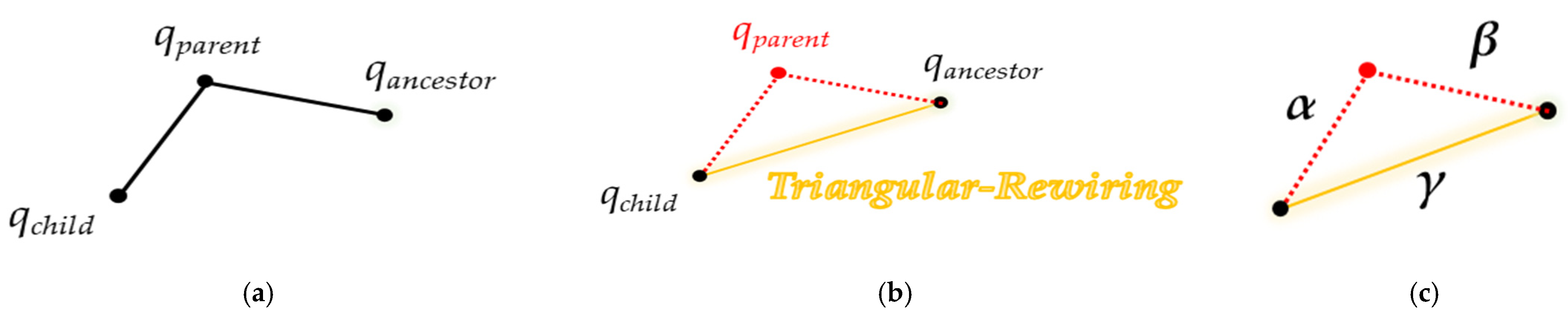
2.2.3. Triangular-RRT-Connect
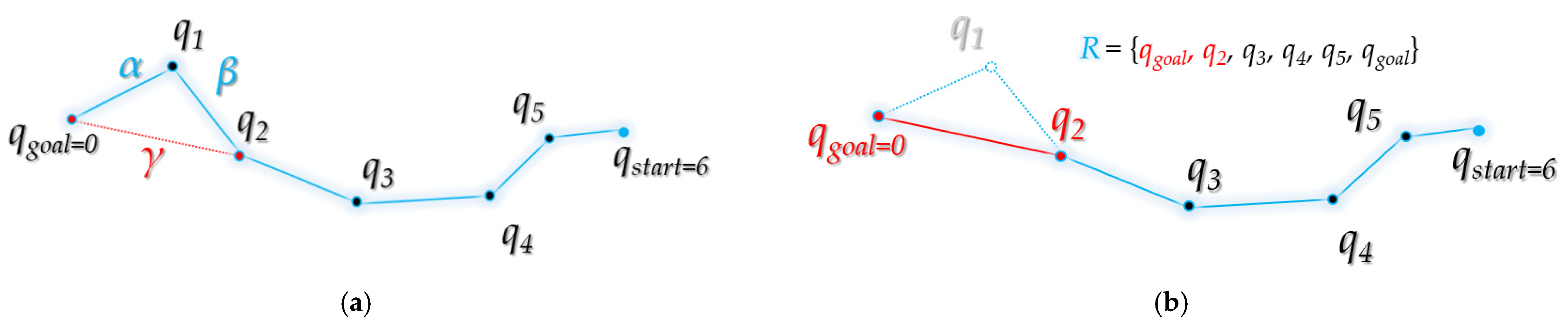
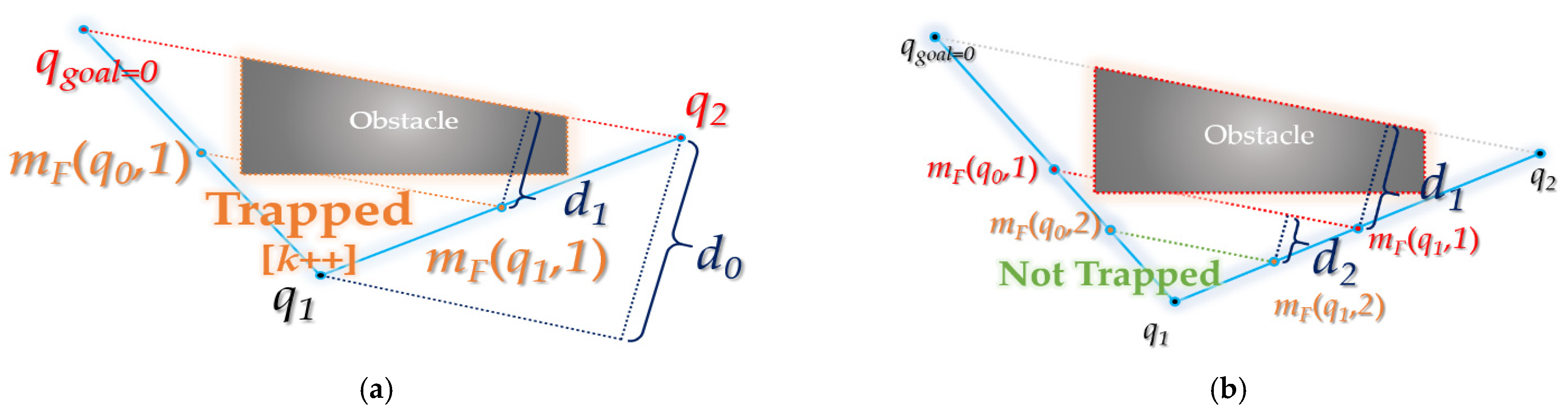
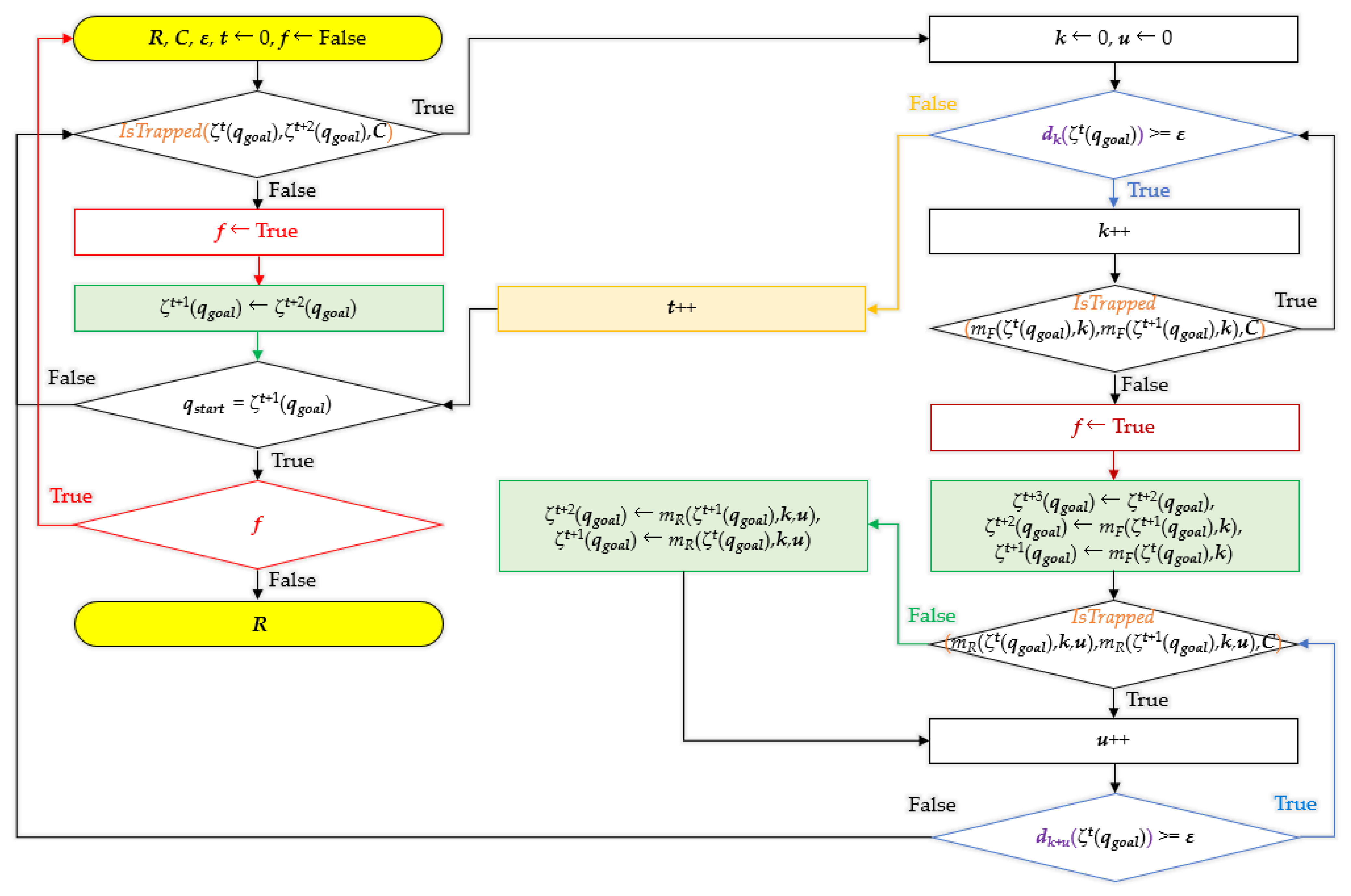
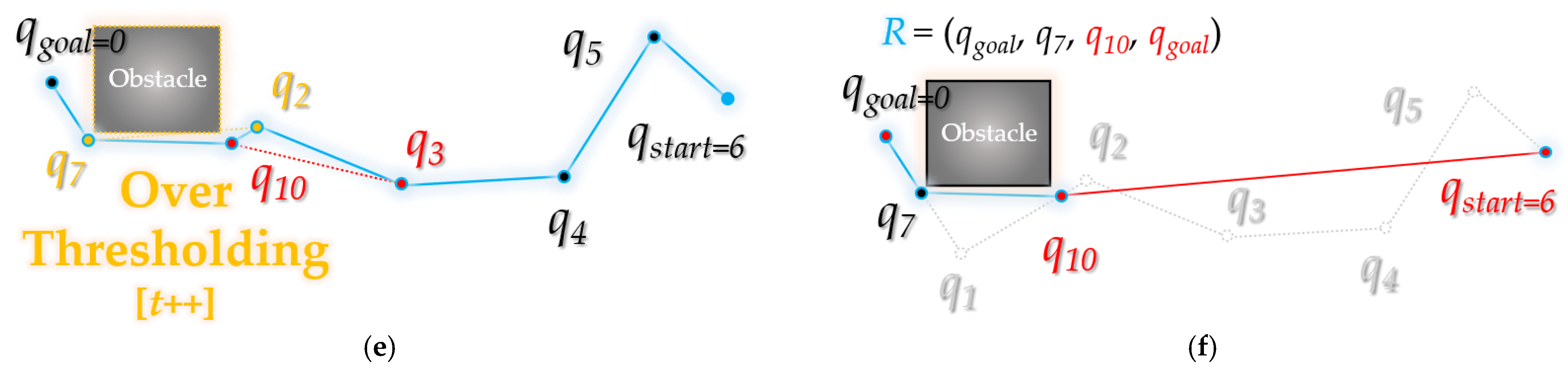
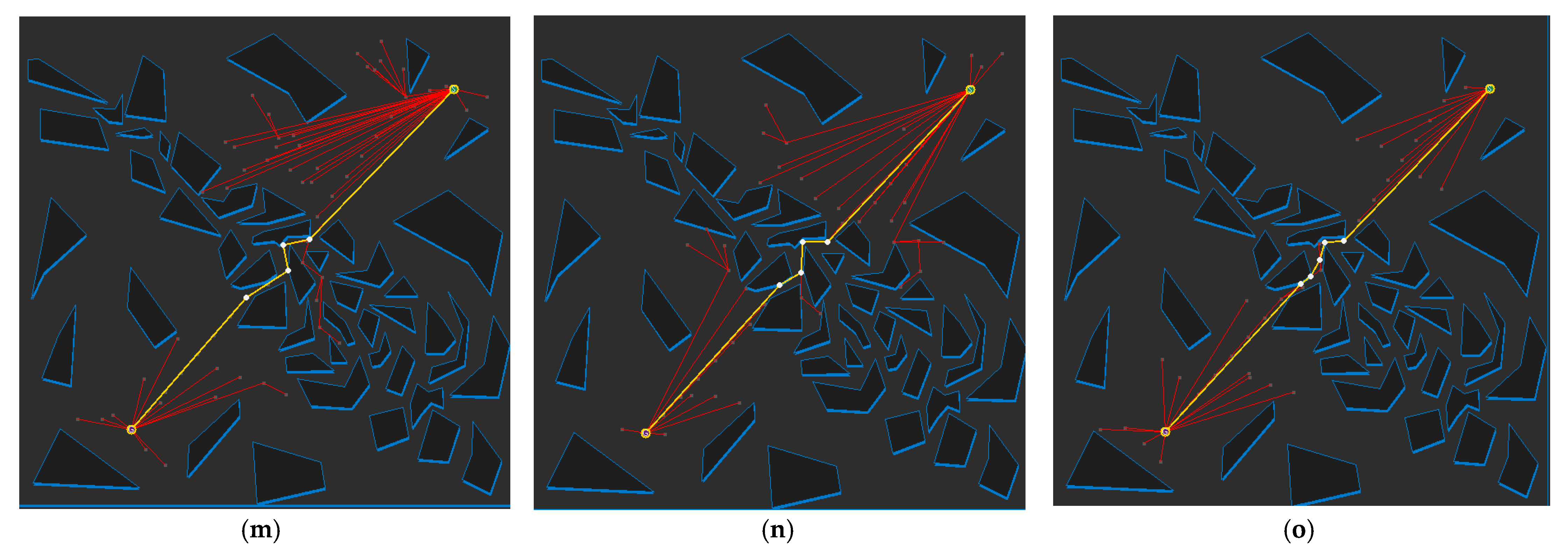
3. Bidirectional Interpolation Method for Post-Processing
3.1. Forward Interpolation Process
3.1.1. Pseudocode of Forward Interpolation Process
| Algorithm 1 Pseudocode of Forward Interpolation Process. | |
| Input: | |
| R ← path from {RRT/RRT-Connect/Tri-RRT/Tri-RRT-Connect/…} | |
| C ← position set of all (measured) boundary points in all (known) obstacles | |
| ε ← threshold value of minimum clearance | |
| Output: | |
| R ← modified path R | |
| Initialize: | |
| fmodify ← true | |
ProcedureForwardInterpolationProcess | |
| Begin | |
| 1 | WhilefmodifyDo |
| 2 | fmodify ← false //is the path modified |
| 3 | t ← 0 //index of the currently focused point |
| 4 | qchild ← first point in R |
| 5 | qparent ← next point of qchild in R |
| 6 | While not [qparent is last point in R] Do |
| 7 | qancestor ← next point of qparent in R |
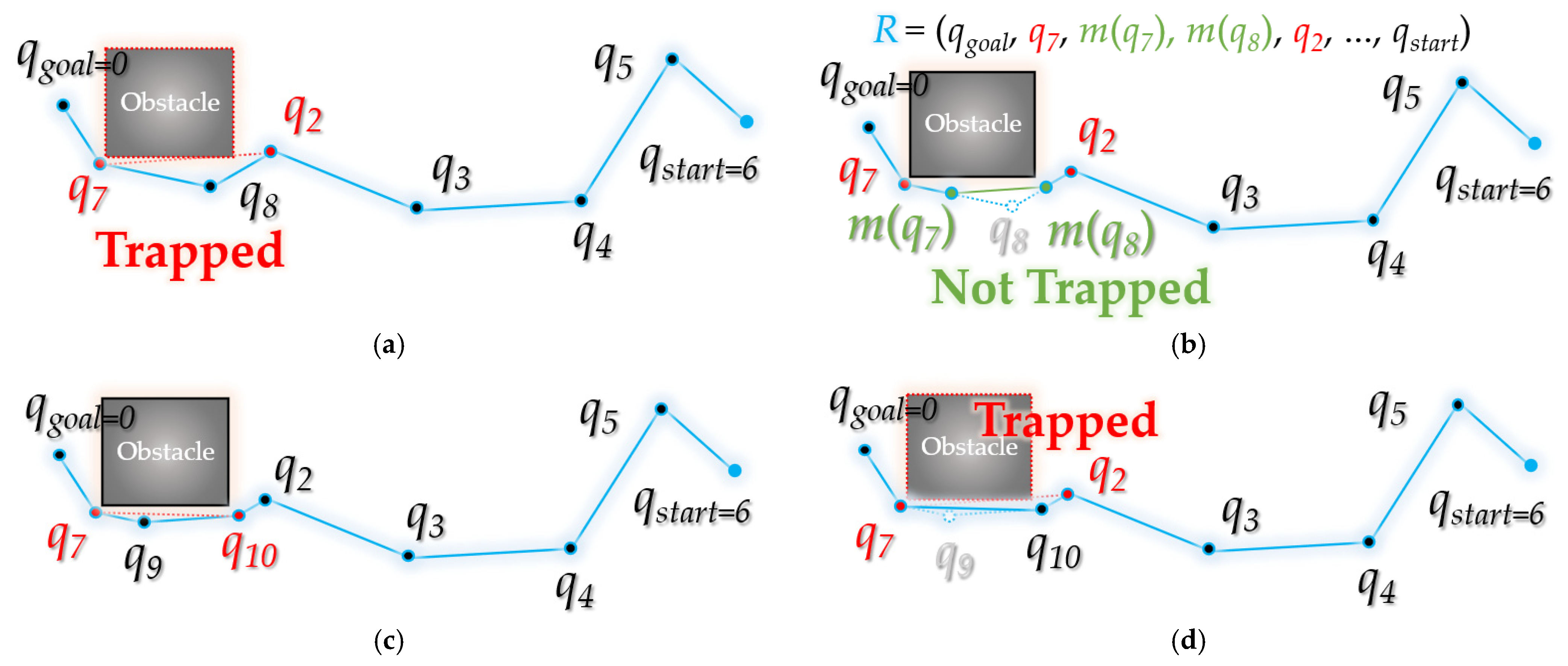
| 8 | If not isTrapped(qchild, qancestor, C) Then R ← postTriangular(R, ε, t, fmodify) |
| 9 | Else |
| 10 | R ← interpolation(R, C, ε, t, fmodify) |
| 11 | qchild ← t-th point in R |
| 12 | qparent ← next point of qchild in R |
| End | |
| Algorithm 2 Pseudocode of the Post Triangular Function. | |
| Input: | |
| R ← path R from postTriProcOfMidInterpolation | |
| t ← point index t from postTriProcOfMidInterpolation | |
| fmodify ← boolean fmodify from postTriProcOfMidInterpolation | |
| Output: | |
| R ← modified path R | |
| fmodify ← result of boolean fmodify //return by reference | |
ProcedurepostTriangularfromForwardInterpolationProcess | |
| Begin | |
| 1 | qchild ← t-th point in R |
| 2 | qparent ← next point of qchild in R |
| 3 | qancestor ← next point of qparent in R |
| 4 | R ← Delete path<qchild, qparent> and path<qparent, qancestor> from R |
| 5 | R ← Insert path<qchild, qancestor> to R |
| 6 | fmodify ← true |
| End | |
| Algorithm 3 Pseudocode of the Interpolation Function. | |
| Input: | |
| R ← path R from ForwardInterpolationProcess | |
| C ← position set C from ForwardInterpolationProcess | |
| ε ← threshold value ε from ForwardInterpolationProcess | |
| t ← point index t from ForwardInterpolationProcess | |
| fmodify ← boolean fmodify from ForwardInterpolationProcess | |
| Output: | |
| R ← modified path R | |
| t ← updated point Index t //return by reference | |
| fmodify ← result of boolean fmodify //return by reference | |
| Initialize: | |
| qchild ← t-th point in R | |
| qparent ← next point of qchild in R | |
| qancestor ← next point of qparent in R | |
ProcedureinterpolationfromForwardInterpolationProcess | |
| Begin | |
| 1 | d ← altitude of triangle consisting of qchild, qparent, and qancestor with base<qchild, qancestor> |
| 2 | ma ← midpoint between qchild and qparent |
| 3 | mb ← midpoint between qparent and qancestor |
| 4 | WhiletrueDo |
| 5 | If d >= ε Then |
| 6 | If not isTrapped(ma, mb, C) Then |
| 7 | R ← Delete path<qchild, qparent> and path<qparent, qancestor> from R |
| 8 | R ← Insert path<qchild, ma>, path<ma, mb>, and path<mb, qancestor> to R |
| 9 | fmodify ← true |
| 10 | Break |
| 11 | Else |
| 12 | d ← d/2 |
| 13 | ma ← midpoint between ma and qparent |
| 14 | mb ← midpoint between mb and qparent |
| 15 | Else |
| 16 | t ← t + 1 |
| 17 | Break |
| End | |
3.1.2. Pseudocode of the Post Triangular Function from Forward Interpolation Process
3.1.3. Pseudocode of Interpolation Function from Forward Interpolation Process
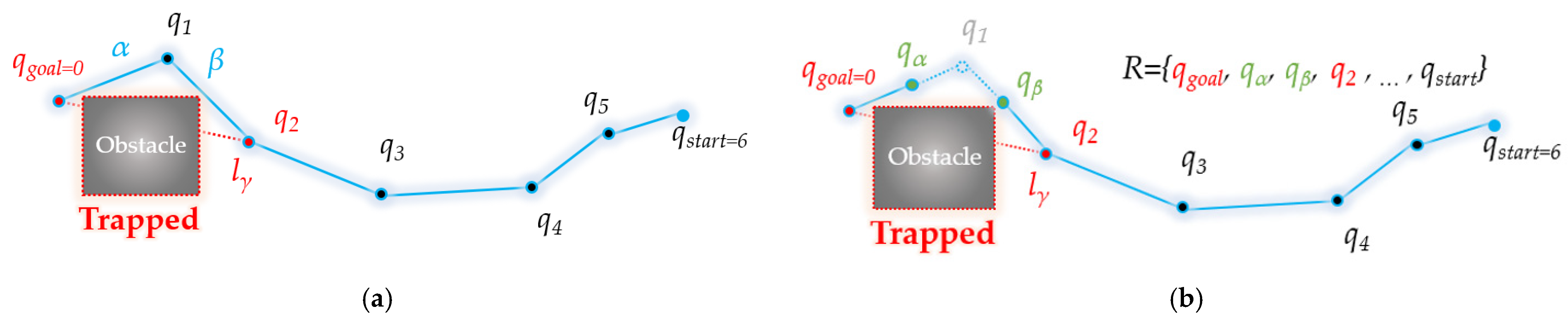
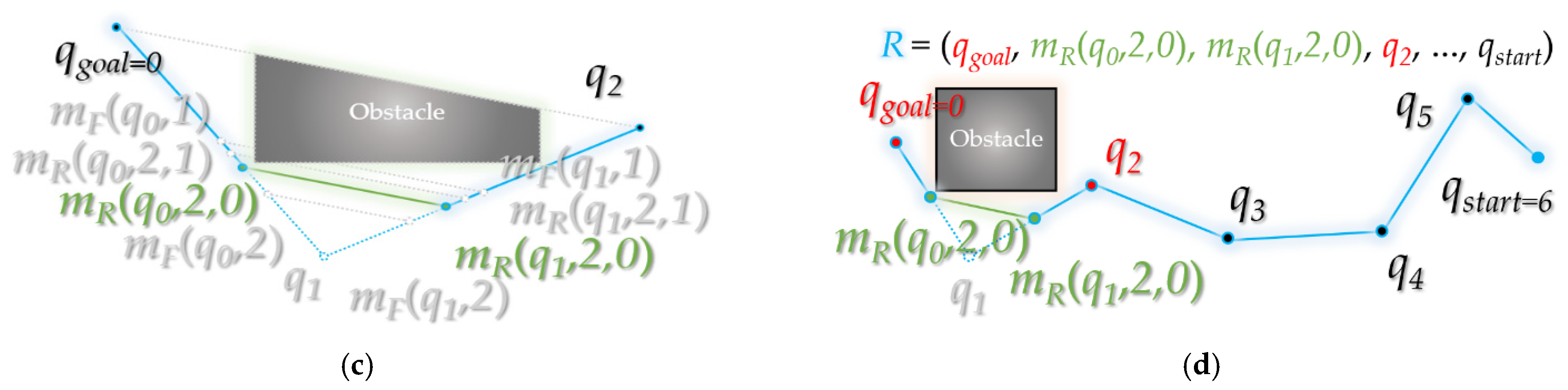
3.2. Backward Interpolation Process
Pseudocode Backward Interpolation Process
| Algorithm 4 Pseudocode of Backward Interpolation Process. | |
| Input: R ← path R from ForwardInterpolationProcess C ← position set C from ForwardInterpolationProcess ε ← threshold value ε from ForwardInterpolationProcess t ← point index t from ForwardInterpolationProcess fmodify ← boolean fmodify from ForwardInterpolationProcess Output: R ← modified path R t ← updated point index t //return by reference fmodify ← result of boolean fmodify //return by reference Initialize: qchild ← t-th point in R qparent ← next point of qchild in R qancestor ← next point of qparent in R | |
ProcedureinterpolationfromForwardInterpolationProcess | |
| Begin | |
| 1 | d ← altitude of triangle consisting of qchild, qparent, and qancestor with base<qchild, qancestor> |
| 2 | ma ← midpoint between qchild and qparent |
| 3 | mb ← midpoint between qparent and qancestor |
| 4 | WhiletrueDo |
| 5 | If d >= ε Then |
| 6 | If not isTrapped(ma, mb, C) Then |
| 7 | R ← Delete path<qchild, qparent> and path<qparent, qancestor> from R |
| 8 | mbackA ← external division point of line segment<qparent, ma> with the ratio 3:1 |
| 9 | mbackB ← external division point of line segment<qparent, mb> with the ratio 3:1 |
| 10 | While true Do |
| 11 | mfreeA ← ma |
| 12 | mfreeB ← mb |
| 13 | If not isTrapped(mbackA, mbackB, C) Then |
| 14 | ma ← mbackA |
| 15 | mb ← mbackB |
| 16 | Else Break |
| 17 | d ← d/2 |
| 18 | If not d >= ε Then Break |
| 19 | mbackA ← external division point of line segment <mfreeA, ma> with the ratio 3:1 |
| 20 | mbackB ← external division point of line segment <mfreeB, mb> with the ratio 3:1 |
| 21 | R ← Insert path<qchild, ma>, path<ma, mb> and path<mb, qancestor> to R |
| 22 | fmodify ← true |
| 23 | Break |
| 24 | Else |
| 25 | d ← d/2 |
| 26 | ma ← midpoint between ma and qparent |
| 27 | mb ← midpoint between mb and qancestor |
| 28 | Else |
| 29 | t ← t + 1 |
| 30 | Break |
| End | |
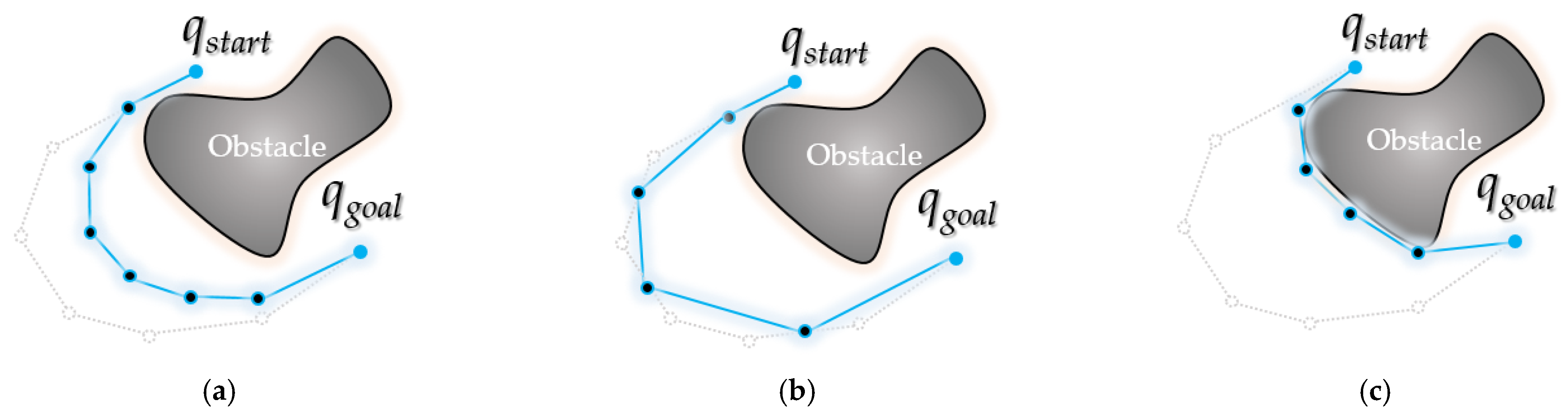
3.3. Overview of Bidirectional Interpolation Method
4. Experimental Results
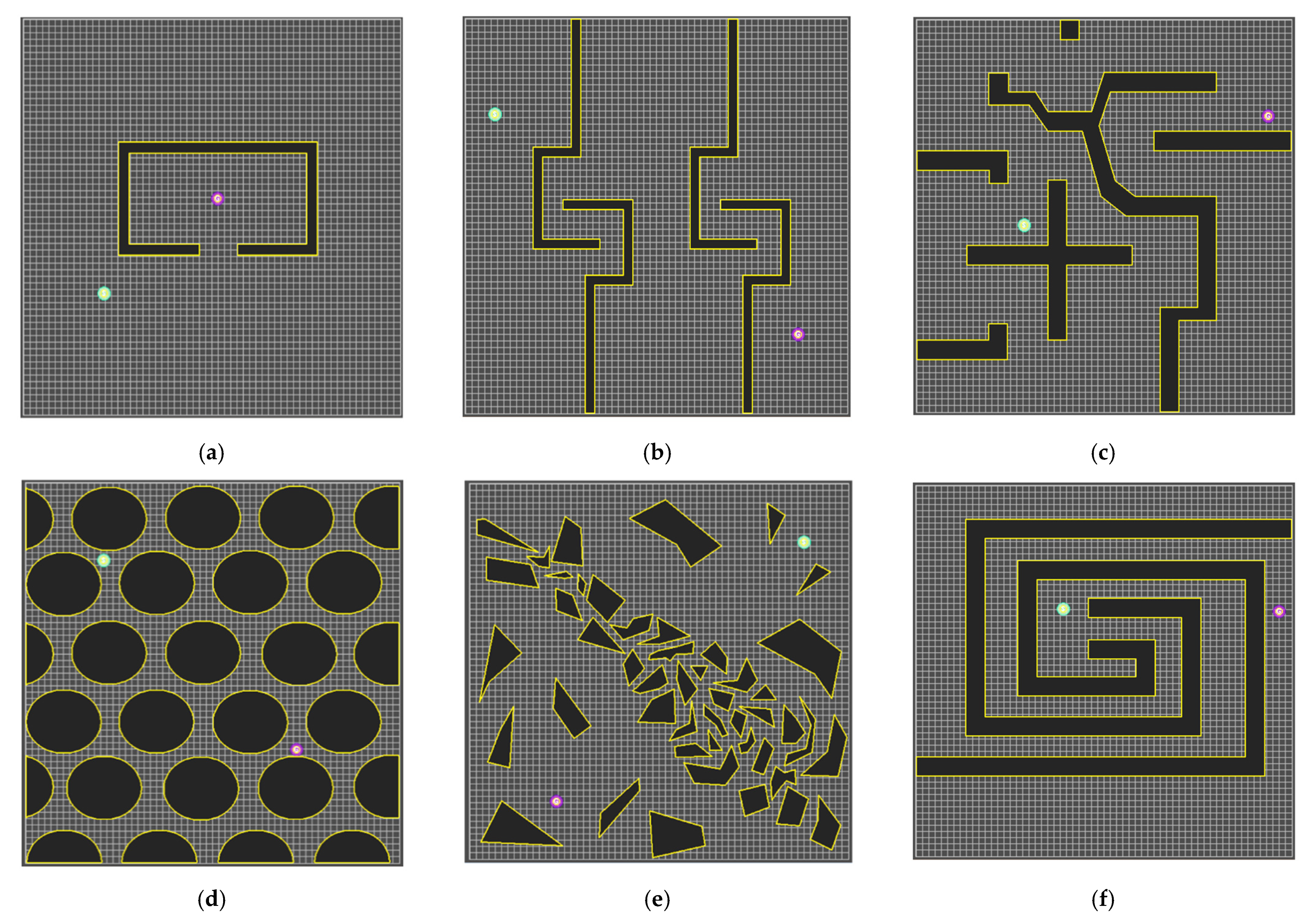
4.1. Experimental Environment
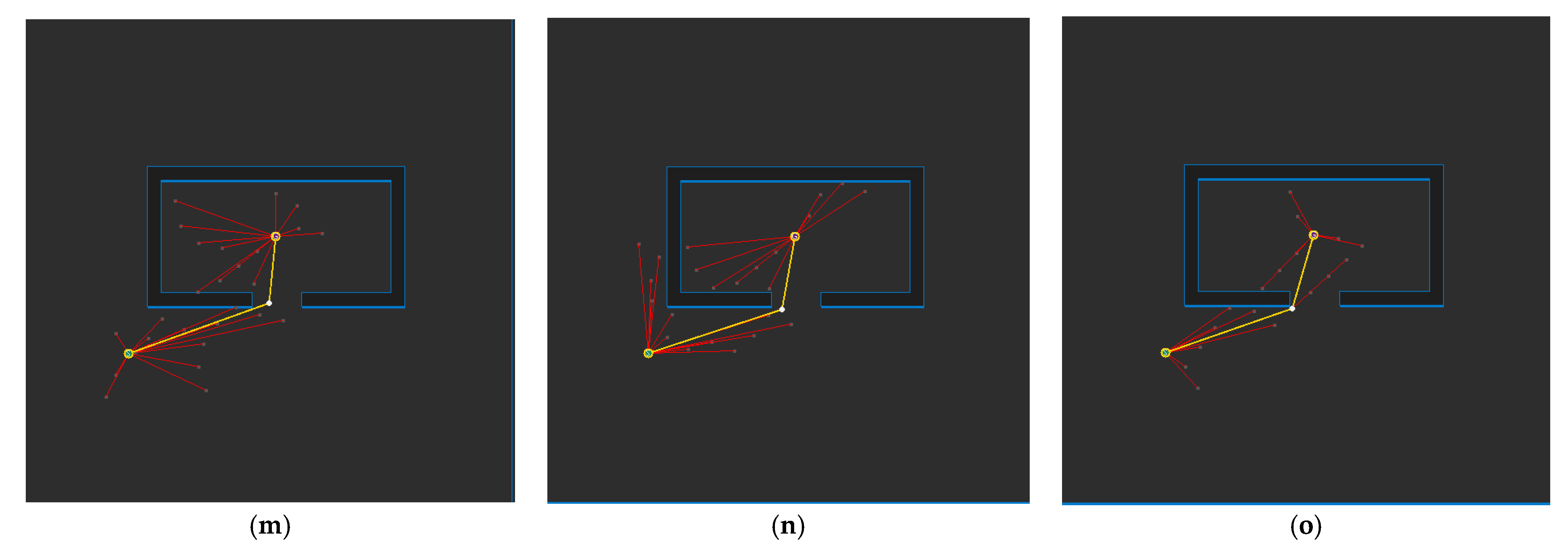
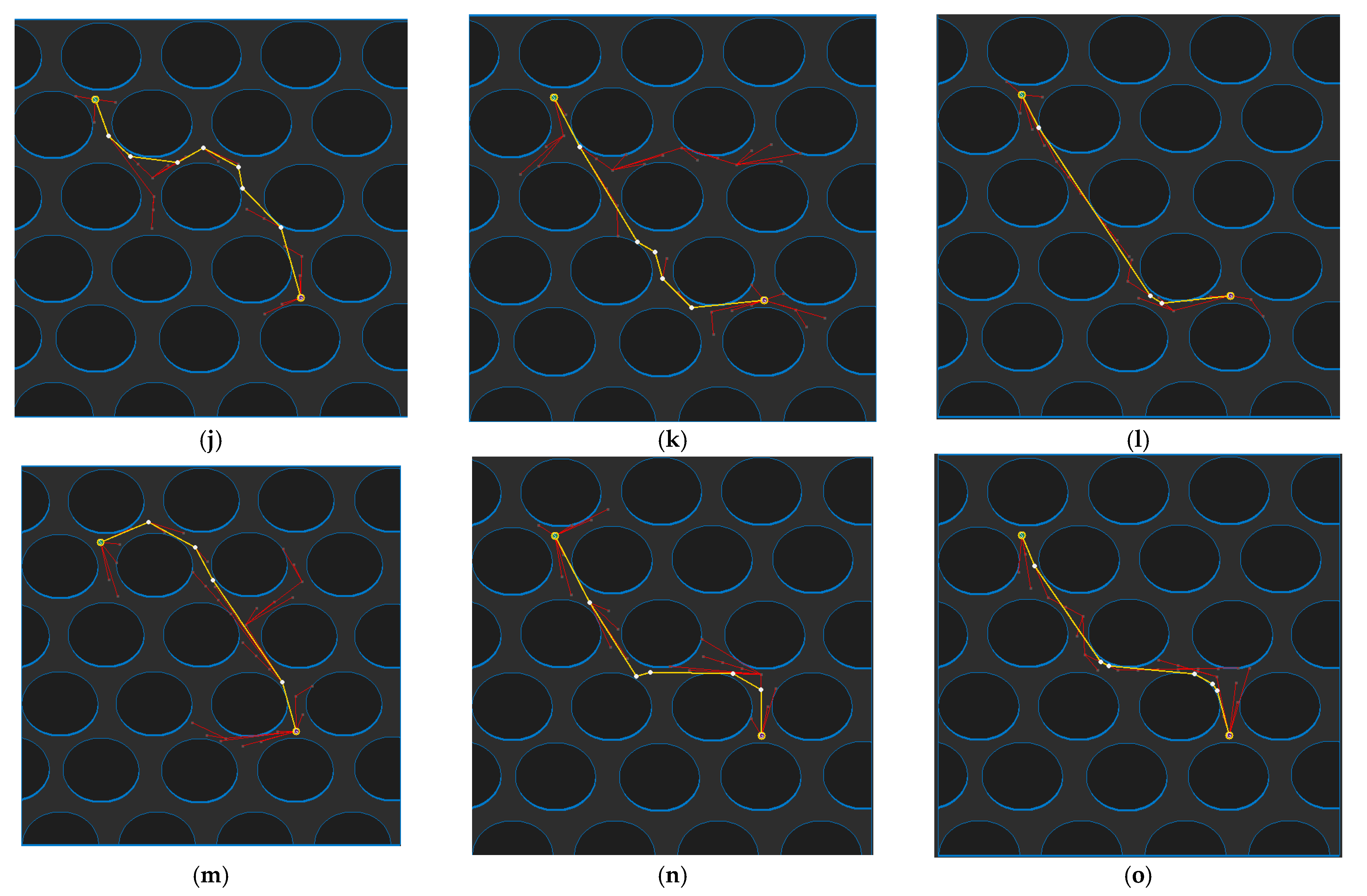
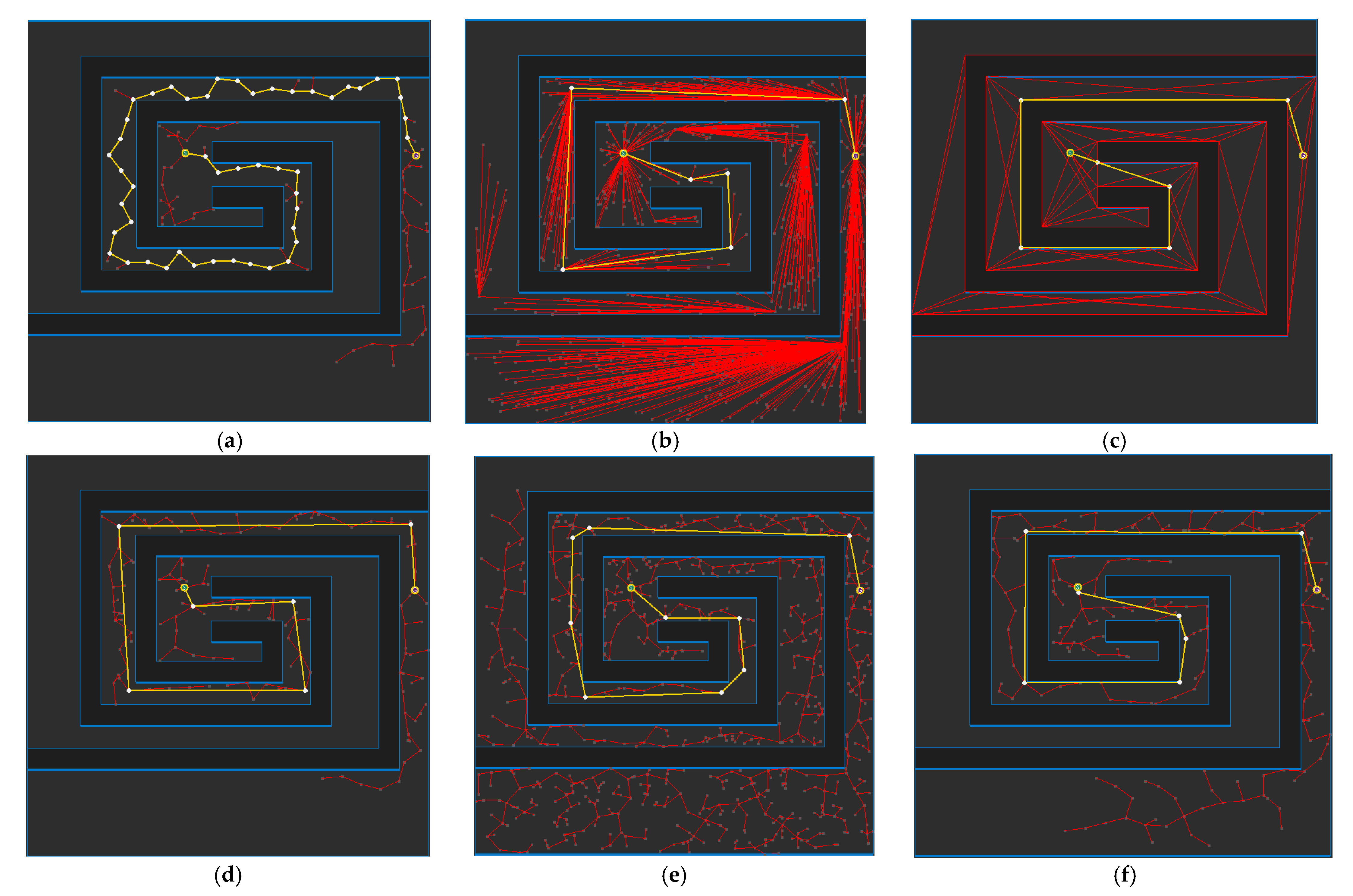
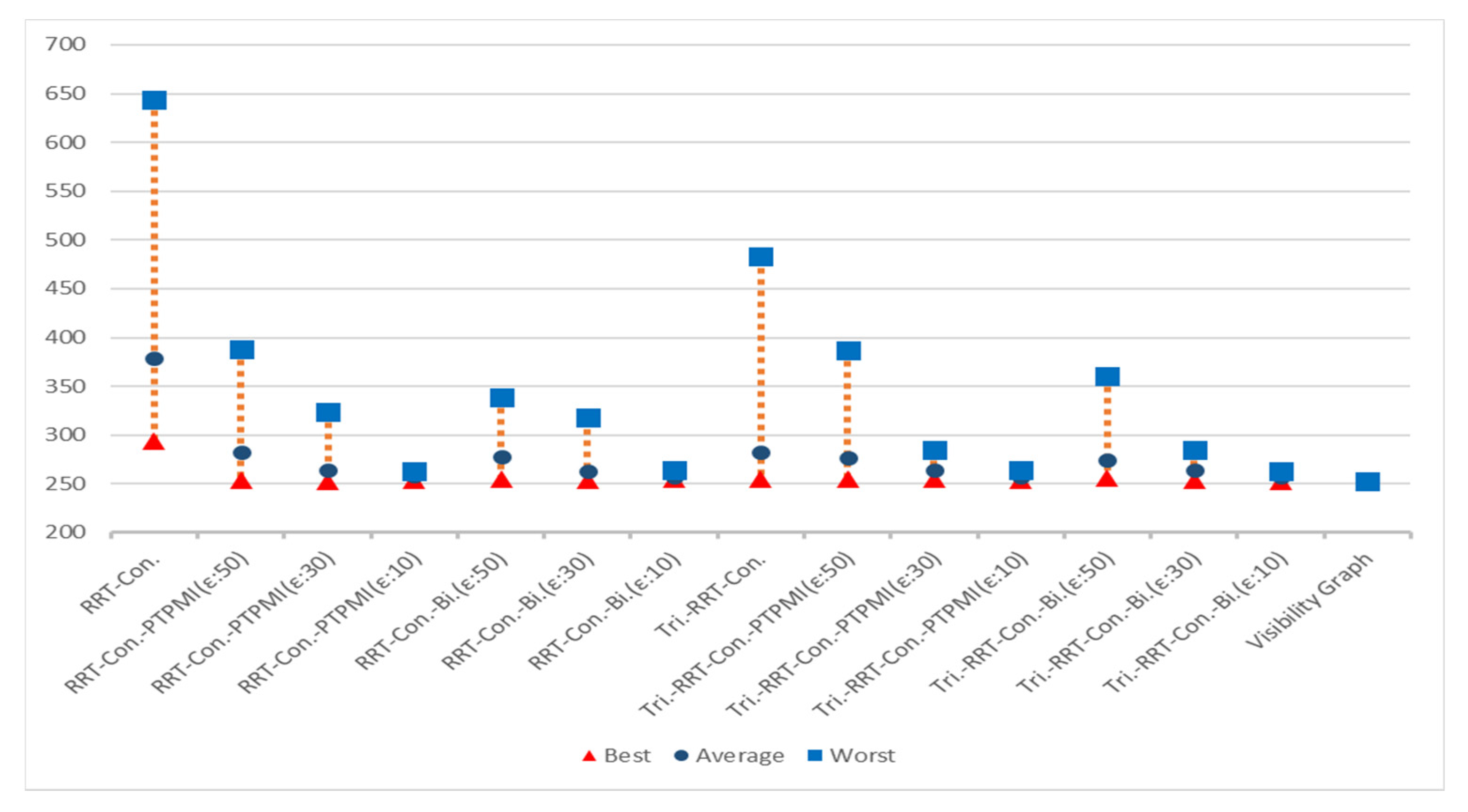
4.2. Experimental Results and Analysis for Each Map
4.3. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schwab, K. The Fourth Industrial Revolution; Currency: New York, NY, USA, 2017. [Google Scholar]
- Marin-Plaza, P.; Hussein, A.; Martin, D.; Escalera, A.D.L. Global and local path planning study in a ROS-based research platform for autonomous vehicles. J. Adv. Transp. 2018, 2018, 6392697. [Google Scholar] [CrossRef]
- Sariff, N.; Buniyamin, N. An overview of autonomous mobile robot path planning algorithms. In Proceedings of the IEEE 4th Student Conference on Research and Development, Selangor, Malaysia, 28–29 June 2006; pp. 183–188. [Google Scholar]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning; Springer: London, UK, 1998. [Google Scholar]
- Kang, J.-G.; Jung, J.-W. Post Triangular Rewiring Method for Shorter RRT Robot Path Planning. Int. J. Fuzzy Log. Intell. Syst. 2021, 21, 213–221. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Roy, D. Visibility graph based spatial path planning of robots using configuration space algorithms. Robot. Auton. Syst. 2009, 24, 1–9. [Google Scholar] [CrossRef]
- Katevas, N.I.; Tzafestas, S.G.; Pnevmatikatos, C.G. The approximate cell decomposition with local node refinement global path planning method: Path nodes refinement and curve parametric interpolation. J. Intell. Robot. Syst. 1998, 22, 289–314. [Google Scholar] [CrossRef]
- Warren, C.W. Global Path Planning using Artificial Potential Fields. In Proceedings of the International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 316–321. [Google Scholar]
- Jeong, I.-B.; Lee, S.-J.; Kim, J.-H. Quick-RRT*: Triangular inequality-based implementation of RRT* with improved initial solution and convergence rate. Expert Syst. Appl. 2019, 123, 82–90. [Google Scholar] [CrossRef]
- Kwon, J.; Choi, K. Kinodynamic Model Identification: A Unified Geometric Approach. IEEE Trans. Robot. 2021, 37, 1100–1114. [Google Scholar] [CrossRef]
- Kurzer, K. Path Planning in Unstructured Environments: A Real-Time Hybrid A* Implementation for Fast and Deterministic Path Generation for the KTH Research Concept Vehicle. Master’s Thesis, KTH Royal Institute of Technology School of Engineering Sciences, Stockholm, Sweden, 2016. [Google Scholar]
- Buniyamin, N.; Ngah, W.W.; Sariff, N.; Mohamad, Z. A simple local path planning algorithm for autonomous mobile robots. Int. J. Syst. Appl. Eng. Dev. 2011, 5, 151–159. [Google Scholar]
- Donald, B.; Xavier, P.; Canny, J.; Reif, J. Kinodynamic motion planning. J. ACM 1993, 40, 1048–1066. [Google Scholar] [CrossRef]
- Wang, J.; Li, B.; Meng, M.Q.-H. Kinematic Constrained Bi-directional RRT with Efficient Branch Pruning for robot path planning. Expert Syst. Appl. 2021, 170, 114541. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Kang, J.-G.; Choi, Y.-S.; Jung, J.-W. An Enhancement Method of Rapidly-exploring Random Tree Robot Path Planning using Midpoint Interpolation. Appl. Sci. 2021, 11, 8483. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Education: Delhi, India, 2009. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.-W.; So, B.-C.; Kang, J.-G.; Lim, D.-W.; Son, Y. Expanded Douglas–Peucker polygonal approximation and opposite angle based exact cell decomposition for path planning with curvilinear obstacles. Appl. Sci. 2019, 9, 638. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.-W.; Park, J.-S.; Kang, T.-W.; Kang, J.-G.; Kang, H.-W. Mobile Robot Path Planning Using a Laser Range Finder for Environments with Transparent Obstacles. Appl. Sci. 2020, 10, 2799. [Google Scholar] [CrossRef] [Green Version]
- Geraerts, R.; Overmars, M.H. A comparative study of probabilistic roadmap planners. In Algorithmic Foundations of Robotics V; Springer: Berlin/Heidelberg, Germany, 2004; pp. 43–57. [Google Scholar]
- Kuffner, J.J., Jr.; LaValle, S.M. RRT-connect: An Efficient Approach to Single-query Path Planning. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 995–1001. [Google Scholar]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal Sampling based Path Planning Focused via Direct Sampling of an Admissible Ellipsoidal Heuristic. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2997–3004. [Google Scholar]
- Kang, J.-G.; Lim, D.-W.; Choi, Y.-S.; Jang, W.-J.; Jung, J.-W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.-W.; So, B.-C.; Kang, J.-G.; Jang, W.-J. Circumscribed Douglas-Peucker Polygonal Approximation for Curvilinear Obstacle Representation. In Proceedings of the IEEE 2019 7th International Conference on Robot Intelligence Technology and Applications (RiTA), Daejeon, Korea, 1–3 November 2019; pp. 237–241. [Google Scholar]
- Han, J. Mobile robot path planning with surrounding point set and path improvement. Appl. Soft Comput. 2017, 57, 35–47. [Google Scholar] [CrossRef]
- Yoon, H.U.; Lee, D.-W. Subplanner algorithm to escape from local minima for artificial potential function based robotic path planning. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 263–275. [Google Scholar] [CrossRef]














| H/W | Spec. |
|---|---|
| CPU | Intel Core i7-6700k 4.00 GHz (8 CPUs) |
| RAM | 32,768 MB (32 GB DDR4) |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 379 (150%) | 283 (112%) | 264 (104%) | 258 (102%) | 278 (110%) | 263 (104%) | 257 (101%) |
| Planning time (ms) | <0 | <0 | <0 | <0 | 1 | <0 | <0 |
| Performance | Triangular-RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 282 (111%) | 277 (109%) | 264 (104%) | 258 (102%) | 274 (108%) | 264 (104%) | 257 (101%) |
| Planning time (ms) | <0 | <0 | <0 | <0 | <0 | <0 | <0 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
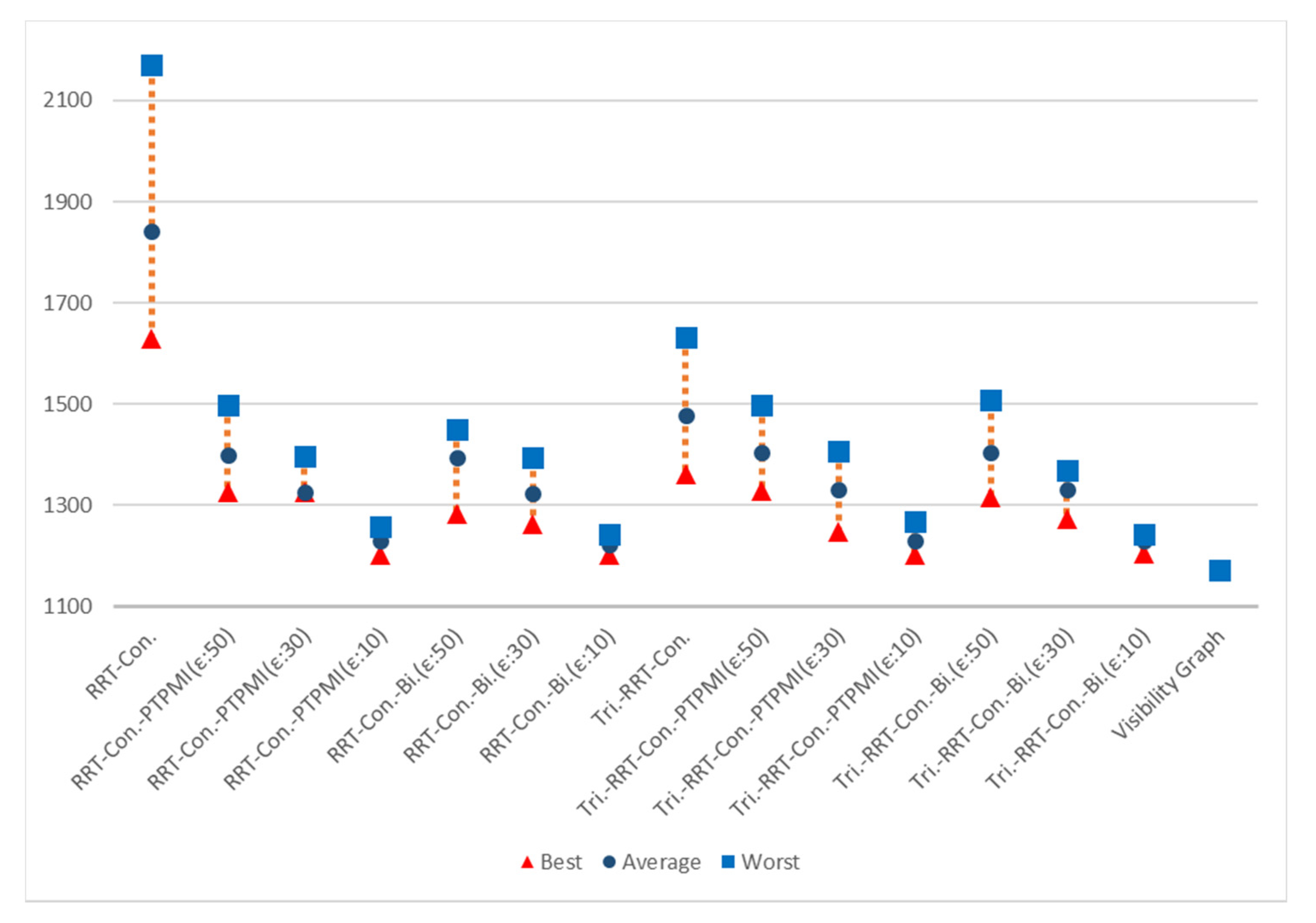
| Path length (px) | 1843 (157%) | 1399 (119%) | 1326 (113%) | 1230 (105%) | 1395 (119%) | 1324 (112%) | 1223 (104%) |
| Planning time (ms) | 220 | 242 | 264 | 250 | 243 | 272 | 223 |
| Performance | Triangular-RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 1478 (126%) | 1405 (120%) | 1331 (113%) | 1230 (105%) | 1404 (120%) | 1331 (113%) | 1229 (105%) |
| Planning time (ms) | 195 | 197 | 194 | 214 | 205 | 181 | 194 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
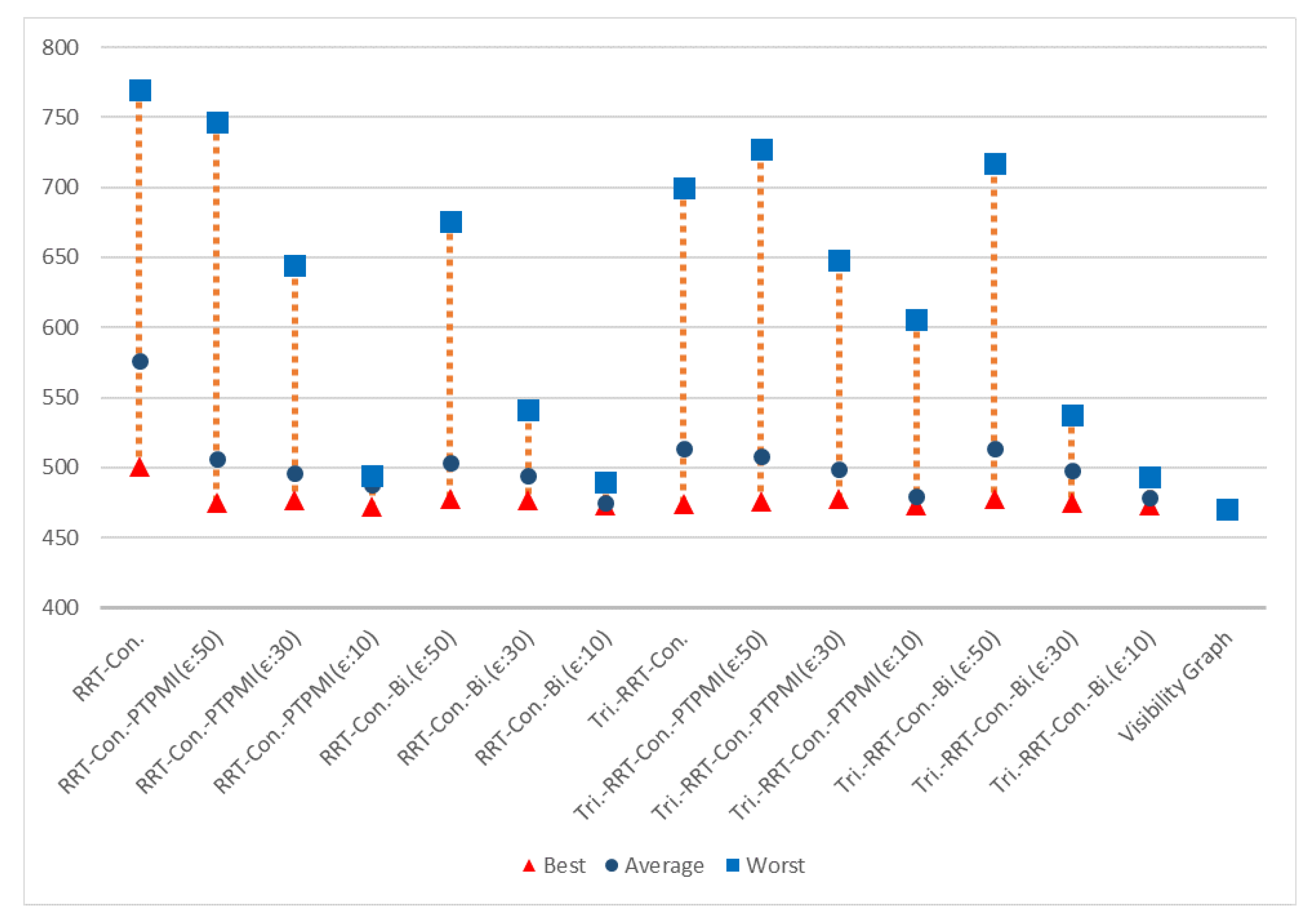
| Path length (px) | 1002 (140%) | 788 (110%) | 757 (106%) | 729 (102%) | 784 (110%) | 755 (106%) | 726 (102%) |
| Planning time (ms) | 9 | 10 | 10 | 9 | 8 | 11 | 12 |
| Performance | Triangular-RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 813 (114%) | 787 (110%) | 753 (105%) | 729 (102%) | 781 (109%) | 750 (105%) | 727 (102%) |
| Planning time (ms) | 7 | 10 | 9 | 10 | 9 | 9 | 9 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 576 (122%) | 506 (108%) | 496 (105%) | 488 (104%) | 504 (107%) | 494 (105%) | 475 (101%) |
| Planning time (ms) | 1 | 2 | 4 | 2 | 1 | 3 | 2 |
| Performance | TriangularRRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
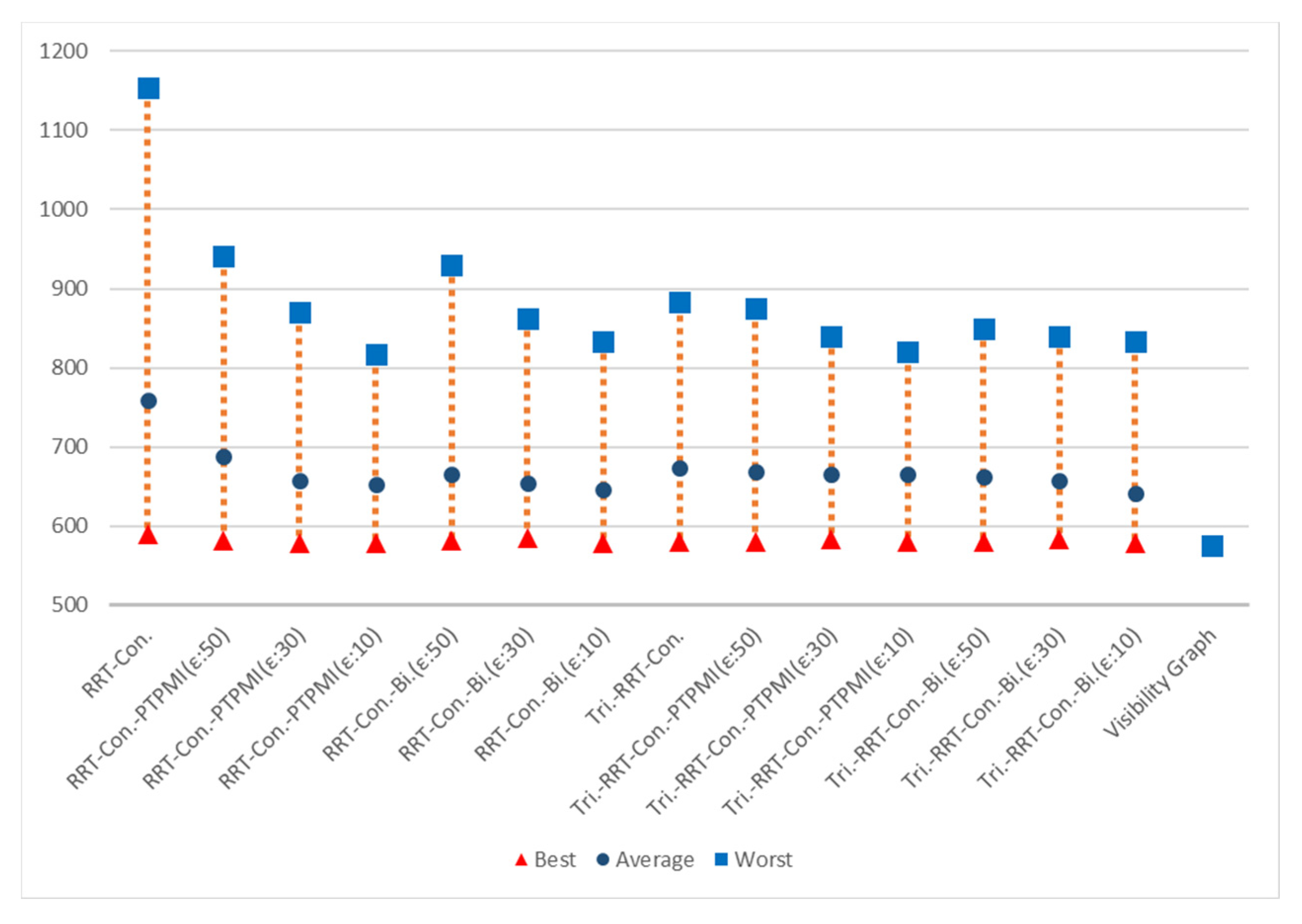
| Path length (px) | 514 (109%) | 508 (108%) | 499 (106%) | 480 (102%) | 514 (109%) | 499 (106%) | 479 (102%) |
| Planning time (ms) | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 759 (132%) | 689 (120%) | 657 (114%) | 653 (113%) | 666 (117%) | 655 (114%) | 646 (112%) |
| Planning time (ms) | 1 | 2 | 2 | 4 | 2 | 2 | 2 |
| Performance | Triangular-RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 673 (117%) | 669 (116%) | 666 (116%) | 665 (115%) | 663 (115%) | 658 (114%) | 641 (111%) |
| Planning time (ms) | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 1478 (127%) | 1292 (111%) | 1257 (108%) | 1189 (102%) | 1286 (110%) | 1254 (108%) | 1187 (102%) |
| Planning time (ms) | 24 | 24 | 27 | 26 | 30 | 26 | 28 |
| Performance | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Path length (px) | 1293 (111%) | 1282 (110%) | 1253 (108%) | 1189 (102%) | 1279 (110%) | 1250 (107%) | 1186 (102%) |
| Planning time (ms) | 23 | 24 | 23 | 22 | 23 | 22 | 23 |
| Map No. | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | Visibility Graph | ||||
|---|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | |||
| Map 1 | 379 (150%) | 283 (112%) | 264 (104%) | 258 (102%) | 278 (110%) | 263 (104%) | 257 (101%) | 253 |
| Map 2 | 1843 (157%) | 1399 (119%) | 1326 (113%) | 1230 (105%) | 1395 (119%) | 1324 (112%) | 1223 (104%) | 1172 |
| Map 3 | 1002 (140%) | 788 (110%) | 757 (106%) | 729 (102%) | 784 (110%) | 755 (106%) | 726 (102%) | 714 |
| Map 4 | 576 (122%) | 506 (108%) | 496 (105%) | 488 (104%) | 504 (107%) | 494 (105%) | 475 (101%) | 470 |
| Map 5 | 759 (132%) | 689 (120%) | 657 (114%) | 653 (113%) | 666 (117%) | 655 (114%) | 646 (112%) | 576 |
| Map 6 | 1478 (127%) | 1292 (111%) | 1257 (108%) | 1189 (102%) | 1286 (110%) | 1254 (108%) | 1187 (102%) | 1165 |
| Map No. | Triangular-RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | Visibility Graph | ||||
|---|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | |||
| Map 1 | 282 (111%) | 277 (109%) | 264 (104%) | 257 (101%) | 274 (108%) | 264 (104%) | 257 (101%) | 253 |
| Map 2 | 1478 (126%) | 1405 (120%) | 1331 (113%) | 1230 (105%) | 1404 (120%) | 1331 (113%) | 1229 (105%) | 1172 |
| Map 3 | 813 (114%) | 787 (110%) | 753 (105%) | 729 (102%) | 781 (109%) | 750 (105%) | 727 (102%) | 714 |
| Map 4 | 514 (109%) | 508(108%) | 499(106%) | 480(102%) | 514(109%) | 499(106%) | 479(102%) | 470 |
| Map 5 | 673 (117%) | 669 (116%) | 666 (116%) | 665 (115%) | 663 (115%) | 658 (114%) | 641 (111%) | 576 |
| Map 6 | 1293 (111%) | 1282 (110%) | 1253 (108%) | 1189 (102%) | 1279 (110%) | 1250 (107%) | 1186 (102%) | 1165 |
| Map No. | RRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Map 1 | <0 | <0 | <0 | <0 | 1 | <0 | <0 |
| Map 2 | 220 | 242 | 264 | 250 | 243 | 272 | 223 |
| Map 3 | 9 | 10 | 10 | 9 | 8 | 11 | 12 |
| Map 4 | 1 | 2 | 4 | 2 | 1 | 3 | 2 |
| Map 5 | 1 | 2 | 2 | 4 | 2 | 2 | 2 |
| Map 6 | 24 | 24 | 27 | 26 | 30 | 26 | 28 |
| Map No. | TriangularRRT-Connect | PTPMI Method | Bidirectional Interpolation Method | ||||
|---|---|---|---|---|---|---|---|
| ε: 50 px | ε: 30 px | ε: 10 px | ε: 50 px | ε: 30 px | ε: 10 px | ||
| Map 1 | <0 | <0 | <0 | <0 | <0 | <0 | <0 |
| Map 2 | 195 | 197 | 194 | 214 | 205 | 181 | 194 |
| Map 3 | 7 | 10 | 9 | 10 | 9 | 9 | 9 |
| Map 4 | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
| Map 5 | 1 | 1 | 1 | 2 | 2 | 1 | 1 |
| Map 6 | 27 | 24 | 20 | 22 | 19 | 22 | 23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, T.-W.; Kang, J.-G.; Jung, J.-W. A Bidirectional Interpolation Method for Post-Processing in Sampling-Based Robot Path Planning. Sensors 2021, 21, 7425. https://doi.org/10.3390/s21217425
Kang T-W, Kang J-G, Jung J-W. A Bidirectional Interpolation Method for Post-Processing in Sampling-Based Robot Path Planning. Sensors. 2021; 21(21):7425. https://doi.org/10.3390/s21217425
Chicago/Turabian StyleKang, Tae-Won, Jin-Gu Kang, and Jin-Woo Jung. 2021. "A Bidirectional Interpolation Method for Post-Processing in Sampling-Based Robot Path Planning" Sensors 21, no. 21: 7425. https://doi.org/10.3390/s21217425
APA StyleKang, T.-W., Kang, J.-G., & Jung, J.-W. (2021). A Bidirectional Interpolation Method for Post-Processing in Sampling-Based Robot Path Planning. Sensors, 21(21), 7425. https://doi.org/10.3390/s21217425








