An Electromagnetic Time-Reversal Imaging Algorithm for Moisture Detection in Polymer Foam in an Industrial Microwave Drying System
Abstract
:1. Introduction
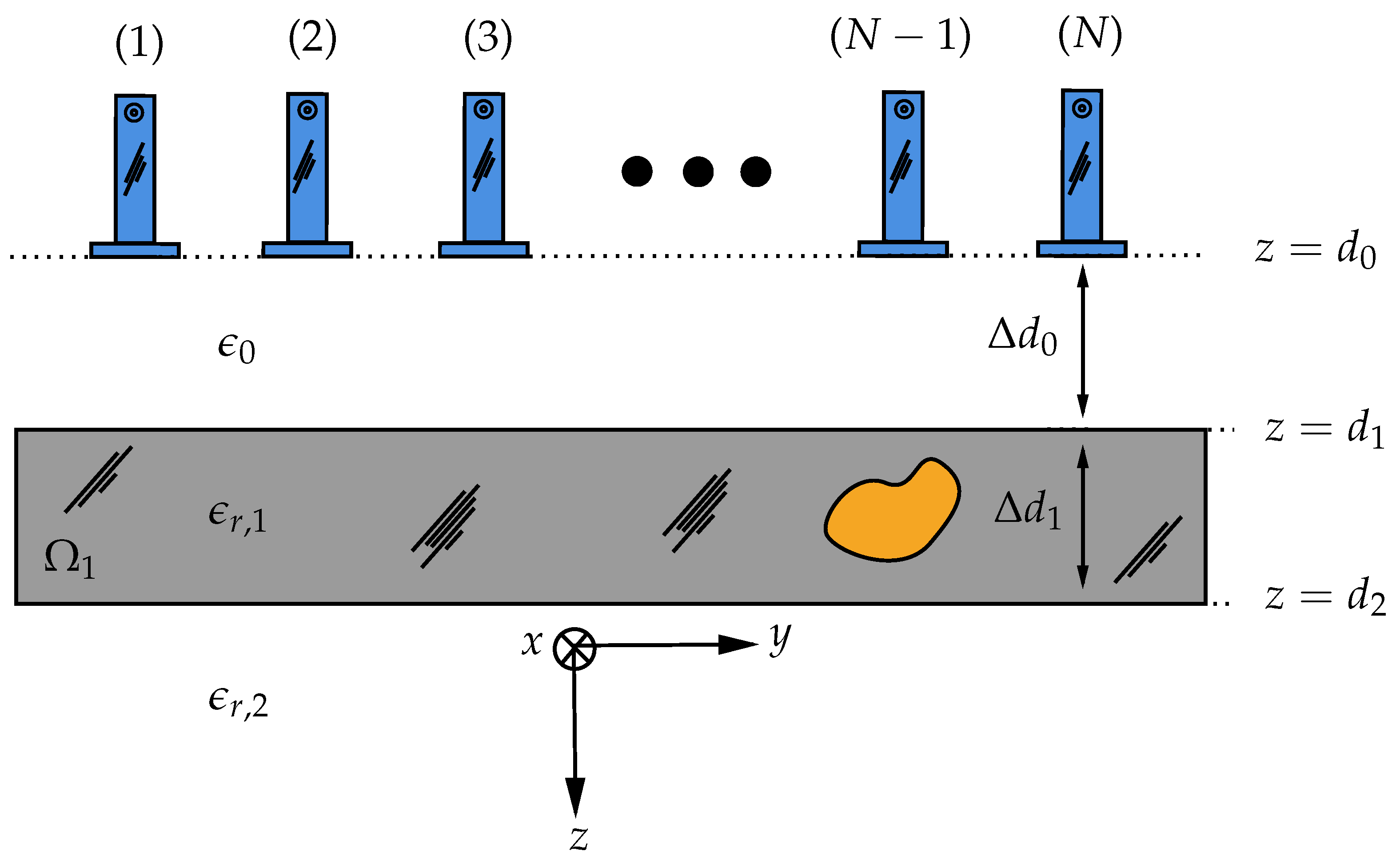
2. Problem Formulation
2.1. Scattering Model and Time-Reversal Imaging
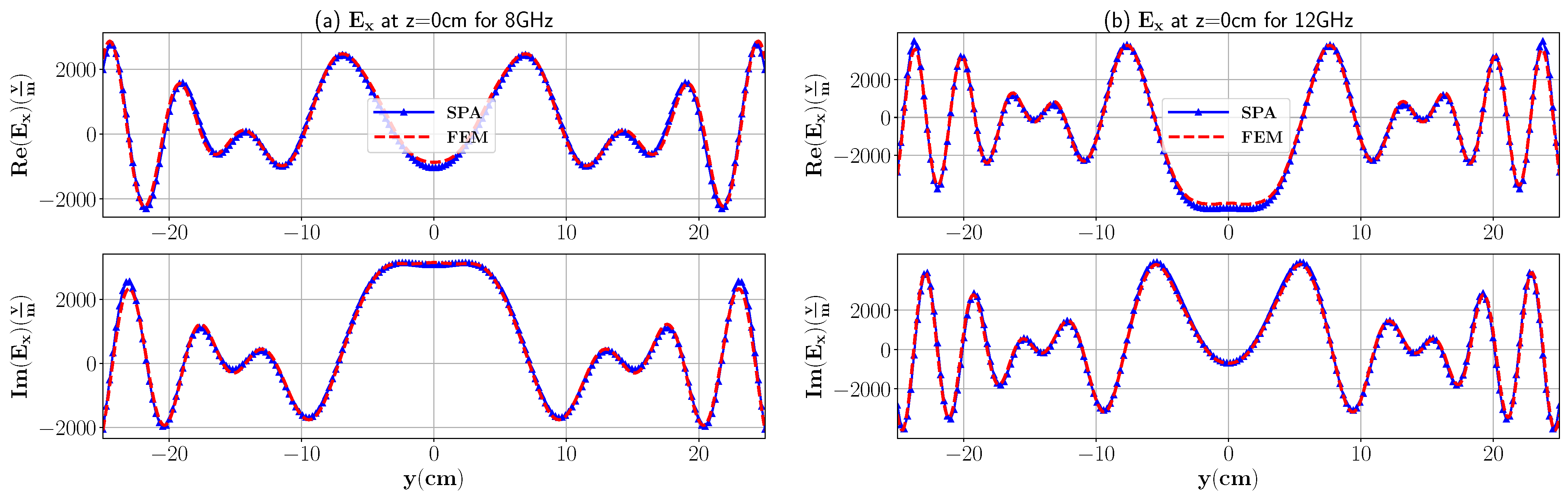
2.2. Dyadic Green Function of Multilayered Media
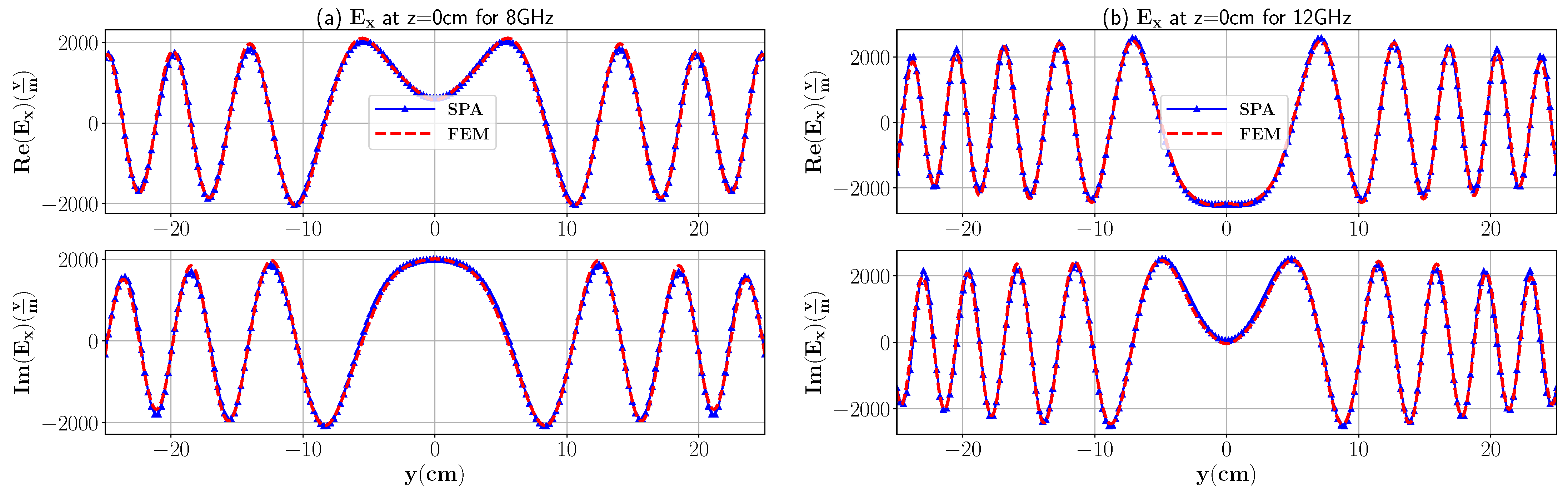
3. TRI-DORT Simulation Results
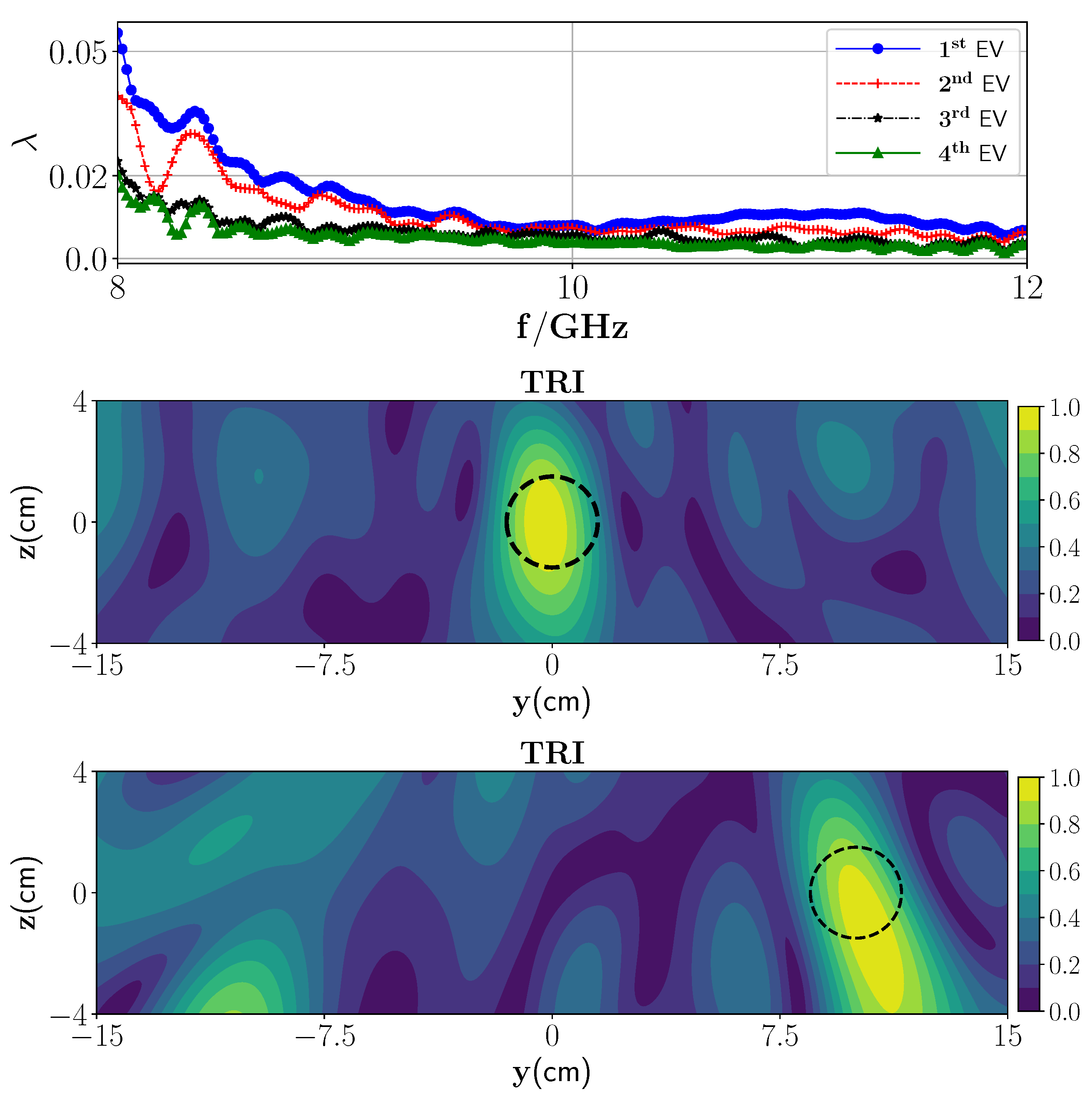
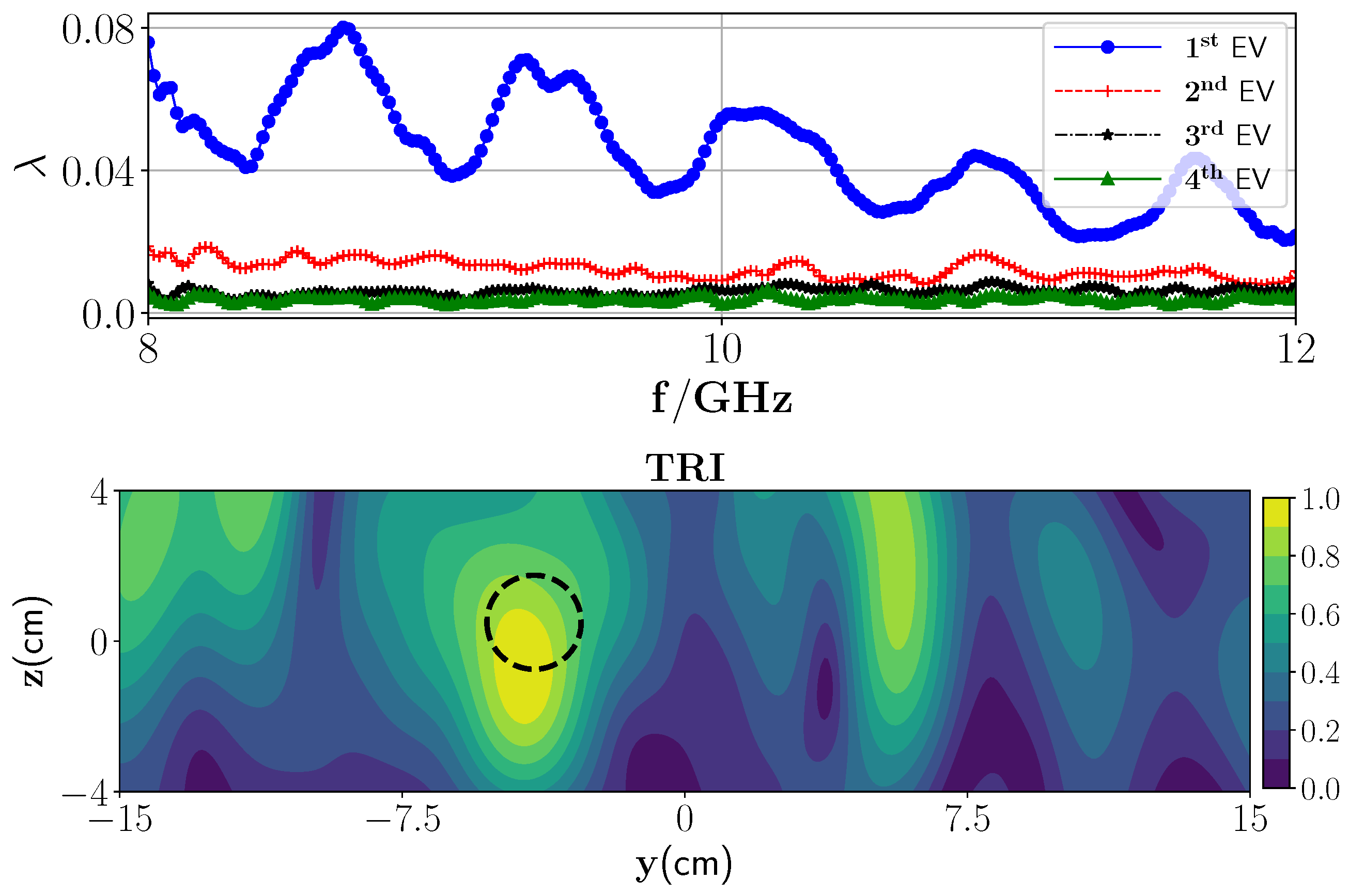
3.1. Low-Contrast Media
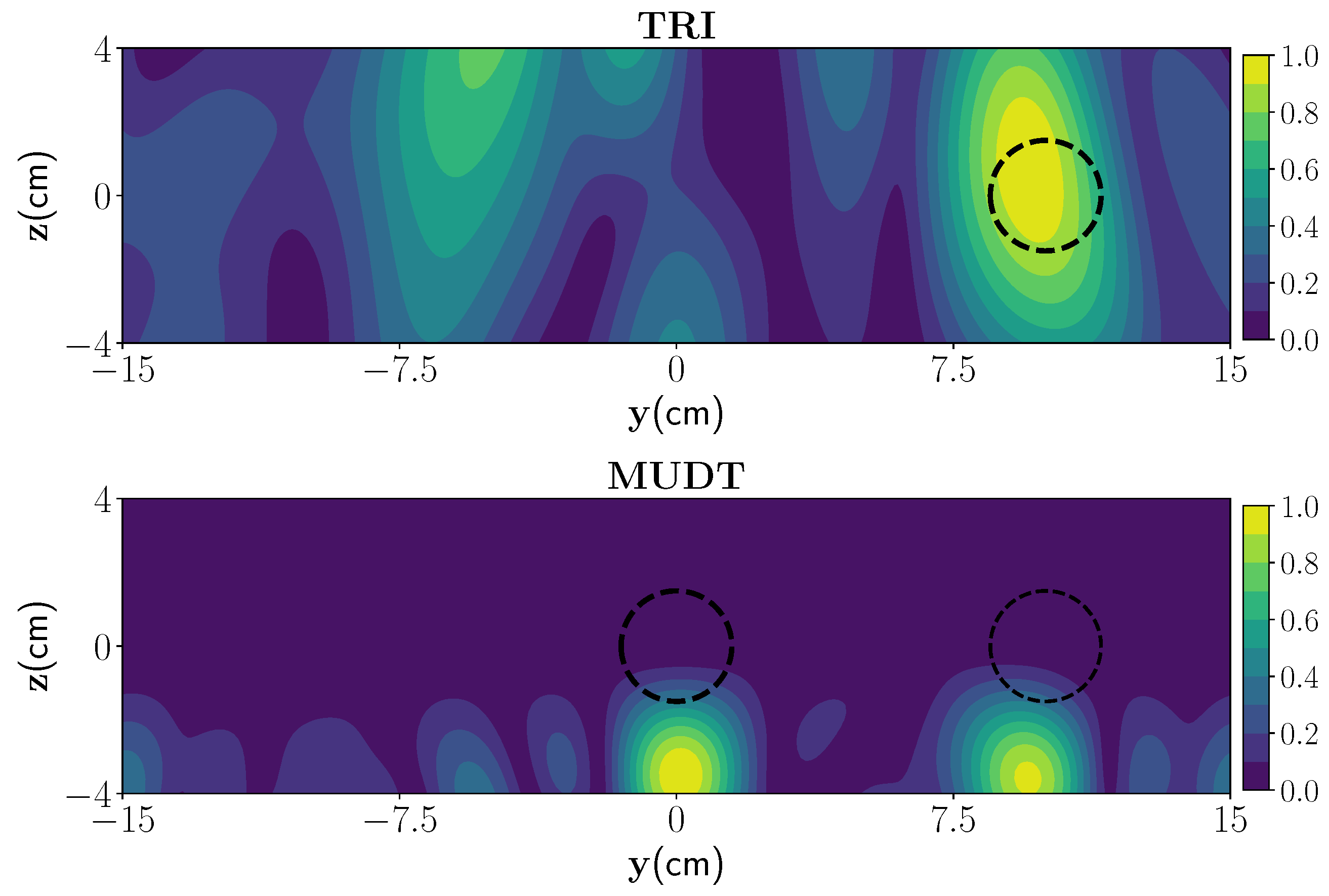
3.2. High-Contrast Media
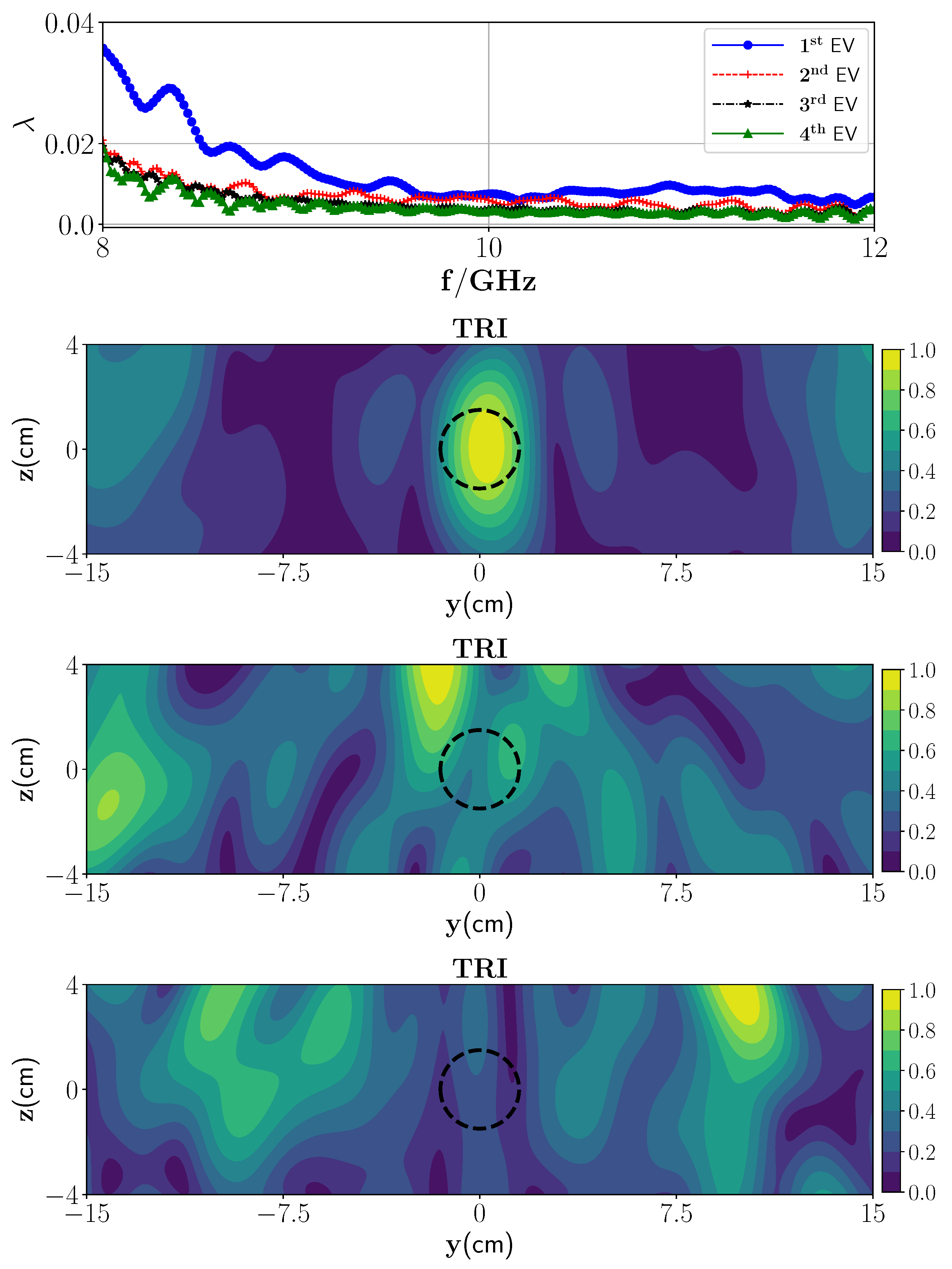
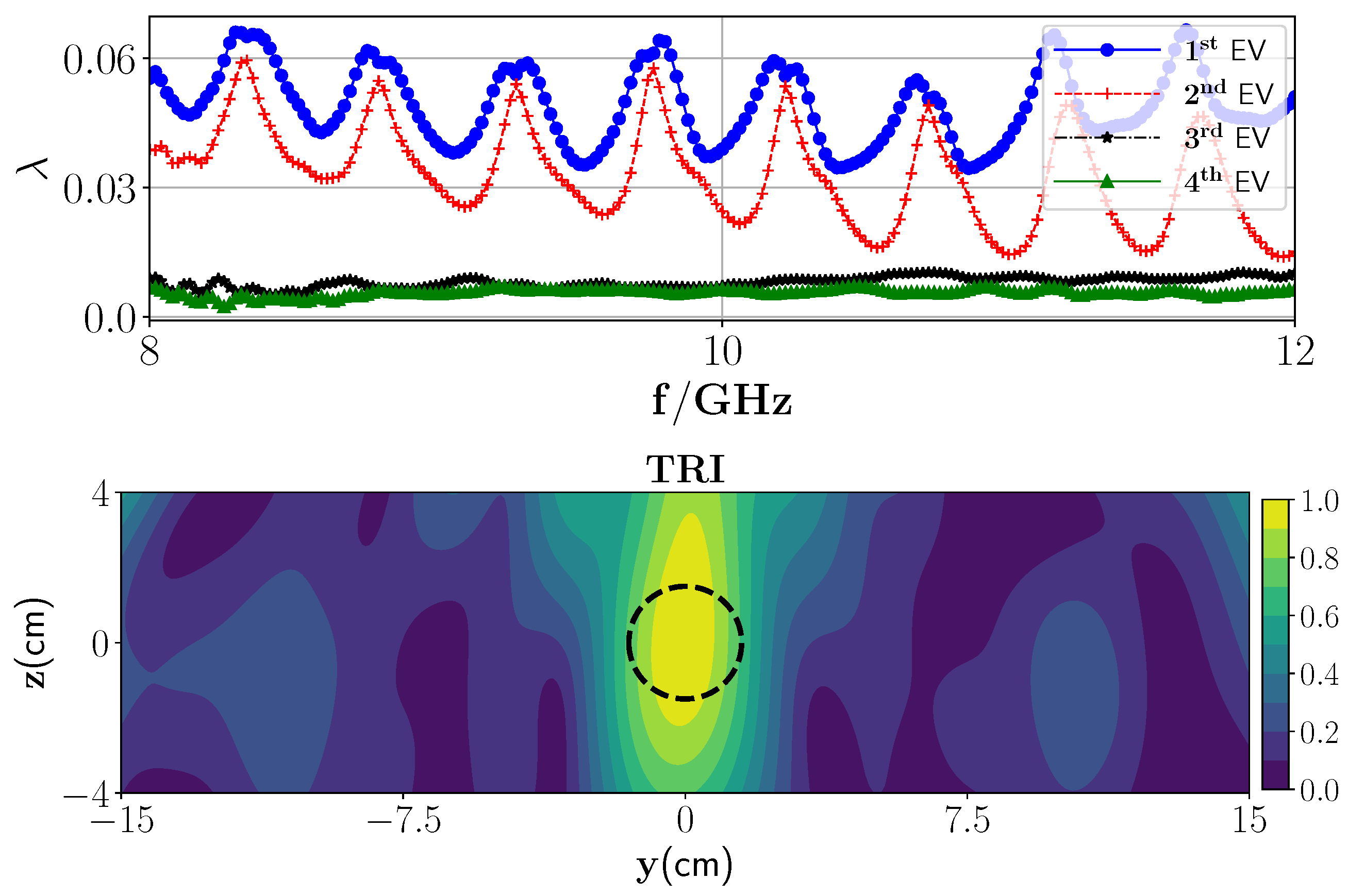
3.3. Single Frequency TRI
3.4. Moderately Rough Surface
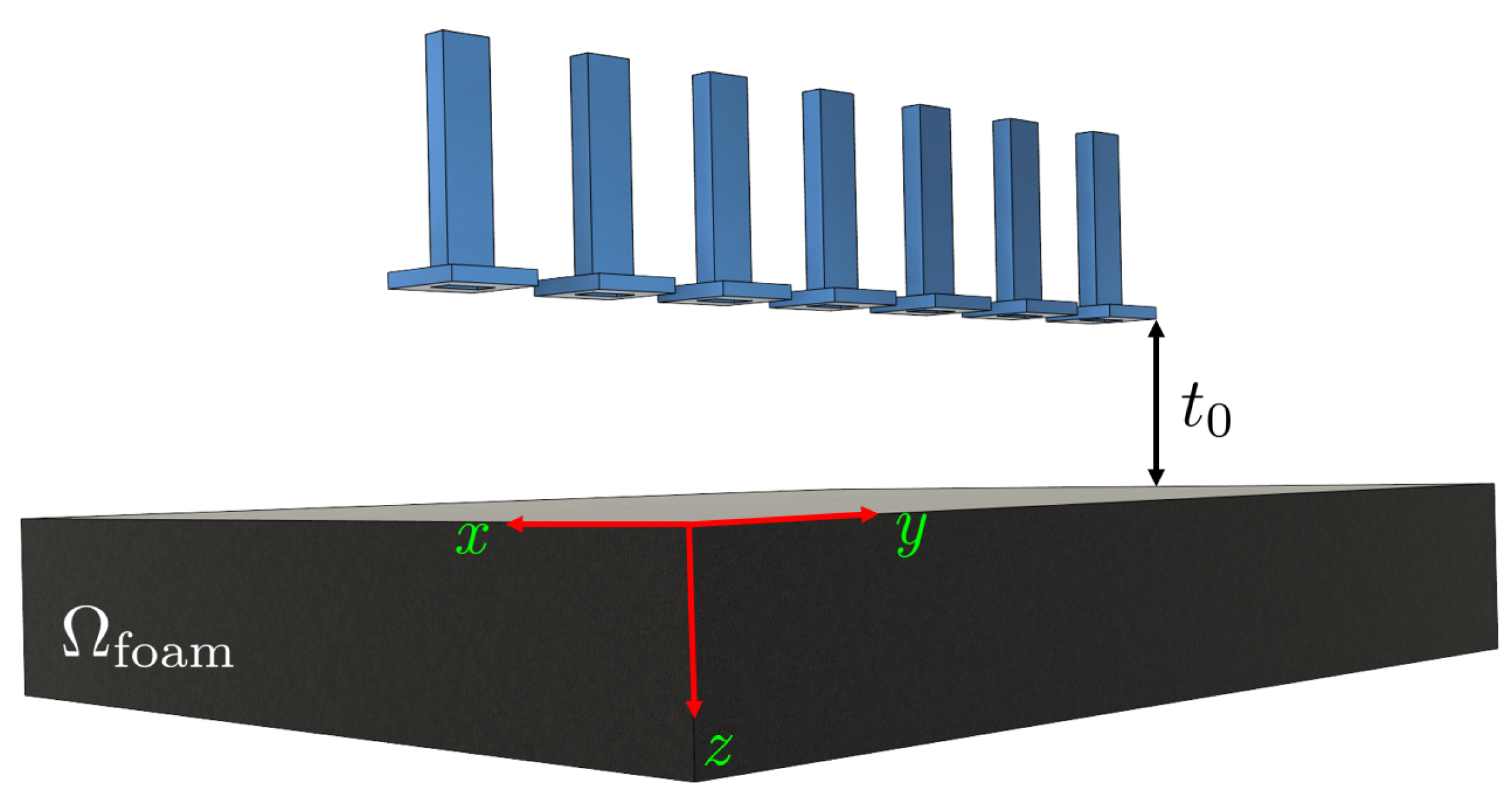
4. Experimental Results
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Roussy, G.; Bennani, A.; Thiebaut, J. Temperature runaway of microwave irradiated materials. J. Appl. Phys. 1987, 62, 1167–1170. [Google Scholar] [CrossRef]
- Li, Z.; Raghavan, G.; Orsat, V. Temperature and power control in microwave drying. J. Food Eng. 2010, 97, 478–483. [Google Scholar] [CrossRef]
- Martynenko, A.; Buck, A. Intelligent Control in Drying; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Mehdizadeh, M. Microwave/RF Applicators and Probes, 2nd ed.; William Andrew Publishing: Boston, MA, USA, 2015. [Google Scholar] [CrossRef]
- Sun, Y. Adaptive and Intelligent Temperature Control of Microwave Heating Systems with Multiple Sources. Ph.D. Thesis, KIT Scientific Publishing, Karlsruhe, Germany, 2016. [Google Scholar]
- Link, G.; Ramopoulos, V. Simple analytical approach for industrial microwave applicator design. Chem. Eng. Process. Process Intensif. 2018, 125, 334–342. [Google Scholar] [CrossRef]
- Link, G.; Kayser, T.; Koester, F.; Weiss, R.; Betz, S.; Wiesehoefer, R.; Sames, T.; Boulkertous, N.; Teufl, D.; Zaremba, S.; et al. Faserverbund-Leichtbau mit Automatisierter Mikrowellenprozesstechnik Hoher Energieeffizienz (FLAME): Schlussbericht des BMBF-Verbundprojektes; KIT Scientific Reports; Technical Report; Karlsruher Institut für Technologie: Karlsruhe, Germany, 2015; Volume 7701. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, H. Microwave Tomography for Industrial Process Imaging: Example Applications and Experimental Results. IEEE Antennas Propag. Mag. 2017, 59, 61–71. [Google Scholar] [CrossRef]
- Tobon Vasquez, J.A.; Scapaticci, R.; Turvani, G.; Ricci, M.; Farina, L.; Litman, A.; Casu, M.R.; Crocco, L.; Vipiana, F. Noninvasive Inline Food Inspection via Microwave Imaging Technology: An Application Example in the Food Industry. IEEE Antennas Propag. Mag. 2020, 62, 18–32. [Google Scholar] [CrossRef]
- Becker, F.; Schwabig, C.; Krause, J.; Leuchs, S.; Krebs, C.; Gruna, R.; Kuter, A.; Langle, T.; Nuessler, D.; Beyerer, J. From Visual Spectrum to Millimeter Wave: A Broad Spectrum of Solutions for Food Inspection. IEEE Antennas Propag. Mag. 2020, 62, 55–63. [Google Scholar] [CrossRef]
- Mohammed, B.J.; Abbosh, A.M.; Mustafa, S.; Ireland, D. Microwave System for Head Imaging. IEEE Trans. Instrum. Meas. 2014, 63, 117–123. [Google Scholar] [CrossRef]
- Bialkowski, M.; Ireland, D.; Wang, Y.; Abbosh, A. Ultra-wideband array antenna system for breast imaging. In Proceedings of the 2010 Asia-Pacific Microwave Conference, Yokohama, Japan, 7–10 December 2010; pp. 267–270. [Google Scholar]
- Klemm, M.; Craddock, I.J.; Leendertz, J.A.; Preece, A.; Benjamin, R. Radar-Based Breast Cancer Detection Using a Hemispherical Antenna Array—Experimental Results. IEEE Trans. Antennas Propag. 2009, 57, 1692–1704. [Google Scholar] [CrossRef] [Green Version]
- Mojabi, P.; Ostadrahimi, M.; Shafai, L.; LoVetri, J. Microwave tomography techniques and algorithms: A review. In Proceedings of the 2012 15 International Symposium on Antenna Technology and Applied Electromagnetics, Toulouse, France, 25–28 July 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Ghasr, M.T.; Simms, D.; Zoughi, R. Multimodal Solution for a Waveguide Radiating Into Multilayered Structures—Dielectric Property and Thickness Evaluation. IEEE Trans. Instrum. Meas. 2009, 58, 1505–1513. [Google Scholar] [CrossRef]
- Chang, C.W.; Chen, K.M.; Qian, J. Nondestructive determination of electromagnetic parameters of dielectric materials at X-band frequencies using a waveguide probe system. IEEE Trans. Instrum. Meas. 1997, 46, 1084–1092. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, K.; Song, R.; Ye, X.; Wang, G.; Chen, X. Learning-Based Quantitative Microwave Imaging With a Hybrid Input Scheme. IEEE Sens. J. 2020, 20, 15007–15013. [Google Scholar] [CrossRef]
- Massa, A.; Marcantonio, D.; Chen, X.; Li, M.; Salucci, M. DNNs as Applied to Electromagnetics, Antennas, and Propagation—A Review. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2225–2229. [Google Scholar] [CrossRef]
- Xiao, L.Y.; Li, J.; Han, F.; Hu, H.J.; Zhuang, M.; Liu, Q.H. Super-Resolution 3-D Microwave Imaging of Objects with High Contrasts by a Semijoin Extreme Learning Machine. IEEE Trans. Microw. Theory Tech. 2021, 69, 4840–4855. [Google Scholar] [CrossRef]
- Lähivaara, T.; Yadav, R.; Link, G.; Vauhkonen, M. Estimation of Moisture Content Distribution in Porous Foam Using Microwave Tomography With Neural Networks. IEEE Trans. Comput. Imaging 2020, 6, 1351–1361. [Google Scholar] [CrossRef]
- Yadav, R.; Omrani, A.; Link, G.; Vauhkonen, M.; Lähivaara, T. Microwave Tomography Using Neural Networks for Its Application in an Industrial Microwave Drying System. Sensors 2021, 21, 6919. [Google Scholar] [CrossRef] [PubMed]
- Fink, M. Time reversal of ultrasonic fields. I. Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 555–566. [Google Scholar] [CrossRef]
- Wu, F.; Thomas, J.L.; Fink, M. Time reversal of ultrasonic fields. Il. Experimental results. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 567–578. [Google Scholar] [CrossRef] [PubMed]
- Cassereau, D.; Fink, M. Time-reversal of ultrasonic fields. III. Theory of the closed time-reversal cavity. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 579–592. [Google Scholar] [CrossRef] [PubMed]
- Prada, C.; Fink, M. Eigenmodes of the time reversal operator: A solution to selective focusing in multiple-target media. Wave Motion. 1994, 20, 151–163. [Google Scholar] [CrossRef]
- Stang, J.; Haynes, M.; Carson, P.; Moghaddam, M. A Preclinical System Prototype for Focused Microwave Thermal Therapy of the Breast. IEEE Trans. Biomed. Eng. 2012, 59, 2431–2438. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.L.; Wu, F.; Fink, M. Time Reversal Focusing Applied to Lithotripsy. Ultrason. Imaging 1996, 18, 106–121. [Google Scholar] [CrossRef]
- Ebrahimi-Zadeh, J.; Dehmollaian, M.; Mohammadpour-Aghdam, K. Electromagnetic Time-Reversal Imaging of Pinholes in Pipes. IEEE Trans. Antennas Propag. 2016, 64, 1356–1363. [Google Scholar] [CrossRef]
- Bas, P.L.; Abeele, K.V.D.; Santos, S.D.; Goursolle, T.; Matar, O. Experimental Analysis for Nonlinear Time Reversal Imaging of Damaged Materials. In Proceedings of the ECNDT 2006, Berlin, Germany, 25–29 September 2006. [Google Scholar]
- Omrani, A.; Moghadasi, M.; Dehmollaian, M. Localisation and permittivity extraction of an embedded cylinder using decomposition of the time reversal operator. IET Microwaves Antennas Propag. 2020, 14, 851–859. [Google Scholar] [CrossRef]
- Fouda, A.E.; Teixeira, F.L.; Yavuz, M.E. Imaging and tracking of targets in clutter using differential time-reversal. In Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP), Rome, Italy, 11–15 April 2011; pp. 569–573. [Google Scholar]
- Yavuz, M.E.; Teixeira, F.L. Space–Frequency Ultrawideband Time-Reversal Imaging. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1115–1124. [Google Scholar] [CrossRef]
- Liu, D.; Kang, G.; Li, L.; Chen, Y.; Vasudevan, S.; Joines, W.; Liu, Q.H.; Krolik, J.; Carin, L. Electromagnetic time-reversal imaging of a target in a cluttered environment. IEEE Trans. Antennas Propag. 2005, 53, 3058–3066. [Google Scholar] [CrossRef]
- Moghadasi, S.M.; Dehmollaian, M.; Rashed-Mohassel, J. Time Reversal Imaging of Deeply Buried Targets Under Moderately Rough Surfaces Using Approximate Transmitted Fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3897–3905. [Google Scholar] [CrossRef]
- Moghadasi, S.M.; Dehmollaian, M. Buried-Object Time-Reversal Imaging Using UWB Near-Ground Scattered Fields. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7317–7326. [Google Scholar] [CrossRef]
- Sadeghi, S.; Mohammadpour-Aghdam, K.; Ren, K.; Faraji-Dana, R.; Burkholder, R.J. A Pole-Extraction Algorithm for Wall Characterization in Through-the-Wall Imaging Systems. IEEE Trans. Antennas Propag. 2019, 67, 7106–7113. [Google Scholar] [CrossRef]
- Sadeghi, S.; Mohammadpour-Aghdam, K.; Faraji-Dana, R.; Burkholder, R.J. A Novel Algorithm for Wall Characterization in Through the wall Imaging based on Spectral Analysis. In Proceedings of the 2018 18th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Waterloo, ON, Canada, 19–22 August 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Ren, K.; Burkholder, R.J. A Uniform Diffraction Tomographic Imaging Algorithm for Near-Field Microwave Scanning Through Stratified Media. IEEE Trans. Antennas Propag. 2016, 64, 5198–5207. [Google Scholar] [CrossRef]
- Omrani, A.; Link, G.; Jelonnek, J. A Multistatic Uniform Diffraction Tomographic Algorithm for Real-Time Moisture Detection. In Proceedings of the 2020 IEEE Asia-Pacific Microwave Conference (APMC), Hong Kong, China, 8–11 December 2020; pp. 437–439. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogenous Media; IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Chew, W.; Wang, Y. Reconstruction of two-dimensional permittivity distribution using the distorted Born iterative method. IEEE Trans. Med. Imaging 1990, 9, 218–225. [Google Scholar] [CrossRef]
- Tai, C.T. Dyadic Green’s Functions in Electromagnetic Theory; IEEE Press: New York, NY, USA, 1994. [Google Scholar]
- Sadeghi, S.; Mohammadpour-Aghdam, K.; Faraji-Dana, R.; Burkholder, R.J. A DORT-Uniform Diffraction Tomography Algorithm for Through-the-Wall Imaging. IEEE Trans. Antennas Propag. 2020, 68, 3176–3183. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E.; Bhatia, A.B.; Clemmow, P.C.; Gabor, D.; Stokes, A.R.; Taylor, A.M.; Wayman, P.A.; Wilcock, W.L. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Soldatov, S.; Kayser, T.; Link, G.; Seitz, T.; Layer, S.; Jelonnek, J. Microwave cavity perturbation technique for high-temperature dielectric measurements. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Devaney, A.J.; Dennison, M. Inverse scattering in inhomogeneous background media. Inverse Probl. 2003, 19, 855–870. [Google Scholar] [CrossRef]
- Kim, S.; Edelmann, G.F.; Kuperman, W.A.; Hodgkiss, W.S.; Song, H.C.; Akal, T. Spatial resolution of time-reversal arrays in shallow water. J. Acoust. Soc. Am. 2001, 110, 820–829. [Google Scholar] [CrossRef]
- Yavuz, M.E.; Teixeira, F.L. Ultrawideband Microwave Sensing and Imaging Using Time-Reversal Techniques: A Review. Remote Sens. 2009, 1, 466–495. [Google Scholar] [CrossRef] [Green Version]
- Janalizadeh, R.C.; Zakeri, B. A Source-Type Best Approximation Method for Imaging Applications. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 1707–1710. [Google Scholar] [CrossRef]
- Liu, D.; Vasudevan, S.; Krolik, J.; Bal, G.; Carin, L. Electromagnetic Time-Reversal Source Localization in Changing Media: Experiment and Analysis. IEEE Trans. Antennas Propag. 2007, 55, 344–354. [Google Scholar] [CrossRef] [Green Version]
- Peitgen, H.O.; Saupe, D. (Eds.) The Science of Fractal Images; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Omrani, A.; Yadav, R.; Link, G.; Vauhkonen, M.; Lähivaara, T.; Jelonnek, J. A Combined Microwave Imaging Algorithm for Localization and Moisture Level Estimation in Multilayered Media. In Proceedings of the 2021 15th European Conference on Antennas and Propagation (EuCAP), Düsseldorf, Germany, 22–26 March 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yadav, R.; Omrani, A.; Vauhkonen, M.; Link, G.; Lähivaara, T. Microwave Tomography for Moisture Level Estimation Using Bayesian Framework. In Proceedings of the 2021 15th European Conference on Antennas and Propagation (EuCAP), Düsseldorf, Germany, 22–26 March 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Asymptotic Expansion of Integrals. In Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999; pp. 247–316. [Google Scholar]
- Norman Bleistein, R.A.H. Asymptotic Expansions of Integrals; Holt, Rinehart and Winston: New York, NY, USA, 1975. [Google Scholar]

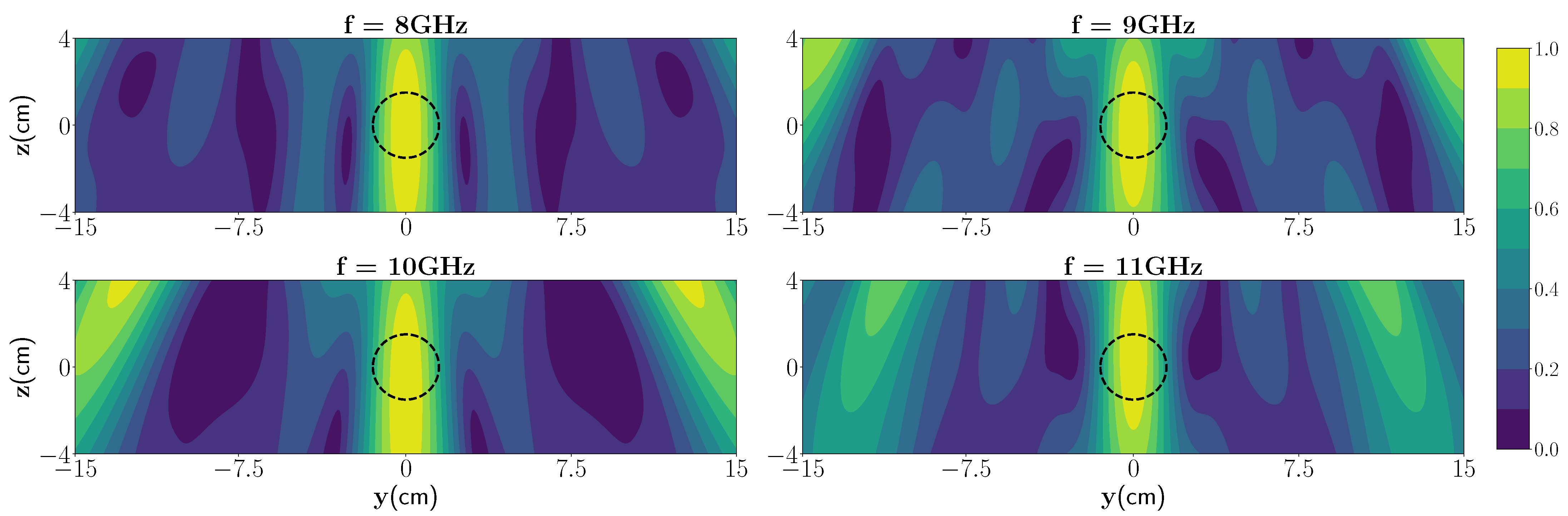
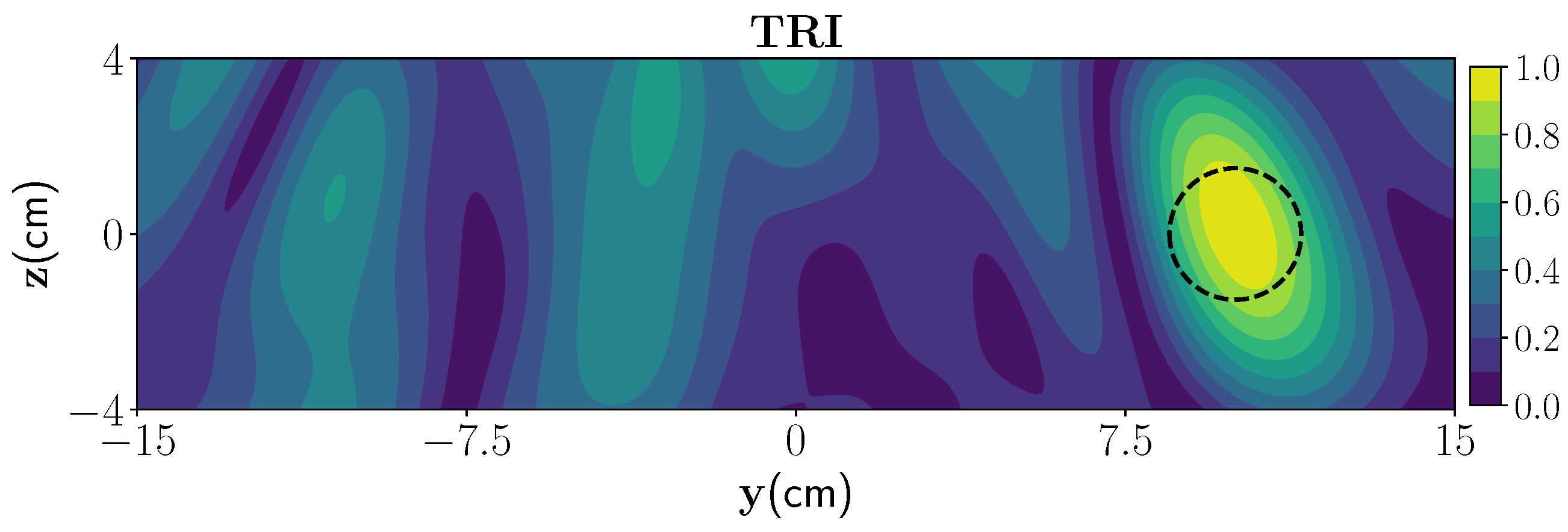

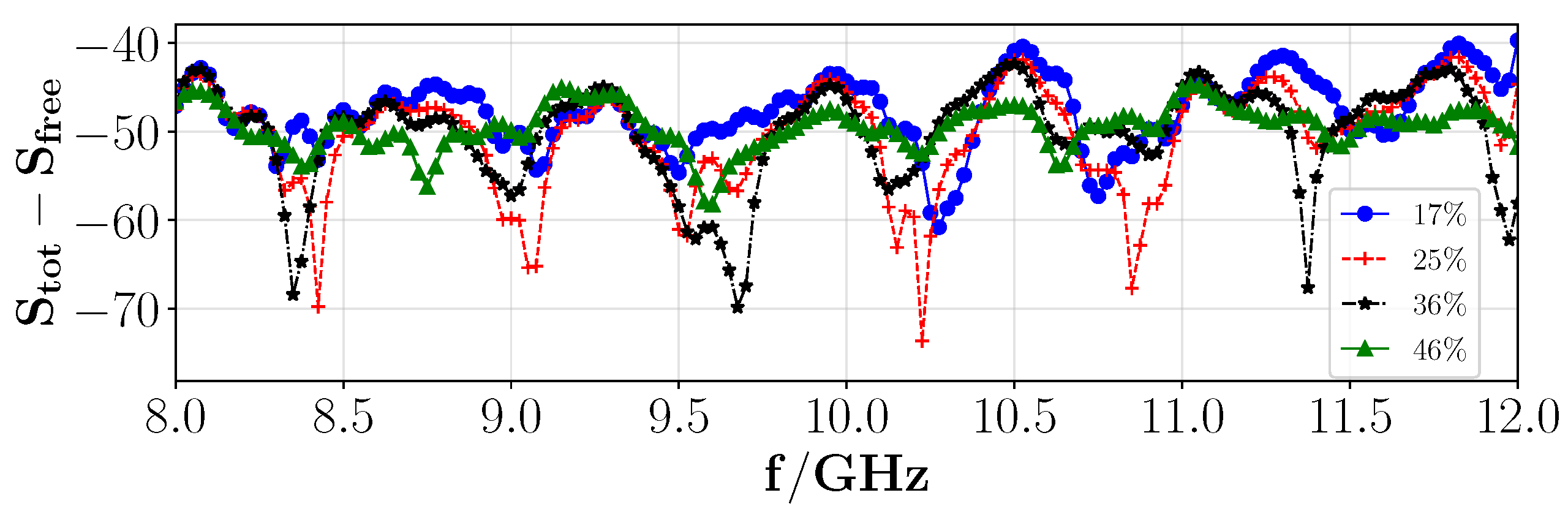
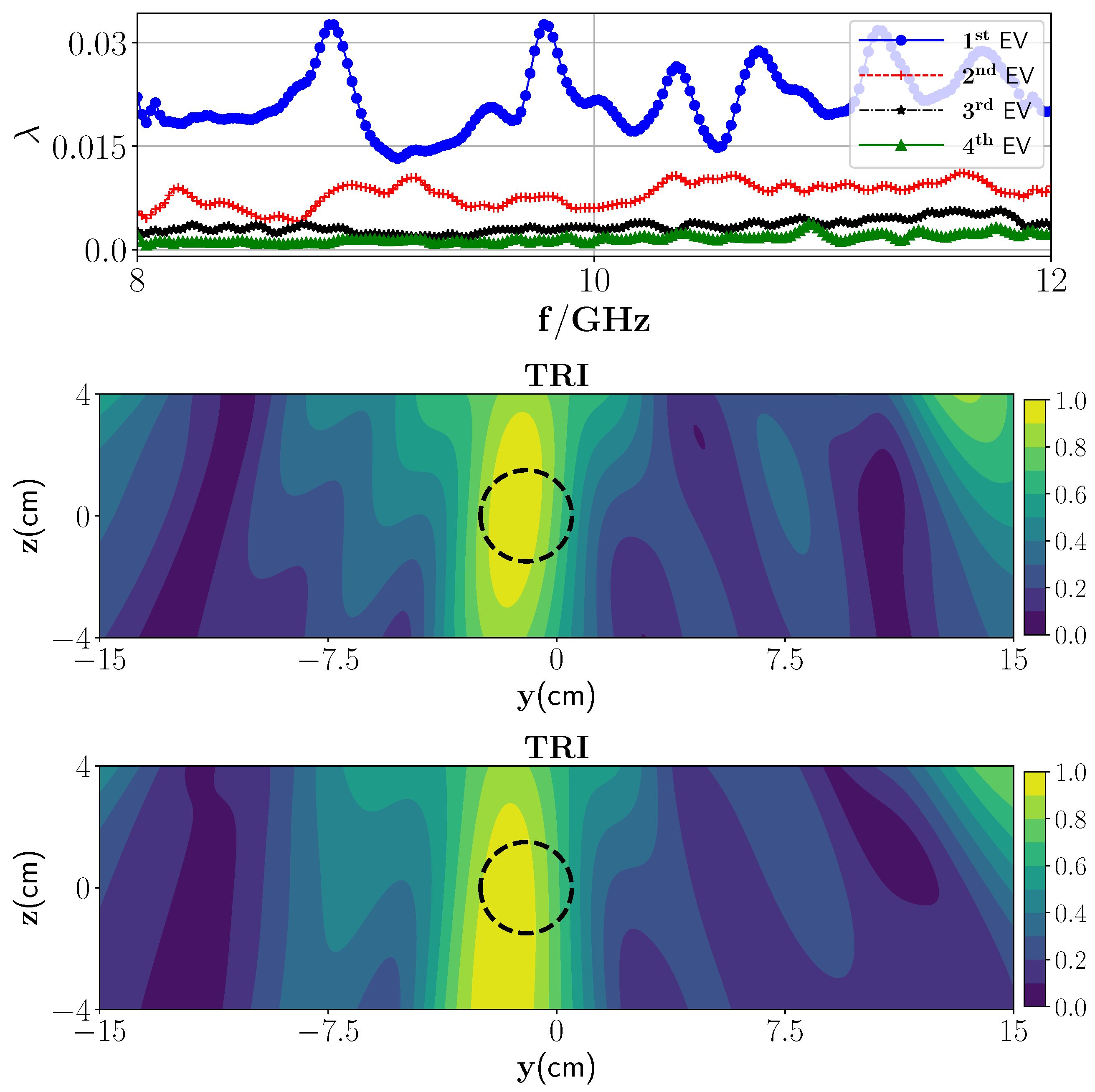
| NRMS % | 1.76 | 2.06 | 2.11 | 2.74 |
| M% | 0 | 30 | 36 |
|---|---|---|---|
| NRMS % | 2.42 | 1.89 | 1.94 | 2.15 |
| f (GHz) | 8 | 9 | 10 | 11 |
|---|---|---|---|---|
| 6.6654 | 2.029 | 2.4659 | 2.694 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omrani, A.; Yadav, R.; Link, G.; Lähivaara, T.; Vauhkonen, M.; Jelonnek, J. An Electromagnetic Time-Reversal Imaging Algorithm for Moisture Detection in Polymer Foam in an Industrial Microwave Drying System. Sensors 2021, 21, 7409. https://doi.org/10.3390/s21217409
Omrani A, Yadav R, Link G, Lähivaara T, Vauhkonen M, Jelonnek J. An Electromagnetic Time-Reversal Imaging Algorithm for Moisture Detection in Polymer Foam in an Industrial Microwave Drying System. Sensors. 2021; 21(21):7409. https://doi.org/10.3390/s21217409
Chicago/Turabian StyleOmrani, Adel, Rahul Yadav, Guido Link, Timo Lähivaara, Marko Vauhkonen, and John Jelonnek. 2021. "An Electromagnetic Time-Reversal Imaging Algorithm for Moisture Detection in Polymer Foam in an Industrial Microwave Drying System" Sensors 21, no. 21: 7409. https://doi.org/10.3390/s21217409
APA StyleOmrani, A., Yadav, R., Link, G., Lähivaara, T., Vauhkonen, M., & Jelonnek, J. (2021). An Electromagnetic Time-Reversal Imaging Algorithm for Moisture Detection in Polymer Foam in an Industrial Microwave Drying System. Sensors, 21(21), 7409. https://doi.org/10.3390/s21217409







