Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation
2.2. BiLSTM-Based Deep Neural Network Model
3. Results
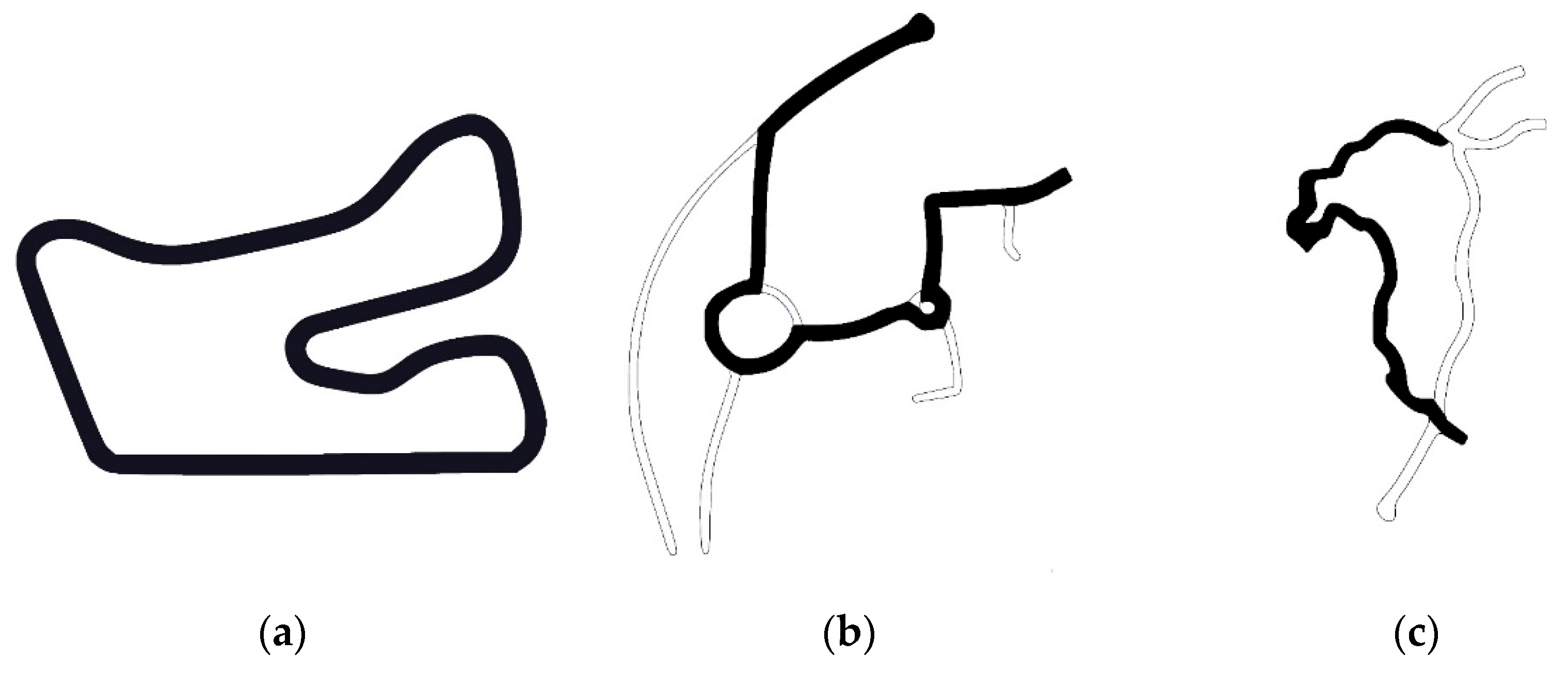
3.1. Vehicle Model Validation and Dataset Generation
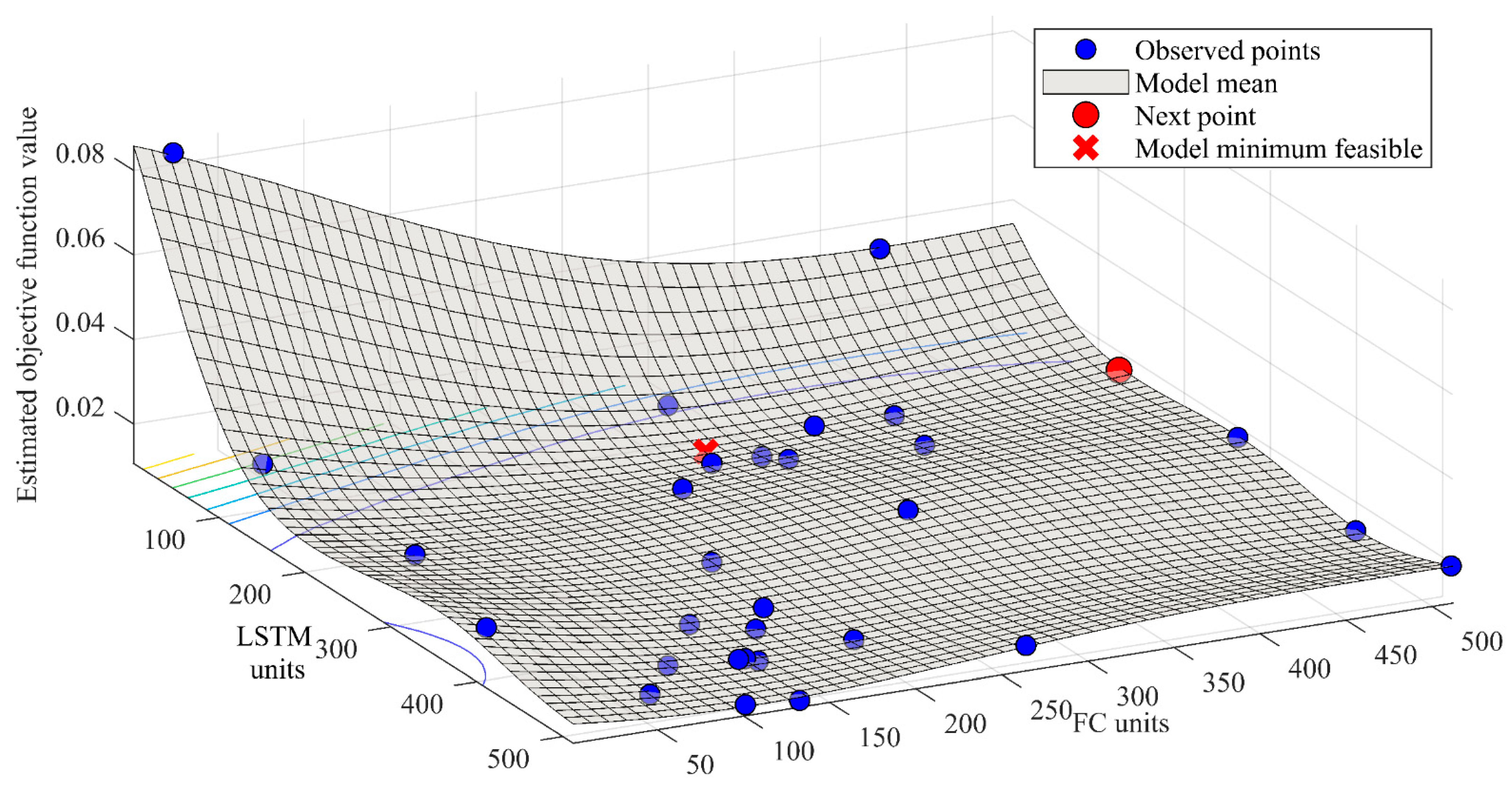
3.2. Results of Hyperparameter Optimisation
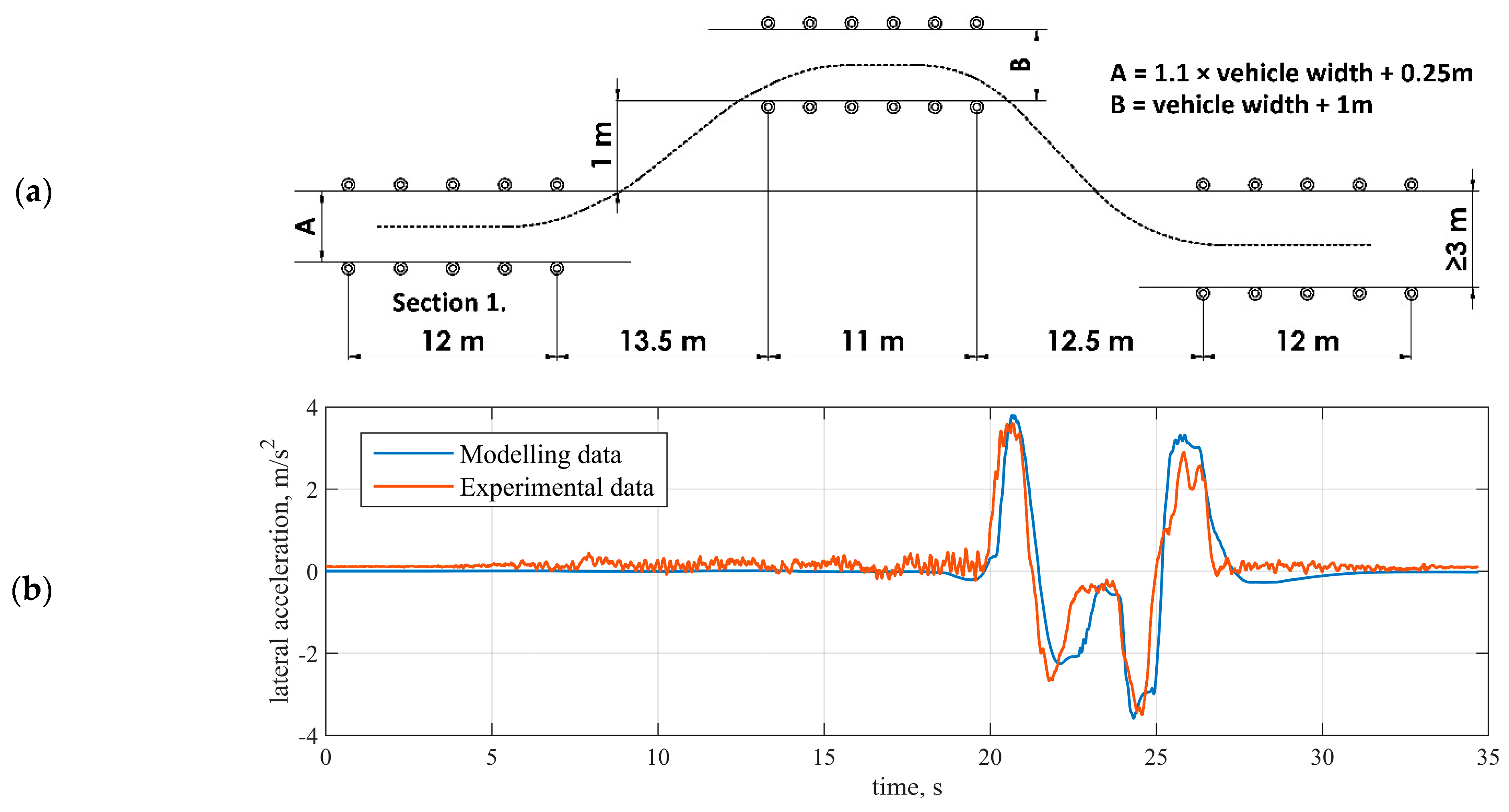
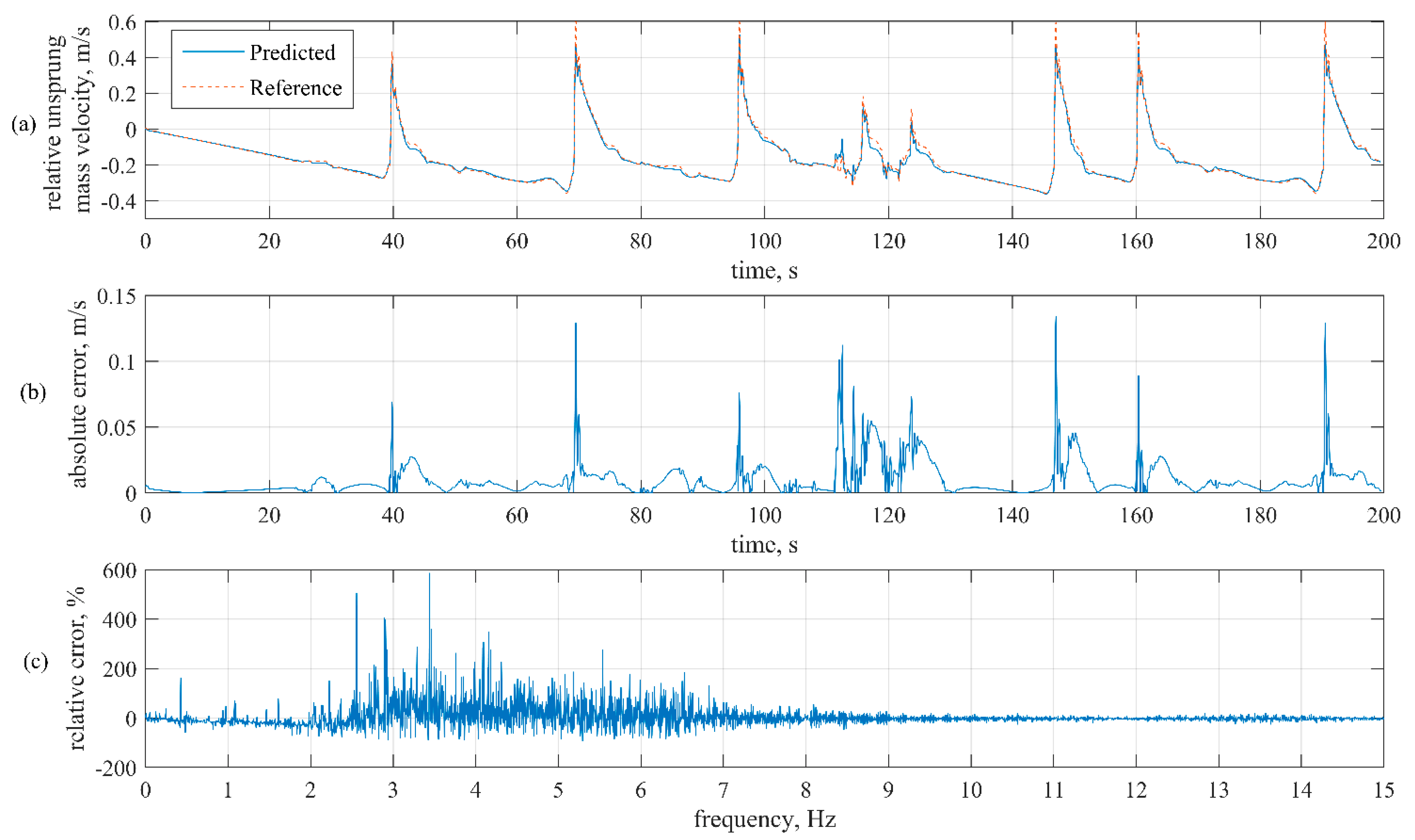
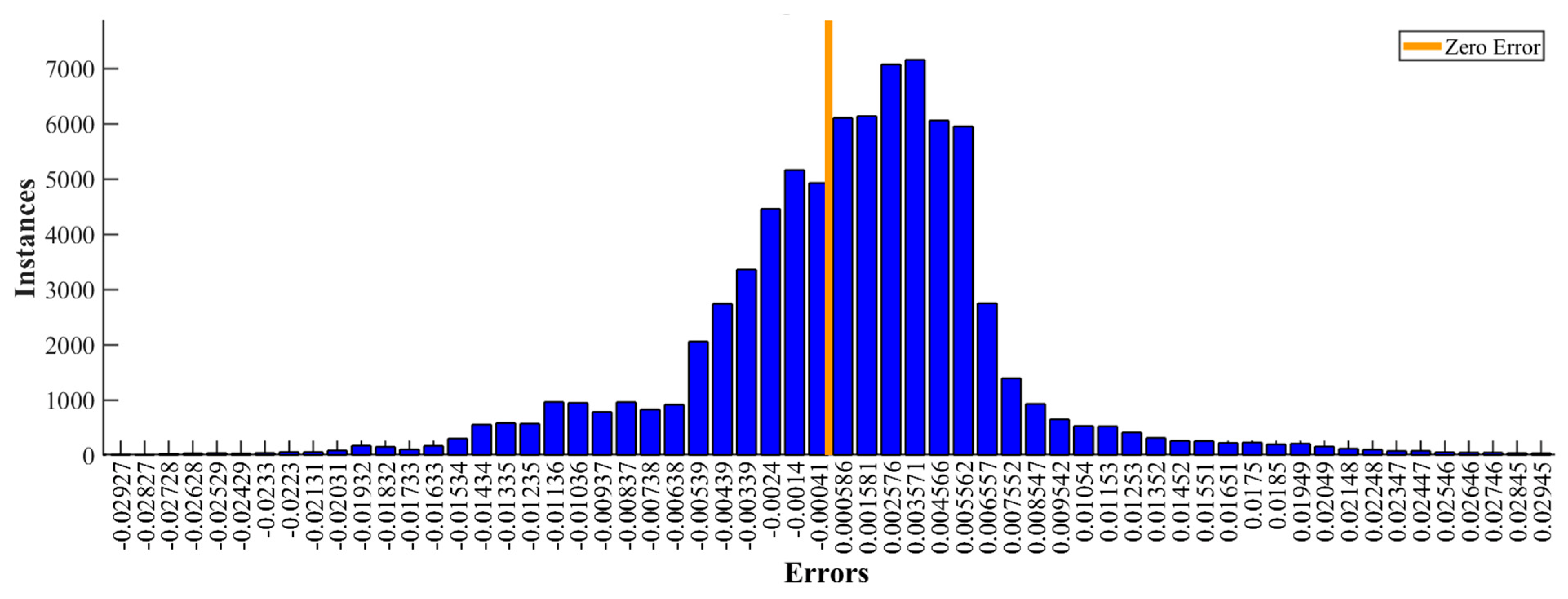
3.3. Virtual Sensor Validation and Testing
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Campbell, S.; O’Mahony, N.; Krpalcova, L.; Riordan, D.; Walsh, J.; Murphy, A.; Ryan, C. Sensor Technology in Autonomous Vehicles: A review. In Proceedings of the 29th Irish Signals and Systems Conference, Belfast, UK, 21–22 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kocić, J.; Jovičić, N.; Drndarević, V. Sensors and Sensor Fusion in Autonomous Vehicles. In Proceedings of the 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 420–425. [Google Scholar] [CrossRef]
- Marti, E.; de Miguel, M.A.; Garcia, F.; Perez, J. A Review of Sensor Technologies for Perception in Automated Driving. IEEE Intell. Transp. Syst. Mag. 2019, 11, 94–108. [Google Scholar] [CrossRef] [Green Version]
- Pinchon, N.; Cassignol, O.; Nicolas, A.; Bernardin, F.; Leduc, P.; Tarel, J.P.; Brémond, P.; Bercier, E.; Brunet, J. All-Weather Vision for Automotive Safety: Which Spectral Band? In Advanced Microsystems for Automotive Applications 2018. AMAA 2018; Lecture Notes in Mobility; Dubbert, J., Muller, B., Meyer, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–15. [Google Scholar] [CrossRef] [Green Version]
- Skrickij, V.; Šabanovič, E.; Shi, D.; Ricci, S.; Rizzetto, L.; Bureika, G. Visual Measurement System for Wheel–Rail Lateral Position Evaluation. Sensors 2021, 21, 1297. [Google Scholar] [CrossRef] [PubMed]
- Kerst, S.; Shyrokau, B.; Holweg, E. Reconstruction of wheel forces using an intelligent bearing. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2016, 9, 196–203. [Google Scholar] [CrossRef]
- Iyer, K.; Shyrokau, B.; Ivanov, V. Offline and Online Tyre Model Reconstruction by Locally Weighted Projection Regression. In Proceedings of the IEEE 16th International Workshop on Advanced Motion Control (AMC), Campus Kristiansand, Kristiansand, Norway, 20–22 April 2020; pp. 311–316. [Google Scholar] [CrossRef]
- Kabadayi, S.; Pridgen, A.; Julien, C. Virtual sensors: Abstracting data from physical sensors. In Proceedings of the International Symposium on a World of Wireless, Mobile and Multimedia Networks, Buffalo-Niagara Falls, NY, USA, 26–29 June 2006; pp. 587–592. [Google Scholar] [CrossRef] [Green Version]
- Martin, D.; Kuhl, N.; Satzger, G. Virtual Sensors. Bus. Inf. Syst. Eng. 2021, 63, 315–323. [Google Scholar] [CrossRef]
- Li, H.; Yu, D.; Braun, J.E. A review of virtual sensing technology and application in building systems. HVAC&R Res. 2011, 17, 619–645. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Z.; Xiong, B.; Vilathgamuwa, D.M. Adaptive Ensemble-Based Electrochemical-Thermal-Degradation State Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Kerst, S.; Shyrokau, B.; Holweg, E. A Model-based approach for the estimation of bearing forces and moments using outer ring deformation. IEEE Trans. Ind. Electron. 2019, 67, 461–470. [Google Scholar] [CrossRef]
- Wei, Z.; Hu, J.; He, H.; Li, Y.; Xiong, B. Load Current and State-of-Charge Coestimation for Current Sensor-Free Lithium-Ion Battery. IEEE Trans. Power Electron. 2021, 36, 10970–10975. [Google Scholar] [CrossRef]
- Mattera, C.G.; Quevedo, J.; Escobet, T.; Shaker, H.R.; Jradi, M. A Method for Fault Detection and Diagnostics in Ventilation Units Using Virtual Sensors. Sensors 2018, 18, 3931. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hensel, B.; Kabitzsch, K. Generator for modular virtual sensors. In Proceedings of the IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 6–9 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, W.; Gao, S.; He, X.; Lu, J. Sensor Fault Diagnosis of Autonomous Underwater Vehicle Based on LSTM. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 6067–6072. [Google Scholar] [CrossRef]
- Kerst, S.; Shyrokau, B.; Holweg, E. A semi-analytical bearing model considering outer race flexibility for model based bearing load monitoring. Mech. Syst. Signal Process. 2018, 104, 384–397. [Google Scholar] [CrossRef]
- Acosta, R.M.; Kanarachos, S.; Fitzpatrick, M. A Virtual Sensor for Integral Tire Force Estimation using Tire Model-Less Approaches and Adaptive Unscented Kalman Filter. In Proceedings of the 14th International Conference on Informatics in Control, Automatics and Robotics, Madrid, Spain, 26–28 July 2017. [Google Scholar] [CrossRef]
- Zaharia, C.; Clenci, A. Study on Virtual Sensors and Their Automotive Applications. Sci. Bull. Automot. Ser. 2013, 23, 68–74. Available online: https://automotive.upit.ro/index_files/2013/2013_A_8_.pdf (accessed on 15 May 2021).
- Kahraman, K.; Emirler, T.M.; Centürk, M.; Güvenç, B.A.; Güvenç, L.; Efendioĝlu, B. Estimation of Vehicle Yaw Rate Using a Virtual Sensor with a Speed Scheduled Observer. IFAC Proc. Vol. 2010, 43, 632–637. [Google Scholar] [CrossRef]
- Skrickij, V.; Savitski, D.; Ivanov, V.; Skačkauskas, P. Investigation of Cavitation Process in Monotube Shock Absorber. Int. J. Automot. Technol. 2018, 19, 801–810. [Google Scholar] [CrossRef]
- Ricciardi, V.; Ivanov, V.; Dhaens, M.; Vandersmissen, B.; Geraerts, M.; Savitski, D.; Augsburg, K. Ride Blending Control for Electric Vehicles. World Electr. Veh. J. 2019, 10, 36. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, M.Q.; Canale, M.; Sename, O.; Dugard, L. A Model Predictive Control approach for semi-active suspension control problem of a full car. In Proceedings of the IEEE 55th Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 2016; pp. 721–726. [Google Scholar] [CrossRef] [Green Version]
- Milanese, M.; Ruiz, F.; Taragna, M. Linear virtual sensors for vertical dynamics of vehicles with controlled suspensions. In Proceedings of the European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 1257–1263. [Google Scholar] [CrossRef]
- Pletschen, N.; Badur, P. Nonlinear State Estimation in Suspension Control Based on Takagi-Sugeno Model. IFAC Proc. Vol. 2014, 47, 11231–11237. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Dong, M.; Qin, Y.; Du, Y.; Zhao, F.; Gu, L. Suspension system state estimation using adaptive Kalman filtering based on road classification. Veh. Syst. Dyn. 2017, 55, 371–398. [Google Scholar] [CrossRef]
- Jeong, K.; Choi, S.B. Vehicle Suspension Relative Velocity Estimation Using a Single 6-D IMU Sensor. IEEE Trans. Veh. Technol. 2019, 68, 7309–7318. [Google Scholar] [CrossRef]
- Vazquez, A.G.A.; Vaseur, C.; Correa-Victorino, A.; Charara, A. Road profile and suspension state estimation boosted with vehicle dynamics conjectures. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1809–1815. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Liu, S. Mechanical State Prediction Based on LSTM Neural Network. In Proceedings of the 36th Chinese Control Conference (CCC), Dialan, China, 26–28 July 2017. [Google Scholar] [CrossRef]
- Abdelgawad, N.E.A.; El Mahdy, A.; Gomaa, W.; Shoukry, A. Estimating Vehicle Speed on Highway Roads from Smartphone Sensors Using Deep Learning Models. In Proceedings of the IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 979–986. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, W.; Zou, S.; Zhang, H.; Luan, Z. A Reliable Vehicle Lateral Velocity Estimation Methodology based on SBI-LSTM during GPS-outage. IEEE Sens. J. 2020, 21, 15485–15495. [Google Scholar] [CrossRef]
- Vaseur, C.; Van Aalst, S. Test Results at Ford Lommel Proving Ground ESR 11 (Version Final) [Data Set]; Interdisciplinary Training Network in Multi-Actuated Ground Vehicles: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- ISO 3888-2:2011. Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre—Part 2: Obstacle Avoidance Manoeuvre; International Organization for Standardization: Geneva, Switzerland; Available online: https://www.iso.org/standard/57253.html (accessed on 20 May 2021).


| Parameter | Symbol | Value |
|---|---|---|
| Wheelbase | L | 2.675 m |
| Distance between front axle and COG | b | 1.439 m |
| Distance between rear axle and COG | a | 1.236 m |
| Height of COG above ground | h | 0.65 m |
| Vehicle mass | m | 2442 kg |
| Total unsprung mass | mu | 126.2 kg |
| Distance between left track and COG | d | 0.778 m |
| Distance between right track and COG | c | 0.847 m |
| Track width | T | 1.625 m |
| Wheel rotational inertia | J | 0.9 kg m2 |
| Tire stiffness | Kt | 225,368 N/m |
| Loaded tire radius | Rl | 0.343 m |
| Tire size | 235/55/R19 | |
| Pitch inertia | 642.3 kg m2 | |
| Roll inertia | 2892 kg m2 | |
| Yaw inertia | 3231 kg m2 |
| Input Parameters | Output Parameters | ||||
|---|---|---|---|---|---|
| Input Nr. | Name | Units | Output Nr. | Name | Units |
| 1 | Sprung mass acceleration (X axis) | m/s2 | 1 | Unsprung mass relative velocity (Z axis) front left | m/s |
| 2 | Sprung mass acceleration (Y axis) | m/s2 | 2 | Unsprung mass relative velocity (Z axis) front right | m/s |
| 3 | Sprung mass acceleration (Z axis) | m/s2 | 3 | Unsprung mass relative velocity (Z axis) rear left | m/s |
| 4 | Sprung mass angular rate (X axis) | deg/s | 4 | Unsprung mass relative velocity (Z axis) rear right | m/s |
| 5 | Sprung mass angular rate (Y axis) | deg/s | |||
| 6 | Sprung mass angular rate (Z axis) | deg/s | |||
| 7 | Vehicle’s longitudinal velocity | m/s | |||
| 8 | Steering angle of front left wheel | deg | |||
| 9 | Steering angle of front right wheel | deg | |||
| 10 | Wheel speed of front left wheel | m/s | |||
| 11 | Wheel speed of front right wheel | m/s | |||
| 12 | Wheel speed of rear left wheel | m/s | |||
| 13 | Wheel speed of rear right wheel | m/s | |||
| 14 | Vehicle’s steering angle | deg | |||
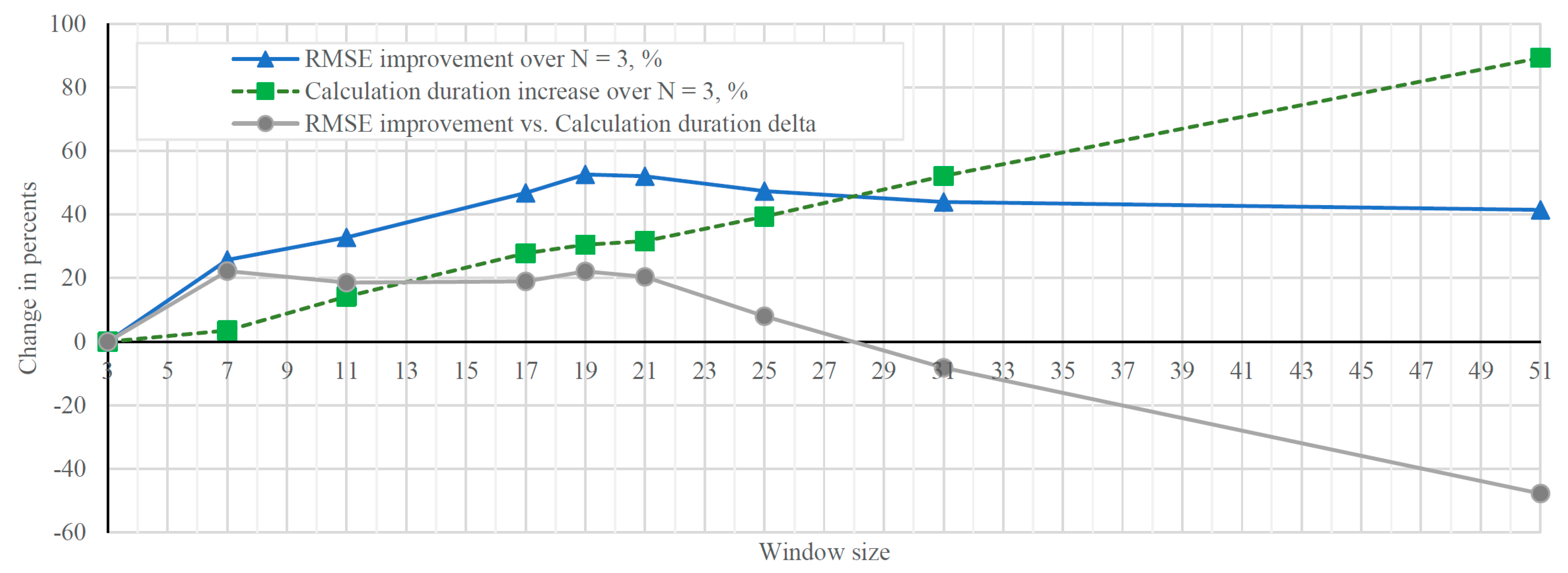
| Window Size | Selected Parameters | RMSE | Relative Error, % | Calculation Duration, ms/Sample | Relative Calculation Duration, % | |
|---|---|---|---|---|---|---|
| BiLSTM Units | FC Units | |||||
| 3 | 360 | 403 | 0.0171 | 100.0 | 1.89 | 100.0 |
| 7 | 502 | 295 | 0.0127 | 74.3 | 1.96 | 103.5 |
| 11 | 202 | 312 | 0.0115 | 67.3 | 2.16 | 114.2 |
| 17 | 512 | 111 | 0.0091 | 53.2 | 2.42 | 127.8 |
| 19 | 167 | 256 | 0.0081 | 47.4 | 2.47 | 130.5 |
| 21 | 137 | 298 | 0.0082 | 48.0 | 2.49 | 131.6 |
| 25 | 207 | 511 | 0.0090 | 52.6 | 2.63 | 139.4 |
| 31 | 116 | 345 | 0.0096 | 56.1 | 2.88 | 152.1 |
| 51 | 137 | 298 | 0.0100 | 58.5 | 3.58 | 189.3 |
| Scenario | RMSE | Accuracy, % | ||||
|---|---|---|---|---|---|---|
| FL | FR | RL | RR | Overall | ||
| Heilbronn track, Aggressive driver (training) | 0.0034 | 0.0033 | 0.0035 | 0.0034 | 0.0034 | 96.5 |
| Heilbronn track, Offensive driver (training) | 0.0021 | 0.0020 | 0.0021 | 0.0020 | 0.0021 | 97.5 |
| Heilbronn track, Normal driver (training) | 0.0027 | 0.0026 | 0.0027 | 0.0026 | 0.0027 | 97.1 |
| Rural track, Aggressive driver (training) | 0.0068 | 0.0069 | 0.0072 | 0.0071 | 0.0070 | 94.1 |
| Rural track, Offensive driver (training) | 0.0027 | 0.0028 | 0.0028 | 0.0029 | 0.0028 | 96.9 |
| Rural track, Normal driver (training) | 0.0045 | 0.0046 | 0.0042 | 0.0044 | 0.0044 | 96.0 |
| Hockenheimring track, Aggressive driver (validation) | 0.0167 | 0.0180 | 0.0157 | 0.0158 | 0.0166 | 92.4 |
| Hockenheimring track, Offensive driver (validation) | 0.0053 | 0.0054 | 0.0046 | 0.0050 | 0.0051 | 96.7 |
| Hockenheimring track, Normal driver (validation) | 0.0086 | 0.0091 | 0.0070 | 0.0078 | 0.0081 | 95.8 |
| Constant turn with radius of 100 m at 50 km/h (testing) | 0.0013 | 0.0013 | 0.0013 | 0.0013 | 0.0013 | 98.9 |
| Constant turn with radius of 100 m at 75 km/h (testing) | 0.0025 | 0.0036 | 0.0044 | 0.0041 | 0.0037 | 97.5 |
| Constant turn with radius of 100 m at 100 km/h (testing) | 0.0393 | 0.0296 | 0.0500 | 0.0500 | 0.0431 | 69.4 |
| Constant turn with radius of 30 m at 30 km/h (testing) | 0.0008 | 0.0011 | 0.0011 | 0.0011 | 0.0010 | 98.5 |
| Constant turn with radius of 30 m at 50 km/h (testing) | 0.0148 | 0.0125 | 0.0189 | 0.0203 | 0.0169 | 81.0 |
| Constant turn with radius of 60 m at 50 km/h (testing) | 0.0008 | 0.0010 | 0.0012 | 0.0012 | 0.0011 | 99.0 |
| Constant turn with radius of 60 m at 75 km/h (testing) | 0.0313 | 0.0252 | 0.0397 | 0.0411 | 0.0349 | 68.4 |
| Double lane change (ISO-3888-2) at 30 km/h (testing) | 0.0014 | 0.0013 | 0.0017 | 0.0014 | 0.0015 | 97.6 |
| Sine with Dwell 60 deg at 40 km/h (testing) | 0.0029 | 0.0020 | 0.0031 | 0.0022 | 0.0026 | 97.2 |
| Sine with Dwell 60 deg at 60 km/h (testing) | 0.0101 | 0.0061 | 0.0108 | 0.0067 | 0.0087 | 93.3 |
| Sine with Dwell 60 deg at 80 km/h (testing) | 0.0189 | 0.0133 | 0.0203 | 0.0138 | 0.0169 | 90.3 |
| Sine with Dwell 80 deg at 40 km/h (testing) | 0.0037 | 0.0028 | 0.0043 | 0.0025 | 0.0034 | 96.3 |
| Sine with Dwell 80 deg at 60 km/h (testing) | 0.0130 | 0.0081 | 0.0145 | 0.0081 | 0.0113 | 91.7 |
| Sine with Dwell 60 deg at 80 km/h (testing) | 0.0284 | 0.0226 | 0.0312 | 0.0231 | 0.0266 | 84.8 |
| Bumpy road at 15 km/h (testing) | 0.0154 | 0.0164 | 0.0209 | 0.0146 | 0.0170 | 75.1 |
| Bumpy road at 25 km/h (testing) | 0.0223 | 0.0236 | 0.0298 | 0.0209 | 0.0223 | 77.9 |
| Bumpy road at 32 km/h (testing) | 0.0347 | 0.0359 | 0.0472 | 0.0390 | 0.0395 | 74.3 |
| Slalom 18 m at 15 km/h (testing) | 0.0013 | 0.0014 | 0.0016 | 0.0013 | 0.0014 | 96.2 |
| Slalom 18 m at 25 km/h (testing) | 0.0012 | 0.0013 | 0.0013 | 0.0012 | 0.0012 | 98.8 |
| Slalom 18 m at 35 km/h (testing) | 0.0025 | 0.0017 | 0.0024 | 0.0019 | 0.0021 | 97.5 |
| Accuracy of all tracks combined | 91.2 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šabanovič, E.; Kojis, P.; Šukevičius, Š.; Shyrokau, B.; Ivanov, V.; Dhaens, M.; Skrickij, V. Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation. Sensors 2021, 21, 7139. https://doi.org/10.3390/s21217139
Šabanovič E, Kojis P, Šukevičius Š, Shyrokau B, Ivanov V, Dhaens M, Skrickij V. Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation. Sensors. 2021; 21(21):7139. https://doi.org/10.3390/s21217139
Chicago/Turabian StyleŠabanovič, Eldar, Paulius Kojis, Šarūnas Šukevičius, Barys Shyrokau, Valentin Ivanov, Miguel Dhaens, and Viktor Skrickij. 2021. "Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation" Sensors 21, no. 21: 7139. https://doi.org/10.3390/s21217139
APA StyleŠabanovič, E., Kojis, P., Šukevičius, Š., Shyrokau, B., Ivanov, V., Dhaens, M., & Skrickij, V. (2021). Feasibility of a Neural Network-Based Virtual Sensor for Vehicle Unsprung Mass Relative Velocity Estimation. Sensors, 21(21), 7139. https://doi.org/10.3390/s21217139










