Depth Data Denoising in Optical Laser Based Sensors for Metal Sheet Flatness Measurement: A Deep Learning Approach
Abstract
:1. Introduction
2. Industrial Context
Actual Sensor Installation
3. Noise Model for Synthetic Data Generation
4. Deep Learning Denoising Approaches
5. Proposed Deep Learning Image Denoising Architecture
5.1. Network Architecture
5.2. Training the Model
6. Dataset
6.1. Real Production Line Data
7. Results
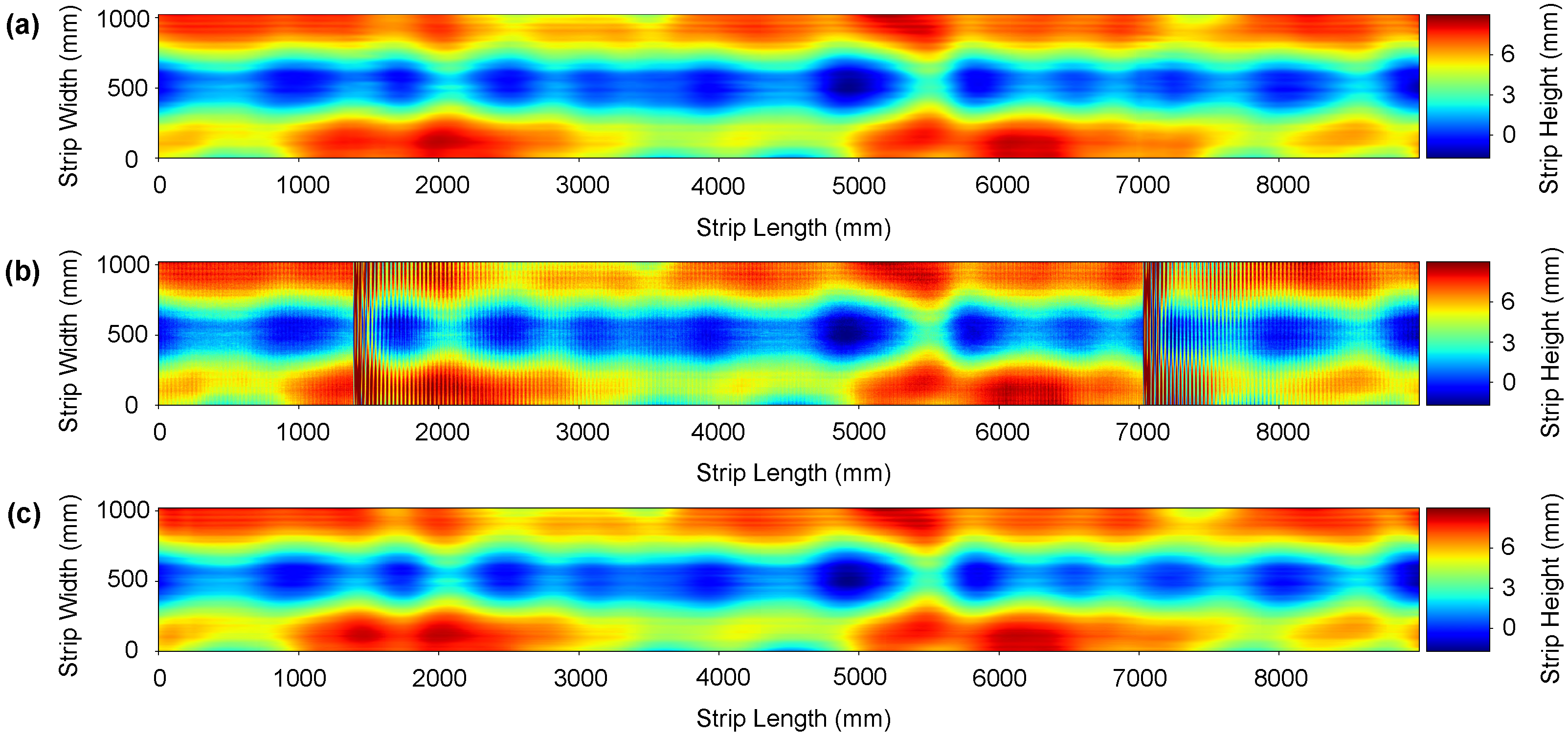
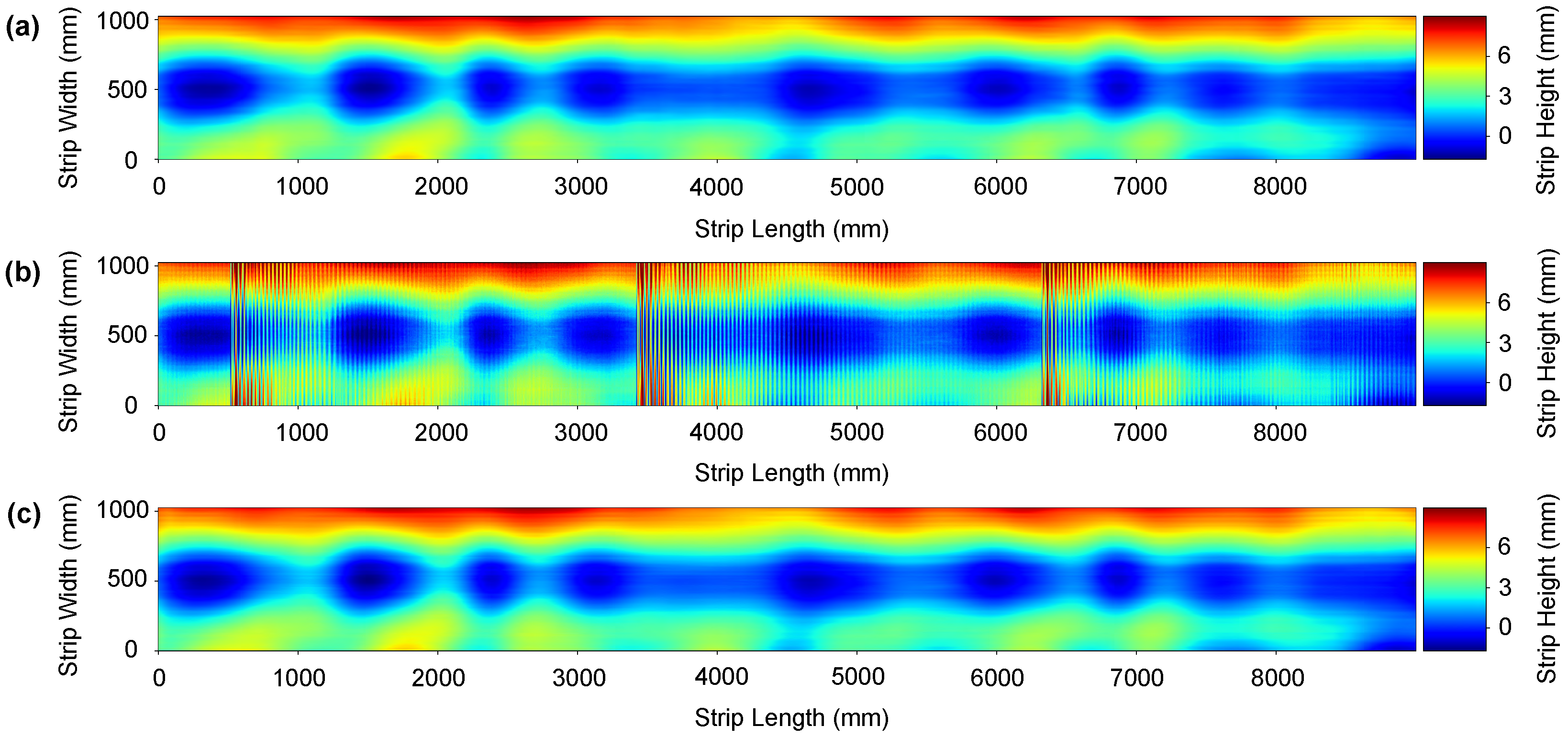
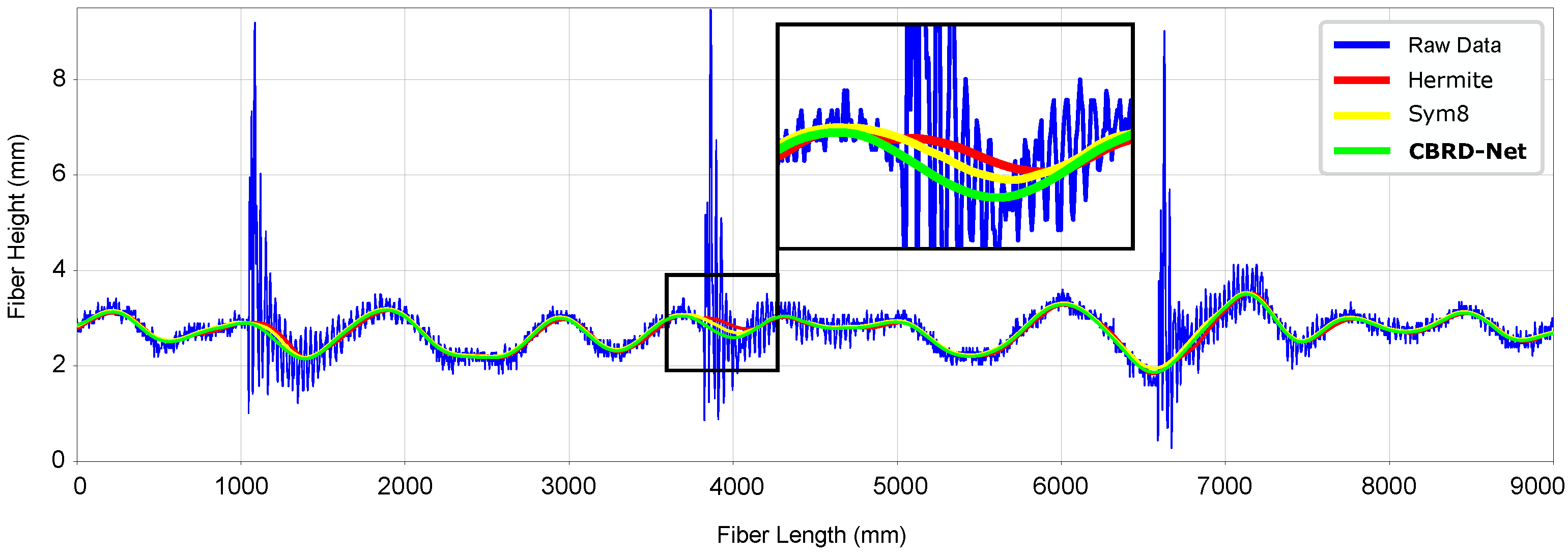
7.1. Synthetic Data Results
7.2. Real Data Results
7.3. Ablation Studies
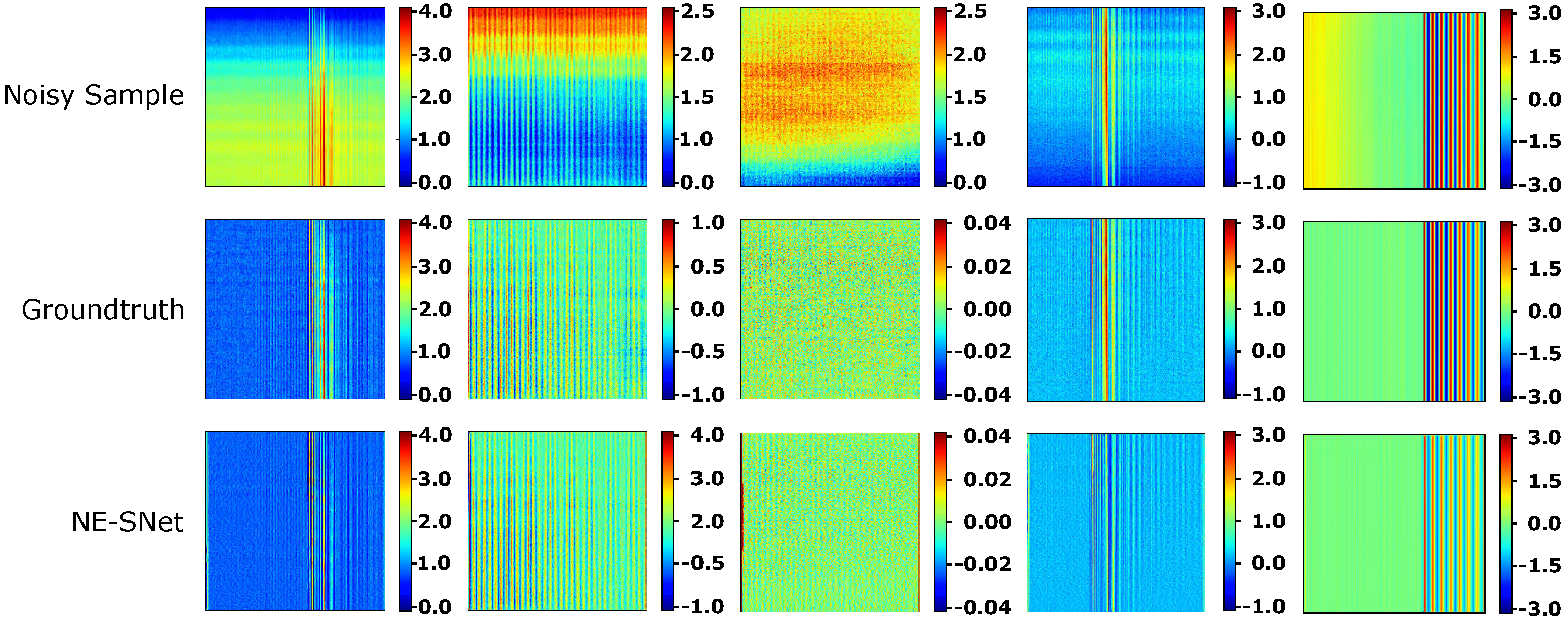
7.3.1. Effect of the NE-SNet Subnetwork
7.3.2. Effect of Synthetic and Real Data
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| DAE | Denoising Autoencoders |
| CDAE | Convolutional Denoising Autoencoders |
| GAN | Generative Adversarial Network |
| SGD | Stochastic Gradient Descent |
| CBRDNet | Convolutional Blind Residual Denoising Network |
| NE-SNet | Noise Estimation Subnetwork |
| NR-SNet | Noise Removal Subnetwork |
| ADAM | Adaptive Moment Estimation |
| ReLU | Rectified Linear Unit |
| BN | Batch Normalization |
| Conv2D | 2D Convolution Layer |
| HSLA | High-Strength Low-Alloy |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| MaxAE | Maximum Absolute Error |
| STD | Standard Deviation |
| RMSE | Root Mean Squared Error |
| CMM | Coordinate Measuring Machine |
| Db | Daubechies |
| Coif | Coiflets |
| Sym | Symlets |
| Fk | Fejer-Korovkin |
| Dmey | Meyer |
References
- Jouet, J.; Francois, G.; Tourscher, G.; de Lamberterie, B. Automatic flatness control at Solmer hot strip mill using the Lasershape sensor. Iron Steel Eng. 1988, 65, 50–56. [Google Scholar]
- Chiarella, M.; Pietrzak, K.A. An Accurate Calibration Technique for 3D Laser Stripe Sensors. In Optics, Illumination, and Image Sensing for Machine Vision IV; Svetkoff, D.J., Ed.; International Society for Optics and Photonics, SPIE, Bellingham: Washington, CA, USA, 1990; Volume 1194, pp. 176–185. [Google Scholar] [CrossRef]
- Álvarez, H.; Alonso, M.; Sánchez, J.R.; Izaguirre, A. A Multi Camera and Multi Laser Calibration Method for 3D Reconstruction of Revolution Parts. Sensors 2021, 21, 765. [Google Scholar] [CrossRef]
- Siekański, P.; Magda, K.; Malowany, K.; Rutkiewicz, J.; Styk, A.; Krzesłowski, J.; Kowaluk, T.; Zagórski, A. On-line laser triangulation scanner for wood logs surface geometry measurement. Sensors 2019, 19, 1074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kierkegaard, P.; Classon, L.A. A new-generation optical flatness measurement system. Iron Steel Technol. 2015, 12, 76–81. [Google Scholar]
- Kierkegaard, P. Developments and Benefits from Optical Flatness Measurement in Strip Processing Lines. In Proceedings of the Congreso y Exposición Nacional de la Industria del Acero, CONAC, Monterrey, Mexico, 8–20 November 2016; pp. 1–15. [Google Scholar]
- Pernkopf, F. 3D surface acquisition and reconstruction for inspection of raw steel products. Comput. Ind. 2005, 56, 876–885. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Molleda, J.; Garcia, D.F.; Bulnes, F.G. Removing vibrations in 3D reconstruction using multiple laser stripes. Opt. Lasers Eng. 2014, 53, 51–59. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Garcia, D.F. Robust registration for removing vibrations in 3D reconstruction of web material. Opt. Lasers Eng. 2015, 68, 135–148. [Google Scholar] [CrossRef]
- Alonso, M.; Izaguirre, A.; Andonegui, I.; Graña, M. Optical Dual Laser Based Sensor Denoising for Online Metal Sheet Flatness Measurement Using Hermite Interpolation. Sensors 2020, 20, 5441. [Google Scholar] [CrossRef]
- Alonso, M.; Izaguirre, A.; Andonegui, I.; Graña, M. An Application of Laser Measurement to On-Line Metal Strip Flatness Measurement. In Proceedings of the 15th International Conference on Soft Computing Models in Industrial and Environmental Applications (SOCO 2020), Burgos, Spain, 16–18 September 2020; Springer International Publishing: Cham, Switzerland, 2021; pp. 835–842. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Borselli, A.; Colla, V.; Vannucci, M.; Veroli, M. A fuzzy inference system applied to defect detection in flat steel production. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Borselli, A.; Colla, V.; Vannucci, M. Surface Defects Classification in Steel Products: A Comparison between Different Artificial Intelligence-based Approaches. In Proceedings of the 11th IASTED International Conference on Artificial Intelligence and Applications, AIA 2011, Innsbruck, Austria, 14–16 February 2011. [Google Scholar] [CrossRef]
- Xu, K.; Xu, Y.; Zhou, P.; Wang, L. Application of RNAMlet to surface defect identification of steels. Opt. Lasers Eng. 2018, 105, 110–117. [Google Scholar] [CrossRef]
- Brandenburger, J.; Colla, V.; Nastasi, G.; Ferro, F.; Schirm, C.; Melcher, J. Big Data Solution for Quality Monitoring and Improvement on Flat Steel Production. IFAC-PapersOnLine 2016, 49, 55–60. [Google Scholar] [CrossRef]
- Appio, M.; Ardesi, A.; Lugnan, A. Automatic Surface Inspection in Steel Products ensures Safe, Cost-Efficient and Timely Defect Detection in Production. In Proceedings of the AISTech-Iron and Steel Technology Conference, São Paulo, Brazil, 2–4 October 2018; pp. 89–101. [Google Scholar] [CrossRef]
- Graña, M.; Alonso, M.; Izaguirre, A. A Panoramic Survey on Grasping Research Trends and Topics. Cybern. Syst. 2019, 50, 40–57. [Google Scholar] [CrossRef]
- Chong, E.; Han, C.; Park, F. Deep Learning Networks for Stock Market Analysis and Prediction: Methodology, Data Representations, and Case Studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.W.; Lin, X. Big Data Deep Learning: Challenges and Perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Villanustre, F.; Khoshgoftaar, T.M.; Seliya, N.; Wald, R.; Muharemagic, E. Deep learning applications and challenges in big data analytics. J. Big Data 2015, 2, 1. [Google Scholar] [CrossRef] [Green Version]
- Affonso, C.; Rossi, A.L.D.; Vieira, F.H.A.; de Leon Ferreira de Carvalho, A.C.P. Deep learning for biological image classification. Expert Syst. Appl. 2017, 85, 114–122. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Geng, J.; Su, Z.; Zhang, W.; Li, J. Real-Time Classification of Steel Strip Surface Defects Based on Deep CNNs. In Proceedings of the 2018 Chinese Intelligent Systems Conference, Vol II; Springer: Singapore, 2019; pp. 257–266. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Peng, L.; An, R.; Jin, X. Application of convolutional neural networks for prediction of strip flatness in tandem cold rolling process. J. Manuf. Process. 2021, 68, 512–522. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length, and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 1994, 6, 3–10. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [Green Version]
- Bank, D.; Koenigstein, N.; Giryes, R. Autoencoders. arXiv 2021, arXiv:2003.05991. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and Composing Robust Features with Denoising Autoencoders. In Proceedings of the 25th International Conference on Machine Learning, ICML’08, Helsinki, Finland, 5–9 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 1096–1103. [Google Scholar] [CrossRef] [Green Version]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2017, arXiv:1609.04747. [Google Scholar]
- Gondara, L. Medical Image Denoising Using Convolutional Denoising Autoencoders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; IEEE Computer Society: Los Alamitos, CA, USA, 2016; pp. 241–246. [Google Scholar] [CrossRef] [Green Version]
- Masci, J.; Meier, U.; Cireşan, D.; Schmidhuber, J. Stacked Convolutional Auto-Encoders for Hierarchical Feature Extraction. In Proceedings of the Artificial Neural Networks and Machine Learning—ICANN 2011, Espoo, Finland, 14–17 June 2011; Honkela, T., Duch, W., Girolami, M., Kaski, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 52–59. [Google Scholar]
- Li, H.; Xu, Z.; Taylor, G.; Goldstein, T. Visualizing the Loss Landscape of Neural Nets. arXiv 2017, arXiv:1712.09913. [Google Scholar]
- Roy, H.; Chaudhury, S.; Yamasaki, T.; DeLatte, D.; Ohtake, M.; Hashimoto, T. Lunar surface image restoration using U-net based deep neural networks. arXiv 2019, arXiv:1904.06683. [Google Scholar]
- Lee, S.; Negishi, M.; Urakubo, H.; Kasai, H.; Ishii, S. Mu-net: Multi-scale U-net for two-photon microscopy image denoising and restoration. Neural Netw. 2020, 125, 92–103. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, R.; Gonsalves, T. Comparing U-Net Based Models for Denoising Color Images. AI 2020, 1, 465–486. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef] [Green Version]
- Jansson, A.; Humphrey, E.; Montecchio, N.; Bittner, R.; Kumar, A.; Weyde, T. Singing voice separation with deep U-Net convolutional networks. In Proceedings of the 18th International Society for Music Information Retrieval Conference, Suzhou, China, 23–27 October 2017. [Google Scholar]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward Convolutional Blind Denoising of Real Photographs. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 1712–1722. [Google Scholar]
- Guo, B.; Song, K.; Dong, H.; Yan, Y.; Tu, Z.; Zhu, L. NERNet: Noise estimation and removal network for image denoising. J. Vis. Commun. Image Represent. 2020, 71, 102851. [Google Scholar] [CrossRef]
- Tian, C.; Xu, Y.; Zuo, W. Image denoising using deep CNN with batch renormalization. Neural Netw. 2020, 121, 461–473. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [Green Version]
- Buades, A.; Coll, B.; Morel, J.M. A Review of Image Denoising Algorithms, with a New One. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Limshuebchuey, A.; Duangsoithong, R.; Saejia, M. Comparison of Image Denoising using Traditional Filter and Deep Learning Methods. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 193–196. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief review of image denoising techniques. Vis. Comput. Ind. Biomed. Art 2019, 2, 7. [Google Scholar] [CrossRef] [Green Version]
- Testolin, A.; Stoianov, I.; De Filippo De Grazia, M.; Zorzi, M. Deep Unsupervised Learning on a Desktop PC: A Primer for Cognitive Scientists. Front. Psychol. 2013, 4, 251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, H.; Grosse, R.; Ranganath, R.; Ng, A. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; p. 77. [Google Scholar] [CrossRef]
- Lan, R.; Zou, H.; Pang, C.; Zhong, Y.; Liu, Z.; Luo, X. Image denoising via deep residual convolutional neural networks. Signal Image Video Process. 2021, 15, 1–8. [Google Scholar] [CrossRef]
- Seib, V.; Lange, B.; Wirtz, S. Mixing Real and Synthetic Data to Enhance Neural Network Training—A Review of Current Approaches. arXiv 2020, arXiv:2007.08781. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; Volume 1502. [Google Scholar] [CrossRef] [Green Version]
- Masters, D.; Luschi, C. Revisiting Small Batch Training for Deep Neural Networks. arXiv 2018, arXiv:1804.07612. [Google Scholar]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- ASTM International. ASTM A1030/A1030M-11, Measuring Flatness Characteristics of Steel Sheet Products, Standard Practice for; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Butterworth, S. On the theory of filter amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Oppenheim, A.; Schafer, R.; Buck, J.; Lee, L. Discrete-Time Signal Processing, Prentice Hall international editions; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Schafer, R.W. What Is a Savitzky-Golay Filter? [Lecture Notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Weinberg, L.; Slepian, P. Takahasi’s Results on Tchebycheff and Butterworth Ladder Networks. IRE Trans. Circuit Theory 1960, 7, 88–101. [Google Scholar] [CrossRef]
- Daubechies, I. Ten Lectures on Wavelets; Society for Industrial and Applied Mathematics, 3600 University City Science Center: Philadelphia, PA, USA, 1992. [Google Scholar]
- Meyer, Y. Ondelettes et Opérateurs; Number v. 1 in Actualités Mathématiques: Hermann, MS, USA, 1990. [Google Scholar]
- Nielsen, M. On the Construction and Frequency Localization of Finite Orthogonal Quadrature Filters. J. Approx. Theory 2001, 108, 36–52. [Google Scholar] [CrossRef] [Green Version]
- ASTM International. ASTM A568/A568M-17a, Standard Specification for Steel, Sheet, Carbon, Structural, and High-Strength, Low-Alloy, Hot-Rolled and Cold-Rolled, General Requirements for; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Peng, Z.; Wang, G. Study on Optimal Selection of Wavelet Vanishing Moments for ECG Denoising. Sci. Rep. 2017, 7, 4564. [Google Scholar] [CrossRef] [PubMed]
- Galiano, G.; Velasco, J. On a nonlocal spectrogram for denoising one-dimensional signals. Appl. Math. Comput. 2014, 244, 859–869. [Google Scholar] [CrossRef] [Green Version]


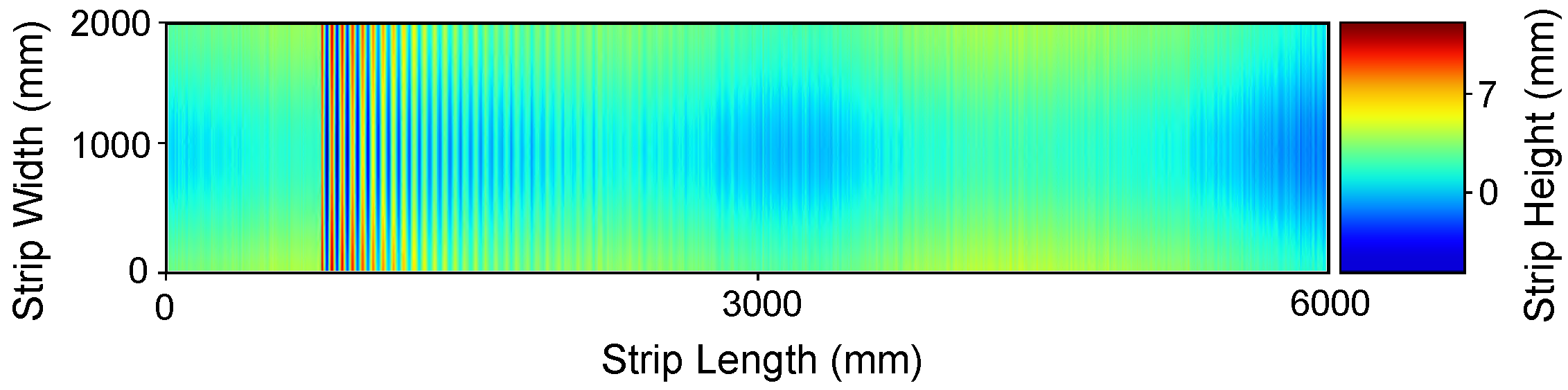
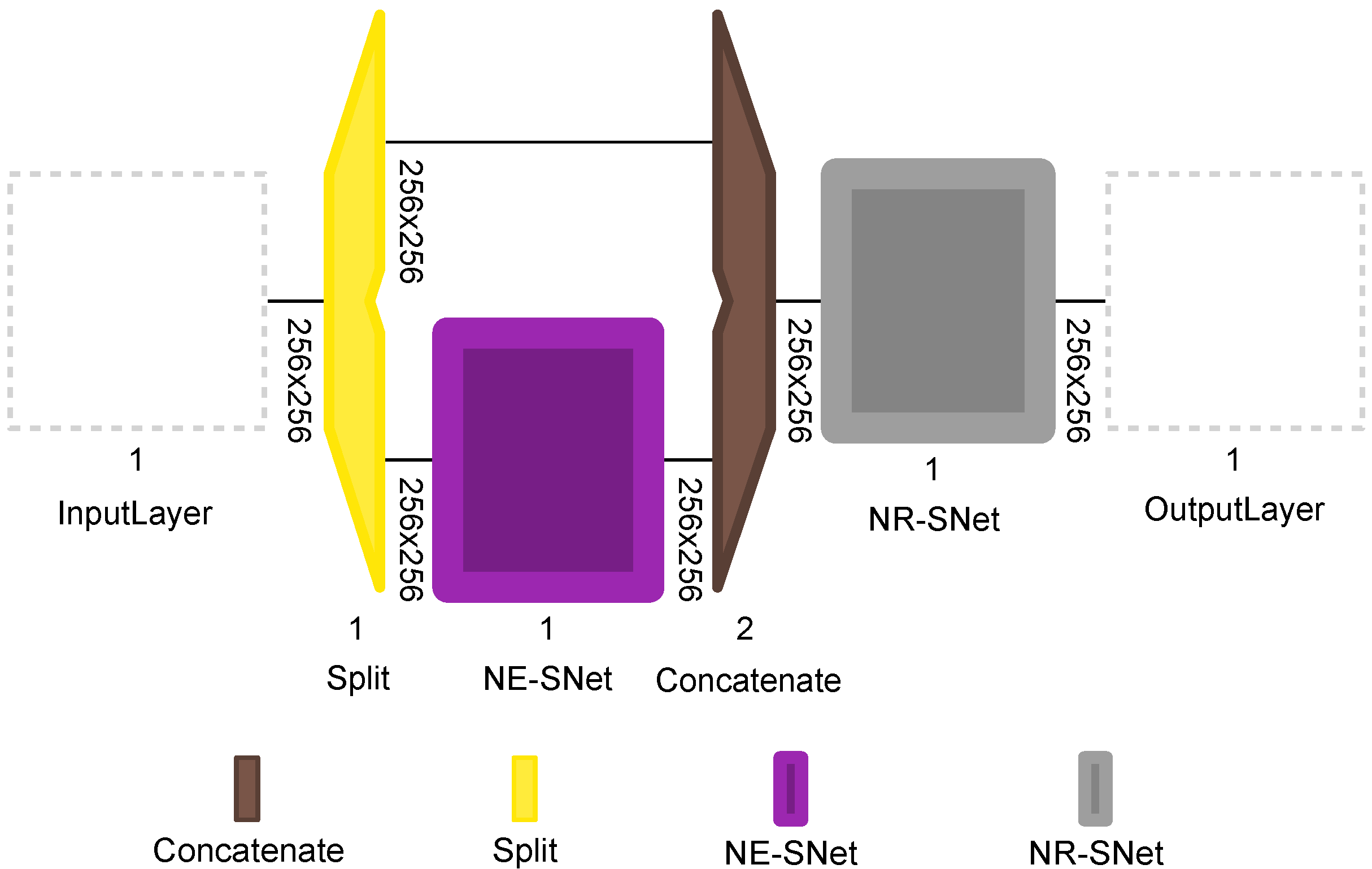
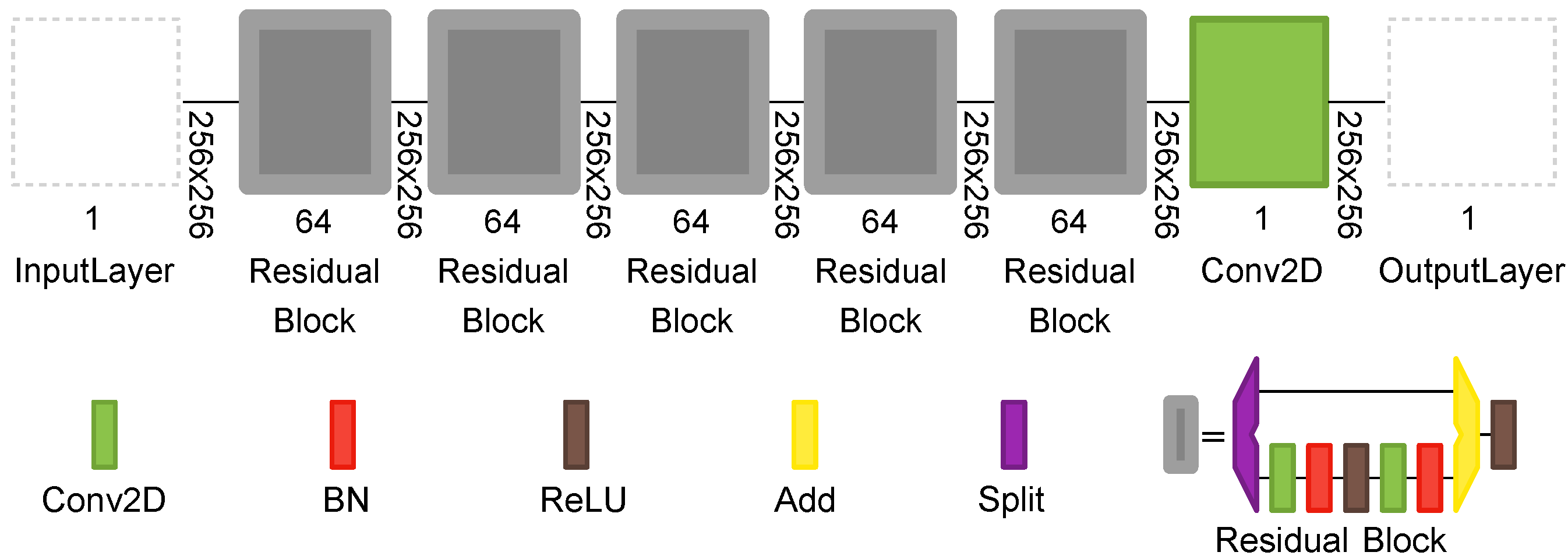
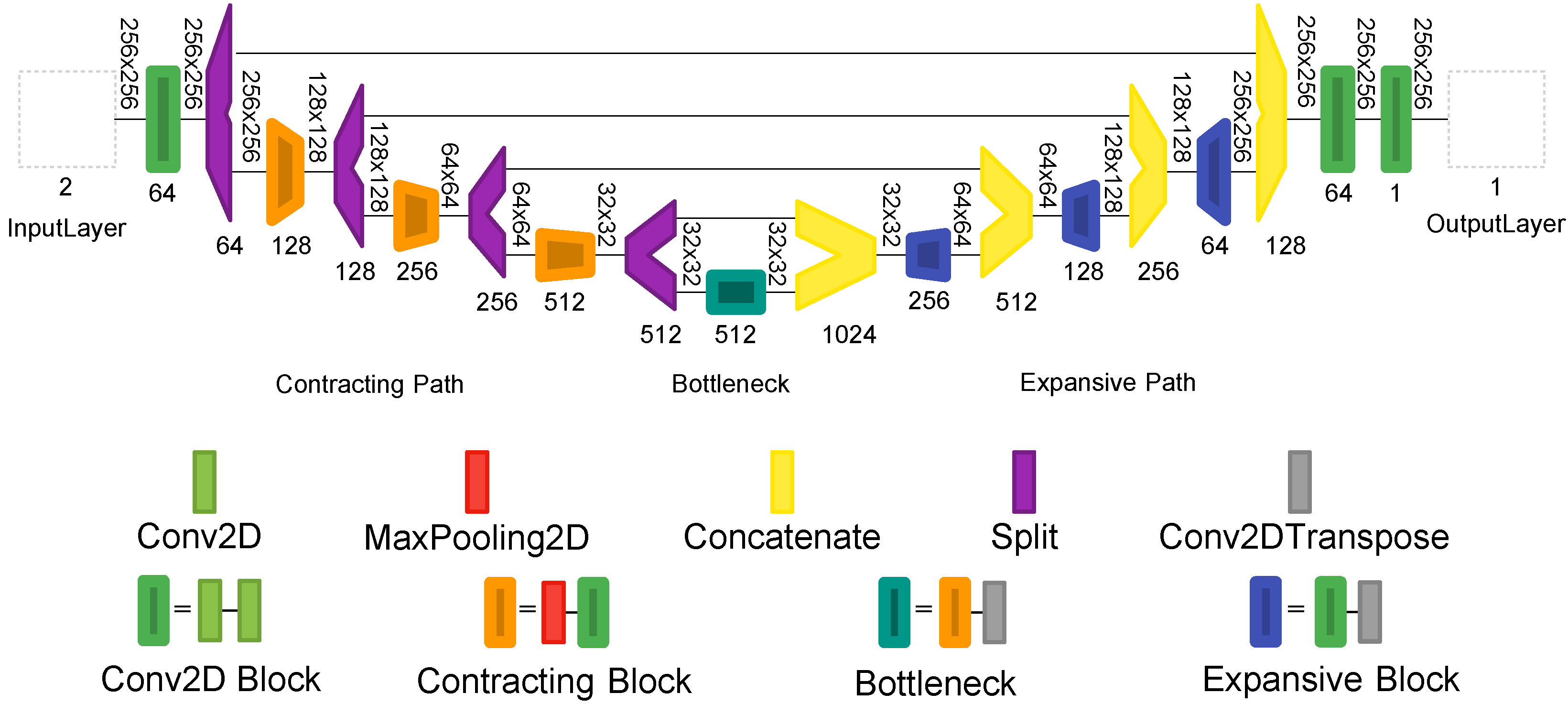

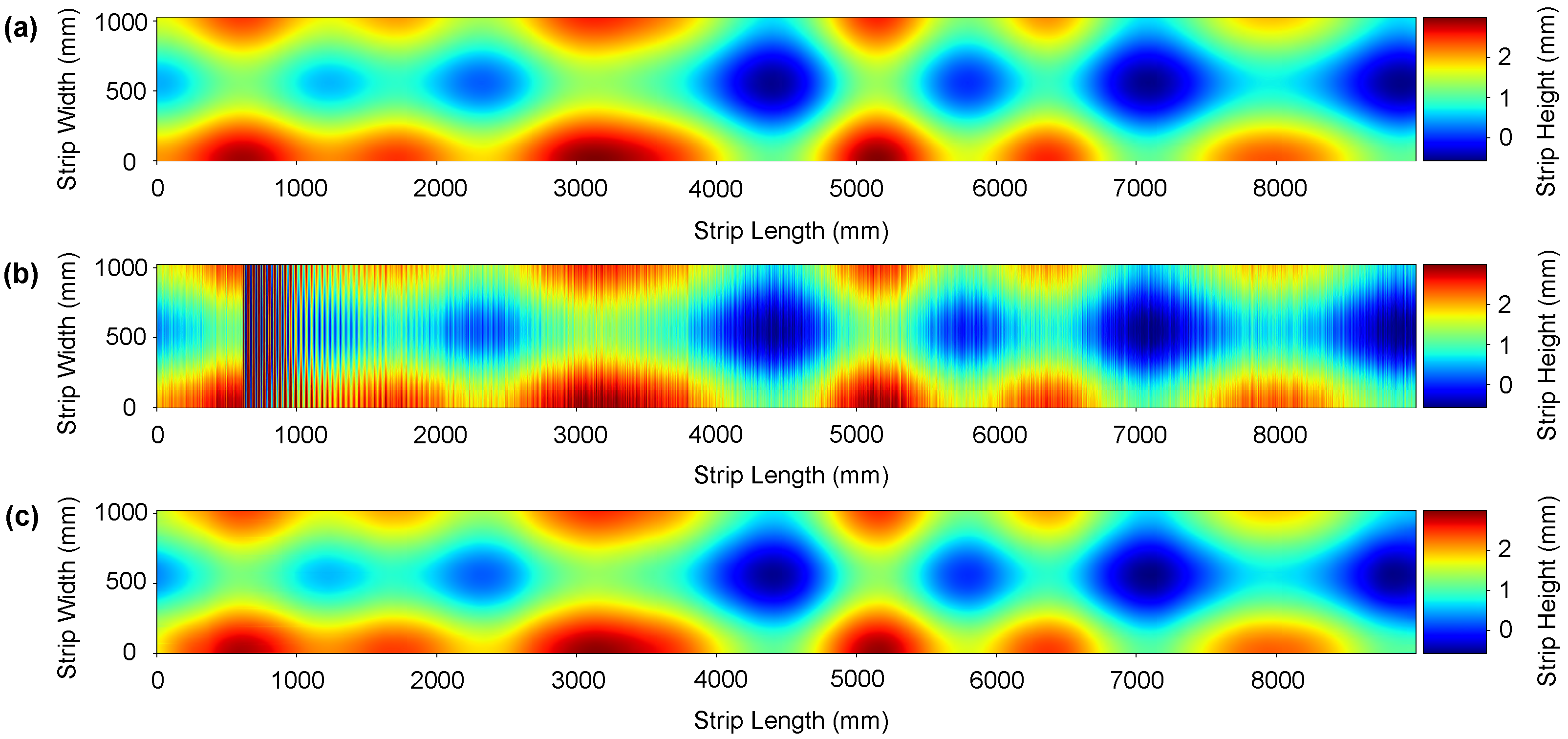
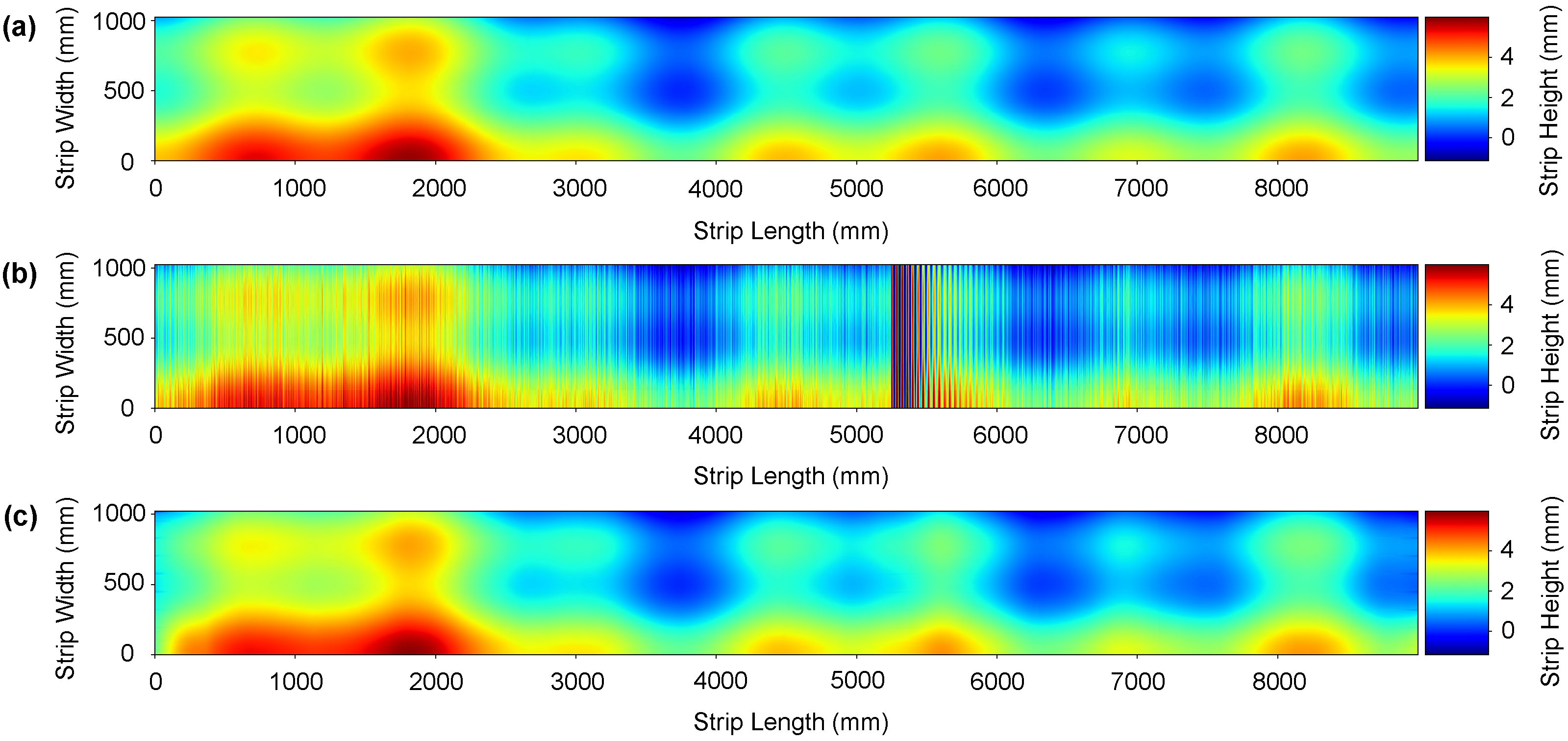
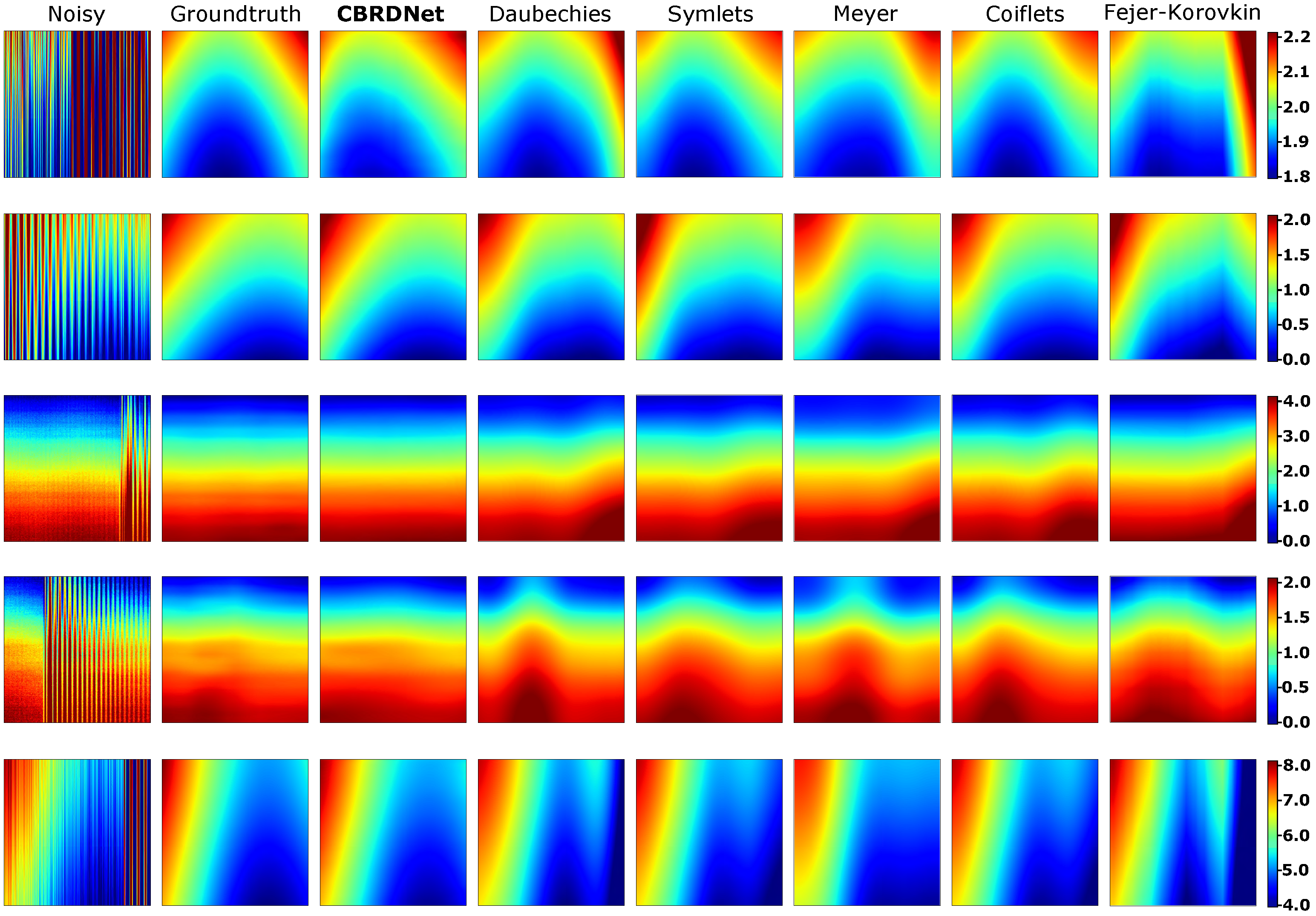
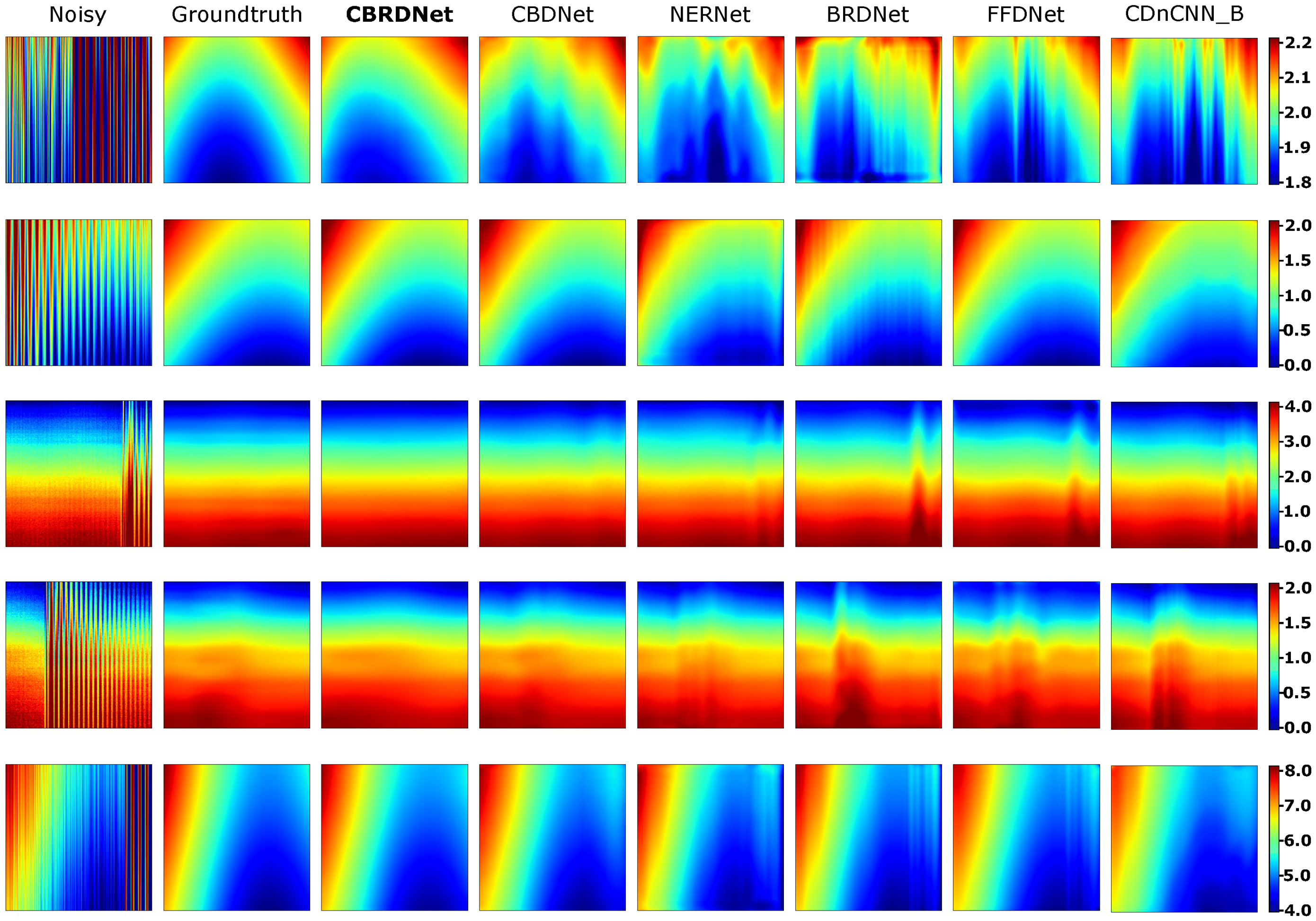
| Coil | w × h (mm) | Young (GPa) | Poisson | Yield Stress (MPa) |
|---|---|---|---|---|
| S235JR | 1050 × 3 | 205 | 0.301 | 215 |
| S235JR | 2000 × 8 | 205 | 0.301 | 215 |
| S420ML | 1650 × 7 | 190 | 0.290 | 410 |
| S355M | 1500 × 3 | 190 | 0.290 | 360 |
| S500MC | 1050 × 3 | 210 | 0.304 | 500 |
| S500MC | 1850 × 6 | 210 | 0.304 | 500 |
| Method | CNN-2D/1D/2D | Blind/Non Blind | MAE * | MaxAE * | STD * | RMSE * |
|---|---|---|---|---|---|---|
| CBRDNet-ReLu (ours) | CNN-2D | Blind | 0.140 | 0.376 | 0.136 | 0.147 |
| CBRDNet-LeakyReLu (ours) | CNN-2D | Blind | 0.160 | 0.466 | 0.154 | 0.172 |
| CBDNet | CNN-2D | Blind | 0.172 | 0.520 | 0.162 | 0.185 |
| NERNet | CNN-2D | Blind | 0.184 | 0.499 | 0.175 | 0.195 |
| BRDNet | CNN-2D | Blind | 0.198 | 0.659 | 0.184 | 0.212 |
| FFDNet | CNN-2D | Non Blind | 0.224 | 0.501 | 0.201 | 0.252 |
| CDnCNN_B | CNN-2D | Blind | 0.312 | 0.840 | 0.308 | 0.342 |
| Sym8 | 2D | NA | 0.176 | 0.543 | 0.170 | 0.188 |
| Coif4 | 2D | NA | 0.180 | 0.591 | 0.179 | 0.190 |
| Db8 | 2D | NA | 0.181 | 0.622 | 0.179 | 0.201 |
| Dmey | 2D | NA | 0.256 | 0.942 | 0.282 | 0.291 |
| Fk8 | 2D | NA | 0.390 | 1.998 | 0.588 | 0.390 |
| Hermite | 1D | NA | 0.413 | 1.150 | 0.380 | 0.459 |
| Butterworth | 1D | NA | 0.760 | 4.423 | 0.735 | 0.781 |
| Savitzky-Golay | 1D | NA | 0.842 | 6.436 | 0.779 | 0.853 |
| Moving Average | 1D | NA | 0.801 | 5.463 | 0.928 | 0.865 |
| Chebyshev Type II | 1D | NA | 0.828 | 5.040 | 0.828 | 0.903 |
| Method | CNN-2D/1D/2D | MAE * | MaxAE * | STD * | RMSE * |
|---|---|---|---|---|---|
| CBRDNet (Full Model) | CNN-2D | 0.140 | 0.376 | 0.136 | 0.147 |
| CBRDNet (No NE-SNet) | CNN-2D | 0.305 | 1.043 | 0.284 | 0.385 |
| CBDNet | CNN-2D | 0.172 | 0.520 | 0.162 | 0.185 |
| Sym8 | 2D | 0.176 | 0.543 | 0.170 | 0.188 |
| Hermite | 1D | 0.413 | 1.150 | 0.380 | 0.459 |
| Method | MAE * | MaxAE * | STD * | RMSE * |
|---|---|---|---|---|
| Mixed dataset results | ||||
| CBRDNet | 0.140 | 0.376 | 0.136 | 0.147 |
| CBRDNet (Synth) | 0.260 | 0.496 | 0.248 | 0.265 |
| CBRDNet (Real) | 0.180 | 0.401 | 0.175 | 0.186 |
| Synthetic dataset results | ||||
| CBRDNet | 0.190 | 0.410 | 0.181 | 0.195 |
| CBRDNet (Synth) | 0.110 | 0.206 | 0.128 | 0.129 |
| CBRDNet (Real) | 0.280 | 0.526 | 0.254 | 0.292 |
| Real dataset results | ||||
| CBRDNet | 0.147 | 0.386 | 0.142 | 0.154 |
| CBRDNet (Synth) | 0.282 | 0.366 | 0.265 | 0.291 |
| CBRDNet (Real) | 0.159 | 0.396 | 0.155 | 0.161 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, M.; Maestro, D.; Izaguirre, A.; Andonegui, I.; Graña, M. Depth Data Denoising in Optical Laser Based Sensors for Metal Sheet Flatness Measurement: A Deep Learning Approach. Sensors 2021, 21, 7024. https://doi.org/10.3390/s21217024
Alonso M, Maestro D, Izaguirre A, Andonegui I, Graña M. Depth Data Denoising in Optical Laser Based Sensors for Metal Sheet Flatness Measurement: A Deep Learning Approach. Sensors. 2021; 21(21):7024. https://doi.org/10.3390/s21217024
Chicago/Turabian StyleAlonso, Marcos, Daniel Maestro, Alberto Izaguirre, Imanol Andonegui, and Manuel Graña. 2021. "Depth Data Denoising in Optical Laser Based Sensors for Metal Sheet Flatness Measurement: A Deep Learning Approach" Sensors 21, no. 21: 7024. https://doi.org/10.3390/s21217024
APA StyleAlonso, M., Maestro, D., Izaguirre, A., Andonegui, I., & Graña, M. (2021). Depth Data Denoising in Optical Laser Based Sensors for Metal Sheet Flatness Measurement: A Deep Learning Approach. Sensors, 21(21), 7024. https://doi.org/10.3390/s21217024






