Hybrid Cyber Petri net Modelling, Simulation and Analysis of Master-Slave Charging for Wireless Rechargeable Sensor Networks
Abstract
1. Introduction
- (1)
- Considering the disadvantages of single fixed or mobile charging, we propose a new charging paradigm. The number and location of fixed chargers are constrained by the growth rate of actual electric quantity, and the optimization goal is to maximize the total actual electric quantity of sensor nodes with fixed charging. Then, a mobile charger takes turns charging the remaining nodes with the optimization goal of minimizing the travelling distance.
- (2)
- Wireless charging for the WRSN is a hybrid system including discrete event decision and continuous energy transfer, in which there are energy flow, data flow and control flow relationships. In addition, a formal specification with graph-mathematical characterization ability is beneficial to the analysis and application of such system. As a result, the Hybrid Cyber Petri net System is proposed based on the classical Petri net to model the Master-Slave Charging.
- (3)
- Because Master-Slave Charging is NP-complete, it is difficult to solve using the traditional optimization method. A greedy-genetic algorithm is proposed by adding greedy crossover and mutation operators in a genetic algorithm, which enhances the local search capability and can be used for reference to solve the chargers’ scheduling problem.
2. Related Work
2.1. Petri Net
2.2. Wireless Charging
3. System Model
3.1. Syetem Model of Wireless Charging
3.2. Petri Net Model
- (1)
- ;
- (2)
- ;
- (3)
- .
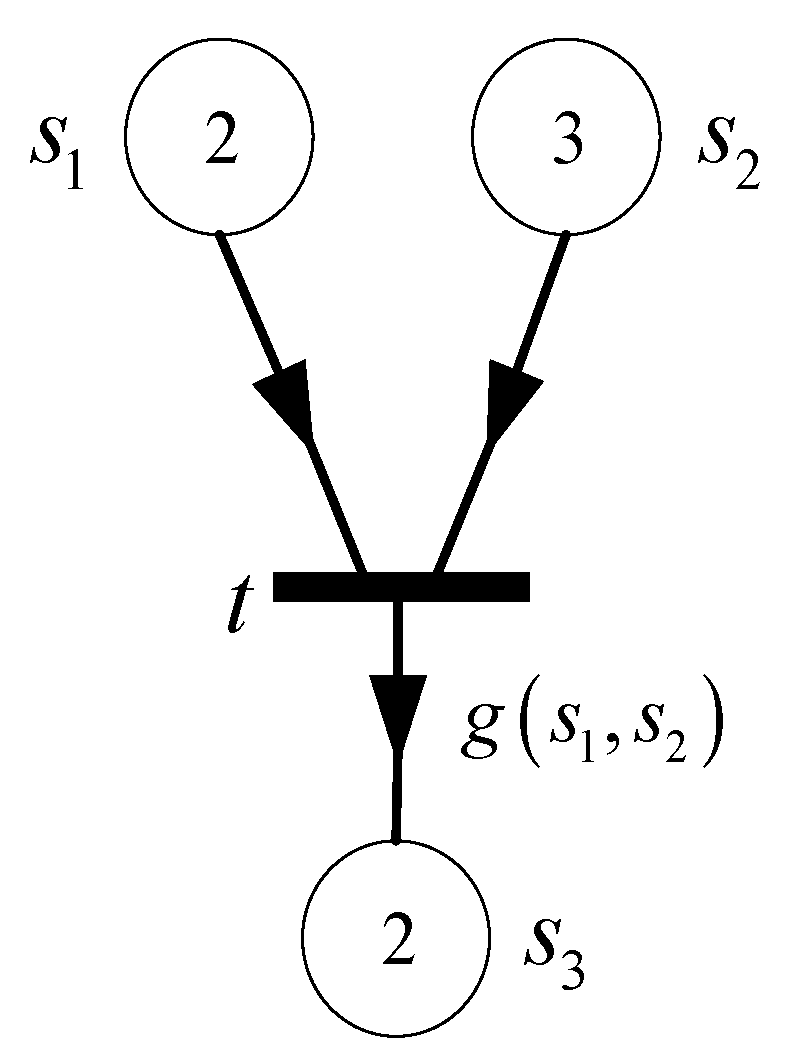
- (1)
- is a directed net, which is named the basic net of;
- (2)
- is the capacity function of;
- (3)
- is the weight function of;
- (4)
- ,is the marking, andis the initial marking.
- (1)
- is a directed net, which is named the basic net of;
- (2)
- is the weight function of,, if and only if;
- (3)
- is the initial marking.
- (1)
- is a directed net, which is named the basic net of;
- (2)
- is the capacity function of, and,whereis a set of real numbers;andis lower and upper of;
- (3)
- is the weight function, whereis the set of functional expressions for;
- (4)
- is the marking, andis the initial marking.
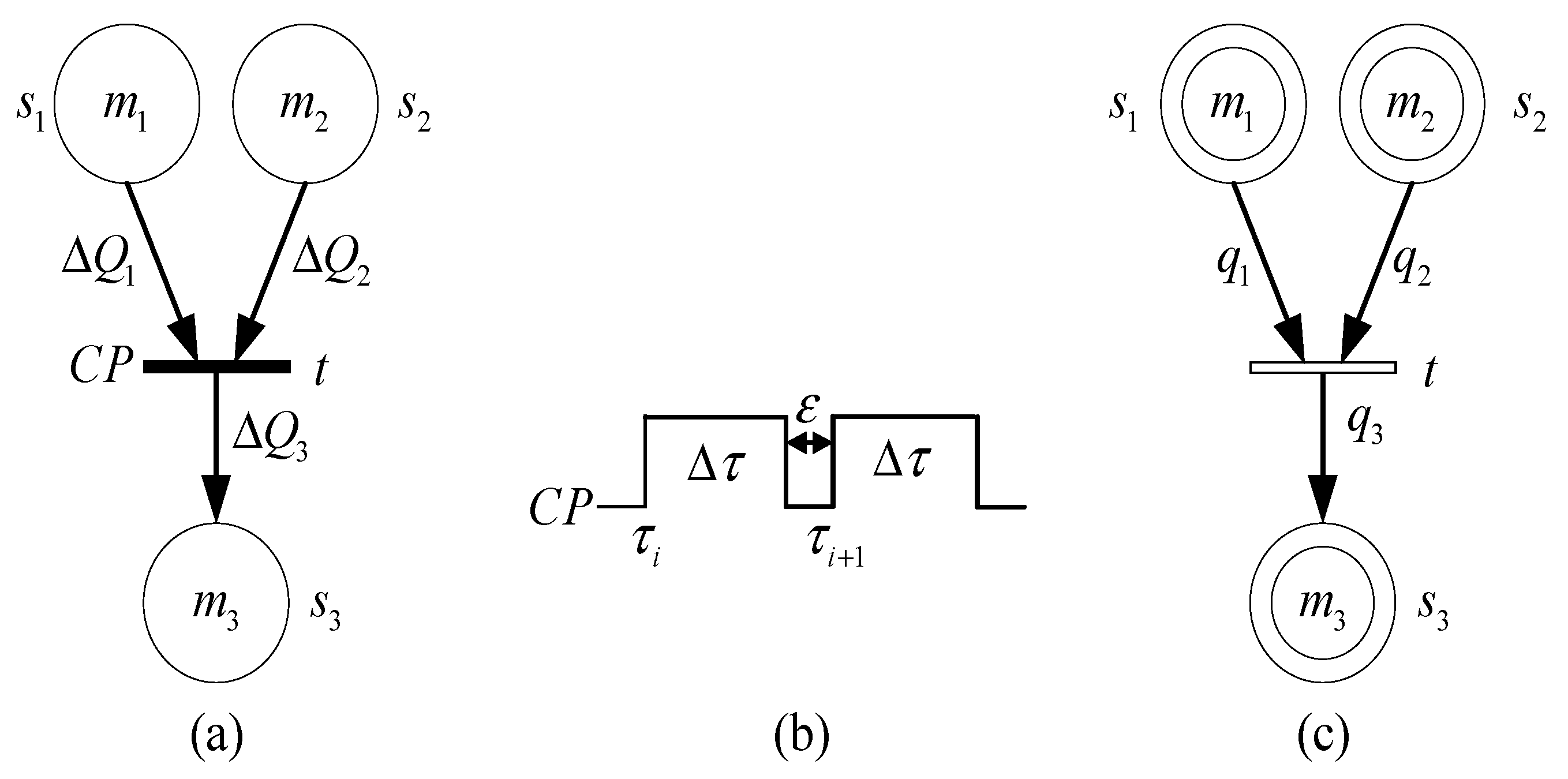
- (1)
- The weight is changed to the function of ;
- (2)
- The capacity of place is limited;
- (3)
- The marking and weight can be real numbers.
- (1)
- is a directed net, which is named the basic net of;
- (2)
- is the capacity function of;
- (3)
- is the weight function, whereis the set of functional expressions forand;
- (4)
- is the marking, andis the initial marking.
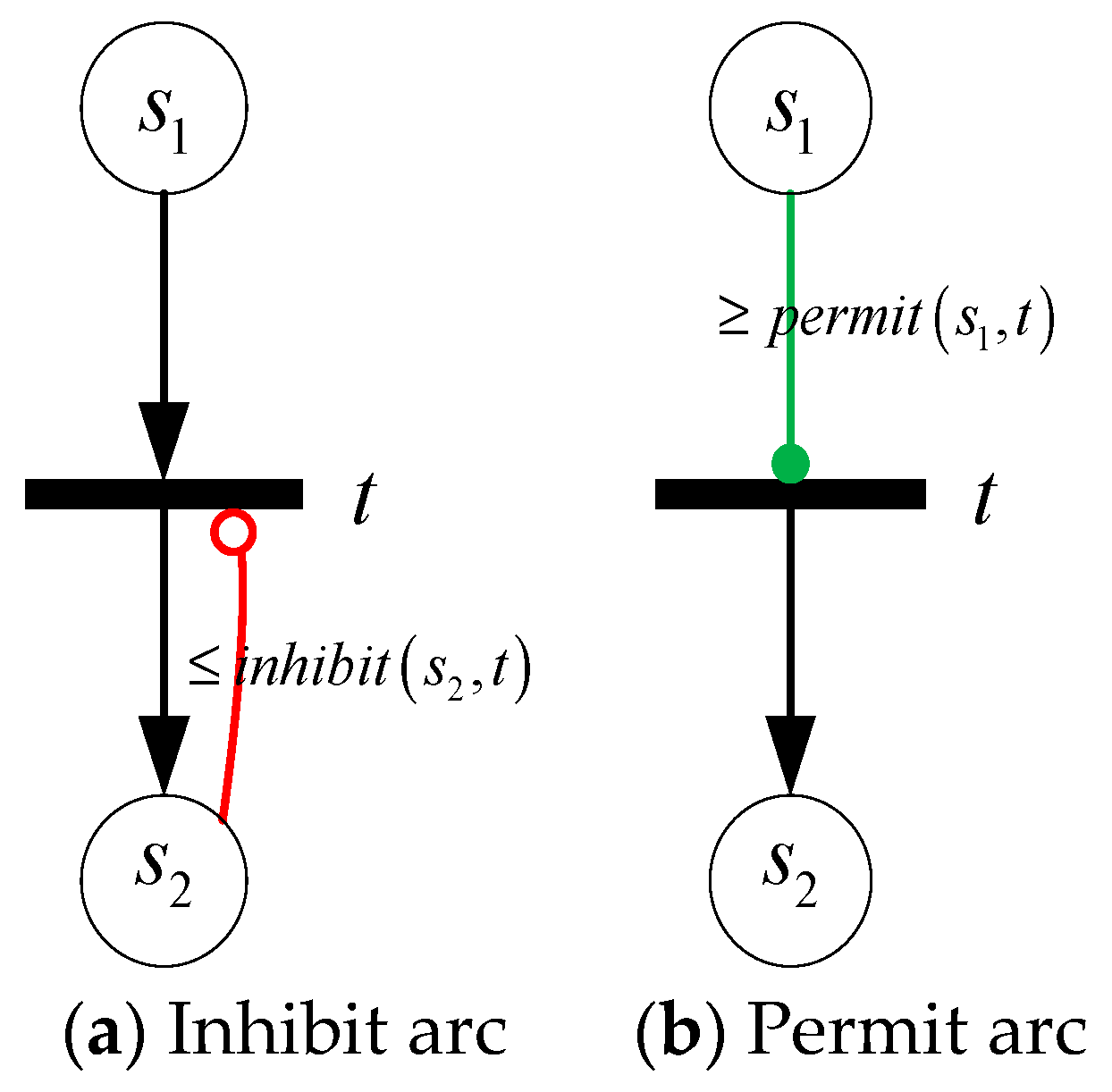
- (1)
- is a directed net, which is named the basic net of;
- (2)
- ,andis discrete place and continuous place, respectively;
- (3)
- ,andis discrete transition and continuous transition, respectively;
- (4)
- ,,and;,,,andis the flow, read, write, inhibitor and permission relationship;
- (5)
- is the lower and upper capacity function of, and, whereis a set of real numbers;
- (6)
- is the weight function, whereis the set of functional expressions for;
- (7)
- is the marking, andis the initial marking.
4. HCPNS Modelling Approach of a Master-Slave Charging System
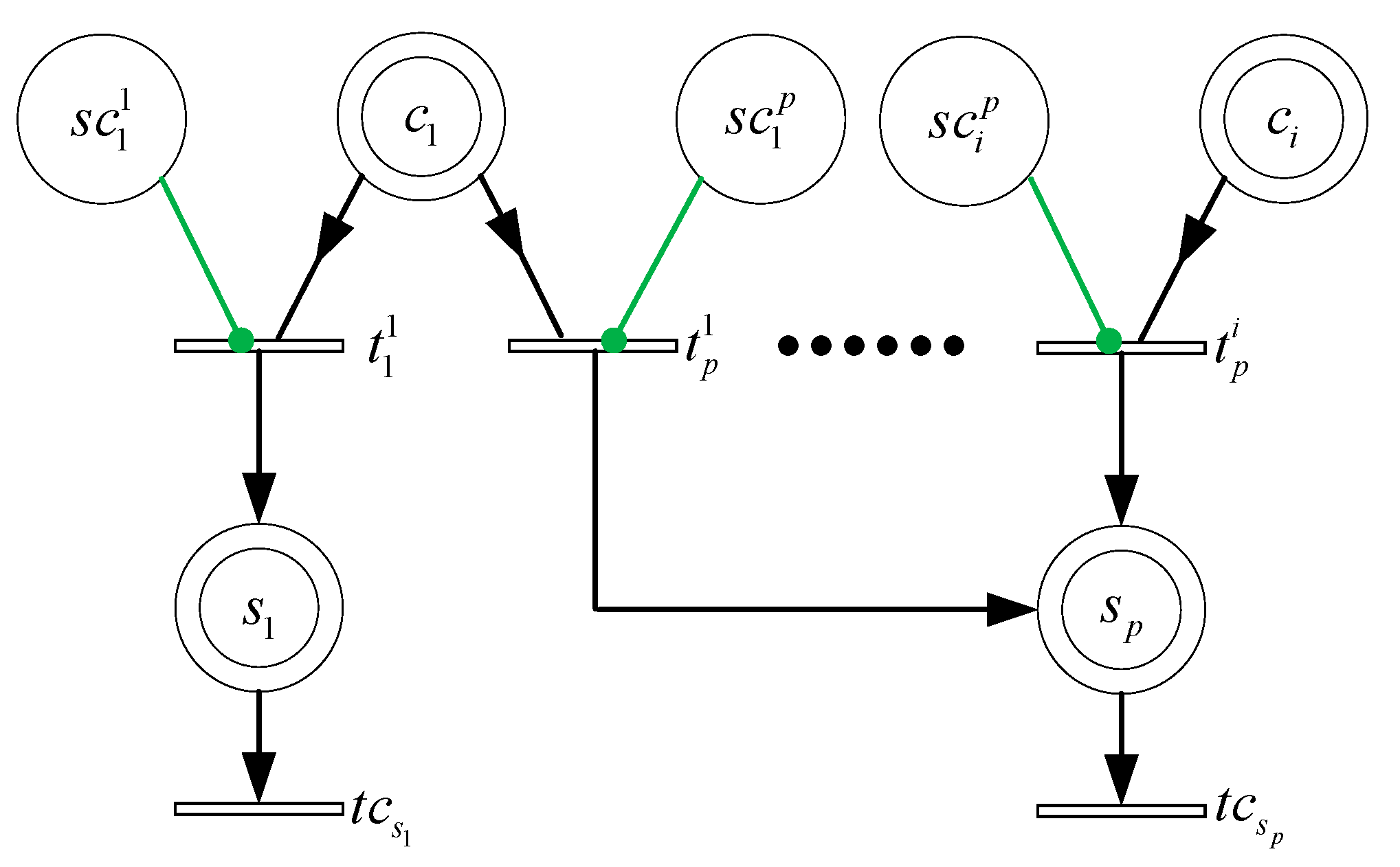
4.1. Fixed Charging Subnet
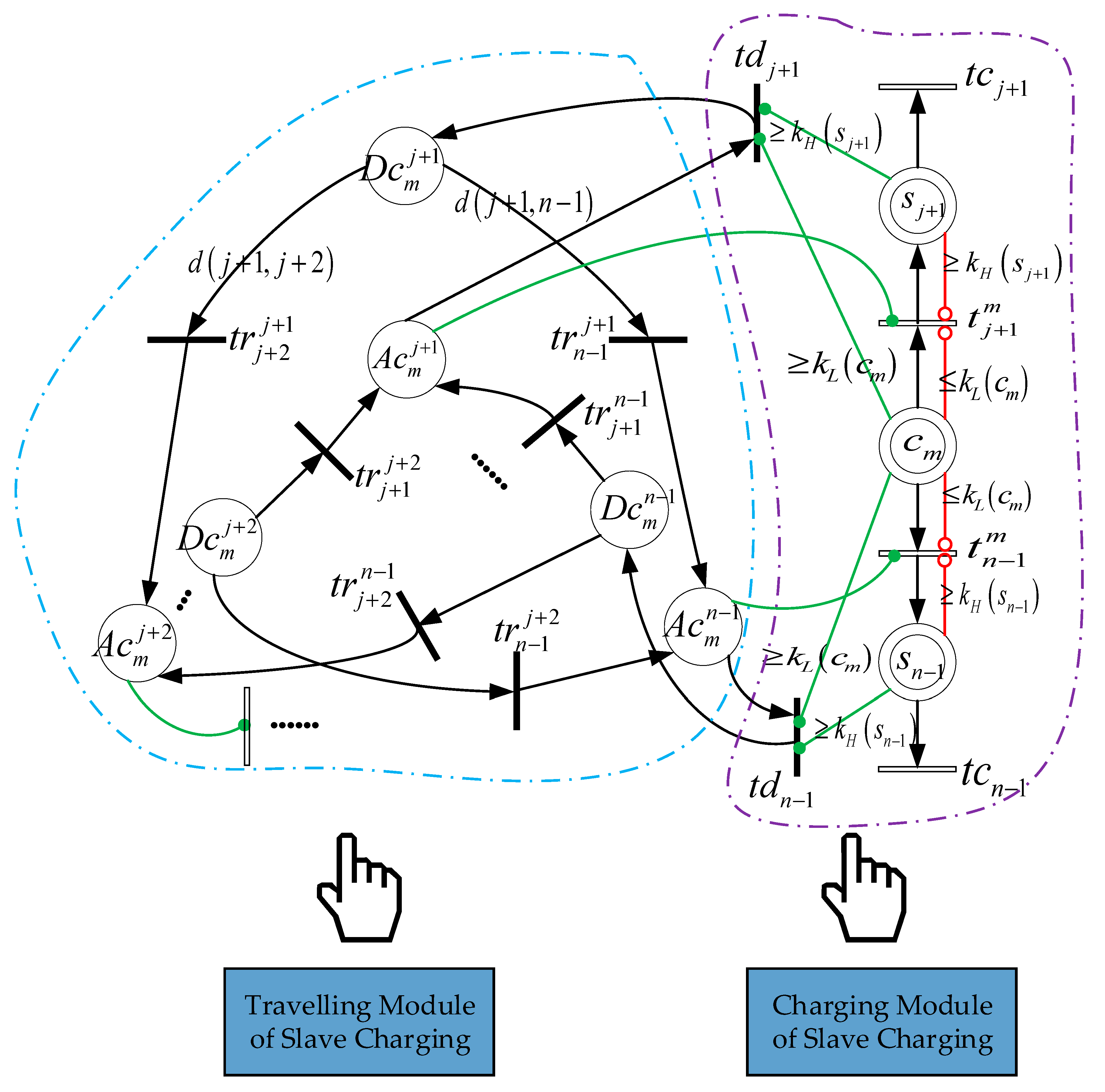
4.2. Mobile Charging Subnet
5. Simulation and Numeric Results
5.1. Simulation Setup and Environment Parameters
- (1)
- Total AEQ: The actual electric quantity received by fixed charging. As the objective of master mode, this metric implies the efficiency of our algorithm.
- (2)
- Proportion of fully-charged sensors: The ratio of fully-charged sensors to all the sensors.
- (3)
- Exceeded energy: Additional energy that the chargers can provide when nodes are fully charged. Since the mobile charger will leave once the node is fully charged, there is no exceeded energy in slave mode.
- (4)
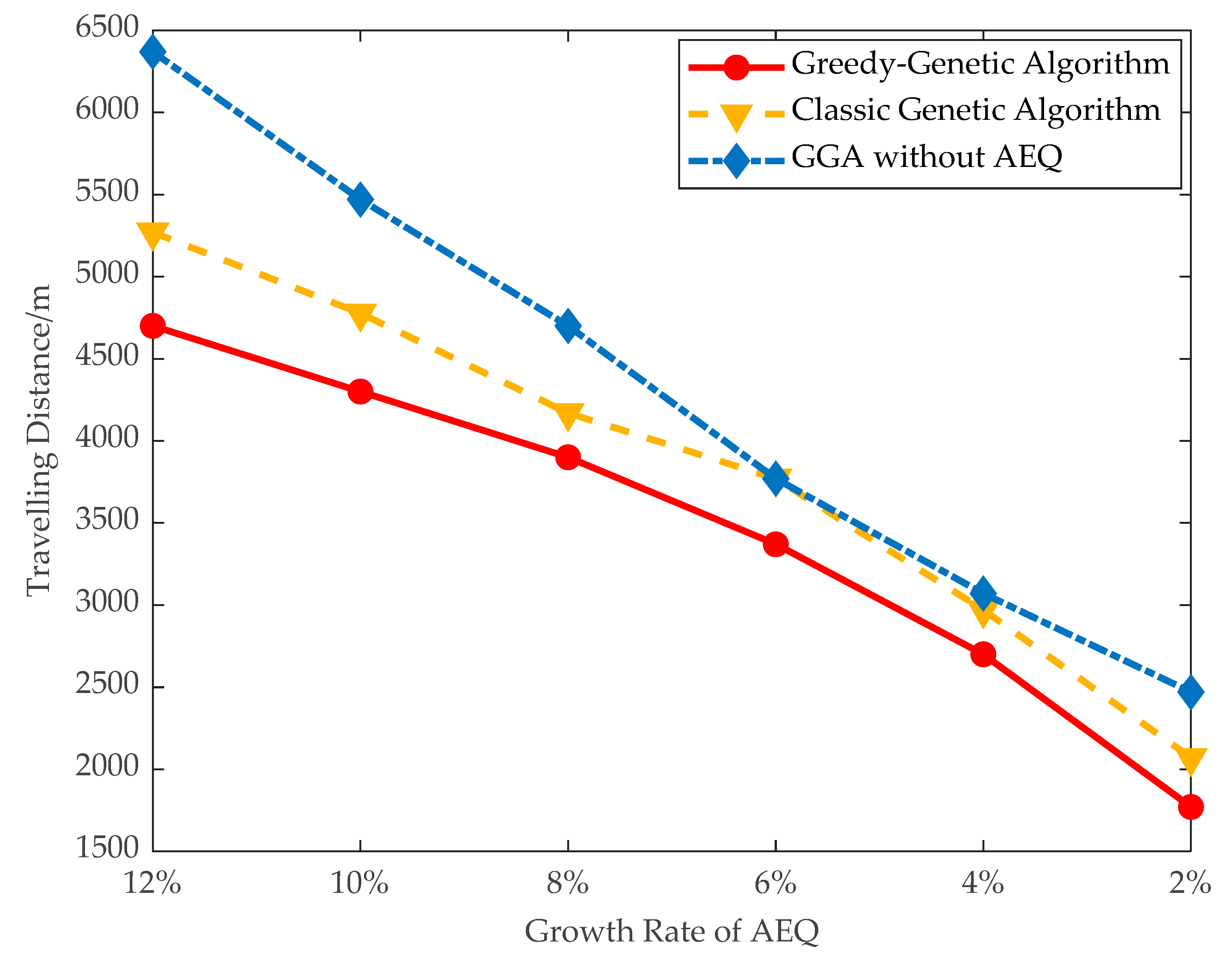
- Traveling distance of the mobile charger: The total distance of the mobile charger from and back to the base station.
- (5)
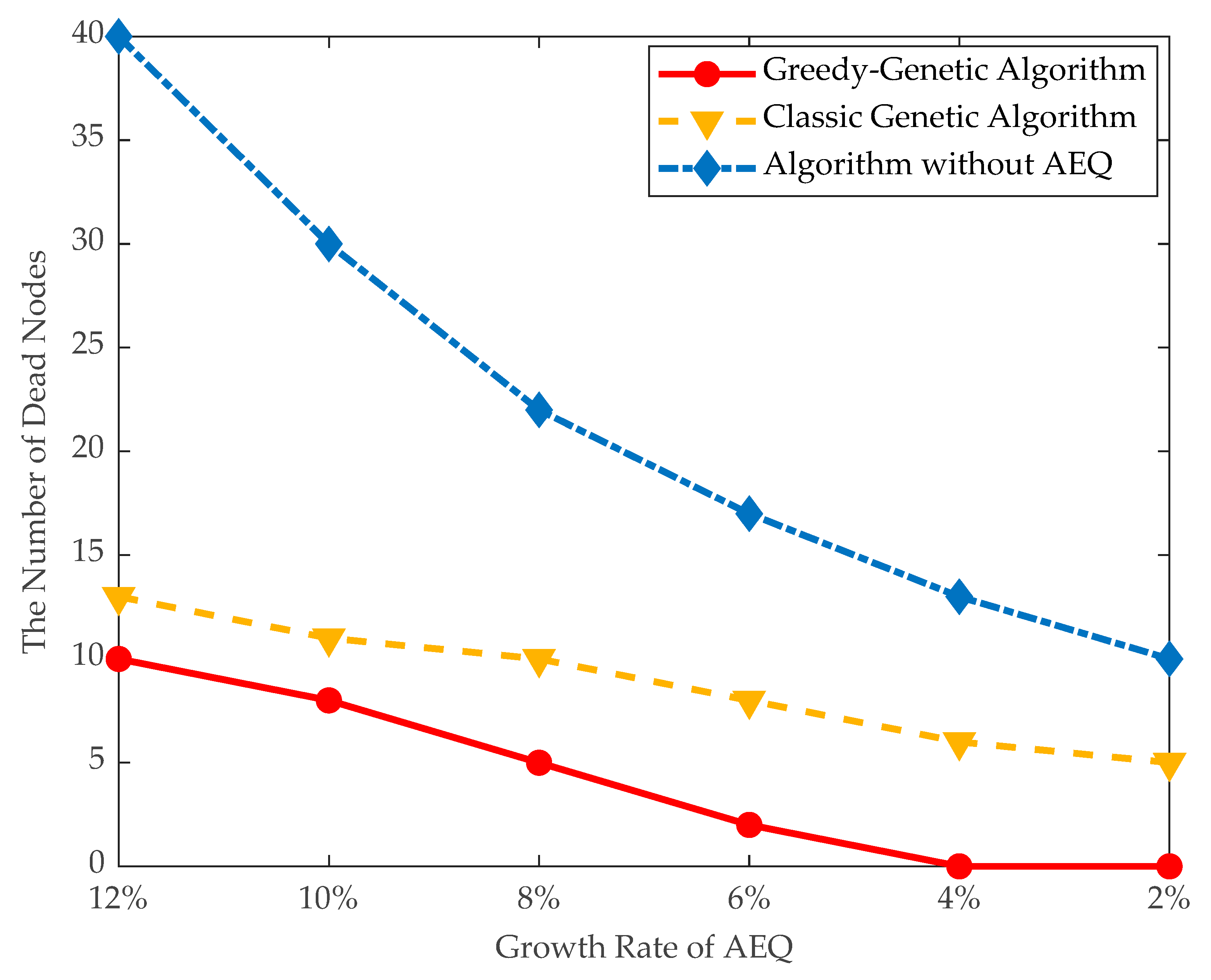
- Number of dead nodes: The number of nodes running out of energy. This metric implied the effect of AEQ growth threshold on network performance.
5.2. Performance
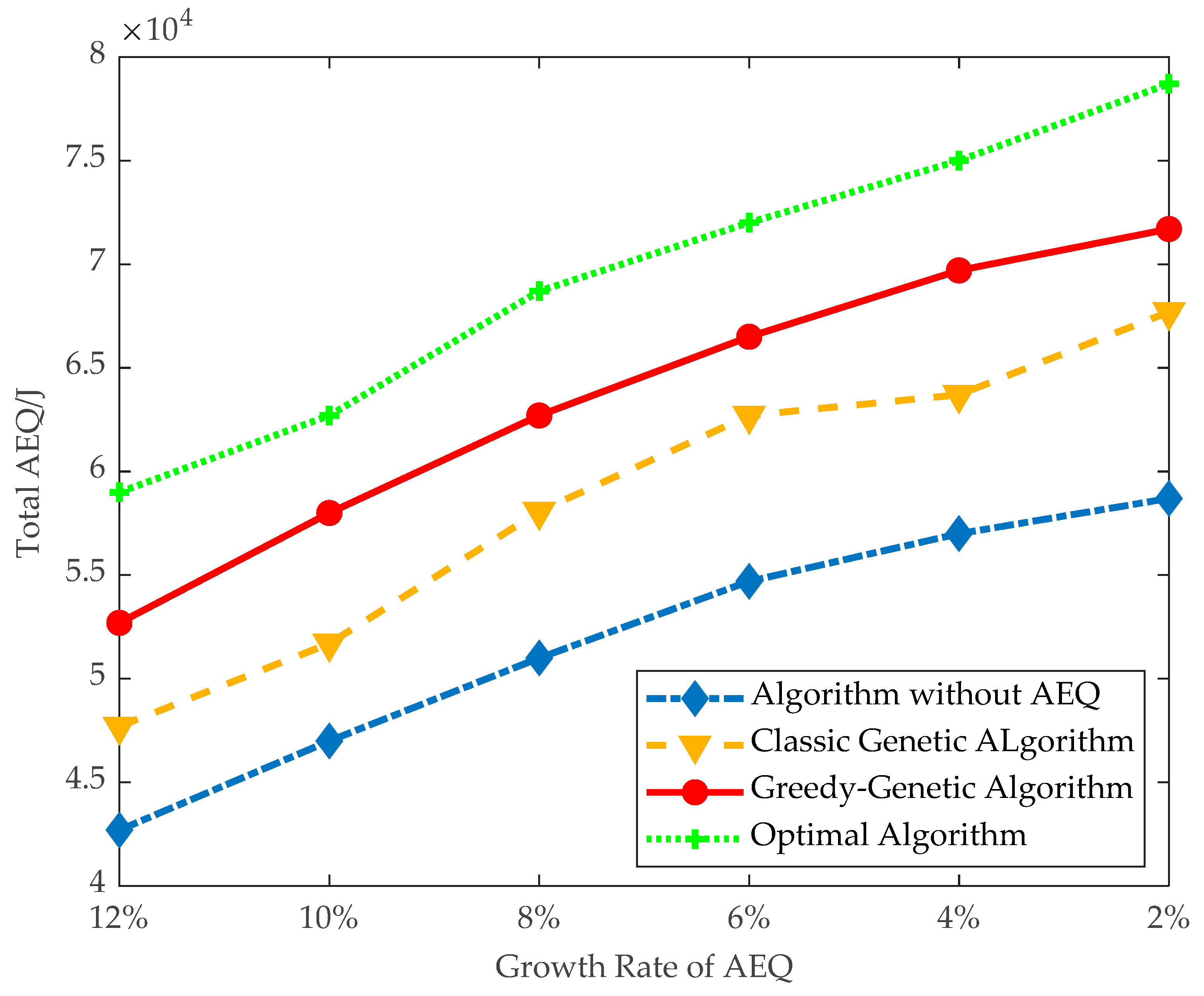
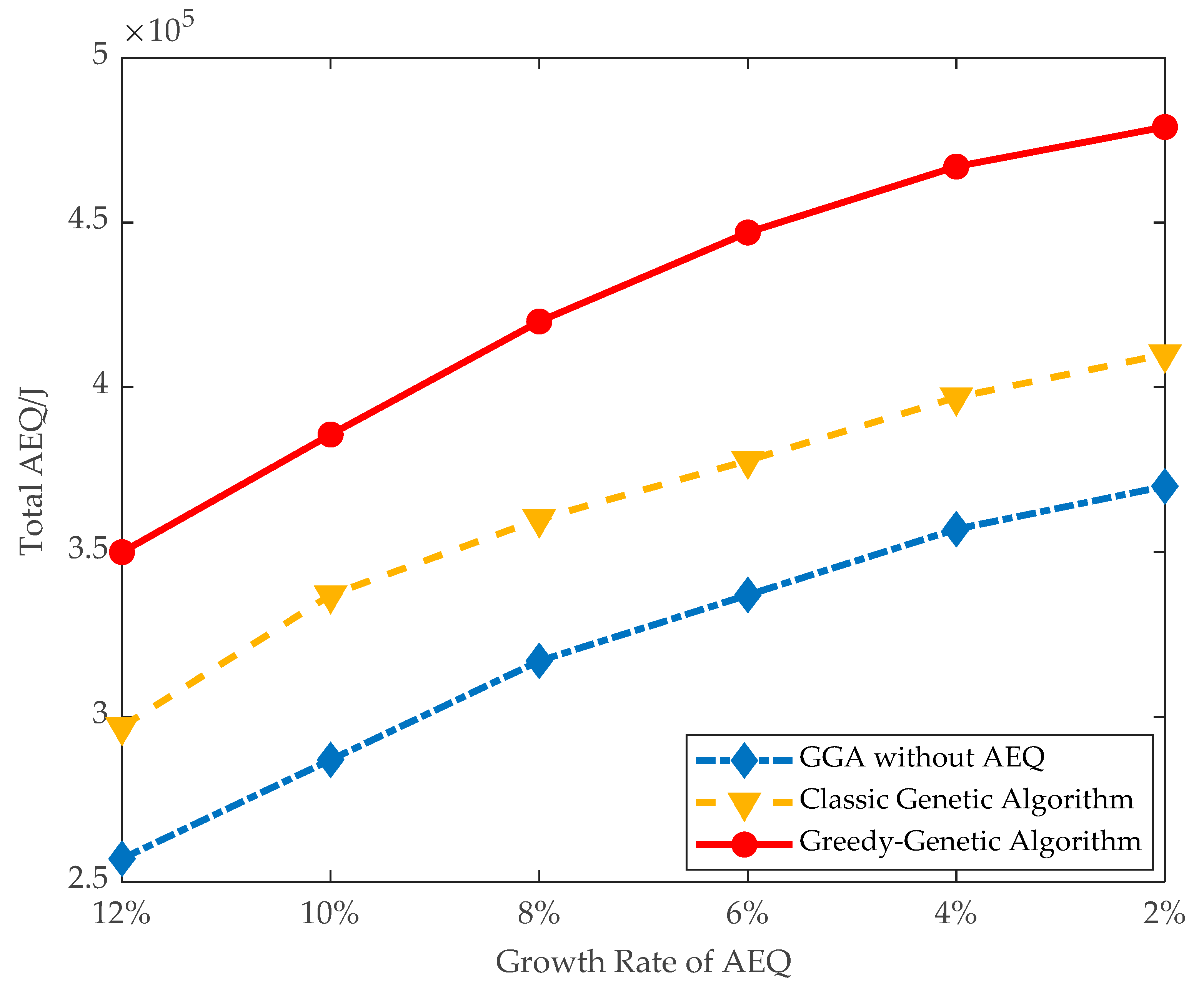
- (1)
- Total AEQ: The total AEQ on both data instances are evaluated by setting the threshold of AEQ growth rate between 2% and 12%. Each different setup is run 10 times, and the average of them will be taken.
- (2)
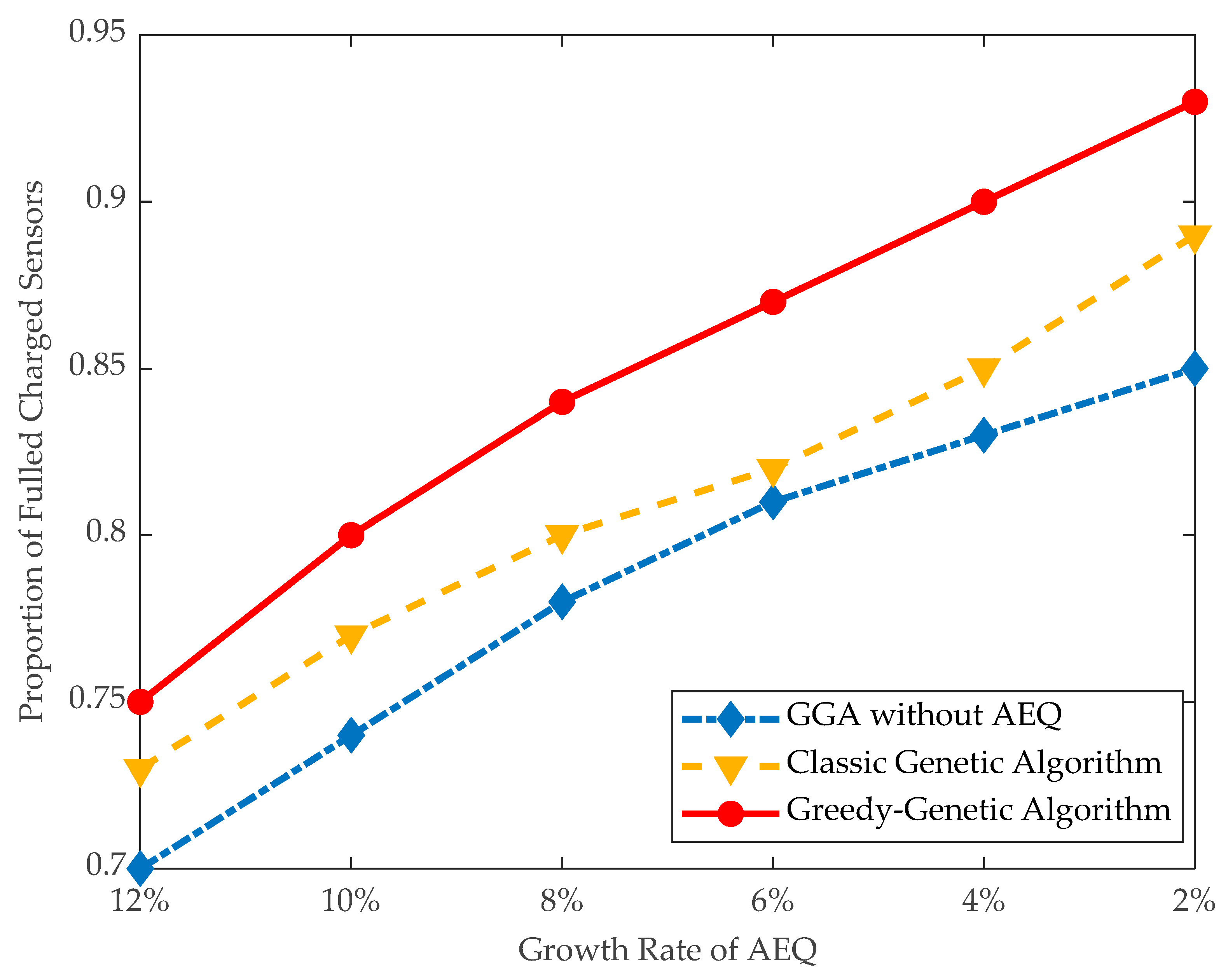
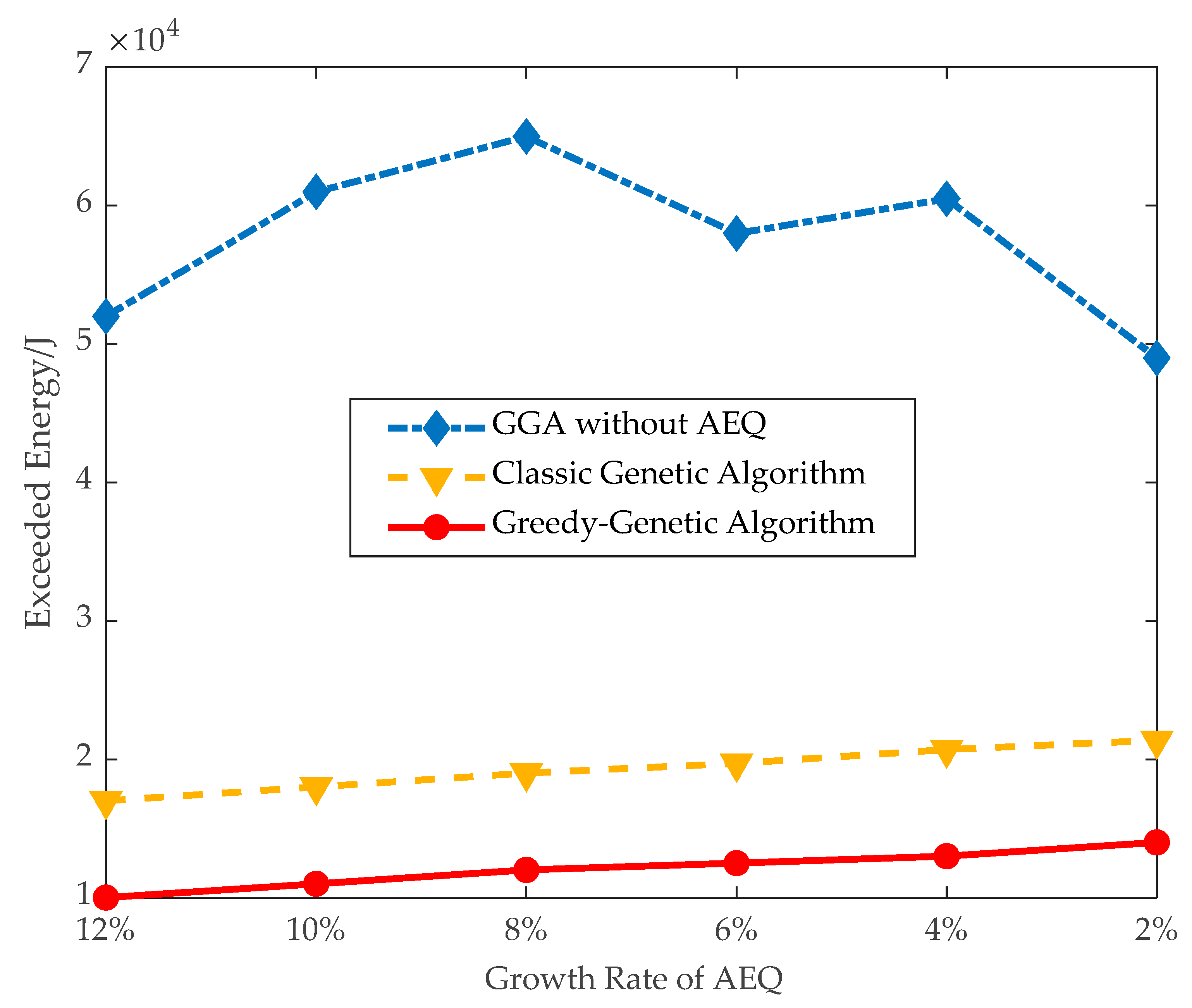
- Effectiveness of applying AEQ: The effectiveness of AEQ is evaluated in terms of the proportion of fully charged and exceeded energy in large instances.
- (3)
- Traveling distance and dead nodes: The traveling distance of the mobile charger and number of dead nodes are evaluated in large data instances. As shown in Figure 12 and Figure 13, when the threshold of AEQ growth rate is 10%, the number of dead nodes is 8 and the traveling distance of the mobile charger is 4300 m. When the threshold of AEQ growth rate is 8%, the traveling distance of the mobile charger is 3900 m and the number of dead nodes is 5. This comparison demonstrates that both the traveling distance and number of dead nodes are turning down with the decrement of the threshold of AEQ growth rate. This is because the lower threshold of the AEQ growth rate allows more fixed chargers to be placed, reducing the number of nodes with mobile charging, thereby easing the burden on the mobile charger and decreasing the waiting time of nodes.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless charging technologies: Fundamentals, standards, and network applications. IEEE Commun. Surv. Tutor. 2016, 18, 1413–1452. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless networks with RF energy harvesting: A contemporary survey. IEEE Commun. Surv. Tutor. 2015, 17, 757–789. [Google Scholar] [CrossRef]
- Bai, X.; Han, W.-Y.; Xu, L.-J.; Zhang, J.-W.; Li, Y.-X. A radio frequency and vibration energy harvesting antenna based on piezoelectric material. Int. J. Rf Microw. Comput. Aided Eng. 2020, 30. [Google Scholar] [CrossRef]
- Lai, W.Y.; Hsiang, T.R. Wireless charging deployment in sensor networks. Sensors 2019, 19, 201. [Google Scholar] [CrossRef]
- Madhja, A.; Nikoletseas, S.; Raptisab, T.P. Hierarchical, collaborative wireless energy transfer in sensor networks with multiple mobile chargers. Comput. Netw. 2016, 97, 98–112. [Google Scholar] [CrossRef]
- Lin, C.; Lin, C.; Wu, J.; Liu, Z.; Obaidat, M.S.; Yu, W.C.; Wu, G. GTCharge: A game theoretical collaborative charging scheme for wireless rechargeable sensor networks. J. Syst. Softw. 2016, 121, 88–104. [Google Scholar] [CrossRef]
- Fu, L.; Cheng, P.; Gu, Y.; Chen, J.; He, T. Optimal charging in wireless rechargeable sensor networks. IEEE Trans. Veh. Technol. 2016, 65, 278–291. [Google Scholar] [CrossRef]
- Jiang, G.Y.; Lam, S.; Sun, Y.; Tu, L.; Wu, J. Joint charging tour planning and depot positioning for wireless sensor networks using mobile chargers. IEEE ACM Trans. Netw. 2017, 25, 2250–2266. [Google Scholar] [CrossRef]
- Wang, W.; Jing, H.; Liao, J.; Yin, F.; Yuan, P.; Chen, L. A safe charging algorithm based on multiple mobile chargers. Sensors 2020, 20, 2937. [Google Scholar] [CrossRef]
- Qin, H.Y.; Xu, L. Petri-net based modelling and multi-objective optimal deployment for WRSN. Control Eng. Appl. Inform. 2020, 22, 3–12. [Google Scholar]
- Lee, J. A petri net design of command filters for semiautonomous mobile sensor networks. IEEE Trans. Ind. Electr. 2008, 55, 1835–1841. [Google Scholar] [CrossRef]
- Yu, Z.H.; Fu, X.; Cai, Y.; Vuran, M.C. A reliable energy-efficient multi-level routing algorithm for wireless sensor networks using fuzzy petri nets. Sensors 2011, 11, 3381–3400. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, M.C.; Mateo, J.A.; Macia, H.; Pardo, J.J.; Olivares, T. Formal modelling and performance evaluation of a novel role-based Routing Algorithm for wireless sensor networks. In Proceedings of the 2012 18th Annual International Conference on Advanced Computing and Communications (ADCOM), Electronics CityHosur Main Road, Bangalore, India, 14–16 December 2012. [Google Scholar]
- Ruiz, M.C.; Garrido-Hidalgo, C.; Gruska, D.P.; Olivares, T.; Hortelano, D.; Roda-Sanchez, L. Modeling and evaluation of a power-aware algorithm for IoT bluetooth low energy devices. In Proceedings of the 2019 IEEE International Conference on Smart Internet of Things (SmartIoT), Tianjin, China, 8–9 November 2019. [Google Scholar]
- Mostafa, A.; Hassan, K. Robust energy harvesting aware clustering with fuzzy petri net reasoning algorithm. In Proceedings of the 2014 IEEE 10th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Larnaca, Cyprus, 8–10 October 2014. [Google Scholar]
- Moreno, J.C.M.; Castro, D.M.; Ramrez, J.L.V. Design of discrete event systems supported on wireless sensors and actuator networks using colored Petri Nets. In Proceedings of the 2015 IEEE 2nd Colombian Conference on Automatic Control (CCAC), Manizales, Colombia, 14–16 October 2015. [Google Scholar]
- Abrishambaf, R.; Cabral, J.; Monteiro, J.; Bal, M. An energy aware design flow of distributed industrial wireless sensor and actuator networks. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015. [Google Scholar]
- Jiang, F.C.; Jou, I.; Leu, F.-Y. Approaching green sensor field using queue-based optimization technique. J. Netw. Comput. Appl. 2016, 66, 128–136. [Google Scholar] [CrossRef]
- Berrachedi, A.; Boukala-Ioualalen, M. Evaluation of the energy consumption and the packet loss in WSNs using deterministic stochastic petri nets. In Proceedings of the 2016 30th International Conference on Advanced Information Networking and Applications Workshops (WAINA), Crans-Montana, Switzerland, 23–25 March 2016. [Google Scholar]
- Kostin, A.E.; Fanaeian, Y.; Al-Wattar, H. Anycast tree-based routing in mobile wireless sensor networks with multiple sinks. Wirel. Netw. 2016, 22, 579–598. [Google Scholar] [CrossRef]
- Le, K.; Pham, B.; Tram, Q.; Bui, T.; Quan, T. CODE-WSN: A formal modelling tool for congestion detection on wireless sensor networks. In Proceedings of the 2018 IEEE World Symposium on Communication Engineering (WSCE), Singapore, 26–28 December 2018. [Google Scholar]
- Riouali, Y.; Benhlima, L.; Bah, S. Extended batches petri nets based system for road traffic management in WSNs. J. Sens. Actuator Netw. 2017, 6, 30. [Google Scholar] [CrossRef]
- Mahjoub, Y.I.; El-Alaouia, E.h.C.; Nait-Sidi-Mohb, A. Modeling and developing a conflict-aware scheduling in urban transportation networks. Future Gener. Comput. Syst. Int. J. Esci. 2020, 107, 1026–1036. [Google Scholar] [CrossRef]
- He, S.; Chen, J.; Jiang, F.; Yau, D.K.Y.; Xing, G.; Sun, Y. Energy provisioning in wireless rechargeable sensor networks. IEEE Trans. Mob. Comp. 2013, 12, 1931–1942. [Google Scholar] [CrossRef]
- Jiang, J.R.; Liao, J.-H. Efficient wireless charger deployment for wireless rechargeable sensor networks. Energies 2016, 9, 696. [Google Scholar] [CrossRef]
- Yao, K.H.; Jiang, J.R.; Tsai, C.H.; Wu, Z.S. Evolutionary beamforming optimization for radio frequency charging in wireless rechargeable sensor networks. Sensors 2017, 17, 1918. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.H.; Yang, M.; Wang, A.M.; Zhang, Y. Charging nodes deployment optimization in wireless rechargeable sensor network. In Proceedings of the 2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017. [Google Scholar]
- Yang, M.; Wang, A.M.; Sun, G.; Zhang, Y. Deploying charging nodes in wireless rechargeable sensor networks based on improved firefly algorithm. Comput. Electr. Eng. 2017, 72, 719–731. [Google Scholar] [CrossRef]
- Dai, H.P.; Liu, Y.; Chen, G.; Wu, X.; He, T.; Liu, A.X.; Zhao, Y. SCAPE: Safe charging with adjustable power. IEEE ACM Trans. Netw. 2018, 26, 520–533. [Google Scholar] [CrossRef]
- Dai, H.P.; Dai, H.; Ma, H.; Liu, A.X.; Chen, G. Radiation constrained scheduling of wireless charging tasks. IEEE ACM Trans. Netw. 2018, 26, 314–327. [Google Scholar] [CrossRef]
- Li, L.L.; Dai, H.; Chen, G.; Zheng, J.; Dou, W.; Wu, X. Radiation constrained fair charging for wireless power transfer. ACM Trans. Sens. Netw. 2019, 15, 33. [Google Scholar] [CrossRef]
- Wan, P.; Cheng, W.; Wu, B.; Wang, G. An algorithm to optimize deployment of charging base stations for WRSN. Eur. J. Wirel. Commun. Netw. 2019, 63. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Ye, F.; Yang, Y. A mobile data gathering framework for wireless rechargeable sensor networks with vehicle movement costs and capacity constraints. IEEE Trans. Comput. 2016, 65, 2411–2427. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Yang, Y.Y.; Ye, F. Combining solar energy harvesting with wireless charging for hybrid wireless sensor networks. IEEE Trans. Mob. Comput. 2018, 17, 560–576. [Google Scholar] [CrossRef]
- Fu, L.; He, L.; Cheng, P.; Gu, Y.; Pan, J.; Chen, J. ESync: Energy synchronized mobile charging in rechargeable wireless sensor networks. IEEE Trans. Veh. Technol. 2016, 65, 7415–7431. [Google Scholar] [CrossRef]
- Shu, Y.; Shin, K.G.; Chen, J.; Sun, Y. Joint energy replenishment and operation scheduling in wireless rechargeable sensor networks. IEEE Trans. Ind. Inform. 2017, 13, 125–134. [Google Scholar] [CrossRef]
- Shu, Y.; Yousefi, H.; Cheng, P.; Chen, J.; Gu, Y.J.L.; He, T.; Shin, K.G. Near-optimal velocity control for mobile charging in wireless rechargeable sensor networks. IEEE Trans. Mob. Comput. 2016, 15, 1699–1713. [Google Scholar] [CrossRef]
- Lin, C.; Wang, K.; Chu, Z.H.; Wang, K.; Deng, J.; Obaidat, M.S.; Wu, G.W. Hybrid charging scheduling schemes for three-dimensional underwater wireless rechargeable sensor networks. J. Syst. Softw. 2018, 146, 42–58. [Google Scholar] [CrossRef]
- Liu, K.Y.; Peng, J.; He, L.; Pan, J.P.; Li, S.; Ling, M.; Huang, Z.W. An active mobile charging and data collection scheme for clustered sensor networks. IEEE Trans. Veh. Technol. 2019, 68, 5100–5113. [Google Scholar] [CrossRef]
- Sheikhi, M.; Kashi, S.S.; Samaee, Z. Energy provisioning in wireless rechargeable sensor networks with limited knowledge. Wirel. Netw. 2019, 25, 3531–3544. [Google Scholar] [CrossRef]
- Ai, Z.; Liu, Y.; Song, F. A smart collaborative charging algorithm for mobile power distribution in 5G networks. IEEE Access 2018, 6, 28668–28679. [Google Scholar] [CrossRef]
- Mo, L.; Dobre, O.A.; Ngatched, T.M.N.; Armada, A.G. Energy-aware multiple mobile chargers coordination for wireless rechargeable sensor networks. IEEE Internet Things J. 2019, 6, 8202–8214. [Google Scholar] [CrossRef]
- Lyu, Z.W.; Wei, Z.; Wang, X.; Fan, Y.; Xia, C.; Shi, L. A periodic multinode charging and data collection scheme with optimal traveling path in WRSNs. IEEE Syst. J. 2020, 14, 3518–3529. [Google Scholar] [CrossRef]
- Tian, M.Q.; Jiao, W.; Liu, J. The charging strategy of mobile charging vehicles in wireless rechargeable sensor networks with heterogeneous sensors. IEEE Access 2020, 8, 73096–73110. [Google Scholar] [CrossRef]
- Xie, L.; Shi, Y.; Hou, Y.T.; Lou, W.; Sherali, H.D.; Midkiff, S.F. Multi-node wireless energy charging in sensor networks. IEEE ACM Trans. Netw. 2015, 23, 437–450. [Google Scholar] [CrossRef]
- Labadi, K.; Benarbia, T.; Barbot, J.; Hamaci, S.; Omari, A. Stochastic petri net modeling, simulation and analysis of public bicycle sharing systems. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1380–1395. [Google Scholar] [CrossRef]


| Notation | Description |
|---|---|
| n | number of sensor nodes |
| m | number of chargers |
| source power of the charger | |
| power consumption rate of sensor node | |
| received power of from | |
| consumed energy of | |
| Er() | energy received by |
| energy needed to be full of | |
| actual electric quantity of | |
| growth rate of actual electric quantity | |
| energy consumption per time unit of travelling by | |
| charging period of fixed chargers |
| Name | Function |
|---|---|
| Represents the charger . | |
| Specify whether the sensor node is within the radiation of . It is the case when . | |
| Represents the node . Its marking corresponds to the current energy. | |
| Used to model the charging for by the charger . | |
| Used to model the consumption of the sensor node . |
| Name | Function |
|---|---|
| Specify whether the mobile charger reach the node . It is the case when . | |
| Represents the mobile charger . Its marking corresponds to the current energy. | |
| Specify whether the mobile charger can leave the node . It is the case when . | |
| Used to model the charging for by the mobile charger . | |
| Used to model the mobile charger’s travelling from the nth to the n−1th node. | |
| Used to model the leaving from the n−1th node. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Zhao, B.; Xu, L.; Bai, X. Hybrid Cyber Petri net Modelling, Simulation and Analysis of Master-Slave Charging for Wireless Rechargeable Sensor Networks. Sensors 2021, 21, 551. https://doi.org/10.3390/s21020551
Qin H, Zhao B, Xu L, Bai X. Hybrid Cyber Petri net Modelling, Simulation and Analysis of Master-Slave Charging for Wireless Rechargeable Sensor Networks. Sensors. 2021; 21(2):551. https://doi.org/10.3390/s21020551
Chicago/Turabian StyleQin, Huaiyu, Buhui Zhao, Leijun Xu, and Xue Bai. 2021. "Hybrid Cyber Petri net Modelling, Simulation and Analysis of Master-Slave Charging for Wireless Rechargeable Sensor Networks" Sensors 21, no. 2: 551. https://doi.org/10.3390/s21020551
APA StyleQin, H., Zhao, B., Xu, L., & Bai, X. (2021). Hybrid Cyber Petri net Modelling, Simulation and Analysis of Master-Slave Charging for Wireless Rechargeable Sensor Networks. Sensors, 21(2), 551. https://doi.org/10.3390/s21020551





