Physician-Friendly Tool Center Point Calibration Method for Robot-Assisted Puncture Surgery
Abstract
1. Introduction
2. Materials and Methods
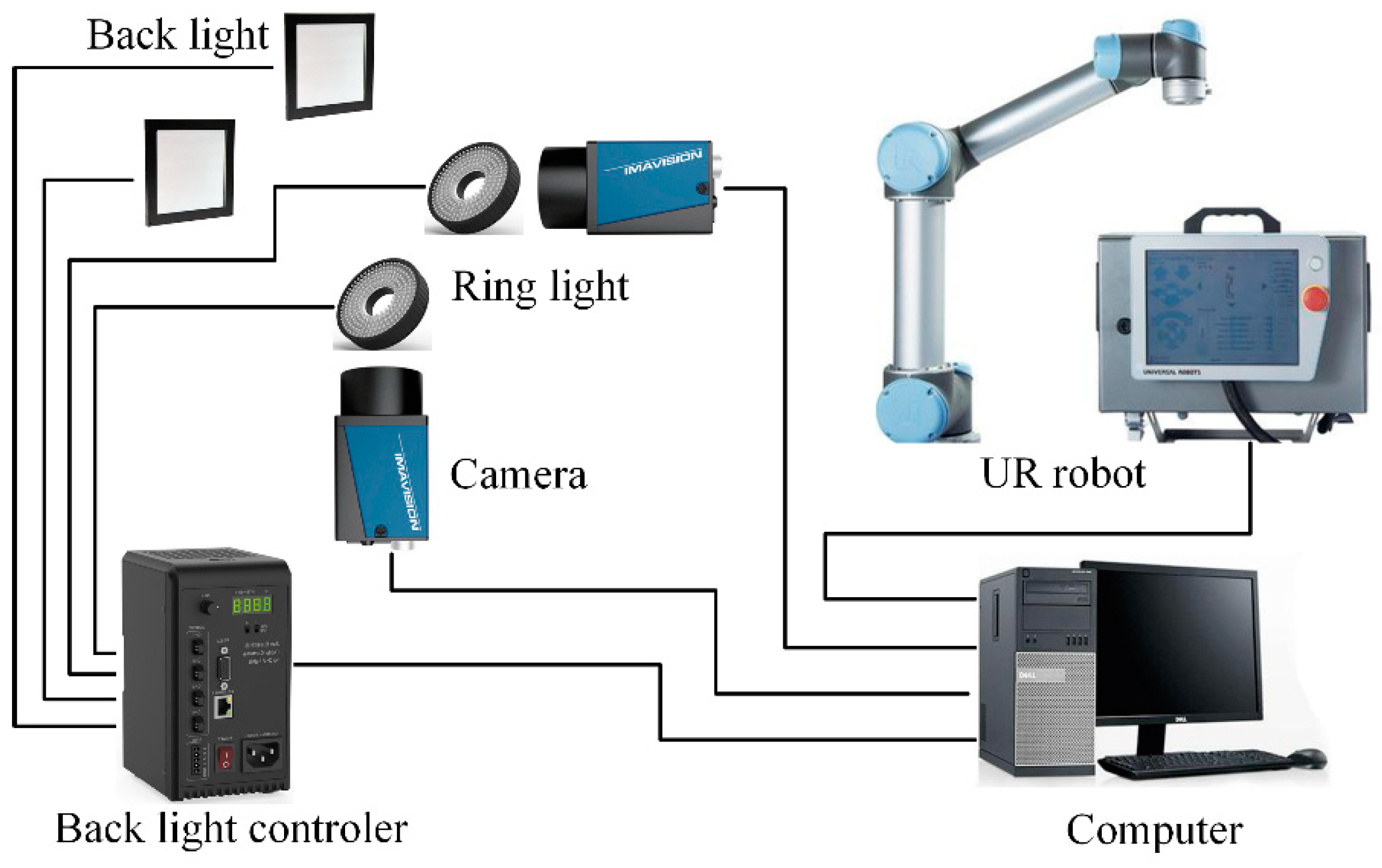
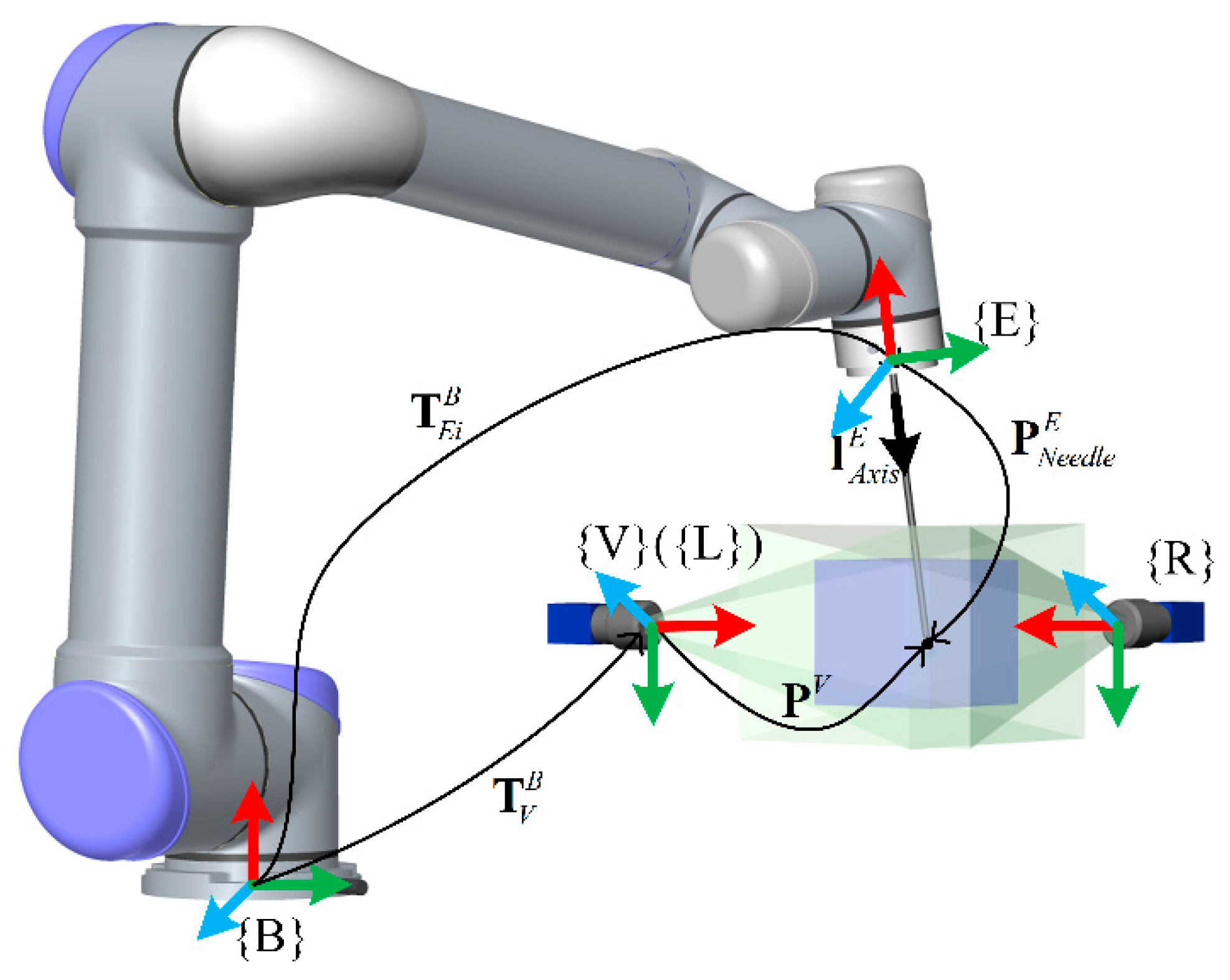
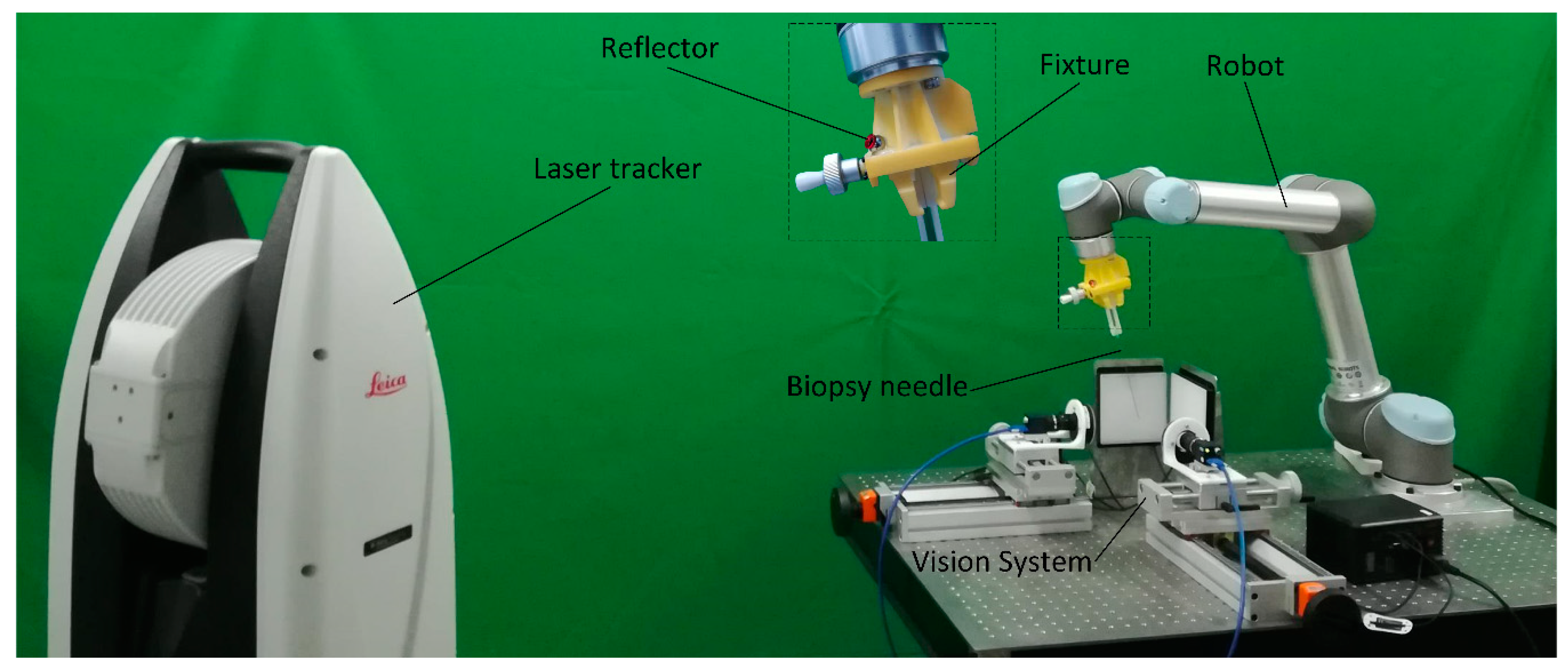
2.1. System Constitution
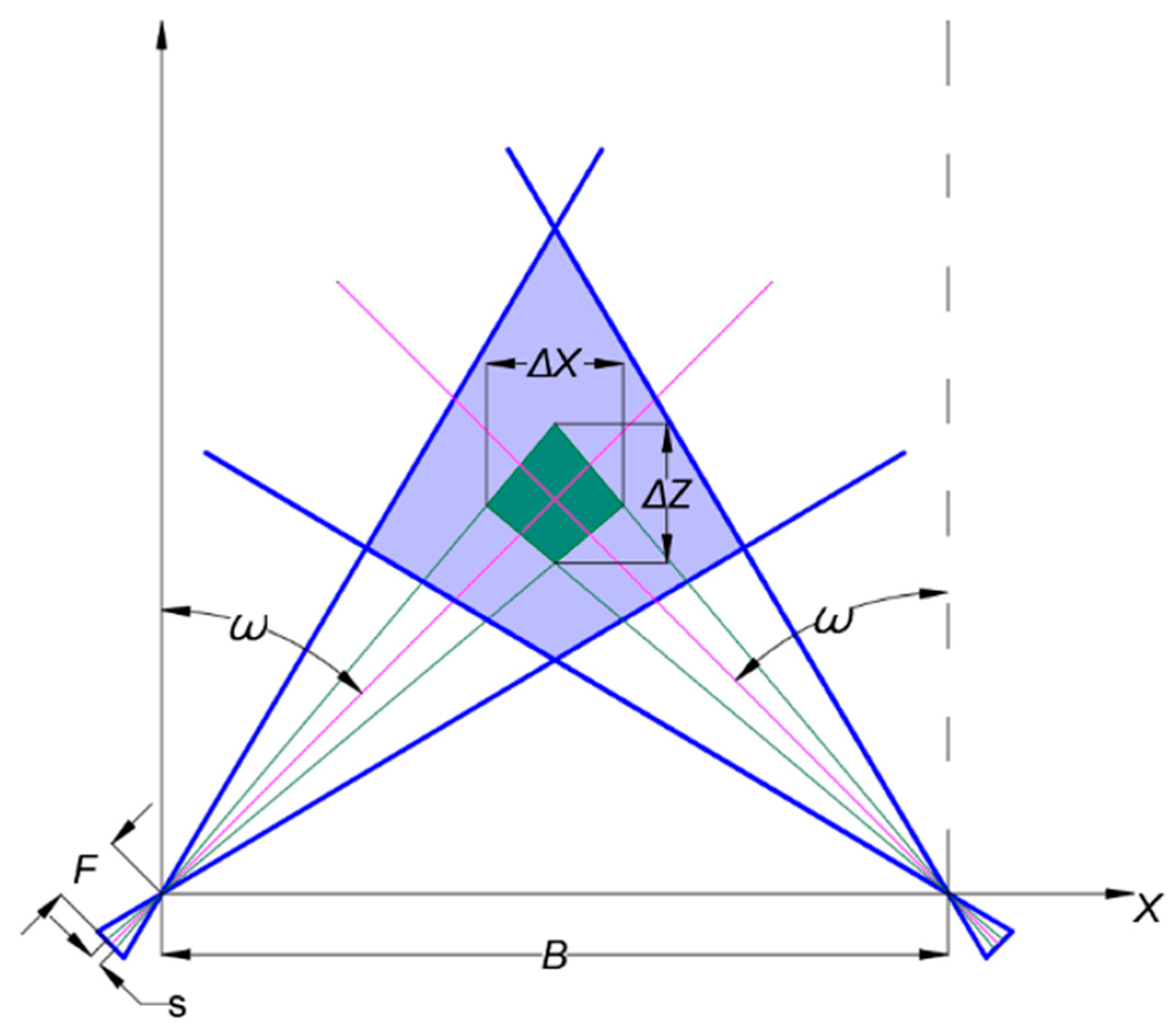
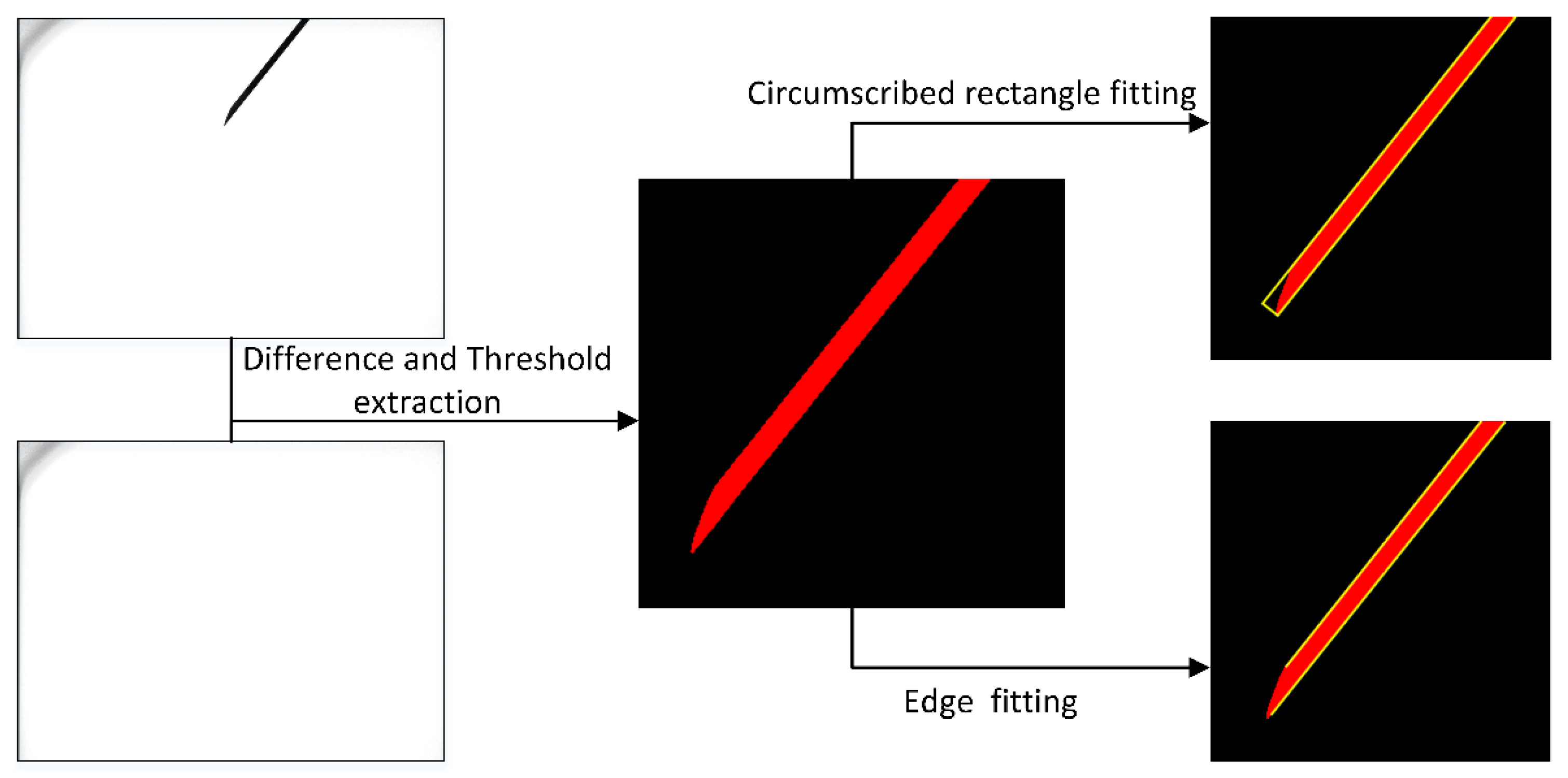
2.2. Binocular System Design and Image Processing
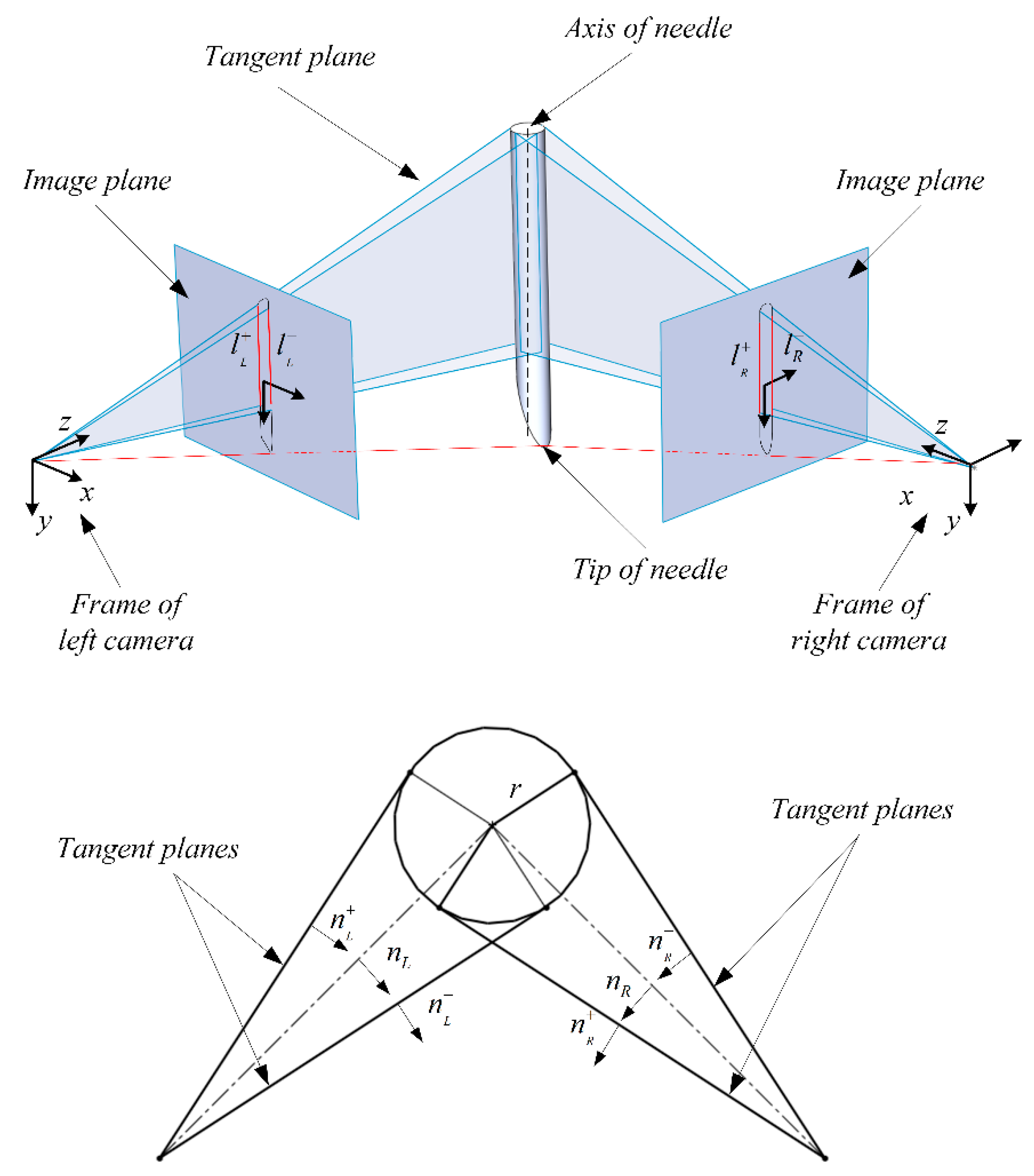
2.3. Positioning Needle
- (a)
- Take gray pictures when no objects are placed in the binocular system and record separately as and ;
- (b)
- Control the robot moving the needle tip to different positions within the measurement range of the binocular system and take pictures and ();
- (c)
- Subtract the image that contains the needle tip from the image that corresponds to the initial state of the camera without the needle tip using formula . The gray value of pixels less than 0 is truncated to 0 and greater than 255 is truncated to 255;
- (d)
- Select the pixels from whose gray values fulfill the condition based on the experience of the experimental;
- (e)
- The resulting image will contain the needle and partial noise. We calculate the size of all of the connected domains in the image and keep the largest connected domain. Then correct image distortion. Then, using a circular structure with a radius of 5 pixels, we perform a morphological opening operation on the image to smooth the outline of the needle.
- (f)
- Calculate the maximum circumscribed rectangle of the needle in the image and calculate the coordinates of all pixels where the short side intersects the boundary of the needle. Take the average of all intersection coordinates as the pixel coordinates of the needle tip.
- (g)
- Fit the edge of the needle with a polygon. Extract the two longest straight lines as input for calculating the needle direction.
2.4. TCP Calibration Algorithm
3. Experimental Design
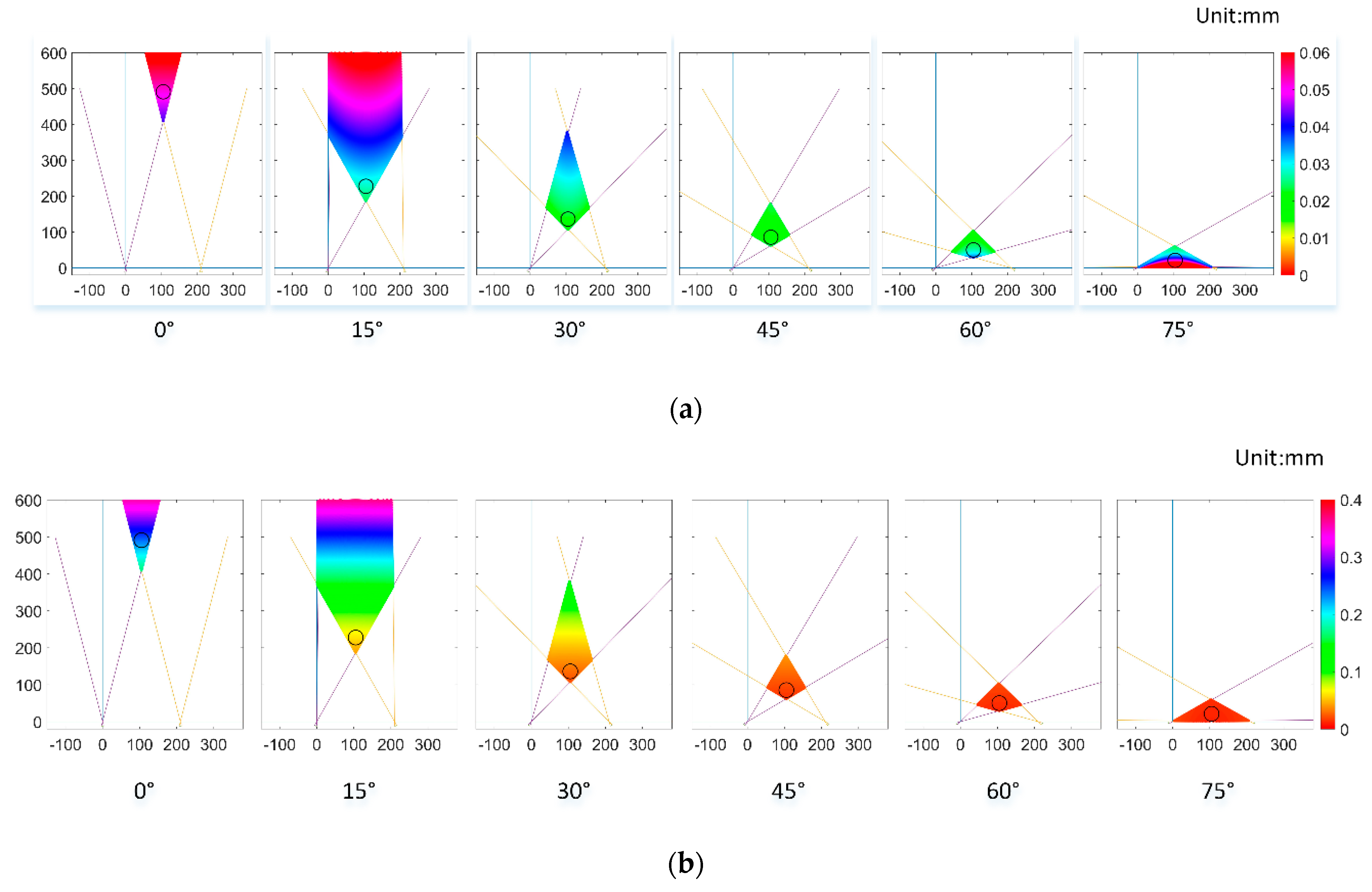
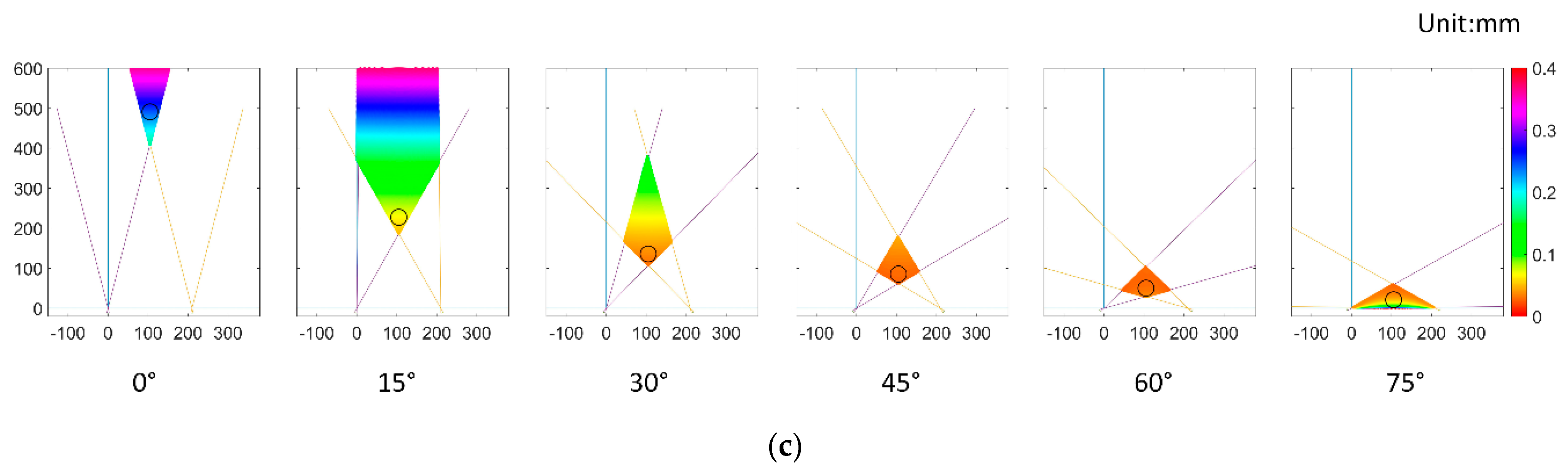
3.1. Accuracy Evaluation of Vision System
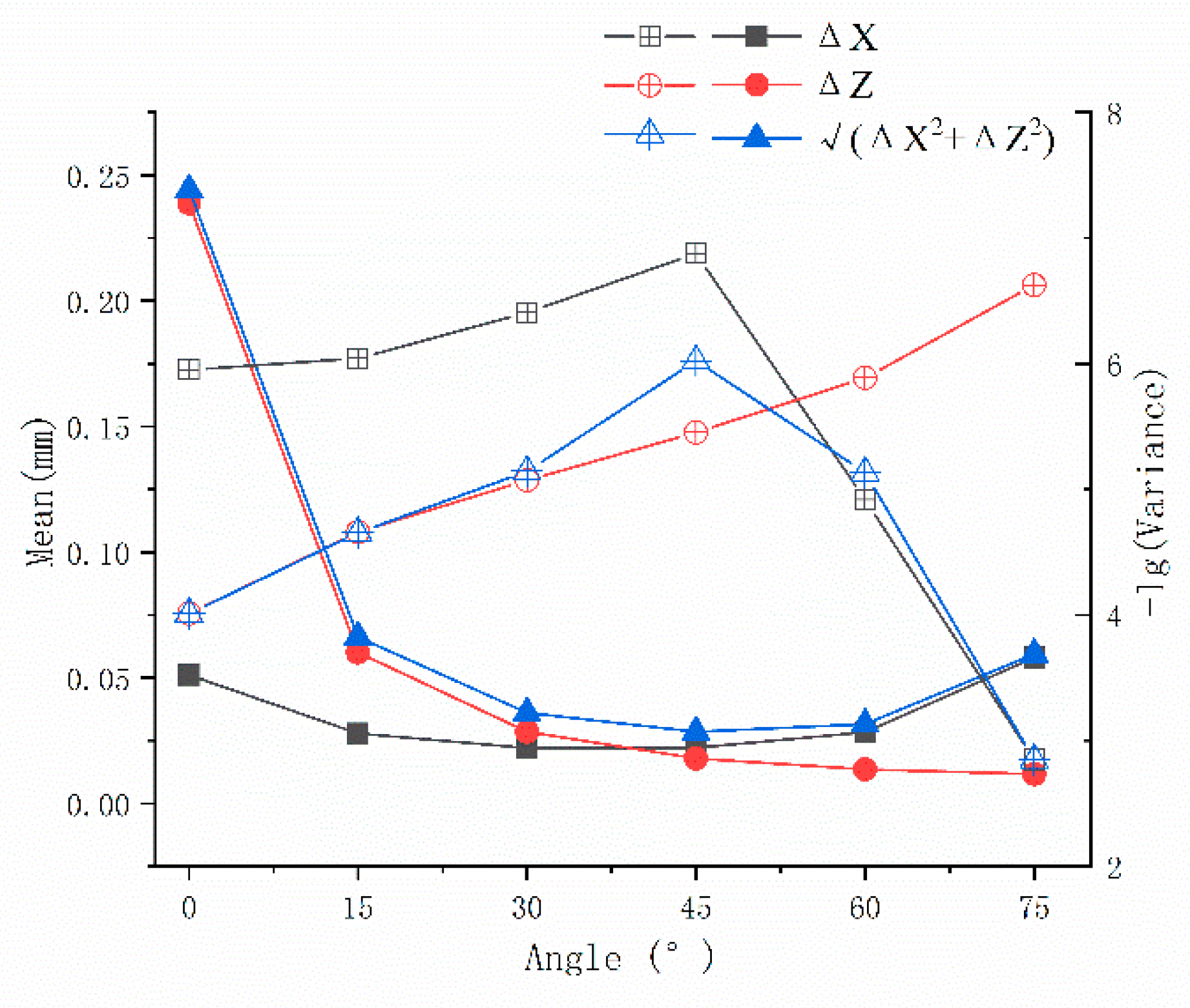
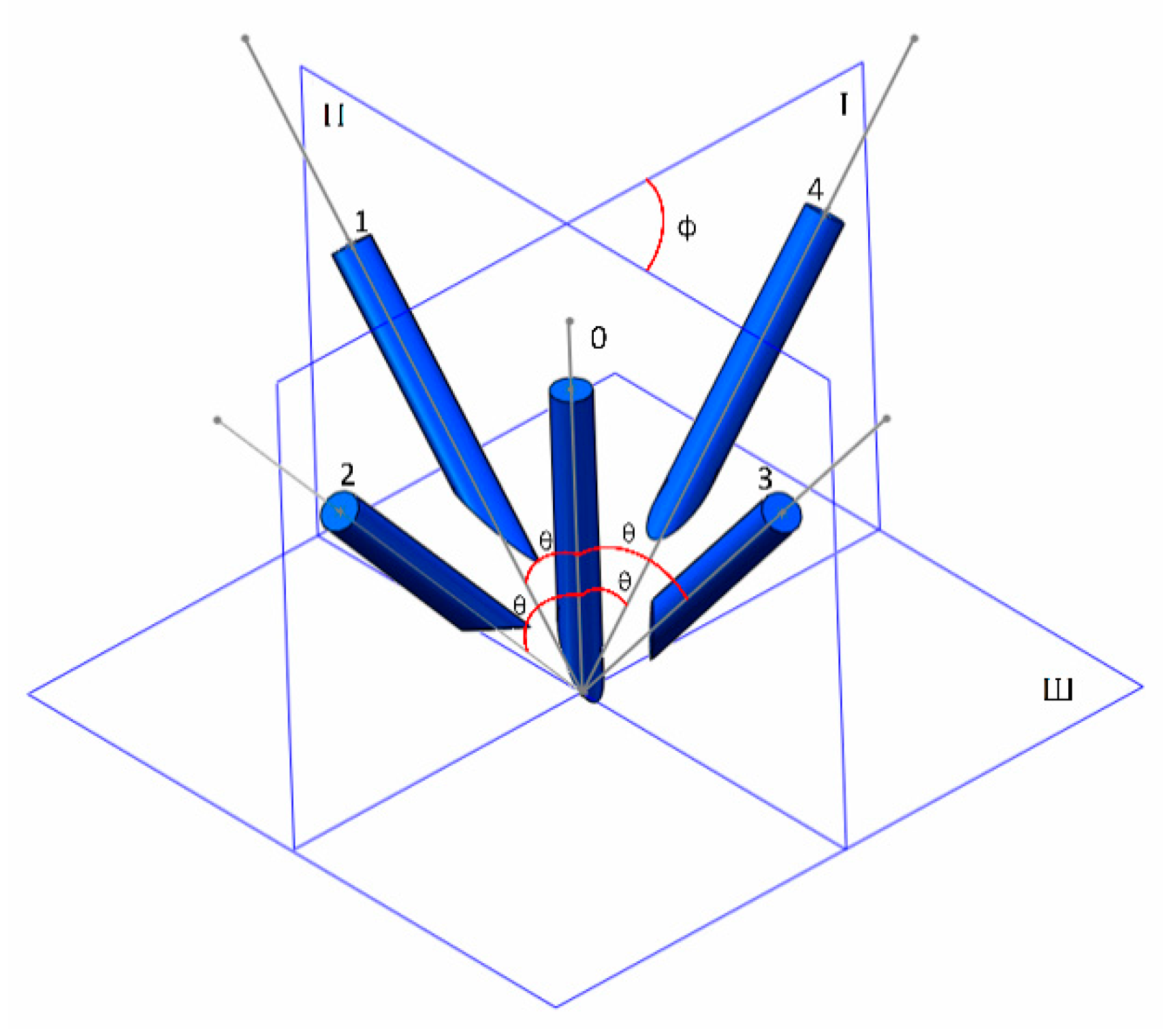
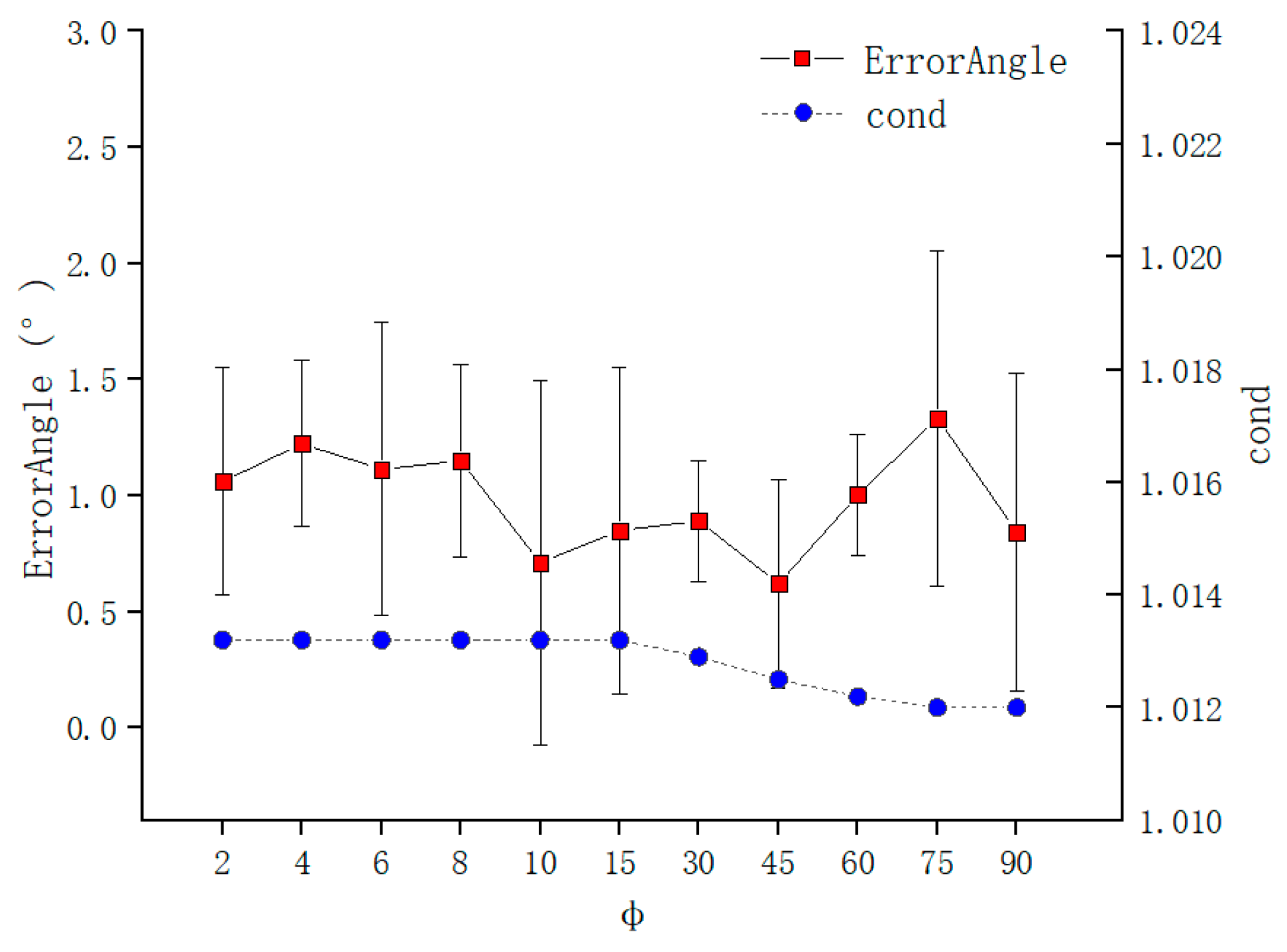
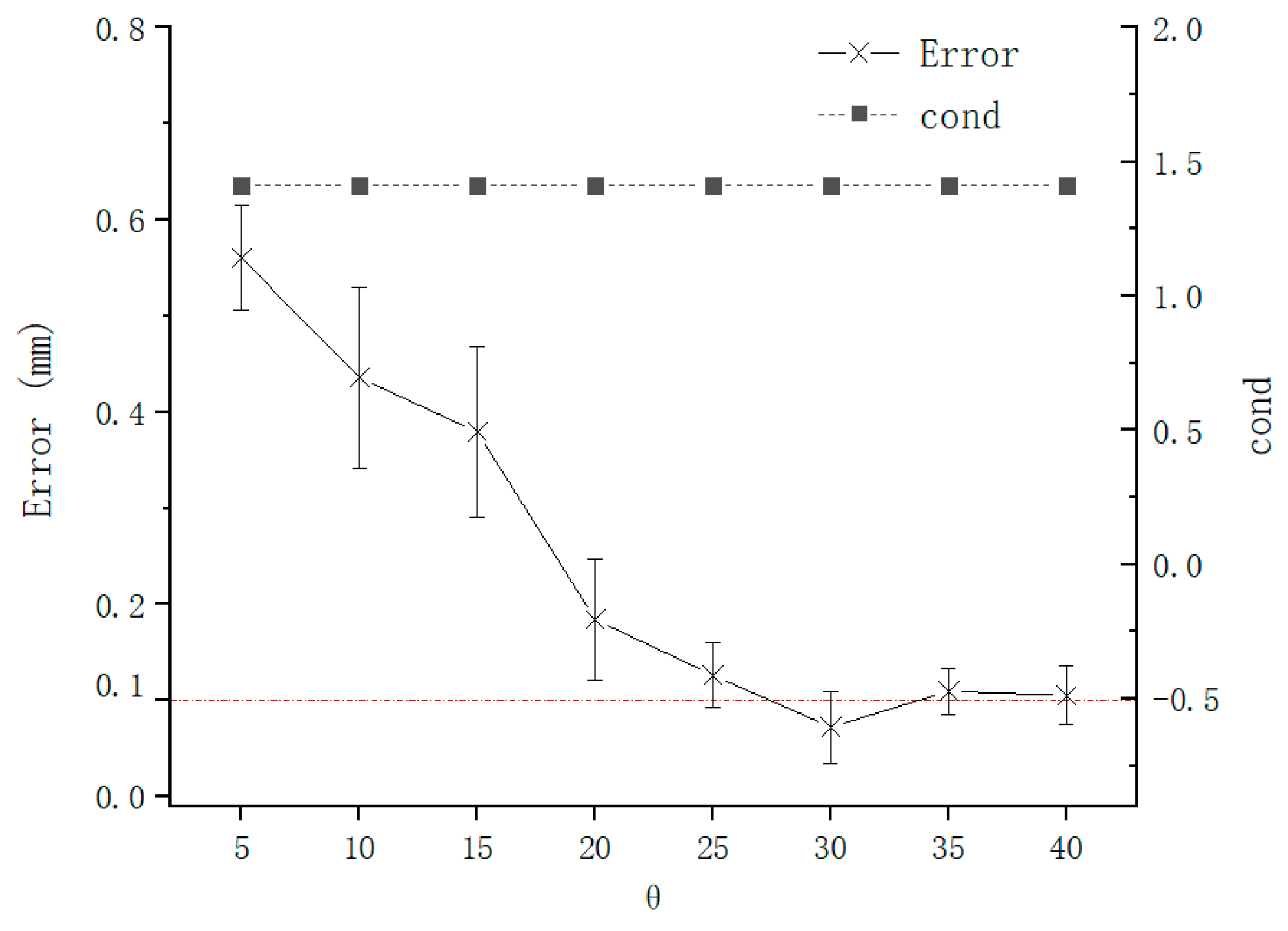
3.2. TCP Calibration Accuracy under Different Configurations
- θ was fixed, and was changed. This configuration would change .
- was fixed, and θ was changed. This configuration would change .
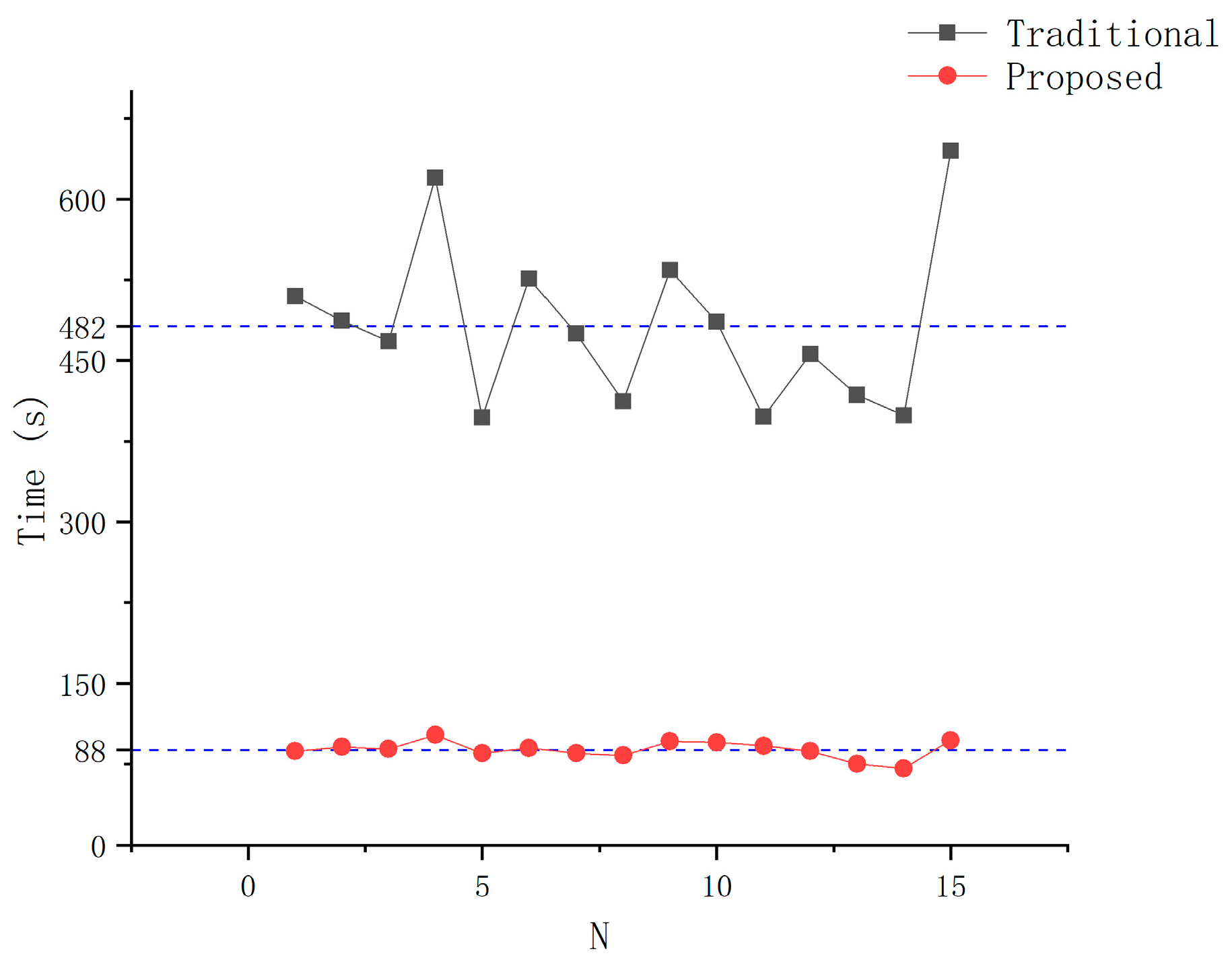
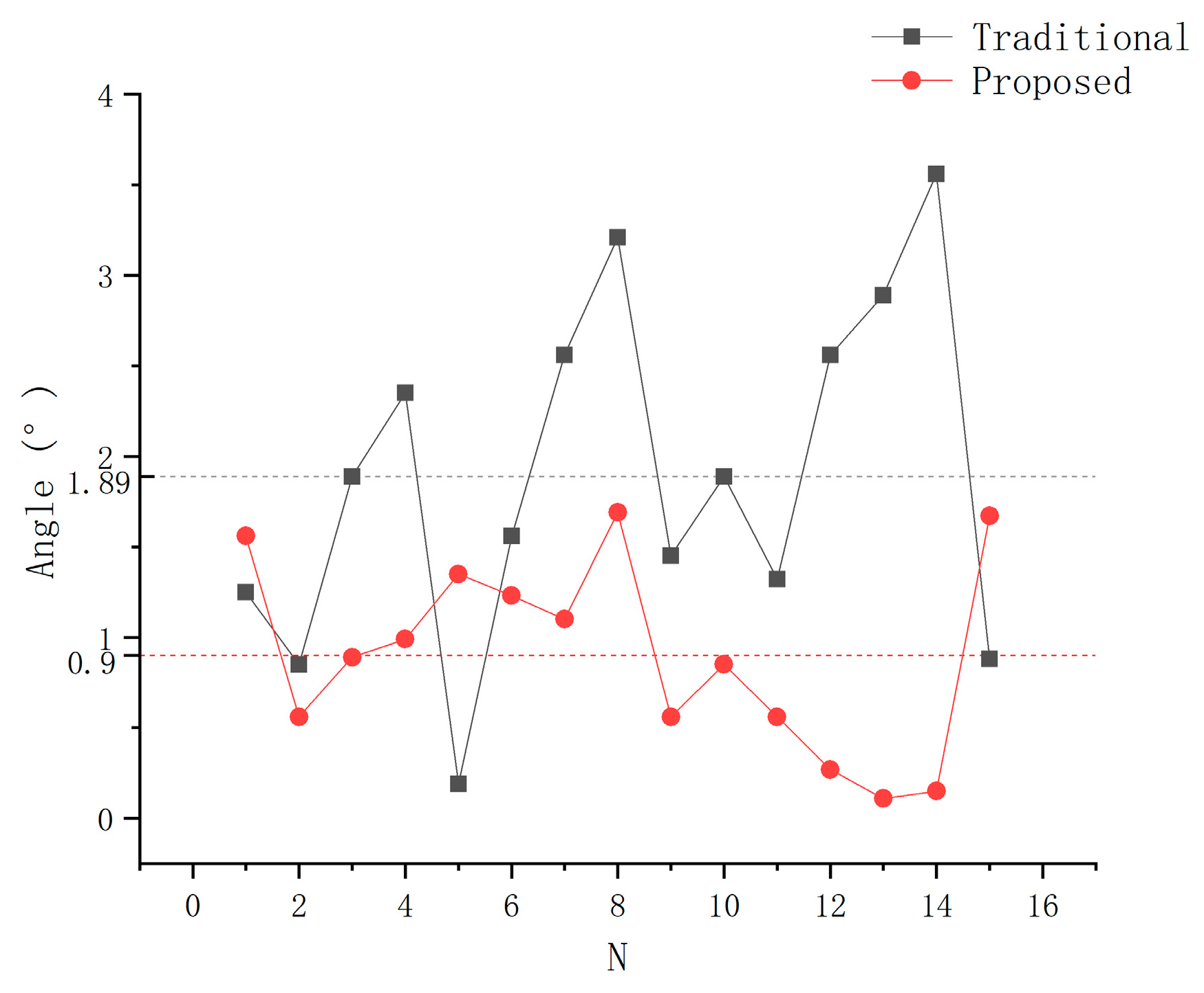
3.3. Comparison of the TCP Calibration with Traditional Methods
4. Results and Discussion
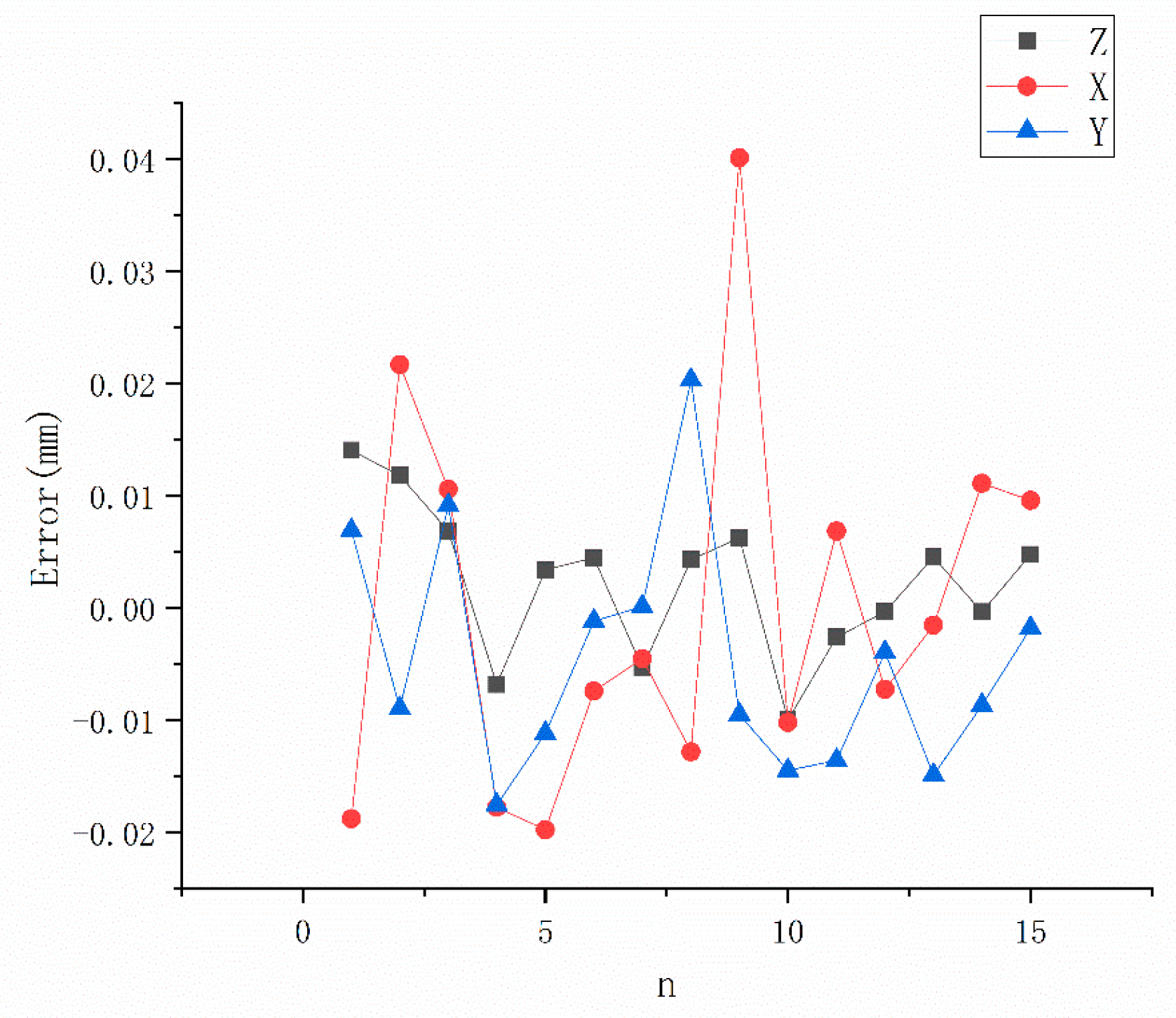
4.1. Accuracy Evaluation of Vision System
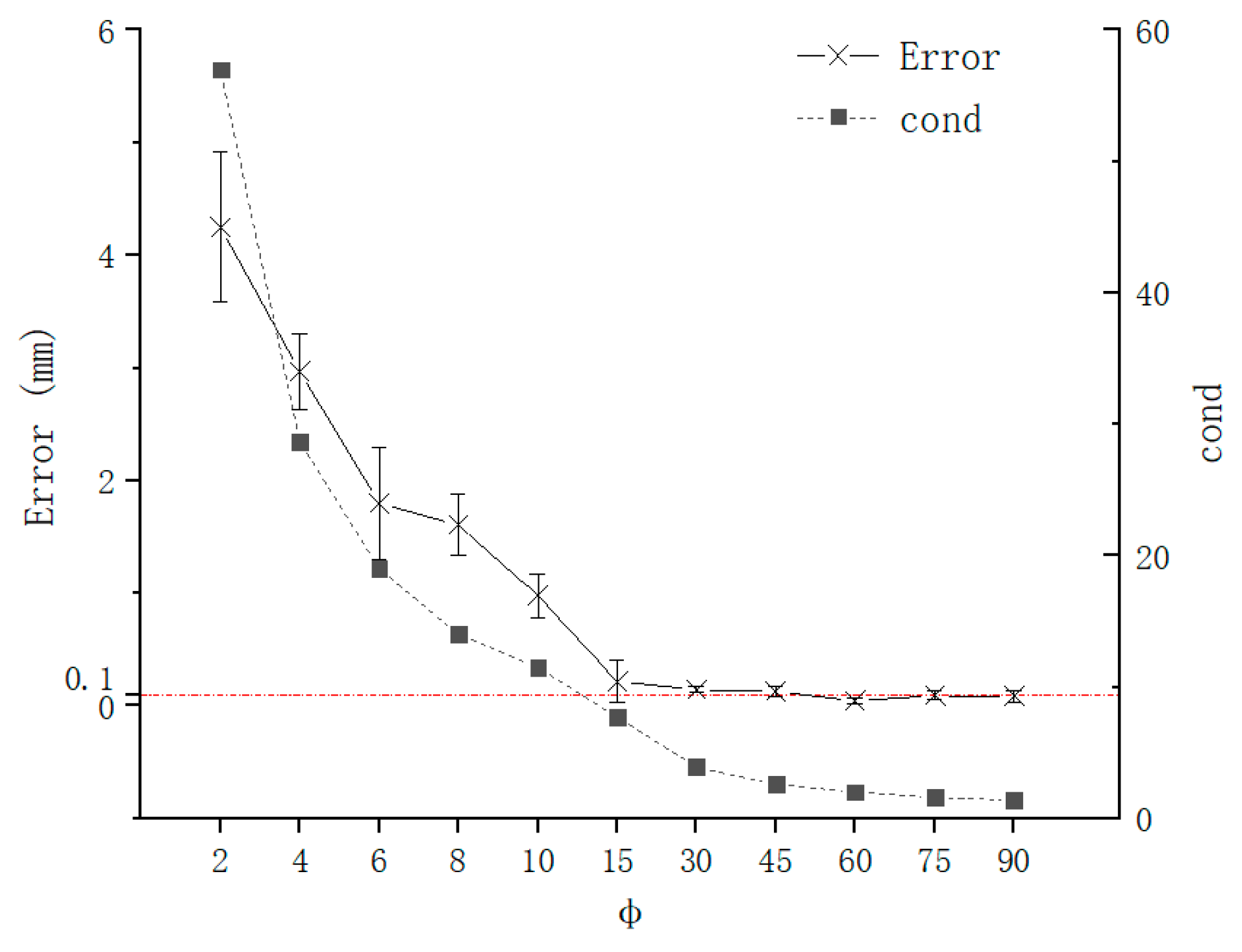
4.2. TCP Calibration Accuracy under Different Configurations
4.3. Comparison of TCP Calibration with Traditional Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Podder, T.K.; Beaulieu, L.; Caldwell, B.; Cormack, R.A.; Crass, J.B.; Dicker, A.P.; Fenster, A.; Fichtinger, G.; Meltsner, M.A.; Moerland, M.A. AAPM and GEC-ESTRO guidelines for image-guided robotic brachytherapy: Report of Task Group 192. Med. Phys. 2014, 41, 101501. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Yu, X.; Li, C.; Li, G.; Zhang, X.; Li, L. Space calibration of the cranial and maxillofacial robotic system in surgery. Comput. Assist. Surg. 2016, 21, 54–60. [Google Scholar] [CrossRef][Green Version]
- Zequn, L.; Changle, L.; Xuehe, Z.; Gangfeng, L.; Jie, Z. The Robot System for Brachytherapy. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 25–29. [Google Scholar]
- Cai, Y.; Gu, H.; Li, C.; Liu, H. Easy industrial robot cell coordinates calibration with touch panel. Robot. Comput. -Integr. Manuf. 2018, 50, 276–285. [Google Scholar] [CrossRef]
- Nof, S.Y. Handbook of Industrial Robotics; John Wiley & Sons: Hoboken, NJ, USA, 1999; ISBN 0-471-17783-0. [Google Scholar]
- Mizuno, T.; Hara, R.; Nishi, H. Method for Automatically Setting a Tool Tip Point. U.S. Patent 4,979,127, 18 December 1990. [Google Scholar]
- Shuo, X.; Bosheng, Y.; Ming, J. Study of robot tool coordibate frame calibration. Mach. Electron. 2012, 6, 60–63. [Google Scholar]
- Ge, J.; Gu, H.; Qi, L.; Li, Q. An automatic industrial robot cell calibration method. In Proceedings of the ISR/Robotik 2014, 41st International Symposium on Robotics, Munich, Germany, 2–3 June 2014; pp. 1–6. [Google Scholar]
- Zhuang, H.; Motaghedi, S.H.; Roth, Z.S. Robot calibration with planar constraints. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 1, pp. 805–810. [Google Scholar]
- Gu, H.; Li, Q.; Li, J. Quick robot cell calibration for small part assembly. In Proceedings of the 14th IFToMM World Congress, Taipei, Taiwan, 25–30 October 2015. [Google Scholar]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Pan, B.; Yu, L.; Zhang, Q. Review of single-camera stereo-digital image correlation techniques for full-field 3D shape and deformation measurement. Sci. China Technol. Sci. 2018, 61, 2–20. [Google Scholar] [CrossRef]
- Draelos, M.; Tang, G.; Keller, B.; Kuo, A.; Hauser, K.; Izatt, J.A. Optical Coherence Tomography Guided Robotic Needle Insertion for Deep Anterior Lamellar Keratoplasty. IEEE Trans. Biomed. Eng. 2020, 67, 2073–2083. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Draelos, M.; Tang, G.; Qian, R.; Kuo, A.; Izatt, J.; Hauser, K. Toward Autonomous Robotic Micro-Suturing using Optical Coherence Tomography Calibration and Path Planning. arXiv 2020, arXiv:2002.00530. [Google Scholar]
- Zhou, M.; Huang, K.; Eslami, A.; Roodaki, H.; Zapp, D.; Maier, M.; Lohmann, C.P.; Knoll, A.; Nasseri, M.A. Precision Needle Tip Localization Using Optical Coherence Tomography Images for Subretinal Injection. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4033–4040. [Google Scholar]
- Changjie, L.; Rongxing, B.; Yin, G.; Shibin, Y.; Yi, W. Calibration method of TCP based on stereo vision robot. Infrared Laser Eng. 2015, 44, 1912–1917. [Google Scholar]
- Luo, R.C.; Wang, H. Automated Tool Coordinate Calibration System of an Industrial Robot. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5592–5597. [Google Scholar]
- Wang, Z.; Liu, Z.; Ma, Q.; Cheng, A.; Liu, Y.; Kim, S.; Deguet, A.; Reiter, A.; Kazanzides, P.; Taylor, R.H. Vision-Based Calibration of Dual RCM-Based Robot Arms in Human-Robot Collaborative Minimally Invasive Surgery. IEEE Robot. Autom. Lett. 2018, 3, 672–679. [Google Scholar] [CrossRef]
- Zhang, X.; Song, Y.; Yang, Y.; Pan, H. Stereo vision based autonomous robot calibration. Robot. Auton. Syst. 2017, 93, 43–51. [Google Scholar] [CrossRef]
- Huang, C.; Guu, Y.; Chen, Y.-L.; Chu, C.; Chen, C. An automatic calibration method of TCP of robot arms. In Proceedings of the 4th International Conference on Production Automation and Mechanical Engineering, Montreal, QC, Canada, 3–4 August 2018; pp. 3–4. [Google Scholar]
- Yang, L.; Wang, B.; Zhang, R.; Zhou, H.; Wang, R. Analysis on Location Accuracy for the Binocular Stereo Vision System. IEEE Photonics J. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Zhu, C.; Yu, S.; Liu, C.; Jiang, P.; Shao, X.; He, X. Error estimation of 3D reconstruction in 3D digital image correlation. Meas. Sci. Technol. 2019, 30, 025204. [Google Scholar] [CrossRef]
- Yuntong, D. External Parameters Optimization and High-Precision Pose Recognition in Multi-Camera Measurement. Ph.D. Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]
- Zhang, G. Vision Measurement; Science Press: Beijing, China, 2008; pp. 145–147. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003; pp. 152–191. [Google Scholar]
- Doignon, C.; de Mathelin, M. A Degenerate Conic-Based Method for a Direct Fitting and 3-D Pose of Cylinders with a Single Perspective View. In Proceedings of the Proceedings 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 4220–4225. [Google Scholar]
- Becke, M.; Schlegl, T. Least squares pose estimation of cylinder axes from multiple views using contour line features. In Proceedings of the IECON 2015 41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 001855–001861. [Google Scholar]
- Navab, N.; Appel, M. Canonical Representation and Multi-View Geometry of Cylinders. Int. J. Comput. Vis. 2006, 2, 133–149. [Google Scholar] [CrossRef]
- Huang, J.-B.; Chen, Z.; Chia, T.-L. Pose determination of a cylinder using reprojection transformation. Pattern Recognit. Lett. 1996, 17, 1089–1099. [Google Scholar] [CrossRef]
- Becke, M. On modeling and least squares fitting of cylinders from single and multiple views using contour line features. In Proceedings of the 9th International Conference on Intelligent Robotics and Applications (ICIRA), Portsmouth, UK, 24–27 August 2015; pp. 372–385. [Google Scholar]
- Ma, Q.; Goh, Z.; Ruan, S.; Chirikjian, G.S. Probabilistic approaches to the $$ AXB = YCZ $$AXB=YCZcalibration problem in multi-robot systems. Auton Robot 2018, 42, 1497–1520. [Google Scholar] [CrossRef]
- Sun, Y.; Pan, B.; Guo, Y.; Fu, Y.; Niu, G. Vision-based hand–eye calibration for robot-assisted minimally invasive surgery. Int. J. Cars 2020. [Google Scholar] [CrossRef] [PubMed]
- Shah, M.; Eastman, R.D.; Hong, T. An overview of robot-sensor calibration methods for evaluation of perception systems. In Proceedings of the Workshop on Performance Metrics for Intelligent Systems, College Park, MD, USA, 20–22 March 2012; pp. 15–20. [Google Scholar]
- Li, P.; Yang, Z.; Jiang, S. Needle-tissue interactive mechanism and steering control in image-guided robot-assisted minimally invasive surgery: A review. Med Biol. Eng. Comput. 2018, 56, 931–949. [Google Scholar] [CrossRef] [PubMed]
- Demmel, J.W. Applied Numerical Linear Algebra; SIAM: Philadelphia, PA, USA, 1997; pp. 117–118. [Google Scholar]



| Right Camera | Left Camera | |
|---|---|---|
| Focus(mm) | 12.39 | 12.41 |
| Cell Width (Sx) (μm) | 1.25 | 1.25 |
| Cell Height (Sy) (μm) | 1.25 | 1.25 |
| Center Column (Cx) (pixel) | 2387.07 | 2433.72 |
| Center Row (Cy) (pixel) | 1820.48 | 1861.79 |
| 2nd Order Radial Distortion (K1) (1/pixel2) | 8.90 × 10−10 | 8.80 × 10−10 |
| 4th Order Radial Distortion (K2) (1/pixel4) | 3.42 × 10−17 | −1.06 × 10−16 |
| 6th Order Radial Distortion (K3) (1/pixel6) | −3.06 × 10−24 | 1.99 × 10−23 |
| 2nd Order Tangential Distortion (P1) (1/pixel2) | 1.89 × 10−13 | 1.41 × 10−13 |
| 2nd Order Tangential Distortion (P2) (1/pixel2) | −1.56 × 10−13 | 1.56 × 10−14 |
| Image Width (pixel) | 4912 | 4912 |
| Image Height (pixel) | 3684 | 3684 |
| Relative position (mm) | 162.39, −4.7 × 10−5, 157.34 | |
| Relative pose (°) | 2.93, 270.23, 3.06 | |
| Reprojection error (pixel) | 0.28 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, C.; Fan, Y.; Zhang, X.; Zhao, J. Physician-Friendly Tool Center Point Calibration Method for Robot-Assisted Puncture Surgery. Sensors 2021, 21, 366. https://doi.org/10.3390/s21020366
Zhang L, Li C, Fan Y, Zhang X, Zhao J. Physician-Friendly Tool Center Point Calibration Method for Robot-Assisted Puncture Surgery. Sensors. 2021; 21(2):366. https://doi.org/10.3390/s21020366
Chicago/Turabian StyleZhang, Leifeng, Changle Li, Yilun Fan, Xuehe Zhang, and Jie Zhao. 2021. "Physician-Friendly Tool Center Point Calibration Method for Robot-Assisted Puncture Surgery" Sensors 21, no. 2: 366. https://doi.org/10.3390/s21020366
APA StyleZhang, L., Li, C., Fan, Y., Zhang, X., & Zhao, J. (2021). Physician-Friendly Tool Center Point Calibration Method for Robot-Assisted Puncture Surgery. Sensors, 21(2), 366. https://doi.org/10.3390/s21020366






