Determining Surface Shape of Translucent Objects with the Combination of Laser-Beam-Based Structured Light and Polarization Technique
Abstract
:1. Introduction
2. Theoretical Analysis and Mathematical Description of the Proposed Method
2.1. Generation and Propagation of the Sinusoidal Fringe Signal
2.2. Reflection and Transmission of the Projected Sinusoidal Fringe Signal on the Surface of the Translucent Object
2.3. Separating from
2.3.1. Removing the Effect of Using an Optical Filter
2.3.2. Eliminating the Effect of and Using a Polarizer
3. Technical Analysis of Measurement and Reconstruction
4. Experimental Results and Discussion
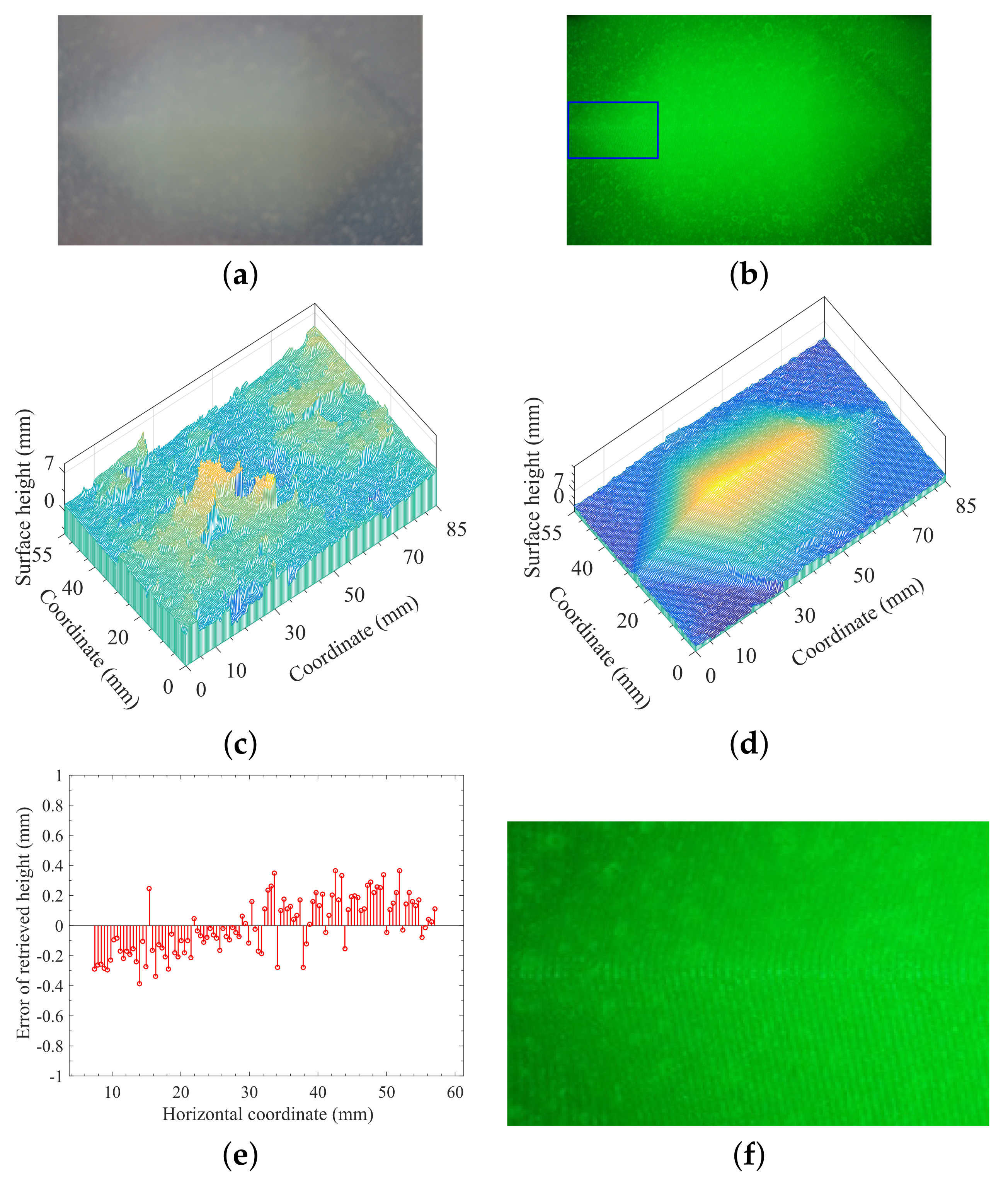
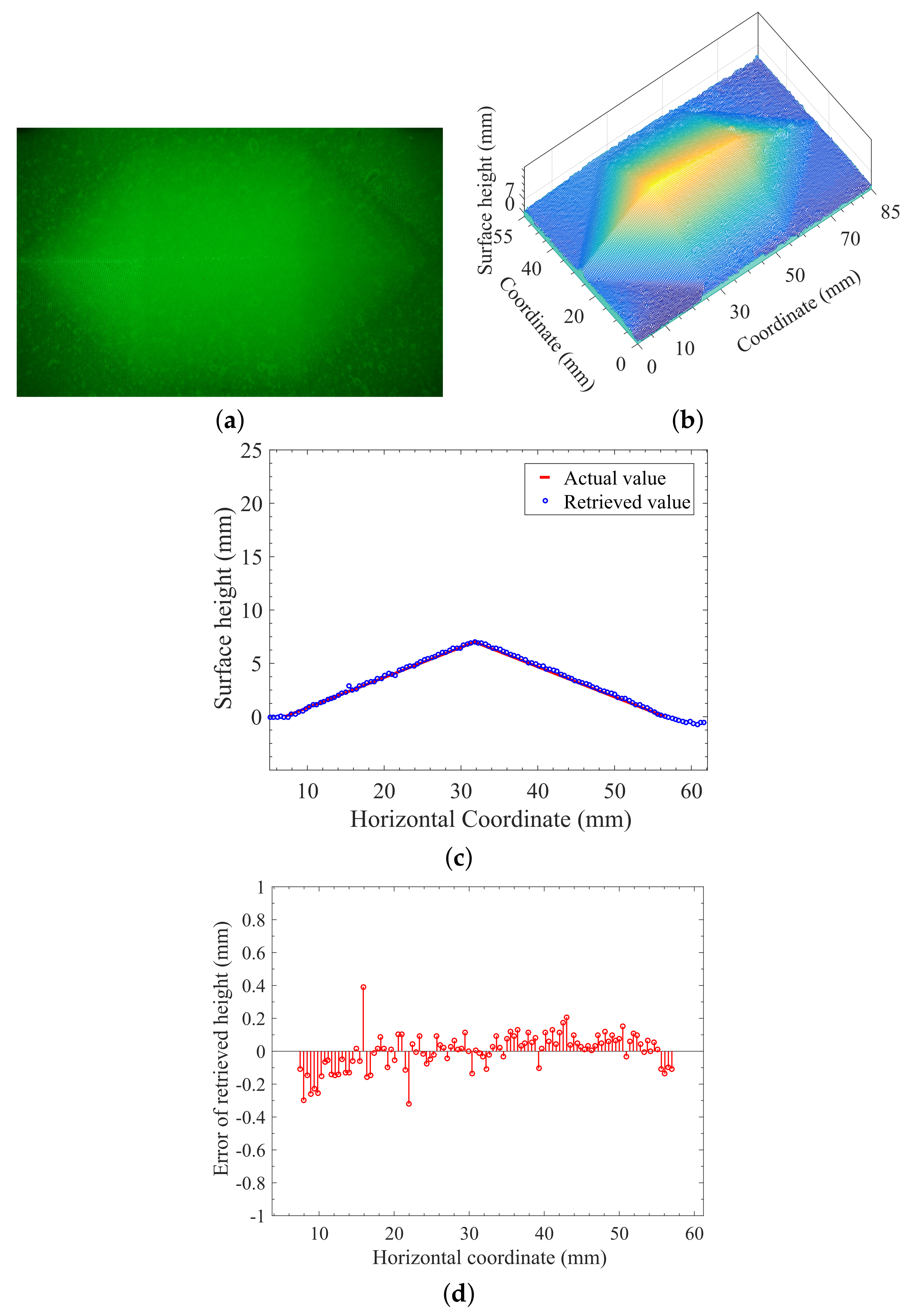
4.1. Measurement and Reconstruction of a 3D Translucent Object Using Optical Filter
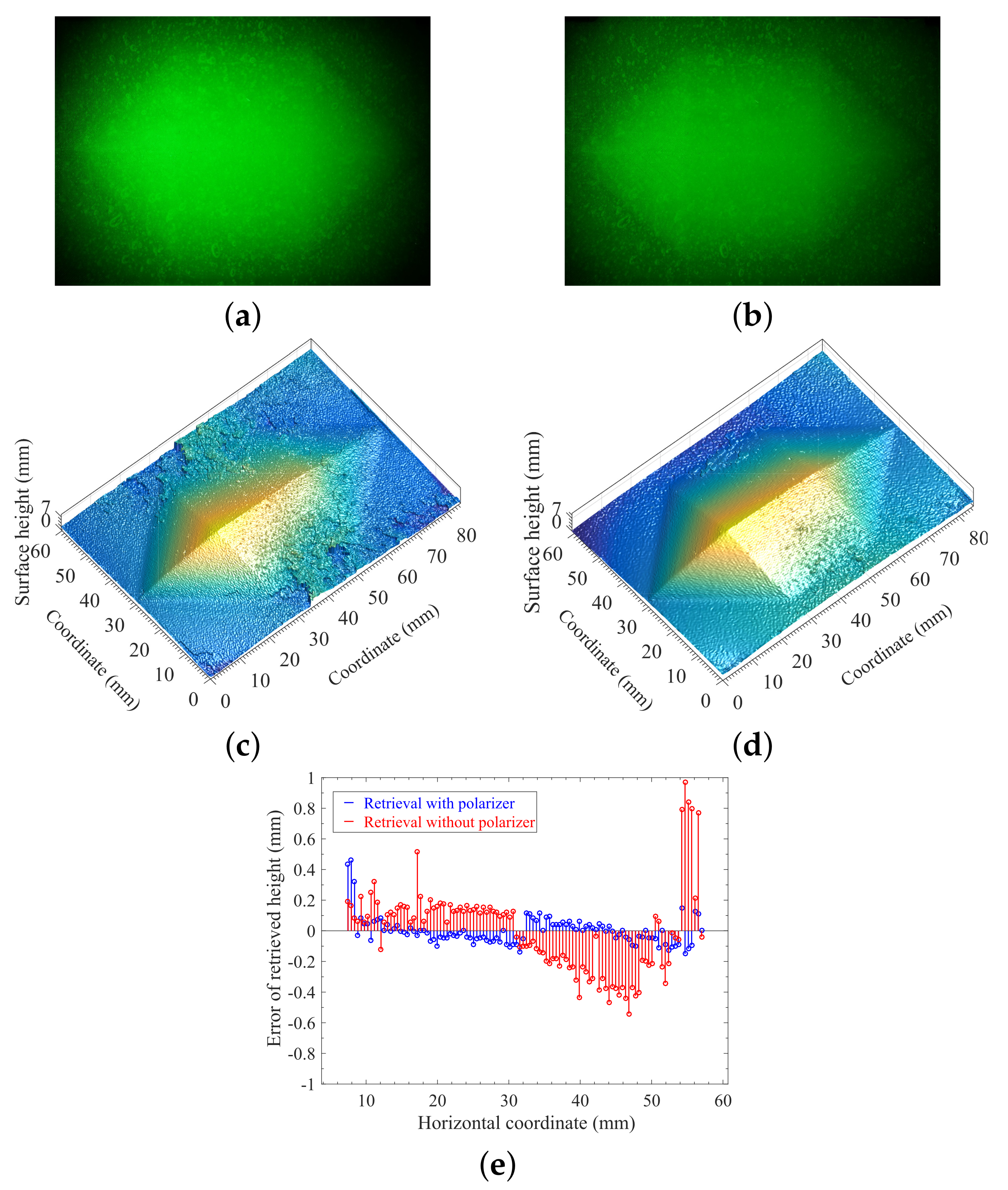
4.2. Measurement and Reconstruction of a 3D Translucent Object Using Optical Polarizer
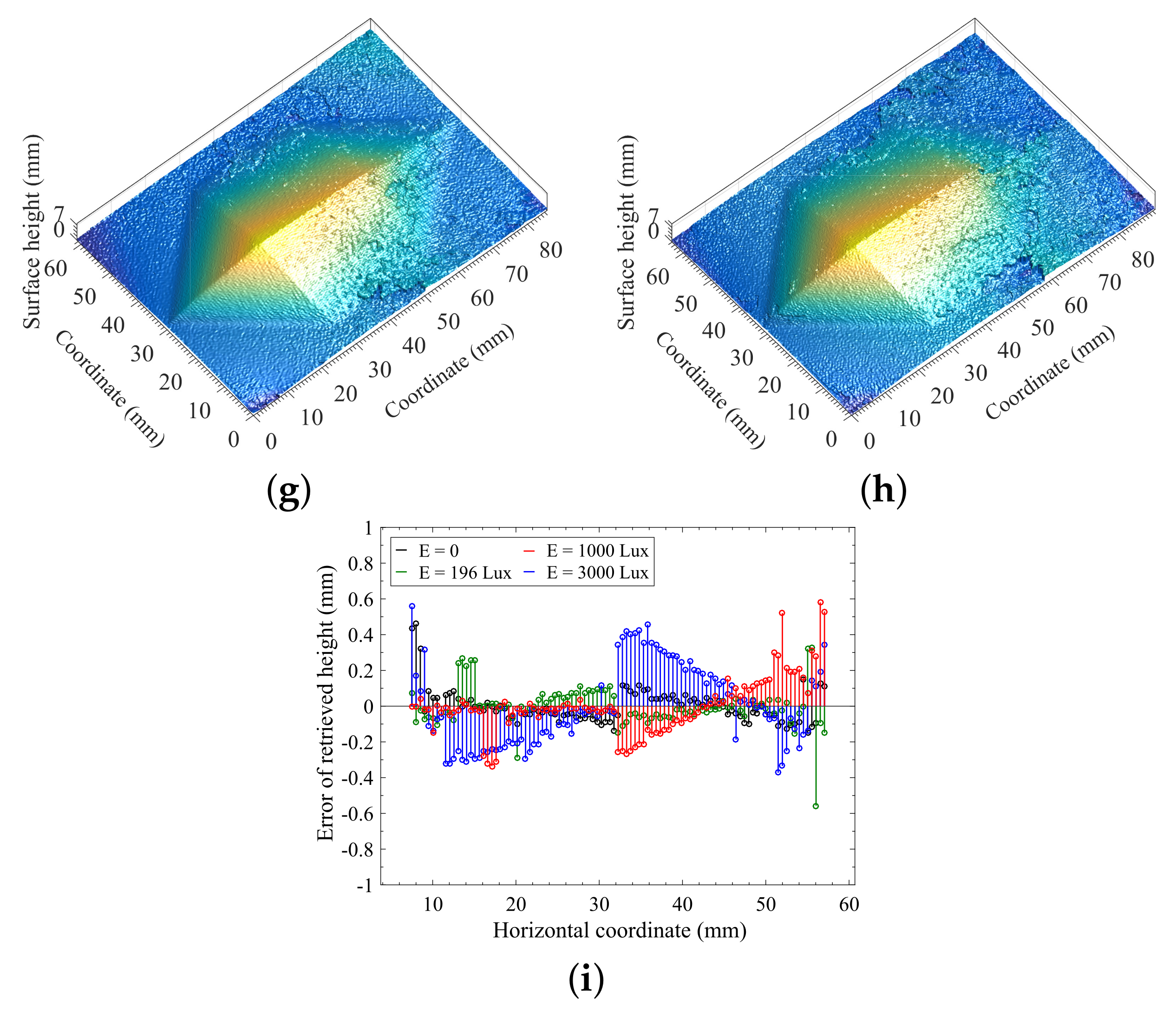
4.3. Measurement and Reconstruction of 3D Translucent Objects under Different Background Illumination
4.4. Analysis and Discussion of the Accuracy of Reconstruction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holroyd, M.; Lawrence, J. An analysis of using high-frequency sinusoidal illumination to measure the 3D shape of translucent objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2985–2991. [Google Scholar] [CrossRef]
- Ihrke, I.; Kutulakos, K.N.; Lensch, H.P.A.; Magnor, M.; Heidrich, W. Transparent and specular object reconstruction. Comput. Graph. Forum 2010, 29, 2400–2426. [Google Scholar] [CrossRef]
- Park, J.; Sabharwal, A.; Veeraraghavan, A. Direct-global separation for improved imaging photoplethysmography. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1375–1384. [Google Scholar] [CrossRef]
- Subpa-Asa, A.; Fu, Y.; Zheng, Y.; Amano, T.; Sato, T. Separating the direct and global components of a single image. J. Inf. Process. 2018, 26, 755–767. [Google Scholar] [CrossRef] [Green Version]
- Nayar, S.K.; Krishnan, G.; Grossberg, M.D.; Raskar, R. Fast separation of direct and global components of a scene using high frequency illumination. ACM Trans. Graph. 2006, 25, 935–944. [Google Scholar] [CrossRef]
- Rao, L.; Da, F. Local blur analysis and phase error correction method for fringe projection profilometry systems. Appl. Opt. 2018, 57, 4267–4276. [Google Scholar] [CrossRef]
- Torii, M.; Okabe, T.; Amano, T. Multispectral direct-global separation of dynamic scenes. In Proceedings of the 19th IEEE Winter Conference on Applications of Computer Vision, Waikoloa Village, HI, USA, 8–10 January 2019; pp. 1923–1931. [Google Scholar] [CrossRef]
- Lockerman, Y.D.; Brenner, S.; Lanzone, J.; Doronin, A.; Rushmeier, H. Testing spatial patterns for acquiring shape and subsurface scattering properties. Electron. Imaging 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Rowe, M.P.; Pugh, E.N.; Tyo, J.S.; Engheta, N. Polarization-difference imaging: A biologically inspired technique for observation through scattering media. Opt. Lett. 1995, 20, 608–610. [Google Scholar] [CrossRef]
- Tyo, J.S.; Rowe, M.P.; Pugh, E.N., Jr.; Engheta, N. Target detection in optically scattering media by polarization-difference imaging. Appl. Opt. 1996, 35, 1855–1870. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Lensch, H.P.A.; Fuchs, C.; Seidel, H.-P. Polarization and phase-shifting for 3D scanning of translucent objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1829–1836. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Zhao, H.; Jiang, H.; Li, X. High-accuracy 3D shape measurement of translucent objects by fringe projection profilometry. Opt. Express 2019, 27, 18421–18434. [Google Scholar] [CrossRef]
- Lutzke, P.; Kuhmstedt, P.; Notni, G. Measuring error compensation on three-dimensional scans of translucent objects. Opt. Eng. 2011, 50, 063601. [Google Scholar] [CrossRef]
- Ohtani, K.; Li, L.; Baba, M. Determining surface shape of translucent objects by using laser rangefinder. In Proceedings of the 2013 IEEE/SICE International Symposium on System Integration, Kobe, Japan, 15–17 December 2013; pp. 454–459. [Google Scholar] [CrossRef]
- Inoshita, C.; Mukaigawa, Y.; Matsushita, Y.; Yagi, Y. Surface normal deconvolution: Photometric stereo for optically thick translucent objects. Lect. Notes Comput. Sci. 2014, 8690, 346–359. [Google Scholar] [CrossRef]
- Lutzke, P.; Heist, S.; Kuhmstedt, P.; Kowarschik, R.; Notni, G. Monte Carlo simulation of three-dimensional measurements of translucent objects. Opt. Eng. 2015, 54, 084111. [Google Scholar] [CrossRef]
- Jiang, H.; Zhai, H.; Xu, Y.; Li, X.; Zhao, H. 3D shape measurement of translucent objects based on Fourier single-pixel imaging in projector-camera system. Opt. Express 2019, 27, 33564–33574. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Agrawal, A.; Veeraraghavan, A.; Narasimhan, S.G. A practical approach to 3D scanning in the presence of inter-reflections, subsurface scattering and defocus. Int. J. Comput. Vis. 2013, 102, 33–55. [Google Scholar] [CrossRef]
- Gkioulekas, I.; Walter, B.; Adelson, E.H.; Bala, K.; Zickler, T. On the appearance of translucent edges. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5528–5536. [Google Scholar] [CrossRef] [Green Version]
- Goodman, J.W. Introduction to Fourier Optics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1996; Chapter 3. [Google Scholar]
- Reichelt, A.; Storck, E.; Wolff, U. Near field diffraction pattern behind a sinusoidal phase grating. Opt. Commun. 1971, 3, 169–172. [Google Scholar] [CrossRef]
- Harvey, J.E.; Pfisterer, R.N. Understanding diffraction grating behavior: Including conical diffraction and Rayleigh anomalies from transmission gratings. Opt. Eng. 2019, 58, 087105. [Google Scholar] [CrossRef]
- Smolka, F.M.; Hill, H.A. Room temperature vulcanizing silicone rubber as an optical element. Appl. Opt. 1977, 16, 292–293. [Google Scholar] [CrossRef] [PubMed]
- Shackelford, J.F. Introduction to Materials Science for Engineers; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Academic: New York, NY, USA, 1978. [Google Scholar]
- Chen, B.; Stamnes, K.; Stamnes, J.J. Validity of the diffusion approximation in bio-optical imaging. Appl. Opt. 2001, 40, 6356–6366. [Google Scholar] [CrossRef]
- Umeyama, S.; Godin, G. Separation of diffuse and specular components of surface reflection by use of polarization and statistical analysis of images. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 639–647. [Google Scholar] [CrossRef]
- Li, H.; Chen, B.; Feng, K.; Ma, H. Modulation transfer function measurement method for fiber optic imaging bundles. Opt. Laser Technol. 2008, 40, 415–519. [Google Scholar] [CrossRef]
- Chen, B.; Li, H.; Yue, J.; Shi, P. Fourier-transform-based surface measurement and reconstruction of human face using the projection of monochromatic structured light. Sensors 2021, 21, 2529. [Google Scholar] [CrossRef]
- Chen, B.; Gao, H.; Li, H.; Ma, H.; Gao, P.; Chu, P.; Shi, P. Indoor and outdoor surface measurement of 3D objects under different background illuminations and wind conditions using laser-beam-based sinusoidal fringe projections. Photonics 2021, 8, 178. [Google Scholar] [CrossRef]
- Takeda, M.; Mutoh, K. Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 1983, 22, 3977–3982. [Google Scholar] [CrossRef] [PubMed]
- Maurel, A.; Cobelli, P.; Pagneux, V.; Petitjeans, P. Experimental and theoretical inspection of the phase-to-height relation in Fourier transform profilometry. Appl. Opt. 2009, 48, 380–392. [Google Scholar] [CrossRef] [PubMed]
- Zappa, E.; Busca, G. Static and dynamic features of Fourier transform profilometry: A review. Opt. Laser Eng. 2012, 50, 1140–1151. [Google Scholar] [CrossRef]
- Yun, H.; Li, B.; Zhang, S. Pixel-by-pixel absolute three-dimensional shape meausrement with Fourier transform profilometry. Appl. Opt. 2017, 56, 1472–1480. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Gao, N.; Xiao, Y.; Gao, F.; Jiang, X. Single-shot 3D shape measurement of discontinuous objects based on a coaxial fringe projection system. Appl. Opt. 2019, 58, A169–A178. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Shi, P.; Wang, Y.; Xu, Y.; Ma, H.; Wang, R.; Zheng, C.; Chu, P. Determining Surface Shape of Translucent Objects with the Combination of Laser-Beam-Based Structured Light and Polarization Technique. Sensors 2021, 21, 6587. https://doi.org/10.3390/s21196587
Chen B, Shi P, Wang Y, Xu Y, Ma H, Wang R, Zheng C, Chu P. Determining Surface Shape of Translucent Objects with the Combination of Laser-Beam-Based Structured Light and Polarization Technique. Sensors. 2021; 21(19):6587. https://doi.org/10.3390/s21196587
Chicago/Turabian StyleChen, Bingquan, Peng Shi, Yanhua Wang, Yongze Xu, Hongyang Ma, Ruirong Wang, Chunhong Zheng, and Pengcheng Chu. 2021. "Determining Surface Shape of Translucent Objects with the Combination of Laser-Beam-Based Structured Light and Polarization Technique" Sensors 21, no. 19: 6587. https://doi.org/10.3390/s21196587
APA StyleChen, B., Shi, P., Wang, Y., Xu, Y., Ma, H., Wang, R., Zheng, C., & Chu, P. (2021). Determining Surface Shape of Translucent Objects with the Combination of Laser-Beam-Based Structured Light and Polarization Technique. Sensors, 21(19), 6587. https://doi.org/10.3390/s21196587






