Design and Optimization of a Linear Wavenumber Spectrometer with Cylindrical Optics for Line Scanning Optical Coherence Tomography
Abstract
:1. Introduction
2. Theory and Properties
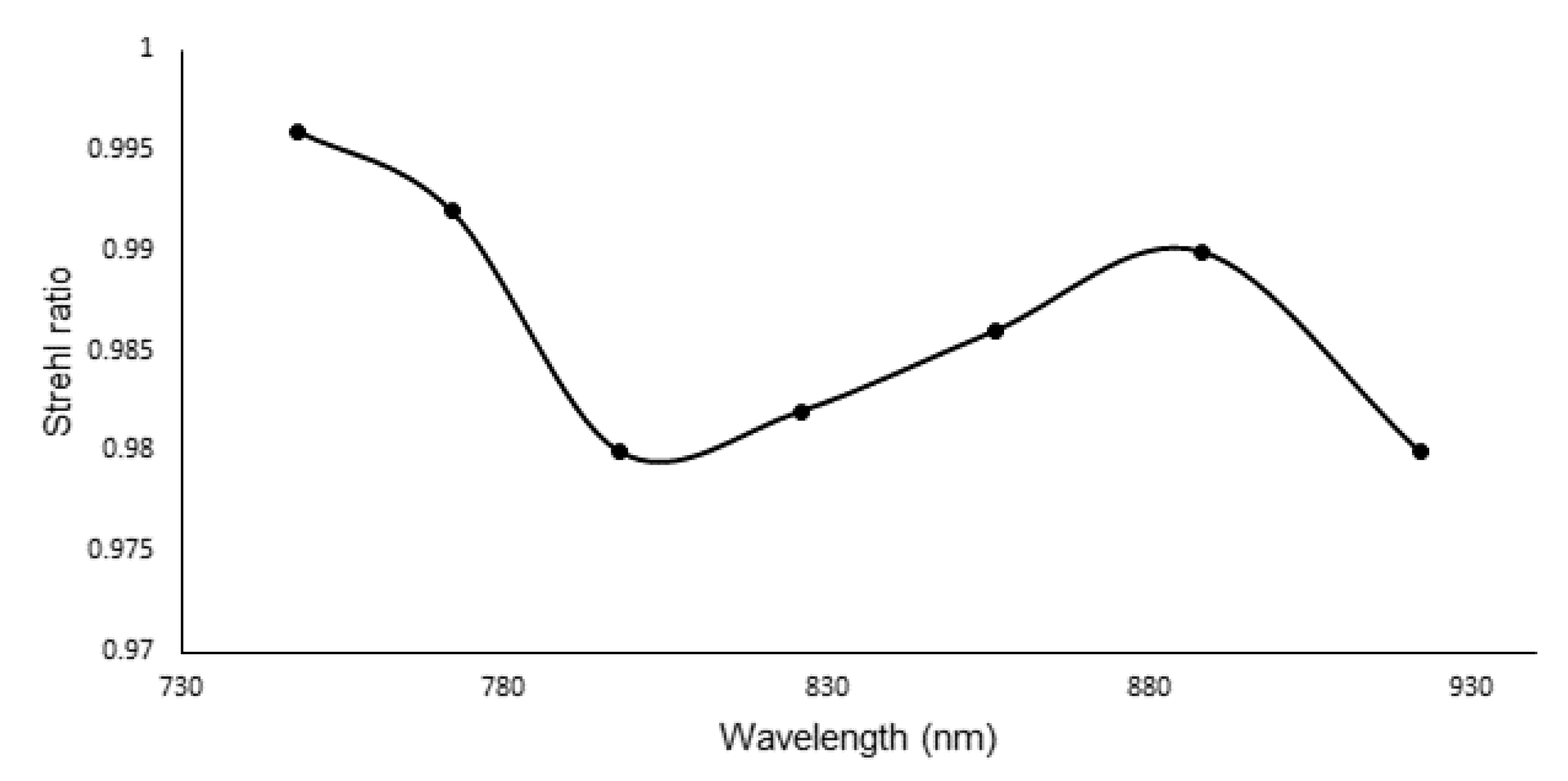
3. The Optical Design of the Spectrometer Based on Transmission Grating
Spectrometer Analysis
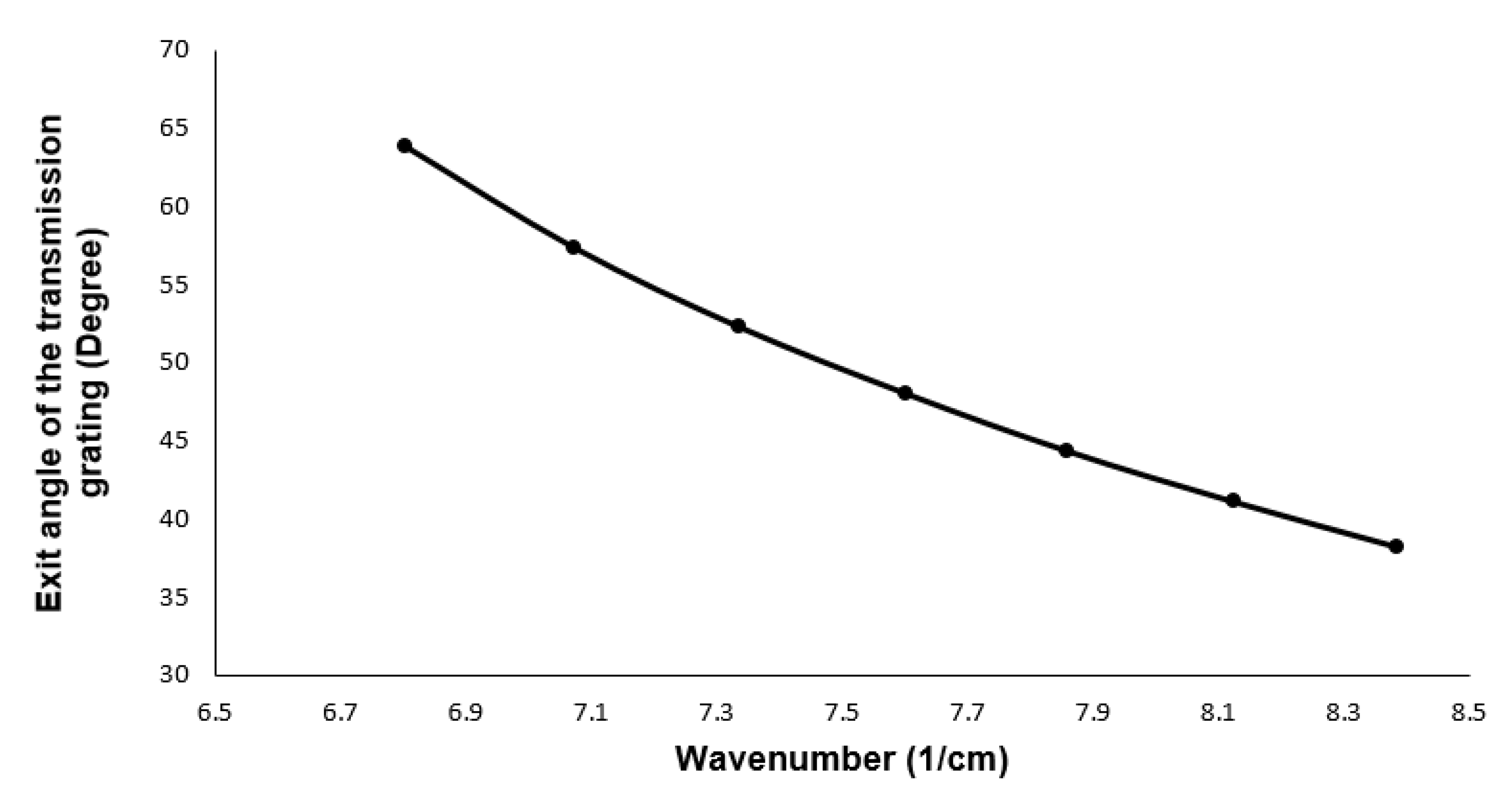
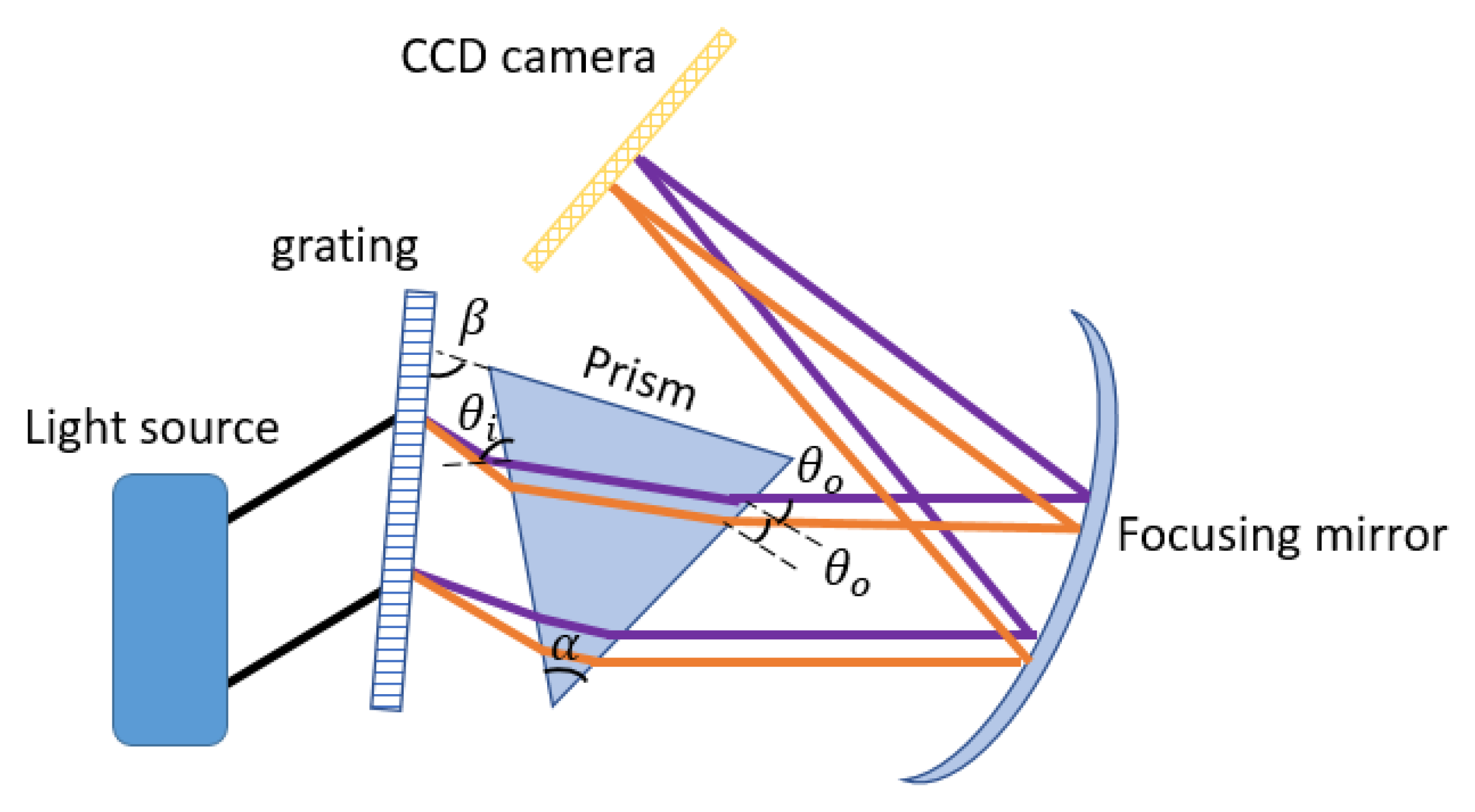
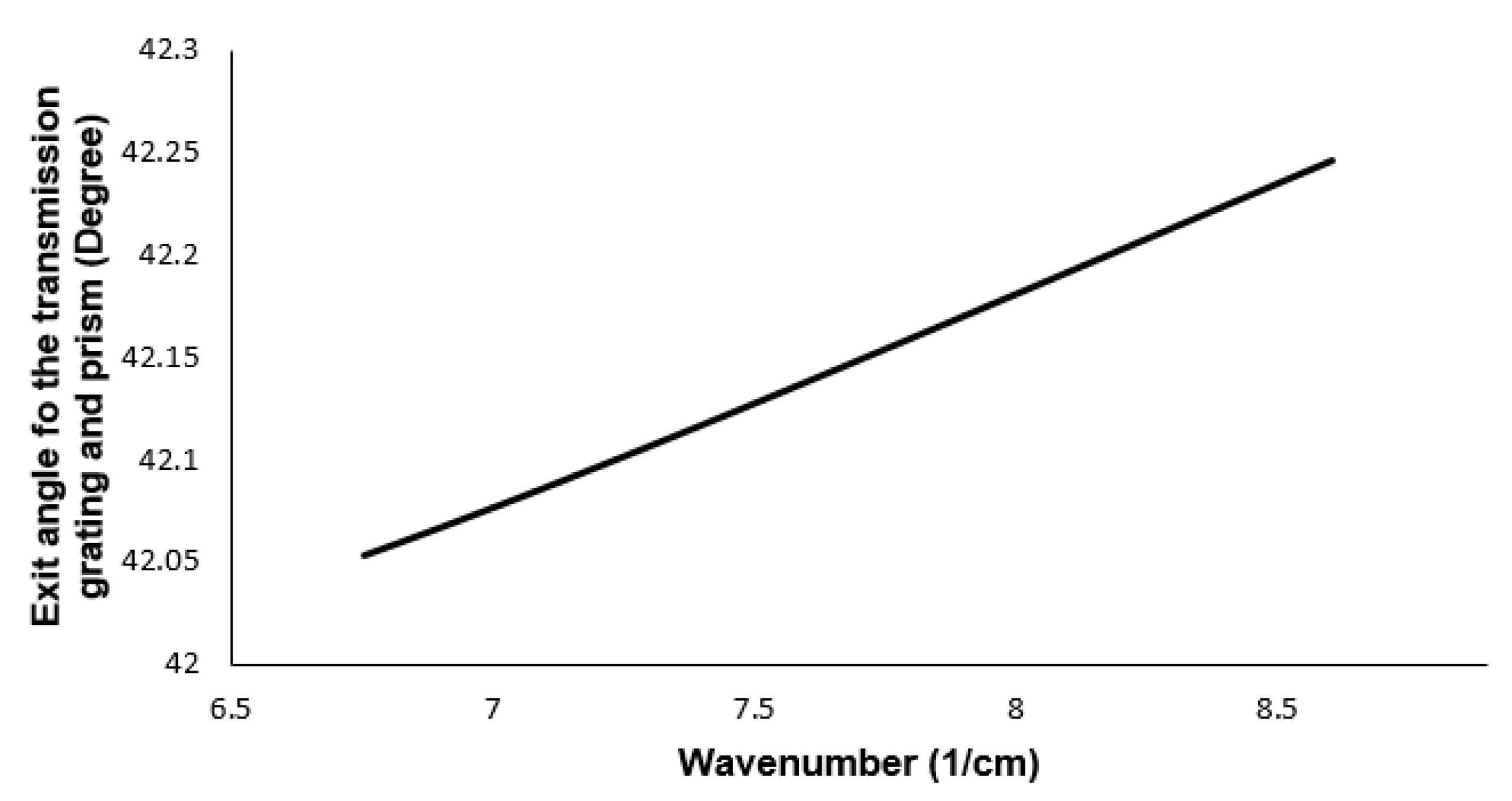
4. The Optical Design of the Spectrometer Based on Transmission Grating and Prism
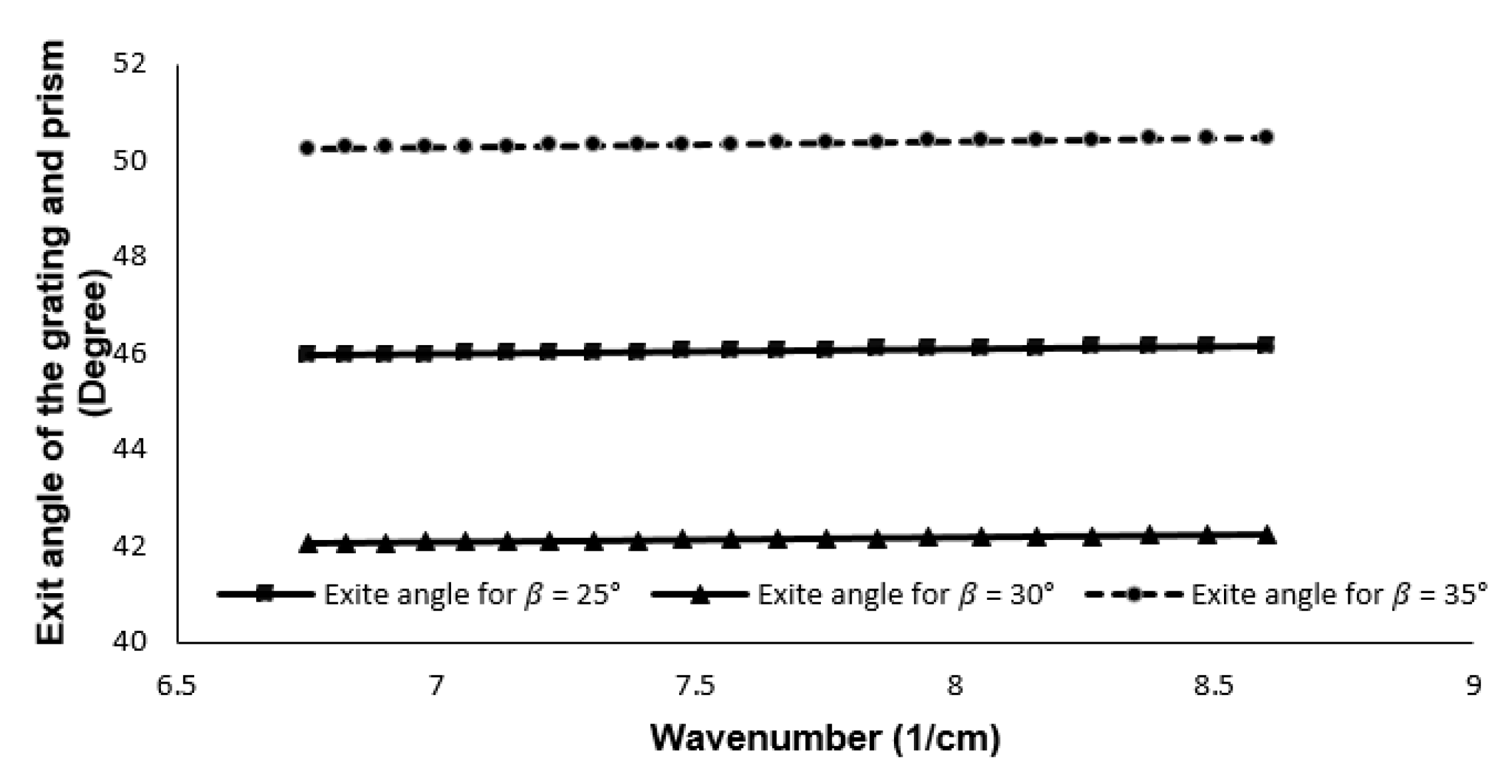
Spectrometer Analysis
5. The Optical Design of the Linear All-Reflective Spectrometer
5.1. Spectrometer Analysis
5.2. Comparison of the Spectrometer Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tomlins, P.H.; Wang, R.K. Theory, developments and applications of optical coherence tomography. J. Phys. D Appl. Phys. 2005, 38, 2519. [Google Scholar] [CrossRef]
- Drexler, W.; Fujimoto, J.G. Optical Coherence Tomography: Technology and Applications; Springer: Berlin, Germany, 2008. [Google Scholar]
- Fercher, A.F.; Hitzenberger, C.K.; Kamp, G.; El-Zaiat, S.Y. Measurement of intraocular distances by backscattering spectral interferometry. Opt. Commun. 1995, 117, 43–48. [Google Scholar] [CrossRef]
- Hausler, G.; Lindner, M.W. Coherence radar and spectral radar-new tools for dermatological diagnosis. J. Biomed. Opt. 1998, 3, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Sun, S.; Wang, X.; Zhang, H.; He, C.; Wang, J.; Gu, X.; Liu, Y. Optimization of linear-wavenumber spectrometer for high-resolution spectral domain optical coherence tomography. Opt. Commun. 2017, 405, 171–176. [Google Scholar] [CrossRef]
- Dorrer, C.; Belabas, N.; Likforman, J.P.; Joffre, M. Spectral resolution and sampling issues in Fourier-transform spectral interferometry. JOSA B 2000, 17, 1795–1802. [Google Scholar] [CrossRef]
- Hu, Z.; Rollins, A.M. Fourier domain optical coherence tomography with a linear-in-wavenumber spectrometer. Opt. Lett. 2007, 32, 3525–3527. [Google Scholar] [CrossRef] [PubMed]
- Gelikonov, V.; Gelikonov, G.; Shilyagin, P. Linear-wavenumber spectrometer for high-speed spectral-domain optical coherence tomography. Opt. Spectrosc. 2009, 106, 459–465. [Google Scholar] [CrossRef]
- Kamal, M.; Sivakumar, N.R.; Packirisamy, M. Optimized off-axis cylindrical mirror-focused line-scanning system for optical coherence tomography imaging applications. J. Biomed. Opt. 2012, 17, 056006. [Google Scholar] [CrossRef] [PubMed]
- van Leeuwen, T.G.; Faber, D.J.; Aalders, M.C. Measurement of the axial point spread function in scattering media using single-mode fiber-based optical coherence tomography. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 227–233. [Google Scholar] [CrossRef]
- Li, P.; An, L.; Lan, G.; Johnstone, M.; Malchow, D.S.; Wang, R.K. Extended imaging depth to 12 mm for 1050-nm spectral domain optical coherence tomography for imaging the whole anterior segment of the human eye at 120-kHz A-scan rate. J. Biomed. Opt. 2013, 18, 016012. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- An, L.; Li, P.; Lan, G.; Malchow, D.; Wang, R.K. High-resolution 1050 nm spectral domain retinal optical coherence tomography at 120 kHz A-scan rate with 6.1 mm imaging depth. Biomed. Opt. Express 2013, 4, 245–259. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Li, G. Design of ak-space spectrometer for ultra-broad waveband spectral domain optical coherence tomography. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Pan, Y.; Rollins, A.M. Analytical model of spectrometer-based two-beam spectral interferometry. Appl. Opt. 2007, 46, 8499–8505. [Google Scholar] [CrossRef] [PubMed]
- Lachance, G.P.; Boisselier, É.; Boukadoum, M.; Miled, A. Assessment of a Grism-based spectrometer design for neurotransmitter detection: Preliminary results. In Nanoscale Imaging, Sensing, and Actuation for Biomedical Applications XVIII; SPIE BiOS, 2021, Online Only 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11658, p. 116580C. [Google Scholar]
- Boppart, S.A.; Bouma, B.E.; Pitris, C.; Southern, J.F.; Brezinski, M.E.; Fujimoto, J.G. In vivo cellular optical coherence tomography imaging. Nat. Med. 1998, 4, 861–865. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yu, X.; Ge, X.; Wu, X.; Wang, X.; Bo, E.; Wang, N.; Liu, X.; Ni, G.; Liu, L. Design and optimization of a spectrometer for high-resolution SD-OCT. Laser Phys. Lett. 2019, 16, 045603. [Google Scholar] [CrossRef]
- Marvdashti, T.; Lee, H.Y.; Ellerbee, A.K. High-resolution spectrometer: Solution to the axial resolution and ranging depth trade-off of SD-OCT. In Advanced Biomedical and Clinical Diagnostic Systems XI; International Society for Optics and Photonics: San Francisco, CA, USA, 2013; Volume 8572, p. 85720I. [Google Scholar]
- Karam, R. Fresnel’s original interpretation of complex numbers in 19th century optics. Am. J. Phys. 2018, 86, 245–249. [Google Scholar] [CrossRef]
- Ogien, J.; Levecq, O.; Azimani, H.; David, A.; Xue, W.; Siret, D.; Perrot, J.L.; Dubois, A. Line-field confocal optical coherence tomography. In Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXIII; International Society for Optics and Photonics: San Francisco, CA, USA, 2019; Volume 10867, p. 108670U. [Google Scholar]
- Chen, W.; Xu, Y.; Zhang, H.; Liu, P.; Jiao, G. Optical lenses design and experimental investigations of a dynamic focusing unit for a CO2 laser scanning system. In Laser Beam Shaping XVII; International Society for Optics and Photonics: San Francisco, CA, USA, 2016; Volume 9950, p. 995006. [Google Scholar]
- Lee, S.S.; Song, W.; Choi, E.S. Spectral Domain Optical Coherence Tomography Imaging Performance Improvement Based on Field Curvature Aberration-Corrected Spectrometer. Appl. Sci. 2020, 10, 3657. [Google Scholar] [CrossRef]
- Samadi, S.; Narayanswamy, S.; Dargahi, J. Design of an All-reflective Line Based Spectrometer for Optical Coherence Tomography. In Proceedings of the 2020 Photonics North (PN), Niagara Falls, ON, Canada, 26–28 May 2020; p. 1. [Google Scholar]
- Kamal, M.; Sivakumar, N.; Packirisamy, M. Design of a spectrometer for all-reflective optics-based line scan Fourier domain optical coherence tomography. In Photonics North 2010; International Society for Optics and Photonics: Niagara Falls, ON, Canada, 2010; Volume 7750, p. 775020. [Google Scholar]
- Kamal, M.; Narayanswamy, S.; Packirisamy, M. Design of spectrometer for high-speed line field optical coherence tomography. In Photonics North 2011; International Society for Optics and Photonics: Ottawa, ON, Canada, 2011; Volume 8007, p. 80071J. [Google Scholar]
- Kamal, M.; Sivakumar, N.; Packirisamy, M. Optical modeling of a line-scan optical coherence tomography system for high-speed three-dimensional endoscopic imaging. In Photonics North 2009; International Society for Optics and Photonics: Quebec, QC, Canada, 2009; Volume 7386, p. 738607. [Google Scholar]
- Payne, A.; Podoleanu, A.G. Direct electronic linearization for camera-based spectral domain optical coherence tomography. Opt. Lett. 2012, 37, 2424–2426. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Lopera, S.; Restrepo, R. Design of a Linear in Wavenumber Spectrometer. In Proceedings of the Latin America Optics and Photonics Conference, Lima, Peru, 12–15 November 2018; p. W2B-3. [Google Scholar]




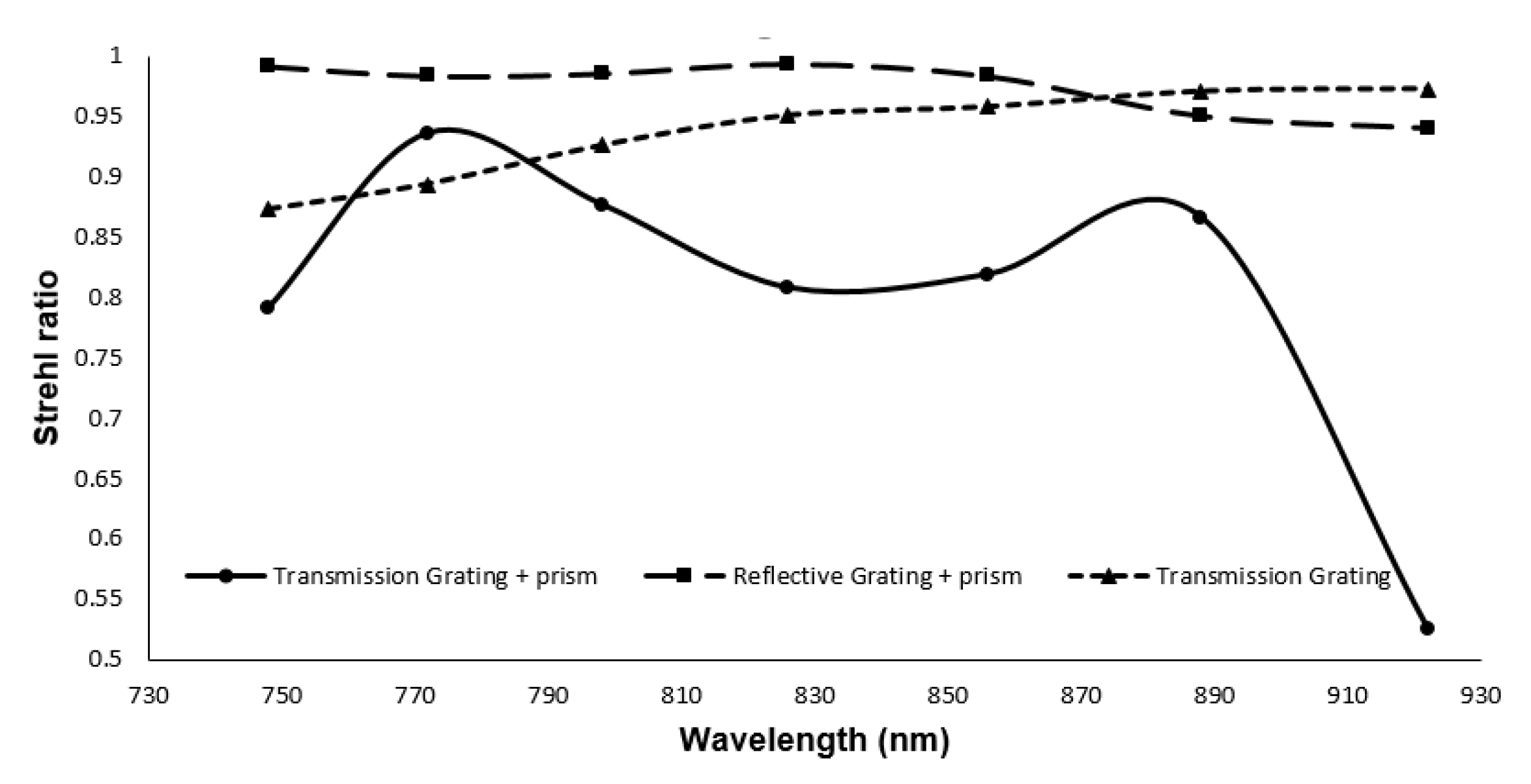
| Spectrometer Design | Wavelength (nm) | Nonlinearity Error | SR Ratio |
|---|---|---|---|
| Transmission Grating | 730–930 | 147.0115 | 0.98–0.996 |
| Transmission grating and prism | 730–930 | 0.0149 | 0.55–0.95 |
| Reflective grating and prism | 730–930 | 0.03517 | 0.95–0.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samadi, S.; Dargahi, J.; Narayanswamy, S. Design and Optimization of a Linear Wavenumber Spectrometer with Cylindrical Optics for Line Scanning Optical Coherence Tomography. Sensors 2021, 21, 6463. https://doi.org/10.3390/s21196463
Samadi S, Dargahi J, Narayanswamy S. Design and Optimization of a Linear Wavenumber Spectrometer with Cylindrical Optics for Line Scanning Optical Coherence Tomography. Sensors. 2021; 21(19):6463. https://doi.org/10.3390/s21196463
Chicago/Turabian StyleSamadi, Sevin, Javad Dargahi, and Sivakumar Narayanswamy. 2021. "Design and Optimization of a Linear Wavenumber Spectrometer with Cylindrical Optics for Line Scanning Optical Coherence Tomography" Sensors 21, no. 19: 6463. https://doi.org/10.3390/s21196463
APA StyleSamadi, S., Dargahi, J., & Narayanswamy, S. (2021). Design and Optimization of a Linear Wavenumber Spectrometer with Cylindrical Optics for Line Scanning Optical Coherence Tomography. Sensors, 21(19), 6463. https://doi.org/10.3390/s21196463






