Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization
Abstract
:1. Introduction
2. Materials and Methods
2.1. Intensity of Light with Hybrid Polarization at the Focus
2.2. Energy Flow at the Focus of the Light with Hybrid Polarization
2.3. SAM in the Strong Focus of a Field with Hybrid Polarization
3. Results and Discussion
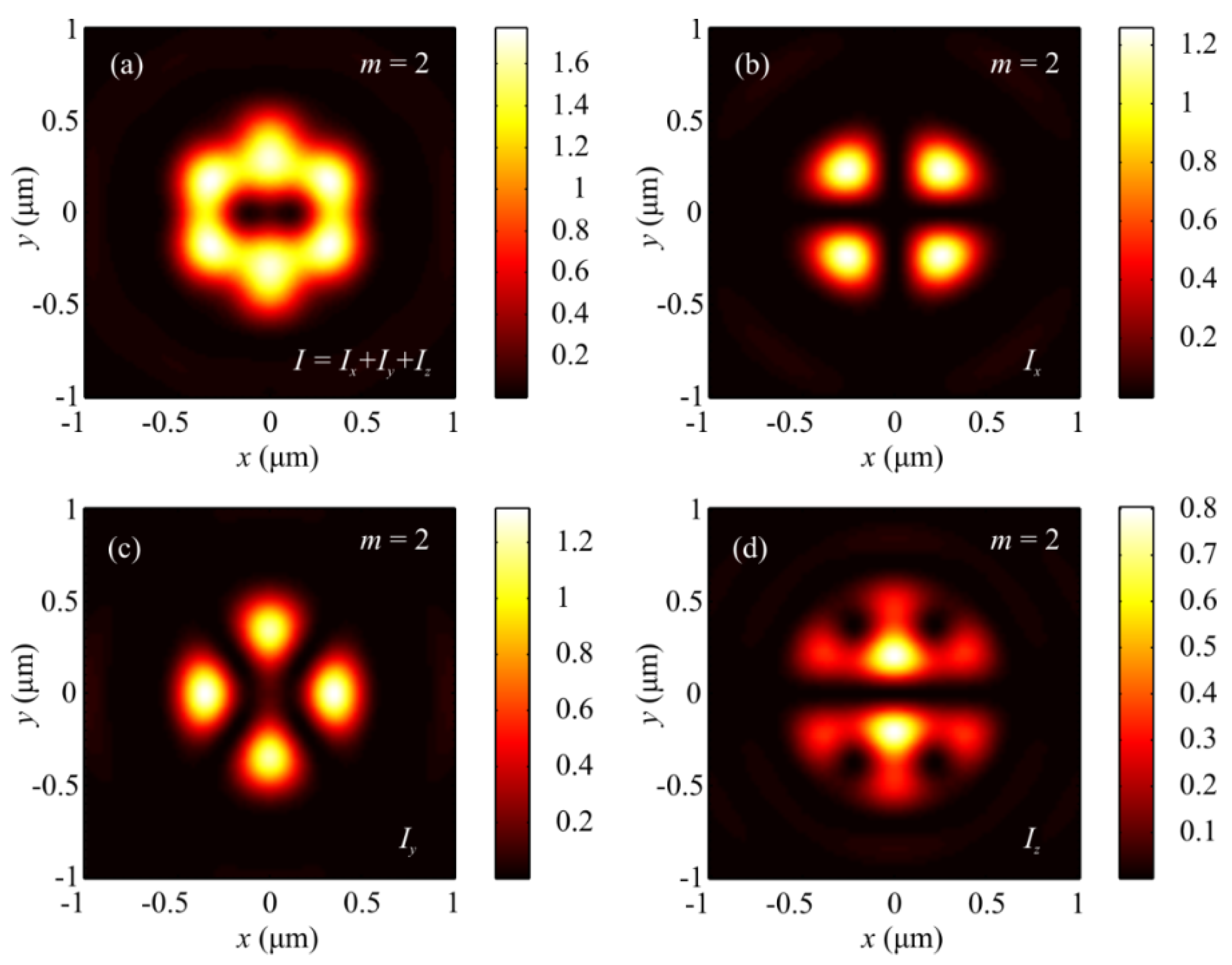
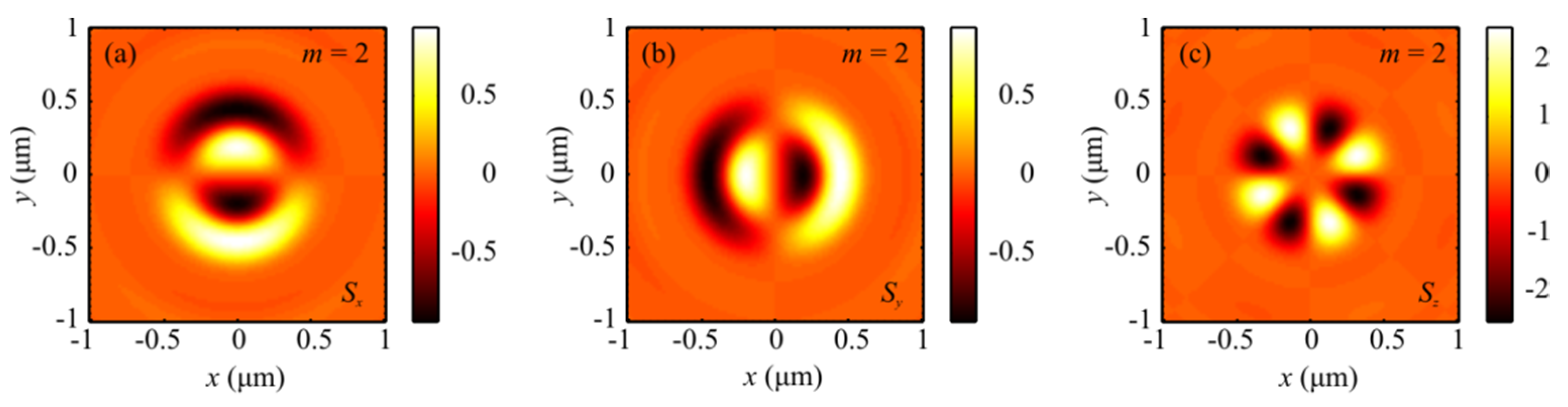
3.1. Results of the Numerical Simulation of Focusing Light with Hybrid Polarization
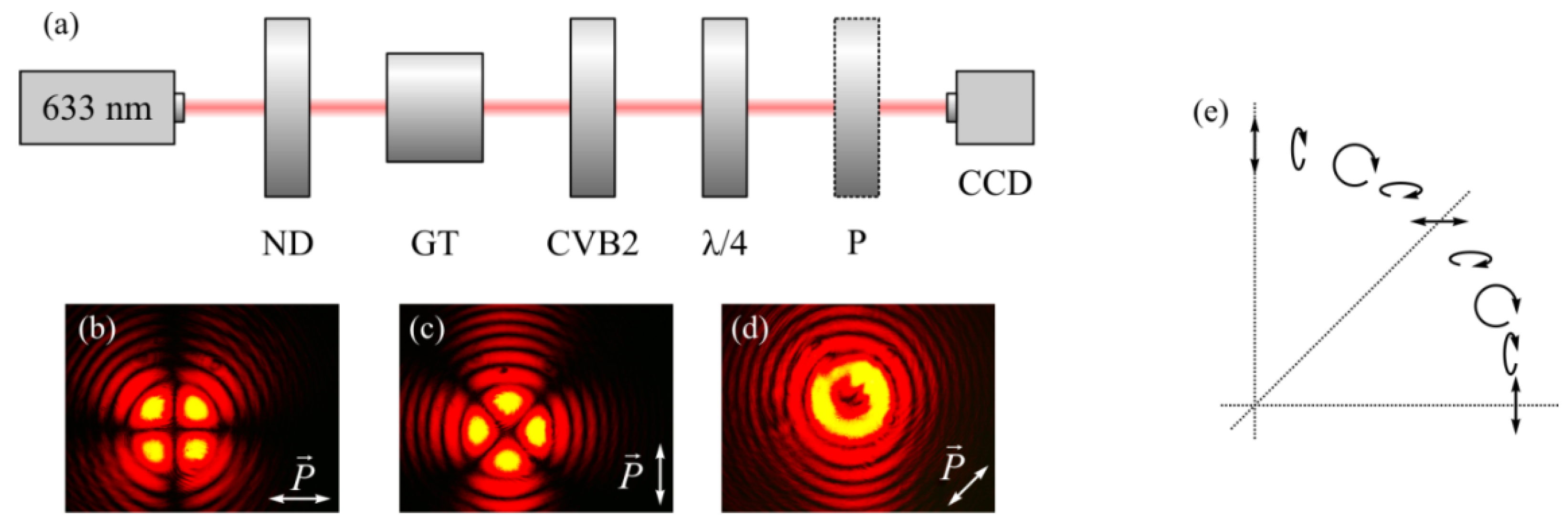
3.2. Experiment
3.3. Optical Setup and Metalens
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Richards, B.; Wolf, E. Electromagnetic Diffraction in Optical Systems. II. Structure of the Image Field in an Aplanatic System. Proc. R. Soc. A 1959, 253, 358–379. [Google Scholar]
- Quabis, S.; Dorn, R.; Eberler, M.; Glöckl, O.; Leuchs, G. Focusing light to a tighter spot. Opt. Commun. 2000, 179, 1–7. [Google Scholar] [CrossRef]
- Kozawa, Y.; Sato, S. Sharper focal spot formed by higher-order radially polarized laser beams. J. Opt. Soc. Am. A 2007, 24, 1793–1798. [Google Scholar] [CrossRef]
- Hao, B.; Leger, J. Experimental measurement of longitudinal component in the vicinity of focused radially polarized beam. Opt. Express 2007, 15, 3550–3556. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Wang, G.; Zeng, X.; Sui, G.; Zhang, R.; Zhan, Q. Focusing properties of radially polarized helico-conical Lorentz-Gauss beam. Optik 2017, 136, 289–294. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Edgar, J.S.; Jeffries, G.D.M.; McGloin, D.; Chiu, D.T. Spin-to-orbital angular momentum conversion in a strongly focused optical beam. Phys. Rev. Lett. 2007, 99, 073901. [Google Scholar] [CrossRef]
- Bekshaev, A. Spin–orbit interaction of light and diffraction of polarized beams. J. Opt. 2017, 19, 085602. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Nalimov, A.G.; Kovalev, A.A.; Porfirev, A.P.; Stafeev, S.S. Spin-orbit and orbit-spin conversion in the sharp focus of laser light: Theory and experiment. Phys. Rev. A 2020, 102, 033502. [Google Scholar] [CrossRef]
- Du, L.; Man, Z.; Zhang, Y.; Min, C.; Zhu, S.; Yuan, X. Manipulating orbital angular momentum of light with tailored in-plane polarization states. Sci. Rep. 2017, 7, 41001. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Pu, J. Tight focusing of elliptically polarized vortex beams. Appl. Opt. 2009, 48, 1288–1294. [Google Scholar] [CrossRef]
- Gao, X.-Z.; Pan, Y.; Zhang, G.-L.; Zhao, M.-D.; Ren, Z.-C.; Tu, C.-G.; Li, Y.-N.; Wang, H.T. Redistributing the energy flow of tightly focused ellipticity-variant vector optical fields. Photon. Res. 2017, 5, 640–648. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Kovalev, A.A.; Nalimov, A.G. Energy density and energy flux in the focus of an optical vortex: Reverse flux of light energy. Opt. Lett. 2018, 43, 2921–2924. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Gu, B.; Rui, G.; Lv, C.; He, J.; Cui, Y. Conservation of the spin angular momentum in second-harmonic generation with elliptically polarized vortex beams. Appl. Phys. Lett. 2019, 114, 101101. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical vector beams: From mathematical concepts to applications. Adv. Opt. Photonics 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Wang, X.-L.; Chen, J.; Li, Y.; Ding, J.; Guo, C.-S.; Wang, H.-T. Optical orbital angular momentum from the curl of polarization. Phys. Rev. Lett. 2010, 105, 253602. [Google Scholar] [CrossRef]
- Wang, X.-L.; Li, Y.; Chen, J.; Guo, C.-S.; Ding, J.; Wang, H.-T. A new type of vector fields with hybrid states of polarization. Opt. Express 2010, 18, 10786–10795. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Chen, Z.; Pu, J. Tight focusing properties of hybridly polarized vector beams. J. Opt. Soc. Am. A 2012, 29, 1099–1104. [Google Scholar] [CrossRef]
- Meng, P.; Man, Z.; Konijnenberg, A.P.; Urbach, H.P. Angular momentum properties of hybrid cylindrical vector vortex beams in tightly focused optical systems. Opt. Express 2019, 27, 35336–35348. [Google Scholar] [CrossRef] [Green Version]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Sharp Focusing of a Hybrid Vector Beam with a Polarization. Photonics 2021, 8, 227. [Google Scholar] [CrossRef]
- Lerman, G.M.; Stern, L.; Levy, U. Generation and tight focusing of hybridly polarized vector beams. Opt. Express 2010, 18, 27650–27657. [Google Scholar] [CrossRef]
- Hu, H.; Xiao, P. The tight focusing properties of spatial hybrid polarization vector beam. Optik 2013, 124, 2406–2410. [Google Scholar] [CrossRef]
- Naidoo, D.; Roux, F.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef] [Green Version]
- D’Errico, A.; Maffei, M.; Piccirillo, B.; de Lisio, C.; Cardano, F.; Marrucci, L. Topological features of vector vortex beams perturbed with uniformly polarized light. Sci. Rep. 2017, 7, 40195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, R.; Chen, P.; Tang, J.; Duan, W.; Ge, S.-J.; Ma, L.-L.; Wu, R.-X.; Hu, W.; Lu, Y.-Q. Perfect Higher-Order Poincaré Sphere Beams from Digitalized Geometric Phases. Phys. Rev. Appl. 2018, 10, 034061. [Google Scholar] [CrossRef]
- Lu, T.H.; Huang, T.D.; Wang, J.G.; Wang, L.W.; Alfano, R.R. Generation of flower high-order Poincaré sphere laser beams from a spatial light modulator. Sci. Rep. 2016, 6, 39657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khonina, S.N.; Ustinov, A.V.; Fomchenkov, S.A.; Porfirev, A.P. Formation of hybrid higher-order cylindrical vector beams using binary multi-sector phase plates. Sci. Rep. 2018, 8, 14320. [Google Scholar] [CrossRef] [Green Version]
- Khonina, S.N. Vortex beams with high-order cylindrical polarization: Features of focal distributions. Appl. Phys. B 2019, 125, 100. [Google Scholar] [CrossRef]
- Rashid, M.; Maragò, O.M.; Jones, P.H. Focusing of high order cylindrical vector beams. J. Opt. A Pure Appl. Opt. 2009, 11, 065204. [Google Scholar] [CrossRef]
- Liu, Y.; Ke, Y.; Zhou, J.; Liu, Y.; Luo, H.; Wen, S.; Fan, D. Generation of perfect vortex and vector beams based on Pancharatnam-Berry phase elements. Sci. Rep. 2017, 7, 44096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Zhu, Z.; Wang, X.; Gong, L.; Wang, M.; Nie, S. Propagation evolution of an off-axis high-order cylindrical vector beam. J. Opt. Soc. Am. A 2014, 31, 2356–2361. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Sharp focusing of a light field with polarization and phase singularities of an arbitrary order. Comput. Opt. 2019, 43, 337–346. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S. A transverse energy flow at the tight focus of light with higher-order circular-azimuthal polarization. Comput. Opt. 2021, 45, 311–318. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Reverse and toroidal flux of light fields with both phase and polarization higher-order singularities in the sharp focus area. Opt. Express 2019, 27, 16689–16702. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Energy backflow in the focus of a light beam with phase or polarization singularity. Phys. Rev. A 2019, 99, 033840. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Nalimov, A.G.; Stafeev, S.S. Exploiting the circular polarization of light to obtain a spiral energy flow at the subwavelength focus. J. Opt. Soc. Am. B 2019, 36, 2850–2855. [Google Scholar] [CrossRef]
- He, Y.; Xie, Z.; Yang, B.; Chen, X.; Liu, J.; Ye, H.; Zhou, X.; Li, Y.; Chen, S.; Fan, D. Controllable photonic spin Hall effect with phase function construction. Photonics Res. 2020, 8, 963–971. [Google Scholar] [CrossRef]
- Sarbort, M.; Hola, M.; Pavelka, J.; Schovanek, P.; Rerucha, S.; Oulehla, J.; Fort, T.; Lasar, J. Comparison of three focus sensors for optical topography measurement of rough surfaces. Opt. Express 2019, 27, 33459. [Google Scholar] [CrossRef]
- Qi, M.; Zhang, N.M.Y.; Li, K.; Tjin, S.C.; Wei, L. Hybrid Plasmonic Fiber-Optic Sensors. Sensors 2020, 20, 3266. [Google Scholar] [CrossRef]
- Ding, Z.; Stubbs, J.M.; McRae, D.; Blacquiere, J.M.; Lagugné-Labarthet, F.; Mittler, S. A Mass-Producible and Versatile Sensing System: Localized Surface Plasmon Resonance Excited by Individual Waveguide Modes. ACS Sens. 2018, 3, 334–341. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, C.; Yang, Y.; Zhu, S.; Yuan, X.-C. Focused cylindrical vector beam assisted microscopic pSPR biosensor with an ultra wide dynamic range. Opt. Lett. 2012, 37, 2091–2093. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Wang, Y.; Yang, Y.; Zhang, C.; Weng, X.; Zhu, S.; Yuan, X. Real-time subcellular imaging based on graphene biosensors. Nanoscale 2018, 10, 1759–1765. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Huang, T.; Han, L.; Su, H.; Wang, H.; Liu, M.; Zhang, W.; Wang, X.; Mei, T. Tip-Enhanced Raman Spectroscopy with High-Order Fiber Vector Beam Excitation. Sensors 2018, 18, 3841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, H.; Qiu, J.; Wang, P.; Shang, Y.; Zhang, L.; Wei, H.; Pang, F. Cylindrical Vector Beam for Vector Magnetic Field Sensing Based on Magnetic Fluid. IEEE Photonics Technol. Lett. 2021, 33, 703–706. [Google Scholar] [CrossRef]
- Sergey-St/Richwolf. Available online: https://github.com/Sergey-St/richwolf (accessed on 2 September 2021).









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotlyar, V.V.; Stafeev, S.S.; Kozlova, E.S.; Nalimov, A.G. Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization. Sensors 2021, 21, 6424. https://doi.org/10.3390/s21196424
Kotlyar VV, Stafeev SS, Kozlova ES, Nalimov AG. Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization. Sensors. 2021; 21(19):6424. https://doi.org/10.3390/s21196424
Chicago/Turabian StyleKotlyar, Victor V., Sergey S. Stafeev, Elena S. Kozlova, and Anton G. Nalimov. 2021. "Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization" Sensors 21, no. 19: 6424. https://doi.org/10.3390/s21196424
APA StyleKotlyar, V. V., Stafeev, S. S., Kozlova, E. S., & Nalimov, A. G. (2021). Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization. Sensors, 21(19), 6424. https://doi.org/10.3390/s21196424







