Development of an Analytic Convection Model for a Heated Multi-Hole Probe for Aircraft Applications
Abstract
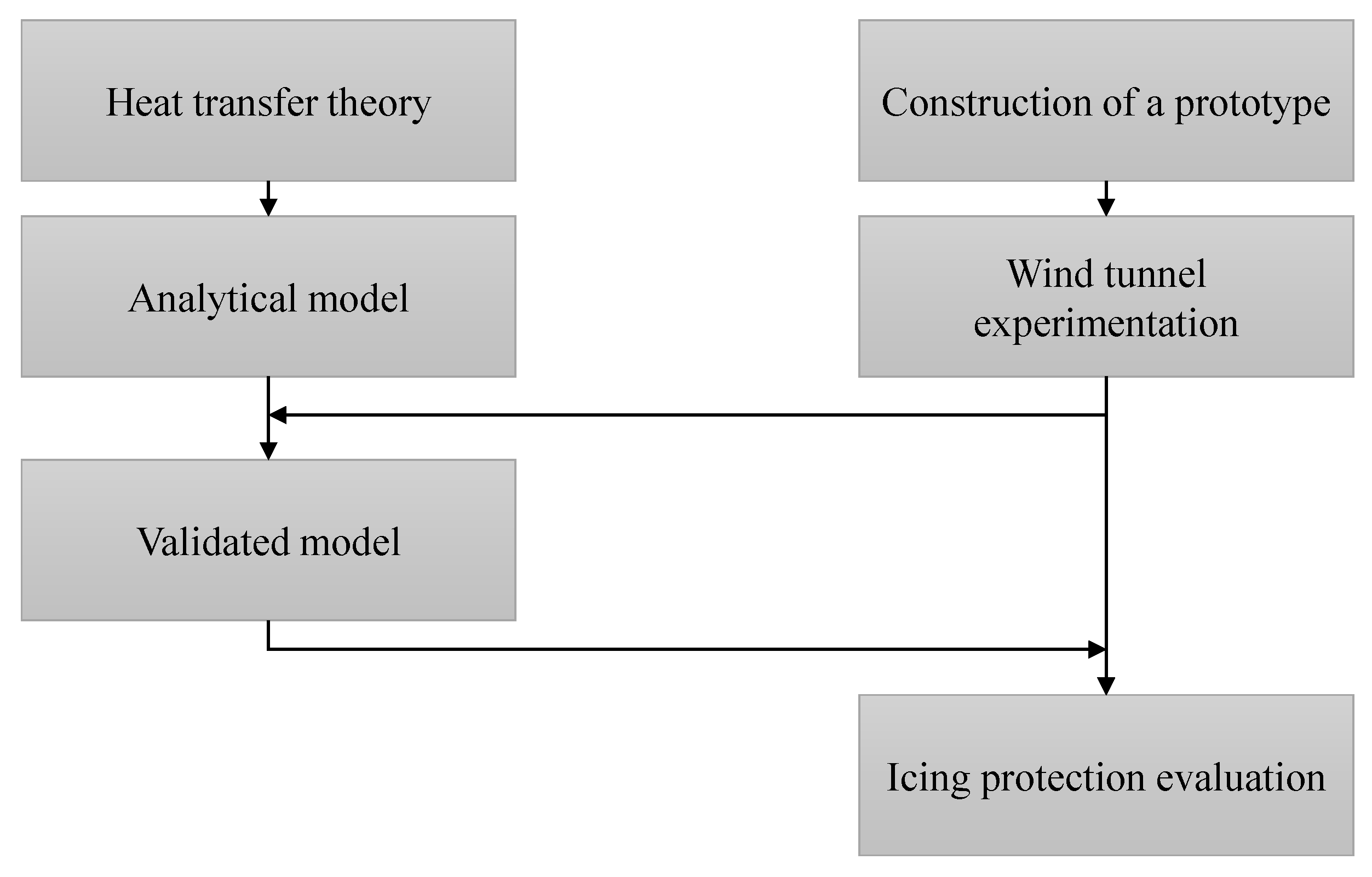
:1. Introduction and Motivation
2. Theory and Analytical Model
2.1. Heat Convection Theory
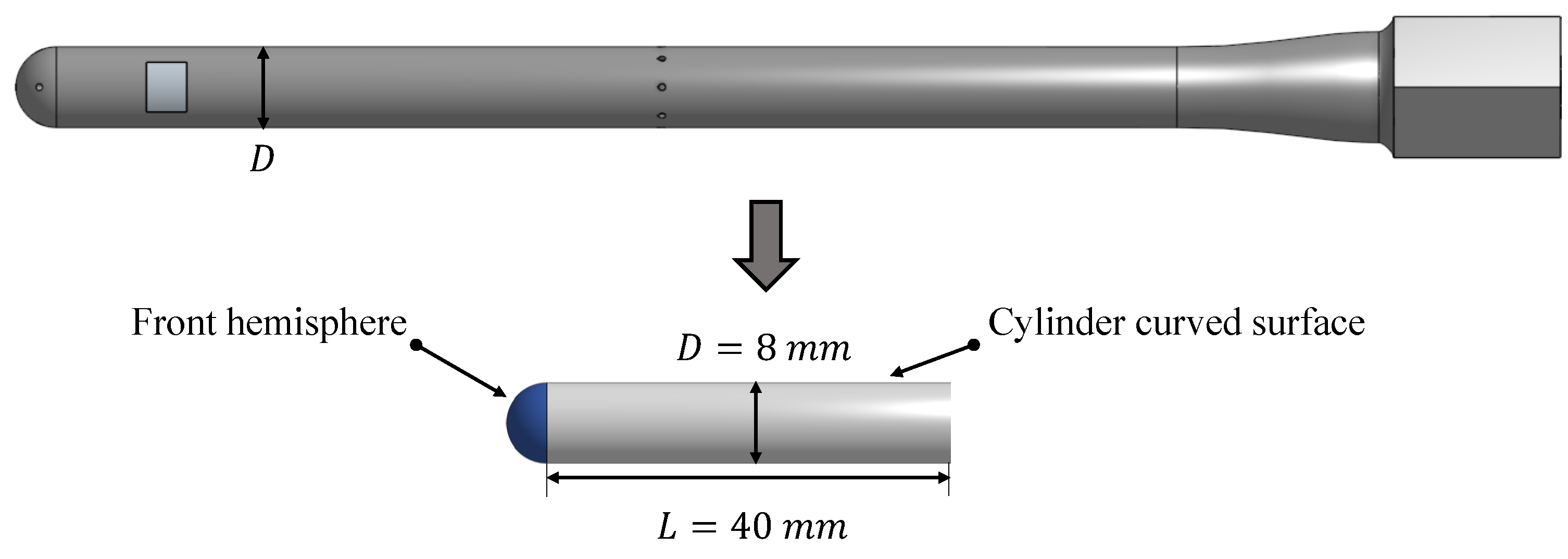
2.2. Heat Convection Model for the Heated Probe
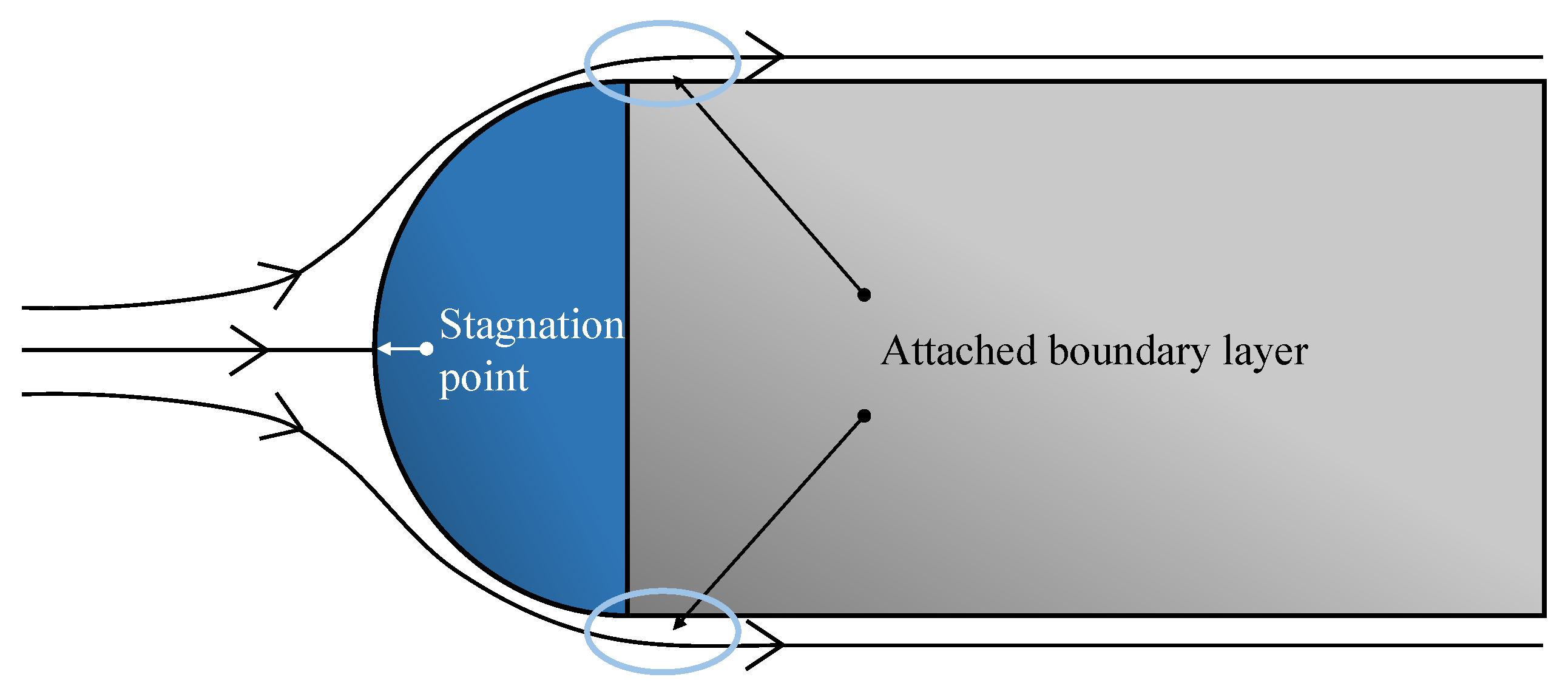
2.2.1. The Front Hemisphere
2.2.2. The Curved Surface of a Cylinder in Axial Flow
2.2.3. Resulting Analytical Model
3. Experimental Setup and Probe Assembly
4. Results
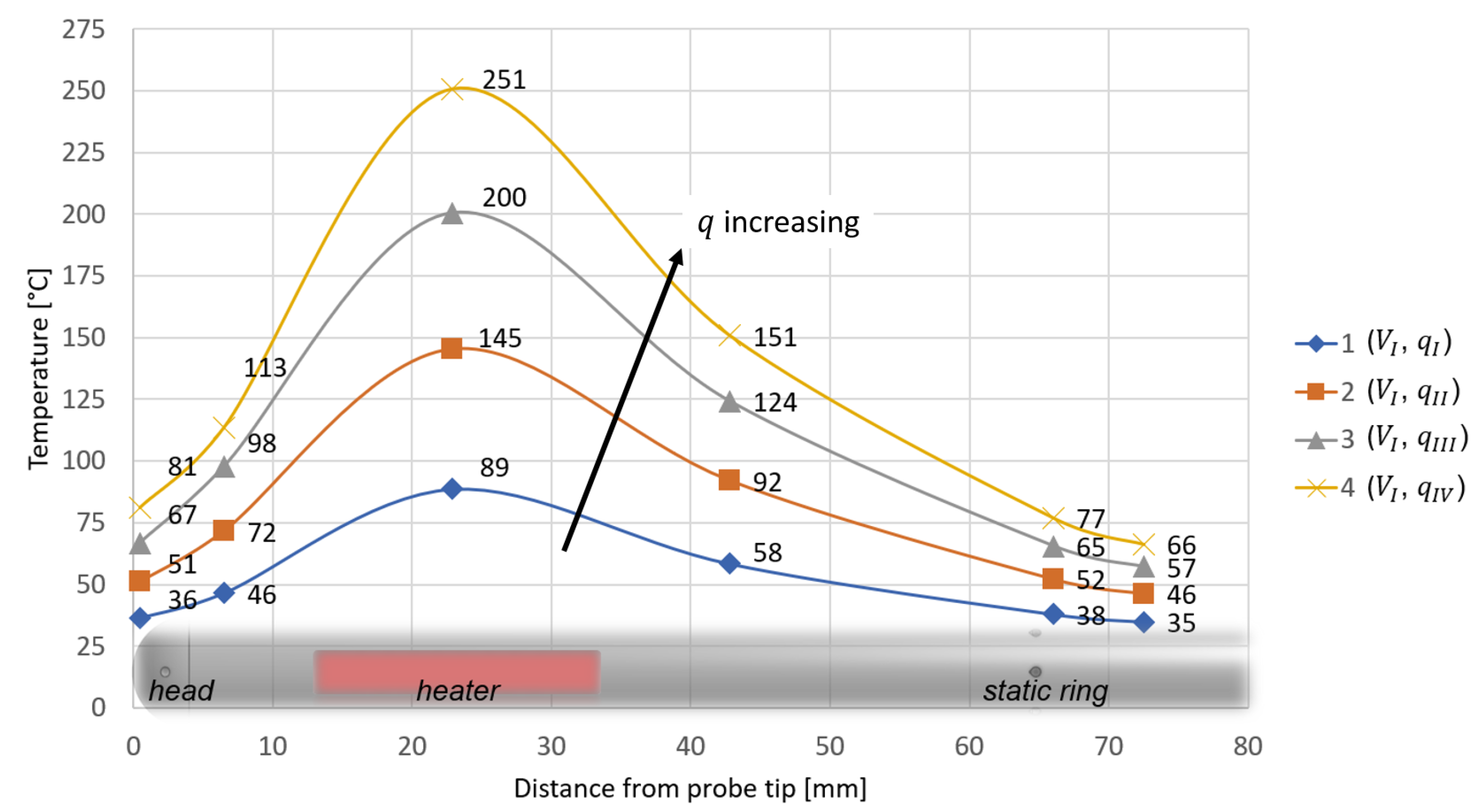
4.1. Temperature Measurements
4.2. Comparison to the Analytical Model
4.3. Evaluation of the Heating System Anti-Icing Capability
5. Discussion and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| IPS | Icing Protection System |
| PBF | Powder Bed Fusion |
| UAV | Unmanned Aerial Vehicles |
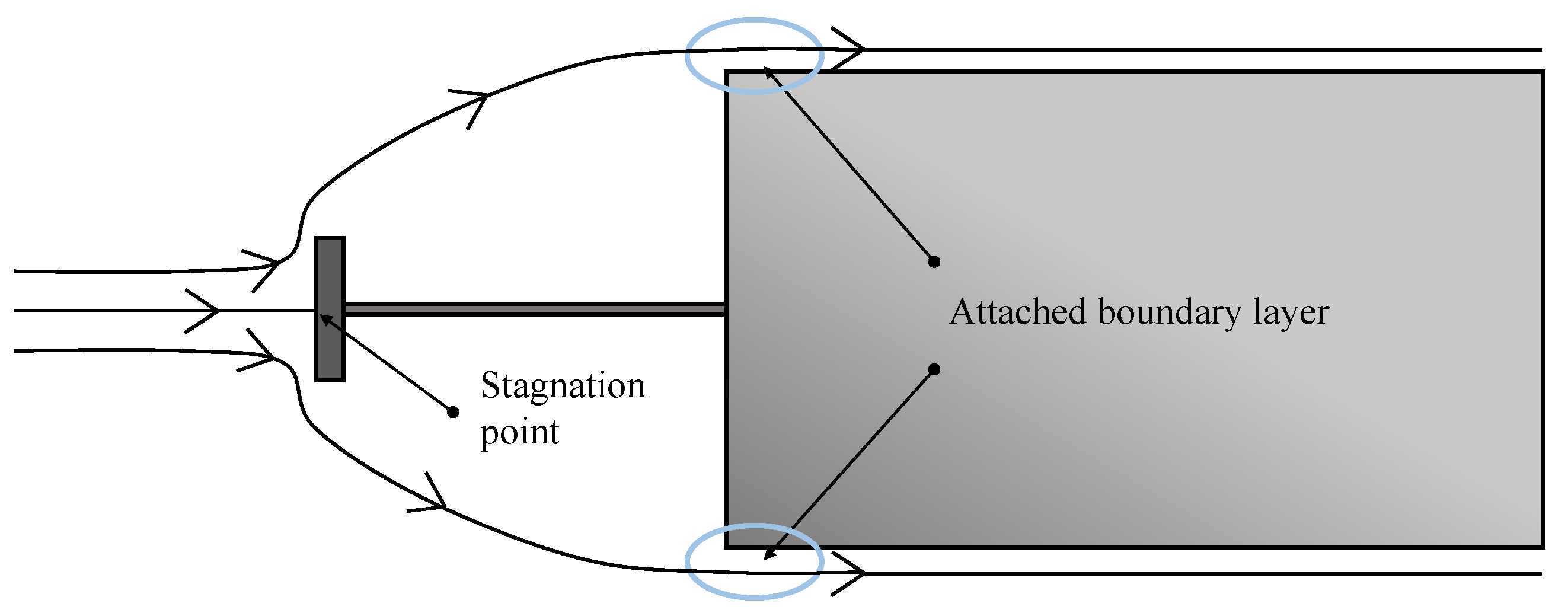
Appendix A. Additional Information of the Front Hemisphere Heat Convection
Appendix A.1. Experimental Explanation
The heat transfer from this part of the sphere is dominating but, as the contribution from the rear part increases faster with increasing Reynolds number, both become equally important at 70,000.

Appendix A.2. Mathematical Explanation
References
- Ng, T.S. Flight Systems and Control; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Korsun, O.N.; Poplavskii, B.K. Estimation of systematic errors of onboard measurement of angle of attack and sliding angle based on integration of data of satellite navigation system and identification of wind velocity. J. Comput. Syst. Sci. Int. 2011, 50, 130–143. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Bailey, S.C.C. An approach to minimize aircraft motion bias in multi-hole probe wind measurements made by small unmanned aerial systems. Atmos. Meas. Tech. 2021, 14, 173–184. [Google Scholar] [CrossRef]
- Kim, S.H.; Kang, Y.J.; Myong, R.S.; Cho, T.H.; Park, Y.M.; Choi, I.H. Calibration of a Five-Hole Multi-Function Probe for Helicopter Air Data Sensors. Int. J. Aeronaut. Space Sci. 2009, 10, 43–51. [Google Scholar] [CrossRef] [Green Version]
- Uzol, O.; Katz, J. Flow Measurement Techniques in Turbomachinery. In Springer Handbook of Experimental Fluid Mechanics; Tropea, C., Yarin, A.L., Foss, J.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 919–957. [Google Scholar] [CrossRef]
- Heckmeier, F.M.; Breitsamter, C. Aerodynamic probe calibration using Gaussian process regression. Meas. Sci. Technol. 2020, 31, 125301. [Google Scholar] [CrossRef]
- United States Committee on Extension to the Standard Atmosphere. U.S. Standard Atmosphere, 1976; U.S. Government Printing Office: Washington, DC, USA, 1976.
- Iwago, M.; Fukudome, K.; Mamori, H.; Fukushima, N.; Yamamoto, M. Fundamental Investigation to Predict Ice Crystal Icing in Jet Engine. In Recent Asian Research on Thermal and Fluid Sciences; Suryan, A., Doh, D.H., Yaga, M., Zhang, G., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020; pp. 305–318. [Google Scholar] [CrossRef]
- Arizmendi, B.; Morelli, M.; Parma, G.; Zocca, M.; Quaranta, G.; Guardone, A. In-flight Icing: Modeling, Prediction, and Uncertainty. In Optimization under Uncertainty with Applications to Aerospace Engineering; Vasile, M., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 455–506. [Google Scholar] [CrossRef]
- Jackson, D.A. Concept of a Pitot tube able to detect blockage by ice, volcanic ash, sand and insects, and to clear the tube. Photonic Sens. 2015, 5, 298–303. [Google Scholar] [CrossRef] [Green Version]
- Shinkafi, A.; Lawson, C. Enhanced Method of Conceptual Sizing of Aircraft Electro-Thermal De-icing System. Int. J. Aerosp. Mech. Eng. 2014, 8, 1073–1080. [Google Scholar]
- Bergman, T.L.; Incropera, F.P. Fundamentals of Heat and Mass Transfer, 7th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Karwa, R. Heat and Mass Transfer; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Zohuri, B. Dimensional Analysis and Self-Similarity Methods for Engineers and Scientists; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar] [CrossRef] [Green Version]
- Taler, D. Numerical Modelling and Experimental Testing of Heat Exchangers; Springer International Publishing: Cham, Switzerland, 2019; Volume 161. [Google Scholar] [CrossRef]
- Aufdermaur, A.N.; Joss, J. A wind tunnel investigation on the local heat transfer from a sphere, including the influence of turbulence and roughness. Z. FÜR Angew. Math. Phys. Zamp 1967, 18, 852–866. [Google Scholar] [CrossRef]
- Eastop, T.; Smith, C. Heat transfer from a sphere to an air stream at sub-critical Reynolds numbers. Trans. Instn chem. Engrs 1972, 50, 26–31. [Google Scholar]
- Will, J.B.; Kruyt, N.P.; Venner, C.H. An experimental study of forced convective heat transfer from smooth, solid spheres. Int. J. Heat Mass Transf. 2017, 109, 1059–1067. [Google Scholar] [CrossRef]
- Wiberg, R.; Lior, N. Heat transfer from a cylinder in axial turbulent flows. Int. J. Heat Mass Transf. 2005, 48, 1505–1517. [Google Scholar] [CrossRef]
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khorram Niaki, M.; Nonino, F. The Management of Additive Manufacturing; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Boerner, M.; Niehuis, R. Development of an additive manufactured miniaturized wedge probe optimized for 2D transonic wake flow measurements. In XXIV Biannual Symposium on Measuring Techniques in Turbomachinery; MTT: Prague, Czech Republic, 2018. [Google Scholar]
- Heckmeier, F.M.; Iglesias, D.; Kreft, S.; Kienitz, S.; Breitsamter, C. Development of unsteady multi-hole pressure probes based on fiber-optic pressure sensors. Eng. Res. Express 2019, 1, 025023. [Google Scholar] [CrossRef] [Green Version]
- Datasheet: IEC Mineral Insulated Thermocouples—0.5 mm, RS. Available online: https://docs.rs-online.com/0a7f/0900766b815bb421.pdf (accessed on 16 July 2021).

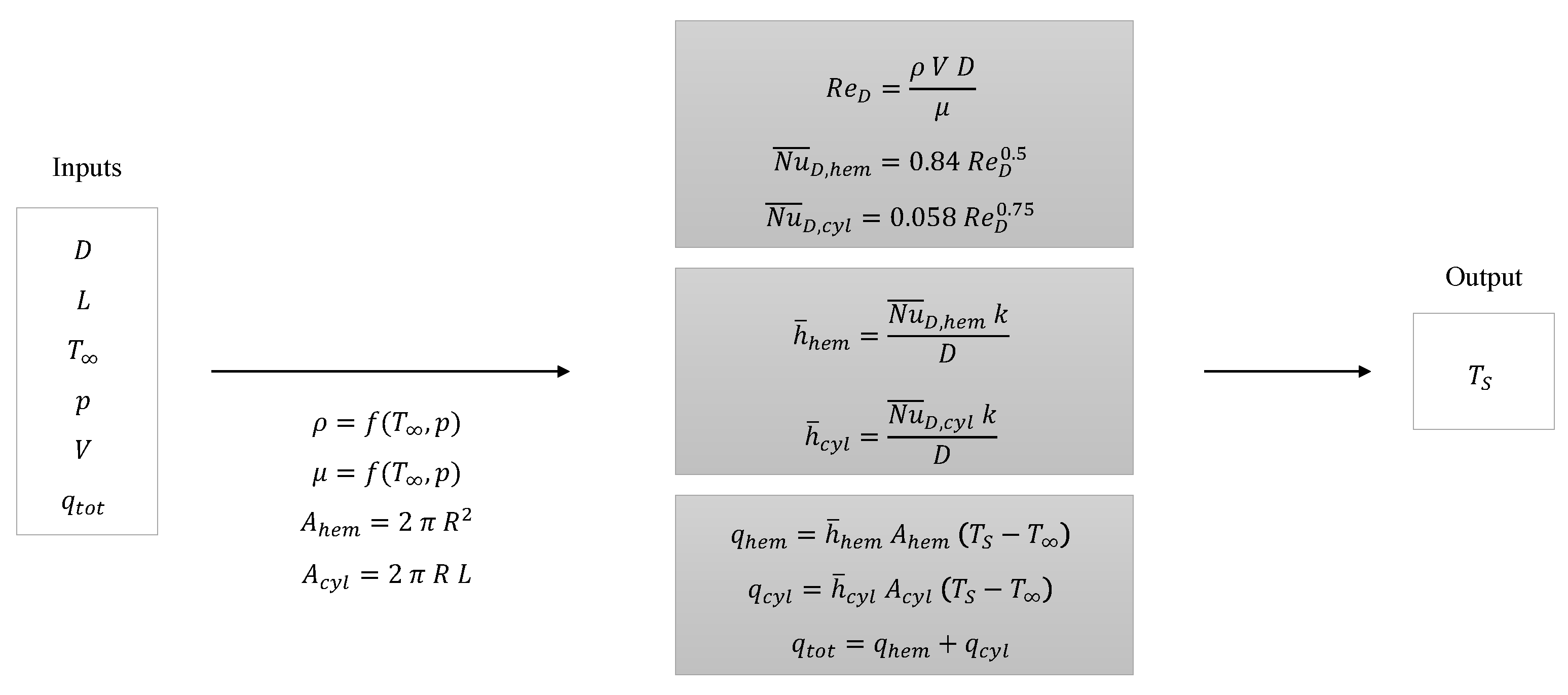


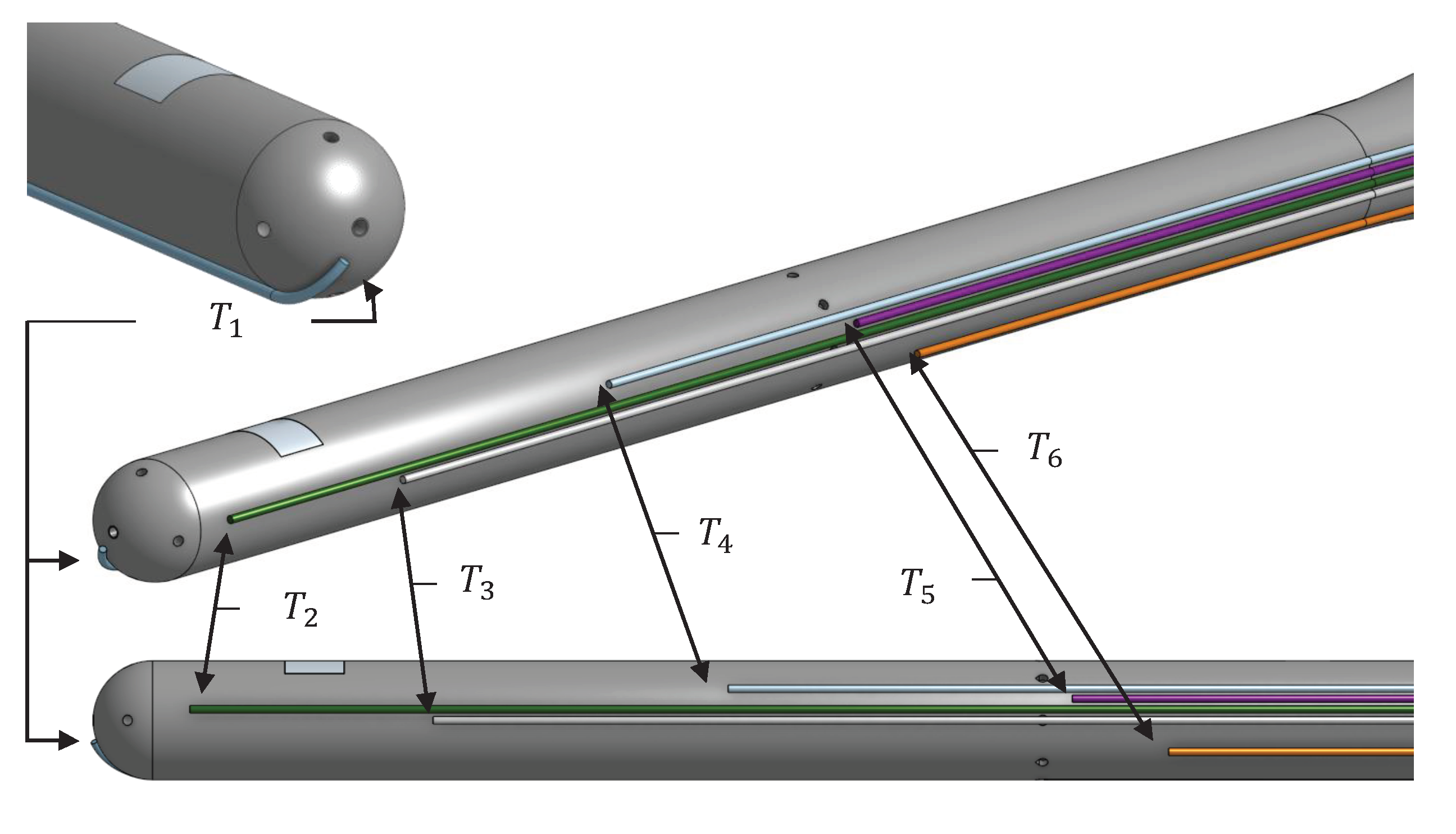
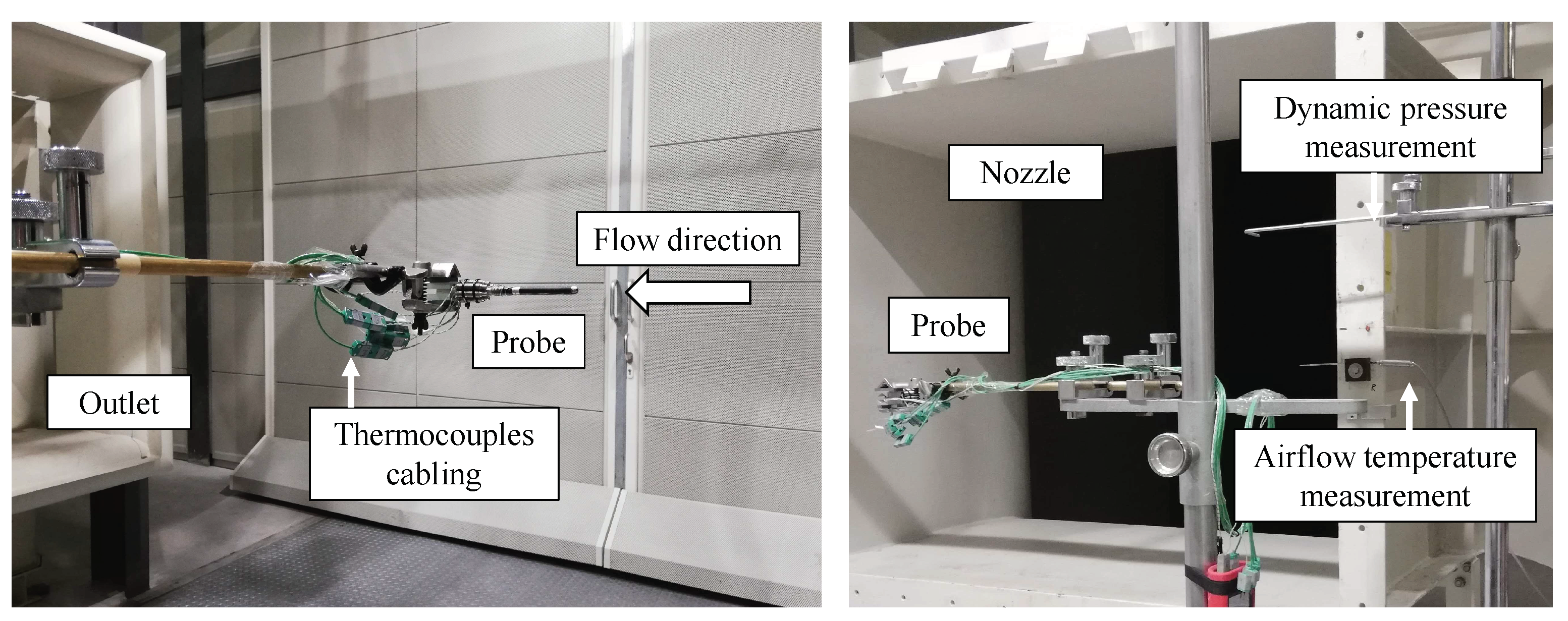
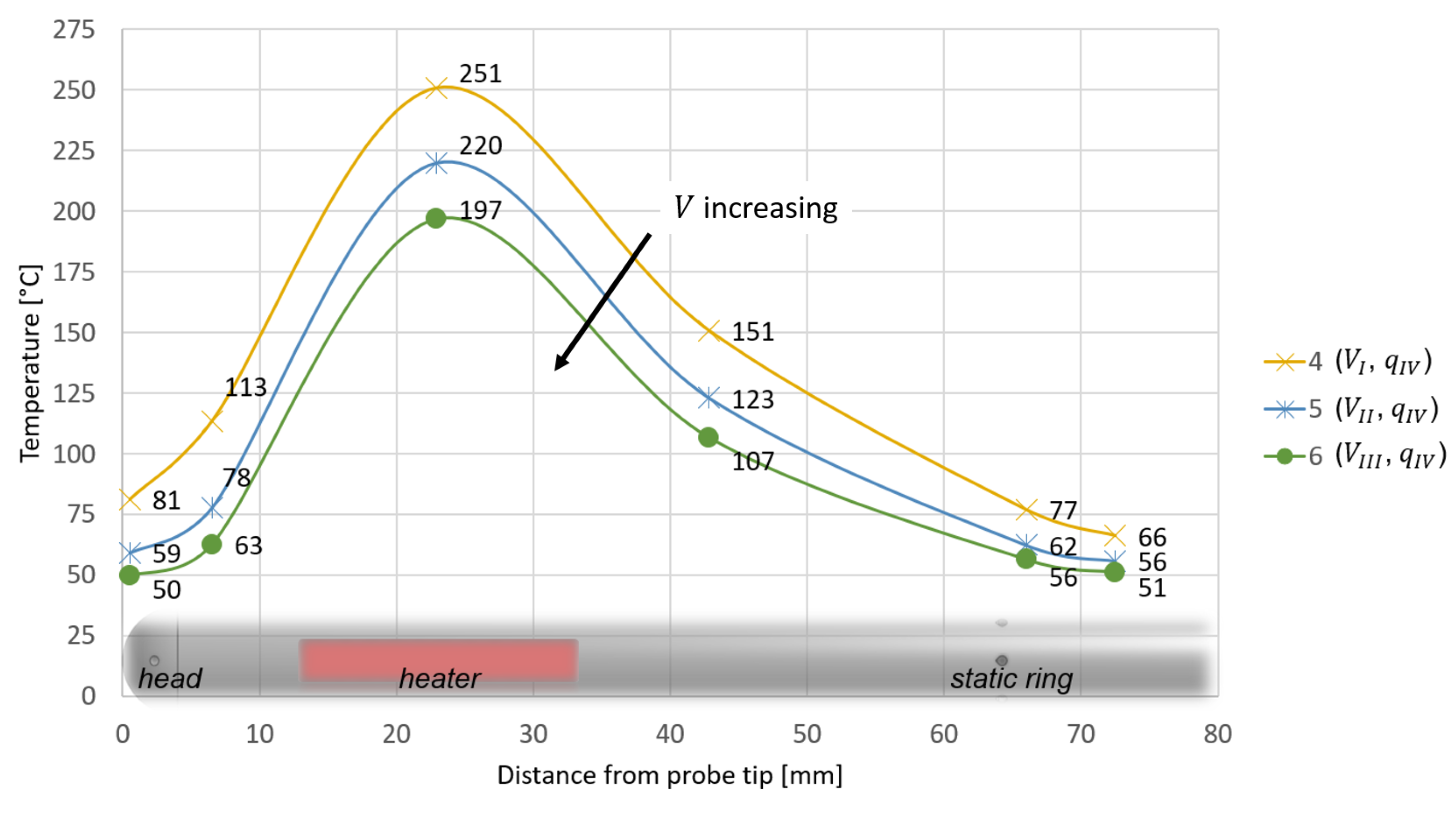
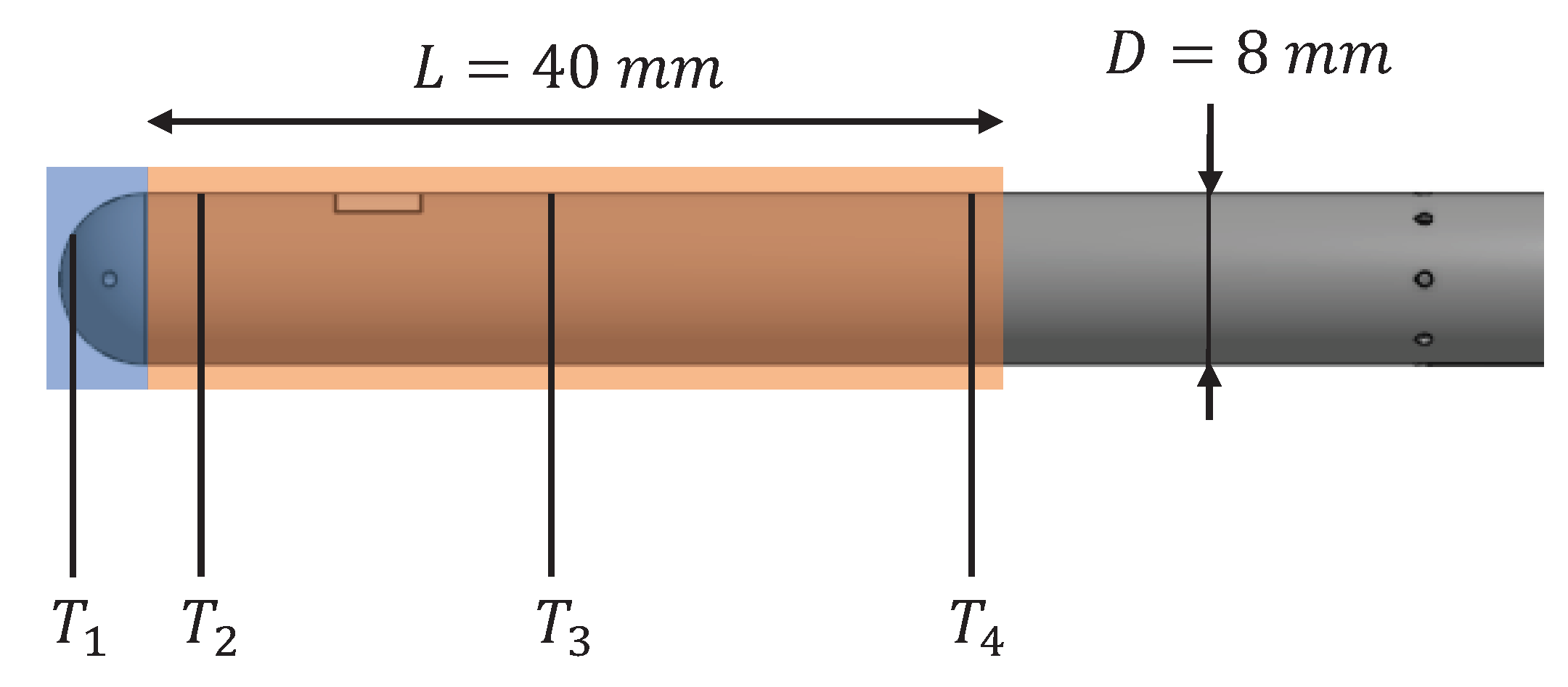

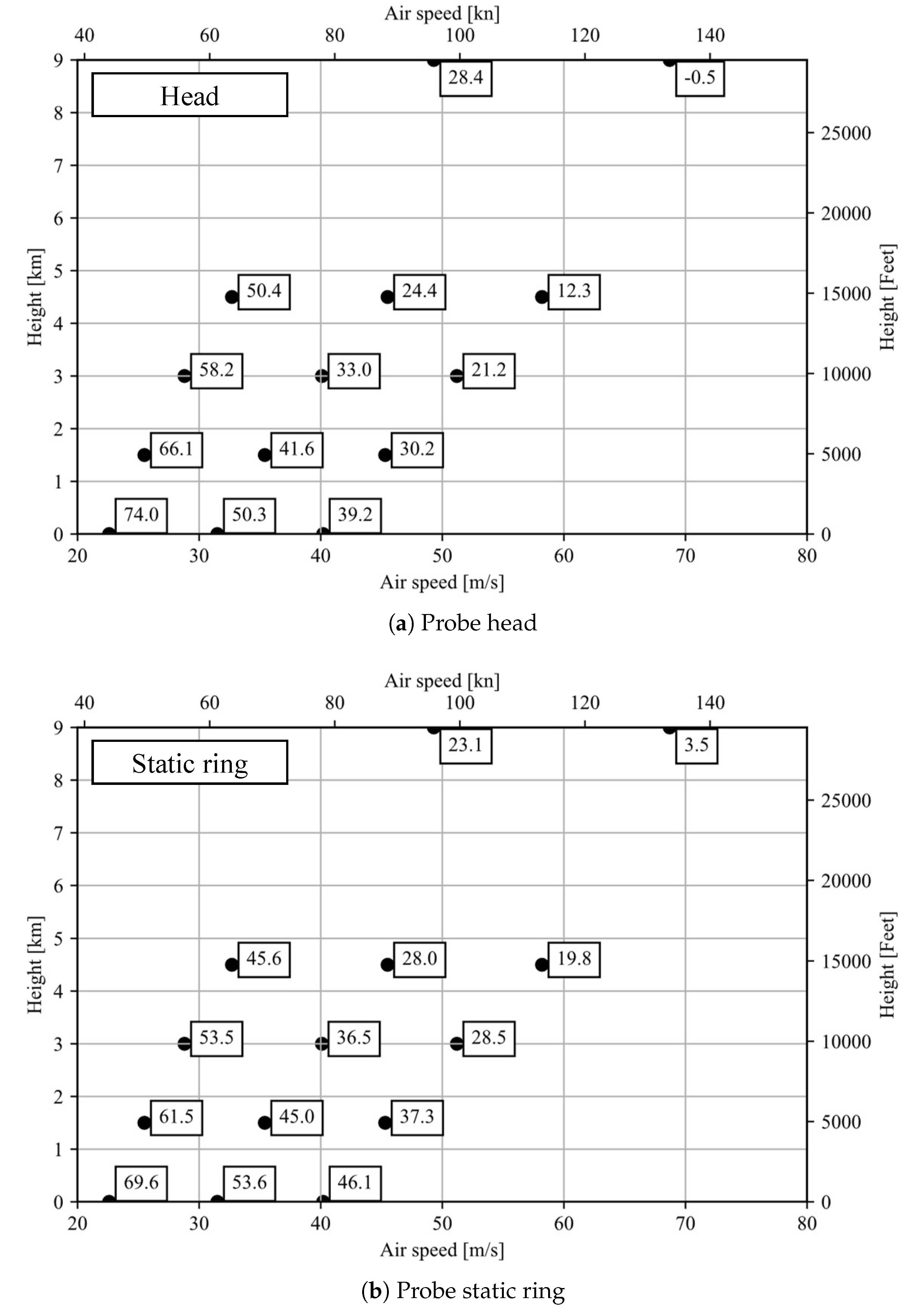

| Configuration | V [m/s] | q [W] |
|---|---|---|
| 1 | 25 () | 10 () |
| 2 | 25 () | 20 () |
| 3 | 25 () | 30 () |
| 4 | 25 () | 40 () |
| 4 | 25 () | 40 () |
| 5 | 35 () | 40 () |
| 6 | 45 () | 40 () |
| T1 | T2 | T3 | T4 | T5 | T6 | |
|---|---|---|---|---|---|---|
| Distance from probe tip [mm] | 0.5 | 6.5 | 22.9 | 42.8 | 66.0 | 72.5 |
| Config. | T∞ | T1 | T2 | T3 | T4 | T5 | T6 |
|---|---|---|---|---|---|---|---|
| 1 | 22.7 | 36.5 | 46.5 | 88.6 | 58.4 | 37.9 | 34.8 |
| 2 | 23.1 | 51.1 | 71.6 | 145.3 | 92.1 | 52.2 | 46.2 |
| 3 | 23.4 | 66.8 | 97.6 | 200.5 | 124.1 | 65.5 | 57.0 |
| 4 | 23.8 | 81.3 | 113.5 | 250.7 | 150.9 | 77.0 | 66.3 |
| 5 | 24.9 | 59.1 | 77.8 | 219.8 | 123.1 | 62.4 | 55.8 |
| 6 | 26.3 | 49.7 | 62.7 | 196.8 | 106.8 | 56.4 | 51.2 |
| Config. | Tanalytical [C] | Ttest [C] | [C] | [%] |
|---|---|---|---|---|
| 1 | 61.0 | 64.5 | −3.5 | −4.4% |
| 2 | 99.6 | 103.0 | −3.4 | −2.9% |
| 3 | 140.1 | 140.7 | −0.6 | −0.4% |
| 4 | 176.3 | 171.7 | 4.6 | 2.5% |
| 5 | 144.6 | 140.2 | 4.4 | 2.8% |
| 6 | 126.2 | 122.1 | 4.1 | 3.0% |
| Config. | T1 | T5 |
|---|---|---|
| Head | Static Ring | |
| 4 | 81.3 | 77.0 |
| 5 | 59.1 | 62.4 |
| 6 | 49.7 | 56.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieto Muro, P.; Heckmeier, F.M.; Jenkins, S.; Breitsamter, C. Development of an Analytic Convection Model for a Heated Multi-Hole Probe for Aircraft Applications. Sensors 2021, 21, 6218. https://doi.org/10.3390/s21186218
Nieto Muro P, Heckmeier FM, Jenkins S, Breitsamter C. Development of an Analytic Convection Model for a Heated Multi-Hole Probe for Aircraft Applications. Sensors. 2021; 21(18):6218. https://doi.org/10.3390/s21186218
Chicago/Turabian StyleNieto Muro, Pablo, Florian M. Heckmeier, Sean Jenkins, and Christian Breitsamter. 2021. "Development of an Analytic Convection Model for a Heated Multi-Hole Probe for Aircraft Applications" Sensors 21, no. 18: 6218. https://doi.org/10.3390/s21186218
APA StyleNieto Muro, P., Heckmeier, F. M., Jenkins, S., & Breitsamter, C. (2021). Development of an Analytic Convection Model for a Heated Multi-Hole Probe for Aircraft Applications. Sensors, 21(18), 6218. https://doi.org/10.3390/s21186218







