Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison
Abstract
:1. Introduction
2. Magnetic Field Sensor’s Error Sources and Measurement Model
- Bias, or offset; all magnetic sensors suffer from bias, which is a constant distortion. In many cases, it is the most important defect in the sensor’s overall error. A vector, , is used to model it.
- Scale-factor error represents the input-output gain error of the sensor. It is modeled by a diagonal matrix, .
- Cross-coupling or non-orthogonality inaccuracies are resulted by the non-ideal alignment of the sensor’s axes during manufacturing and are modeled by a matrix, .
- Soft-iron distortion is caused by ferromagnetic materials in the vicinity of the sensor, attached to the sensor’s coordinate frame. Those materials do not generate their own magnetic field, but instead alter the existing magnetic field locally, resulting in a measurement discrepancy. This effect is modeled by a matrix, .
- Hard-iron distortion is due to magnetic materials attached to the sensor’s coordinate frame. As a consequence of the persistent magnetic field created by those materials, the sensor’s output has a constant bias. Hard-iron distortion is modeled by a vector, .
- Random noise is the stochastic error in the sensor’s output. It is induced by the sensor’s mechanical and electrical architecture. It is modeled by a vector, , and it is most commonly assumed to be a sequence of white noise, i.e., .
3. Alonso and Shuster (TWOSTEP)
3.1. Initial Estimate
3.2. Solution Improvement Step
| Algorithm 1: Alonso and Shuster (TWOSTEP) [1] |
Step 1: Calculate by using (4)–(6) Step 2: Calculate the centered values (7) Step 3: Calculate centered estimate and covariance matrix (8) Step 5: Calculate and from (10) Step 6: Update using (9) Step 7: Calculate following (12) Step 8: Repeat steps 4–7 until is sufficiently small Step 9: Apply SVD on (13) and define matrix W Step 10: Calculate (14) and (15) |
4. Crassidis et al.
| Algorithm 2: Crassidis et al. [6] |
Step 1: Initialize and Step 2: for each measurement do: Calculate (4) Extract and from (16) Calculate (20) and (19) Calculate Kalman Gain (18) Update estimation: Update covariance matrix: (18) Step 3: Extract and from (16) |
5. Dorveaux et al.
| Algorithm 3: Dorveaux et al. [3] |
Step 1: Initialize using (24). Step 2: Minimize (25) using least squares and derive and . Step 3: Use and to calculate from (26). Step 4: Calculate and using (28). Step 5: Evaluate the cost function from (29). Step 6: Repeat steps 2-5 until is sufficiently small. |
6. Vasconcelos et al.
Initial Estimate
| Algorithm 4: Vasconcelos et al. [2] |
Initial Estimate Step 2: Calculate p using (39) Newton Method Step 4: Use the initial estimates and to initialize x according to (34). Step 5: Update x using (35). Step 6: Evaluate the cost function of (33). Step 7: Repeat Steps 5–6 until becomes sufficiently small. Step 8: Split x into and h and calculate . |
7. Ali et al.
| Algorithm 5: Ali et al. [7] |
Step 1: Initialize for and set Step 2: Find Particle i best: Global best: and Step 3: for each particle i do Update (47) Calculate (45) if and if and Step 4: Repeat Step 3 until an exit condition is met |
8. Wu and Shi
Initial Estimate
| Algorithm 6: Wu and Shi [4] |
Initial Estimate Step 1: Calculate , from (55) and form the matrix . Step 2: Find the eigenvector of corresponding to its minimum (or zero) eigenvalue and denote it as . Step 3: Calculate where . Step 4: Extract , b and c from z. Step 5: Calculate an initial estimate of the unknowns using (57). Gauss–Newton Method Step 6: Use the initial estimates to initialize the vector x of (53) Step 7: Update x using (54). Step 8: Evaluate the cost of (52). Step 9: Repeat steps 7-8 until becomes sufficiently small. |
9. Papafotis and Sotiriadis (MAG.I.C.AL.)
10. Algorithm Evaluation and Comparison
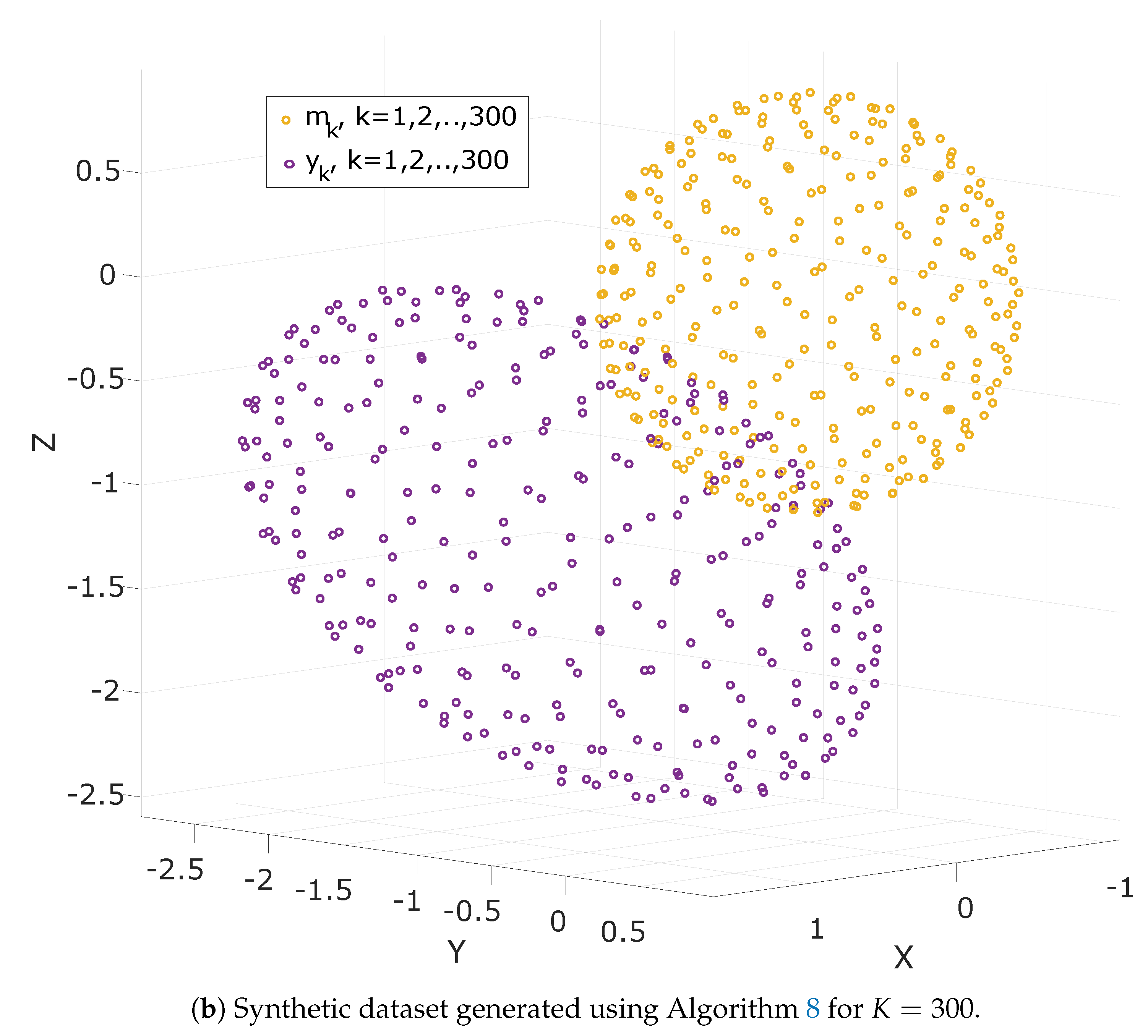
10.1. Synthetic Data Generation
| Algorithm 8: Generation of synthetic data |
Step 1:Initialize the number of measurements K and the radius of sphere r Step 2: Calculate Golden Ratio: Step 3: for each do: Step 4: Pick the scaling parameter, , the perturbation matrix, E and the perturbation vector, e. Step 5: Calculate T and h according to (66). Step 6: Generate a sequence of white noise: Step 7: Calculate the measurement vectors: (2) |
10.1.1. Experiment Setup and Evaluation Criteria
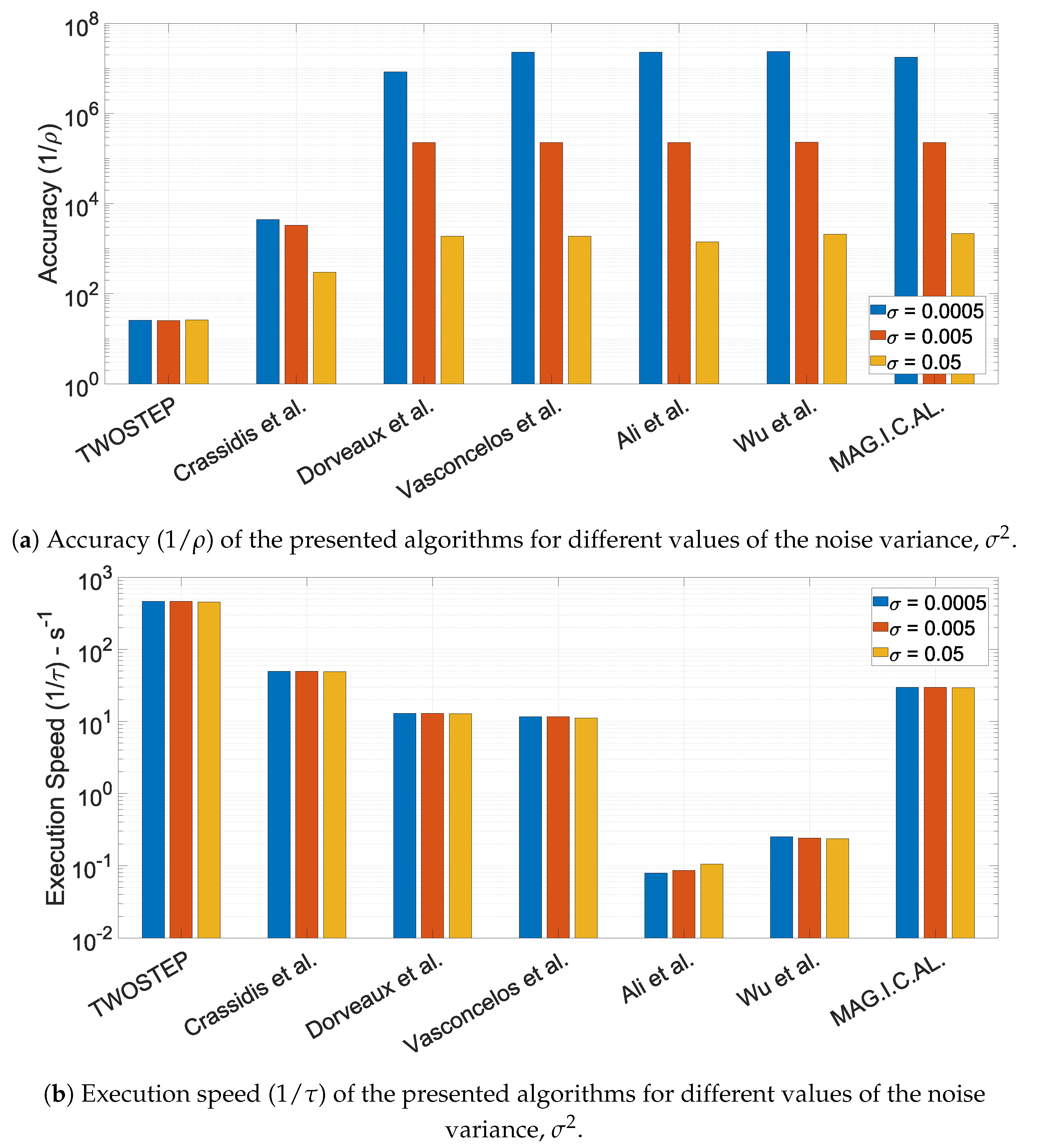
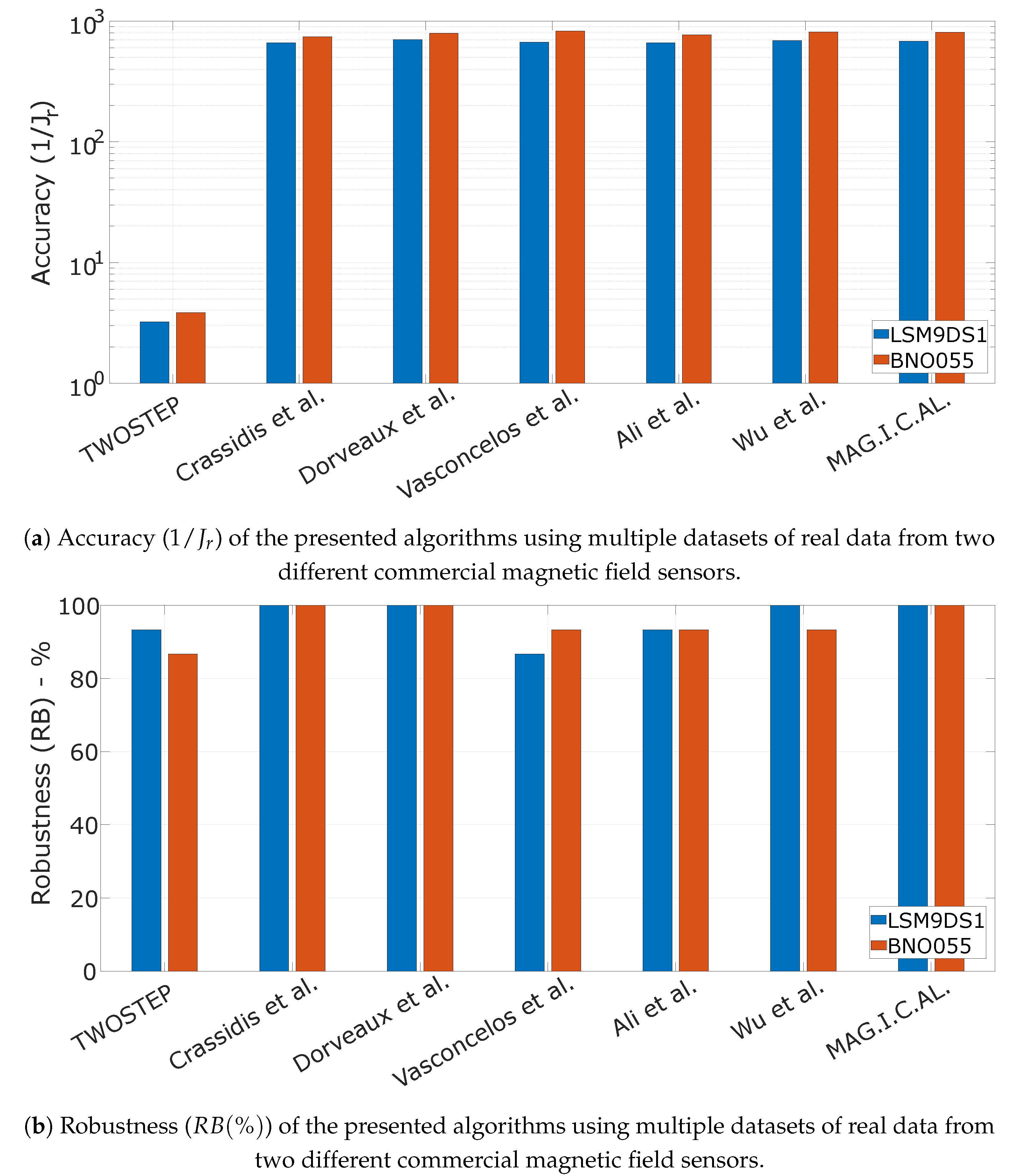
- Accuracy is defined as the mean value of the cost J, defined in (74), across all N executions with meaningful output.
- Mean execution time is defined as the mean value of the execution time of an algorithm.
- Robustness is defined as the percentage of datasets for which each algorithm successfully derived a meaningful solution.
10.1.2. Baseline Evaluation
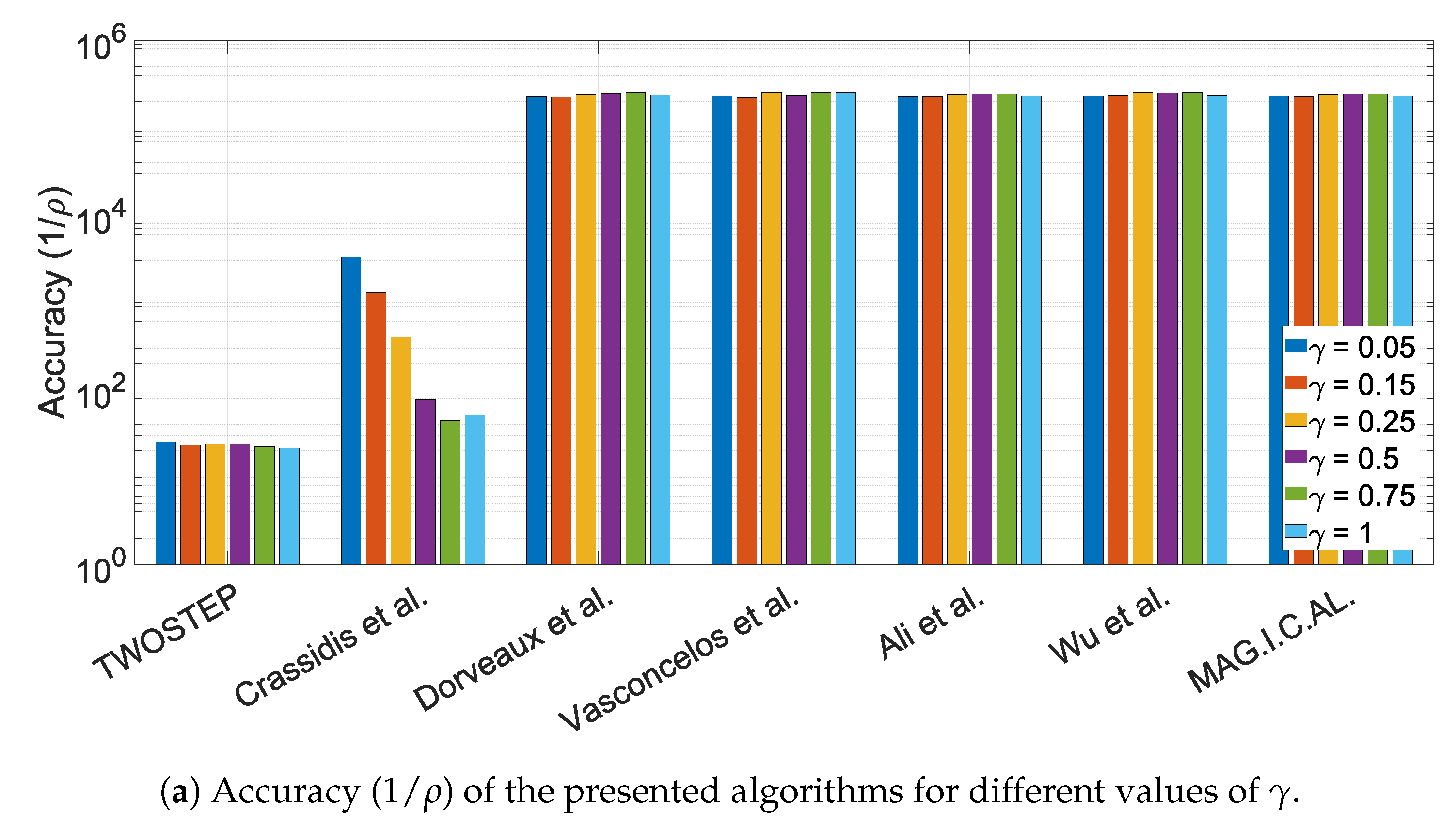
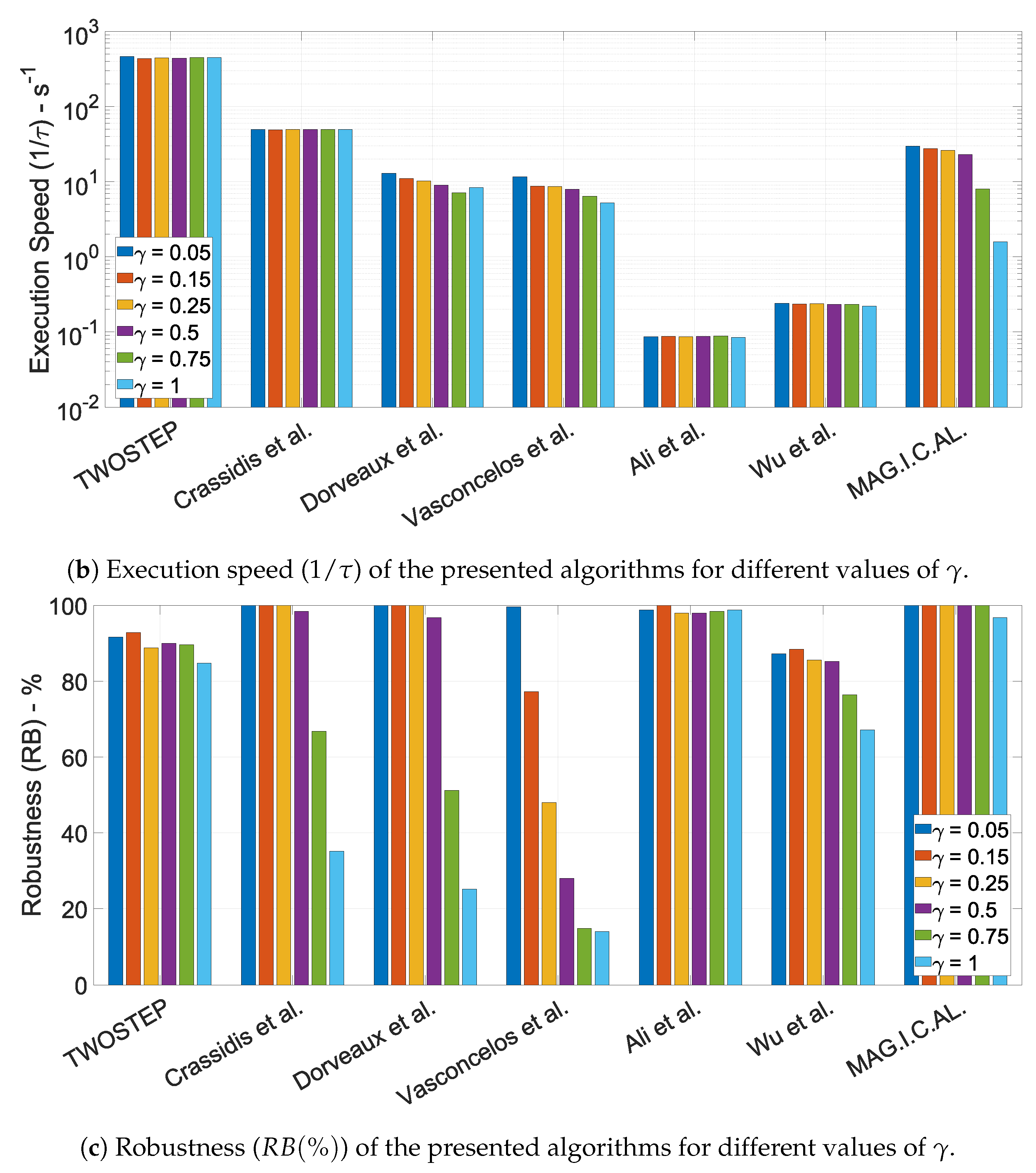
10.1.3. The Effect of the Offset Perturbation Parameter,
10.1.4. The Effect of the Calibration Matrix Perturbation Parameter,
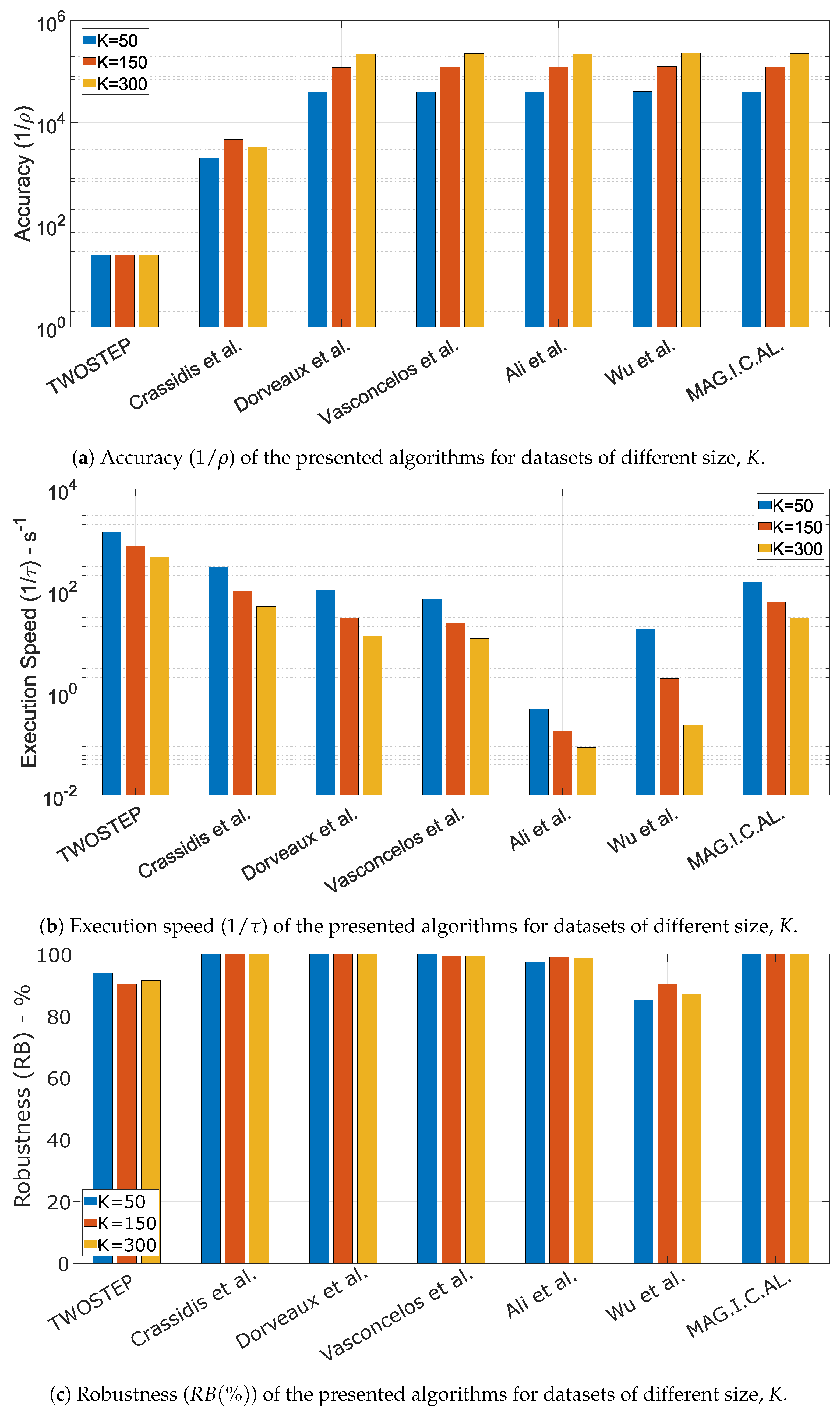
10.1.5. The Effect of Dataset Size, K
10.1.6. The Effect of the Noise Variance,
10.2. Algorithm Evaluation Using Real Data
11. Conclusions
- ✓
- TWOSTEP: Extremely time efficient. Works effectively for small distortions. Has low accuracy in general. The method can be generalized to on-orbit calibration.
- ✓
- Crassidis et al.: Easy to implement. Extremely time efficient. Works effectively for small to medium distortions. The method can be generalized to on-orbit calibration. It is the only algorithm that provides online update. It can be considered as a more accurate and effective version of TWOSTEP with similar time complexity.
- ✓
- Dorveaux et al.: Easy to implement. Moderately time efficient. Robust and accurate, but vulnerable to large values of bias.
- ✓
- Vasconcelos et al.: Difficult to implement. Characterized by high time-complexity. Exceptional accuracy and robustness for small distortions.
- ✓
- Ali et al.: Robust and accurate. Very high computational cost. Some prior knowledge of the search space is beneficial. At the beginning of the algorithm, the unknown variables are randomized and, thus, it is not always ensured that the algorithm will reach an optimal point. Thus, a couple of repetitions might be needed. Using modern PSO algorithms which can constrain the search space and handle a few variable inequalities increases the algorithm’s performance significantly.
- ✓
- Wu and Shi: Difficult to implement. Characterized by high time-complexity. Exceptional accuracy even with larger distortion. We noticed a 1% failure of finding an initial estimate due to inadequacy of applying Cholesky decomposition.
- ✓
- MAG.I.C.AL: Easy to implement. Moderately time efficient. Exceptional robustness and accuracy in both synthetic and real data experiments.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Gradient Vector and Hessian Matrix for the Algorithm of Vasconcelos et al.
Appendix A.2. Gradient Vector and Hessian Matrix for the Algorithm of Wu and Shi
References
- Alonso, R.; Shuster, M.D. Complete Linear Attitude-Independent Magnetometer Calibration. J. Astronaut. Sci. 2002, 50, 477–490. [Google Scholar] [CrossRef]
- Vasconcelos, J.F.; Elkaim, G.; Silvestre, C.; Oliveira, P.; Cardeira, B. Geometric Approach to Strapdown Magnetometer Calibration in Sensor Frame. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1293–1306. [Google Scholar] [CrossRef] [Green Version]
- Dorveaux, E.; Vissière, D.; Martin, A.; Petit, N. Iterative calibration method for inertial and magnetic sensors. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 8296–8303. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Shi, W. On Calibration of Three-Axis Magnetometer. IEEE Sens. J. 2015, 15, 6424–6431. [Google Scholar] [CrossRef] [Green Version]
- Papafotis, K.; Sotiriadis, P.P. MAG.I.C.AL.—A Unified Methodology for Magnetic and Inertial Sensors Calibration and Alignment. IEEE Sens. J. 2019, 19, 8241–8251. [Google Scholar] [CrossRef]
- Crassidis, J.; Lai, K.L.; Herman, R.R. Real-Time Attitude-Independent Three-Axis Magnetometer Calibration. J. Guid. Control Dyn. 2005, 28, 115–120. [Google Scholar] [CrossRef]
- Ali, A.; Siddharth, S.; Syed, Z.; El-Sheimy, N. Swarm Optimization-Based Magnetometer Calibration for Personal Handheld Devices. Sensors 2012, 12, 12455–12472. [Google Scholar] [CrossRef] [Green Version]
- Papafotis, K.; Sotiriadis, P.P. Accelerometer and Magnetometer Joint Calibration and Axes Alignment. Technologies 2020, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Kok, M.; Hol, J.D.; Schön, T.B.; Gustafsson, F.; Luinge, H. Calibration of a magnetometer in combination with inertial sensors. In Proceedings of the 2012 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 787–793. [Google Scholar]
- Wu, Y.; Zou, D.; Liu, P.; Yu, W. Dynamic Magnetometer Calibration and Alignment to Inertial Sensors by Kalman Filtering. IEEE Trans. Control Syst. Technol. 2018, 26, 716–723. [Google Scholar] [CrossRef] [Green Version]
- Kok, M.; Schön, T.B. Maximum likelihood calibration of a magnetometer using inertial sensors. IFAC Proc. Vol. 2014, 47, 92–97. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, Z. A new calibration method for tri-axial field sensors in strap-down navigation systems. Meas. Sci. Technol. 2012, 23, 105105. [Google Scholar] [CrossRef]
- Cao, G.; Xu, X.; Xu, D. Real-Time Calibration of Magnetometers Using the RLS/ML Algorithm. Sensors 2020, 20, 535. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hadjigeorgiou, N.; Asimakopoulos, K.; Papafotis, K.; Sotiriadis, P.P. Vector Magnetic Field Sensors: Operating Principles, Calibration and Applications. IEEE Sens. J. 2020, 21, 12531–12544. [Google Scholar] [CrossRef]
- IAGA Division V; Working Group 8. Revision of International Geomagnetic Reference Field released. EOS Trans. 1996, 77, 153. [Google Scholar] [CrossRef]
- Gambhir, B. Determination of Magnetometer Biases Using Module RESIDG; Technical Report; Computer Sciences Corporation: Falls Church, VA, USA, 1975. [Google Scholar]
- LERNER, G. Spacecraft Attitude Determination and Control; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Alonso, R.; Shuster, M.D. TWOSTEP: A fast robust algorithm for attitude-independent magnetometer-bias determination. J. Astronaut. Sci. 2002, 50, 433–451. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Applications; Brooks Cole/Cengage Learning: Belmont, CA, USA, 2007. [Google Scholar]
- Crassidis, J.L.; Markley, F.L.; Lightsey, E.G. Global Positioning System Integer Ambiguity Resolution without Attitude Knowledge. J. Guid. Control Dyn. 1999, 22, 212–218. [Google Scholar] [CrossRef] [Green Version]
- Crassidis, J.L. Optimal Estimation of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Springmann, J.C.; Cutler, J.W. Attitude-Independent Magnetometer Calibration with Time-Varying Bias. J. Guid. Control Dyn. 2012, 35, 1080–1088. [Google Scholar] [CrossRef]
- Foster, C.C. Elkaim, Extension of a two-step calibration methodology to include nonorthogonal sensor axes. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1070–1078. [Google Scholar] [CrossRef]
- Gebre-Egziabher, D.; Elkaim, G.; Powell, J.; Parkinson, B. Calibration of Strapdown Magnetometers in Magnetic Field Domain. J. Aerosp. Eng. 2006, 19, 87–102. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Kennedy, J.; Obaiahnahatti, B.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Academic Press: San Francisco, CA, USA, 2001; Volume 1, pp. 1931–1938. [Google Scholar]
- Magnus Erik Hvass Pedersen. Good Parameters for Particle Swarm Optimization; Hvass Laboratories. 2010. Available online: https://www.semanticscholar.org/paper/Good-Parameters-for-Particle-Swarm-Optimization-Pedersen/a4ad7500b64d70a2ec84bf57cfc2fedfdf770433 (accessed on 31 July 2021).
- Mezura-Montes, E.; Coello, C. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Helwig, S.; Branke, J.; Mostaghim, S. Experimental Analysis of Bound Handling Techniques in Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2013, 17, 259–271. [Google Scholar] [CrossRef]
- MATLAB. Optimization Toolbox; The MathWorks Inc.: Natick, MA, USA, 1999. [Google Scholar]
- Roberts, M. How to Evenly Distribute Points on a Sphere More Effectively than the Canonical Fibonacci Lattice. Available online: http://extremelearning.com.au/how-to-evenly-distribute-points-on-a-sphere-more-effectively-than-the-canonical-fibonacci-lattice/ (accessed on 22 May 2021).
- Gonzalez, A. Measurement of Areas on a Sphere Using Fibonacci and Latitude–Longitude Lattices. Math. Geosci. 2010, 42, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Schonemann, P. A generalized solution of the orthogonal procrustes problem. Psychometrika 1966, 31, 1–10. [Google Scholar] [CrossRef]



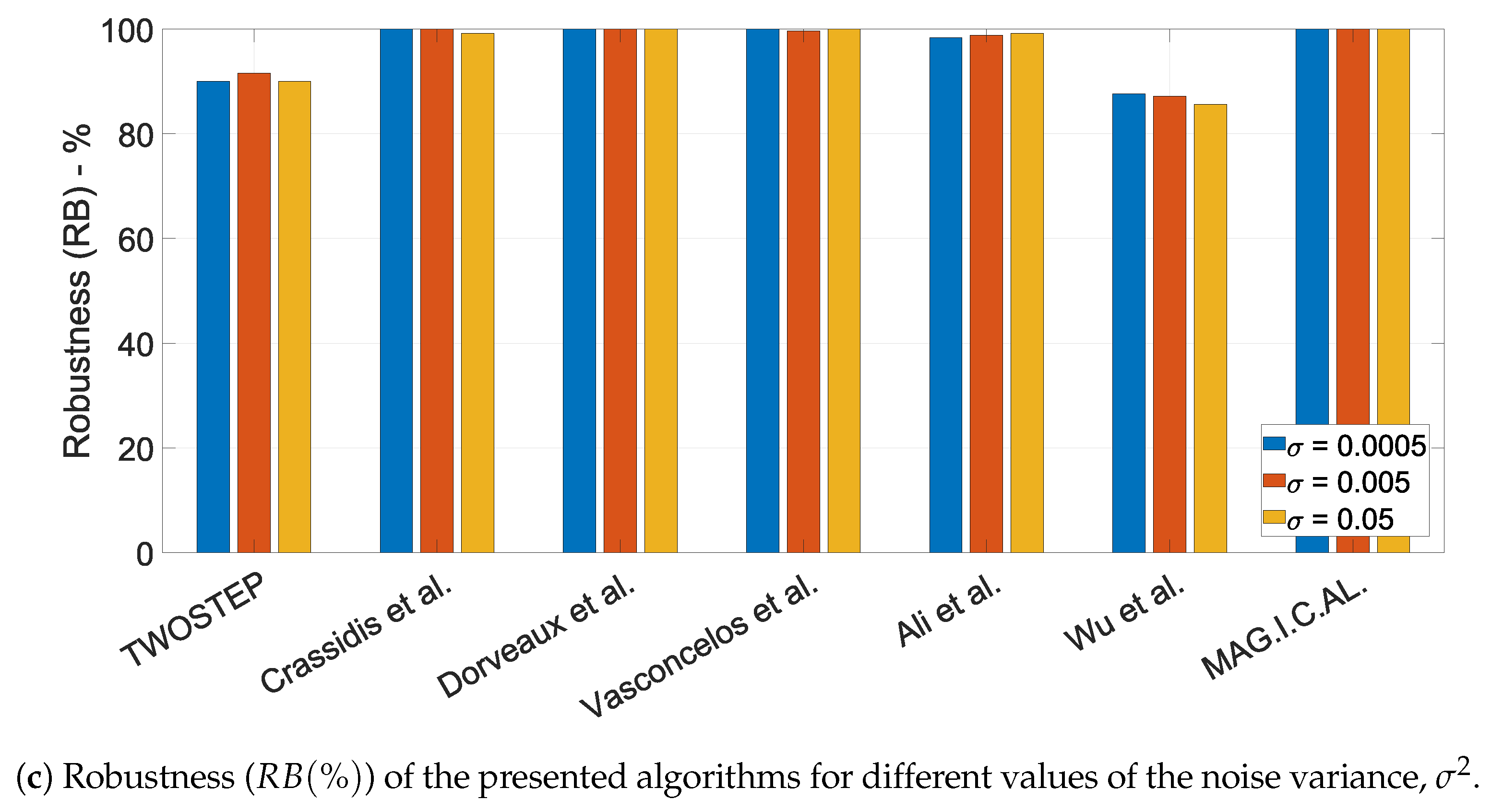
| Euclidean Norm | |
| Frobenius Norm | |
| vec (·) | Vectorization of Matrix |
| diag(·) | Diagonal Matrix |
| chol (·) | Cholesky Factorization |
| Identity Matrix | |
| Zero Vector | |
| Normal Distribution | |
| Uniform Distribution | |
| ∇ | Gradient Vector |
| Hessian Matrix | |
| ⊗ | Kronecker Product |
| Orthogonal Group of dimension 3 | |
| 3D Rotation Group | |
| Group of Upper Triangular Matrices |
| Algorithm | Accuracy () | Robustness () | Execution Speed () |
|---|---|---|---|
| TWOSTEP [1] | 455 | ||
| Crassidis et al. [6] | |||
| Dorveaux et al. [3] | |||
| Vasconcelos et al. [2] | |||
| Ali et al. [7] | |||
| Wu and Shi [4] | |||
| MAG.I.C.AL [5] |
| BNO055 | LSM9DS1TR | |
|---|---|---|
| Measurement Range | Gauss | Gauss |
| Sampling Rate | 30 Hz | 80 Hz |
| Measurement Resolution | 16 bits | 16 bits |
| Algorithm | Simplicity | Robustness | Accuracy | Efficiency |
|---|---|---|---|---|
| TWOSTEP | ✓✓ | ✓✓ | ✓ | ✓✓✓ |
| Crassidis et al. | ✓✓✓ | ✓✓ | ✓ | ✓✓✓ |
| Dorveaux et al. | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓✓ |
| Vasconcelos et al. | ✓ | ✓ | ✓✓ | ✓ |
| Ali et al. | ✓✓ | ✓✓✓ | ✓✓✓ | ✓ |
| Wu and Shi | ✓ | ✓ | ✓✓✓ | ✓ |
| MAG.I.C.AL | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papafotis, K.; Nikitas, D.; Sotiriadis, P.P. Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison. Sensors 2021, 21, 5288. https://doi.org/10.3390/s21165288
Papafotis K, Nikitas D, Sotiriadis PP. Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison. Sensors. 2021; 21(16):5288. https://doi.org/10.3390/s21165288
Chicago/Turabian StylePapafotis, Konstantinos, Dimitris Nikitas, and Paul P. Sotiriadis. 2021. "Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison" Sensors 21, no. 16: 5288. https://doi.org/10.3390/s21165288
APA StylePapafotis, K., Nikitas, D., & Sotiriadis, P. P. (2021). Magnetic Field Sensors’ Calibration: Algorithms’ Overview and Comparison. Sensors, 21(16), 5288. https://doi.org/10.3390/s21165288








