Deep Learning of Explainable EEG Patterns as Dynamic Spatiotemporal Clusters and Rules in a Brain-Inspired Spiking Neural Network
Abstract
:1. Introduction
- Detecting informative spatiotemporal variables with respect to the dynamic evolving spike-driven patterns during the learning process in SNN models. This resulted in improving the output prediction/classification accuracy.
- Extracting spatiotemporal rules of spike occurrence during the dynamic clustering, which enhanced the interpretability and explainability of SNN learning behavior.
2. Materials and Methods
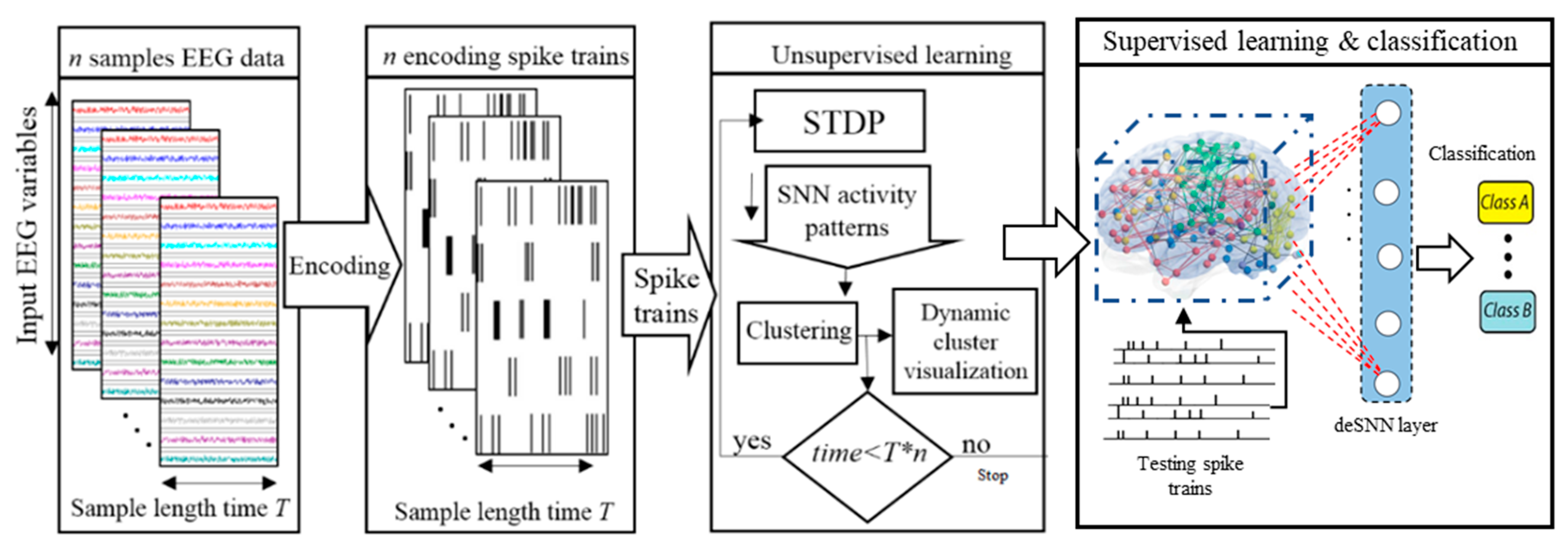
2.1. Method for Dynamic Spatiotemporal Clustering of Streaming Data in Spiking Neural Networks
- Spatiotemporal data encoding.
- SNN mapping and initializing.
- Unsupervised learning in SNN and simultaneously clustering the neurons.
- Quantitative analysis of the dynamic clustering patterns.
- Spatiotemporal fuzzy clustering.
- Spatiotemporal rule extraction from SNN clustering patterns.
- Supervised learning and pattern classification.
| Algorithm 1. The dynamic spatiotemporal clustering algorithm at time point t of the unsupervised learning process. |
| Input: Input spike data , number of neurons in the SNN model , number of input variables , connection weights , and parameter , STDP, time Output: A vector of labelled neurons k, vector of spik events for each cluster 1: Procedure 2: 3: , 4: For each time point t from the input stream data Do 5: 6: 7: 8: 9: Visualization of the clusters 10: Spatiotemporal rules within each cluster Do 11: If 12: Cluster fires as active event in time . 13: End if 14: End for 15: Algorithms to generate a set of spatiotemporal rules 16: End of procedure |
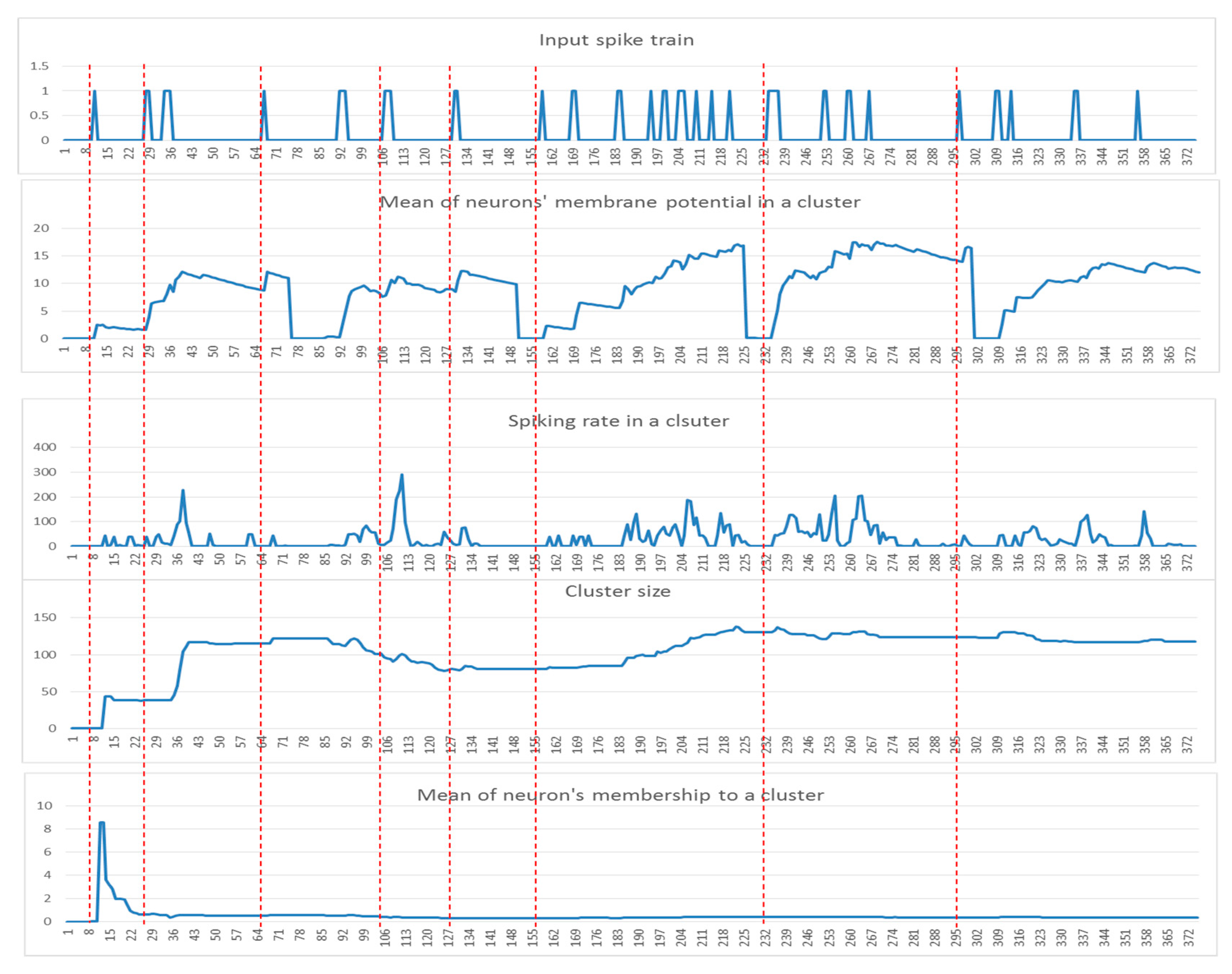
2.2. SNN Model Explainability through Dynamic Clustering Method
- Input spike train to an SNN model.
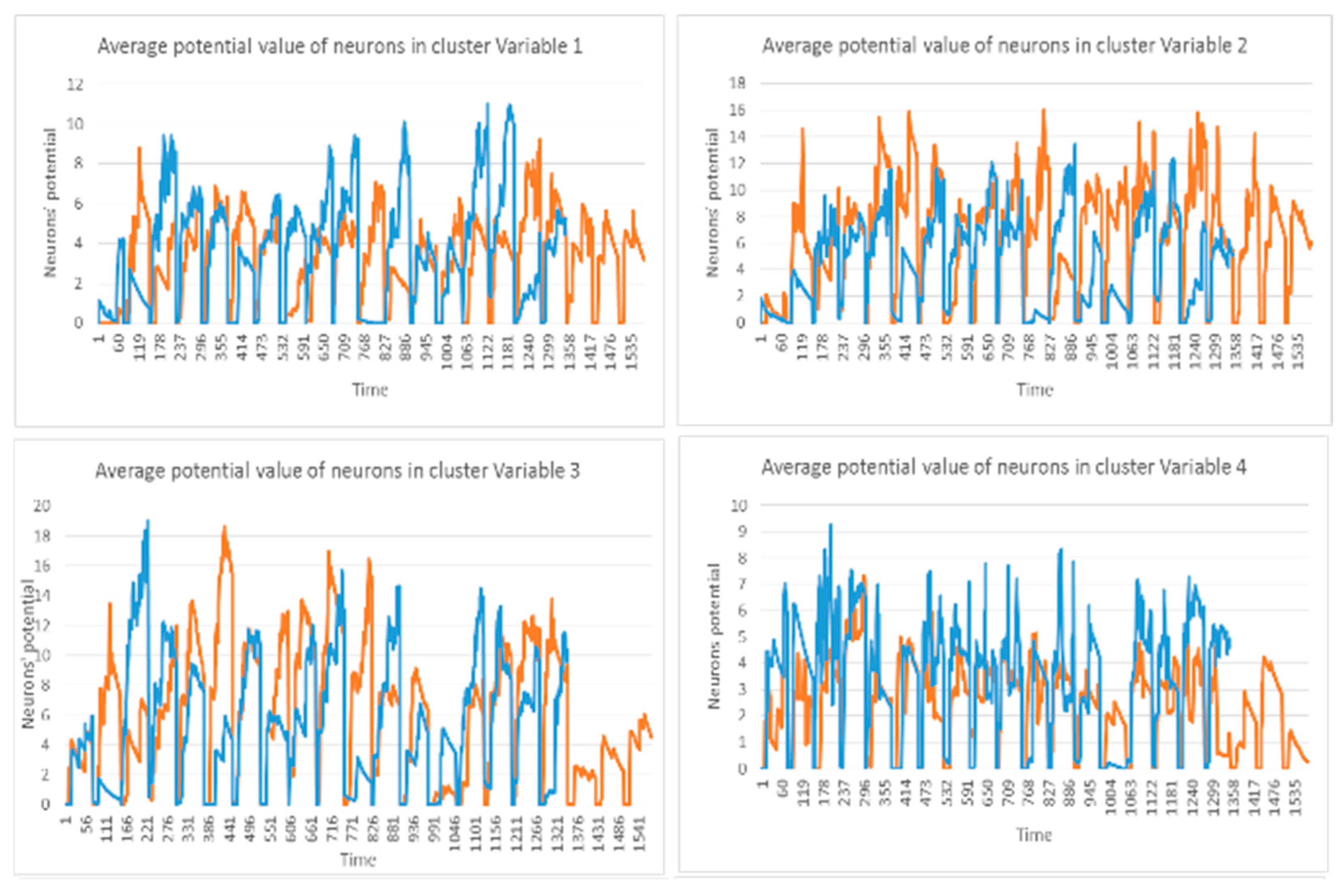
- The mean of the cluster’s postsynaptic potentials , indicated by .
- The mean of the cluster’s spiking rates, indicated by .
- The size of the cluster (number of neurons).
- The mean of the neuron’s memberships (the number of spikes received by neurons from the cluster center).
- Among these five patterns of the cluster evolution, we further investigated the patterns using the following techniques:
- Local maximum the maximum value of the was measured for each data sample.
- The area under a curve: this is computed from the of each data sample defined by where l is the length of each sample (time points).
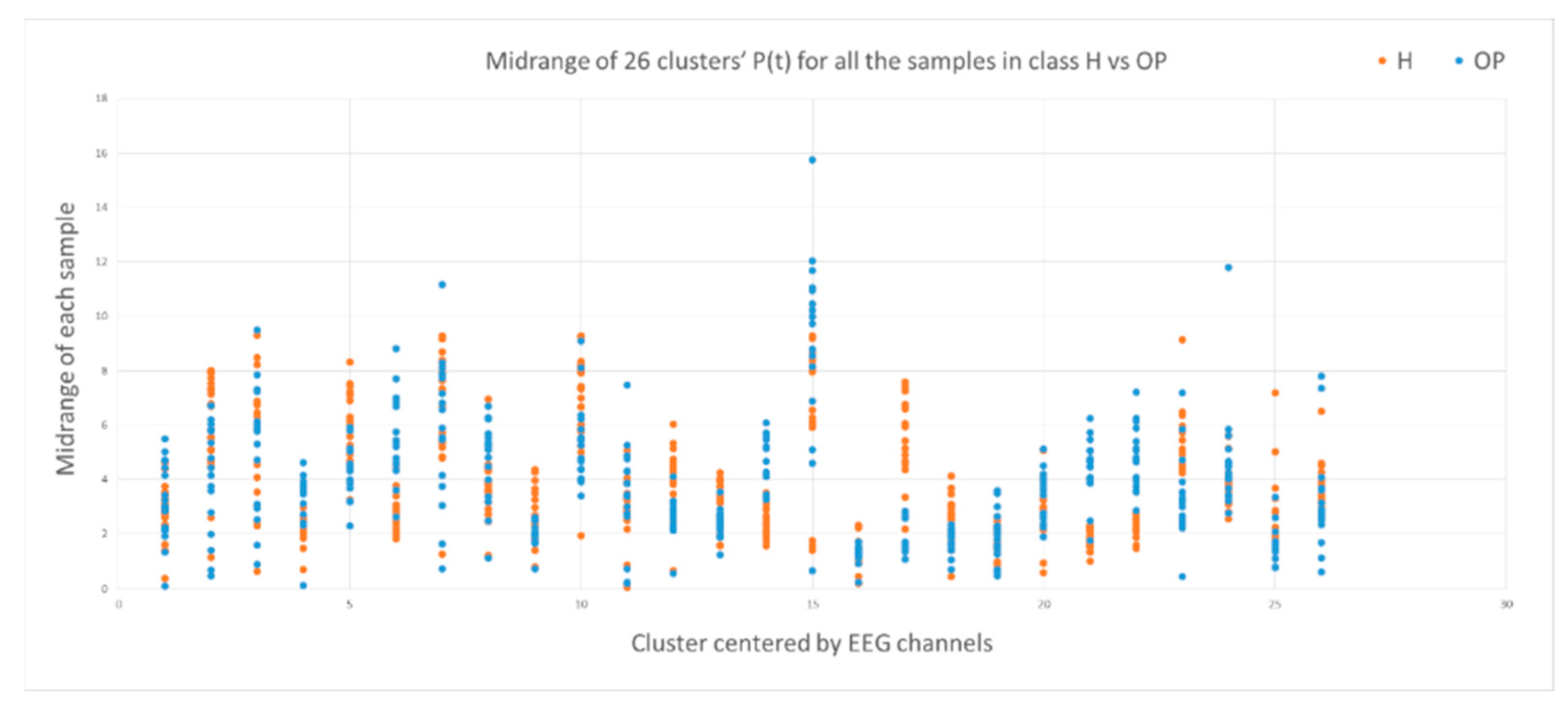
- Mid of potential: this is an average of the min value and max value in the , measured through .
2.3. Spatiotemporal Fuzzy Clusters in SNN Models
2.4. Enhancing the SNN Explainability through Spatiotemporal Spike Rule Extraction
| Algorithm 2. Defining the order of the time interval when spike actions A are detected. |
| Inputs: Cluster , Number of clusters , timeseries, temporal length , Spike-events in clusters and spike time-interval Outputs: Rules as set of Action A and time orders Procedure: For //for all the clusters While If ( //sequential number of spikes End If End while End For Print sets of Actions as Rules For c = 1 to Ord For t = 1 to T If Ord End For End For End of Procedure |
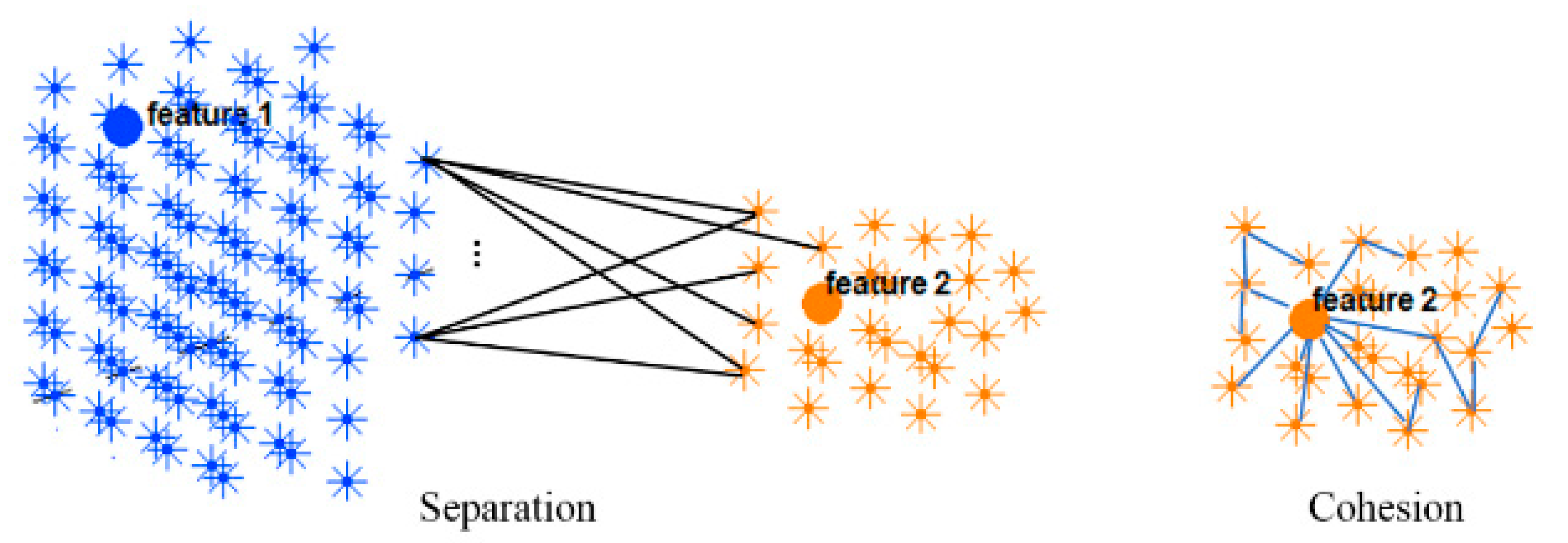
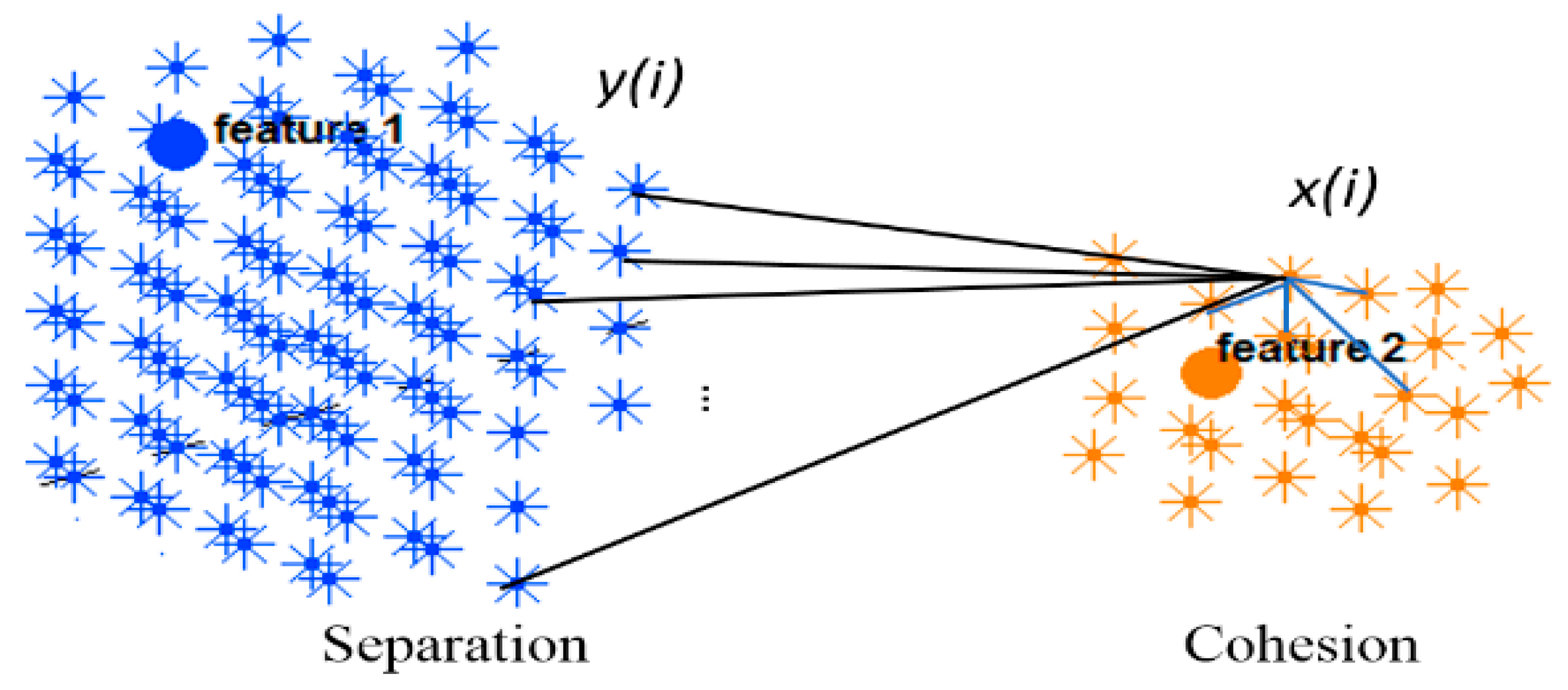
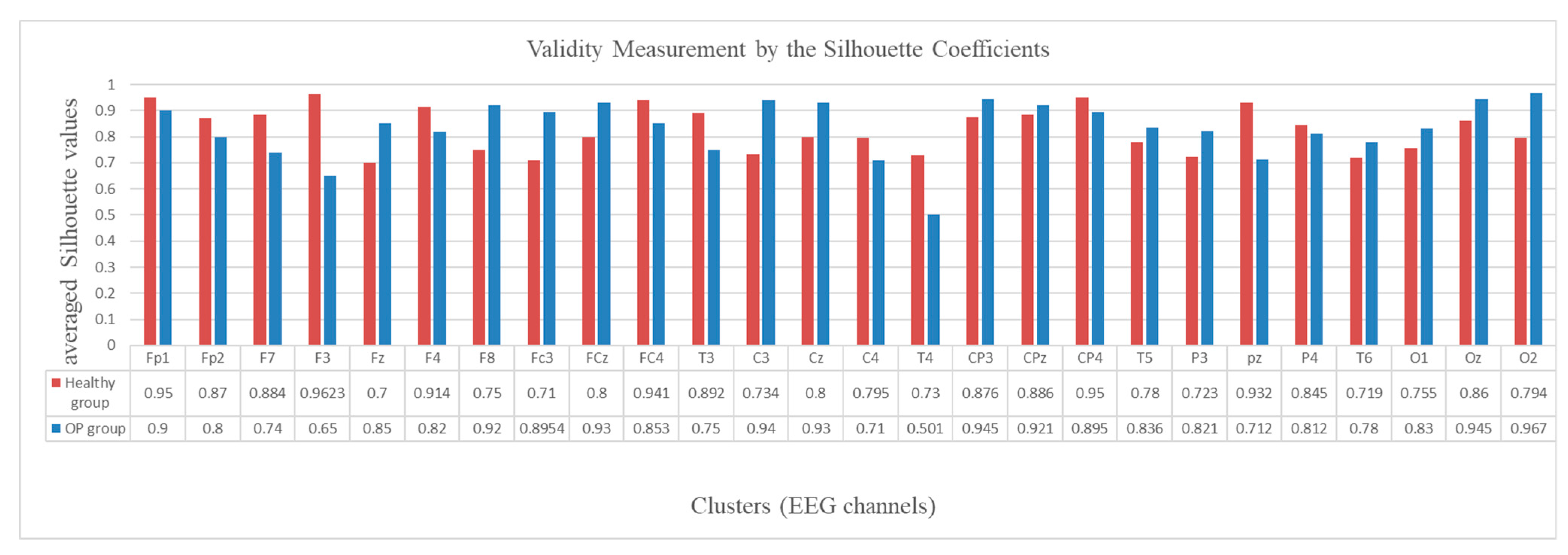
2.5. Validity Measurement of the SNN Clustering
3. Results: Dynamic SNN Clustering of EEG Data, Spatiotemporal Rule Extraction and Feature Selection
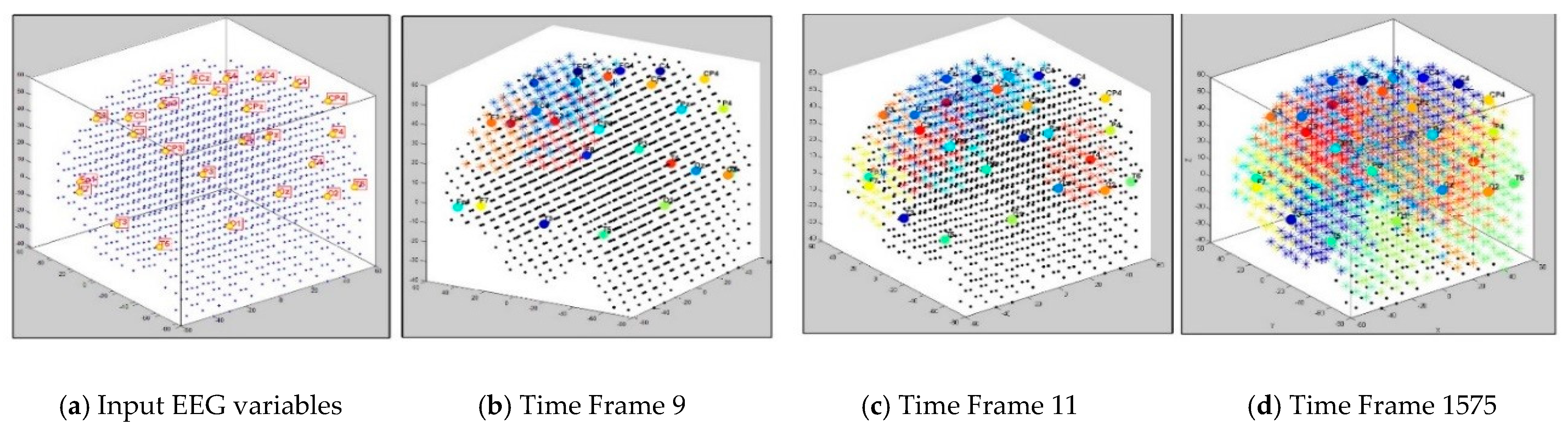
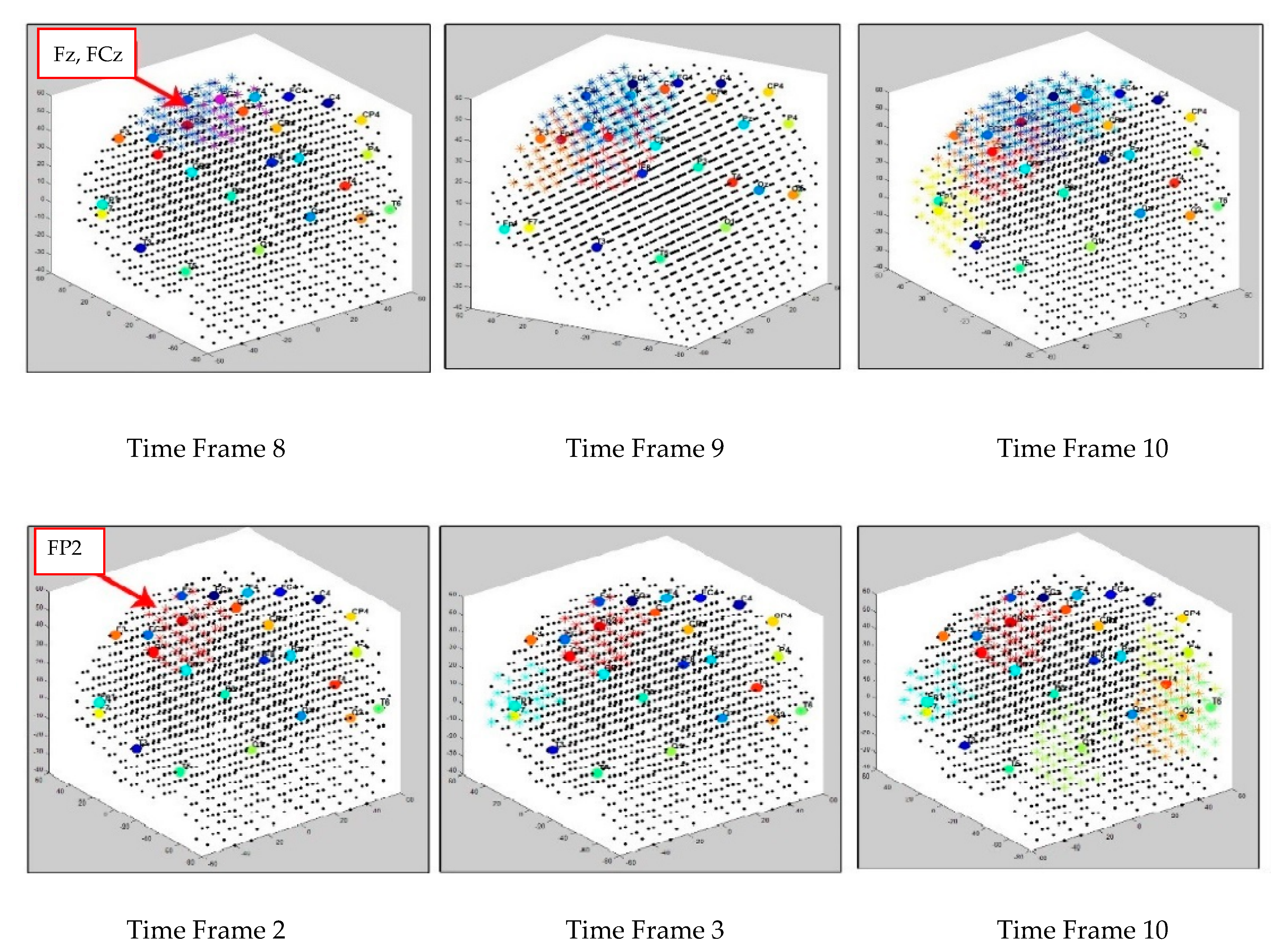
3.1. Dynamic Spatiotemporal Clustering in SNN while Streaming EEG Data
3.2. Feature Selection through Modelling Dynamic Clustering Patterns in SNN
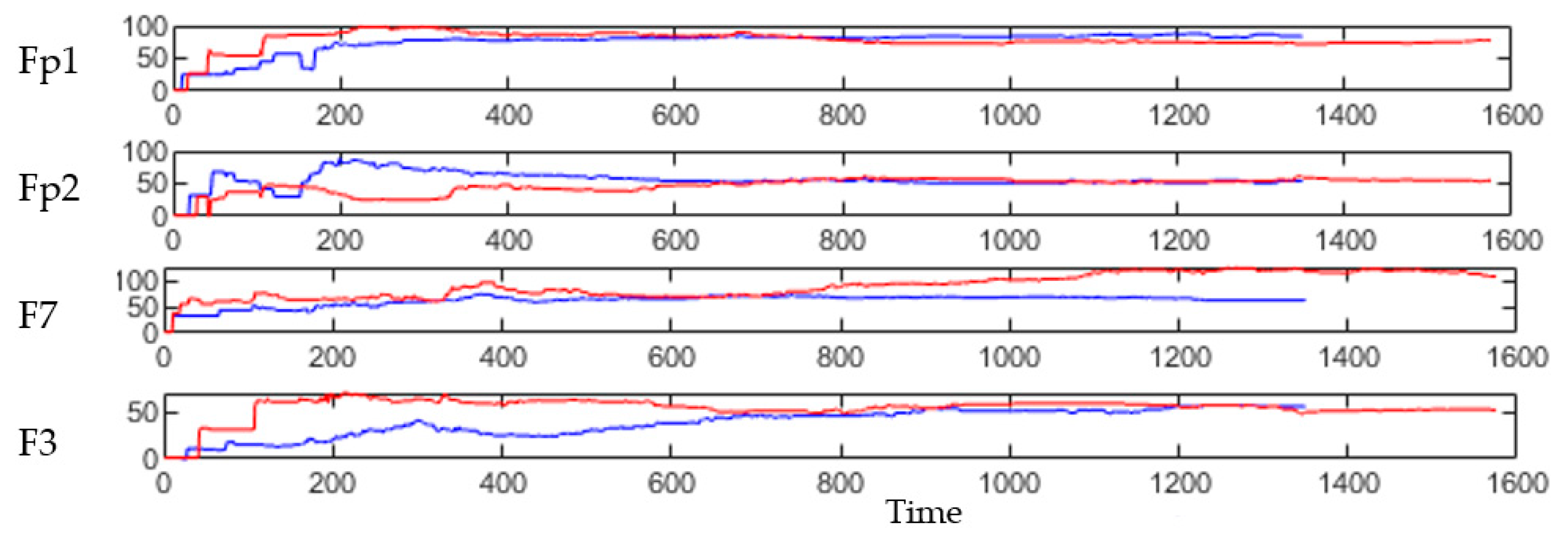
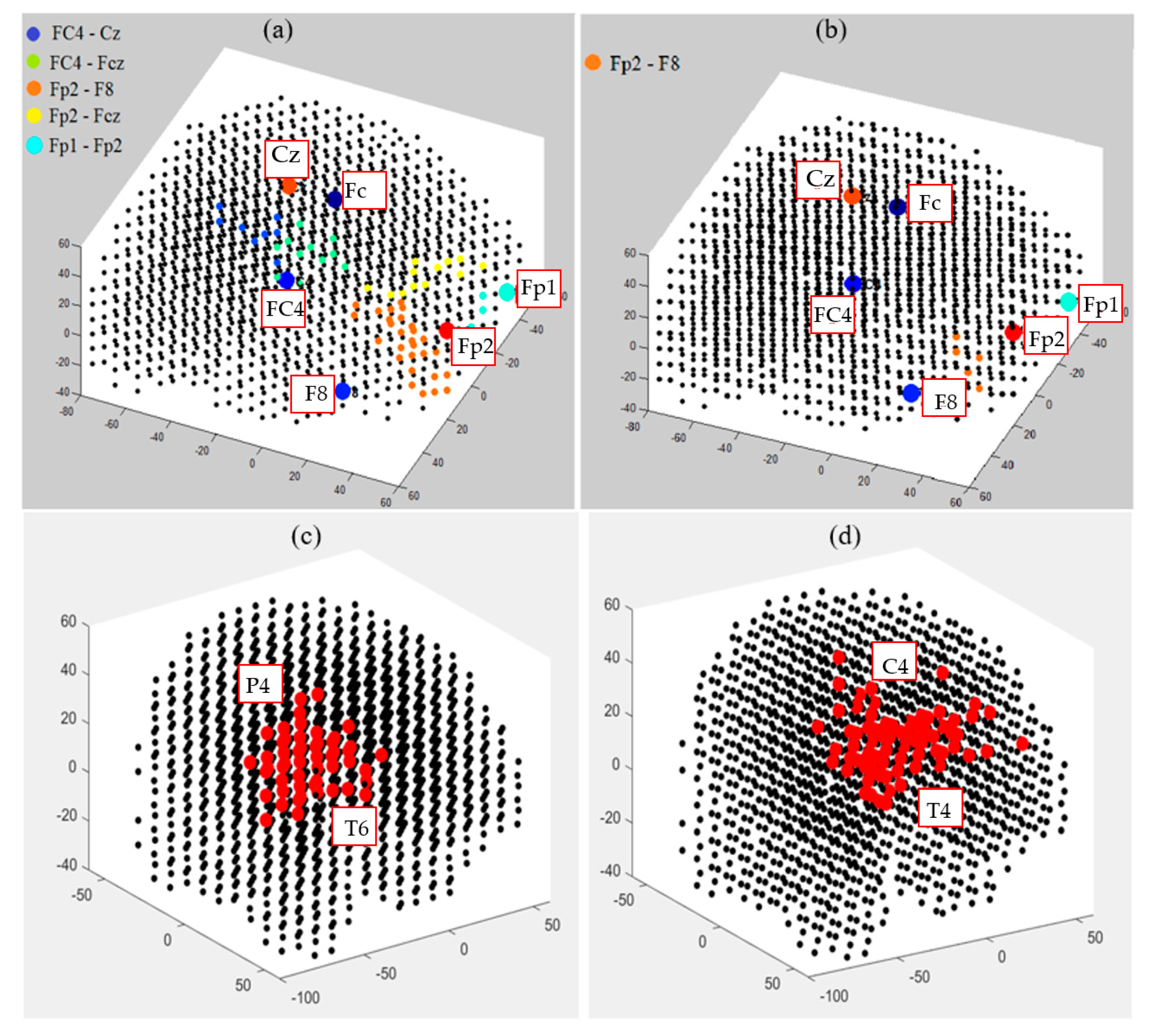
3.3. Spatiotemporal Fuzzy Clusters in SNN Models of EEG from Control and OP Groups
3.4. Capturing Spatiotemporal Spike Events during Unsupervised Learning in SNN Models
4. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Kim, G.; Kim, K.; Choi, S.; Jang, H.J.; Jung, S.-O. Area-and Energy-Efficient STDP Learning Algorithm for Spiking Neural Network SoC. IEEE Access 2020, 8, 216922–216932. [Google Scholar] [CrossRef]
- Bensimon, M.; Greenberg, S.; Haiut, M. Using a Low-Power Spiking Continuous Time Neuron (SCTN) for Sound Signal Processing. Sensors 2021, 21, 1065. [Google Scholar]
- Asghar, M.S.; Arslan, S.; Kim, H. A Low-Power Spiking Neural Network Chip Based on a Compact LIF Neuron and Binary Exponential Charge Injector Synapse Circuits. Sensors 2021, 21, 4462. [Google Scholar] [CrossRef]
- Lobov, S.A.; Chernyshov, A.V.; Krilova, N.P.; Shamshin, M.O.; Kazantsev, V.B. Competitive learning in a spiking neural network: Towards an intelligent pattern classifier. Sensors 2020, 20, 500. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alzhrani, W.; Doborjeh, M.; Doborjeh, Z.; Kasabov, N. Emotion Recognition and Understanding Using EEG Data in A Brain-Inspired Spiking Neural Network Architecture. In Proceedings of the International Joint Conference on Neural Networks IJCNN 2021, Shenzhen, China, 18–22 July 2021; pp. 1–10. [Google Scholar]
- Doborjeh, M.G.; Kasabov, N. Personalised modelling on integrated clinical and EEG spatio-temporal brain data in the NeuCube spiking neural network system. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1373–1378. [Google Scholar]
- Doborjeh, M.; Kasabov, N.; Doborjeh, Z.; Enayatollahi, R.; Tu, E.; Gandomi, A.H. Personalised modelling with spiking neural networks integrating temporal and static information. Neural Netw. 2019, 119, 162–177. [Google Scholar] [CrossRef]
- Durai, M.; Sanders, P.; Doborjeh, Z.; Wendt, A.; Kasabov, N.; Searchfield, G. Prediction of tinnitus masking benefit within a case series using a spiking neural network model. In Progress in Brain Research; Waxman, S., Stein, D.G., Swaab, D., Fields, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Doborjeh, Z.G. Modelling of Spatiotemporal EEG and ERP Brain Data for Dynamic Pattern Recognition and Brain State Prediction using Spiking Neural Networks: Methods and Applications in Psychology. Ph.D. Thesis, Auckland University of Technology, Auckland, New Zealand, 2019. [Google Scholar]
- Doborjeh, Z.; Doborjeh, M.; Taylor, T.; Kasabov, N.; Wang, G.Y.; Siegert, R.; Sumich, A. Spiking neural network modelling approach reveals how mindfulness training rewires the brain. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Doborjeh, Z.; Doborjeh, M.; Crook-Rumsey, M.; Taylor, T.; Wang, G.Y.; Moreau, D.; Krägeloh, C.; Wrapson, W.; Siegert, R.J.; Kasabov, N.; et al. Interpretability of Spatiotemporal Dynamics of the Brain Processes Followed by Mindfulness Intervention in a Brain-Inspired Spiking Neural Network Architecture. Sensors 2020, 20, 7354. [Google Scholar] [CrossRef] [PubMed]
- Kasabov, N.; Zhou, L.; Doborjeh, M.G.; Doborjeh, Z.G.; Yang, J. New algorithms for encoding, learning and classification of fMRI data in a spiking neural network architecture: A case on modeling and understanding of dynamic cognitive processes. IEEE Trans. Cogn. Dev. Syst. 2016, 9, 293–303. [Google Scholar] [CrossRef]
- Kasabov, N.K.; Doborjeh, M.G.; Doborjeh, Z.G. Mapping, learning, visualization, classification, and understanding of fMRI data in the NeuCube evolving spatiotemporal data machine of spiking neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 887–899. [Google Scholar] [CrossRef]
- Doborjeh, M.G.; Capecci, E.; Kasabov, N. Classification and segmentation of fMRI spatio-temporal brain data with a NeuCube evolving spiking neural network model. In Proceedings of the 2014 IEEE Symposium on Evolving and Autonomous Learning Systems (EALS), Orlando, FL, USA, 9–12 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 73–80. [Google Scholar]
- Doborjeh, M.G.; Kasabov, N. Dynamic 3D clustering of spatio-temporal brain data in the NeuCube spiking neural network architecture on a case study of fMRI data. In International Conference on Neural Information Processing; Springer: Cham, Switzerland, 2015; pp. 191–198. [Google Scholar]
- Capecci, E.; Doborjeh, Z.G.; Mammone, N.; la Foresta, F.; Morabito, F.C.; Kasabov, N. Longitudinal study of Alzheimer’s disease degeneration through EEG data analysis with a NeuCube spiking neural network model. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1360–1366. [Google Scholar]
- Kasabov, N.K. NeuCube: A spiking neural network architecture for mapping, learning and understanding of spatio-temporal brain data. Neural Netw. 2014, 52, 62–76. [Google Scholar] [CrossRef]
- Kasabov, N.K. Time-Space, Spiking Neural Networks and Brain-Inspired Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Kumarasinghe, K.; Kasabov, N.; Taylor, D. Deep learning and deep knowledge representation in Spiking Neural Networks for Brain-Computer Interfaces. Neural Netw. 2020, 121, 169–185. [Google Scholar] [CrossRef]
- Doborjeh, M.G.; Kasabov, N.; Doborjeh, Z.G. Evolving, dynamic clustering of spatio/spectro-temporal data in 3D spiking neural network models and a case study on EEG data. Evol. Syst. 2017, 9, 195–211. [Google Scholar] [CrossRef] [Green Version]
- Dhoble, K.; Nuntalid, N.; Indiveri, G.; Kasabov, N. Online spatio-temporal pattern recognition with evolving spiking neural networks utilising address event representation, rank order, and temporal spike learning. In Proceedings of the 2012 international joint conference on Neural networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Sengupta, N.; Kasabov, N. Spike-time encoding as a data compression technique for pattern recognition of temporal data. Inf. Sci. 2017, 406, 133–145. [Google Scholar] [CrossRef]
- Schrauwen, B.; van Campenhout, J. BSA, a fast and accurate spike train encoding scheme. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. 2825–2830. [Google Scholar]
- Bohte, S.M. The evidence for neural information processing with precise spike-times: A survey. Nat. Comput. 2004, 3, 195–206. [Google Scholar] [CrossRef] [Green Version]
- Talairach, J. 3-dimensional proportional system; an approach to cerebral imaging. co-planar stereotaxic atlas of the human brain. Thieme 1988, 1–122. [Google Scholar]
- Koessler, L.; Maillard, L.; Benhadid, A.; Vignal, J.P.; Felblinger, J.; Vespignani, H.; Braun, M. Automated cortical projection of EEG sensors: Anatomical correlation via the international 10–10 system. Neuroimage 2009, 46, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Braitenberg, V.; Schüz, A. Cortex: Statistics and Geometry of Neuronal Connectivity; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Knight, B.W. Dynamics of encoding in a population of neurons. J. Gen. Physiol. 1972, 59, 734–766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, S.; Miller, K.D.; Abbott, L.F. Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 2000, 3, 919–926. [Google Scholar] [CrossRef]
- Zhou, D.; Bousquet, O.; Lal, T.N.; Weston, J.; Schölkopf, B. Learning with local and global consistency. Adv. Neural Inf. Process. Syst. 2004, 16, 321–328. [Google Scholar]
- Doborjeh, M.G.; Wang, G.Y.; Kasabov, N.K.; Kydd, R.; Russell, B. A spiking neural network methodology and system for learning and comparative analysis of EEG data from healthy versus addiction treated versus addiction not treated subjects. IEEE Trans. Biomed. Eng. 2015, 63, 1830–1841. [Google Scholar] [CrossRef]
- Tan, P.-N.; Steinbach, M.; Kumar, V. Introduction to Data Mining; Pearson Education India: New Delhi, India, 2016. [Google Scholar]
- Zhao, Y.; Karypis, G. Evaluation of hierarchical clustering algorithms for document datasets. In Proceedings of the Eleventh International Conference on Information and Knowledge Management, McLean, VA, USA, 4–9 November 2002; pp. 515–524. [Google Scholar]
- Kasabov, N.; Dhoble, K.; Nuntalid, N.; Indiveri, G. Dynamic evolving spiking neural networks for on-line spatio-and spectro-temporal pattern recognition. Neural Netw. 2013, 41, 188–201. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, S.; Gautrais, J. Rank order coding. In Computational Neuroscience; Springer: Berlin/Heidelberg, Germany, 1998; pp. 113–118. [Google Scholar]

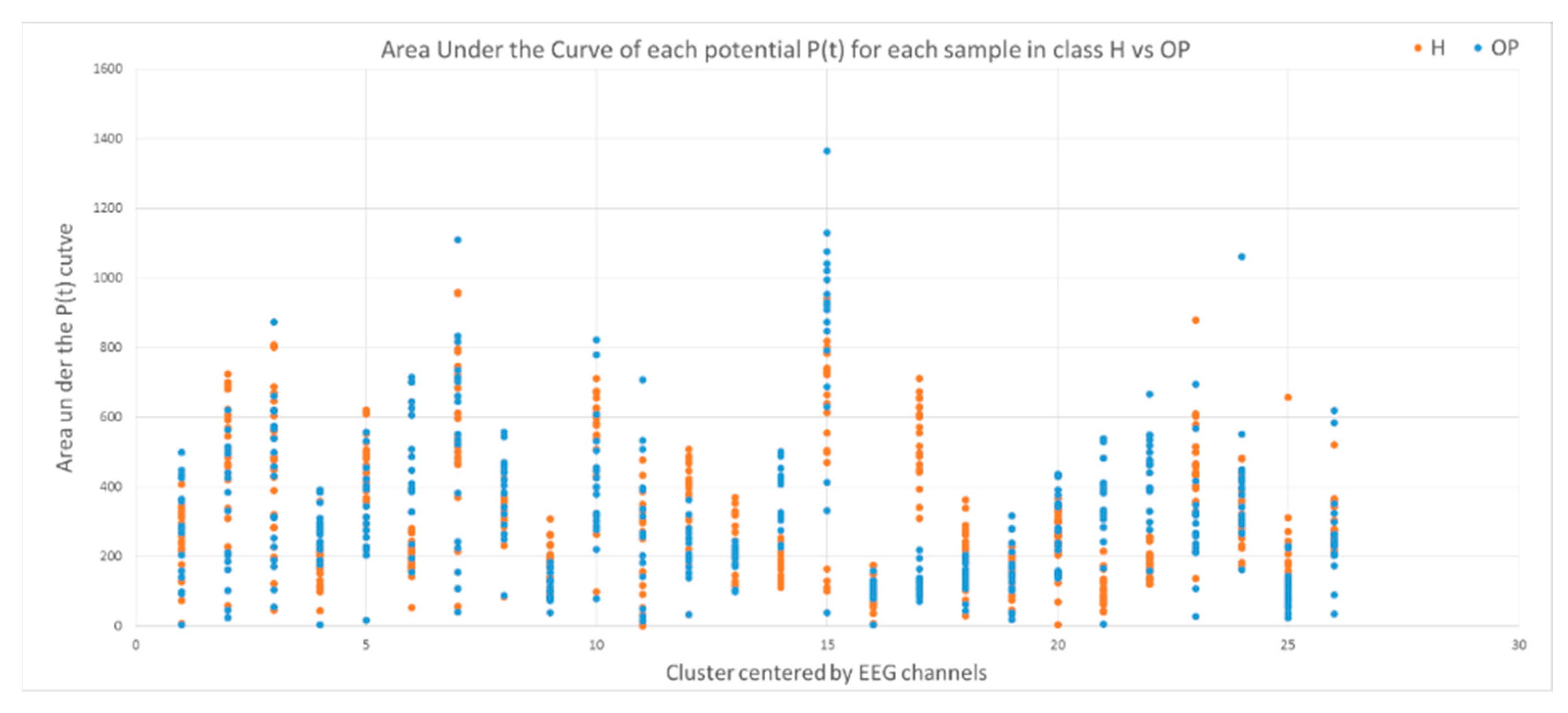

| Area under Curve | ||||||||
|---|---|---|---|---|---|---|---|---|
| -Value | EEG Channel | Channel Index | -Value | EEG Channel | Channel Index | -Value | EEG Channel | Channel Index |
| 2.4 × 10−11 | CPz | 17 | 1.2 × 10−11 | CPz | 17 | −1 × 10−11 | CPz | 17 |
| 2.2 × 10−9 | C4 | 14 | 1.3 × 10−8 | C4 | 14 | 8.4 × 10−9 | C4 | 14 |
| 4.7 × 10−9 | Pz | 21 | 2.4 × 10−8 | P4 | 22 | 1.7 × 10−8 | Pz | 21 |
| 9.9 × 10−9 | P4 | 22 | 1.8 × 10−7 | Pz | 21 | 4.9 × 10−8 | P4 | 22 |
| 0.00001 | F4 | 6 | 7.3 × 10−6 | F4 | 6 | 2.2 × 10−6 | F4 | 6 |
| 0.00008 | C3 | 12 | 3.9 × 10−5 | C3 | 12 | 8.2 × 10−5 | C3 | 12 |
| 0.00008 | Fz | 5 | 0.0007 | T6 | 23 | 0.0001 | Fz | 5 |
| 0.0002 | T6 | 23 | 0.002 | Fz | 5 | 0.0003 | T6 | 23 |
| Methods | SNN | SVM | MLP | MLR | ECM |
|---|---|---|---|---|---|
| 26 variables (reported in [33]) | 85.00 | 68.00 | 78.00 | 68.00 | 70.00 |
| 8 selected variables (feature selection) | 92.00 | 70.00 | 80.00 | 72.00 | 78.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doborjeh, M.; Doborjeh, Z.; Kasabov, N.; Barati, M.; Wang, G.Y. Deep Learning of Explainable EEG Patterns as Dynamic Spatiotemporal Clusters and Rules in a Brain-Inspired Spiking Neural Network. Sensors 2021, 21, 4900. https://doi.org/10.3390/s21144900
Doborjeh M, Doborjeh Z, Kasabov N, Barati M, Wang GY. Deep Learning of Explainable EEG Patterns as Dynamic Spatiotemporal Clusters and Rules in a Brain-Inspired Spiking Neural Network. Sensors. 2021; 21(14):4900. https://doi.org/10.3390/s21144900
Chicago/Turabian StyleDoborjeh, Maryam, Zohreh Doborjeh, Nikola Kasabov, Molood Barati, and Grace Y. Wang. 2021. "Deep Learning of Explainable EEG Patterns as Dynamic Spatiotemporal Clusters and Rules in a Brain-Inspired Spiking Neural Network" Sensors 21, no. 14: 4900. https://doi.org/10.3390/s21144900
APA StyleDoborjeh, M., Doborjeh, Z., Kasabov, N., Barati, M., & Wang, G. Y. (2021). Deep Learning of Explainable EEG Patterns as Dynamic Spatiotemporal Clusters and Rules in a Brain-Inspired Spiking Neural Network. Sensors, 21(14), 4900. https://doi.org/10.3390/s21144900









