Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver
Abstract
1. Introduction
- 1.
- Unlike accuracy optical ranging sensors that relies on high precision pointing mechanism [22,27], microwave ranging can be realized by transceiver antenna with a few degrees wide main lobe angle. At the same time, microwave ranging can operate in a pseudo-code mode or carrier mode for coarse or precise ranging if necessary, as required by mission control, providing a flexible solution to the GNC system;
- 2.
- Good inheritance of microwave ranging technology from existing space experience [28];
- 3.
- As an essential supplement to the MWR system, BeiDou III B1C/B2a dual frequency navigation signal receiving and processing technology can be fully tested and verified in an SFF mission. The receiver can provide high accuracy time synchronization solutions, with precision to a nanosecond, served as a time scale benchmark between formation satellites. Moreover, the receiver can provide precise stand-alone navigation solutions using a precise orbit determination algorithm;
- 4.
- Microwaves can also be used for real-time data transmission between spacecrafts for original science data exchange, for differential GPS measurement data transmission for relative navigation, and, possibly, as a backup channel for mission telemetry, track, and command (TT&C) system.
2. Earth’s Gravity Field Detection Mission and Payloads
2.1. EGFD Mission Analysis
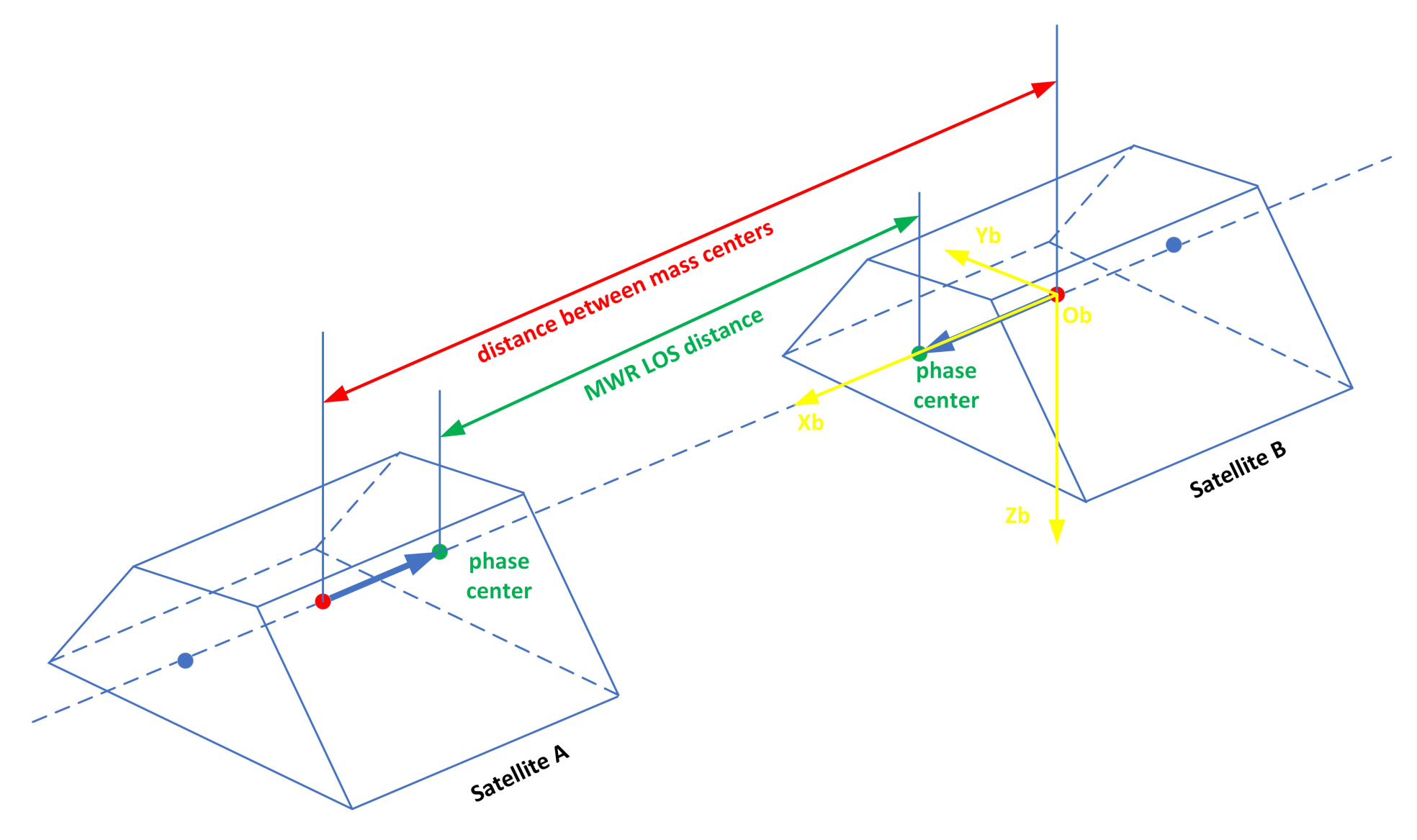
2.1.1. Measurement of LOS Distance and Its Rate between Antenna Phase Centers by MWR
2.1.2. Calculation of the LOS Distance Change and Its Rate between Centroids
2.2. MWR System Design and Development
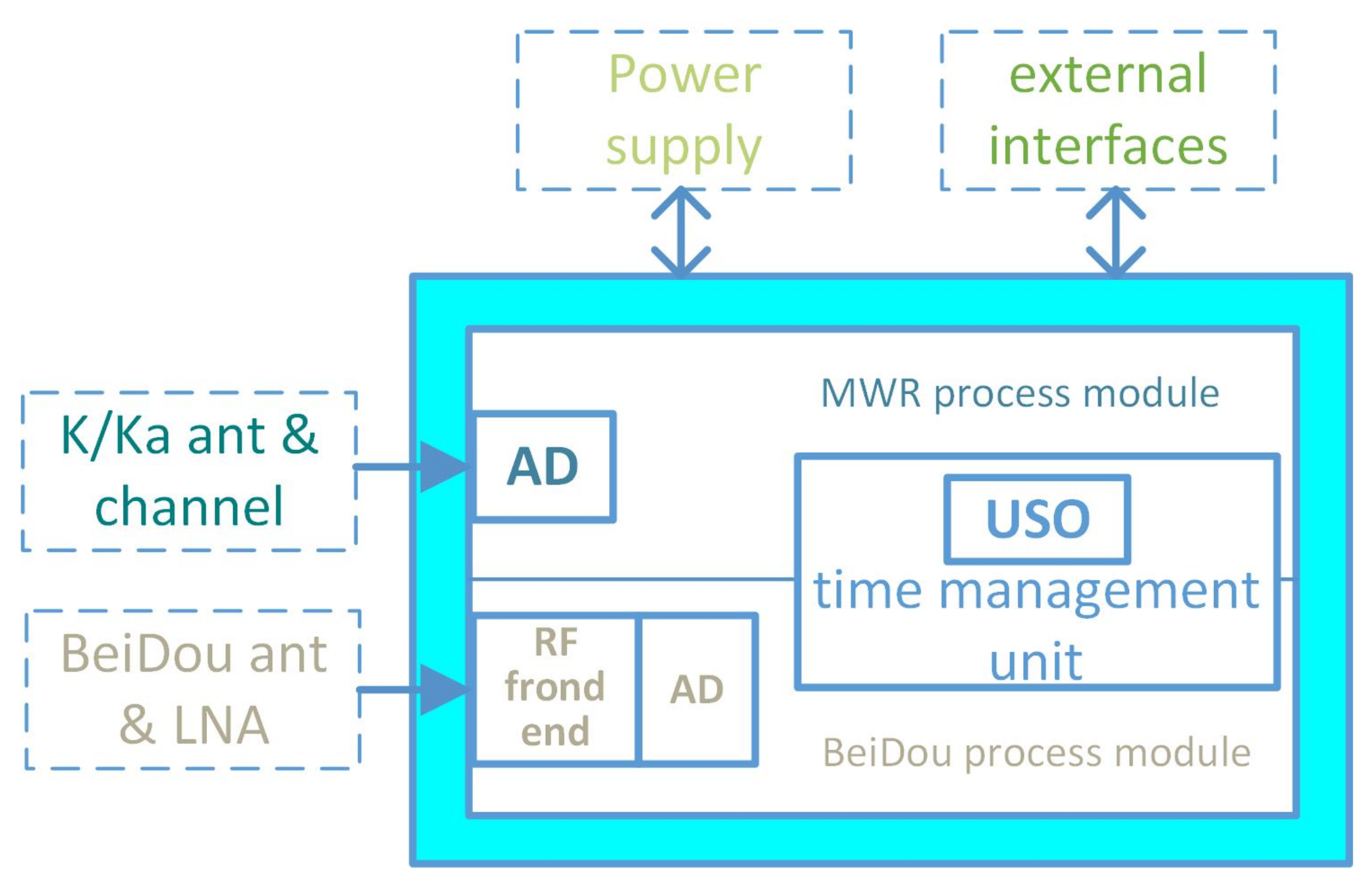
2.2.1. MWR System Composition
- 1.
- Single horn antenna, used to transmit and receive K/Ka band dual frequency microwave signals (shared by both transmit and receive dual frequencies);
- 2.
- USO is used as the frequency reference of the whole system;
- 3.
- The K/Ka transmitter is used for up converting the reference frequency to generate K/Ka transmitting carrier frequency;
- 4.
- The K/Ka receiver uses the carrier frequency of the K/Ka transmitter as the mixing frequency, down converts the receiving carrier to the designed phase measurement frequency, about 500 KHz;
- 5.
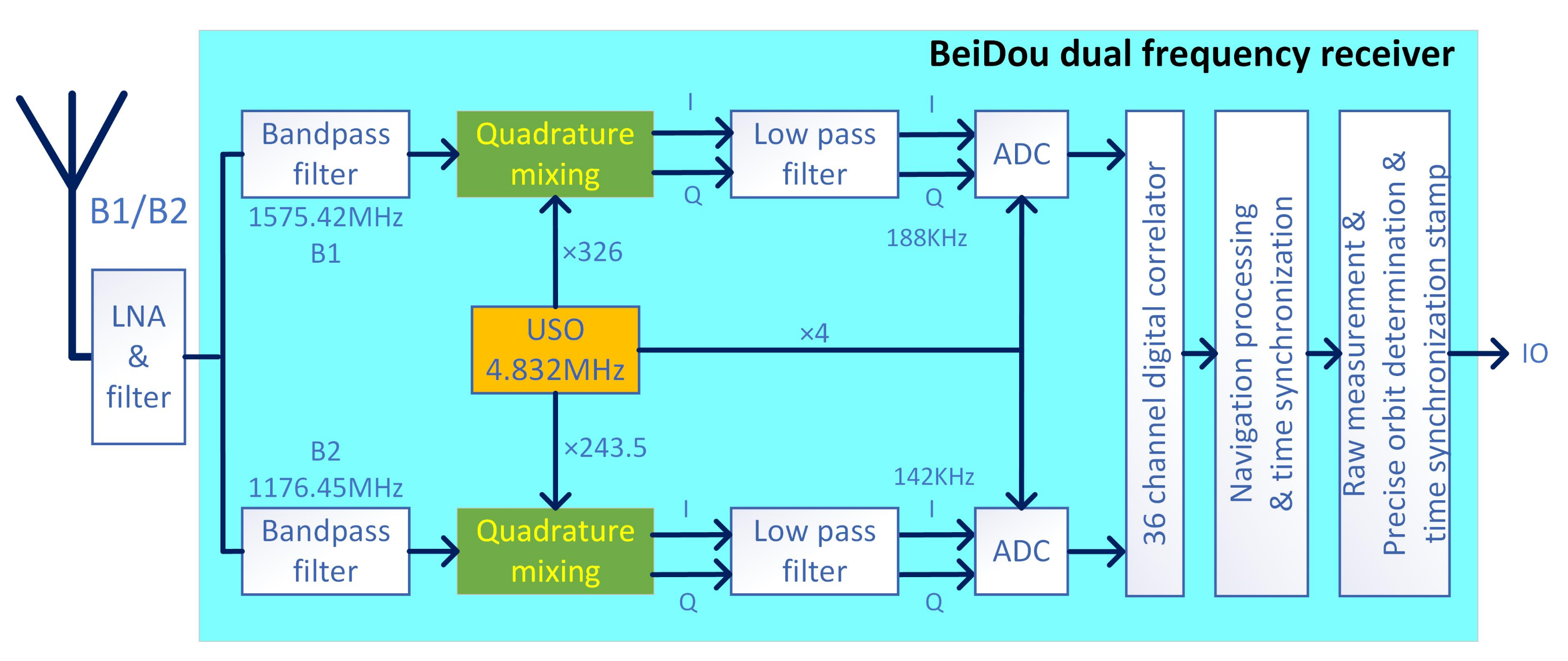
- BeiDou receiving antenna and BeiDou receiving channel take USO as frequency reference, completing BeiDou B1C/B2a signal receiving, frequency down conversion, filtering, amplification, and, finally, output intermediate frequency (IF) signal to digital signal processing unit;
- 6.
- The digital signal processing unit receives carrier phase measurement with frequency of about 500 KHz from K/Ka receiver, completes high-precision carrier phase extraction, and receives IF signal from BeiDou B1C/B2a receiving channel, completes acquisition of pseudo range and carrier phase observation and navigation calculation, finally outputs scientific data and navigation data to satellite platform on-board data handling (OBDH) system. The distance, velocity, acceleration, and other information between formation satellites can be obtained through ground processing.
2.2.2. MWR System Errors Analysis
- 1.
- Time delay stability of RF channel and stability of antenna phase center, a crucial segment to ensure the high precision of measurement of the MWR system, which are mainly affected by the temperature stability. Since the MWR system measures inter-satellite distance change and its rate, there is no strict requirement for equipment absolute time delay, but it requires equipment to have high delay stability, including stability of antenna phase center and time delay stability of RF channel. Those two stabilities are highly sensitive to the change of the ambient temperature, therefore it is necessary to make high-precision temperature control method key components of MWR equipment. The satellite platform is required to conduct high-precision temperature control for MWR, providing there are ideal environment conditions for the highly sensitive oscillator and antenna material structure;
- 2.
- Multi path error. If the geometric relationship between transmitter and receiver changes, multipath will introduce a variable range offset which is difficult to correct. Here we solve it by using the typical antenna and satellite front panel and setting the satellite pointing requirements through high-precision attitude control.The other MWR related error sources including:
- 3.
- Ionospheric delay error. The K/Ka dual frequency measurement technique is adopted to correct the influence of ionospheric refraction, aiming to achieve microns level ranging accuracy;
- 4.
- Frequency source noise. In order to minimize the influence of the medium and long-term phase noise and inter-satellite relative frequency drift from the USO reference frequency source, the DOWR technique is adopted;
- 5.
- Time tag error [31]. To ensure that the change of inter-satellite distance measured at the time tag is equals to the real value in instant, the DOWR technique requires accurate synchronization during ranging process. Suppose we have the nominal frequency of 500∼700 kHz for difference frequency phase measurement method, in order to achieve cycle detect accuracy, the time tag error is required to be less than kHz ns. BeiDou receiver can be used to achieve time synchronization between formation satellites (with synchronization accuracy better than 0.1 ns), so that the carrier phase measurement calibration time of MWR systems can be accurately aligned for two satellites;
- 6.
- Instant distance correction error. The distance between two formation satellites is constantly changing during the DOWR process. Assuming that we have the ideal situation of an accurately synchronized MWR system, the receiving time of the two satellites at the end ranging time is accurately synchronized. However, the inter-satellite distance obtained by satellite A at the receiving time and the inter-satellite distance obtained by satellite B at the same time are different from each other, because the satellite moves at a high speed (about 7.8 km/s for 500 km orbit altitude) during the ranging process (about 1ms for 270 km formation distance). The obtained distances are , and neither of them are the inter-satellite distance at the receiving time, that is, the DOWR is not the same distance when two satellites move at high speed along the same direction, nor the real inter-satellite distance at the receiving time. In this way, the accurate correction of the instant inter-satellite distance is needed when the DOWR measurement is conducted, as shown in Figure 3. Precise orbit determination with the BeiDou receiver can realize precise correction of instant inter-satellite distance, here we call it light-time correction.
3. Precise Time Synchronize and Beidou Receiver
3.1. Time Synchronize Solutions of MWR System
- •
- First, by using oscillator: The stability of the oscillator is required to reach s, but the performance of the current oscillator available cannot reach this level;
- •
- Second, using homologous rubidium or a cesium clock for precise time-transfer, but the two formation satellites cannot be wired connected in orbit. The precise wireless time-transfer technology with stability and reliability is still under research currently;
- •
- Third, the precise time interval counter is used to determine the precise time differential measurement, still, the two formation satellites cannot be connected in orbit for measurement;
- •
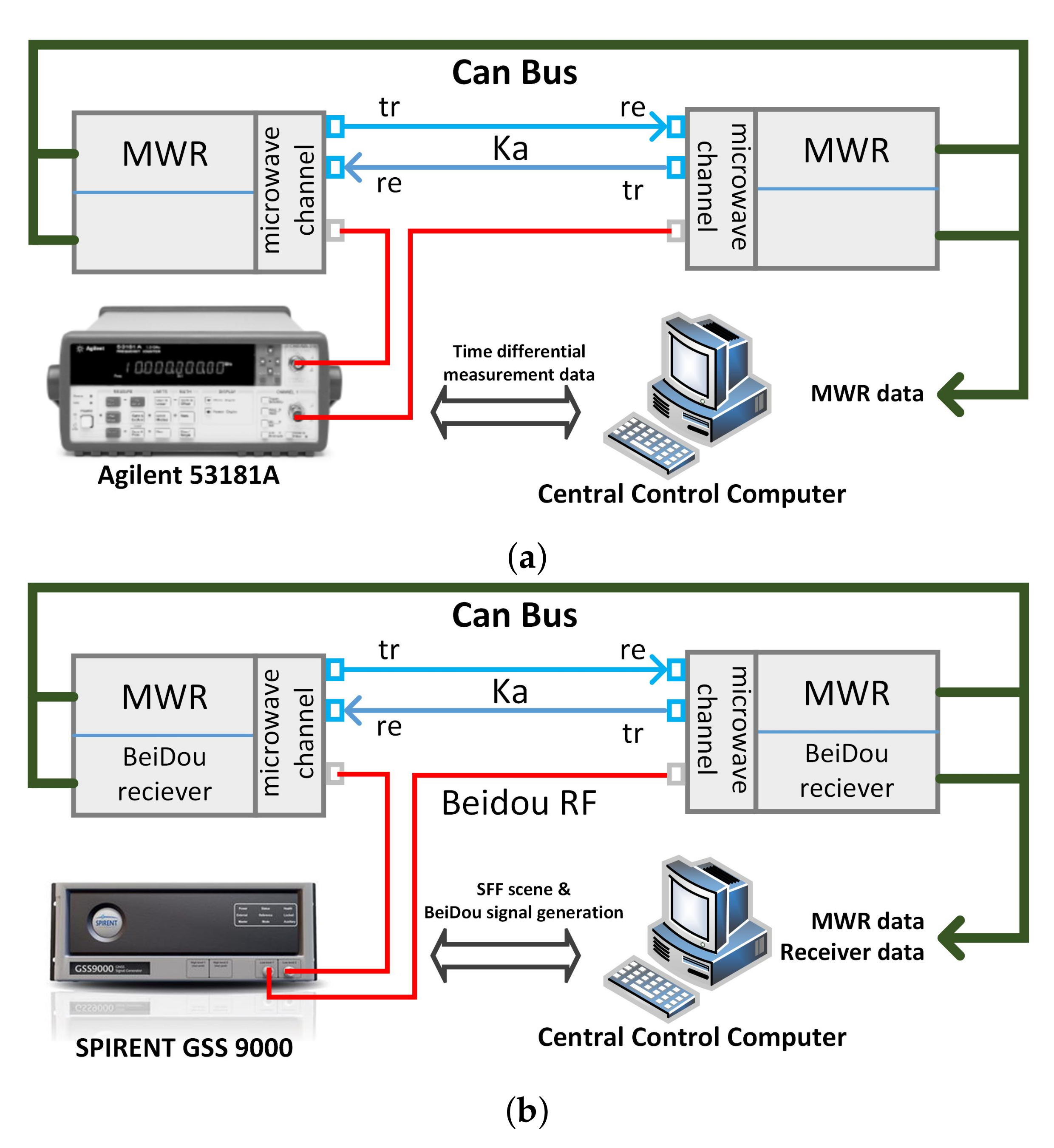
- Finally, the two formation satellites are equipped with dual frequency BeiDou receivers, respectively. Through synchronous sampling, the MWR data are stamped with BeiDou time tag. The down-link transmitted BeiDou observation data are processed after the formation mission on the ground. The relative positioning accuracy of 2–3 cm and the time synchronize accuracy of 0.1 ns can be obtained by using carrier phase differential positioning algorithm, which meets the requirements of the MWR system.
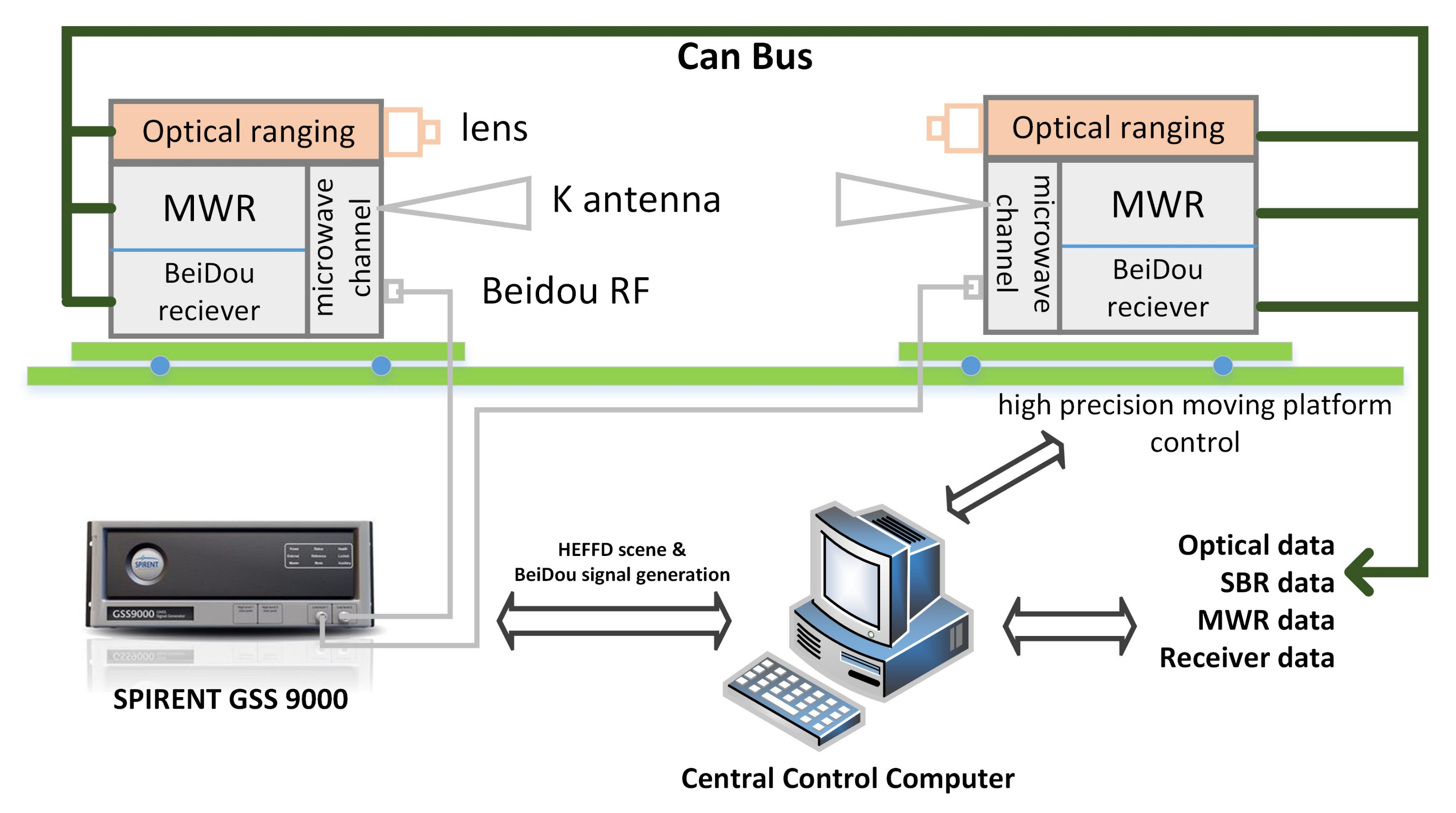
3.2. Design and Develop of Beidou Dual Frequency Receiver
4. Test and Simulations
4.1. Assessment of MWR Ranging Accuracy
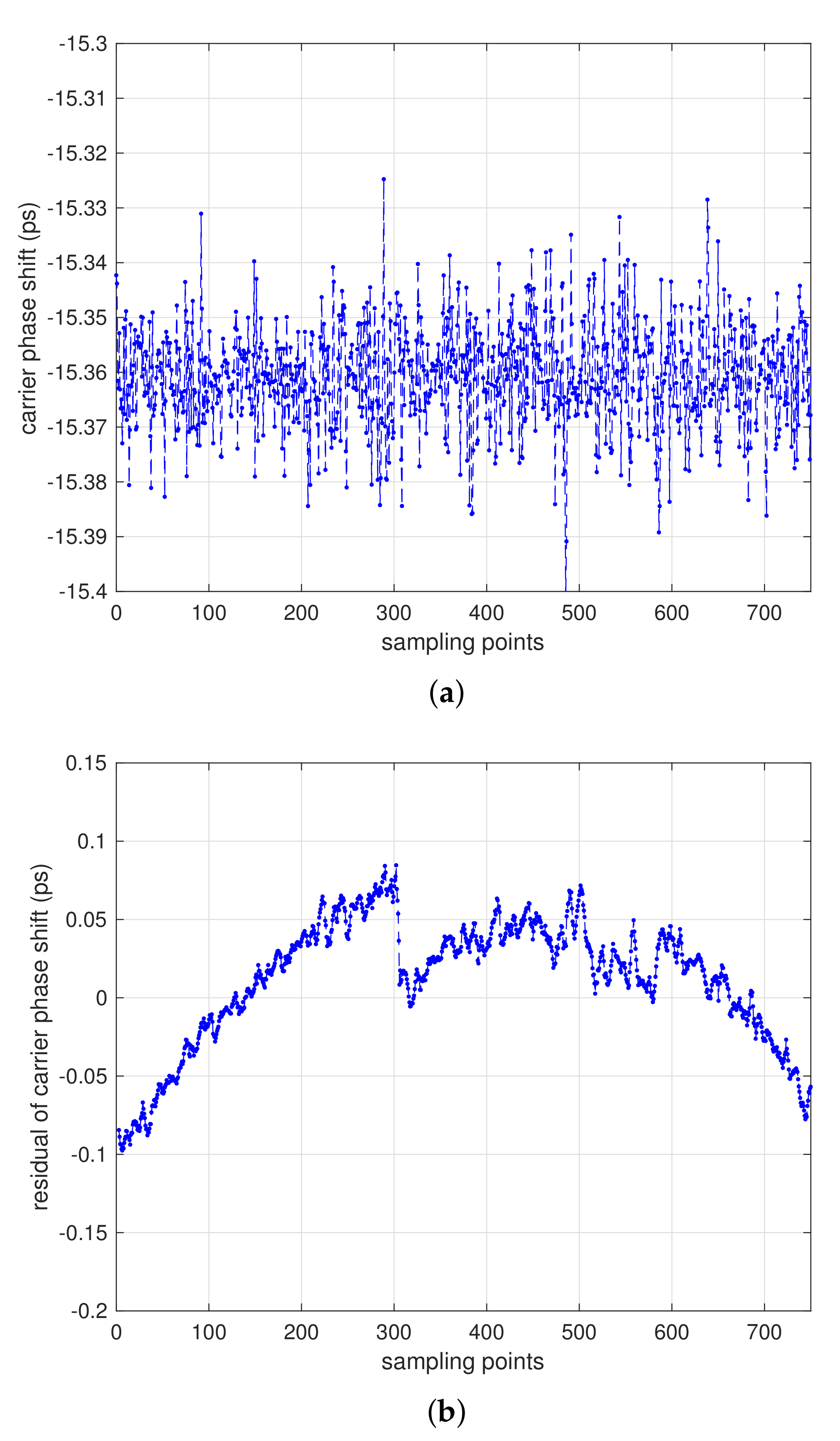
4.1.1. Test of Time Synchronize Performance
4.1.2. Test of Ranging Accuracy Using DOWR Measurement
4.2. Relative Navigation Performance Using Mwr Measurement
4.2.1. Hardware in Loop Simulation Platform
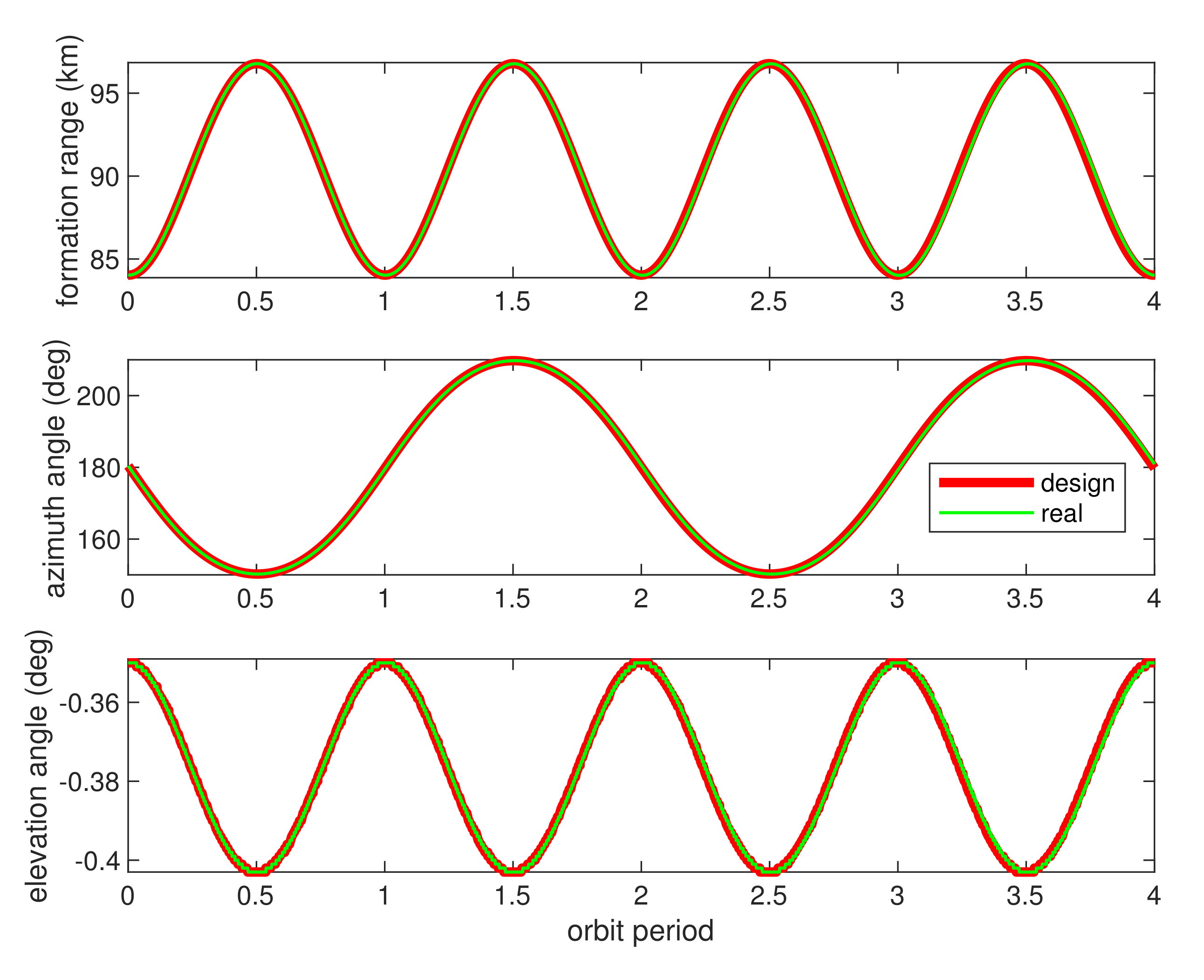
4.2.2. Mission Orbit Analysis
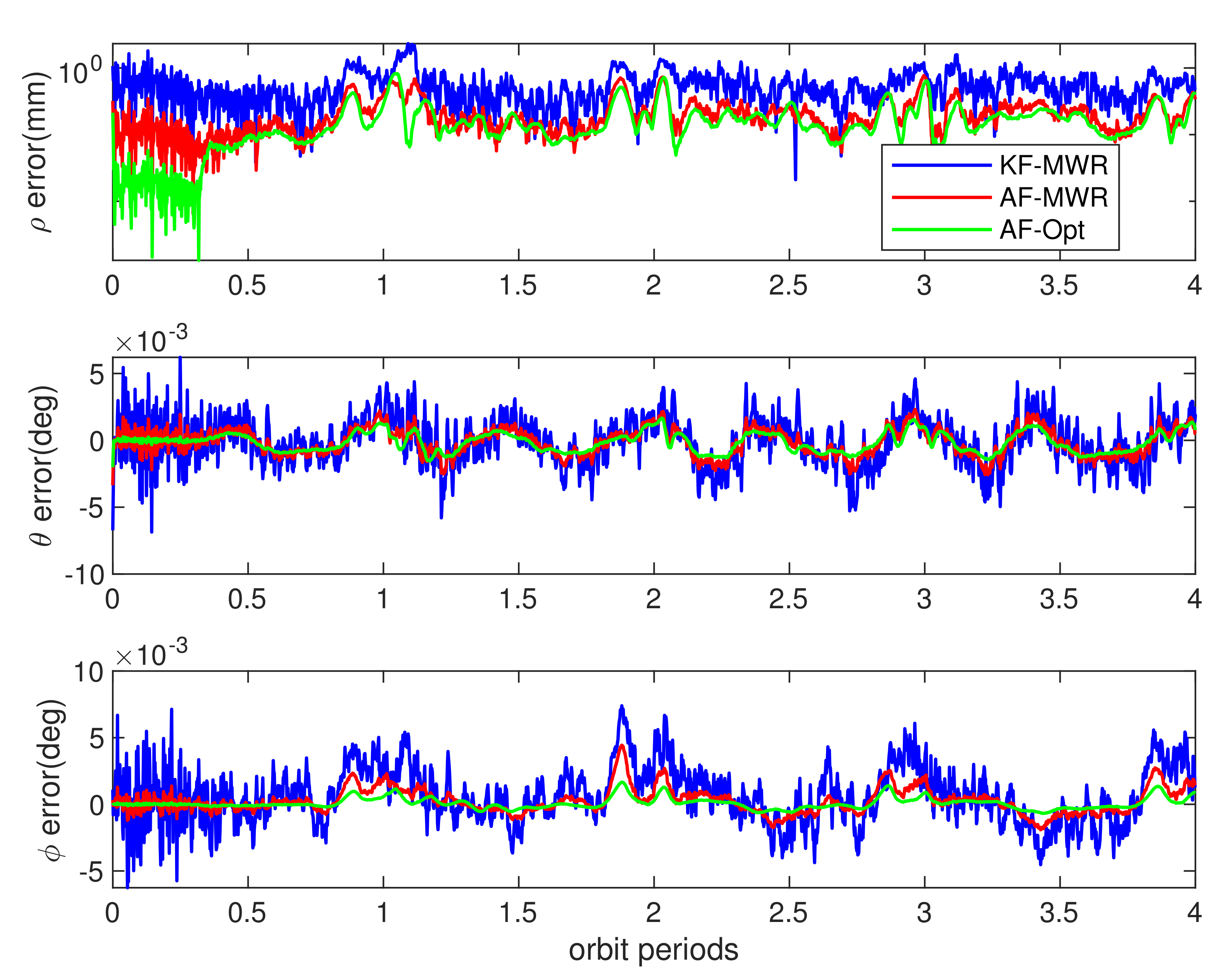
4.2.3. Relative Navigation Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MWR | Microwave ranging |
| GRACE | Gravity recovery and climate experiment |
| EGF | Earth’s gravity field |
| DEM | Digital elevation models |
| SFF | Spacecraft formation flying |
| LEO | Low Earth orbit |
| HEO | Highly elliptical orbit |
| DOWR | Dual one-way ranging |
| HIL | Hardware in loop |
| 6-DOF | Six degrees of freedom |
| CAN | Controller Area Network |
| GNC | Guidance, navigation, and control |
| ISL | Inter-satellite-link |
| NASA | National Aeronautics and Space Administration |
| ESA | European Space Agency |
| EGFD | Earth’s gravity field detection |
| TT&C | Telemetry, track, and command |
| LOS | Line of sight |
| USO | Ultra-stable oscillator |
| KBR | K-band ranging |
| IF | Intermediate frequency |
| OBDH | On-board data handling |
| RF | Radio frequency |
| POD | Precise orbit determination |
| LO | Local oscillator |
| NCO | Numerically controlled oscillator |
| SAR | Synthetic aperture radar |
| In-SAR | Interferometric synthetic-aperture radar |
| GA | Gravitational accelerations |
| NGA | Non-gravitational accelerations |
| RMS | Root mean square |
References
- Alfriend, K.; Vadali, S.R.; Gurfil, P.; How, J.; Breger, L. Spacecraft Formation Flying: Dynamics, Control and Navigation; Elsevier: Amsterdam, The Netherlands, 2009; Volume 2. [Google Scholar]
- Busse, F.D. Precise Formation-State Estimation in Low Earth Orbit Using Carrier Differential GPS. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Tapley, B.D.; Flechtner, F.; Bettadpur, S.V.; Watkins, M.M. The Status and Future Prospect for GRACE after the First Decade. AGU Fall Meet. Abstr. 2013, G32A–01. Available online: https://ui.adsabs.harvard.edu/abs/2013AGUFM.G32A..01T/abstract (accessed on 1 April 2014).
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The gravity recovery and climate experiment follow-on mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the global mass change data record: GRACE Follow-On instrument and science data performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Behzadpour, S.; Mayer-Gürr, T.; Krauss, S. GRACE Follow-On accelerometer data recovery. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021297. [Google Scholar] [CrossRef]
- Bryant, R.; Moran, M.S.; McElroy, S.A.; Holifield, C.; Thome, K.J.; Miura, T.; Biggar, S.F. Data continuity of Earth observing 1 (EO-1) Advanced Land I satellite image (ALI) and Landsat TM and ETM+. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 1204–1214. [Google Scholar] [CrossRef]
- Persson, S.; Veldman, S.; Bodin, P. PRISMA––A formation flying project in implementation phase. Acta Astronaut. 2009, 65, 1360–1374. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Hengl, T.; Reuter, H.I. Geomorphometry: Concepts. Software, Applications; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Wilson, J.P. Environmental Applications of Digital Terrain Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- TanDEM-X, Science Service System. 2003. Available online: https://tandemx-science.dlr.de/ (accessed on 1 February 2004).
- Hawker, L.; Neal, J.; Bates, P. Accuracy assessment of the TanDEM-X 90 Digital Elevation Model for selected floodplain sites. Remote Sens. Environ. 2019, 232, 111319. [Google Scholar] [CrossRef]
- Pollack, S.E. Analytic and Interferometric Techniques for the Laser Interferometer Space Antenna. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2005. [Google Scholar]
- Nagano, S.; Yoshino, T.; Kunimori, H.; Hosokawa, M.; Kawamura, S.; Sato, T.; Ohkawa, M. Displacement measuring technique for satellite-to-satellite laser interferometer to determine Earth’s gravity field. Meas. Sci. Technol. 2004, 15, 2406. [Google Scholar] [CrossRef]
- Dehne, M.; Cervantes, F.G.; Sheard, B.; Heinzel, G.; Danzmann, K. Laser interferometer for spaceborne mapping of the Earth’s gravity field. J. Physics Conf. Ser. 2009, 154, 012023. [Google Scholar] [CrossRef]
- Danzmann, K.; Rüdiger, A. LISA technology—Concept, status, prospects. Class. Quantum Gravity 2003, 20, S1. [Google Scholar] [CrossRef]
- Shaddock, D.; Ware, B.; Halverson, P.G.; Spero, R.E.; Klipstein, B. Overview of the LISA Phasemeter. Aip Conf. Proc. 2006, 873, 654–660. [Google Scholar]
- Wand, V. Interferometry at Low Frequencies: Optical Phase Measurement for LISA and LISA Pathfinder. Ph.D. Thesis, Gottfried Wilhelm Leibniz Universität Hannover, Hannover, Germany, 2007. [Google Scholar]
- Bender, P.L.; Hall, J.L.; Ye, J.; Klipstein, W.M. Satellite-satellite laser links for future gravity missions. Space Sci. Rev. 2003, 108, 377–384. [Google Scholar] [CrossRef]
- Müller, V. Laser Ranging Interferometer on GRACE Follow-On: Current Status. EGU Gen. Assem. Conf. Abstr. 2020, 10566. Available online: https://ui.adsabs.harvard.edu/abs/2020EGUGA..2210566M/abstract (accessed on 1 December 2020).
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.B.; Barr, D.C.; Bize, M.P.; Bogan, C.; Braxmaier, C.; Burke, M.J. In-orbit performance of the GRACE follow-on laser ranging interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef]
- Sheard, B.S.; Heinzel, G.; Danzmann, K.; Shaddock, D.A.; Klipstein, W.M.; Folkner, W.M. Intersatellite laser ranging instrument for the GRACE follow-on mission. J. Geod. 2012, 86, 1083–1095. [Google Scholar] [CrossRef]
- Goswami, S.; Devaraju, B.; Weigelt, M.; Mayer-Gürr, T. Analysis of GRACE range-rate residuals with focus on KBR instrument system noise. Adv. Space Res. 2018, 62, 304–316. [Google Scholar] [CrossRef]
- Darbeheshti, N.; Wegener, H.; Müller, V.; Naeimi, M.; Heinzel, G.; Hewitson, M. Instrument data simulations for GRACE Follow-on: Observation and noise models. Earth Syst. Sci. Data 2017, 9, 833–848. [Google Scholar] [CrossRef]
- Wang, X.; Gong, D.; Jiang, Y.; Mo, Q.; Kang, Z.; Shen, Q.; Wu, S.; Wang, D. A Submillimeter-Level Relative Navigation Technology for Spacecraft Formation Flying in Highly Elliptical Orbit. Sensors 2020, 20, 6524. [Google Scholar] [CrossRef]
- Koch, A.; Sanjuan, J.; Gohlke, M.; Mahrdt, C.; Brause, N.; Braxmaier, C.; Heinzel, G. Line of sight calibration for the laser ranging interferometer on-board the GRACE Follow-On mission: On-ground experimental validation. Opt. Express 2018, 26, 25892–25908. [Google Scholar] [CrossRef]
- Shao, F. Long March 2C rocket “one rocket three satellites” launched successfully. China Equip. Eng. 2017, 20, 4. [Google Scholar]
- Wang, F. Study on Center of Mass Calibration and K-Band Ranging System Calibration of the GRACE Mission. The University of Texas at Austin. 2003. Available online: https://www.proquest.com/openview/a71fc96d0a089e7a5589da7add99b1a1/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 1 January 2004).
- Ko, U.; Tapley, B.D.; Ries, J.C.; Bettadpur, S.V. Analysis of the Characteristics of the GRACE Dual One-Way Ranging System. AGU Fall Meet. Abstr. 2007, 2007, G33A-0895. [Google Scholar]
- Chen, L.; Wang, Y.; Zhang, C. Analysis of time and frequency error in dual-one-way ranging. In Proceedings of the 2012 2nd IEEE International Conference on Remote Sensing, Environment and Transportation Engineering, Nanjing, China, 1–3 June 2012; pp. 1–4. [Google Scholar]
- Kim, J. Simulation Study of a Low-Low Satellite-to-Satellite Tracking Mission. The University of Texas at Austin. 2000. Available online: https://www.proquest.com/openview/5d2b158f2e818bb1c89225d74e15391c/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 1 January 2001).
- Kim, J.; Tapley, B.D. Optimal frequency configuration for dual one-way ranging systems. J. Spacecr. Rocket. 2005, 42, 749–751. [Google Scholar] [CrossRef]
- Kim, J. Measurement time synchronization for a satellite-to-satellite ranging system. In Proceedings of the 2007 IEEE International Conference on Control, Automation and Systems, Seoul, Korea, 17–20 October 2007; pp. 190–194. [Google Scholar]
- Kim, J.; Lee, S.W. Flight performance analysis of GRACE K-band ranging instrument with simulation data. Acta Astronaut. 2009, 65, 1571–1581. [Google Scholar] [CrossRef]
- Eggleston, J.M.; Dunning, R.S. Analytical Evaluation of a Method of Midcourse Guidance for Rendezvous with Earth Satellites; NASA TD-883; National Aeronautics and Space Administration: Washington, DC, USA, 1961.
- Bettadpur, S. Gravity Recovery and Climate Experiment, Product Specification Document; Rev 4.6 May 29 2012, GRACE 327-720, CSR-GR-03-02; Center for Space Research, The University of Texas: Austin, TX, USA, 2012. [Google Scholar]
- Wang, X. Improved adaptive filter with application to relative navigation. GPS Solut 2011, 15, 121–128. [Google Scholar] [CrossRef]







| Error Sources | Error Uncertainty | Means of Improvement |
|---|---|---|
| Phase measurement resolution | less than 1 m | (1) Selection of K/Ka frequency band; (2) Differential frequency phase measurement. |
| Time delay stability of RF channel/antenna phase center | less than 3 m/K | (1) Selection control of electronic components/low thermal coefficient machining materials; (2) Minimize the waveguide connection length; (3) Thermo control of MWR equipment. |
| Multi path error | less than 3 m | (1) Improve the pointing accuracy of formation satellites and minimize the multipath; (2) Strict requirements for antenna installation. |
| Ionospheric delay error | less than 2 m | K/Ka dual frequency measurement and correct |
| Frequency source noise | less than 3 m | (1) Low phase noise design of USO and microwave direct multiple locking; (2) Satellite platform control of thermal, magnetic field, radiation and vibration protection; (3) DOWR to eliminate the influence of medium/ long-term stability. |
| Time tag error | less than 1 m | (1) Integrated design of MWR and BeiDou, synchronous data sampling with the same time tag; (2) Achieving the precise time synchronization accuracy of 0.1 ns between satellites with post data process; (3) MWR observation data with BeiDou precise time tag synchronous resampling. |
| Instant distance correction error | less than 5 m | Corrected according to the precise orbit determination data. |
| Error Sources | Error Uncertainty | Means of Improvement |
|---|---|---|
| Attitude pointing control | less than 2 m | Precise attitude and pointing control support from satellite ADCS and orbit control system.* |
| Geometric stability | less than 5 m/orbit | Guaranteed from satellite platform structural design. |
| Centroid stability | less than 2 m | Guaranteed from satellite platform centroid stability design. |
| Items | Model |
|---|---|
| GA—the geopotential effect of the Earth | 20th order and degree |
| GA—Sun, and Moon gravities | DE405/LE405 planetary ephemerides model |
| GA—solid Earth tides | IERS Conventions 1996 |
| GA—ocean tides | Center for Space Research 3.0 model |
| NGA—the atmospheric drag | NRLMSISE-00 empirical model |
| NGA—the solar radiation pressure | IERS Standards 1992 |
| Items | Unit | KF-MWR | AF-MWR | AF-Opt |
|---|---|---|---|---|
| range | m | 935.26 | 417.91 | 301.82 |
| range rate | m/s | 1.05 | 0.87 | 0.65 |
| azimuth | deg | |||
| azimuth rate | deg/s | |||
| elevation | deg | |||
| elevation rate | deg/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wu, S.; Gong, D.; Shen, Q.; Wang, D.; Damaren, C. Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver. Sensors 2021, 21, 4883. https://doi.org/10.3390/s21144883
Wang X, Wu S, Gong D, Shen Q, Wang D, Damaren C. Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver. Sensors. 2021; 21(14):4883. https://doi.org/10.3390/s21144883
Chicago/Turabian StyleWang, Xiaoliang, Shufan Wu, Deren Gong, Qiang Shen, Dengfeng Wang, and Christopher Damaren. 2021. "Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver" Sensors 21, no. 14: 4883. https://doi.org/10.3390/s21144883
APA StyleWang, X., Wu, S., Gong, D., Shen, Q., Wang, D., & Damaren, C. (2021). Evaluation of Precise Microwave Ranging Technology for Low Earth Orbit Formation Missions with Beidou Time-Synchronize Receiver. Sensors, 21(14), 4883. https://doi.org/10.3390/s21144883







