Abstract
The forecast of electricity demand has been a recurrent research topic for decades, due to its economical and strategic relevance. Several Machine Learning (ML) techniques have evolved in parallel with the complexity of the electric grid. This paper reviews a wide selection of approaches that have used Artificial Neural Networks (ANN) to forecast electricity demand, aiming to help newcomers and experienced researchers to appraise the common practices and to detect areas where there is room for improvement in the face of the current widespread deployment of smart meters and sensors, which yields an unprecedented amount of data to work with. The review looks at the specific problems tackled by each one of the selected papers, the results attained by their algorithms, and the strategies followed to validate and compare the results. This way, it is possible to highlight some peculiarities and algorithm configurations that seem to consistently outperform others in specific settings.
1. Introduction
Electricity is expected to increase its prevalence as the main energy vector in the near future for industrial, domestic and transportation use. This emphasizes the importance of electricity demand forecast, as it has a direct impact on many operational and business processes. Electricity demand is typically known as load in the electrical engineering jargon, we will use both terms interchangeably. For decades, load forecast has been a recurrent research topic and a framework for the evolution of Machine Learning (ML) approaches based on Artificial Neural Networks (ANN), which are inherently suitable to deal with non-linearities and multiple types of inputs [1,2]. Presently, the massive deployment of smart meters and sensors along the grid yields a propitious environment for the optimization of such techniques.
The literature accumulated on the topic of load forecast using ANN-based models over the last 20 years is vast and difficult to grasp. This paper aims at classifying and reviewing the most relevant works. Our focus is on identifying what algorithm performs better for specific electricity demand problems and under what circumstances, including the selection of input variables and the optimal combination of parameters. Other distinguishing aspects of this systematic review are the following:
- We analyze the Key Performance Indicators (KPIs) used to evaluate the accuracy of the predictions and to compare the performance of different algorithms. In this regard, the predominance of some metrics in the literature (e.g., MAPE, the Mean Absolute Percentage Error) often leads to overlooking important quality parameters, such as the distribution of the error and the maximum forecast error.
- We look at other fundamental aspects in ML problems, such as the data pre-processing techniques, the selection of training and validation sets, the tuning of the hyper-parameters of the model, the graphical representations and the presentation of the results.
- Last but not least, we discuss the ability to publicly access the datasets used to carry out the experiments and to validate the results and the code of each one of the selected papers. Lack of access makes the results of many papers very hard or impossible to reproduce, reducing their impact as sources of innovation and knowledge.
Previous reviews of approaches for electricity demand forecast (see [3,4,5]) surveyed the use of ANN-based techniques in a shallower manner, as they covered other ML techniques too. Other surveys looked at general uses of ML in energy systems, not only for load but also for generation, and not restricted to electricity but considering any sources of energy [6,7]. Our exclusive focus on ANN for electricity demand forecast allows providing deeper insight, to the point of questioning aspects that have been traditionally taken for granted, such as the non-linear nature of the forecast problem (to be discussed in Section 4.3.3). It is worth noting, though, that we cover not only pure uses of ANNs, but also hybrid approaches in which ANNs are combined with other algorithms and/or used to process the data in early or final stages.
2. Methodology
Initially, we used Elsevier’s ScienceDirect, Scopus and IEEE Xplore to search for relevant papers, thus ensuring essential quality requirements and coverage of the most relevant publications. We obtained an initial list by performing search queries for the keywords “ANN”, “neural networks”, “forecast”, “prediction”, “electricity”, “load”, “forecasting” and “machine learning”. We also considered related papers that were recommended by the search engines and met the search requirements. Next, we left out all the papers that did not include ANN-based mechanisms or dealt with other energy sources than electricity —still, we included papers that compared ANN-based methods to other approaches such as Support Vector Machines (SVM). We proceeded iteratively to include all the papers referenced in the state-of-the-art section of papers already included in our set.
Table 1 shows the sites from where we downloaded the papers covered in the review. 55% of them were retrieved from IEEE Explorer, acknowledging the fact that many relevant papers on electric load forecasting papers have been traditionally presented in IEEE conferences. MDPI and ScienceDirect also hosted a relevant number of original papers.

Table 1.
Sources of papers for the review.
Having selected the papers, we put them on a data sheet with different columns to look at the specifics of each one. The columns were:
- Type of problem to solve.
- Algorithms used.
- Supporting tools.
- Input variables.
- Dataset characteristics.
- Performance indicators.
- Results.
- Particularities.
In the last column we wrote down comments about what made each paper different from others. This helped us to analyze and compare the different papers focusing on specific aspects that we will cover in the review. A simplified version of this table is included in Section 5 to be used as a quick reference by the readers.
3. State-of-the-Art ANN-Based Algorithms Used in Load Forecasting Problems
Some of the reviewed papers use single ANN-based algorithms, whereas others combine them with other techniques. The single algorithms are the following:
- The Multi-Layer Perceptron (MLP) refers to a canonical feedforward artificial neural network, which typically consists of one input layer, one output layer and a set of hidden layers in between. Early works showed that a single hidden layer is sufficient to yield a universal approximator of any function, and so MLPs were commonly used in papers from the 1990s and early 2000s. However they have been progressively replaced by more sophisticated recursive algorithms, which can better capture the complex patterns of load time series. The most recent papers included in Section 5 show how recursive ANN-based approaches typically outperform MLP.
- Self-Organizing Maps (SOM) are neural network-based dimensionality reduction algorithms, generally used to represent a high-dimensional dataset as a two-dimensional discretized pattern. They are also called feature maps, as they are essentially re-training the features of the input data and grouping them according to similarity parameters. SOMs are used to recognize common patterns in the input space and train distinct ANNs to be used with the different patterns [35].
- Deep Learning refers to ANN networks capable of unsupervised learning from data that are unstructured or unlabeled. The adjective “deep” comes from the use of multiple hidden layers in the network to progressively extract higher-level features from the raw input.
- Many authors (e.g., [20,47,52]) use variants of Recursive Neural Networks (RNNs) that have the capability of learning from previous load time series. Others use Long Short-Term Memory (LSTM) networks, a special kind of RNNs that can learn from long-term dependencies. These were introduced by Hochreiter and Schmidhuber [57] in 1997 and refined and popularized by many authors in subsequent works. Several of the most recent papers included in the review conclude that LSTM variants achieve low forecasting errors outperforming other algorithms in their experiments.
The hybrid ANN-based algorithms found in the reviewed papers fall into three approaches:
- ANN and Genetic Algorithms (ANN-GA). In these works, the idea of the genetic algorithms is to iteratively apply three operations (referred to as selection, crossing and mutation) in order to optimize different parameters of the ANNs. For example, Wang et al. [33] used the GA to improve specifically the back-propagation weights, whereas Azadeh et al. [36] used GAs to tune all the parameters of an MLP.
- ANN and Particle Swarm Optimization (ANN-PSO). PSO is another optimization technique that tries to improve a candidate solution in a search-space with regard to a given measure of quality. It is a metaheuristic (i.e., it makes few or no assumptions about the problem being optimized) that can search very large spaces of candidate solutions, but it cannot guarantee that an optimal solution is ever found. As an example, Son and Kim [58] used PSO to select the 10 most relevant variables to be used as input for SVR (Support Vector Machine Regression) and ANN algorithms. Likewise, He and Xu [22] proposed the use of PSO to optimize the back-propagation process to tune the parameters of an MLP.
- Adaptive Neuro-Fuzzy Inference System (ANFIS). Developed in 1993 by Jang [59], ANFIS overcomes the deficient parts of ANNs and fuzzy logic by combining both technologies. It is used in [3] to model load demand problems. It uses fuzzy inference in its internal layers which allows the model to be less dependent on proficient knowledge, improving its learning and making it more adaptable.
Recent papers combine at least two ANN-based algorithms. For instance, Ref. [32] integrates LSTM with Deep Neural Networks (DNN) to forecast load demand from previous time series and to predict from meteorological input variables. In this case, LSTM captures the load forecast due to previous values thanks to its recursion features, and the DNN gives a more accurate value for the load demand specifically owing to the weather conditions.
4. Particularities of Electric Load Demand As a Problem for ANNs
In this section, we shall highlight particular aspects about the use of ANNs for load forecasting. These are questions that must be taken into account in any research work, as they condition the type of algorithms that may be used.
4.1. Prediction Range
According to the time range of the prediction, we can distinguish three categories that have been used in the definition of energy forecast problems, at least since 1995 [10]:
- Short-term load forecasting (STLF) refers to predictions up to 1 day ahead.
- Medium-term load forecasting (MTLF) refers to 1 day to 1 year ahead.
- Long-term load forecasting (LTLF) refers to 1–10 years ahead.
Table 2 shows that most of the reviewed papers that use ANN-based algorithms do so for STLF problems. Therefore, we can safely assume that ANN-based algorithms have been widely recognized as suitable for short-term prediction.

Table 2.
Type of used input variables.
STLF has become particularly important (hence the greater presence in the scientific literature) since the massive introduction of renewable energy sources, as the forecasts help the electric companies to plan the production mix more efficiently. STLF is crucial for electric intra-day markets, where 1-day ahead forecasts are used to fix the prices for the next day considering the expected demand. STLF is also important for the operation of electric companies and microgrids, where the predicted demand may drive operative decisions in order to be properly covered by the generation sources. Many electric operators are supporting these research efforts by providing significant amounts of data and funding.
ANN-based algorithms have been also proven to work well for MTLF when they can capture weekly and seasonal patterns, as it happens with the recursion techniques of LSTM [43]. LTLF problems, in turn, seem harder to solve by using ML algorithms only. The expected demand in the next years depends heavily on demographic, geopolitical and technological evolution variables, which are hard to turn into numbers and for which there are no historical data to learn from.
4.2. Load Forecasting as a Sequence Prediction Problem
In the electricity forecast field, sequences are typically series of past ordered load values, indexed by time. Brownlee [60] differentiated two types of prediction problems:
- Sequence prediction: from a sequence of values a single value is predicted. For example, from a time series of previous load values we obtain a prediction for the next load value.
- Sequence-to-Sequence (S2S) prediction: we do not obtain a single value but a sequence of predicted values, defining how the load will evolve in a range of future time steps.
Our review covers papers featuring both approaches, and even combined strategies (e.g., [19]).
4.3. Input Variables
In many cases the selection of input variables is determined by the available data. All the papers covered in this review consider the previous load (directly or applying some kind of transformation) as one of the input variables of the ML algorithm. In many cases, a time series of previous load is the only input to the algorithm, which is required to learn from past values only. In other cases, it is common to use additional data such as weather variables and economic activity indicators [29,33,58]. Table 3 shows the distribution of the input variables used in the analyzed papers.

Table 3.
Type of used input variables.
Weather variables—especially temperature—are known to have a linear influence on the electricity demand [47]. Extensive analyses of the influence of weather variables, daylight hours and human activity can be found in [18,61]. It has been shown (see [33]) that the load data over the same period or previous periods have greater influence, though, as those values of electric load implicitly capture effects of climate, daylight hours and human habits.
In the electricity market, real-time price depends on the generation of renewable sources, current demand and socio-economic factors. Real-time price has not been considered as an input variable for STLF problems in the reviewed papers. However it exhibits a relevant non-linear correlation with power load as shown in [62].
The values provided by the Advanced Metering Infrastructure (AMIs) deployed by electric companies give the amount of energy consumed during a period of time (typically 1 h and 24 h) but there are also sensors that can provide instantaneous values of consumed power. They are all valid for the predictions, but energy values in KW/h or W/h are the most commonly used in forecasting problems. The AMIs can also provide the peak values directly and in many cases the forecasting is focused on the peak values only, not on aggregated consumption.
To identify the predictive value of input variables, several authors have made correlation analysis between the different input variables and the power load [18,42]. However, recent papers propose more advanced alternatives such as Kendall rank and Copula functions [62,63] which are more suitable to identify non-linear relationships between input and output variables. The use of LASSO (Least Absolute Shrinkage and Selection Operator) regression analysis to select the most relevant features is also proposed as an effective approach [45]. This technique enables the selection of the features to optimize the performance of the model. Feature selection is important to improve the performance of models with a huge number of features, typically those which include socio-economic variables.
4.3.1. Sources of Input Data
All the reviewed papers used time series of previous electric demand to train and test the models. Table 4 shows the sources of the data.

Table 4.
Origin of load time-series data.
Many of the papers focused on certain geographic areas, so they handled problems of aggregated demand from thousands or millions of consumers. The use of ANN-based models to these problems has shown very good performance. The demand prediction problems using smart meter and microgrid data, in turn, seem to be in an early stage of evolution, as they handle load patterns whose distributions differ significantly from those of aggregated demands.
Several studies have proved that forecast is much more accurate when it is done over aggregated data. For example, Kong et al. [31] propose the use of a clustering technique called DBSCAN (Density-Based Spatial Clustering of Application with Noise) to evaluate consistency in daily power profile, finding that aggregated data presents fewer outliers, which favors ANN convergence. The same authors compared the forecast accuracy of individual meters and checked how it improves with the level of aggregation, discovering that the aggregation of forecasts is more accurate than the forecast of the aggregation. Regarding the patterns of individual consumers, lifestyles are clearly reflected in energy consumption as consumers typically have common and repetitive behaviors [64].
4.3.2. Pre-Processing of Input Variables
The importance of data pre-processing is a well-known topic in data science [65]. Any forecasting problem requires processing of data before feeding them to whichever ML algorithm. However, most of the papers covered in this review do not explain the way they pre-process the numeric data.
The pre-processing may differ depending on the used algorithm, but it will typically involve the following steps when using ANN-algorithms:
- Data cleaning. Either due to errors in the sensors or in the data processing, the time series may include invalid or missing data, making it necessary to apply conventional mechanisms to modify these values. For example, depending on the type and amount of missing data, different approaches can be used, such as dropping the variable or completing with the mean or the last observed value. Removal of duplicate rows may be also needed at this initial stage. Very few papers explain whether any of these techniques was used, even when they may have a significant effect on the model’s performance.
- Data validation. It is necessary to validate the data, especially when they come directly from AMI devices and they have not been obtained from public databases. Data visualization techniques can help to check if the data match expected patterns. It is worth noting that smart meters typically send the measured values using PLC (Power Line Communication) technologies, which may be affected by different electromagnetic interference sources [66]. This makes it especially important to verify the integrity of the data before training the model. Detection and removal of outlier values is typically performed to optimize the training of ANN-based models. Ref. [46] proposes the use of PCA (Principal Component Analysis) as an effective outlier detection approach.
- Data transformation. This phase includes different types of transformations of the data, such as change of units or data aggregation. Data aggregation from individual sources is a common practice to achieve data reduction, change of scale and minimize variability. More advanced transformation techniques are aimed at rescaling the features in order to make the algorithm to converge faster and properly and minimize the forecasting error. The most common rescaling approaches are normalization and standardization:
- Normalization refers to the process of scaling the original data range to values between 0 and 1. It is useful when the data have varying scales and the used algorithm does not make assumptions about their distribution (as is the case of ANNs).
- Standardization consists of re-scaling the data so that the mean of the values is 0 and the standard deviation is 1. Variables that are measured at different scales would not contribute equally to the analysis and might end up creating biased results through the ANNs. Standardization also avoids problems that would stem from measurements expressed with different units.
- Dimensionality reduction techniques are typically used in machine learning problems in order to optimize the model generation by reducing the number of input variables. However, only a few of the reviewed papers require the usage these techniques due to the low number of input variables.
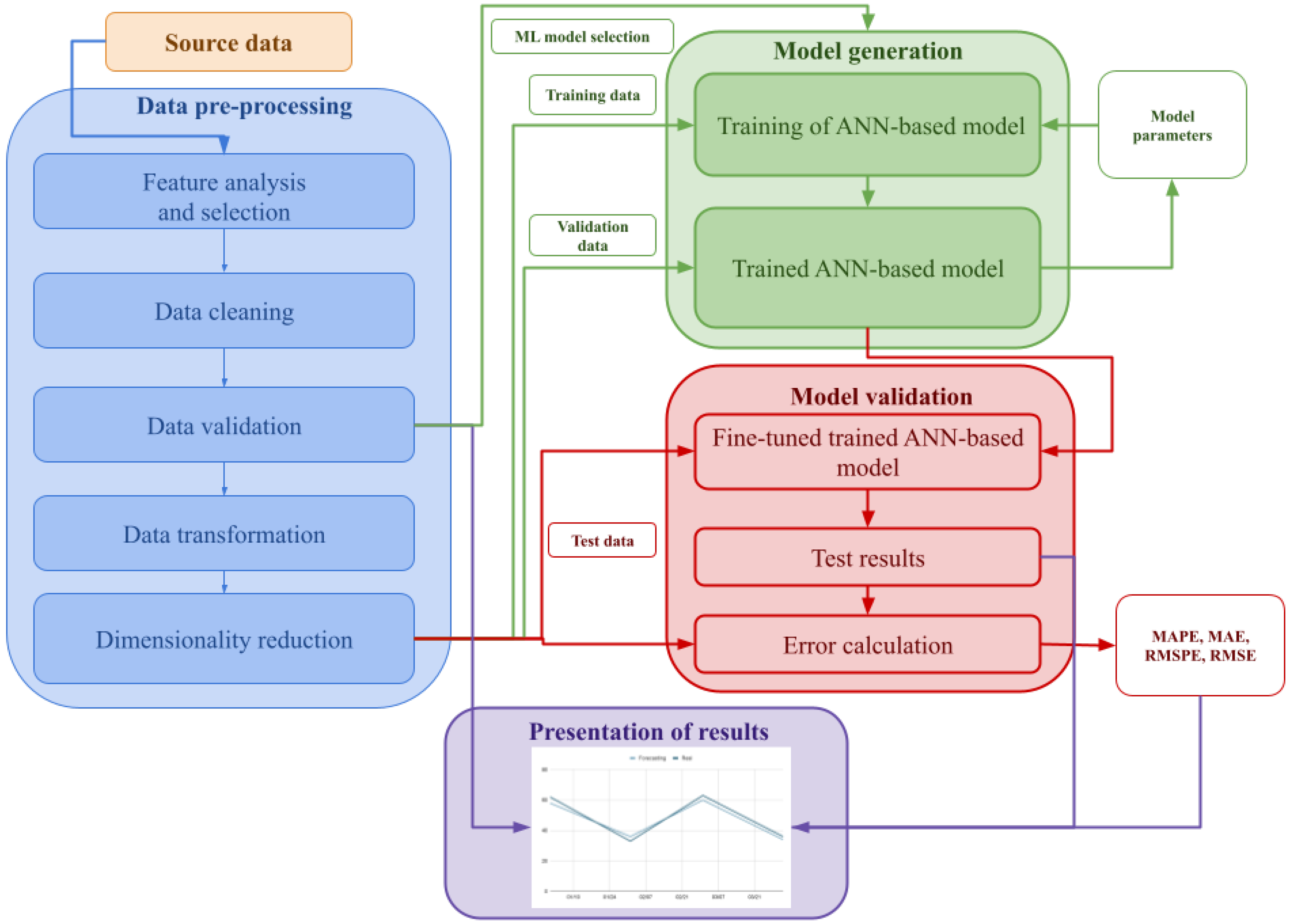
The blue box in Figure 1 presents a generalization of the pre-processing steps found in the reviewed papers. As already mentioned, many authors do not explain how the raw data are pre-processed, even though any omission or error in this process may lead to inaccurate and suboptimal models.
Figure 1.
Generalization of the steps documented in the reviewed papers.
4.3.3. Non-Linearity with Respect to Input Variables
In almost all the reviewed papers, the authors mention the fact that electricity demand is inherently non-linear, and therefore algorithms designed for linear problems are not a good choice for forecasting. This is typically taken for granted, without referring to papers that include mathematical analyses of demand time series in order to calculate the degree of linearity regarding the input variables. In this line, Darbellay and Slama [34] carried out a correlation analysis that suggests that LTLF—at least with the data available from the Czech Republic—was primarily a linear problem. This was confirmed by the comparison of the predictions. Knowing that, the same authors discussed the conditions under which ANNs could be superior to linear models. It is relevant to note that the computational cost of ANN-based algorithms can be easily afforded by research centers and companies of any size at present. Therefore, the superior mathematical knowledge required to create adapted linear models may not be worth even when the algorithms are typically lighter than the training and optimization process of ANN-based algorithms.
4.4. Output Variables
In the reviewed papers we found two main possible output variables:
- A time series of expected demand for the future, i.e., a list of the demand values predicted for specific moments.
- The load peak value of the electric grid at some point in the future (e.g., next day or next week peak).
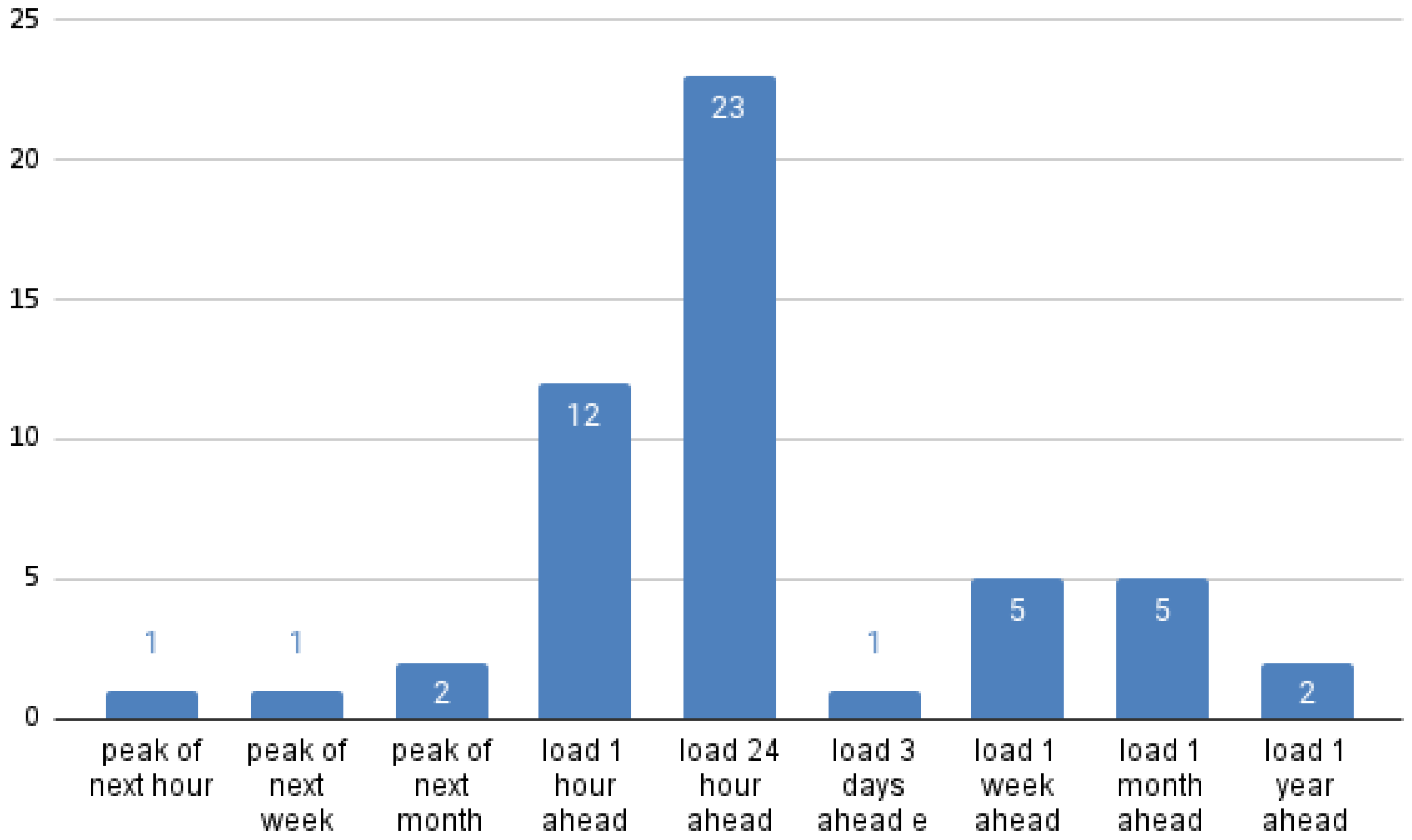
As shown in Figure 2, the most common output is the 24-h ahead prediction. As we explained before, this is especially relevant because the production is scheduled according to the negotiation of the intra-day electricity markets.
Figure 2.
Output variables of the reviewed papers that focus on STLF and MTLF. Some papers are counted in several columns.
Figure 2 also shows that the number of papers that look at peak values only ([8,37,56]) is very low compared to those that predict the load time series, and none of those was published after 2011. Narrowing to peak values was apparently done to simplify the problem, but currently predicting a complete time series is more useful for operative purposes (and, of course, peak values can be drawn from the predicted time series).
Almost all the reviewed papers present models that generate a predicted value for future points in time. Other authors [67] propose models that produce forecast probability density functions (PDF) so that it is possible to know the degree of uncertainty of each result. The suitability of a PDF as the output of the model depends on the type of problem that needs to be solved. A PDF may provide valuable information, for example, when it is important to know the probability of rare events that can compromise the supply. The loss of information with single-point forecasting is especially relevant when the forecasting model produces fat-tailed PDFs [68].
4.5. Measuring and Comparing Performance
The reviewed papers typically used the same data set with different algorithms or variants to decide which one performs better. Several Key Performance Indicators (KPI) have been used in order to compare their results.
Most of the works compare the results of the simulation algorithm with the actual values. The most common metrics to do so is the Mean Absolute Percentage Error (MAPE), given by Equation (1), where N represents the number of predicted values, is the predicted value at t and is the actual value which corresponds to the predicted value. MAPE gives a measurement of how accurate the prediction is, based on the average percentage of error of each predicted value.
The Mean Absolute Error (MAE), given by Equation (2), is equivalent to the MAPE but gives an absolute value for the error rather than a percentage.
When the same dataset is used to compare the prediction algorithms, both MAPE and MAE can be used; however, they are not helpful to compare results from different datasets. Even with the same dataset, the use of MAE may lead to confusing results if the units of any output are modified. Thus, MAPE is more common in the reviewed papers.
The second most common KPI is the Root Mean Square Percentage Error (RMSPE), given by Equation (3). While the MAPE gives the same weight to all errors, the RMSPE penalizes variance, since it gives more weight to larger absolute values than errors with smaller absolute values. Like in the case of the MAE, there is an absolute version called RMSE (Equation (4))that gives more weight to larger errors.
RMSPE is considered more suitable to show bigger deviations and helps to provide a complete picture of the error distribution (see [69]); however, it is not commonly used in the analyzed papers. Chai and Draxler [69] claim that RMSE is more appropriate than MAE when the error distribution is expected to be Gaussian, but this is often disregarded in the reviewed papers even though it would help to extract more information from the results.
The following are other variables found in the literature, depending of the purpose of the research work:
- The Maximum Negative Error (MNE) and Maximum Positive Error (MPE) give the maximum negative and positive difference, respectively, between a predicted value and a real value. These values can be more relevant than the average error for some applications (e.g., to forecast the fuel stockage in a power plant).
- The Residual Sum of Squares (RSS) is the sum of the squares of residuals (deviations predicted from actual values of data). It can be calculated from the RMSE. It measures the discrepancy between the data and an estimation model.
- The Standard Deviation of Residuals describes the difference in standard deviations of observed values versus predicted values as shown by points in a regression analysis.
- The comparison of the correlation between the time series produced by different algorithms and the real validation set is used by some authors to measure quality [13], too.
Computing the values above allows comparing the results attained by different techniques. However, such a simple analysis may not be very meaningful, especially when the difference between algorithms is small or the dataset is not very long. In this line, Kandananond [48] used Wilcoxson signed-rank and paired t-tests to compare the results offered by ANN, MLR and ARIMA. The p-values obtained were above , so he concluded that the results were not meaningful and there was no real advantage of ANN over ARIMA or MLR.
4.6. Forecasting Model Generation Process
Figure 1 shows the steps typically followed by the reviewed papers to validate their proposed models by obtaining meaningful results from the input data. The process is not significantly different from the flows typically used in ML problems.
Once the data have been pre-processed following the steps presented in Section 4.3.2, they are typically divided in two sets: training and test. The training data are in turn divided into training and validation datasets. First, the training data is used to train the model. The initial version of the model is validated with the validation dataset. After this process, it may be necessary to tune the hyperparameters of the model or, in the specific case of ANN-based models, to introduce some changes to the topology of the neural network. Then the model is tested again with the test dataset and its performance is measured by calculating the error with regard to the real data.
Graphical representations of the final results are included in almost all the reviewed papers. It is also common to support model selection decisions with different data visualization techniques to describe the patterns and characteristics of the original data.
Despite the fact that this structure is common to most of the reviewed papers, the authors typically introduce innovations in either the methodology or the algorithms and techniques used in the different stages of the process. The parts where more innovative approaches can be found are:
- The use of clustering and other categorization techniques with load input data in order to tune the model depending on the patterns found therein [31,35,49,51];
- The ML algorithm proposed to build the forecasting model. The proposed models are typically compared with commonly used ML models. Section 5 includes an exhaustive list of both the ML algorithm being tested and the alternative options.
- As mentioned in Section 4.5, authors use different alternatives to analyze and compare the performance of the different ML algorithms [13,40,48]. However, the comparison of MAPE and RMSE values is the most typical choice.
4.7. Reproducibility of Forecasting Experiments
As shown in Table 5, we found that less than 40% of the reviewed papers used publicly accessible data that could be used to reproduce the experiment. In the other cases, the researchers typically had some type of agreement with the operator providing the data, and the original data are not accessible. This makes the experiments hard to reproduce and validate, especially in the case of new algorithms. In any case, aggregated demand and generation data are commonly available in developed countries. In contrast, smart meter data are harder to achieve owing to data protection laws, but it is possible to gain access to anonymized load time series of individual and industrial consumers, which can be freely used for experiments.

Table 5.
Data source in the reviewed papers.
Another factor that affects the reproducibility of the experiments are the tools and the code used to conduct them. The growing adoption of ML algorithms to extract value from the massive amount of data available in numerous fields of applications has fostered an active open-source ML community. Some of the most relevant ML and data science related projects (e.g., PyTorch, Tensorflow and its high-level API Keras) are supported by big Internet companies. Research in ML can now take advantage of these valuable tools, reducing the programming efforts and making it easier to focus on the problems and try different alternatives. In Table 6, we see that MATLAB remains the main tool used in the reviewed papers, while several authors used code implemented ad-hoc. The tool used for the implementation is not even mentioned by many authors.

Table 6.
Tools used in the reviewed papers.
Regarding the code used to conduct the experiments, only one of the reviewed papers offers it to the reader [52]. However, sharing the code seems to be a growing trend in data science and ML papers [70] so it may happen as well for load demand forecasting papers in the near future.
5. Summary of the Reviewed Papers
Given the perspective of the previous section, next we provide a table (Table 7) containing the most relevant information from the reviewed papers, including the following:

Table 7.
Reviewed papers.
- Title and reference.
- Year of publication.
- Goal.
- Algorithms and optimization techniques used.
- Performance of the best algorithm.
Most of the papers used MAPE (and in some cases other related values) as the metrics to compare the performance of the algorithms. To give the reader a reference of the performance of each algorithm, we only include the MAPE value in the table. When other non-normalized values were used, we did not include them in the table to keep it coherent and avoid misunderstandings. If, in some specific case, the MAPE was not the most relevant value, it is indicated in the Best algorithm column.
6. Conclusions
The use of ANN-based ML algorithms for electricity demand forecasting is an idea that goes back to the 1990s, but continues to be the subject of intensive research presently. Chronologically, the papers we have reviewed show how ANNs evolved from a sensible and promising concept—due to the cyclic nature of load demand—to a widely used reality in production environments.
This review is aimed at providing a valuable asset for researchers. Bearing this goal in mind, we analyzed 50 research works to extract their common patterns and also the main differences in terms of methodology and algorithms. We want to highlight four aspects to be considered for future forecasting experiments: performance comparison, best performing algorithms, influence of aggregation level, and experiment reproducibility.
6.1. Performance Comparison
The generalized use of MAPE to measure the performance of the algorithms allows to extract some relevant conclusions. The first is that ANN-based algorithms (and especially LSTM, which is the most used algorithm in the reviewed papers) have proved to achieve very good results in aggregated load forecast, and that their predictions get typically more accurate as the number of electricity consumers grows. A significant number of recent papers show MAPE values below 3% for the best cases.
Regarding the ability to compare the different algorithms, we understand that just comparing the MAPE values from different papers can give a raw orientation for future research works. However, we are also aware that this is not the best approach, since they are making predictions over different datasets, which in many cases are not accessible to the scientific community. Additionally, using the MAPE as the single KPI may not be always fair, since the RMSE may be a better metric for many applications where high forecast errors must be avoided. It is worth noting that recently published papers typically include (at least) both values, which a positive practice to enable more complete comparisons in the future.
6.2. The Best Performing Algorithms
ANN-based approaches that can capture recurrent patterns (such as RNN and, specifically, LSTM) proved to perform well for load demand problems. In consequence, most of the papers covered in this survey featured one ANN-based algorithm as the best alternative compared to other approaches. However, there are some exceptions. For instance, in [58] a combination of PSO with SVR turned out to perform slightly better than PSO with ANN-based algorithms; Ref. [43] found the autoregressive models of ARIMA to outperform RNN and LSTM for STLF problems; SVM worked better than MLP in an STLF problem in [3]; and SVM was found to be more reliable and stable than ANN for mid-term load forecasting in [29].
In general, combinations of MLP or LTSM with other algorithms do not attain a substantial advantage over the original algorithms, but the papers that compare innovative combinations typically show them as the optimal option. There are innovative models, though, whose authors claim to obtain MAPE values below 1% [71]. However, without an extensive validation using different datasets, it remains unclear whether the model really shows a very good performance for generic load demand problems, or the results may be due to an over-fitted model (e.g., one that provides very good results only for the dataset with which it has been trained). An alternative to obtain more accurate models—at the cost of a higher complexity—could be the kind of combinations of different ANN-based algorithms as proposed in [32].
6.3. Influence of the Aggregation Level in Model Performance
The accuracy of STLF and MTLF predictions for aggregated demand of a huge number of consumers is good in general, which makes modern ANN-based algorithms a good tool for commercial and research purposes. In turn, load forecasting in microgrids is a challenging problem according to the results provided by the analyzed papers. The MAPE results are typically above 10%. Still, this could be good enough, inasmuch as recent advances in energy storage techniques can easily absorb the forecast errors.
The problem of individual user load forecasting seems to be the hardest to resolve, which is understandable due to the nature of some human behaviors. The high MAPE values attained by the few papers that tackle this problem (such as [31]) suggest that ANN may not be the best approach if very high precision is needed. Again, the importance of individual consumer forecast is lower than aggregated load from the point of view of the industry, due to the recent improvements in power storage technologies that can absorb load oscillation in isolated systems. In any case, we understand that there is still room for improvement for microgrids and individual load demand forecast models.
6.4. Benchmarks and Reproducibility
To make an unbiased assessment of the performance of the different algorithms, load demand papers should use a common reference benchmark, which does not exist yet. This could use publicly available datasets, in addition to other specific ones. For example, the comprehensive list of smart meter time series included in [73] could be used as a starting point to define a reference dataset to test the performance of the different algorithms in equivalent conditions. In the same line, the publication of results without making the source code and datasets available makes it hard or impossible to reproduce the results. Fortunately, sharing the source code is also becoming common in recent years [70], so we are optimistic in this sense. Without a doubt, this will help to take forecasting closer to the limits of ML techniques in the next few years.
Author Contributions
Conceptualization, A.R.-P. and M.L.-N.; methodology, A.R.-P.; software, A.R.-P.; validation, A.R.-P., M.L.-N. and J.J.P.-A.; formal analysis, A.R.-P.; investigation, A.R.-P.; resources, A.R.-P.; data curation, A.R.-P.; writing—original draft preparation, A.R.-P.; writing—review and editing, A.R.-P., M.L.-N. and J.J.P.-A.; visualization, A.R.-P.; supervision, M.L.-N. and J.J.P.-A.; project administration, M.L.-N.; funding acquisition, J.J.P.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the University of Vigo from the European Regional Development Fund (ERDF), in part by the Galician Regional Government under the Program for the Consolidation and Structuring of Competitive Research Groups under Grant ED431B 2020/34, in part by the atlanTTic Research Center for Telecommunication Technologies, and in part by the Ministerio de Educación y Ciencia, Gobierno de España Research Project under Grant TIN2017-87604-R.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the papers included in this systematic review have been downloaded from the original publisher sites and are available to any researcher. Some of the publisher platforms may require a subscription to be able to read and download the papers.
Conflicts of Interest
The authors declare no conflict of interest. They do not have either a professional or an academic relationship with any of authors of the reviewed papers.
Abbreviations
The following abbreviations are used in this manuscript:
| AMI | Advanced Metering Infrastructure |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive integrated moving average |
| ARMAX | Autoregressive–moving-average model |
| BFGS | Broyden–Fletcher–Goldfarb–Shanno |
| BP | Back-Propagation |
| BPN | Back-Propagation Network |
| BR | Bayesian Regularization |
| ENN | Evolving Neural Network |
| FFNN | Feed Forward Neural Network |
| FFANN | Feedforward Artificial Neural Network |
| GBRT | Gradient Boosted Regression Trees |
| LM | Levenberg Marquardt (BP algorithm) |
| DNN | Deep Neural Network |
| GA | Genetic Algorithm |
| GMDH | Group Method Data Handling |
| KPI | Key Performance Indicator |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MHS | Modified Harmony Search |
| ML | Machine Learning |
| MLP | Multi-Layer Perceptron |
| MLR | Multiple Linear Regression |
| MTLF | Medium-Term Load Forecast |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LSTM | Long-Short Term Memory networks |
| LTLF | Short-Term Load Forecast |
| PCA | Principal Component Analysis |
| Probability Distribution Function | |
| PDRNN | Diagonal Recurrent Neural Networks |
| PJM | Pennsylvania, New Jersey, and Maryland |
| PSO | Particle Swarm Optimization |
| RBF | Radial Basis Function |
| RBM | Restricted Boltzmann Machine |
| RMSE | Root Mean Square Error |
| RMSPE | Root Mean Square Percentage Error |
| RNN | Recurrent Neural Network |
| SBMO | Sequential Model-Based Global Optimization |
| SFNN | Self-organising Fuzzy Neural Network |
| SOM | Self-Organizing Map |
| STLF | Short-Term Load Forecast |
| SVM | Support Vector Machine |
| SVR | Support Vector Machine Regression |
| WEFuNN | Weighted Evolving Fuzzy Neural Network |
References
- Lee, K.Y.; Park, J.H.; Chang, S.H. Short-term load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1992, 7, 124–130. [Google Scholar] [CrossRef]
- Peng, T.M.; Hubele, N.F.; Karady, G.G. An conceptual approach to the application of neural networks for short term load forecasting. In Proceedings of the IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; pp. 2942–2945. [Google Scholar]
- Zor, K.; Timur, O.; Teke, A. A state-of-the-art review of artificial intelligence techniques for short-term electric load forecasting. In Proceedings of the 2017 6th International Youth Conference on Energy (IYCE), Budapest, Hungary, 21–24 June 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Fallah, S.N.; Deo, R.C.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef] [Green Version]
- Alfares, H.; Mohammad, N. Electric load forecasting: Literature survey and classification of methods. Int. J. Syst. Sci. 2002, 33, 23–34. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef] [Green Version]
- Metaxiotis, K.; Kagiannas, A.; Askounis, D.; Psarras, J. Artificial intelligence in short term electric load forecasting: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2003, 44, 1525–1534. [Google Scholar] [CrossRef]
- Moharari, N.S.; Debs, A.S. An artificial neural network based short term load forecasting with special tuning for weekends and seasonal changes. In Proceedings of the Second International Forum on Applications of Neural Networks to Power Systems, Yokohama, Japan, 19–22 April 1993; pp. 279–283. [Google Scholar] [CrossRef]
- Mori, H.; Ogasawara, T. A recurrent neural network for short-term load forecasting. In Proceedings of the Second International Forum on Applications of Neural Networks to Power Systems, Yokohama, Japan, 19–22 April 1993; pp. 395–400. [Google Scholar] [CrossRef]
- Srinivasa, N.; Lee, M.A. Survey of hybrid fuzzy neural approaches to electric load forecasting. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Part 5, Vancouver, BC, Canada, 22–25 October 1995; pp. 4004–4008. [Google Scholar]
- Mohammed, O.; Park, D.; Merchant, R.; Dinh, T.; Tong, C.; Azeem, A.; Farah, J.; Drake, C. Practical experiences with an adaptive neural network short-term load forecasting system. IEEE Trans. Power Syst. 1995, 10, 254–265. [Google Scholar] [CrossRef]
- Marin, F.J.; Garcia-Lagos, F.; Joya, G.; Sandoval, F. Global model for short-term load forecasting using artificial neural networks. IEEE Gener. Transm. Distrib. 2002, 149, 121–125. [Google Scholar] [CrossRef] [Green Version]
- Abu-El-Magd, M.A.; Findlay, R.D. A new approach using artificial neural network and time series models for short term load forecasting. In Proceedings of the CCECE 2003—Canadian Conference on Electrical and Computer Engineeringl Toward a Caring and Humane Technology (Cat. No.03CH37436), Montreal, QC, Canada, 4–7 May 2003; Volume 3, pp. 1723–1726. [Google Scholar] [CrossRef]
- Izzatillaev, J.; Yusupov, Z. Short-term load forecasting in grid-connected microgrid. In Proceedings of the 2019 7th International Istanbul Smart Grids and Cities Congress and Fair (ICSG), Istanbul, Turkey, 25–26 April 2019; pp. 71–75. [Google Scholar]
- Twanabasu, S.R.; Bremdal, B.A. Load forecasting in a Smart Grid oriented building. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013; pp. 1–4. [Google Scholar]
- Emre, A.; Hocaoglu, F.O. Electricity demand forecasting of a micro grid using ANN. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–23 March 2018; pp. 1–5. [Google Scholar]
- Gezer, G.; Tuna, G.; Kogias, D.; Gulez, K.; Gungor, V.C. PI-controlled ANN-based energy consumption forecasting for smart grids. In Proceedings of the ICINCO 2015—12th International Conference on Informatics in Control, Automation and Robotics, Colmar, France, 21–23 July 2015; pp. 110–116. [Google Scholar] [CrossRef]
- Huang, Q.; Li, Y.; Liu, S.; Liu, P. Hourly load forecasting model based on real-time meteorological analysis. In Proceedings of the 2016 8th International Conference on Computational Intelligence and Communication Networks (CICN), Tehri, India, 23–25 December 2016; pp. 488–492. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using Deep Neural Networks. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7046–7051. [Google Scholar] [CrossRef] [Green Version]
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. In Proceedings of the 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm), Sydney, Australia, 6–9 November 2016; pp. 308–313. [Google Scholar] [CrossRef]
- He, Y.; Xu, Q. Short-term power load forecasting based on self-adapting PSO-BP neural network model. In Proceedings of the 2012 Fourth International Conference on Computational and Information Sciences, Chongqing, China, 17–19 August 2012; pp. 1096–1099. [Google Scholar] [CrossRef]
- Jigoria-Oprea, D.; Lustrea, B.; Kilyeni, S.; Barbulescu, C.; Kilyeni, A.; Simo, A. Daily load forecasting using recursive Artificial Neural Network vs. classic forecasting approaches. In Proceedings of the 2009 5th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 28–29 May 2009; pp. 487–490. [Google Scholar] [CrossRef]
- Tee, C.Y.; Cardell, J.B.; Ellis, G.W. Short-term load forecasting using artificial neural networks. In Proceedings of the 41st North American Power Symposium, Starkville, MS, USA, 4–6 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Dudek, G. Short-term load cross-forecasting using pattern-based neural models. In Proceedings of the 2015 16th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 20–22 May 2015; pp. 179–183. [Google Scholar] [CrossRef]
- Keitsch, K.A.; Bruckner, T. Input data analysis for optimized short term load forecasts. In Proceedings of the 2016 IEEE Innovative Smart Grid Technologies—Asia (ISGT-Asia), Melbourne, Australia, 28 November–1 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, N.K.; Singh, A.K.; Paliwal, N. Neural network based short-term electricity demand forecast for Australian states. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Mitchell, G.; Bahadoorsingh, S.; Ramsamooj, N.; Sharma, C. A comparison of artificial neural networks and support vector machines for short-term load forecasting using various load types. In Proceedings of the 2017 IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Pan, X.; Lee, B. A comparison of support vector machines and artificial neural networks for mid-term load forecasting. In Proceedings of the 2012 IEEE International Conference on Industrial Technology, Athens, Greece, 19–21 March 2012; pp. 95–101. [Google Scholar] [CrossRef]
- Narayan, A.; Hipel, K.W. Long short term memory networks for short-term electric load forecasting. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 2573–2578. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Bashari, M.; Rahimi-Kian, A. Forecasting electric load by aggregating meteorological and history-based deep learning modules. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, Y.; Zhao, W.; Mao, Y. Dynamic neural network based genetic algorithm optimizing for short term load forecasting. In Proceedings of the 2010 Chinese Control and Decision Conference, Xuzhou, China, 26–28 May 2010; pp. 2701–2704. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Slama, M. Forecasting the short-term demand for electricity: Do neural networks stand a better chance? Int. J. Forecast. 2000, 16, 71–83. [Google Scholar] [CrossRef]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sánchez-Esguevillas, A.; Lloret, J. Artificial neural networks for short-term load forecasting in microgrids environment. Energy 2014, 75, 252–264. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Tarverdian, S.; Saberi, M. Integration of artificial neural networks and genetic algorithm to predict electrical energy consumption. Appl. Math. Comput. 2007, 186, 1731–1741. [Google Scholar] [CrossRef]
- Chang, P.-C.; Fan, C.-Y.; Lin, J.-J. Monthly electricity demand forecasting based on a weighted evolving fuzzy neural network approach. Int. J. Electr. Power Energy Syst. 2011, 33, 17–27. [Google Scholar] [CrossRef]
- Dash, P.K.; Satpathy, H.P.; Liew, A.C. A real-time short-term peak and average load forecasting system using a self-organising fuzzy neural network. Eng. Appl. Artif. Intell. 1998, 11, 307–316. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Forecasting electrical consumption by integration of Neural Network, time series and ANOVA. Appl. Math. Comput. 2007, 186, 1753–1761. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Santana, Á.L.; Conde, G.B.; Rego, L.P.; Rocha, C.A.; Cardoso, D.L.; Costa, J.C.W.; Bezerra, U.H.; Francês, C.R.L. PREDICT—Decision support system for load forecasting and inference: A new undertaking for Brazilian power suppliers. Int. J. Electr. Power Energy Syst. 2012, 38, 33–45. [Google Scholar] [CrossRef]
- Bunnoon, P.; Chalermyanont, K.; Limsakul, C. Multi-substation control central load area forecasting by using HP-filter and double neural networks (HP-DNNs). Int. J. Electr. Power Energy Syst. 2013, 44, 561–570. [Google Scholar] [CrossRef]
- Rahman, A.; Srikumar, V.; Smith, A.D. Predicting electricity consumption for commercial and residential buildings using deep recurrent neural networks. Appl. Energy 2018, 212, 372–385. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. A Deep Learning Approach to Forecasting Monthly Demand for Residential–Sector Electricity. Sustainability 2020, 12, 3103. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Qin, Y.; Wang, S.; Wang, X.; Wang, C. Electricity consumption probability density forecasting method based on LASSO-Quantile Regression Neural Network. Appl. Energy 2019, 233–234, 565–575. [Google Scholar] [CrossRef] [Green Version]
- Hernandez, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J. Short-Term Load Forecasting for Microgrids Based on Artificial Neural Networks. Energies 2013, 6, 1385–1408. [Google Scholar] [CrossRef] [Green Version]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef] [Green Version]
- Kandananond, K. Forecasting Electricity Demand in Thailand with an Artificial Neural Network Approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Zhai, M.-Y. Day-Ahead Prediction of Microgrid Electricity Demand Using a Hybrid Artificial Intelligence Model. Processes 2019, 7, 320. [Google Scholar] [CrossRef] [Green Version]
- Amjady, N.; Keynia, F. A New Neural Network Approach to Short Term Load Forecasting of Electrical Power Systems. Energies 2011, 4, 488–503. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef] [Green Version]
- Hossen, T.; Plathottam, S.J.; Angamuthu, R.K.; Ranganathan, P.; Salehfar, H. Short-term load forecasting using deep neural networks (DNN). In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
- Peng, Y.; Wang, Y.; Lu, X.; Li, H.; Shi, D.; Wang, Z.; Li, J. Short-term load forecasting at different aggregation levels with predictability analysis. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3385–3390. [Google Scholar] [CrossRef] [Green Version]
- Anupiya, N.; Upeka, S.; Kok, W. Predicting Electricity Consumption using Deep Recurrent Neural Networks. arXiv 2019, arXiv:1909.08182. [Google Scholar]
- Hossen, T.; Nair, A.S.; Chinnathambi, R.A.; Ranganathan, P. Residential Load Forecasting Using Deep Neural Networks (DNN). In Proceedings of the 2018 North American Power Symposium (NAPS), Fargo, ND, USA, 9–11 September 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Bunnon, P.; Chalermyanont, K.; Limsakul, C. The Comparision of Mid Term Load Forecasting between Multi-Regional and Whole Country Area Using Artificial Neural Network. Int. J. Comput. Electr. Eng. 2010, 2, 334. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]
- Jang, J.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Brownlee, J. Long Short-Term Memory Networks with Python. Develop Sequence Prediction Models With Deep Learning; Machine Learning Mastery: San Juan, PR, USA, 2017. [Google Scholar]
- Hernández, L.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Cook, D.J.; Chinarro, D.; Gómez, J. A Study of the Relationship between Weather Variables and Electric Power Demand inside a Smart Grid/Smart World Framework. Sensors 2012, 12, 11571–11591. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Liu, R.; Li, H.; Wang, S.; Lu, X. Short-term power load probability density forecasting method using kernel-based support vector quantile regression and Copula theory. Appl. Energy 2017, 185, 254–266. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Zhang, L.; Chen, J.; Wu, G.; Ni, S.; Hu, Z.; Weng, C.; Chen, Z. Multiple-Load Forecasting for Integrated Energy System Based on Copula-DBiLSTM. Energies 2021, 14, 2188. [Google Scholar] [CrossRef]
- Shove, E.; Pantzar, M.; Watson, M. The Dynamics of Social Practice: Everyday Life and How it Changes; SAGE Publications: Southend Oaks, CA, USA, 2012. [Google Scholar]
- Ventseslav, S.; Vanya, M. Impact of data preprocessing on machine learning performance. In Proceedings of the International Conference on Information Technologies (InfoTech-2013), Singapore, 1–2 December 2013. [Google Scholar]
- Sendin, A.; Peña, I.; Angueira, P. Strategies for Power Line Communications Smart Metering Network Deployment. Energies 2014, 7, 2377–2420. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Wang, Y. Short-term wind power prediction based on EEMD-LASSO-QRNN model. Appl. Soft Comput. 2021, 105, 107288. [Google Scholar] [CrossRef]
- Taleb, N.N.; Bar-Yam, Y.; Cirillo, P. On single point forecasts for fat-tailed variables. Int. J. Forecast. 2020. [Google Scholar] [CrossRef] [PubMed]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE)or mean absolute error (MAE)? Argum. Against Avoid. RMSE Lit. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Papers with Code. Available online: https://paperswithcode.com/ (accessed on 30 June 2021).
- Chen, J.; Do, Q.H. Forecasting daily electricity load by wavelet neural networks optimized by cuckoo search algorithm. In Proceedings of the 2017 6th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Hamamatsu, Japan, 9–13 July 2017; pp. 835–840. [Google Scholar] [CrossRef]
- Mohammad, F.; Lee, K.B.; Kim, Y.-C. Short Term Load Forecasting Using Deep Neural Networks. arXiv 2018, arXiv:1811.03242. [Google Scholar]
- Wang, Y.; Chen, Q.; Hong, T.; Kang, C. Review of Smart Meter Data Analytics: Applications, Methodologies, and Challenges. IEEE Trans. Smart Grid 2019, 10, 3125–3148. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).