An Autoencoder-Based Deep Learning Approach for Load Identification in Structural Dynamics
Abstract
1. Introduction
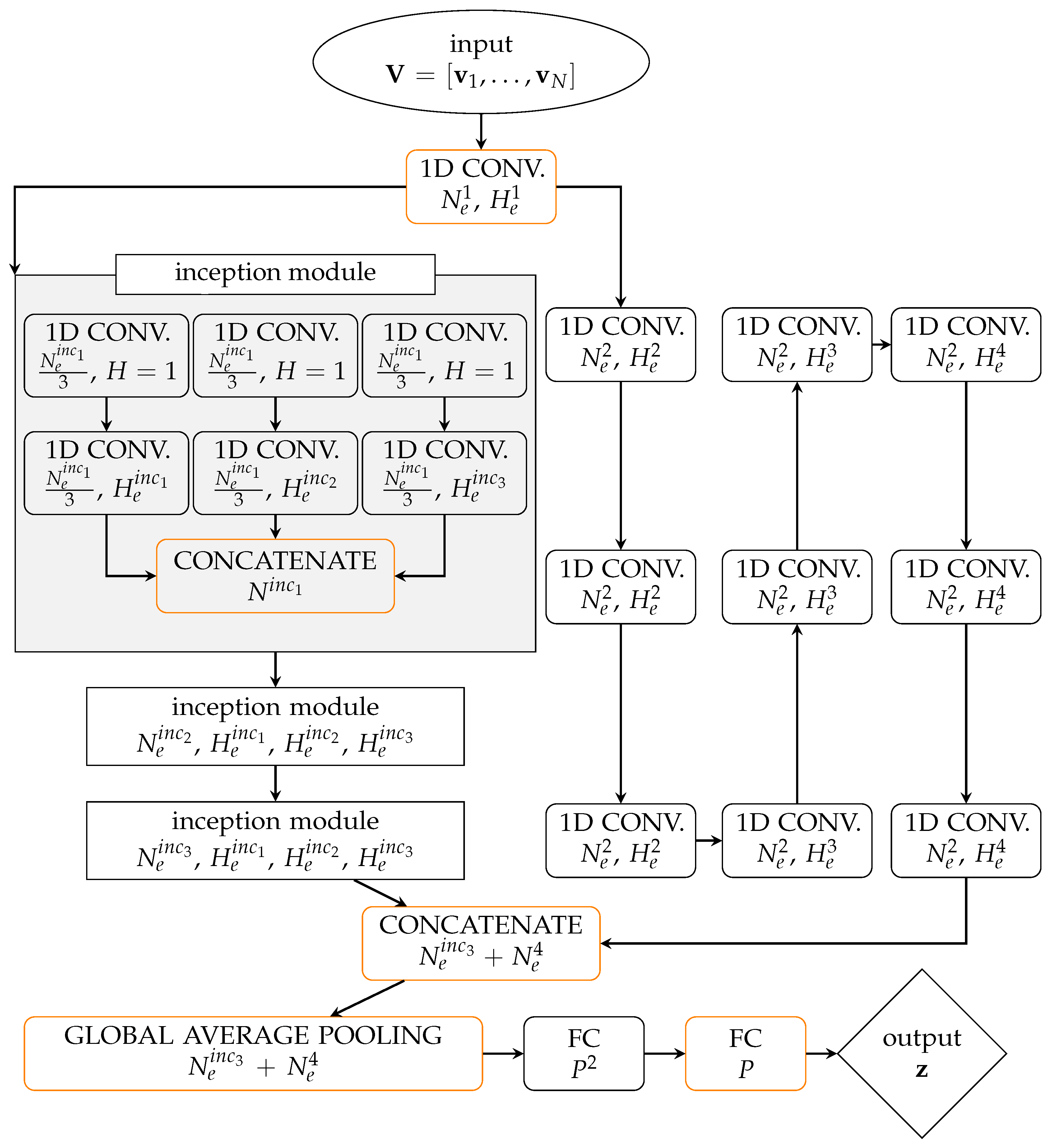
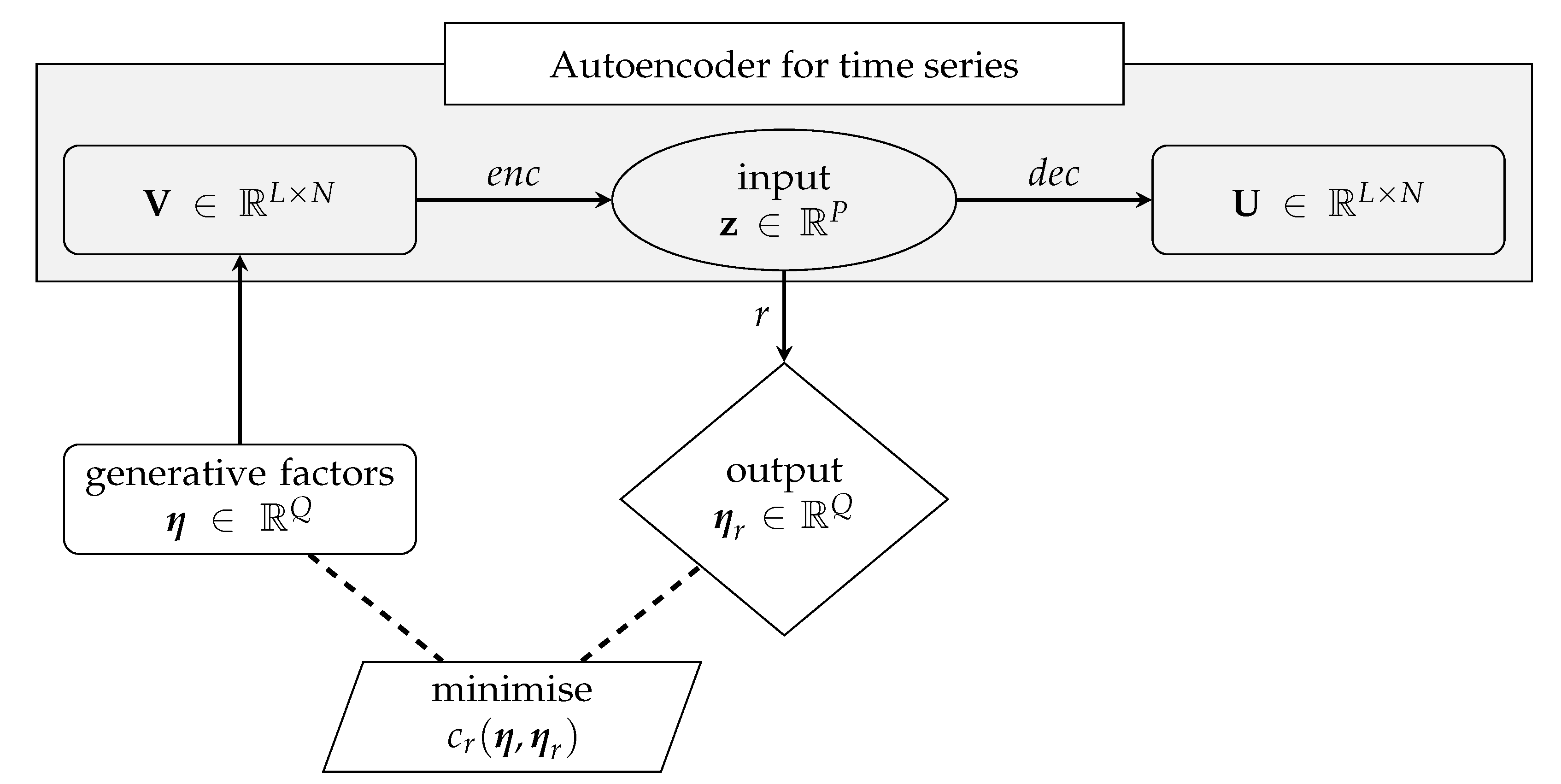
2. Autoencoders for Input (Load) Identification
2.1. Autoencoder Paradigm
2.2. Solving Regression Problems
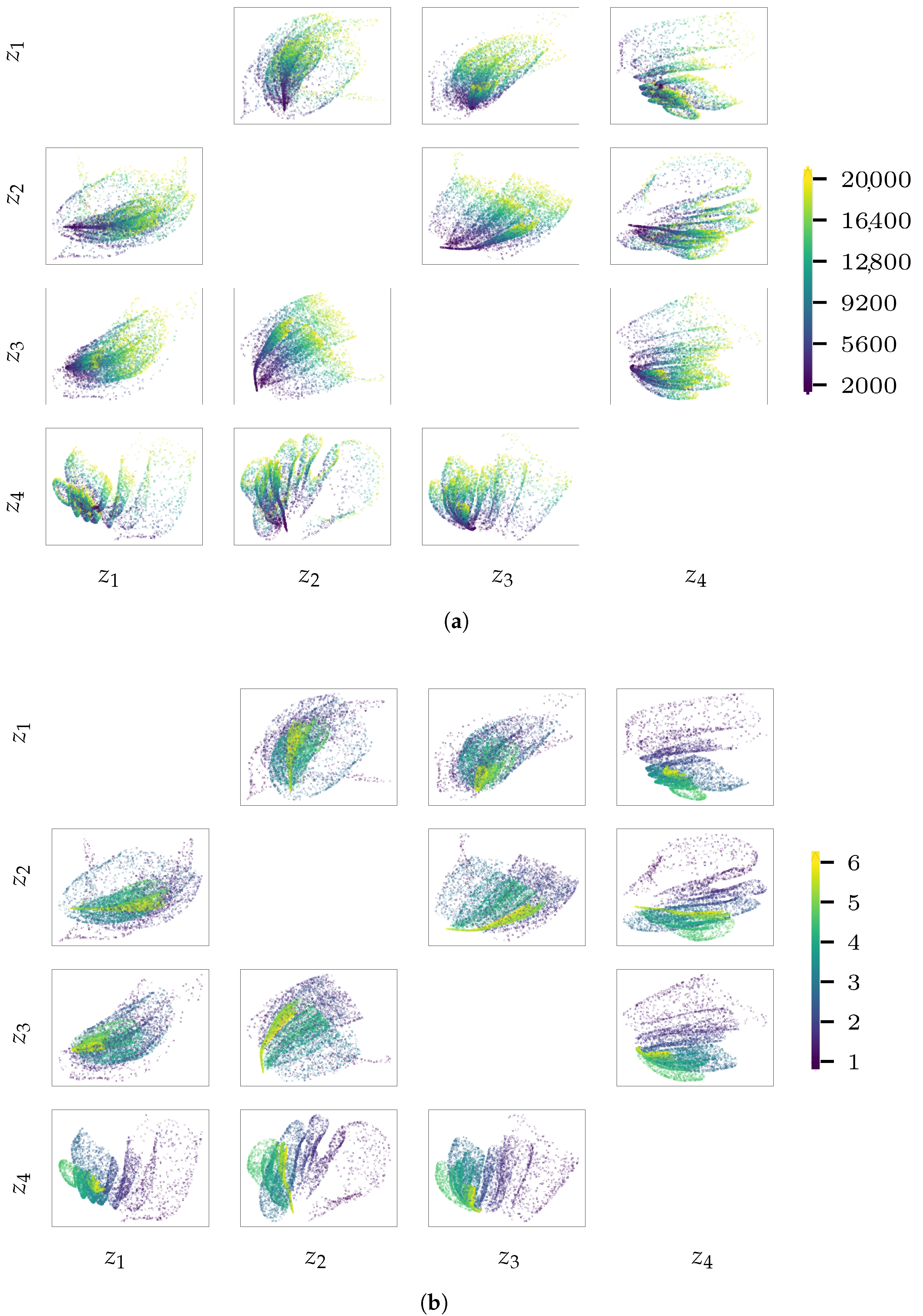
3. Choice of the Latent Dimension
3.1. Generative Factors
3.2. False Nearest Neighbour Heuristics
4. Numerical Results
4.1. Two-Storey Shear Building
4.1.1. Shear Building Model
4.1.2. Signal Reconstruction
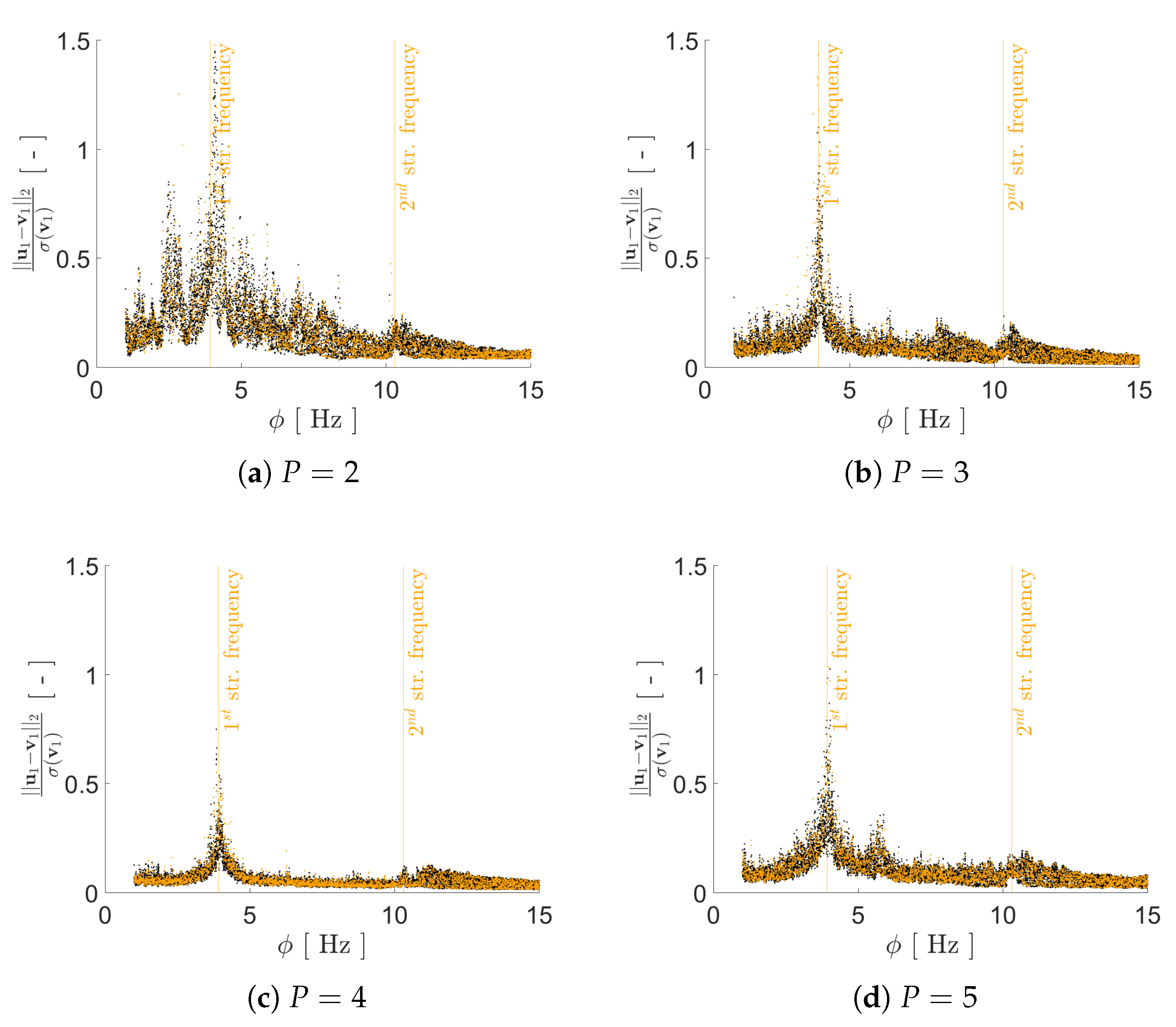
4.1.3. False Nearest Neighbour Heuristics
4.1.4. Load Identification
4.2. Pirelli Tower
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fink, O.; Wang, Q.; Svensén, M.; Dersin, P.; Lee, W.J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.; Prime, M. A Summary Review of Vibration-Based Damage Identification Methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical Damage Classification Under Changing Environmental and Operational Conditions. J. Intell. Mater. Syst. Struct. 2002, 13, 561–574. [Google Scholar] [CrossRef]
- Azam, S.E.; Mariani, S.; Attari, N.K. Online damage detection via a synergy of proper orthogonal decomposition and recursive Bayesian filters. Nonlinear Dyn. 2017, 89, 1489–1511. [Google Scholar] [CrossRef]
- Azam, S.E.; Mariani, S. Online damage detection in structural systems via dynamic inverse analysis: A recursive Bayesian approach. Eng. Struct. 2018, 159, 28–45. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441–445. [Google Scholar] [CrossRef]
- Azam, S.E.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60–61, 866–886. [Google Scholar] [CrossRef]
- Hansen, P.C.; Sekii, T.; Shibahashi, H. The Modified Truncated SVD Method for Regularization in General Form. SIAM J. Sci. Stat. Comput. 1992, 13, 1142–1150. [Google Scholar] [CrossRef]
- Yang, C.; Hou, X.; Chang, S. A synchronous placement and size-based multi-objective optimization method for heat dissipation design on antenna module of space solar power satellite. Sustain. Energy Technol. Assess. 2021, 45, 101183. [Google Scholar] [CrossRef]
- Yang, C. A novel uncertainty-oriented regularization method for load identification. Mech. Syst. Signal Process. 2021, 158, 107774. [Google Scholar] [CrossRef]
- Seo, J.K.; Kim, K.C.; Jargal, A.; Lee, K.; Harrach, B. A Learning-Based Method for Solving Ill-Posed Nonlinear Inverse Problems: A Simulation Study of Lung EIT. SIAM J. Imaging Sci. 2019, 12, 1275–1295. [Google Scholar] [CrossRef]
- Farrar, C.; Worden, K. Structural Health Monitoring a Machine Learning Perspective; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Bergés, M.; Bielak, J.; Garrett, J.H.; Kovačević, J.; Noh, H.Y. Diagnosis algorithms for indirect structural health monitoring of a bridge model via dimensionality reduction. Mech. Syst. Signal Process. 2020, 136, 106454. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Li, J. A Novel Parallel Auto-Encoder Framework for Multi-Scale Data in Civil Structural Health Monitoring. Algorithms 2018, 11, 112. [Google Scholar] [CrossRef]
- Hu, Y.; Palmé, T.; Fink, O. Fault detection based on signal reconstruction with Auto-Associative Extreme Learning Machines. Eng. Appl. Artif. Intell. 2017, 57, 105–117. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Zamir, A.R.; Sax, A.; Shen, W.; Guibas, L.J.; Malik, J.; Savarese, S. Taskonomy: Disentangling Task Transfer Learning. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3712–3722. [Google Scholar] [CrossRef]
- Shen, C.; Qi, Y.; Wang, J.; Cai, G.; Zhu, Z. An automatic and robust features learning method for rotating machinery fault diagnosis based on contractive autoencoder. Eng. Appl. Artif. Intell. 2018, 76, 170–184. [Google Scholar] [CrossRef]
- Fu, T. A review on time series data mining. Eng. Appl. Artif. Intell. 2011, 24, 164–181. [Google Scholar] [CrossRef]
- Gilpin, W. Deep reconstruction of strange attractors from time series. In Proceedings of the 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Virtual Conference, 6–14 December 2020. [Google Scholar]
- Haykin, S. Neural Networks and Learning Machines; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–13. [Google Scholar]
- Rosafalco, L.; Manzoni, A.; Mariani, S.; Corigliano, A. Fully convolutional networks for structural health monitoring through multivariate time series classification. Adv. Model. Simul. Eng. Sci. 2020, 7, 38. [Google Scholar] [CrossRef]
- Rosafalco, L.; Torzoni, M.; Manzoni, A.; Mariani, S.; Corigliano, A. Online structural health monitoring by model order reduction and deep learning algorithms. arXiv 2021, arXiv:2103.14328. [Google Scholar]
- Locatello, F.; Tschannen, M.; Bauer, S.; Rätsch, G.; Schölkopf, B.; Bachem, O. Disentangling Factors of Variations Using Few Labels. In Proceedings of the 8th International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 26–30 April 2020. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR, Las Vegas, NV, USA, 26 June–1 July 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Klambauer, G.; Unterthiner, T.; Mayr, A.; Hochreiter, S. Self-Normalizing Neural Networks. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 971–980. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Arora, S.; Bhaskara, A.; Ge, R.; Ma, T. Provable Bounds for Learning Some Deep Representations. In Proceedings of the 31st International Conference on Machine Learning, Bejing, China, 22–24 June 2014; PMLR: Bejing, China, 2014; Volume 32, pp. 584–592. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 28 March 2020).
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 4 April 2020).
- Dutilleux, P. An Implementation of the “Algorithme à Trous” to Compute the Wavelet Transform; Wavelets; Springer: Berlin/Heidelberg, Germany, 1990; pp. 298–304. [Google Scholar] [CrossRef]
- van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Sudret, B.; Defaux, G.; Pendola, M. Stochastic evaluation of the damage length in RC beams submitted to corrosion of reinforcing steel. Civ. Eng. Environ. Syst. 2007, 24, 165–178. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, ICML, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- He, K.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR, Las Vegas, NV, USA, 26 June–1 July 2015; pp. 5353–5360. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Barbella, G.; Perotti, F.; Simoncini, V. Block Krylov subspace methods for the computation of structural response to turbulent wind. Comput. Methods Appl. Mech. Eng. 2011, 200, 2067–2082. [Google Scholar] [CrossRef]
- Eftekhar Azam, S.; Mariani, S. Investigation of computational and accuracy issues in POD-based reduced order modeling of dynamic structural systems. Eng. Struct. 2013, 54, 150–167. [Google Scholar] [CrossRef]
- Capellari, G.; Chatzi, E.; Mariani, S. Structural Health Monitoring Sensor Network Optimization through Bayesian Experimental Design. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04018016. [Google Scholar] [CrossRef]
- European Commitee for Standardization. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Bruxelles, Belgium, 2003; pp. 66–74. [Google Scholar]
- Corigliano, A.; Mariani, S. Parameter identification in explicit structural dynamics: Performance of the extended Kalman filter. Comput. Methods Appl. Mech. Eng. 2004, 193, 3807–3835. [Google Scholar] [CrossRef]
- Pandey, A.; Biswas, M. Damage Detection in Structures Using Changes in Flexibility. J. Sound Vib. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Yang, C.; Liang, K.; Zhang, X. Strategy for sensor number determination and placement optimization with incomplete information based on interval possibility model and clustering avoidance distribution index. Comput. Methods Appl. Mech. Eng. 2020, 366, 113042. [Google Scholar] [CrossRef]
- Falkner, S.; Klein, A.; Hutter, F. BOHB: Robust and Efficient Hyperparameter Optimization at Scale. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1437–1446. [Google Scholar]
- Clough, R.W.; Penzien, J.; Griffin, D. Dynamics of Structures; American Society of Mechanical Engineers Digital Collection. 1977. Available online: https://asmedigitalcollection.asme.org/ (accessed on 28 March 2020).
- Severini, T.A. Elements of Distribution Theory; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar] [CrossRef]
- Hazra, B.; Sadhu, A.; Roffel, A.J.; Narasimhan, S. Hybrid Time-Frequency Blind Source Separation Towards Ambient System Identification of Structures. Comput. Aided Civ. Infrastruct. Eng. 2012, 27, 314–332. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Behkamal, B.; Mariani, S. Big Data Analytics and Structural Health Monitoring: A Statistical Pattern Recognition-Based Approach. Sensors 2020, 20, 2328. [Google Scholar] [CrossRef] [PubMed]




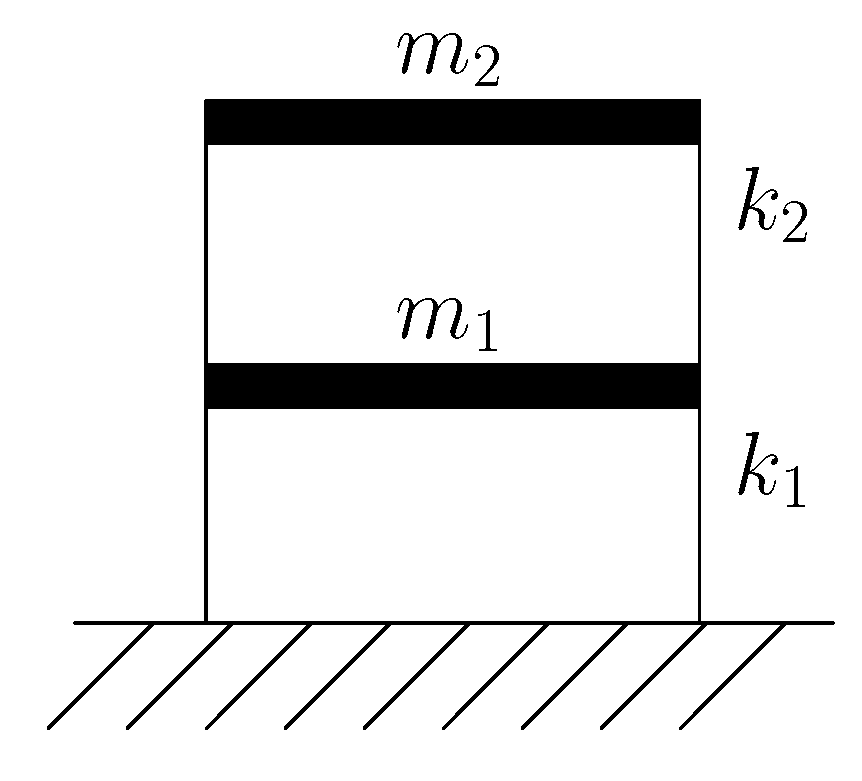



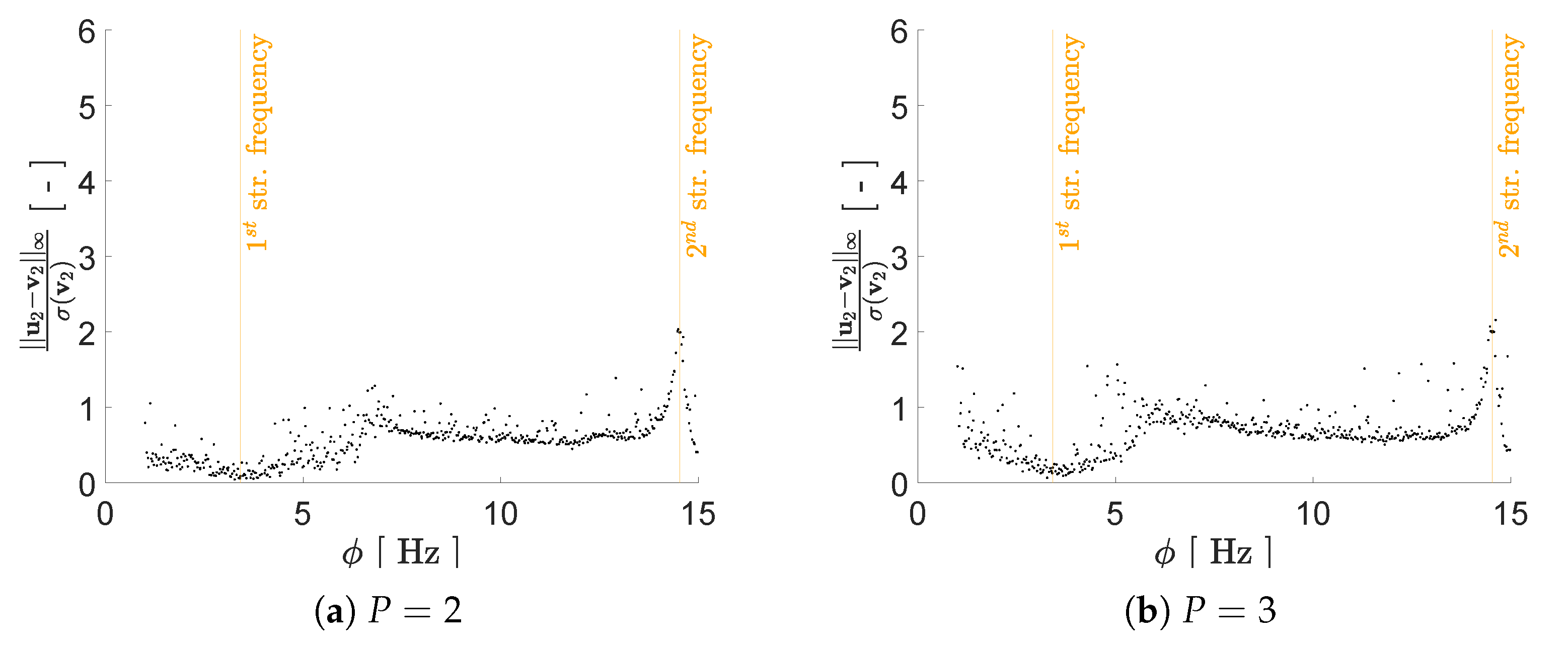
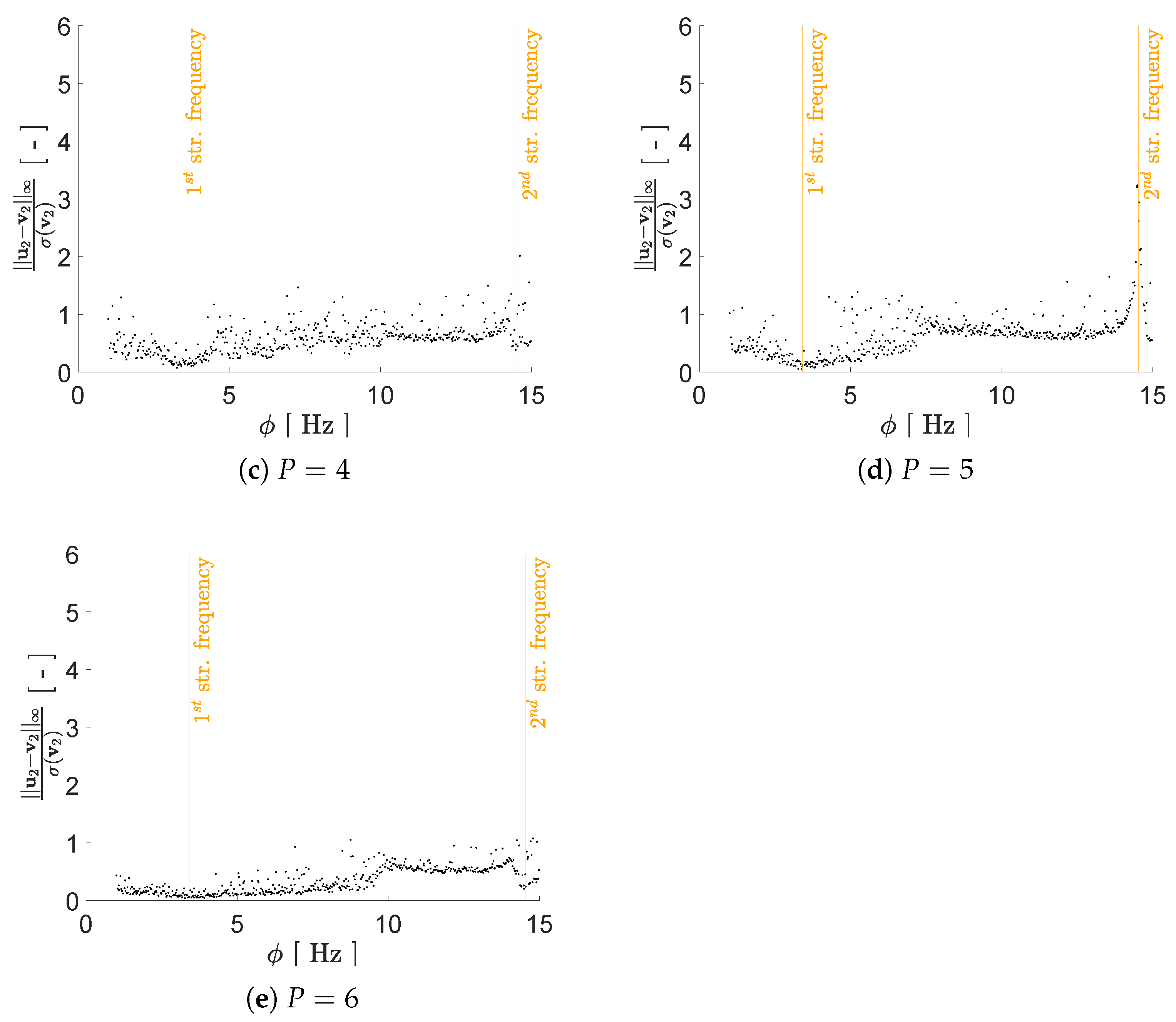
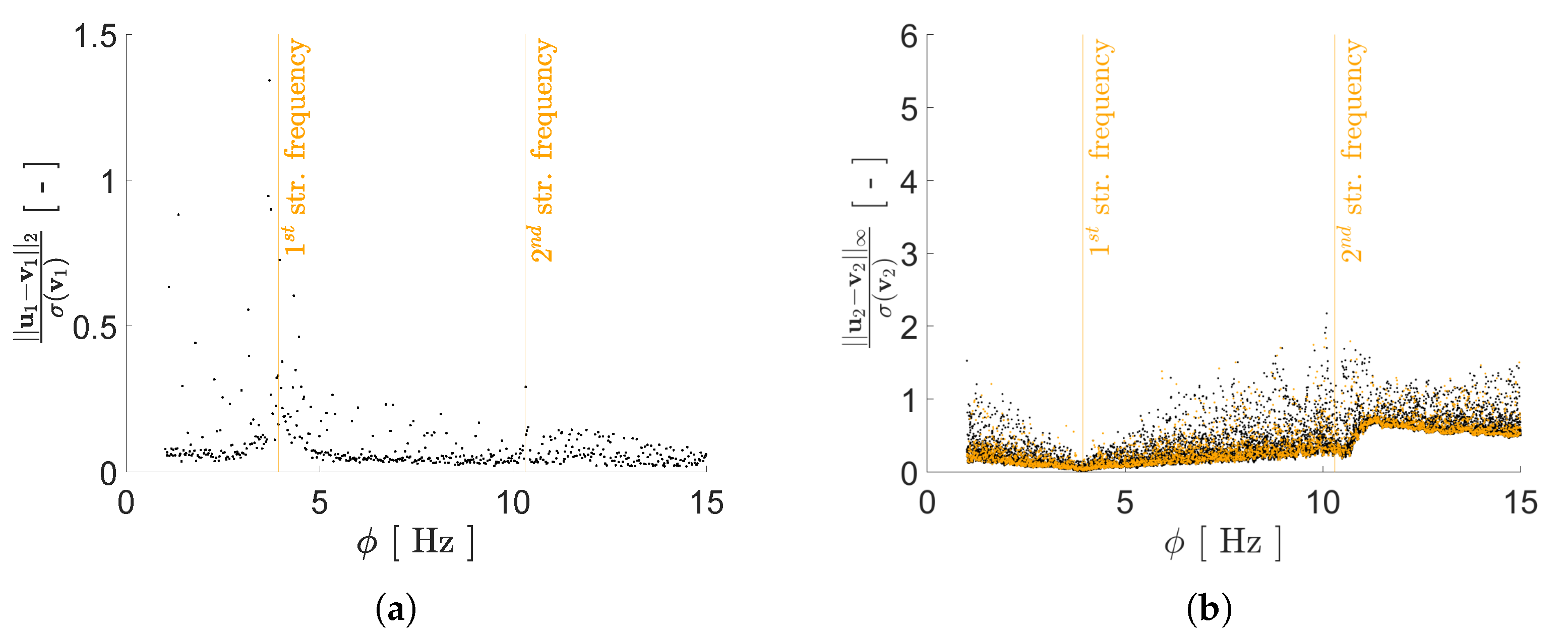



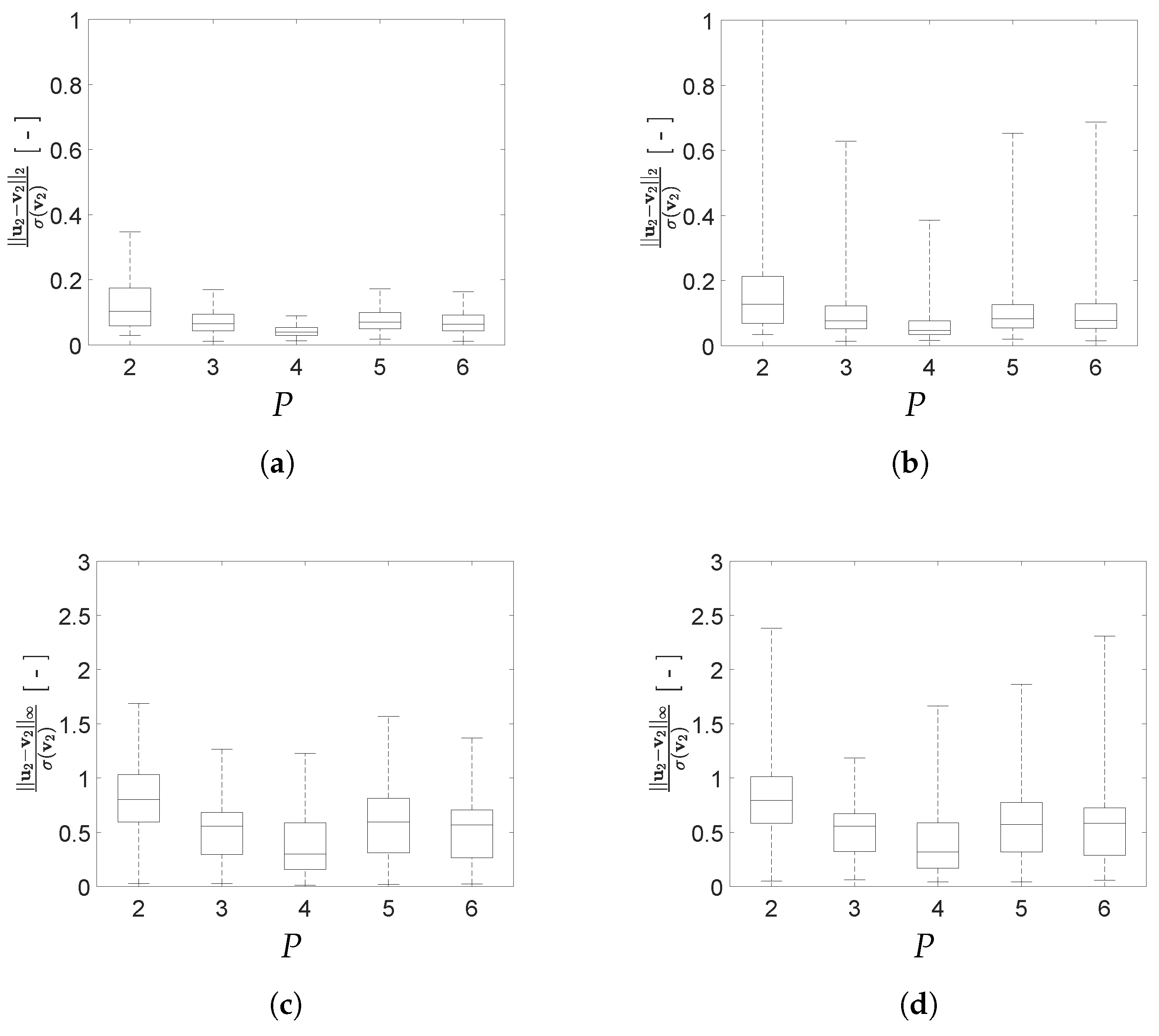

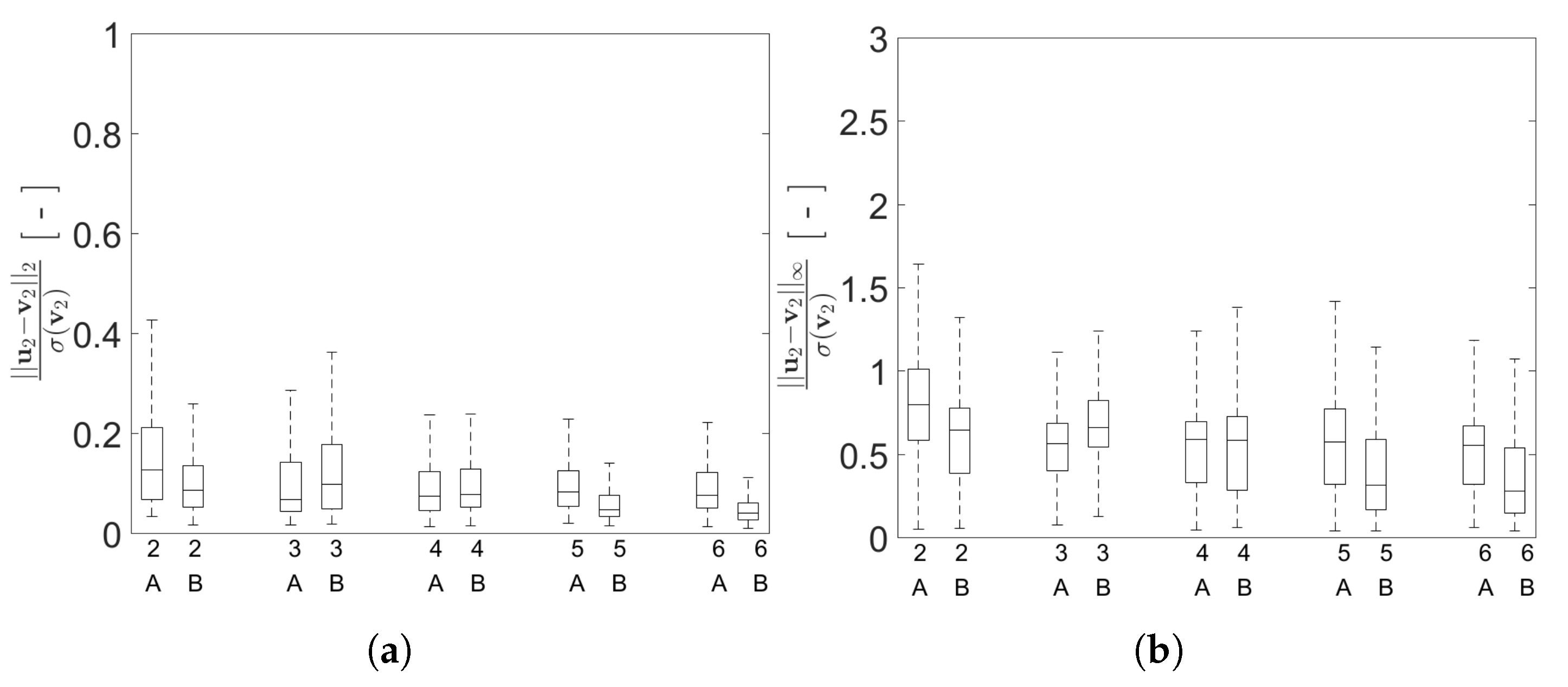




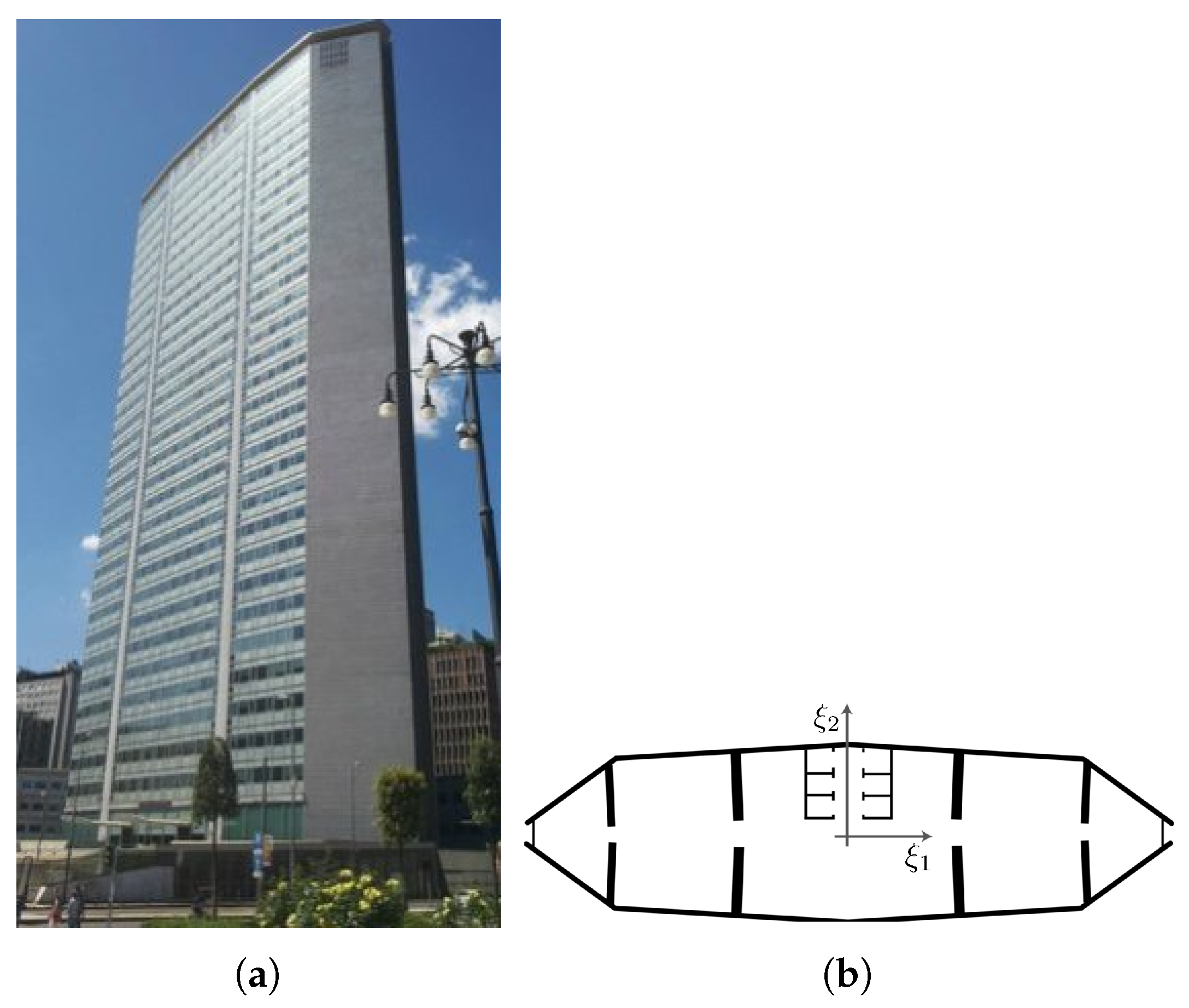



| Configuration A | Configuration B | ||
|---|---|---|---|
| (ton) | 625, 625 | 625, 1250 | |
| () | |||
| (Hz) | 3.93, 10.3 | 3.41, 14.5 |
| standardized norm | |
| standardized norm |
| Encoder | Decoder | ||
|---|---|---|---|
| P | ||||
|---|---|---|---|---|
| RMSE [N] | [-] | RMSE [Hz] | [-] | |
| 2 | 1263 | 0.654 | 1.74 | 0.912 |
| 3 | 1243 | 0.717 | 1.11 | 0.963 |
| 4 | 552 | 0.941 | 0.69 | 0.987 |
| 5 | 1004 | 0.803 | 1.16 | 0.960 |
| 6 | 769 | 0.897 | 1.28 | 0.966 |
| Vibration Mode | Frequency |
|---|---|
| 1 | 0.25 |
| 2 | 1.08 |
| 3 | 2.60 |
| 4 | 4.71 |
| 5 | 7.06 |
| 6 | 8.79 |
| 7 | 9.56 |
| 8 | 9.91 |
| 9 | 11.38 |
| 10 | 13.36 |
| 11 | 14.64 |
| 12 | 18.30 |
| 13 | 22.14 |
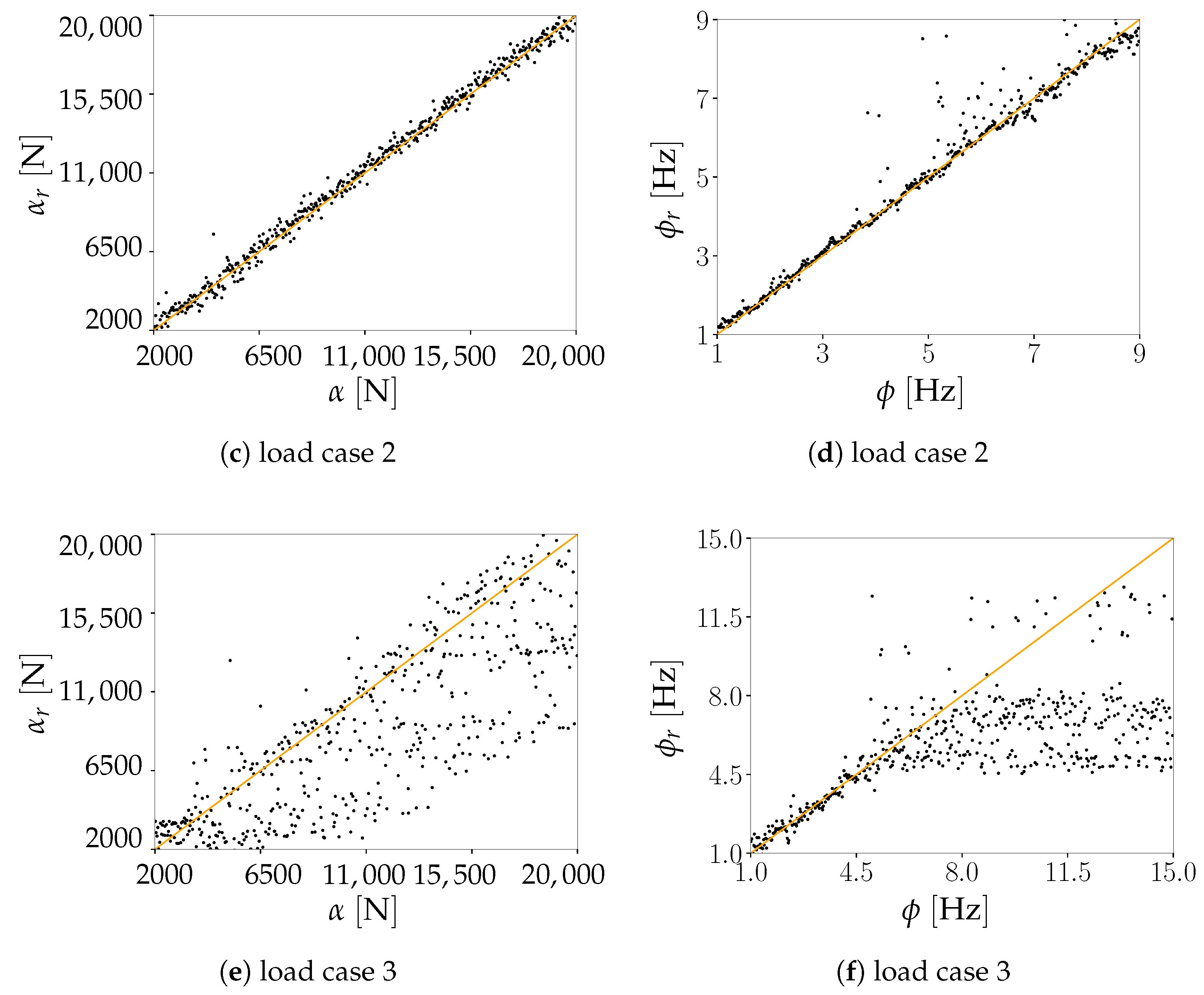
| Load | ||||
|---|---|---|---|---|
| Case | RMSE [N] | [-] | RMSE [Hz] | [-] |
| 1 | 469 | 0.996 | 0.144 | 0.998 |
| 2 | 439 | 0.997 | 0.417 | 0.984 |
| 3 | 3852 | 0.808 | 3.758 | 0.679 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosafalco, L.; Manzoni, A.; Mariani, S.; Corigliano, A. An Autoencoder-Based Deep Learning Approach for Load Identification in Structural Dynamics. Sensors 2021, 21, 4207. https://doi.org/10.3390/s21124207
Rosafalco L, Manzoni A, Mariani S, Corigliano A. An Autoencoder-Based Deep Learning Approach for Load Identification in Structural Dynamics. Sensors. 2021; 21(12):4207. https://doi.org/10.3390/s21124207
Chicago/Turabian StyleRosafalco, Luca, Andrea Manzoni, Stefano Mariani, and Alberto Corigliano. 2021. "An Autoencoder-Based Deep Learning Approach for Load Identification in Structural Dynamics" Sensors 21, no. 12: 4207. https://doi.org/10.3390/s21124207
APA StyleRosafalco, L., Manzoni, A., Mariani, S., & Corigliano, A. (2021). An Autoencoder-Based Deep Learning Approach for Load Identification in Structural Dynamics. Sensors, 21(12), 4207. https://doi.org/10.3390/s21124207








