Spatial Domain Terahertz Image Reconstruction Based on Dual Sparsity Constraints
Abstract
1. Introduction
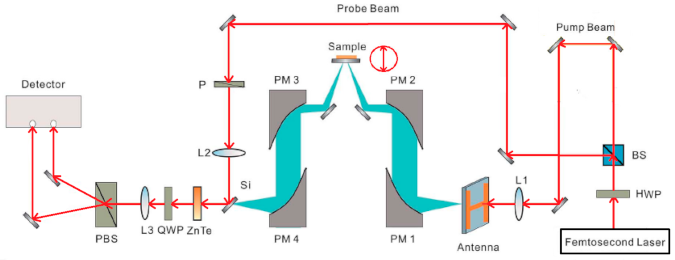
2. Spatial Domain Signal Model of THz-TDS System
3. The Proposed DSC-THz Imaging Method
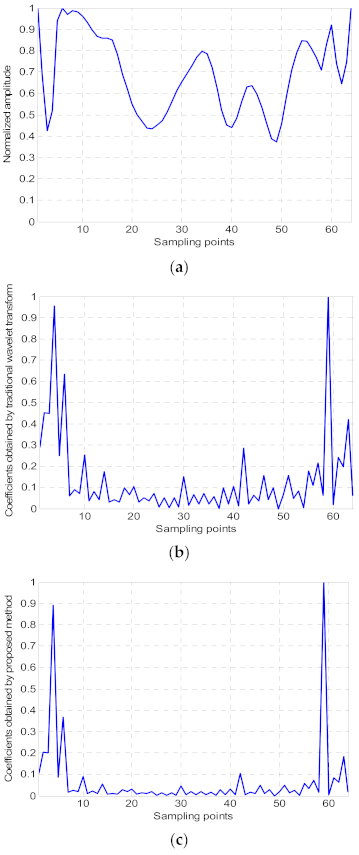
3.1. Proposed DSC-THz Model
3.2. The Proposed Algorithm
| Algorithm 1. Proposed DSC-THz Imaging Algorithm |
| Input: measurement y, measurement matrix R, exponential shift invariant wavelet basis We, horizontal gradient operator , vertical gradient operator . Initialization: ,,,, Loop: set and repeat until () End loop Output: reconstructed terahertz image x. |
3.3. Convergence Analysis
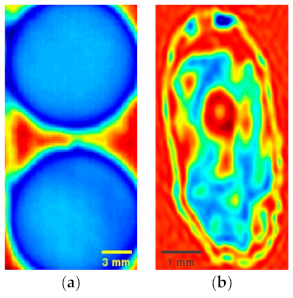
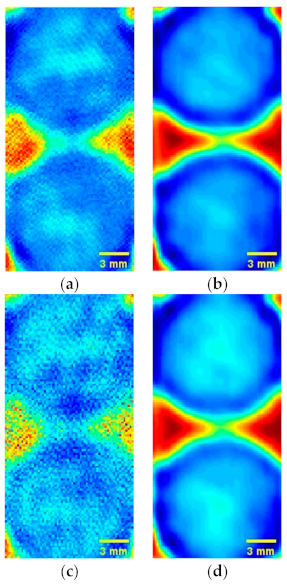
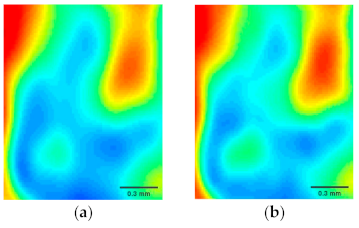
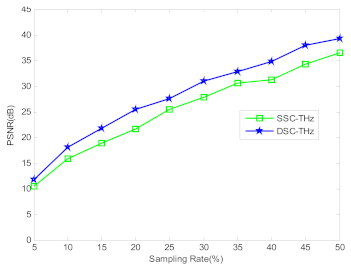
4. Experiments and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mittleman, D.M. Twenty years of terahertz imaging. Opt. Express 2018, 26, 9417–9431. [Google Scholar] [CrossRef] [PubMed]
- Zanotto, L.; Piccoli, R.; Dong, J.; Morandotti, R.; Razzari, L. Single-pixel terahertz imaging: A review. Opto-Electron. Adv. 2020, 3, 20001201–20001215. [Google Scholar] [CrossRef]
- Stantchev, R.I.; Yu, X.; Blu, T.; Pickwell-MacPherson, E. Real-time terahertz imaging with a single-pixel detector. Nat. Commun. 2020, 11, 2535. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Son, J.-H.; Ahn, C.-B. Enhancement of terahertz reflection tomographic imaging by interference cancellation between layers. Opt. Express 2016, 24, 7028–7036. [Google Scholar] [CrossRef]
- Zhai, M.; Locquet, A.; Citrin, D. Pulsed THz imaging for thickness characterization of plastic sheets. NDT E Int. 2020, 116, 102338. [Google Scholar] [CrossRef]
- Redo-Sanchez, A.; Heshmat, B.; Aghasi, A.; Naqvi, S.; Zhang, M.; Romberg, J.; Raskar, R. Terahertz time-gated spectral imaging for content extraction through layered structures. Nat. Commun. 2016, 7, 12665. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, H.; Xia, R.; Liu, Q.; Zhao, B.Y. Time Segmented Image Fusion Based Multi- Depth Defects Imaging Method in Composites With Pulsed Terahertz. IEEE Access 2020, 8, 155529–155537. [Google Scholar] [CrossRef]
- Gowen, A.; O’Sullivan, C.; O’Donnell, C. Terahertz time domain spectroscopy and imaging: Emerging techniques for food process monitoring and quality control. Trends Food Sci. Technol. 2012, 25, 40–46. [Google Scholar] [CrossRef]
- Guerboukha, H.; Nallappan, K.; Skorobogatiy, M. Toward real-time terahertz imaging. Adv. Opt. Photonics 2018, 10, 843–938. [Google Scholar] [CrossRef]
- D’Arco, A.; Di Fabrizio, M.; Dolci, V.; Petrarca, M.; Lupi, S. THz Pulsed Imaging in Biomedical Applications. Condens. Matter 2020, 5, 25. [Google Scholar] [CrossRef]
- Park, J.Y.; Choi, H.J.; Cheon, H.; Cho, S.W.; Lee, S.; Son, J.-H. Terahertz imaging of metastatic lymph nodes using spectroscopic integration technique. Biomed. Opt. Express 2017, 8, 1122–1129. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhang, X.-C. Terahertz imaging via electrooptic effect. IEEE Trans. Microw. Theory Tech. 1999, 47, 2644–2650. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.-C. Terahertz wave reciprocal imaging. Appl. Phys. Lett. 2006, 88, 151107. [Google Scholar] [CrossRef]
- Chan, W.L.; Moravec, M.L.; Baraniuk, R.G.; Mittleman, D. Terahertz imaging with compressed sensing and phase retrieval. Opt. Lett. 2008, 33, 974–976. [Google Scholar] [CrossRef]
- Chan, W.L.; Charan, K.; Takhar, D.; Kelly, K.F.; Baraniuk, R.G.; Mittleman, D. A single-pixel terahertz imaging system based on compressed sensing. Appl. Phys. Lett. 2008, 93, 121105. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, X.; Zhong, J. Single-pixel imaging by means of Fourier spectrum acquisition. Nat. Commun. 2015, 6, 6225. [Google Scholar] [CrossRef]
- Yee, D.-S.; Jin, K.H.; Yahng, J.S.; Yang, H.-S.; Kim, C.Y.; Ye, J.C. High-speed terahertz reflection three-dimensional imaging using beam steering. Opt. Express 2015, 23, 5027–5034. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, X.-K.; Sun, W.-F.; Feng, S.-F.; Ye, J.-S.; Han, P.; Zhang, Y. Reflective Single-Pixel Terahertz Imaging Based on Compressed Sensing. IEEE Trans. Terahertz Sci. Technol. 2020, 10, 495–501. [Google Scholar] [CrossRef]
- Cho, S.-H.; Lee, S.-H.; Nam-Gung, C.; Oh, S.-J.; Son, J.-H.; Park, H.; Ahn, C.-B. Fast terahertz reflection tomography using block-based compressed sensing. Opt. Express 2011, 19, 16401–16409. [Google Scholar] [CrossRef]
- Hwang, B.-M.; Lee, S.H.; Lim, W.-T.; Ahn, C.-B.; Son, J.-H.; Park, H. A Fast Spatial-domain Terahertz Imaging Using Block-based Compressed Sensing. J. Infrared Millim. Terahertz Waves 2011, 32, 1328–1336. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing Sparsity by Reweighted l(1) Minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A New Alternating Minimization Algorithm for Total Variation Image Reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhang, Y.; Peterson, B.S.; Dong, Z. Increasing sparsity in compressed sensing MRI by exponent of wavelet coefficients. In Proceedings of the 19th Annual Meeting of ISMRM, Melbourne, Australia, 1 January 2012; p. 5885. [Google Scholar]
- Goldstein, T.; Osher, S. The Split Bregman Method for L1-Regularized Problems. SIAM J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Li, L.; Xiao, S.; Zhao, Y. Image Compressive Sensing via Hybrid Nonlocal Sparsity Regularization. Sensors 2020, 20, 5666. [Google Scholar] [CrossRef] [PubMed]
- Yin, W.; Osher, S.; Goldfarb, D.; Darbon, J. Bregman iterative algorithms for l1-minimization with applications to compressed sensing. SIAM J. Imaging Sci. 2008, 1, 142–168. [Google Scholar] [CrossRef]
- Cai, J.-F.; Osher, S.; Shen, Z. Linearized Bregman iterations for compressed sensing. Math. Comput. 2009, 78, 1515–1536. [Google Scholar] [CrossRef]
- Cai, J.-F.; Osher, S.; Shen, Z. Linearized Bregman Iterations for Frame-Based Image Deblurring. SIAM J. Imaging Sci. 2009, 2, 226–252. [Google Scholar] [CrossRef]
- Zou, J.; Li, H.; Li, G. Split Bregman Algorithm for Structured Sparse Reconstruction. IEEE Access 2018, 6, 21560–21569. [Google Scholar] [CrossRef]
- Taylor, Z.D.; Singh, R.S.; Culjat, M.O.; Suen, J.Y.; Grundfest, W.S.; Lee, H.; Brown, E.R. Reflective terahertz imaging of porcine skin burns. Opt. Lett. 2008, 33, 1258–1260. [Google Scholar] [CrossRef]
- Jiang, Y.; Ge, H.; Lian, F.; Zhang, Y.; Xia, S. Discrimination of moldy wheat using terahertz imaging combined with multivariate classification. RSC Adv. 2015, 5, 93979–93986. [Google Scholar] [CrossRef]
- Kim, K.W.; Kim, K.S.; Kim, H.; Lee, S.H.; Park, J.H.; Han, J.H.; Seok, S.H.; Park, J.; Choi, Y.; Kim, Y.I.; et al. Terahertz dynamic imaging of skin drug absorption. Opt. Express 2012, 20, 9476–9484. [Google Scholar] [CrossRef] [PubMed]
- Karpowicz, N.; Zhong, H.; Xu, J.; Lin, K.-I.; Hwang, J.-S.; Zhang, X.-C. Comparison between pulsed terahertz time-domain imaging and continuous wave terahertz imaging. Semicond. Sci. Technol. 2005, 20, S293–S299. [Google Scholar] [CrossRef]
- Tewari, P. Reflective Terahertz Imaging for Early Diagnosis of Skin Burn Severity; University of California: Los Angeles, CA, USA, 2013. [Google Scholar]
- Hale, E.T.; Yin, W.T.; Zhang, Y. A fixed-point continuation method for l1-regularized minimization with applications to compressed sensing. SIAM J. Optim. 2008, 19, 1107–1130. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Jiang, Y. Spatial Domain Terahertz Image Reconstruction Based on Dual Sparsity Constraints. Sensors 2021, 21, 4116. https://doi.org/10.3390/s21124116
Ren X, Jiang Y. Spatial Domain Terahertz Image Reconstruction Based on Dual Sparsity Constraints. Sensors. 2021; 21(12):4116. https://doi.org/10.3390/s21124116
Chicago/Turabian StyleRen, Xiaozhen, and Yuying Jiang. 2021. "Spatial Domain Terahertz Image Reconstruction Based on Dual Sparsity Constraints" Sensors 21, no. 12: 4116. https://doi.org/10.3390/s21124116
APA StyleRen, X., & Jiang, Y. (2021). Spatial Domain Terahertz Image Reconstruction Based on Dual Sparsity Constraints. Sensors, 21(12), 4116. https://doi.org/10.3390/s21124116




