Abstract
The use of heart rate variability (HRV) in research has been greatly popularized over the past decades due to the ease and affordability of HRV collection, coupled with its clinical relevance and significant relationships with psychophysiological constructs and psychopathological disorders. Despite the wide use of electrocardiograms (ECG) in research and advancements in sensor technology, the analytical approach and steps applied to obtain HRV measures can be seen as complex. Thus, this poses a challenge to users who may not have the adequate background knowledge to obtain the HRV indices reliably. To maximize the impact of HRV-related research and its reproducibility, parallel advances in users’ understanding of the indices and the standardization of analysis pipelines in its utility will be crucial. This paper addresses this gap and aims to provide an overview of the most up-to-date and commonly used HRV indices, as well as common research areas in which these indices have proven to be very useful, particularly in psychology. In addition, we also provide a step-by-step guide on how to perform HRV analysis using an integrative neurophysiological toolkit, NeuroKit2.
1. Heart Rate Variability for Psychologists: A Review of HRV Metrics and an Analysis Tutorial
A complex and constantly changing heart rate (HR) is an indicator of healthy regulatory systems that can effectively adapt to sudden environmental and psychological challenges [1,2,3,4,5]. Thus, reduced heart rate variability (HRV) has not only been associated with poor cardiovascular health outcomes [6,7,8] and a range of vascular diseases [4,9,10], but also with different mental disorders and cognitive impairments [8,11,12,13,14,15,16,17].
The physiological mechanism underlying HRV exemplifies the tight, yet complex coupling between the brain and the body. Heartbeats are initiated by the impulse generated from the sinoatrial (SA) node—a bundle of specialized cells in the heart. The SA node, dictating the rhythm of heart contractions, is in turn controlled by the complex interactions between different regulatory systems and mechanical activities such as respiration. As the interdependent sources of HR operate on different time scales, HRV is itself unevenly distributed in different frequency bands, with high and low frequency changes corresponding to different neurophysiological mechanisms. Rapid changes of HR reflect the cardiac regulatory influences of the autonomic nervous system (ANS), in tandem with its dynamic interaction with cardiovascular and respiratory activities [10,18,19,20]. On the other hand, slow HR changes reflect bodily fluctuations of lower frequency, such as circadian rhythms, sleep cycles, metabolism, and changes in body temperature and hormonal systems.
The autonomic nervous system (ANS), which influences HR on short-time intervals, is subdivided into two distinct components, namely the sympathetic (SNS) and the parasympathetic nervous system (PNS). The SNS, known as the “quick response” system, predominates during elevated activity and stressful states and its stimulation results in an increase in HR. The PNS, known as the “relaxed response” system, predominates in the quiet and relaxing states, and is related to a decrease in HR. In healthy individuals, the two systems work together (promptly alternating between each other) to maintain the regulatory balance in physiological autonomic function.
In addition to the neural contributions of the two ANS systems, the short-term periodic changes of HR are also influenced by the cyclic activation of the baroreceptors—a mechanical sensor that works to maintain a homeostatic level of blood pressure [21]. When there is an increase in blood pressure, baroreceptors fire to decrease HR and increase the diameter of blood vessels, which subsequently brings the blood pressure back to normal. The opposite effect is observed when the blood pressure decreases. This ability of the body to regulate blood pressure is referred to as baroreflex. The stronger the baroreflex, the more frequently our HR is adjusted to maintain a stable level of blood pressure. Thus, a stronger baroreflex is associated with greater HRV.
The baroreflex is also the autonomic reflex that underlies the physiologic interactions between the cardiovascular and respiratory systems. Specifically, the arterial baroreceptors are also affected by breathing (arterial pressure decreases during inhalation and increases during exhalation), which results in variation in HR during each breathing cycle. This specific influence of respiration on HRV is referred to as respiratory sinus arrhythmia (RSA). RSA can be seen as one of the aspects of HRV and encapsulates the coupling between respiratory and cardiac activity. It has been measured via the proxy of specific HRV indices sensitive to the variability in the respiratory frequency band (e.g., in [22]). However, RSA-specific metrics, which usually require the respiratory signal to quantify selectively the variability related to breathing, provide a more accurate measure of RSA [23].
Due to the different time scales and frequencies at which different systems influence HR, the duration of the cardiac activity recordings naturally limits the sources of variability that can be quantified. While short recordings of 5 min or less can effectively capture high-frequency HRV, long-term recordings of at least 24 h are needed to reliably assess lower-frequency components [18,20]. As long-term recordings capture changes across more diverse situations, they are more reflective of the general state of the system and have been found to be more predictive of health outcomes [24,25,26,27]. However, due to practical considerations, there is a strong interest regarding the reliability (and validity) of indices computed from shorter recordings.
Recent evidence suggests that some HRV indices obtained with time windows as short as 10–30 s are as reliable as short-term HRV indices obtained from more typical (i.e., 5 min or more) recording lengths [28,29,30,31,32,33]. However, this only applies to some “types” of HRV metrics, namely time-domain indices, rather than frequency-domain indices (which require at least 1 min) [33,34] or non-linear indices. Other metrics, specifically targeting long-term changes, can require as long as 24 h of recording to capture the mechanisms of interest. We will discuss these different types of HRV indices in the following section.
2. HRV Indices
When HRV was first recognized as a potential indicator of ANS abnormalities [35], the main method used to quantify it was to measure the amount of variance in inter-beat intervals (IBI)—the time intervals between successive heartbeats. In 1981, Akselrod et al. [36] introduced the power spectral analysis of HR to assess the power (or energy) found within different frequency bands. As different regulatory systems influence HRV at different frequencies, frequency-domain measures allow the assessment of their unique contributions to changes of HR. A few years later, L. Cohen [37] introduced the time-frequency domain measures to capture both the time and frequency variabilities simultaneously. In the same decade, Goldberger and West [38] argued that the HR signal was not simply a product of a regular periodic oscillator; instead, it displayed characteristics of a deterministic chaos—a seemingly random sequence of events with an underlying structure [39,40]. Therefore, in order to capture the complex non-linear dynamic behaviors of the “chaotic” fluctuations of HR, new analytical approaches based on entropy and fractal dimensions were proposed [40,41,42,43]. Since then, the evolution of HRV research has been associated with the emergence of new and supposedly better indices or approaches to quantify and reliably assess HRV, making it a rapidly evolving field heavily connected to mathematical and computational developments.
3. Time-Domain Analysis
Time-domain measures reflect the total variability of HR and are relatively indiscriminate when it comes to precisely quantifying the respective contributions of different underlying regulatory mechanisms [44]. However, this “general” sensitivity can be seen as a positive feature (e.g., in exploratory studies or when specific underlying neurophysiological mechanisms are not the focus). Moreover, as they are easy to compute and interpret, time-domain measures are still among the most commonly reported HRV indices.
4. Deviation-Based Indices
SDNN, measured in the unit of milliseconds (ms), is the standard deviation of the normal beat intervals (denoted NN intervals), i.e., excluding beats related to technical artefacts and physiological artefacts (e.g., similar to ectopic beats—beats that do not arise from SA node depolarizations—and atrial fibrillation). Mathematically, SDNN is the square root of the total variance in the entire recording and, therefore, it encompasses both short-term high frequency variation (mostly due to parasympathetically-mediated RSA [20]) and long-term low frequency components of the HR signals. Some proponents argue that the accuracy of SDNN is higher for longer recording periods, especially over 24 h periods where values of SDNN have been used for cardiac risk stratification in medical settings [20].
Stemming from the concept of SDNN, there are other statistical variables that similarly capture the variance of NN but in a more fine-grained manner. Firstly, the standard deviation of average NN is extracted for each 5 min segment of the long-term HR time series (e.g., 24 h recordings) (SDANN). It is highly correlated with SDNN and has been said to provide little additional information beyond what SDNN is able to [20]. On the other hand, the SDNN index (SDNNI) is the mean of the standard deviations of NN calculated per 5 min segment [20]. While SDANN is an estimate of long-term components contributing to HRV, SDNNI assesses the variability within the short intervals and hence is an estimate of short-term components that modulate HR signals.
While these traditional indices have been recommended by official guidelines [18] and have been extensively used in past research, new metrics are being explored in parallel with the development of the mathematics and statistics fields. Some of them involve certain forms of normalization, such as the Coefficient of Variation of NN (CV), i.e., the ratio of the standard deviation to the mean, which could be more stable when comparing individuals or conditions with different HR baselines [45]. Others involve “robust” alternatives to traditional dispersion indices, such as the Median Absolute Deviation (MAD; a median-based index of variability) or the interquartile range (IQR), that are less influenced by outliers and, thus, less sensitive to measurement errors [46,47].
5. Difference-Based Indices
While the aforementioned indices are calculated directly from the NN sequence, other approaches are derived from the difference between successive NN intervals. These measures include the standard deviation of the successive difference (SDSD), the root mean square of successive difference (RMSSD), the proportion of successive NN intervals that are larger than a given threshold (e.g., 20 ms or 50 ms—pNN20 and pNN50, respectively). As these measures are derived from beat-to-beat differences, they are mostly indicative of short-term variations in HR.
Among the highly correlated difference-based indices, RMSSD is generally preferred by researchers due to its better statistical properties [18,48]. As compared to SDNN, RMSSD is more influenced by the PNS activity and hence is often used to estimate the vagally mediated fluctuations in HR [19,48]). Its statistical robustness makes it well-suited for short-term time windows [30,33,49].
6. Geometric Indices
HRV can also be quantified from geometric (i.e., graphical) representations of NN, in the form of histograms and scatter plots. Such indices include, among others, the HRV triangular index (HTI), the triangular interpolation of NN histogram (TTIN) and other geometrical properties of the NN scatter plots (e.g., Lorenz plots). While geometric methods are less sensitive to measurement errors as compared to basic dispersion-based indices [50], a large number of NN intervals is required for reliable assessment. Therefore, even though 5 min recordings have successfully been used in past research [51], recordings of at least 20 min are recommended for accurate computation [18].
7. Frequency-Domain Analysis
As the different regulatory systems modulate HR at distinct frequencies, frequency-domain indices that reflect the distribution of power across different frequencies bands are particularly suited to assess the specific components of HRV. According to Force [18], the HRV power spectrum can be meaningfully divided into four bands: ultra-low frequency (ULF; ≤0.003 Hz), very low frequency (VLF; 0.0033–0.04 Hz), low frequency (LF; 0.04–0.15 Hz) and high frequency (HF; 0.15–0.4 Hz).
Generally, due to the inherent differences in their signaling mechanisms, the parasympathetic (vagal) modulation of HR, including RSA, is faster than the sympathetic activities. Thus, research suggests that HF and LF are prominent reflections of parasympathetic and sympathetic activity, respectively [44,52]. The ratio of LF to HF power (LF/HF) has also been commonly used as an index of the sympathovagal balance—a measure of the relative contributions of SNS to PNS activity.
HF component is relatively established as an index of the parasympathetic modulation of HR and under controlled conditions, its derivative, LnHF (the natural logarithm of HF) as an estimator of vagal tone [20,44]. However, the concept of tagging a frequency component to a particular division of ANS activities has been controversial for other components. Particularly, the interpretation of LF power as an index of sympathetic activities has been repeatedly challenged. In contrast to the assumption that LF power dominantly represents the sympathetic component, research has shown that it is modulated by both ANS branches as well as baroreceptor activities [18,44,53,54]. There are also mixed findings regarding the exact physiological mechanisms underlying ULF and VLF components [20,27], with the former often being associated with very low-frequency biological processes such as circadian rhythms or metabolisms [55,56] and the latter with body temperature regulation and vasomotor activity [57,58,59].
Another limitation of the frequency-domain approach is pertaining to the inherent differences in the outputs of different spectral analysis algorithms, which make it difficult to compare the absolute values of frequency components across studies [18,60]. For instance, a non-parametric method such as the fast Fourier transform (FFT) periodogram has been argued to overestimate the LF/HF as compared to the Lomb–Scargle (LS) periodogram [60]. Even with the same algorithm, the values of the frequency components can greatly vary depending on the choices of the parameters such as the length of the estimation window or the model order [61].
To allow for more reliable comparison of frequency components across studies, the spectral indices are often normalized by dividing the individual component by the total power. The normalization process allows the normalized components (normalized LF, LFn and normalized HF, HFn) to be less varied by the methodological differences and less sensitive to the changes in total power [18,62]. Depending on the length of the recording, the normalizing denominator (total power) can be with or without the ULF component (sum of power includes ULF, VLF, LF and HF for 24 recordings, and includes VLF, LF and HF for short-term recordings [20]). Even though the normalized spectral HRV indices can be interpreted in the same manner as the absolute values, the general guideline recommends reporting the low-frequency and high-frequency components in both absolute (e.g., LF, HF) and normalized forms (e.g., LFn, HFn) to present a complete picture of the power distribution [18].
8. Time-Frequency Methods of Analysis
The spectral analysis algorithms used in frequency-domain approaches can only compute the power spectrum density (PSD) over the entire recording, failing to account for the temporal variation of the frequency components. To address this limitation, tools to simultaneously capture both time and frequency changes (i.e., a time-frequency approach, TF), have been proposed [37,63]. By evaluating the frequency spectrum over short moving windows, TF methods quantify the instantaneous PSD at any given time [19]. The TF methods include, among others, linear approaches such as the short-time Fourier transform (STFT), the wavelet transform, and quadratic approaches such as the Wigner–Ville distribution (WVD).
As it allows for the integration over both the time and frequency domain, the TF HRV indices usually include the maximum and minimum energy of the time windows in HR signal, the standard deviation between energy of time windows, the total energy of signal in different frequency bands (e.g., energy of VLF, LF or HF), and the corresponding average energy of each band (derived by dividing total energy by length of band). While the TF approaches are believed to be more informative since they provide a means to quantitatively assess the changes in frequency components across time, they are not as widely used as other domains. One current limiting factor is that some of them are computationally expensive, while others, being easier to compute, can hardly provide high accuracy in both time and frequency domains [64,65]. The appeal of TF approaches could be greatly enhanced by addressing these technical challenges, together with future works that investigate the interpretations of relevant TF features extracted from the time-varying spectrum.
9. Non-Linear Dynamics
Recent research has emphasized non-linear interactions of physiological systems underlying cardiovascular regulation [66]. Hence, HRV indices derived from non-linear methods were proposed to adequately characterize the dynamical properties of HR that other methods are unable to [18].
10. Poincaré Plot
The Poincaré plot, whose principles were derived from nonlinear dynamics theory, is one of the most common methods to measure non-linear HRV [67]. It corresponds to a scatterplot of each NN interval plotted against its corresponding preceding interval, which approximates the cardiac system’s evolution [68]. The points are dispersed around the identity line and converge into an ellipsoid configuration. Points above the line represent HR decelerations (NN intervals that are longer than preceding ones) and points below the line of identity indicate HR accelerations [69].
Qualitatively, the Poincaré plot’s shape provides a visual summary of the heart’s behavior [67]. From the plot, outliers such as premature heartbeats and other technical artefacts can be easily removed, something which cannot be done with spectral and most time-domain analyses. On a quantitative level, indices extracted from the plot correspond to time-domain indices. SD1 is the standard deviation of points perpendicular to the identity line and is equivalent to RMSSD [48], describing short-term NN variability. SD2 is the standard deviation of points parallel to the line of identity and is equivalent to SDNN, representing long-term NN variability. The former reflects short-term vagal activity whereas the latter represents sympathetic modulation. A third index, SD1/SD2, describes the ratio of short to long-term variations in NN interval fluctuations and reflects sympathovagal balance [70]. SD1/SD2 has been shown to additionally capture complexity in HR patterns (e.g., healthy heart displays a “comet” shaped Poincaré plot while cardiac abnormalities display atypical “fan” or “complex” shapes [71,72,73]). However, SD1/SD2 seems to be sensitive to the time lag used, with some recent research recommending a lag of five or six heartbeats [72,74]. Nevertheless, there is no consensus on the optimal time lag yet, which itself could be subject to inter-individual differences.
11. Entropy
Entropy-based methods find their roots in information theory in which they are conceptualized as measures of complexity (or “unpredictability”) of a signal. While they originated from fields of thermodynamics [75], their applications have expanded towards the quantification of complexity in physiological systems and have been used widely as a diagnostic tool in biomedicine. The underlying concept of entropy is that it quantifies repetitions of patterns in a signal, with greater entropy indicating higher randomness and unpredictability (and thus, complexity) and lower entropy values implying that the cardiac system is predictable, (i.e., periodic and does not produce much new information) [76]. Common entropy-based methods include approximate entropy (ApEn) [77], sample entropy (SampEn) [78], and multiscale entropy (MSE) [79]. SampEn was built on ApEn [78] and addresses the latter’s tendency to overestimate the amount of regularity in the signal [75,80,81], being in turn more consistent in measuring complexity across different time series lengths [67]. However, another important difference is that ApEn computes regularity based on short time sequences whereas SampEn considers the entire time series [75]. Consequently, ApEn might be better suited to capture short-term HRV changes than SampEn, which is more often used as a global index of variability [76].
However, as higher irregularity is not always equivalent to higher complexity [82], these traditional measures have been shown to falsely quantify random HRV changes in certain pathological conditions as being complex [79,83]. In order to estimate complexity from irregularity statistics more accurately, Costa et al. [83] suggested instead examining irregularity in multiple spatio-temporal scales where SampEn is estimated on more than one scale, giving rise to a new entropy-based method called MSE. Compared to single-scale entropy estimates, MSE has been able to accurately account for lower HRV observed in different cardiac abnormalities, such as atrial fibrillation where there are random outputs in HRV [83]. As MSE formulation does not allow for reliable computation of entropy in short time windows, new methods such as refined MSE (RMSE) [84] and refined composite MSE (RCMSE) [85] have been introduced, though few studies have tested them on HRV [86,87].
The entropy analysis of HRV is an actively evolving field, with more novel approaches being proposed, each claiming to confer certain advantages over more traditional approaches. For example, new measures such as fuzzy entropy (FuzzEn) [88] and fuzzy measure entropy (FuzzyMEn) [89] that were developed to overcome the poor statistical stability of ApEn and SampEn [90,91] have been gaining traction. While a comparison of clinical validity across these entropy measures has been demonstrated in a few studies (e.g., [89,92,93]), the choice of entropy type and the appropriate parameters for entropy calculation is not a straightforward process and investigation into how these factors influence HRV interpretations is still ongoing [94].
12. Fractal Measures
Fractal methods are more recently developed methods to assess noisy and nonstationary time series. In the context of HRV, fractal methods measure the fluctuations of the cardiac system across multiple time scales, where lower self-similarity/self-affinity (i.e., similar structural details at different scales of visualization) may imply a randomly structured, less adaptable and flexible system.
Correlation dimension (CD) is a widely used measure of fractal dimension (an index of how patterns change with the scale at which it is measured). In the case of HRV, CD measures the number of dynamic variables needed to define the underlying system of the HR time series, where a higher CD reflects greater complexity in HRV. Other algorithms for computing fractal dimension also exist, such as the box-counting dimension, and the algorithm by Katz [95] and Higuchi [96], but CD is the most popular by far [67].
In recent years, the most extensively used method in measuring HRV complexity is detrended fluctuation analysis (DFA) [97]. DFA is a measure of the correlations between successive NN intervals at different time scales, and is used to analyze recordings spanning several hours. Its computation disregards nonstationarities in the cardiac time series and hence any spurious correlations due to artifacts of nonstationarity behavior (e.g., trends due to external stimuli) are avoided, an advantage conferred over other fractal methods [98,99]. DFA eventually extracts both long-term correlations and short-term correlations, with anywhere between 4 and 16 heartbeats for the former, and 16 and 64 heartbeats for the latter [98]. The short-term correlations correspond to the baroreceptor reflex whereas the long-term correlations measure regulatory mechanisms in the cardiac system [20]. See Table 1 for a summary of all indices.

Table 1.
A summary of HRV indices according to their respective analysis domains.
13. Respiratory Sinus Arrhythmia (RSA)
RSA refers to the fluctuations of HR at the respiratory frequency, or in other words, the effect of respiratory-gated PNS activity on the heart. As RSA commonly occurs at high-frequency heart rate fluctuations, most studies quantify RSA using the HF component of the spectral measures [100]. Other methods to quantify RSA include the Porges–Bohrer method (PB) [101] and the peak-to-trough algorithm (P2T) [102,103]. PB extracts RSA by removing variances in the HR time series that are not attributable to spontaneous breathing frequencies, and has high accuracy only when there is a low signal-to-noise ratio in the data. On the other hand, P2T derives RSA by finding the difference between the shortest heart period during inhalation and the longest heart period during exhalation per single breath.
Even though the three different RSA indices are highly correlated [102], PB has been shown to be less susceptible to the non-stationarity in the HR signal and the influence of respiration than the HF component or P2T metric [23]. While both HF and P2T may work well in the absence of slow components and trends [23], PB has been proposed to be the most sensitive to vagal activity.
14. HRV in Psychological Research
As mentioned above, the different HRV indices are believed to reflect different physiological mechanisms. It is therefore unsurprising that they are associated with distinct psychological constructs, such as cognitive abilities, neural processes, personality traits and psychopathological disorders.
15. HRV and Self-Control
Based on the neurovisceral integration model [104,105], the neural circuitry implicated in the effective regulation of psychological processes (i.e., emotional and cognitive self-regulation) are also related to the regulation of cardiac autonomic activity. The model has gained ample support over the past decades as mounting evidence emerges, showing a significant relationship between HRV and prefrontal cortex activity [105,106,107,108]. This is in line with studies investigating the relationship between HRV and executive functioning, showing that participants with higher resting HRV (particularly short-term changes) performed better at different executive tasks, such as sustained attention [109,110], working memory [111,112] inhibition [106,113,114,115], and cognitive flexibility [16,116,117]. Additionally, Hansen et al. [111] also highlighted the executive-specific advantage of higher vagally-mediated resting HRV which was not observed in non-executive tasks based on simple reaction time.
Autonomic flexibility (i.e., the ability of ANS to modify bodily states), indexed by HRV, is crucial for adjusting between high and low arousal states, and has thus been related to emotional regulation. In studies that investigated emotional responses to stress, individuals with higher resting RSA had lower perceived (negative) emotional arousal and made greater use of adaptive coping strategies [118,119]. Similarly, individuals with higher HF experience more positive moods, in particular cheerfulness and calmness, and this relationship was mediated by emotion regulation abilities (e.g., ability to engage in situational planning, refocusing, and reappraisal) [120]. This parallels findings reporting that anxious participants experienced a greater decrease in RCMSE during stress exposure [86]. This is in line with neuroimaging findings highlighting the relationship between HRV and the activity of brain regions involved in threat perception and saliency detection such as the amygdala, media prefrontal cortex [121]. Although the evidence in favor of a link between cognitive and affective dysregulation and reduced HRV is robust, the exact physiopsychological mechanisms underlying this association remain to be uncovered [122].
While most of the literature focuses on the role of resting HRV in cognitive control and emotional regulation, another level of analysis of HRV, the phasic HRV, has been less examined but is also of great interest for health and well-being. Resting or tonic HRV is measured at the state of resting, whereas phasic HRV is measured during the state of stress where changes in HRV, relative to baseline, represent the reactivity of the cardiac system to different stimuli. While the advantages of higher tonic HRV have been repeatedly shown in the literature [121], the desirability of phasic HRV changes (increase versus decrease phasic HRV) is context-dependent [123]. Higher phasic HRV suppression (–the autonomic stress response to prepare for fight-or-flight situations [124] has been linked to higher levels of tonic HRV and phasic HRV post-stress, which are indicators of faster recovery [125,126,127,128]. Therefore, researchers have highlighted its potential role as a protective factor against stress [123,129,130]. However, when the stressor requires the engagement of executive functioning [131], higher phasic HRV enhancement is preferred as it indicates greater attentional resources and self-regulatory effort [132,133,134]. Interestingly, by looking at participants’ performance under different levels of perceptual loads, Park et al. [123] observed that individuals with higher tonic HRV can exert regulatory effort (presence of phasic HRV enhancement) and avoid making autonomic stress response (absence of phasic HRV suppression) even under high loads where the task could be a potential stressor. In contrast, individuals with lower tonic HRV experienced autonomic stress response (phasic HRV enhancement) even in low loads condition, suggesting a tendency to appraise even trivial challenges as stressors. Given the significant interaction between tonic and phasic HRV and its potential to provide insight on individual differences in regulatory processes, future studies should investigate not only HRV at rest but also HRV reactivity (changes between rest and event) and HRV recovery (changes between event and post-event) [135].
16. HRV and Psychopathology
Research focusing on the relationship between HRV and mood disorders suggests that, in general, a lower vagal tone (and thus, a lower HRV) is associated with negative outcomes [136]. Short-term HRV indices such has RMSSD, SDANN, HF and non-linear measures such as MSE were found to be significantly reduced in patients with depression [14,137,138] and negatively correlated with symptom severity [139]. Short-term HRV indices are also lower (and correlated with symptoms’ severity [140]) in anxiety disorders, including generalized anxiety disorder (GAD), social anxiety disorder, panic disorder and post-traumatic stress disorder [11,12,14,17,124,141,142,143,144,145,146,147] Additionally, depression with comorbid anxiety has been shown to be associated with greater reduction in HRV as compared to depression alone [15]. In this context, lower HRV has been associated with changes in the sympathovagal balance in favor of a sympathetic predominance, which may subsequently increase cardiovascular risk in these pathologies [146]. Bipolar disorder is also associated with a decreased HRV across a variety of HRV indices, including RMSSD, pNN50, SDNN, HF, LF, and SampEn [148,149,150,151]. A similar pattern would be expected with borderline personality disorder, given the shared physiopsychological mechanisms with bipolar disorder [152]. However, the few studies currently report mixed findings (e.g., a higher HF in BPD patients [153]) vs. lower RSA [154]). Research also suggests a lower HRV with reduced RMSSD, HF, ApEn and SampEn in patients suffering from schizophrenia [149,155,156,157,158], and a correlation with symptoms such as apathy, withdrawal and delusions [159], suggesting a relationship between psychotic symptoms and cardiac autonomic function [149,160].
HRV has been presented as a useful clinical marker of psychopathology, in which it represents the combined effect of parasympathetic inhibition as well as excessive sympathetic activation, reflecting a sub-optimal adaptive response to external and internal changes. Although the specific pathophysiological mechanisms underlying the associations between psychiatric conditions and HRV remain poorly understood, the majority of studies observed significant relationships between the different pathologies and parasympathetic parameters (such as HF and RMSSD, that are particularly sensitive to short-term HR changes). This has led researchers to propose that a restrained vagal activity could be a transdiagnostic biomarker across psychiatric disorders [17,155,161,162]. This hypothesis is further supported by the observation of worsening parasympathetic tone during the chronic course of psychiatric conditions [155,163], and parallel improvements in parasympathetic parameters as symptom severity reduces over the course of treatment [14,145,164,165].
17. HRV as a Therapeutic Target
With the progressive establishment of HRV as a convenient peripheral (and correlational) index of self-regulatory abilities [104,166], its usage in applied settings grew. Recently, the psychophysiological cardiac coherence model has been introduced to promote training to enhance HRV. This model emphasizes the importance of having reciprocal interactions and coherence between the regulatory systems to maximize the adaptability to environmental demands [167,168]. Cardiac coherence refers to a stable state of increased synchrony between the rhythms of different oscillatory systems, typically HR, respiration and blood pressure. In practice, this coherent state is reflected by a more ordered and sine wave-like HRV waveform, oscillating at a frequency approximating 0.1 Hz, the frequency at which the phase synchrony of HR and respiration occurs [169,170].
According to the model, cardiac coherence can be induced by breathing at a steady pace approximating 0.1 Hz (i.e., six breaths per minute). Such deliberate slow-paced breathing (also referred to as “deep breathing,” [170]) maximizes both baroreflex sensitivity and RSA on HR, giving rise to a high-amplitude oscillation of HR [171,172]. According to [172], regular breathing exercising techniques help to continuously stimulate and exercise autonomic reflexes, especially the baroreflex. In fact, deep breathing has been shown to produce significant improvements in cognitive and emotional functioning [167] and different dimensions of health and well-being, such as pain [173], stress and anxiety [174,175], depression [176,177,178], post-traumatic stress disorder [179], or attention-deficit hyperactivity disorder [180]. Different mechanisms have been proposed to explain the therapeutic effects of HRV-focused biofeedback [181], but further investigations are needed to understand, clarify and validate its potential clinical utility.
18. HRV in Practice: A Tutorial Using Python
Over the years, HRV has become a convenient and reliable marker to detect ANS and cardiovascular abnormalities. However, due to the complex mathematical models and theories of signal processing involved, there is a practical barrier for users without the prior technical knowledge, such as many psychology students and researchers, to effectively understand, interpret, produce and reproduce HRV indices. In the following, we will present a step-by-step guide to obtain HRV indices using NeuroKit2 [182]), an open-source Python package that is designed to be friendly to both novice and advanced programmers. Instructions on how to get Python and NeuroKit2 up and running can be found at https://neurokit2.readthedocs.io/en/latest/installation.html (accessed on 3 May 2021). Note that other open-source software such as HeartPy [183], pyHRV [184], hrv [185] and GUI-based software such as KUBIOS© [186], and BIOPAC Acqknowledge software (https://www.biopac.com) (accessed on 3 May 2021) are other alternatives for HRV analysis.
19. Data Preprocessing
Cardiac activity data stored on the disk can be loaded using functions appropriate to the format (e.g., read_bitalino() or read_acqknowledge()). For the purposes of this tutorial, we will download and use an example dataset available in NeuroKit2, which consists of recordings of four participants during 8 min of resting state. Their cardiac activity (ECG) and respiration (RSP) signals were recorded and downsampled to 200 Hz for the purpose of this demonstration (note that higher sampling rates are recommended to maximize the precision of NN intervals).
The data from the first participant is then extracted, stored into an object, and two of its variables (the ECG and RSP signals) are passed to a preprocessing function that will clean the signals and, importantly, find the location of R peaks and respiration cycles. Details about the options and algorithms used are available in the package’s documentation.
# Load data import neurokit2 as nk data_all = nk.data(‘https://raw.githubusercontent.com/neuropsychology/NeuroKit/dev/data/bio_resting_8min_200hz.json’) data_participant = data_all[“S01”] # Access the data of the first participant # Clean signal clean_signals, info = nk.bio_process(ecg=data_participant[“ECG”], rsp=data_participant[“RSP”], sampling_rate=200) # Show the location of the fist 5 R-peaks info[“ECG_R_Peaks”][0:5] ## array([165, 345, 506, 672, 838])
The bio_process() function allows simultaneous processing of different signals using signal-specific pipelines. For instance, for ECG signals, the steps involve minimizing noise in the data, removing artifacts due to environmental or biological sources, as well as extracting all potential peaks (e.g., R-peaks) in the signal before removing peaks that are not of interest (i.e., ectopic peaks).
NeuroKit2 offers flexibility in choosing different processing methods. For this tutorial, we will use the bio_process() function which allows for less customization of the pipeline and relies on sensible default parameters for performing signal-specific operations (i.e., cleaning, peak extraction, rate computation). Alternatively, users can customize their own processing pipeline following the tutorial available on the documentation of NeuroKit2.
20. HRV Analysis
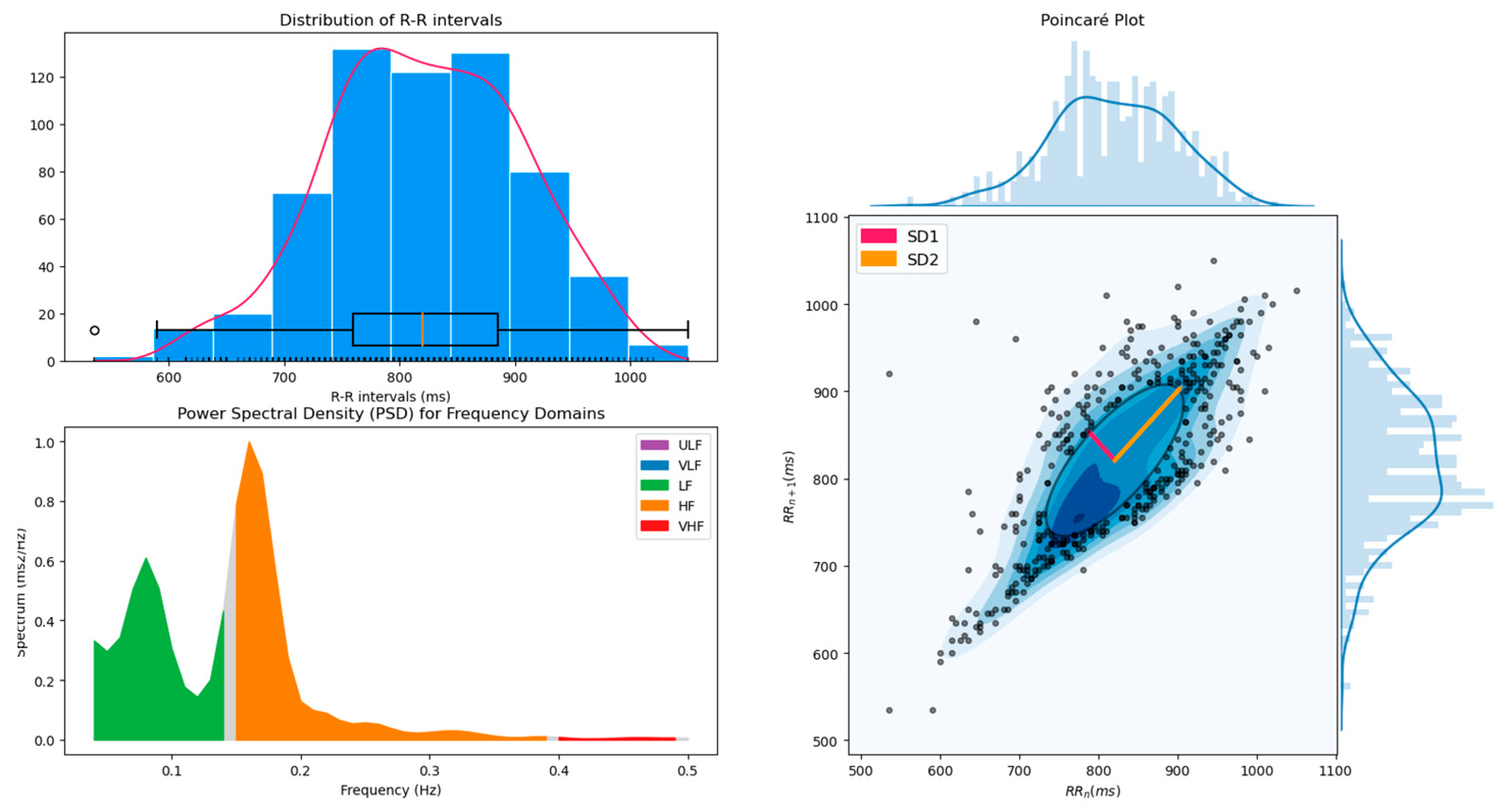
HRV indices of different domains can then be obtained using specific functions such as hrv_time(), hrv_frequency(), hrv_nonlinear() and hrv_rsa(), to which the list of R-peaks location, the sampling rate (200 Hz in this example), and respiration phases (specifically for hrv_rsa()) have to be provided. However, all the available indices can also be computed at once using hrv(), alongside a figure combining useful diagnostic plots (such as the power spectral density and the Poincaré plot) when the show argument is set to True. Table 2 shows an example of the indices output and Figure 1 shows an example of the diagnostic plot.

Table 2.
The hrv() function returns a dataframe containing all the indices as columns.
Figure 1.
Output of the hrv() function showing the distribution of NN intervals, the power spectrum density (PSD) and the Poincaré plot, that can be used as a visual diagnostic tool for HRV.
# Compute all HRV indices and show plots nk.hrv(info, sampling_rate=200, show=True)
21. Multiple Participants Analysis
As the function(s) to compute HRV indices for a participant return a single row dataframe, the process can easily scale up for studies that contain multiple participants by, essentially, binding all the rows together into one dataframe. In the example below, we will demonstrate how to loop through participants, compute HRV indices at each turn and append the data. For more complex or tailored analyses, it is within such loops that additional participant-specific operations can be inserted (e.g., apply specific data preprocessing steps or extract other types of information).
# Load data and create list of participants data_all = nk.data(‘https://raw.githubusercontent.com/neuropsychology/NeuroKit/dev/data/bio_resting_8min_200hz.json’) list_participants = [“S01”, “S02”, “S03”, “S04”] # Loop through participants’ names for participant in list_participants: # Get data of current participant data_participant = data_all[participant] # Clean signal clean_signals, info = nk.bio_process(ecg=data_participant[“ECG”], rsp=data_participant[“RSP”], sampling_rate=200) # Compute HRV indices results = nk.hrv(info, sampling_rate=200, show=False) # Add “Participant” column results[“Participant”] = participant # If participant is not the first, then append the data if participant == “S01”: results_all = results else: results_all = results_all.append(results)
22. Conclusions
Throughthe above literature review related to HRV and its applications in psychology and neuroscience, we demonstrated how HRV analysis can be efficiently performed using NeuroKit2 by computing the indices, creating useful diagnostic plots, as well as by aggregating the indices across multiple subjects. We hope that helping to provide psychologists with a comprehensive list of HRV indices will help to shift the focus from physiological preprocessing and programming technicalities towards the interpretation of the results involving these indices as well as the critical discussion of their limitations.
Given the amount of existing HRV indices, in addition to the lack of clarity regarding their associated physiological mechanisms, psychophysiological researchers might find it difficult to pinpoint which ones to focus on. Time-domain indices have a long history of usage in HRV research, with RMSSD being arguably the most robust measure of vagal tone [44,135]. While these statistical indices are quick to compute, it is crucial to carefully preprocess the HR signal before performing HRV analysis, as their accuracy can be easily affected by outliers and artefacts. In cases of noisy signal, geometrical approaches such as the HTI might be a more viable alternative. Frequency-domain indices may provide greater precision in quantifying autonomic control mechanisms. Among the spectral measures, the relationship between HF and vagal tone has been the most well-established. However, given its sensitivity to processing parameters chosen, it is recommended that HF is interpreted in conjunction with other time-domain indices that are thought to similarly reflect vagal tone (e.g., RMSSD, pNN50, see [135]). Controlled breathing protocols can also be used to minimize variable respiratory influences on HF across different populations (e.g., athletes have slower respiratory rates, children breathe faster, [44,187]). Additionally, although the use of LF/HF has also been quite popular amongst researchers, definitive conclusions about sympathovagal balance based solely on this parameter are ill-advised due to the unclear sources of LF.
While both time- and frequency-domain indices are correlated with non-linear indices, the latter are more reflective of the general complexity of HR signal rather than any specific underlying physiological mechanism [188]. However, theoretical and methodological concerns related to their usage have been raised. Firstly, these indices are very sensitive to the parameters chosen (e.g., window length), with unclear guidelines, rules, or standards for their (optimal) selection. Secondly, while some studies attest to the clinical utility of non-linear HRV dynamics when applied longitudinally (i.e., ability to differentiate progression of cardiovascular diseases), it is not yet clear why certain non-linear methods are better at distinguishing between pathologies. Apart from methods covered in this paper, other methods such as largest Lyapunov exponent (LLE), Hurst exponent (HE) and symbolic dynamics have also gained wide acceptance for assessing various complex systems, but their applications in HRV are substantially less popular than the aforementioned non-linear indices [67]. All in all, it is recommended to treat these indices as complementary measures to traditional linear indices [135,188].
Finally, other considerations influence the choice and interpretation of HRV indices, such as recording length, quality of the recorded signal, breathing methods and participant variables (e.g., age, gender, cardio-related medication, etc.) [18,189]. To facilitate the comparisons of HRV-related results across populations and studies, past studies have attempted to quantify the reference values for HRV measures of different recording lengths (e.g., see [190,191] for long-term recordings; [192,193] for short-term recordings), of different populations (e.g., [194] for healthy school-aged children; [193] for healthy adults) and/or across different demographic characteristics (e.g., [195,196]). Related to this, researchers have provided a comprehensive list of practical recommendations [188] to improve the use of standardized protocols for HRV research. All in all, the focus of the current paper is aimed at providing an overview of HRV indices, their usage in psychological research, and a practical demonstration on how to obtain these indices using NeuroKit2.
Author Contributions
D.M. conceived and T.P. coordinated the study. T.P. and Z.J.L. participated in the manuscript drafting. D.M. and S.H.A.C. performed a critical review of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The authors did not receive support from any organization for the submitted work.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Selye, H. The Stress of Life; Mc Gran-Hill Book Company Inc.: New York, NY, USA, 1956. [Google Scholar]
- Lombardi, F.; Malliani, A.; Pagani, M.; Cerutti, S. Heart Rate Variability and Its Sympatho-Vagal Modulation. Cardiovasc. Res. 1996, 32, 208–216. [Google Scholar] [CrossRef]
- Vila, J.; Guerra, P.; Muñoz, M.A.; Vico, C.; Jesús, M.I.V.-D.; Delgado, L.C.; Perakakis, P.; Kley, E.; Mata, J.L.; Rodríguez, S. Cardiac defense: From attention to action. Int. J. Psychophysiol. 2007, 66, 169–182. [Google Scholar] [CrossRef] [PubMed]
- Obrist, P.A. Cardiovascular Psychophysiology: A Perspective; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Mccraty, R.; Shaffer, F. Heart Rate Variability: New Perspectives on Physiological Mechanisms, Assessment of Self-regulatory Capacity, and Health Risk. Glob. Adv. Heal. Med. 2015, 4, 46–61. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, H.; Larson, M.G.; Venditti, F.J.; Manders, E.S.; Evans, J.C.; Feldman, C.L.; Levy, D. Impact of Reduced Heart Rate Variability on Risk for Cardiac Events: The Framingham Heart Study. Circulation 1996, 94, 2850–2855. [Google Scholar] [CrossRef]
- Ranpuria, R.; Hall, M.; Chan, C.T.; Unruh, M. Heart rate variability (HRV) in kidney failure: Measurement and consequences of reduced HRV. Nephrol. Dial. Transplant. 2007, 23, 444–449. [Google Scholar] [CrossRef]
- Taylor, C.B. Depression, heart rate related variables and cardiovascular disease. Int. J. Psychophysiol. 2010, 78, 80–88. [Google Scholar] [CrossRef]
- Thayer, J.F.; Yamamoto, S.S.; Brosschot, J.F. The relationship of autonomic imbalance, heart rate variability and cardiovascular disease risk factors. Int. J. Cardiol. 2010, 141, 122–131. [Google Scholar] [CrossRef]
- Ziemssen, T.; Siepmann, T. The Investigation of the Cardiovascular and Sudomotor Autonomic Nervous System—A Review. Front. Neurol. 2019, 10, 53. [Google Scholar] [CrossRef]
- Tulen, J.; Bruijn, J.; de Man, K.; van der Velden, E.; Pepplinkhuizen, L.; Veld, A. ’T Anxiety and autonomic regulation in major depressive disorder: An exploratory study. J. Affect. Disord. 1996, 40, 61–71. [Google Scholar] [CrossRef]
- Stein, P.K.; Carney, R.M.; E Freedland, K.; A Skala, J.; Jaffe, A.S.; E Kleiger, R.; Rottman, J.N. Severe depression is associated with markedly reduced heart rate variability in patients with stable coronary heart disease. J. Psychosom. Res. 2000, 48, 493–500. [Google Scholar] [CrossRef]
- Agelink, M.W.; Boz, C.; Ullrich, H.; Andrich, J. Relationship Between Major Depression and Heart Rate Variability.: Clinical Consequences and Implications for Antidepressive Treatment. Psychiatry Res. 2002, 113, 139–149. [Google Scholar] [CrossRef]
- Kemp, A.H.; Quintana, D.S.; Gray, M.A.; Felmingham, K.L.; Brown, K.; Gatt, J.M. Impact of Depression and Antidepressant Treatment on Heart Rate Variability: A Review and Meta-Analysis. Biol. Psychiatry 2010, 67, 1067–1074. [Google Scholar] [CrossRef]
- Kemp, A.H.; Quintana, D.S.; Felmingham, K.L.; Matthews, S.; Jelinek, H.F. Depression, Comorbid Anxiety Disorders, and Heart Rate Variability in Physically Healthy, Unmedicated Patients: Implications for Cardiovascular Risk. PLoS ONE 2012, 7, e30777. [Google Scholar] [CrossRef]
- Gaebler, M.; Daniels, J.K.; Lamke, J.-P.; Fydrich, T.; Walter, H. Heart Rate Variability and Its Neural Correlates During Emotional Face Processing in Social Anxiety Disorder. Biol. Psychol. 2013, 94, 319–330. [Google Scholar] [CrossRef]
- Chalmers, J.A.; Quintana, D.S.; Abbott, M.J.; Kemp, A.H. Anxiety Disorders Are Associated with Reduced Heart Rate Variability: A Meta-Analysis. Front. Psychiatry 2014, 5, 80. [Google Scholar] [CrossRef]
- Force, T. Standards of Measurement, Physiological Interpretation and Clinical Use. Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology. Circulation 1996, 93, 1043–1065. [Google Scholar]
- Shaffer, F.; McCraty, R.; Zerr, C.L. A healthy heart is not a metronome: An integrative review of the heart’s anatomy and heart rate variability. Front. Psychol. 2014, 5, 1040. [Google Scholar] [CrossRef]
- Shaffer, F.; Ginsberg, J. An Overview of Heart Rate Variability Metrics and Norms. Front. Public Health 2017, 5, 258. [Google Scholar] [CrossRef]
- Berntson, G.G.; Bigger, J.T.; Eckberg, D.L.; Grossman, P.; Kaufmann, P.G.; Malik, M.; Nagaraja, H.N.; Porges, S.W.; Saul, J.P.; Stone, P.H.; et al. Heart rate variability: Origins, methods, and interpretive caveats. Psychophysiology 1997, 34, 623–648. [Google Scholar] [CrossRef]
- Yaroslavsky, I.; Bylsma, L.M.; Rottenberg, J.; Kovacs, M. Combinations of Resting RSA and RSA Reactivity Impact Maladaptive Mood Repair and Depression Symptoms. Biol. Psychol. 2013, 94, 272–281. [Google Scholar] [CrossRef]
- Lewis, G.F.; Furman, S.A.; McCool, M.F.; Porges, S.W. Statistical Strategies to Quantify Respiratory Sinus Arrhythmia: Are Commonly Used Metrics Equivalent? Biol. Psychol. 2012, 89, 349–364. [Google Scholar] [CrossRef]
- Bigger Jr, J.T.; Albrecht, P.; Steinman, R.C.; Rolnitzky, L.M.; Fleiss, J.L.; Cohen, R.J. Comparison of Time-and Frequency Domain-Based Measures of Cardiac Parasympathetic Activity in Holter Recordings After Myocardial Infarction. Am. J. Cardiol. 1989, 64, 536–538. [Google Scholar] [CrossRef]
- Fei, L.; Copie, X.; Malik, M.; Camm, A.J. Short-and Long-Term Assessment of Heart Rate Variability for Risk Stratification After Acute Myocardial Infarction. Am. J. Cardiol. 1996, 77, 681–684. [Google Scholar] [CrossRef]
- Nolan, J.; Batin, P.D.; Andrews, R.; Lindsay, S.J.; Brooksby, P.; Mullen, M.; Baig, W.; Flapan, A.D.; Cowley, A.; Prescott, R.J.; et al. Prospective Study of Heart Rate Variability and Mortality in Chronic Heart Failure: Results of the United Kingdom Heart Failure Evaluation and Assessment of Risk Trial (UK-Heart). Circulation 1998, 98, 1510–1516. [Google Scholar] [CrossRef] [PubMed]
- Kleiger, R.E.; Stein, P.K.; Bigger Jr, J.T. Heart Rate Variability: Measurement and Clinical Utility. Ann. Noninvasive Electrocardiol. 2005, 10, 88–101. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, E.B.; Whitsel, E.A.; Evans, G.W.; Prineas, R.J.; Chambless, L.E.; Heiss, G. Repeatability of Heart Rate Variability Measures. J. Electrocardiol. 2004, 37, 163–172. [Google Scholar] [CrossRef] [PubMed]
- McNames, J.; Aboy, M. Reliability and Accuracy of Heart Rate Variability Metrics Versus ECG Segment Duration. Med. Biol. Eng. Comput. 2006, 44, 747–756. [Google Scholar] [CrossRef]
- Salahuddin, L.; Cho, J.; Jeong, M.G.; Kim, D. Ultra short term analysis of heart rate variability for monitoring mental stress in mobile settings. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 23–26 August 2007; pp. 4656–4659. [Google Scholar]
- Nussinovitch, U.; Elishkevitz, K.P.; Katz, K.; Nussinovitch, M.; Segev, S.; Volovitz, B.; Nussinovitch, N. Reliability of Ultra-Short ECG Indices for Heart Rate Variability. Ann. Noninvasive Electrocardiol. 2011, 16, 117–122. [Google Scholar] [CrossRef]
- Munoz, M.L.; van Roon, A.; Riese, H.; Thio, C.; Oostenbroek, E.; Westrik, I.; de Geus, E.J.; Gansevoort, R.; Lefrandt, J.; Nolte, I.M.; et al. Validity of (Ultra-) Short Recordings for Heart Rate Variability Measurements. PLoS ONE 2015, 10, e0138921. [Google Scholar] [CrossRef]
- Baek, H.J.; Cho, C.-H.; Cho, J.; Woo, J. Reliability of Ultra-Short-Term Analysis as a Surrogate of Standard 5-Min Analysis of Heart Rate Variability. Telemed. e-Health 2015, 21, 404–414. [Google Scholar] [CrossRef]
- Castaldo, R.; Montesinos, L.; Melillo, P.; James, C.; Pecchia, L. Ultra-short term HRV features as surrogates of short term HRV: A case study on mental stress detection in real life. BMC Med. Inform. Decis. Mak. 2019, 19, 1–13. [Google Scholar] [CrossRef]
- Hon, E.H.; Lee, S.T. ELECTRONIC EVALUATION OF THE FETAL HEART RATE. VIII. PATTERNS PRECEDING FETAL DEATH, FURTHER OBSERVATIONS. Am. J. Obstet. Gynecol. 1963, 87, 814–826. [Google Scholar]
- Akselrod, S.; Gordon, D.; Ubel, F.A.; Shannon, D.C.; Berger, A.; Cohen, R.J. Power Spectrum Analysis of Heart Rate Fluctuation: A Quantitative Probe of Beat-to-Beat Cardiovascular Control. Science 1981, 213, 220–222. [Google Scholar] [CrossRef]
- Cohen, L. Time-frequency distributions-a review. In Proceedings of the IEEE; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 1989; Volume 77, pp. 941–981. [Google Scholar]
- Goldberger, A.L.; West, B.J. Applications of Nonlinear Dynamics to Clinical Cardiology. Ann. New York Acad. Sci. 1987, 504, 195–213. [Google Scholar] [CrossRef]
- Denton, T.A.; Diamond, G.A.; Helfant, R.H.; Khan, S.; Karagueuzian, H. Fascinating rhythm: A primer on chaos theory and its application to cardiology. Am. Heart J. 1990, 120, 1419–1440. [Google Scholar] [CrossRef]
- Bigger Jr, J.T.; Steinman, R.C.; Rolnitzky, L.M.; Fleiss, J.L.; Albrecht, P.; Cohen, R.J. Power Law Behavior of RR-Interval Variability in Healthy Middle-Aged Persons, Patients with Recent Acute Myocardial Infarction, and Patients with Heart Transplants. Circulation 1996, 93, 2142–2151. [Google Scholar] [CrossRef]
- Lombardi, F.; Sandrone, G.; Mortara, A.; Torzillo, D.; La Rovere, M.T.; Signorini, M.G.; Cerutti, S.; Malliani, A. Linear and nonlinear dynamics of heart rate variability after acute myocardial infarction with normal and reduced left ventricular ejection fraction. Am. J. Cardiol. 1996, 77, 1283–1288. [Google Scholar] [CrossRef]
- Huikuri, H.V.; Mäkikallio, T.H.; Perkiömäki, J. Measurement of heart rate variability by methods based on nonlinear dynamics. J. Electrocardiol. 2003, 36, 95–99. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.B.; Liebovitch, L.S.; West, B.J.; Stanley, H.E. Fractal Physiology. Phys. Today 1995, 48, 66. [Google Scholar] [CrossRef]
- Acharya, U.R.; Joseph, K.P.; Kannathal, N.; Lim, C.M.; Suri, J.S. Heart rate variability: A review. Med Biol. Eng. Comput. 2006, 44, 1031–1051. [Google Scholar] [CrossRef]
- Abdi, H.; Salkind, N. Coefficient of Variation. Encycl. Res. Des. 2012, 1, 169–171. [Google Scholar] [CrossRef]
- Yılmaz, B.; Asyalı, M.H.; Arıkan, E.; Yetkin, S.; Özgen, F. Sleep stage and obstructive apneaic epoch classification using single-lead ECG. Biomed. Eng. Online 2010, 9, 39. [Google Scholar] [CrossRef]
- Almazaydeh, L.; Elleithy, K.; Faezipour, M. Obstructive sleep apnea detection using SVM-based classification of ECG signal features. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 4938–4941. [Google Scholar]
- Ciccone, A.B.; Siedlik, J.A.; Wecht, J.M.; Deckert, J.A.; Nguyen, N.D.; Weir, J.P. Reminder: RMSSD and SD1 are identical heart rate variability metrics. Muscle Nerve 2017, 56, 674–678. [Google Scholar] [CrossRef]
- Esco, M.R.; Flatt, A.A. Ultra-Short-Term Heart Rate Variability Indexes at Rest and Post-Exercise in Athletes: Evaluating the Agreement with Accepted Recommendations. J. Sports Sci. Med. 2014, 13, 535–541. [Google Scholar]
- Malik, M.; Xia, R.; Odemuyiwa, O.; Staunton, A.; Poloniecki, J.; Camm, A.J. Influence of the recognition artefact in automatic analysis of long-term electrocardiograms on time-domain measurement of heart rate variability. Med Biol. Eng. Comput. 1993, 31, 539–544. [Google Scholar] [CrossRef]
- Jovic, A.; Bogunovic, N. Electrocardiogram analysis using a combination of statistical, geometric, and nonlinear heart rate variability features. Artif. Intell. Med. 2011, 51, 175–186. [Google Scholar] [CrossRef]
- Seyd, P.A.; Ahamed, V.T.; Jacob, J.; Joseph, P. Time and frequency domain analysis of heart rate variability and their correlations in diabetes mellitus. Int. J. Biol. Life Sci. 2008, 4, 24–27. [Google Scholar]
- Goldstein, D.S.; Bentho, O.; Park, M.-Y.; Sharabi, Y. Low-frequency power of heart rate variability is not a measure of cardiac sympathetic tone but may be a measure of modulation of cardiac autonomic outflows by baroreflexes. Exp. Physiol. 2011, 96, 1255–1261. [Google Scholar] [CrossRef]
- Billman, G.E. The LF/HF ratio does not accurately measure cardiac sympatho-vagal balance. Front. Physiol. 2013, 4, 26. [Google Scholar] [CrossRef]
- Takabatake, N.; Nakamura, H.; Minamihaba, O.; Inage, M.; Inoue, S.; Kagaya, S.; Yamaki, M.; Tomoike, H. A novel pathophysiologic phenomenon in cachexic patients with chronic obstructive pulmonary disease: The relationship between the circadian rhythm of circulating leptin and the very low-frequency component of heart rate variability. Am. J. Respir. Crit. Care Med. 2001, 163, 1314–1319. [Google Scholar] [CrossRef]
- Barrett, C.J.; Navakatikyan, M.A.; Malpas, S.C. Long-term control of renal blood flow: What is the role of the renal nerves? Am. J. Physiol. Integr. Comp. Physiol. 2001, 280, R1534–R1545. [Google Scholar] [CrossRef] [PubMed]
- Coenen, A.J.; Kitney, R.; Rompelman, O. Thermally elicited entertainment of heart rate variability [proceedings]. J. Physiol. 1977, 270, 5–6. [Google Scholar]
- Bouzida, N.; Bendada, A.; Maldague, X.P. Visualization of body thermoregulation by infrared imaging. J. Therm. Biol. 2009, 34, 120–126. [Google Scholar] [CrossRef]
- Machado, C.; Estevez, M.; Perez-Nellar, J.; Schiavi, A. Residual vasomotor activity assessed by heart rate variability in a brain-dead case. BMJ Case Rep. 2015, 2015. [Google Scholar] [CrossRef]
- Kim, K.K.; Kim, J.S.; Lim, Y.G.; Park, K.S. The effect of missing RR-interval data on heart rate variability analysis in the frequency domain. Physiol. Meas. 2009, 30, 1039–1050. [Google Scholar] [CrossRef]
- Malik, M.; Bigger, J.T.; Camm, A.J.; Kleiger, R.E.; Malliani, A.; Moss, A.J.; Schwartz, P.J. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Eur. Heart J. 1996, 17, 354–381. [Google Scholar] [CrossRef]
- Burr, R.L. Interpretation of Normalized Spectral Heart Rate Variability Indices In Sleep Research: A Critical Review. Sleep 2007, 30, 913–919. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1995; Volume 778. [Google Scholar]
- Elsenbruch, S.; Wang, Z.; Orr, W.C.; Chen, J.D.Z. Time-frequency analysis of heart rate variability using short-time Fourier analysis. Physiol. Meas. 2000, 21, 229–240. [Google Scholar] [CrossRef]
- Mainardi, L.T. On the quantification of heart rate variability spectral parameters using time–frequency and time-varying methods. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 255–275. [Google Scholar] [CrossRef]
- Voss, A.; Schulz, S.; Schroeder, R.; Baumert, M.; Caminal, P. Methods derived from nonlinear dynamics for analysing heart rate variability. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2008, 367, 277–296. [Google Scholar] [CrossRef]
- Henriques, T.; Ribeiro, M.; Teixeira, A.; Castro, L.; Antunes, L.; Costa-Santos, C. Nonlinear Methods Most Applied to Heart-Rate Time Series: A Review. Entropy 2020, 22, 309. [Google Scholar] [CrossRef]
- Brennan, M.; Palaniswami, M.; Kamen, P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? IEEE Trans. Biomed. Eng. 2001, 48, 1342–1347. [Google Scholar] [CrossRef]
- Brennan, M.; Palaniswami, M.; Kamen, P. Poincaré plot interpretation using a physiological model of HRV based on a network of oscillators. Am. J. Physiol. Circ. Physiol. 2002, 283, H1873–H1886. [Google Scholar] [CrossRef]
- Hsu, C.-H.; Tsai, M.-Y.; Huang, G.-S.; Lin, T.-C.; Chen, K.-P.; Ho, S.-T.; Shyu, L.-Y.; Li, C.-Y. Poincaré plot indexes of heart rate variability detect dynamic autonomic modulation during general anesthesia induction. Acta Anaesthesiol. Taiwanica 2012, 50, 12–18. [Google Scholar] [CrossRef]
- Woo, M.A.; Stevenson, W.G.; Moser, D.K.; Trelease, R.B.; Harper, R.M. Patterns of beat-to-beat heart rate variability in advanced heart failure. Am. Heart J. 1992, 123, 704–710. [Google Scholar] [CrossRef]
- Claudia, L.; Oscar, I.; Héctor, P.-G.; Marco, V.J. Poincaré plot indexes of heart rate variability capture dynamic adaptations after haemodialysis in chronic renal failure patients. Clin. Physiol. Funct. Imaging 2003, 23, 72–80. [Google Scholar] [CrossRef]
- Hoshi, R.A.; Pastre, C.M.; Vanderlei, L.C.M.; Godoy, M.F. Poincaré plot indexes of heart rate variability: Relationships with other nonlinear variables. Auton. Neurosci. 2013, 177, 271–274. [Google Scholar] [CrossRef]
- Koichubekov, B.; Riklefs, V.; Sorokina, M.; Korshukov, I.; Turgunova, L.; Laryushina, Y.; Bakirova, R.; Muldaeva, G.; Bekov, E.; Kultenova, M. Informative Nature and Nonlinearity of Lagged Poincaré Plots Indices in Analysis of Heart Rate Variability. Entropy 2017, 19, 523. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef]
- Faes, L.; Gómez-Extremera, M.; Pernice, R.; Carpena, P.; Nollo, G.; Porta, A.; Bernaola-Galván, P. Comparison of methods for the assessment of nonlinearity in short-term heart rate variability under different physiopathological states. Chaos: Interdiscip. J. Nonlinear Sci. 2019, 29, 123114. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale Entropy Analysis of Complex Physiologic Time Series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Al-Angari, H.M.; Sahakian, A.V. Use of Sample Entropy Approach to Study Heart Rate Variability in Obstructive Sleep Apnea Syndrome. IEEE Trans. Biomed. Eng. 2007, 54, 1900–1904. [Google Scholar] [CrossRef]
- Xie, H.-B.; He, W.-X.; Liu, H. Measuring time series regularity using nonlinear similarity-based sample entropy. Phys. Lett. A 2008, 372, 7140–7146. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.-K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Phys. A Stat. Mech. Its Appl. 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Wang, C.-C.; Lee, K.-Y. Time Series Analysis Using Composite Multiscale Entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Wu, S.-D.; Wu, C.-W.; Lin, S.-G.; Lee, K.-Y.; Peng, C.-K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Blons, E.; Arsac, L.M.; Gilfriche, P.; McLeod, H.; Lespinet-Najib, V.; Grivel, E.; Deschodt-Arsac, V. Alterations in heart-brain interactions under mild stress during a cognitive task are reflected in entropy of heart rate dynamics. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Deschodt-Arsac, V.; Blons, E.; Gilfriche, P.; Spiluttini, B.; Arsac, L.M. Entropy in Heart Rate Dynamics Reflects How HRV-Biofeedback Training Improves Neurovisceral Complexity during Stress-Cognition Interactions. Entropy 2020, 22, 317. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Humeau-Heurtier, A. The Multiscale Entropy Algorithm and Its Variants: A Review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Castiglioni, P.; Di Rienzo, M. How the threshold “r” influences approximate entropy analysis of heart-rate variability. Comput. Cardiol. 2008, 561–564. [Google Scholar] [CrossRef]
- Graff, B.; Graff, G.; Kaczkowska, A. Entropy Measures of Heart Rate Variability for Short ECG Datasets in Patients with Congestive Heart Failure. Acta Phys. Pol. B Proc. Suppl. 2012, 5, 153–158. [Google Scholar] [CrossRef]
- Graff, B.; Graff, G.; Makowiec, D.; Kaczkowska, A.; Wejer, D.; Budrejko, S.; Kozlowski, D.; Narkiewicz, K. Entropy Measures in the Assessment of Heart Rate Variability in Patients with Cardiodepressive Vasovagal Syncope. Entropy 2015, 17, 1007–1022. [Google Scholar] [CrossRef]
- Mayer, C.C.; Bachler, M.; Hortenhuber, M.; Stocker, C.; Holzinger, A.; Wassertheurer, S. Selection of entropy-measure parameters for knowledge discovery in heart rate variability data. BMC Bioinform. 2014, 15, 1–11. [Google Scholar] [CrossRef]
- Katz, M.J. Fractals and the analysis of waveforms. Comput. Biol. Med. 1988, 18, 145–156. [Google Scholar] [CrossRef]
- Higuchi, T. Relationship between the fractal dimension and the power law index for a time series: A numerical investigation. Phys. D Nonlinear Phenom. 1990, 46, 254–264. [Google Scholar] [CrossRef]
- Peng, C.-K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Penzel, T.; Kantelhardt, J.W.; Grote, L.; Peter, J.-H.; Bunde, A. Comparison of Detrended Fluctuation Analysis and Spectral Analysis for Heart Rate Variability in Sleep and Sleep Apnea. IEEE Trans. Biomed. Eng. 2003, 50, 1143–1151. [Google Scholar] [CrossRef]
- Echeverria, J.; Woolfson, M.; Crowe, J.; Hayes-Gill, B.; Croaker, G.; Vyas, H. Interpretation of heart rate variability via detrended fluctuation analysis and alpha beta filter. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 467–475. [Google Scholar] [CrossRef]
- Grossman, P.; Taylor, E.W. Toward Understanding Respiratory Sinus Arrhythmia: Relations to Cardiac Vagal Tone, Evolution and Biobehavioral Functions. Biol. Psychol. 2007, 74, 263–285. [Google Scholar] [CrossRef]
- Porges, S.W.; Bohrer, R.E. The Analysis of Periodic Processes in Psychophysiological Research. In Principles of Psychophysiology: Physical, Social, and Inferential Elements; Cacioppo, J.T., Tassinary, L.G., Eds.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Grossman, P.; Van Beek, J.; Wientjes, C. A Comparison of Three Quantification Methods for Estimation of Respiratory Sinus Arrhythmia. Psychophysiology 1990, 27, 702–714. [Google Scholar] [CrossRef]
- Katona, P.G.; Jih, F. Respiratory Sinus Arrhythmia: Noninvasive Measure of Parasympathetic Cardiac Control. Eur. J. Appl. Physiol. 1975, 39, 801–805. [Google Scholar] [CrossRef]
- Thayer, J.F.; Lane, R.D. A model of neurovisceral integration in emotion regulation and dysregulation. J. Affect. Disord. 2000, 61, 201–216. [Google Scholar] [CrossRef]
- Thayer, J.F.; Lane, R.D. Claude bernard and the heart–brain connection: Further elaboration of a model of neurovisceral integration. Neurosci. Biobehav. Rev. 2009, 33, 81–88. [Google Scholar] [CrossRef]
- Thayer, J.F.; Friedman, B.H. Stop that! Inhibition, sensitization, and their neurovisceral concomitants. Scand. J. Psychol. 2002, 43, 123–130. [Google Scholar] [CrossRef]
- Thayer, J.F.; Brosschot, J.F. Psychosomatics and psychopathology: Looking up and down from the brain. Psychoneuroendocrinology 2005, 30, 1050–1058. [Google Scholar] [CrossRef]
- Friedman, B.H. An autonomic flexibility—Neurovisceral integration model of anxiety and cardiac vagal tone. Biol. Psychol. 2007, 74, 185–199. [Google Scholar] [CrossRef] [PubMed]
- Porges, S.W.; Raskin, D.C. Respiratory and heart rate components of attention. J. Exp. Psychol. 1969, 81, 497. [Google Scholar] [CrossRef] [PubMed]
- Richards, J.E.; Casey, B.J. Heart Rate Variability During Attention Phases in Young Infants. Psychophysiology 1991, 28, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Hansen, A.L.; Johnsen, B.H.; Thayer, J.F. Vagal influence on working memory and attention. Int. J. Psychophysiol. 2003, 48, 263–274. [Google Scholar] [CrossRef]
- Hansen, A.L.; Johnsen, B.H.; Thayer, J.F. Relationship between heart rate variability and cognitive function during threat of shock. Anxiety Stress Coping 2009, 22, 77–89. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, B.H.; Thayer, J.F.; Laberg, J.C.; Wormnes, B.; Raadal, M.; Skaret, E.; Kvale, G.; Berg, E. Attentional and physiological characteristics of patients with dental anxiety. J. Anxiety Disord. 2003, 17, 75–87. [Google Scholar] [CrossRef]
- Krypotos, A.-M.; Jahfari, S.; Ast VA van Kindt, M.; Forstmann, B.U. Individual differences in heart rate variability predict the degree of slowing during response inhibition and initiation in the presence of emotional stimuli. Front. Psychol. 2011, 2, 278. [Google Scholar] [CrossRef]
- Park, G.; Van Bavel, J.J.; Vasey, M.W.; Thayer, J.F. Cardiac Vagal Tone Predicts Inhibited Attention to Fearful Faces. Emotion 2012, 12, 1292. [Google Scholar] [CrossRef]
- Colzato, L.S.; Steenbergen, L. High Vagally Mediated Resting-State Heart Rate Variability Is Associated with Superior Action Cascading. Neuropsychologia 2017, 106, 1–6. [Google Scholar] [CrossRef]
- Colzato, L.S.; Jongkees, B.; De Wit, M.; Van Der Molen, M.J.W.; Steenbergen, L. Variable heart rate and a flexible mind: Higher resting-state heart rate variability predicts better task-switching. Cogn. Affect. Behav. Neurosci. 2018, 18, 730–738. [Google Scholar] [CrossRef]
- Fabes, R.A.; Eisenberg, N.; Eisenbud, L. Behavioral and physiological correlates of children’s reactions to others in distress. Dev. Psychol. 1993, 29, 655. [Google Scholar] [CrossRef]
- Fabes, R.A.; Eisenberg, N. Regulatory control and adults’ stress-related responses to daily life events. J. Personal. Soc. Psychol. 1997, 73, 1107. [Google Scholar] [CrossRef]
- Geisler, F.C.; Vennewald, N.; Kubiak, T.; Weber, H. The impact of heart rate variability on subjective well-being is mediated by emotion regulation. Personal. Individ. Differ. 2010, 49, 723–728. [Google Scholar] [CrossRef]
- Thayer, J.F.; Ahs, F.; Fredrikson, M.; Sollers, J.J., III; Wager, T.D. A meta-analysis of heart rate variability and neuroimaging studies: Implications for heart rate variability as a marker of stress and health. Neurosci. Biobehav. Rev. 2012, 36, 747–756. [Google Scholar] [CrossRef]
- Appelhans, B.M.; Luecken, L.J. Heart Rate Variability as an Index of Regulated Emotional Responding. Rev. Gen. Psychol. 2006, 10, 229–240. [Google Scholar] [CrossRef]
- Park, G.; Vasey, M.W.; Van Bavel, J.J.; Thayer, J.F. When Tonic Cardiac Vagal Tone Predicts Changes in Phasic Vagal Tone: The Role of Fear and Perceptual Load. Psychophysiology 2014, 51, 419–426. [Google Scholar] [CrossRef]
- Thayer, J.F.; Friedman, B.H.; Borkovec, T.D. Autonomic characteristics of generalized anxiety disorder and worry. Biol. Psychiatry 1996, 39, 255–266. [Google Scholar] [CrossRef]
- Benvenuti, S.M.; Mennella, R.; Buodo, G.; Palomba, D. Dysphoria is associated with reduced cardiac vagal withdrawal during the imagery of pleasant scripts: Evidence for the positive attenuation hypothesis. Biol. Psychol. 2015, 106, 28–38. [Google Scholar] [CrossRef]
- El-Sheikh, M.; Hinnant, B.; Erath, S. Developmental trajectories of delinquency symptoms in childhood: The role of marital conflict and autonomic nervous system activity. J. Abnorm. Psychol. 2011, 120, 16–32. [Google Scholar] [CrossRef]
- Rottenberg, J.; Salomon, K.; Gross, J.J.; Gotlib, I.H. Vagal Withdrawal to a Sad Film Predicts Subsequent Recovery from Depression. Psychophysiology 2005, 42, 277–281. [Google Scholar] [CrossRef]
- Weber, C.S.; Thayer, J.F.; Rudat, M.; Wirtz, P.H.; Zimmermann-Viehoff, F.; Thomas, A.; Perschel, F.H.; Arck, P.C.; Deter, H.C. Low vagal tone is associated with impaired post stress recovery of cardiovascular, endocrine, and immune markers. Eur. J. Appl. Physiol. 2010, 109, 201–211. [Google Scholar] [CrossRef] [PubMed]
- Beauchaine, T.P.; Gatzke-Kopp, L.; Mead, H.K. Polyvagal Theory and developmental psychopathology: Emotion dysregulation and conduct problems from preschool to adolescence. Biol. Psychol. 2007, 74, 174–184. [Google Scholar] [CrossRef]
- Schwerdtfeger, A.; Derakshan, N. The Time Line of Threat Processing and Vagal Withdrawal in Response to a Self-Threatening Stressor in Cognitive Avoidant Copers: Evidence for Vigilance-Avoidance Theory. Psychophysiology 2010, 47, 786–795. [Google Scholar] [CrossRef] [PubMed]
- Segerstrom, S.C.; Nes, L.S. Heart rate variability reflects self-regulatory strength, effort, and fatigue. Psychol. Sci. 2007, 18, 275–281. [Google Scholar] [CrossRef] [PubMed]
- Butler, E.A.; Wilhelm, F.H.; Gross, J.J. Respiratory Sinus Arrhythmia, Emotion, and Emotion Regulation During Social Interaction. Psychophysiology 2006, 43, 612–622. [Google Scholar] [CrossRef] [PubMed]
- Laborde, S.; Raab, M.; Kinrade, N.P. Is the ability to keep your mind sharp under pressure reflected in your heart? Evidence for the neurophysiological bases of decision reinvestment. Biol. Psychol. 2014, 100, 34–42. [Google Scholar] [CrossRef] [PubMed]
- Laborde, S.; Lautenbach, F.; Allen, M.S. The contribution of coping-related variables and heart rate variability to visual search performance under pressure. Physiol. Behav. 2015, 139, 532–540. [Google Scholar] [CrossRef]
- Laborde, S.; Mosley, E.; Thayer, J.F. Heart rate variability and cardiac vagal tone in psychophysiological research–recommendations for experiment planning, data analysis, and data reporting. Front. Psychol. 2017, 8, 213. [Google Scholar] [CrossRef]
- Beauchaine, T. Vagal tone, development, and Gray’s motivational theory: Toward an integrated model of autonomic nervous system functioning in psychopathology. Dev. Psychopathol. 2001, 13, 183–214. [Google Scholar] [CrossRef]
- Schulz, S.; Koschke, M.; Bar, K.-J.; Voss, A. The altered complexity of cardiovascular regulation in depressed patients. Physiol. Meas. 2010, 31, 303. [Google Scholar] [CrossRef]
- Leistedt, S.J.; Linkowski, P.; Lanquart, J.P.; Mietus, J.; Davis, R.B.; Goldberger, A.L.; Costa, M.D. Decreased neuroautonomic complexity in men during an acute major depressive episode: Analysis of heart rate dynamics. Transl. Psychiatry 2011, 1, e27. [Google Scholar] [CrossRef]
- Koenig, J.; Kemp, A.H.; Beauchaine, T.P.; Thayer, J.F.; Kaess, M. Depression and resting state heart rate variability in children and adolescents—A systematic review and meta-analysis. Clin. Psychol. Rev. 2016, 46, 136–150. [Google Scholar] [CrossRef]
- Piccirillo, G.; Elvira, S.; Bucca, C.; Viola, E.; Cacciafesta, M.; Marigliano, V. Abnormal passive head-up tilt test in subjects with symptoms of anxiety power spectral analysis study of heart rate and blood pressure. Int. J. Cardiol. 1997, 60, 121–131. [Google Scholar] [CrossRef]
- Dalack, G.W.; Roose, S.P. Perspectives on the relationship between cardiovascular disease and affective disorder. J. Clin. Psychiatry 1990, 51, 4–11. [Google Scholar]
- Klein, E.; Cnaani, E.; Harel, T.; Braun, S.; Ben-Haim, S.A. Altered heart rate variability in panic disorder patients. Biol. Psychiatry 1995, 37, 18–24. [Google Scholar] [CrossRef]
- Lakusic, N.; Fuckar, K.; Mahovic, D.; Cerovec, D.; Majsec, M.; Stancin, N. Characteristics of Heart Rate Variability in War Veterans with Post-Traumatic Stress Disorder after Myocardial Infarction. Mil. Med. 2007, 172, 1190–1193. [Google Scholar] [CrossRef]
- Prasko, J.; Latalova, K.; Diveky, T.; Grambal, A.; Kamaradova, D.; Velartova, H.; Salinger, J.; Opavsky, J.; Silhan, P. Panic disorder, autonomic nervous system and dissociation—Changes during therapy. Neuroendocr. Lett. 2011, 32, 101–111. [Google Scholar]
- Hartmann, R.; Schmidt, F.M.; Sander, C.; Hegerl, U. Heart Rate Variability as Indicator of Clinical State in Depression. Front. Psychiatry 2019, 9, 735. [Google Scholar] [CrossRef]
- Dimitriev, D.A.; Saperova, E.V.; Dimitriev, A. State Anxiety and Nonlinear Dynamics of Heart Rate Variability in Students. PLoS ONE 2016, 11, e0146131. [Google Scholar] [CrossRef]
- Kim, K.; Lee, S.; Kim, J.-H. Diminished autonomic neurocardiac function in patients with generalized anxiety disorder. Neuropsychiatr. Dis. Treat. 2016, 12, 3111–3118. [Google Scholar] [CrossRef]
- Cohen, H.; Kaplan, Z.; Kotler, M.; Mittelman, I.; Osher, Y.; Bersudsky, Y. Impaired heart rate variability in euthymic bipolar patients. Bipolar Disord. 2003, 5, 138–143. [Google Scholar] [CrossRef] [PubMed]
- Henry, B.L.; Minassian, A.; Paulus, M.P.; Geyer, M.A.; Perry, W. Heart rate variability in bipolar mania and schizophrenia. J. Psychiatr. Res. 2010, 44, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-S.; Kim, B.; Hong, Y.; Joo, Y.H. Heart rate variability in the subsyndromal depressive phase of bipolar disorder. Psychiatry Clin. Neurosci. 2012, 66, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.-A.; Chang, C.-C.; Tzeng, N.-S.; Kuo, T.B.J.; Lu, R.-B.; Huang, S.-Y. Heart rate variability in unmedicated patients with bipolar disorder in the manic phase. Psychiatry Clin. Neurosci. 2014, 68, 674–682. [Google Scholar] [CrossRef]
- Carr, O.; De Vos, M.; Saunders, K.E.A. Heart rate variability in bipolar disorder and borderline personality disorder: A clinical review. Evid. Based Ment. Health 2017, 21, 23–30. [Google Scholar] [CrossRef]
- Ebner-Priemer, U.W.; Welch, S.S.; Grossman, P.; Reisch, T.; Linehan, M.M.; Bohus, M. Psychophysiological ambulatory assessment of affective dysregulation in borderline personality disorder. Psychiatry Res. 2007, 150, 265–275. [Google Scholar] [CrossRef]
- Weinberg, A.; Klonsky, E.D.; Hajcak, G. Autonomic impairment in Borderline Personality Disorder: A laboratory investigation. Brain Cogn. 2009, 71, 279–286. [Google Scholar] [CrossRef]
- Bär, K.J.; Letzsch, A.; Jochum, T.; Wagner, G.; Greiner, W.; Sauer, H. Loss of efferent vagal activity in acute schizophrenia. J. Psychiatr. Res. 2005, 39, 519–527. [Google Scholar] [CrossRef]
- Jindal, R.; MacKenzie, E.M.; Baker, G.B.; Yeragani, V.K. Cardiac risk and schizophrenia. J. Psychiatry Neurosci. 2005, 30, 393. [Google Scholar]
- Bär, K.-J.; Boettger, M.; Koschke, M.; Schulz, S.; Chokka, P.; Yeragani, V.K.; Voss, A. Non-linear complexity measures of heart rate variability in acute schizophrenia. Clin. Neurophysiol. 2007, 118, 2009–2015. [Google Scholar] [CrossRef]
- Chang, J.S.; Yoo, C.S.; Yi, S.H.; Hong, K.H.; Oh, H.S.; Hwang, J.Y.; Kim, S.-G.; Ahn, Y.M.; Kim, Y.S. Differential pattern of heart rate variability in patients with schizophrenia. Prog. Neuro-Psychopharmacol. Biol. Psychiatry 2009, 33, 991–995. [Google Scholar] [CrossRef]
- Valkonen-Korhonen, M.; Tarvainen, M.; Ranta-Aho, P.; Karjalainen, P.A.; Partanen, J.; Karhu, J.; Lehtonen, J. Heart rate variability in acute psychosis. Psychophysiol. 2003, 40, 716–726. [Google Scholar] [CrossRef]
- Toichi, M.; Kubota, Y.; Murai, T.; Kamio, Y.; Sakihama, M.; Toriuchi, T.; Inakuma, T.; Sengoku, A.; Miyoshi, K. The influence of psychotic states on the autonomic nervous system in schizophrenia. Int. J. Psychophysiol. 1999, 31, 147–154. [Google Scholar] [CrossRef]
- Einvik, G.; Hrubos-Strøm, H.; Randby, A.; Nordhus, I.H.; Somers, V.K.; Omland, T.; Dammen, T. Major Depressive Disorder, Anxiety Disorders, and Cardiac Biomarkers in Subjects at High Risk of Obstructive Sleep Apnea. Psychosom. Med. 2011, 73, 378–384. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Tracey, K.J. The vagus nerve and the inflammatory reflex—Linking immunity and metabolism. Nat. Rev. Endocrinol. 2012, 8, 743–754. [Google Scholar] [CrossRef]
- Moon, E.; Lee, S.-H.; Kim, D.-H.; Hwang, B. Comparative Study of Heart Rate Variability in Patients with Schizophrenia, Bipolar Disorder, Post-traumatic Stress Disorder, or Major Depressive Disorder. Clin. Psychopharmacol. Neurosci. 2013, 11, 137–143. [Google Scholar] [CrossRef]
- Hage, B.; Sinacore, J.; Heilman, K.; Porges, S.W.; Halaris, A. Heart Rate Variability Predicts Treatment Outcome in Major Depression. J. Psychiatry Brain Sci. 2017, 2, 1. [Google Scholar] [CrossRef]
- Park, S.-W.; Lee, J.-H.; Kim, J.; Suh, S.; Lee, M.-S. Changes in heart rate variability in first-episode drug-naïve adolescents with major depressive disorder: A 12-week prospective study. J. Affect. Disord. 2018, 238, 250–255. [Google Scholar] [CrossRef]
- Porges, S.W. The polyvagal perspective. Biol. Psychol. 2007, 74, 116–143. [Google Scholar] [CrossRef]
- McCraty, R.; Atkinson, M.; Tomasino, D.; Bradley, R.T. The coherent heart heart-brain interactions, psychophysiological coherence, and the emergence of system-wide order. Integral Rev. A Transdiscipl. Transcult. J. N. Thought Res. Prax. 2009, 5, 354–381. [Google Scholar]
- McCraty, R.; Zayas, M.A. Cardiac coherence, self-regulation, autonomic stability, and psychosocial well-being. Front. Psychol. 2014, 5, 1090. [Google Scholar] [CrossRef]
- Vaschillo, E.G.; Vaschillo, B.; Lehrer, P.M. Characteristics of Resonance in Heart Rate Variability Stimulated by Biofeedback. Appl. Psychophysiol. Biofeedback 2006, 31, 129–142. [Google Scholar] [CrossRef]
- Lehrer, P.M.; Vaschillo, B.; Zucker, T.; Graves, J.; Katsamanis, M.; Aviles, M.; Wamboldt, F.S. Protocol for Heart Rate Variability Biofeedback Training. Biofeedback 2013, 41, 98–109. [Google Scholar] [CrossRef]
- Vaschillo, E.; Lehrer, P.; Rishe, N.; Konstantinov, M. Heart Rate Variability Biofeedback as a Method for Assessing Baroreflex Function: A Preliminary Study of Resonance in the Cardiovascular System. Appl. Psychophysiol. Biofeedback 2002, 27, 1–27. [Google Scholar] [CrossRef]
- Lehrer, P.M.; Vaschillo, E.; Vaschillo, B.; Lu, S.-E.; Eckberg, D.L.; Edelberg, R.; Shih, W.J.; Lin, Y.; Kuusela, T.A.; Tahvanainen, K.U.O.; et al. Heart Rate Variability Biofeedback Increases Baroreflex Gain and Peak Expiratory Flow. Psychosom. Med. 2003, 65, 796–805. [Google Scholar] [CrossRef]
- Hallman, D.M.; Olsson, E.; Von Schéele, B.; Melin, L.; Lyskov, E. Effects of Heart Rate Variability Biofeedback in Subjects with Stress-Related Chronic Neck Pain: A Pilot Study. Appl. Psychophysiol. Biofeedback 2011, 36, 71–80. [Google Scholar] [CrossRef]
- Henriques, G.; Keffer, S.; Abrahamson, C.; Horst, S.J. Exploring the Effectiveness of a Computer-Based Heart Rate Variability Biofeedback Program in Reducing Anxiety in College Students. Appl. Psychophysiol. Biofeedback 2011, 36, 101–112. [Google Scholar] [CrossRef]
- Goessl, V.C.; Curtiss, J.E.; Hofmann, S.G. The effect of heart rate variability biofeedback training on stress and anxiety: A meta-analysis. Psychol. Med. 2017, 47, 2578–2586. [Google Scholar] [CrossRef]
- Karavidas, M.K.; Lehrer, P.M.; Vaschillo, E.; Vaschillo, B.; Marin, H.; Buyske, S.; Malinovsky, I.; Radvanski, D.; Hassett, A. Preliminary Results of an Open Label Study of Heart Rate Variability Biofeedback for the Treatment of Major Depression. Appl. Psychophysiol. Biofeedback 2007, 32, 19–30. [Google Scholar] [CrossRef]
- Siepmann, M.; Aykac, V.; Unterdörfer, J.; Petrowski, K.; Mueck-Weymann, M. A Pilot Study on the Effects of Heart Rate Variability Biofeedback in Patients with Depression and in Healthy Subjects. Appl. Psychophysiol. Biofeedback 2008, 33, 195–201. [Google Scholar] [CrossRef]
- Caldwell, Y.T.; Steffen, P.R. Adding HRV biofeedback to psychotherapy increases heart rate variability and improves the treatment of major depressive disorder. Int. J. Psychophysiol. 2018, 131, 96–101. [Google Scholar] [CrossRef] [PubMed]
- Ginsberg, J.; Berry, E.M.; Powell, A.D. Cardiac coherence and posttraumatic stress disorder in combat veterans. Altern. Ther. Health Med. 2010, 16, 52–60. [Google Scholar] [PubMed]
- Lloyd, A.; Brett, D.; Wesnes, K. Coherence training in children with attention-deficit hyperactivity disorder: Cognitive functions and behavioral changes. Altern. Ther. Health Med. 2010, 16, 34–42. [Google Scholar] [PubMed]
- Lehrer, P.M.; Gevirtz, R. Heart rate variability biofeedback: How and why does it work? Front. Psychol. 2014, 5, 756. [Google Scholar] [CrossRef]
- Makowski, D.; Pham, T.; Lau, Z.J.; Brammer, J.C.; Lespinasse, F.; Pham, H.; Schölzel, C.; Chen, S.H.A. NeuroKit2: A Python toolbox for neurophysiological signal processing. Behav. Res. Methods 2021, 1–8. [Google Scholar] [CrossRef]
- van Gent, P.; Farah, H.; van Nes, N.; van Arem, B. HeartPy: A novel heart rate algorithm for the analysis of noisy signals. Transp. Res. Part F Traffic Psychol. Behav. 2019, 66, 368–378. [Google Scholar] [CrossRef]
- Gomes, P.; Margaritoff, P.; Silva, H. pyHRV: Development and evaluation of an open-source python toolbox for heart rate variability (HRV). In Proceedings of the Int’l Conference on Electrical, Electronic and Computing Engineering (IcETRAN), Srebrno Jezero, Serbia, 3–6 June 2019; pp. 822–828. [Google Scholar]
- Bartels, R.; Peçanha, T. HRV: A Pythonic package for Heart Rate Variability Analysis. J. Open Source Softw. 2020, 5, 1867. [Google Scholar] [CrossRef]
- Tarvainen, M.P.; Niskanen, J.P.; Lipponen, J.A.; Ranta-Aho, P.O.; Karjalainen, P.A. Kubios HRV–heart rate variability analysis software. Comput. Methods Programs Biomed. 2014, 113, 210–220. [Google Scholar] [CrossRef]
- Saboul, D.; Pialoux, V.; Hautier, C. The breathing effect of the LF/HF ratio in the heart rate variability measurements of athletes. Eur. J. Sport Sci. 2011, 14, S282–S288. [Google Scholar] [CrossRef]
- Sassi, R.; Cerutti, S.; Lombardi, F.; Malik, M.; Huikuri, H.V.; Peng, C.-K.; Schmidt, G.; Yamamoto, Y.; Gorenek, B.; Lip, G.Y.; et al. Advances in heart rate variability signal analysis: Joint position statement by the e-Cardiology ESC Working Group and the European Heart Rhythm Association co-endorsed by the Asia Pacific Heart Rhythm Society. Europace 2015, 17, 1341–1353. [Google Scholar] [CrossRef]
- Catai, A.M.; Pastre, C.M.; de Godoy, M.F.; da Silva, E.; Takahashi, A.C.D.M.; Vanderlei, L.C.M. Heart rate variability: Are you using it properly? Standardisation checklist of procedures. Braz. J. Phys. Ther. 2020, 24, 91–102. [Google Scholar] [CrossRef]
- Aeschbacher, S.; Schoen, T.; Dörig, L.; Kreuzmann, R.; Neuhauser, C.; Schmidt-Trucksäss, A.; Probst-Hensch, N.M.; Risch, M.; Risch, L.; Conen, D. Heart rate, heart rate variability and inflammatory biomarkers among young and healthy adults. Ann. Med. 2016, 49, 32–41. [Google Scholar] [CrossRef]
- Umetani, K.; Singer, D.H.; McCraty, R.; Atkinson, M. Twenty-Four Hour Time Domain Heart Rate Variability and Heart Rate: Relations to Age and Gender Over Nine Decades. J. Am. Coll. Cardiol. 1998, 31, 593–601. [Google Scholar] [CrossRef]
- Nunan, D.; Sandercock, G.R.H.; Brodie, D.A. A Quantitative Systematic Review of Normal Values for Short-Term Heart Rate Variability in Healthy Adults. Pacing Clin. Electrophysiol. 2010, 33, 1407–1417. [Google Scholar] [CrossRef]
- Dantas, E.M.; Kemp, A.H.; Andreão, R.V.; Da Silva, V.J.D.; Brunoni, A.R.; Hoshi, R.A.; Bensenor, I.M.; Lotufo, P.A.; Ribeiro, A.L.P.; Mill, J.G. Reference values for short-term resting-state heart rate variability in healthy adults: Results from the Brazilian Longitudinal Study of Adult Health-ELSA-Brasil study. Psychophysiology 2018, 55, e13052. [Google Scholar] [CrossRef]
- Gąsior, J.S.; Sacha, J.; Pawlowski, M.; Zielinski, J.; Jelen, P.J.; Tomik, A.; Ksiazczyk, T.M.; Werner, B.; Dkabrowski, M.J. Normative values for heart rate variability parameters in school-aged children: Simple approach considering differences in average heart rate. Front. Physiol. 2018, 9, 1495. [Google Scholar] [CrossRef]
- Sammito, S.; Böckelmann, I. Reference values for time- and frequency-domain heart rate variability measures. Heart Rhythm. 2016, 13, 1309–1316. [Google Scholar] [CrossRef]
- Berg, M.E.V.D.; Rijnbeek, P.R.; Niemeijer, M.N.; Hofman, A.; Van Herpen, G.; Bots, M.L.; Hillege, H.; Swenne, C.A.; Eijgelsheim, M.; Stricker, B.H.; et al. Normal Values of Corrected Heart-Rate Variability in 10-Second Electrocardiograms for All Ages. Front. Physiol. 2018, 9, 424. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).