SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR)
Abstract
1. Introduction
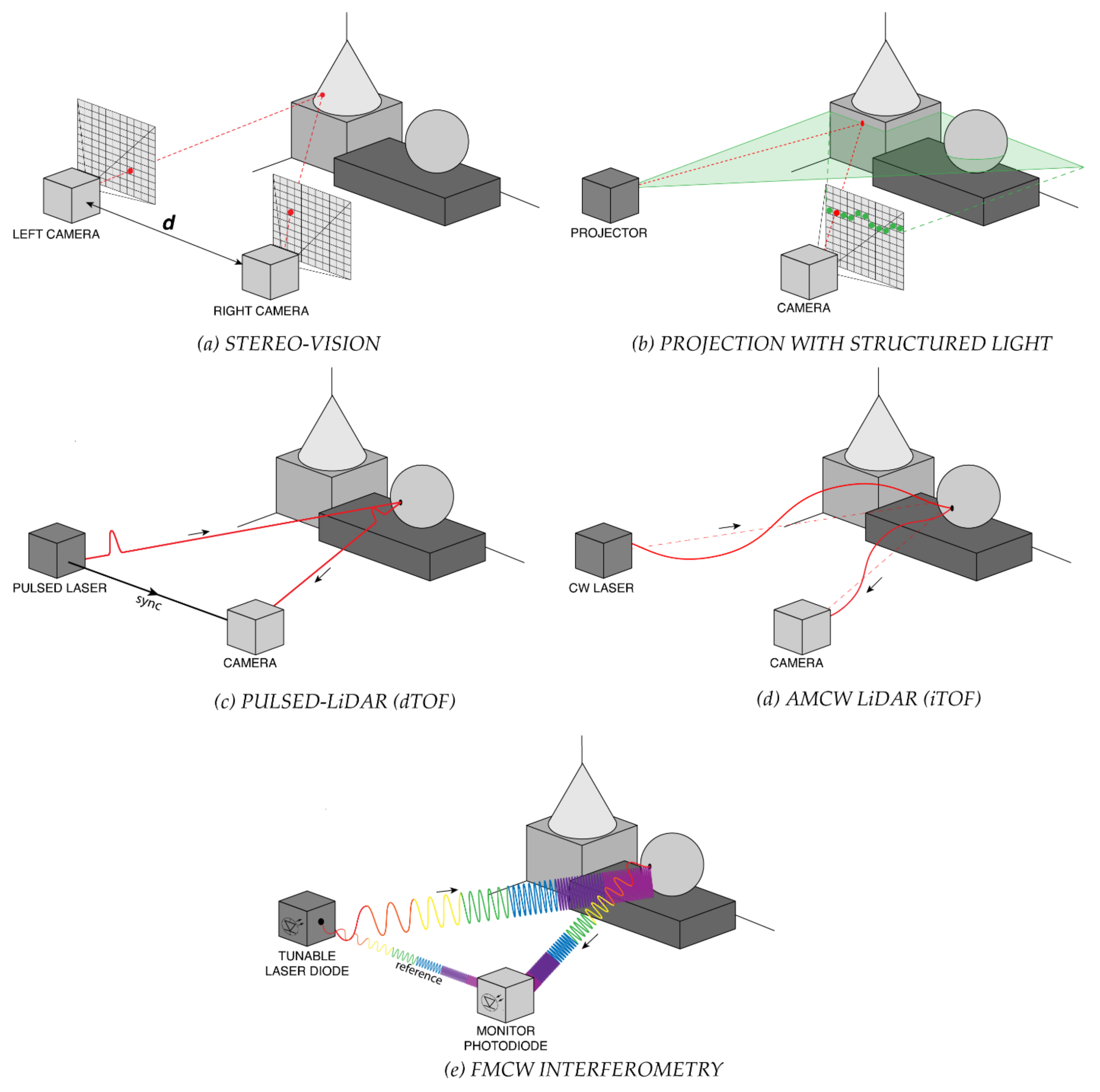
1.1. LiDAR Techniques
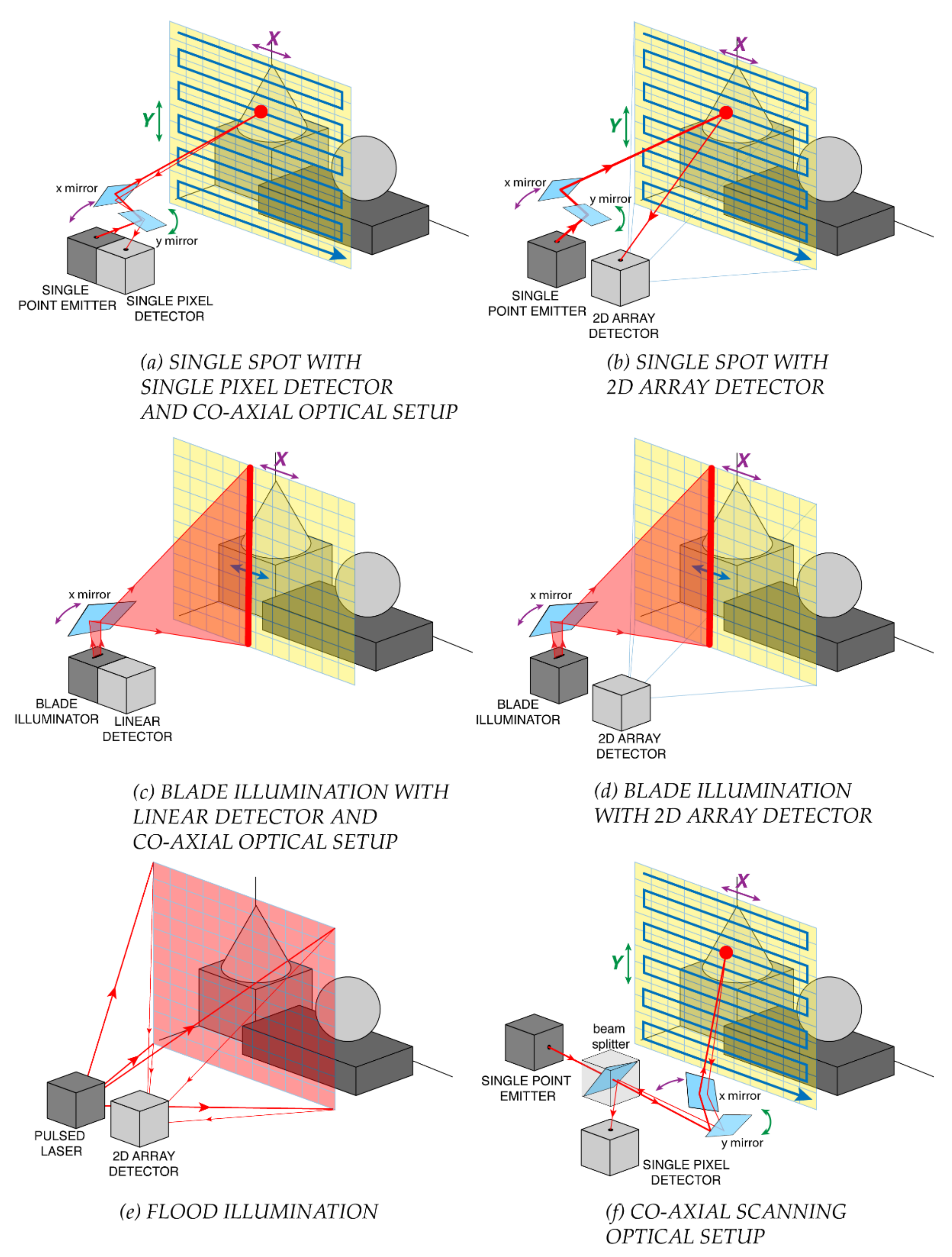
1.2. Illumination Schemes
1.3. Pulsed-LiDAR Requirements and Challenges
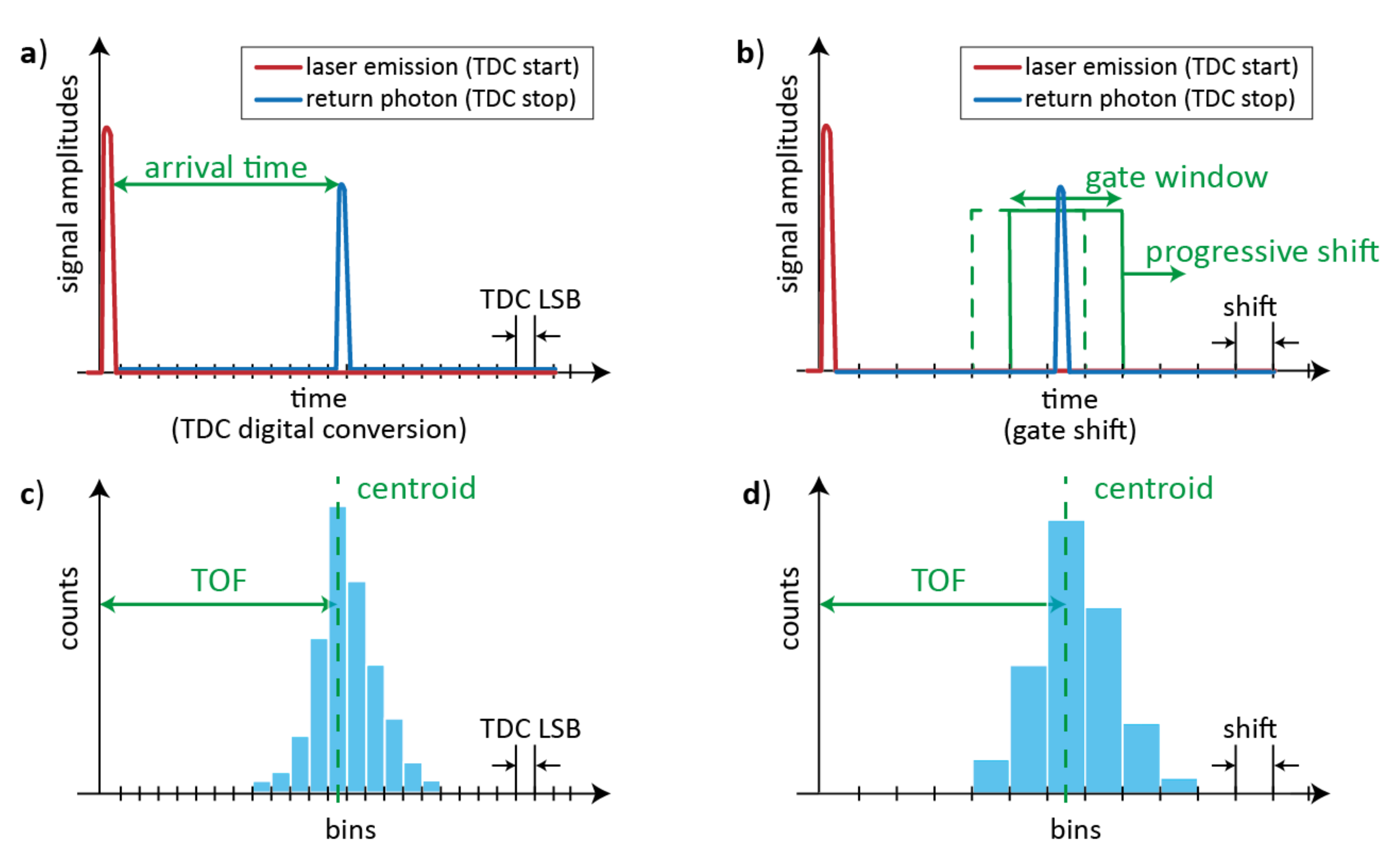
2. Detectors for Pulsed-LiDAR Systems
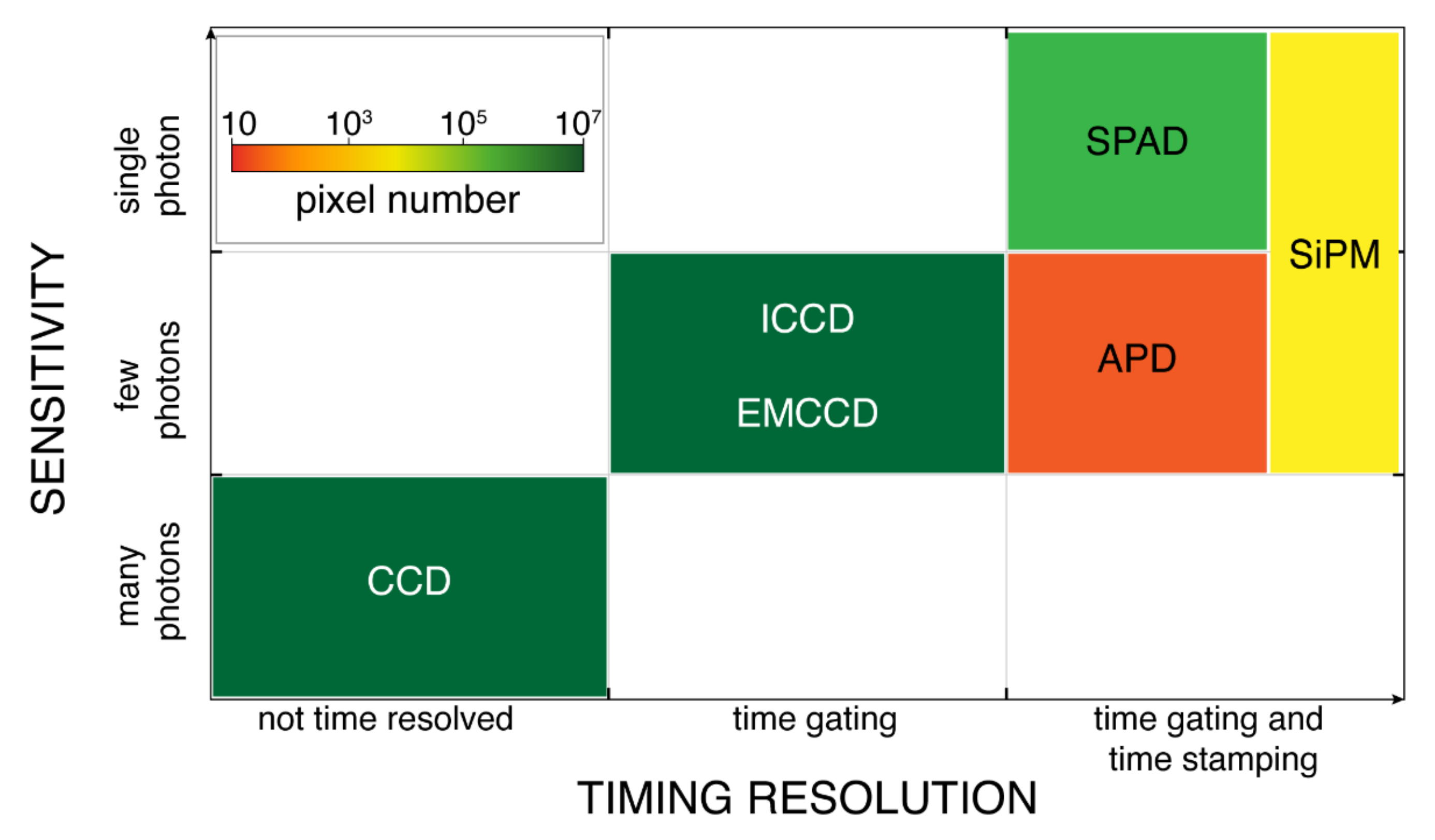
2.1. Detector Technologies
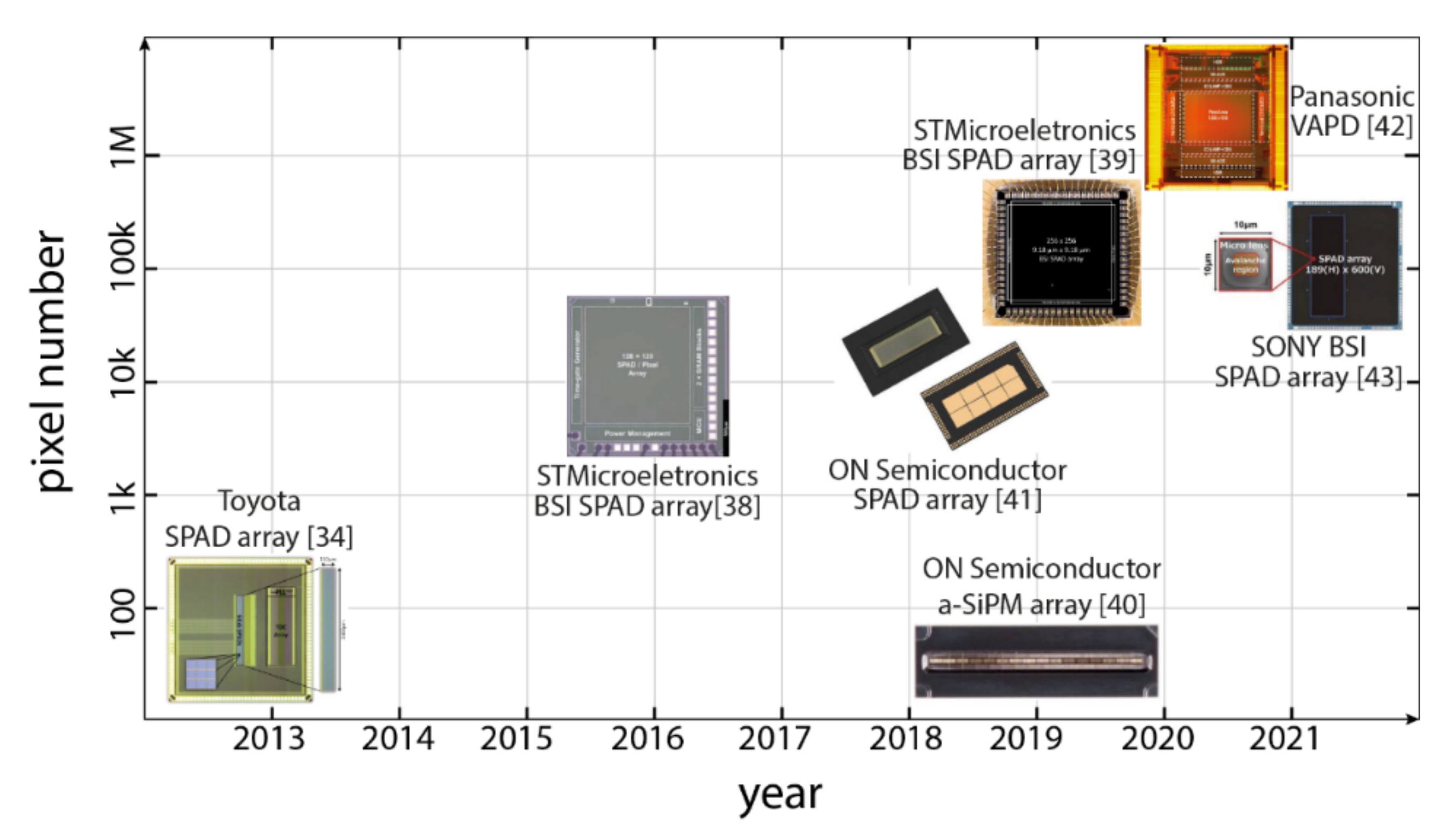
2.2. Commercial SPAD and SiPM Detectors for LiDAR
3. SPAD and SiPM Detectors for Pulsed-LiDAR
3.1. Selected SPAD LiDAR Detectors Architectures
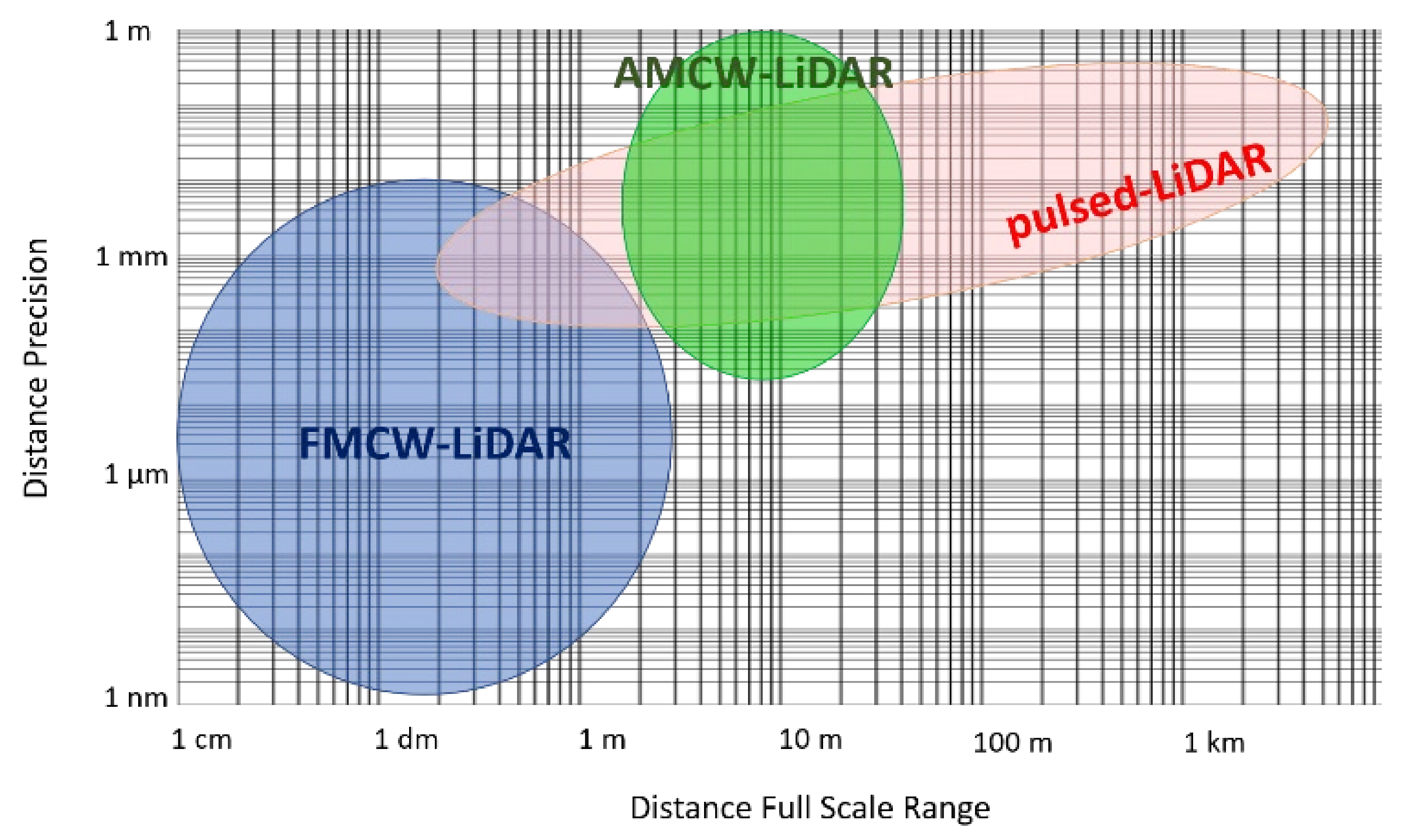
3.2. Maximum Range and Precision
3.3. FOV and Angular Resolution
3.4. Measurement Speed and Background Suppression
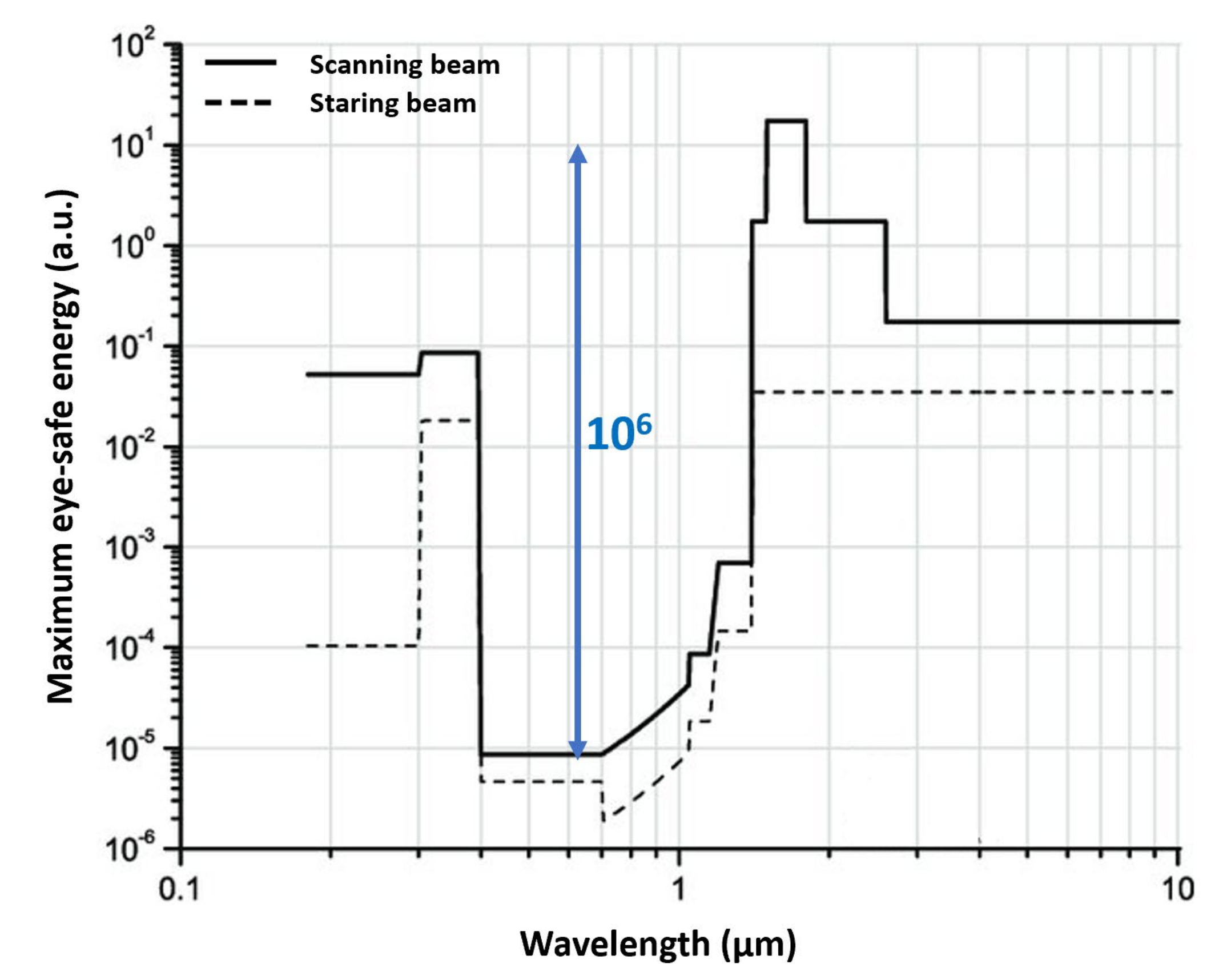
3.5. Eye-Safety
3.6. Interference Robustness for Multi-Camera Operation
4. Discussion on Next Generation Detectors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Lai, B.; Wang, C.; Bian, X.; Yang, W.; Xia, Y.; Lin, X.; Lai, S.H.; Weng, D.; Li, J. Learning to Match 2D Images and 3D LiDAR Point Clouds for Outdoor Augmented Reality. In Proceedings of the IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Atlanta, GA, USA, 22–26 March 2020; pp. 654–655. [Google Scholar]
- Warren, M.E. Automotive LIDAR Technology. In Proceedings of the Symposium on VLSI Circuits, Kyoto, Japan, 9–14 June 2019; pp. C254–C255. [Google Scholar]
- Steger, C.; Ulrich, M.; Wiedemann, C. Machine Vision Algorithms and Applications; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Glennie, C.L.; Carter, W.E.; Shrestha, R.L.; Dietrich, W.E. Geodetic imaging with airborne LiDAR: The Earth's surface revealed. Rep. Prog. Phys. 2013, 76, 086801. [Google Scholar] [CrossRef] [PubMed]
- Yu, A.W.; Troupaki, E.; Li, S.X.; Coyle, D.B.; Stysley, P.; Numata, K.; Fahey, M.E.; Stephen, M.A.; Chen, J.R.; Yang, G.; et al. Orbiting and In-Situ Lidars for Earth and Planetary Applications. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3479–3482. [Google Scholar]
- Pierrottet, D.F.; Amzajerdian, F.; Hines, G.D.; Barnes, B.W.; Petway, L.B.; Carson, J.M. Lidar Development at NASA Langley Research Center for Vehicle Navigation and Landing in GPS Denied Environments. In Proceedings of the IEEE Research and Applications of Photonics In Defense Conference (RAPID), Miramar Beach, FL, USA, 22–24 August 2018; pp. 1–4. [Google Scholar]
- Rangwala, S. Lidar: Lighting the path to vehicle autonomy. SPIE News, March 2021. Available online: https://spie.org/news/photonics-focus/marapr-2021/lidar-lighting-the-path-to-vehicle-autonomy?SSO=1 (accessed on 31 May 2021).
- Hartley, R.I.; Sturm, P. Triangulation. Comput. Vis. Image Underst. 1997, 68, 146–157. [Google Scholar] [CrossRef]
- Bertozzi, M.; Broggi, A.; Fascioli, A.; Nichele, S. Stereo vision-based vehicle detection. In Proceedings of the IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 5 October 2000; pp. 39–44. [Google Scholar]
- Sun, J.; Li, Y.; Kang, S.B.; Shum, H.Y. Symmetric Stereo Matching for Occlusion Handling. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 399–406. [Google Scholar]
- Behroozpour, B.; Sandborn, P.A.M.; Wu, M.C.; Boser, B.E. Lidar System Architectures and Circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
- ENSENSO XR SERIES. Available online: https://en.ids-imaging.com/ensenso-3d-camera-xr-series.html (accessed on 25 May 2021).
- Structure Core. Available online: https://structure.io/structure-core?ref=hackernoon.com (accessed on 25 May 2021).
- Intel® RealSense™ Depth Camera D455. Available online: https://www.intelrealsense.com/depth-camera-d455/ (accessed on 25 May 2021).
- Geng, J. Structured-light 3D surface imaging: a tutorial. Adv. Opt. Photon. 2011, 3, 128–160. [Google Scholar] [CrossRef]
- PRIMESENSE CARMINE. Available online: http://xtionprolive.com/primesense-carmine-1.09?ref=hackernoon.com (accessed on 25 May 2021).
- Structure Sensor: Capture the World in 3D. Available online: https://www.kickstarter.com/projects/occipital/structure-sensor-capture-the-world-in-3d?ref=hackernoon.com (accessed on 25 May 2021).
- Atra ORBBEC. Available online: https://orbbec3d.com/product-astra-pro/?ref=hackernoon.com (accessed on 25 May 2021).
- Smisek, J.; Jancosek, M.; Pajdla, T. 3D with Kinect. In Consumer Depth Cameras for Computer Vision; Springer: Berlin, Germany, 2013; pp. 3–25. [Google Scholar]
- Hansard, M.; Lee, S.; Choi, O.; Horaud, R.P. Time-of-Flight Cameras: Principles, Methods and Applications; Springer: Berlin, Germany, 2012. [Google Scholar]
- Becker, W. Advanced Time-Correlated Single Photon Counting Techniques; Springer: Berlin, Germany, 2005. [Google Scholar]
- Becker, W.; Bergmann, A.; Hink, M.A.; König, K.; Benndorf, K.; Biskup, C. Fluorescence lifetime imaging by time-correlated single-photon counting. Microsc. Res. Tech. 2004, 63, 58–66. [Google Scholar] [CrossRef]
- Becker, W.; Bergmann, A.; Kacprzak, M.; Liebert, A. Advanced time-correlated single photon counting technique for spectroscopy and imaging of biological systems. In Proceedings of the SPIE, Fourth International Conference on Photonics and Imaging in Biology and Medicine, Tianjin, China, 3–6 September 2005; p. 604714. [Google Scholar]
- Bronzi, D.; Zou, Y.; Villa, F.; Tisa, S.; Tosi, A.; Zappa, F. Automotive Three-Dimensional Vision through a Single-Photon Counting SPAD Camera. IEEE Trans. Intell. Transp. Syst. 2016, 17, 782–785. [Google Scholar] [CrossRef]
- Bellisai, S.; Bronzi, D.; Villa, F.; Tisa, S.; Tosi, A.; Zappa, F. Single-photon pulsed light indirect time-of-flight 3D ranging. Opt. Express 2013, 21, 5086–5098. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, Z.; Tian, Y.; Set, S.Y.; Yamashita, S. Comprehensive Ranging Disambiguation for Amplitude-Modulated Continuous-Wave Laser Scanner With Focusing Optics. IEEE Trans. Instrum. Meas. 2021, 70, 8500711. [Google Scholar]
- Lum, D.J.; Knarr, S.H.; Howell, J.C. Frequency-modulated continuous-wave LiDAR compressive depth-mapping. Opt. Express 2018, 26, 15420–15435. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yi, L.; Qu, X. Simultaneous measurements of velocity and distance via a dual-path FMCW lidar system. Opt. Commun. 2020, 474, 126066. [Google Scholar] [CrossRef]
- FMCW Lidar: The Self-Driving Game-Changer. Available online: https://aurora.tech/blog/fmcw-lidar-the-self-driving-game-changer (accessed on 25 May 2021).
- Radar & LiDAR Autonomous Driving Sensors by Mobileye & Intel. Available online: https://static.mobileye.com/website/corporate/media/radar-lidar-fact-sheet.pdf (accessed on 25 May 2021).
- Sesta, V.; Severini, F.; Villa, F.; Lussana, R.; Zappa, F.; Nakamuro, K.; Matsui, Y. Spot Tracking and TDC Sharing in SPAD Arrays for TOF LiDAR. Sensors 2021, 21, 2936. [Google Scholar] [CrossRef]
- Velodyne Lidar-64E High Definition Real-Time 3D LiDAR Sensor. 2018. Available online: https://velodynelidar.com/products/hdl-64e/ (accessed on 20 April 2021).
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Ibrahim, M.F.; Hussain, A. A Survey on LiDAR Scanning Mechanisms. Electronics 2020, 9, 741. [Google Scholar] [CrossRef]
- McCarthy, A.; Ximin, R.; Della Frera, A.; Gemmell, N.R.; Krichel, N.J.; Scarcella, C.; Ruggeri, A.; Tosi, A.; Buller, G.S. Kilometer-range depth imaging at 1550 nm wavelength using an InGaAs/InP single-photon avalanche diode detector. Opt. Express 2013, 21, 22098–22113. [Google Scholar] [CrossRef]
- Lussana, R.; Villa, F.; Dalla Mora, A.; Contini, D.; Tosi, A.; Zappa, F. Enhanced single-photon time-of-flight 3D ranging. Opt. Express 2015, 23, 24962–24973. [Google Scholar] [CrossRef] [PubMed]
- American National Standard for Safe Use of Lasers, ANSI Z136.1-2014. Available online: https://webstore.ansi.org/Standards/LIA/ANSIZ1362014?gclid=Cj0KCQjwktKFBhCkARIsAJeDT0is6PtE21B1PaHKnON-J5vQ5uckb-avkU9UKG_dEEen50sdPyv-SBwaAq3-EALw_wcB (accessed on 31 May 2021).
- Kutila, M.; Pyykönen, P.; Holzhüter, H.; Colomb, M.; Duthon, P. Automotive LiDAR performance verification in fog and rain. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 1695–1701. [Google Scholar]
- De Monte, B.; Bell, R.T. Development of an EMCCD for lidar applications. In Proceeding of SPIE 10565, International Conference on Space Optics—ICSO, Rhodes Island, Greece, 20 November 2017; p. 1056502. [Google Scholar]
- Cester, L.; Lyons, A.; Braidotti, M.C.; Faccio, D. Time-of-Flight Imaging at 10 ps Resolution with an ICCD Camera. Sensors 2019, 19, 180. [Google Scholar] [CrossRef] [PubMed]
- Adamo, G.; Busacca, A. Time of Flight measurements via two LiDAR systems with SiPM and APD. In Proceedings of the AEIT International Annual Conference, Capri, Italy, 5–7 October 2016; pp. 1–5. [Google Scholar]
- Niclass, C.; Soga, M.; Matsubara, H.; Kato, S.; Kagami, M. A 100-m Range 10-Frame/s 340 x 96-Pixel Time-of-Flight Depth Sensor in 0.18 µm CMOS. IEEE J. Solid-State Circuits 2013, 48, 559–572. [Google Scholar] [CrossRef]
- Niclass, C.; Soga, M.; Matsubara, H.; Ogawa, M.; Kagami, M. A 0.18-µm CMOS SoC for a 100-m-Range 10-Frame/s 200×96-Pixel Time-of-Flight Depth Sensor. IEEE J. Solid-State Circuits 2014, 49, 315–330. [Google Scholar] [CrossRef]
- Takai, I.; Matsubara, H.; Soga, M.; Ohta, M.; Ogawa, M.; Yamashita, T. Single-Photon Avalanche Diode with Enhanced NIR-Sensitivity for Automotive LIDAR Systems. Sensors 2016, 16, 459. [Google Scholar] [CrossRef]
- Pellegrini, S.; Rae, B.; Pingault, A.; Golanski, D.; Jouan, S.; Lapeyre, C.; Mamdy, B. Industrialised SPAD in 40 nm technology. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017; pp. 16–16. [Google Scholar]
- Al Abbas, T.; Dutton, N.A.W.; Almer, O.; Pellegrini, S.; Henrion, Y.; Henderson, R.K. Backside illuminated SPAD image sensor with 7. In 83μm pitch in 3D-stacked CMOS technology. In Proceedings of the 2016 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2016; pp. 8.1.1–8.1.4. [Google Scholar]
- Hutchings, S.W.; Johnston, N.; Gyongy, I. A Reconfigurable 3-D-Stacked SPAD Imager with In-Pixel Histogramming for Flash LIDAR or High-Speed Time-of-Flight Imaging. IEEE J. Solid-State Circuits 2019, 54, 2947–2956. [Google Scholar] [CrossRef]
- Gnecchi, S.; Barry, C.; Bellis, S.; Buckley, S.; Jackson, C. Long Distance Ranging Performance of Gen3 LiDAR Imaging System based on 1×16 SiPM Array. In Proceedings of the International Image Sensors Society (IISS) Workshop, Snowbird, UT, USA, 23–27 June 2019; p. 11. [Google Scholar]
- Palubiak, D.; Gnecchi, S.; Jackson, C.; Ma, S.; Skorka, O.; Ispasoiu, R. Pandion: A 400 × 100 SPAD sensor for ToF LiDAR with 5 Hz median DCR and 11 ns mean dead-time. In Proceedings of the International Image Sensors Society (IISS) 2019, Snowbird, Utah, USA, 23–27 June 2019; p. R29. [Google Scholar]
- Okino, T.; Yamada, S.; Sakata, Y.; Takemoto, M.; Nose, Y.; Koshida, H.; Tamaru, M.; Sugiura, Y.; Saito, S.; Koyana, M.; et al. A 1200 × 900 6µm 450fps Geiger-Mode Vertical Avalanche Photodiodes CMOS Image Sensor for a 250m Time-of-Flight Ranging System Using Direct-Indirect-Mixed Frame Synthesis with Configurable-Depth-Resolution Down to 10cm. In Proceedings of the 2020 IEEE International Solid- State Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; pp. 96–98. [Google Scholar]
- Kumagai, O.; Ohmachi, J.; Matsumura, M.; Yagi, S.; Tayu, K.; Amagawa, K.; Matsukawa, T.; Qzawa, Q.; Hirono, D.; Shinozuka, Y.; et al. A 189×600 Back-Illuminated Stacked SPAD Direct Time-of-Flight Depth Sensor for Automotive LiDAR Systems. In Proceedings of the 2021 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 110–112. [Google Scholar]
- Jiang, X.; Wilton, S.; Kudryashov, I.; Itzler, M.A.; Entwistle, M.; Kotelnikov, J.; Katsnelson, A.; Piccione, B.; Owens, M.; Slomkowski, K.; et al. InGaAsP/InP Geiger-mode APD-based LiDAR. In Proceedings of the SPIE 10729, Optical Sensing, Imaging, and Photon Counting: From X-Rays to THz, San Diego, CA, USA, 18 September 2018; p. 107290C. [Google Scholar]
- Perenzoni, M.; Perenzoni, D.; Stoppa, D. A 64 × 64-Pixels Digital Silicon Photomultiplier Direct TOF Sensor With 100-MPhotons/s/pixel Background Rejection and Imaging/Altimeter Mode With 0.14% Precision Up To 6 km for Spacecraft Navigation and Landing. IEEE J. Solid-State Circuits 2017, 52, 151–160. [Google Scholar] [CrossRef]
- Ximenes, A.R.; Padmanabhan, P.; Lee, M.; Yamashita, Y.; Yaung, D.N.; Charbon, E. A 256×256 45/65nm 3D-stacked SPAD-based direct TOF image sensor for LiDAR applications with optical polar modulation for up to 18. In 6dB interference suppression. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 96–98. [Google Scholar]
- Ximenes, A.R.; Padmanabhan, P.; Lee, M.; Yamashita, Y.; Yaung, D.N.; Charbon, E. A Modular, Direct Time-of-Flight Depth Sensor in 45/65-nm 3-D-Stacked CMOS Technology. IEEE J. Solid-State Circuits 2019, 54, 3203–3214. [Google Scholar] [CrossRef]
- Beer, M.; Haase, J.; Ruskowski, J.; Kokozinski, R. Background Light Rejection in SPAD-Based LiDAR Sensors by Adaptive Photon Coincidence Detection. Sensors 2018, 18, 4338. [Google Scholar] [CrossRef]
- Zhang, C.; Lindner, S.; Antolović, I.M.; Pavia, J.M.; Wolf, M.; Charbon, E. A 30-frames/s, 252x144 SPAD Flash LiDAR with 1728 Dual-Clock 48.8-ps TDCs, and Pixel-Wise Integrated Histogramming. IEEE J. Solid-State Circuits 2019, 54, 1137–1151. [Google Scholar] [CrossRef]
- Seo, H.; Yoon, H.; Kim, D.; Kim, J.; Kim, S.J.; Chun, J.H.; Choi, J. A 36-Channel SPAD-Integrated Scanning LiDAR Sensor with Multi-Event Histogramming TDC and Embedded Interference Filter. In Proceedings of the 2020 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 16–19 June 2020; pp. 1–2. [Google Scholar]
- Padmanabhan, P.; Zhang, C.; Cazzaniga, M.; Efe, B.; Xinmenes, A.; Lee, M.; Charbon, E. A 256 × 128 3D-Stacked (45nm) SPAD FLASH LiDAR with 7-Level Coincidence Detection and Progressive Gating for 100m Range and 10klux Background Light. In Proceedings of the 2021 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 111–113. [Google Scholar]
- Gu, Y.; Lu, W.; Niu, Y.; Zhang, Y.; Chen, Z. A High Dynamic Range Pixel Circuit with High-voltage Protection for 128×128 Linear-mode APD Array. In Proceedings of the 2020 IEEE 15th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Kunming, China, 3–6 November 2020; pp. 1–3. [Google Scholar]
- Tontini, A.; Gasparini, L.; Perenzoni, M. Numerical Model of SPAD-Based Direct Time-of-Flight Flash LIDAR CMOS Image Sensors. Sensors 2020, 20, 5203. [Google Scholar] [CrossRef]
- Lee, M.J.; Charbon, E. Progress in single-photon avalanche diode image sensors in standard CMOS: From two-dimensional monolithic to three-dimensional-stacked technology. Jpn. J. Appl. Phys. 2018, 57, 1002A3. [Google Scholar] [CrossRef]
- You, Z.; Parmesan, L.; Pellegrini, S.; Henderson, R.K. 3µm Pitch, 1µm Active Diameter SPAD Arrays in 130 nm CMOS Imaging Technology. In Proceedings of the International Image Sensors Society (IISS) Workshop, Hiroshima, Japan, 30 May–2 June 2017. [Google Scholar]
- Henderson, R.K.; Webster, E.A.G.; Walker, R.; Richardson, J.A.; Grant, L.A. A 3 × 3, 5 µm pitch, 3-transistor single photon avalanche diode array with integrated 11 V bias generation in 90 nm CMOS technology. In Proceedings of the IEEE Int. Electron Devices Meeting, San Francisco, CA, USA, 6–8 December 2010; pp. 336–339. [Google Scholar]
- Morimoto, K.; Charbon, E. High fill-factor miniaturized SPAD arrays with a guard-ring-sharing technique. Opt. Express 2020, 28, 13068–13080. [Google Scholar] [CrossRef]
- Portaluppi, D.; Conca, E.; Villa, F. 32 × 32 CMOS SPAD Imager for Gated Imaging, Photon Timing, and Photon Coincidence. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–6. [Google Scholar] [CrossRef]
- López-Martínez, J.M.; Vornicu, I.; Carmona-Galán, R.; Rodríguez-Vázquez, Á. An Experimentally-Validated Verilog-A SPAD Model Extracted from TCAD Simulation. In Proceedings of the 25th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Bordeaux, France, 9–12 December 2018; pp. 137–140. [Google Scholar]
- Zappa, F.; Tosi, A.; Dalla Mora, A.; Tisa, S. SPICE modeling of single photon avalanche diodes. Sens. Actuators A Phys. 2009, 153, 197–204. [Google Scholar] [CrossRef]
- Villa, F.; Zou, Y.; Dalla Mora, A.; Tosi, A.; Zappa, F. SPICE Electrical Models and Simulations of Silicon Photomultipliers. IEEE Trans. Nucl. Sci. 2015, 62, 1950–1960. [Google Scholar] [CrossRef]
- Gyongy, I.; Hutchings, S.W.; Halimi, A.; Tyler, M.; Chan, S.; Zhu, F.; McLaughlin, S.; Henderson, R.K.; Leach, J. High-speed 3D sensing via hybrid-mode imaging and guided upsampling. Optica 2020, 7, 1253–1260. [Google Scholar] [CrossRef]
- Chan, S.; Halimi, A.; Zhu, F.; Gyongy, I.; Henderson, R.K.; Bowman, R.; McLaughlin, S.; Buller, G.S.; Leach, J. Long-range depth imaging using a single-photon detector array and non-local data fusion. Sci. Rep. 2019, 9, 8075. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Ingle, A.; Gupta, M. Asynchronous Single-Photon 3D Imaging. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 7909–7918. [Google Scholar]
- Vornicu, I.; Darie, A.; Carmona-Galán, R.; Rodríguez-Vázquez, Á. Compact Real-Time Inter-Frame Histogram Builder for 15-Bits High-Speed ToF-Imagers Based on Single-Photon Detection. IEEE Sens. J. 2019, 19, 2181–2190. [Google Scholar] [CrossRef]
- Buttgen, B.; Seitz, P. Robust Optical Time-of-Flight Range Imaging Based on Smart Pixel Structures. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 1512–1525. [Google Scholar] [CrossRef]
- Kostamovaara, J.; Jahromi, S.S.; Keränen, P. Temporal and Spatial Focusing in SPAD-Based Solid-State Pulsed Time-of-Flight Laser Range Imaging. Sensors 2020, 20, 5973. [Google Scholar] [CrossRef]
- Vornicu, I.; López-Martínez, J.M.; Bandi, F.N.; Galán, R.C.; Rodríguez-Vázquez, Á. Design of High-Efficiency SPADs for LiDAR Applications in 110nm CIS Technology. IEEE Sens. J. 2021, 21, 4776–4785. [Google Scholar] [CrossRef]
- Cohen, L.; Matekole, E.S.; Sher, Y.; Istrati, D.; Eisenberg, H.S.; Dowling, J.P. Thresholded Quantum LIDAR: Exploiting Photon-Number-Resolving Detection. Phys. Rev. Lett. 2019, 123, 203601. [Google Scholar] [CrossRef] [PubMed]
- Ulku, A.C.; Bruschini, C.; Antolovic, I.M.; Charbon, E. A 512 × 512 SPAD Image Sensor with Integrated Gating for Widefield FLIM. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 6801212. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, A.T.; Walker, R.; Finlayson, N.; Krstajic, N.; Williams, G.; Girkin, J.; Henderson, R. A CMOS SPAD Line Sensor with Per-Pixel Histogramming TDC for Time-Resolved Multispectral Imaging. IEEE J. Solid-State Circuits 2019, 54, 1705–1719. [Google Scholar] [CrossRef]
| Detector | Technology (nm) | Pixel Number | SPADs per Pixel | PDP @ 905 nm (%) | FF (%) | TDC LSB (ps) | TDC FSR (ns) |
|---|---|---|---|---|---|---|---|
| 2013 Niclass [41] | 180 | 32 × 1 | 12 | N.A.1 | 70 | 208 | 853 |
| 2017 Perenzoni [52] | 150 | 64 × 64 | 8 | N.A.1 | 26.5 | 250 10,000 | 6400 327,000 |
| 2018 Ximenes [53,54] | BSI 45/65 | 8 × 32 | 1 | 7.5 | 31 | 60 | 1000 |
| 2018 Beer [55] | 350 | 192 × 2 | 4 | 2 | 5.3 | 312.5 | N.A. |
| 2019 Zhang [56] | 180 | 252 × 144 | 1 | 5 | 28 | 48.8 | 200 |
| 2019 Hutchings [46] | BSI 90/40 | 256 × 256 2 64 × 64 3 | 1 2 4 × 4 3 | 5 | 51 | 38 4 560 5 | 143 4 9 5 |
| 2020 Seo [57] | 110 | 1 × 36 | 4 | N.A.1 | N.A.1 | 156 | 320 |
| 2021 Padmanabhan [58] | BSI 45/N.A. 1 | 256 × 128 | 1 | N.A.1 | N.A.1 | 60 | 1000 |
| 2021 Kumagai [50] | BSI 90/40 | 63 × 200 31 × 100 | 3 × 3 4 × 4 | 22 | N.A.1 | 1000 | 1800 |
| Detector | Maximum Range (m) | Precision (cm) | FOV | Angular Resolution | Image Resolution | Frame Rate (fps) | Optical System |
|---|---|---|---|---|---|---|---|
| 2013 Niclass [41] | 128 | 3.8 | 170° × 4.5° | 0.5° × 0.05° | 340 × 96 | 10 | 2D Scanning |
| 2017 Perenzoni [52] | 367 2 5862 3 | 20 2 50 3 | N.A.1 | N.A. 1 | 64 × 64 | 7.7 2 7.2 3 | Flash |
| 2018 Ximenes [53,54] | 7 80 | 15 47 | 7° × 7° | 0.02° × 0.02° | 256 × 256 | 0.031 | 2D Scanning |
| 2018 Beer [55] | 6.5 4 | 4.7 | 36° × 1° | 0.2° × 1° | 36 × 1 | 25 | Flash 5 |
| 2019 Zhang [56] | 50 | 0.14 | 40° × 20° | 0.15° × 0.14° | 252 × 144 | 30 | Flash |
| 2019 Hutchings [46] | 50 | N.A.1 | 1.2° × 1.2° | 0.02° × 0.02° | 64 × 64 | 30 | Flash |
| 2020 Seo [57] | 48 | 0.85 | 120° × 8° | 0.05° × 0.2° | 2200 × 36 | 1.18 | 1D Scanning |
| 2021 Padmanabhan [58] | 10 6 | N.A. | 2° × 2° | 0.16° × 0.16° | 128 × 128 | N.A. | Flash |
| 2021 Kumagai [50] | 150 300 | 15 30 | 25.2° × 9.45° | 0.15° × 0.15° | 168 × 63 | 20 | 1D Scanning 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villa, F.; Severini, F.; Madonini, F.; Zappa, F. SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR). Sensors 2021, 21, 3839. https://doi.org/10.3390/s21113839
Villa F, Severini F, Madonini F, Zappa F. SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR). Sensors. 2021; 21(11):3839. https://doi.org/10.3390/s21113839
Chicago/Turabian StyleVilla, Federica, Fabio Severini, Francesca Madonini, and Franco Zappa. 2021. "SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR)" Sensors 21, no. 11: 3839. https://doi.org/10.3390/s21113839
APA StyleVilla, F., Severini, F., Madonini, F., & Zappa, F. (2021). SPADs and SiPMs Arrays for Long-Range High-Speed Light Detection and Ranging (LiDAR). Sensors, 21(11), 3839. https://doi.org/10.3390/s21113839






