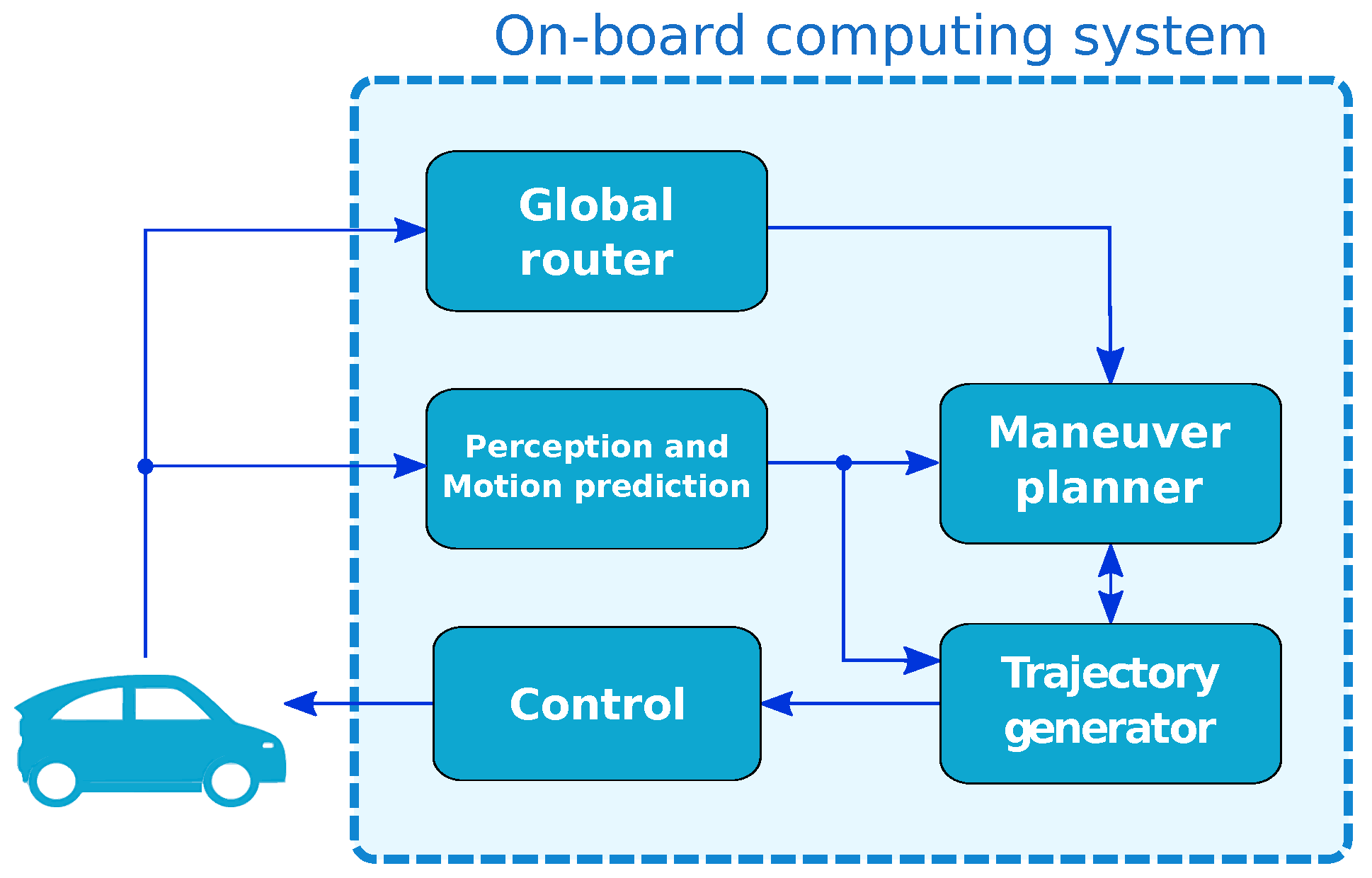
4.1. Trajectory Performance Indicators and Decision Variables
A set of 15
is computed for each trajectory candidate, grouped into four
, as shown in
Table 1. According to [
31], comfort in autonomous vehicles is directly related to acceleration
and jerk
, which explains their central role in comfort
. The longitudinal comfort variable is obtained by combining the mean and maximum values of the longitudinal acceleration and jerk. The lateral comfort not only combines the lateral acceleration and jerk, but it also includes the smoothness of the path, obtained from the first and second derivative of its curvature, as in [
18]. In [
32], the collision risk is minimized by increasing the distance to the existing obstacles in the driving scene; in [
33], the authors propose different metrics such as time headway or lateral and longitudinal distances to surrounding obstacles, and in [
34], the risk metric is directly linked to the lane departure of the vehicle. With this in mind, the safety
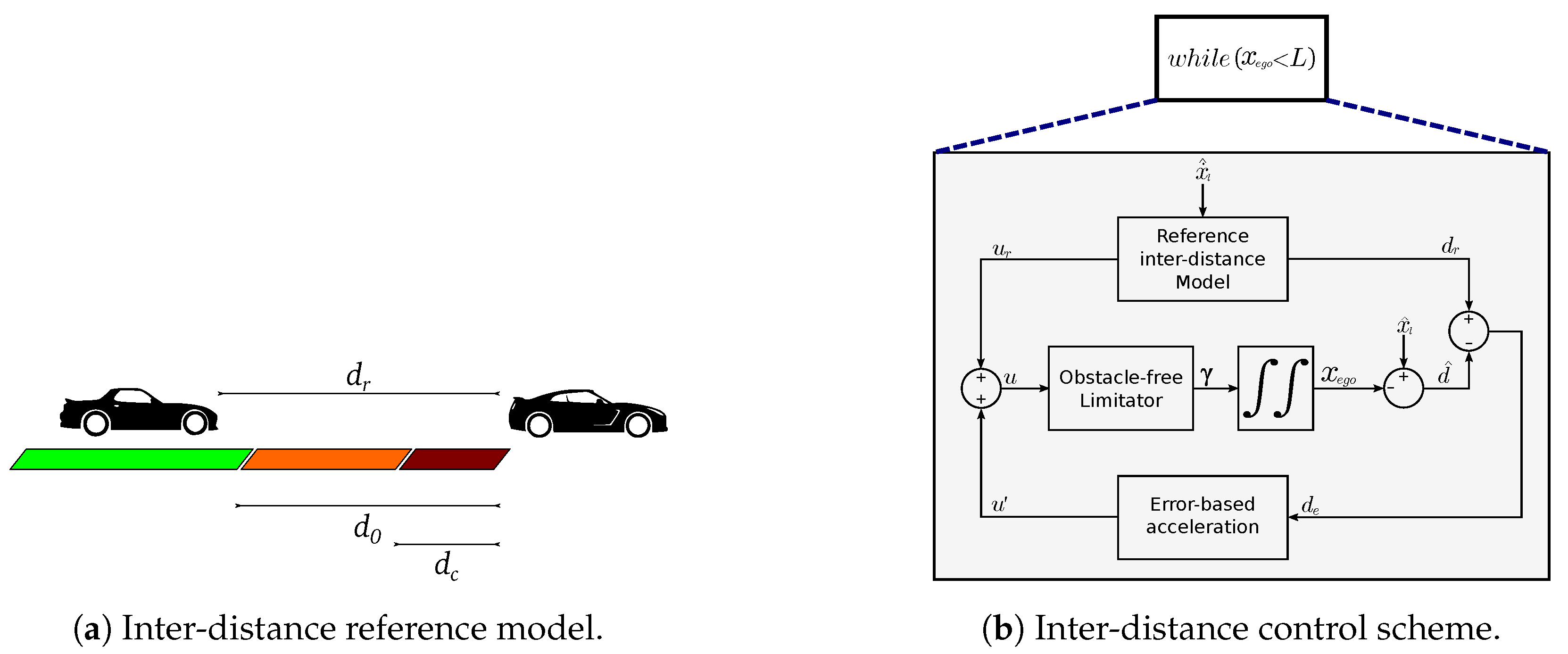
is computed by measuring the distance to static obstacles, the average inter-distance to a leader vehicle (if present) and the lane invasion of the candidates. Most of these
are obtained by evaluating the occupancy polygon of the candidate in the planning grids
and
. Finally, the utility is calculated from the average speed of the candidate and the length of its path. In the end, each
is normalized using a maximum possible value set by design.
4.2. Merit Function
The merit score
assigned to each candidate is calculated by combining the four
with a modified version of the weighted product (WP). This approach was chosen over the weighted sum (WS) because it provides an intrinsic filter (due its multiplication nature) to the candidates that do not perform well in one of the
[
35]. For the sake of illustration, if a candidate has an outstanding longitudinal comfort but keeps a very dangerous inter-distance with the vehicle up front, it should be considered irrelevant. Each
is first weighted using a non-linear weighting function in order to vary its influence in the final merit of the candidate, and then it is multiplied with the other
:
where
represents one of the four decision variables of a candidate
c and
is the weight of that
.
This weighting function is designed to satisfy three properties: (i) it must reinforce the difference between the lower and higher values of
when
; (ii) it must decrease the difference between the lower and higher values of
when
; (iii) values of
near 0 must stay near 0 after being weighted. The weighing function is defined to be bounded in the interval
. In order to meet these properties, the weighing function
is defined as a piecewise function which depends on the value of
. If the value of
is lower than
, the function is similar in shape to the square root function, and if the value of
is higher or equal than
, the weighting function has an exponential behavior. The formal definition of this function is as follows:
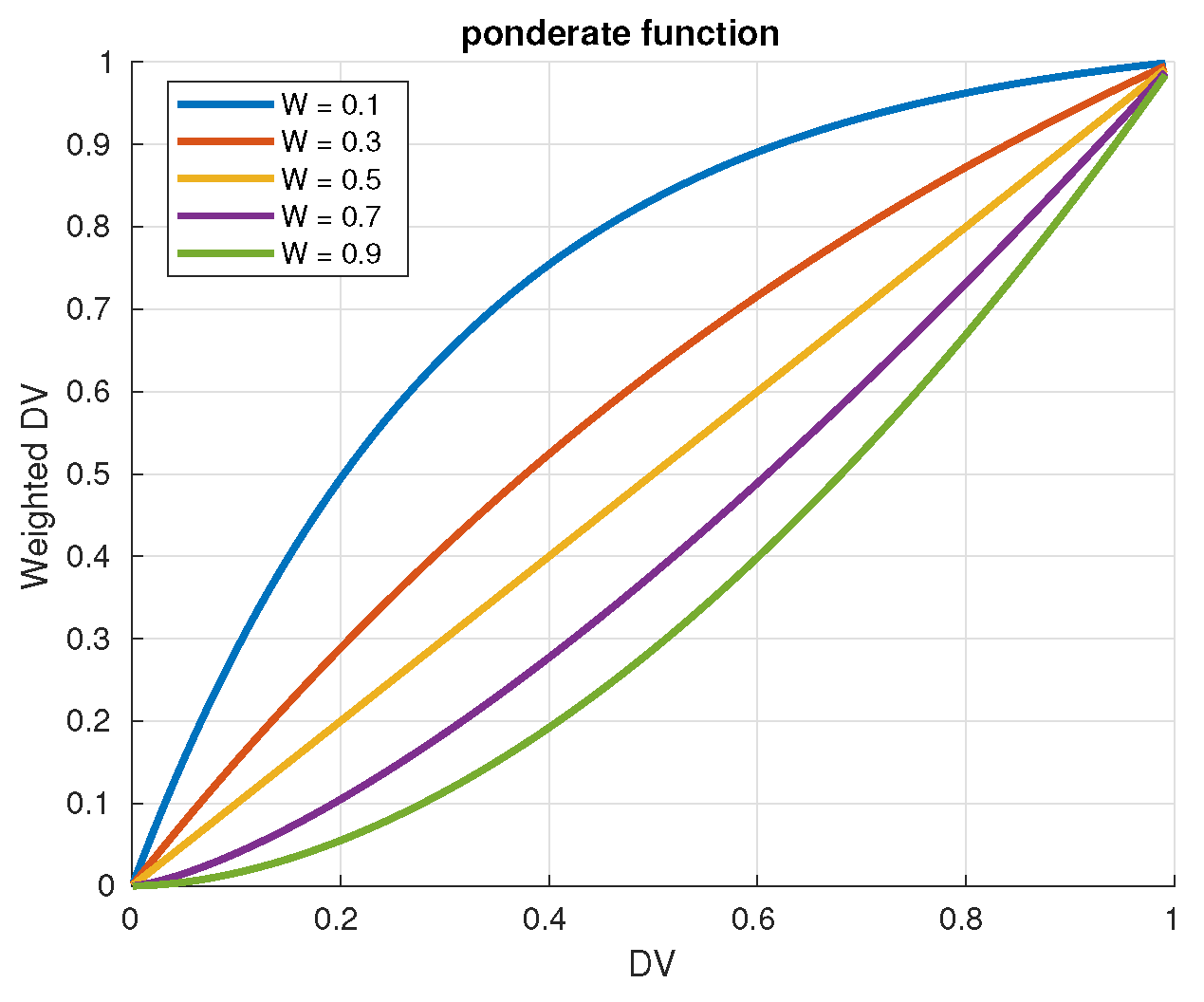
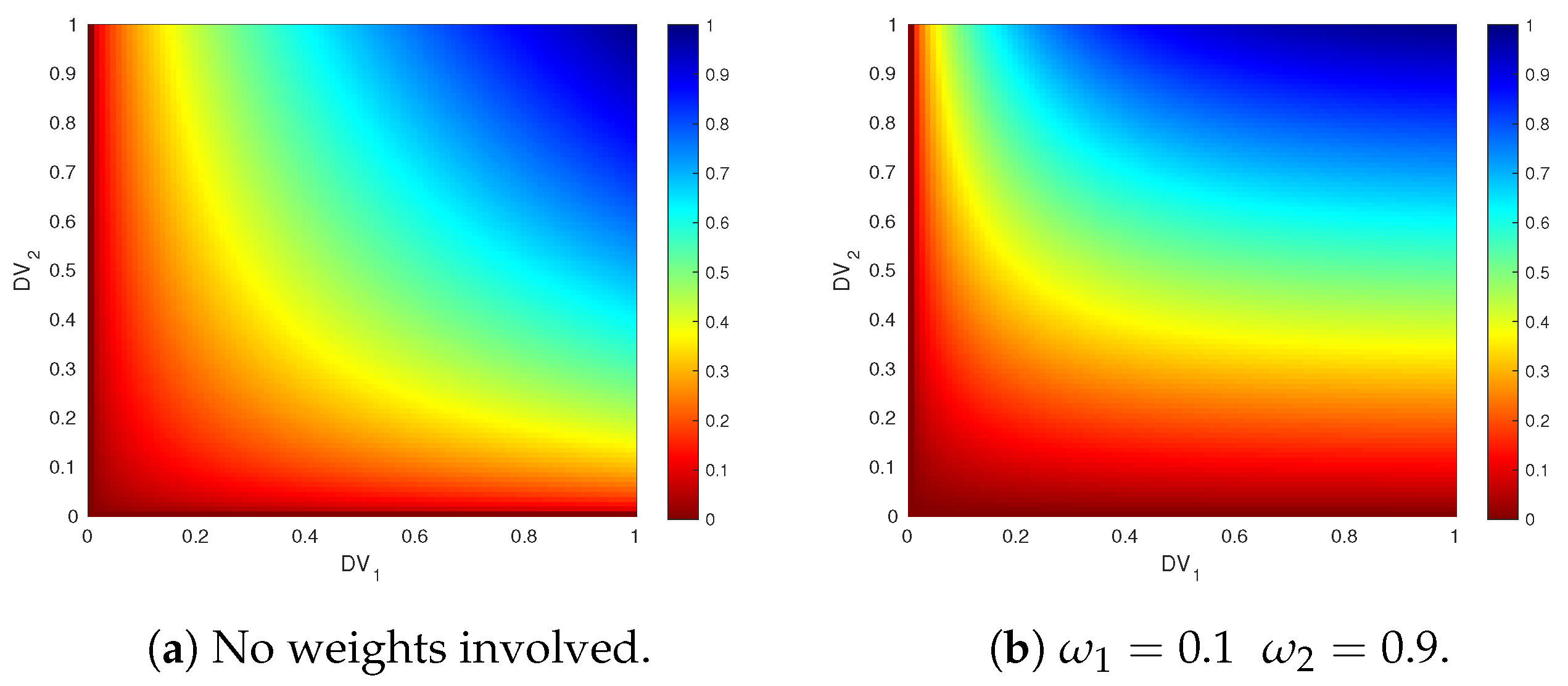
Figure 9 shows how a
is modified with different values of
.
Figure 10 illustrates the performance of the merit function (Equation (
3)) when combining two different
.
Figure 10a shows the merit values after combining the two
with a non-weighted geometric mean, where it can be seen that both
equally affect the resulting merit. In
Figure 10b,
and
have weights
and
, respectively. In this case, the variation of
does not influence the merit function as much as the variation of
, but it gets very close to 0 when values of
are near to 0, as expected for property (iii).
Each
is created from a combination of
, as stated in
Table 1, using the merit function (
3). Accordingly, if a candidate performance is poor for a specific
, then the value of the corresponding
will be low, and the final merit of that candidate will be affected. Since
are defined using a lowest-is-better equation and WP needs a greatest-is-better formulation, they are inverted after being normalized, using, for each of the 15
, the following expression:
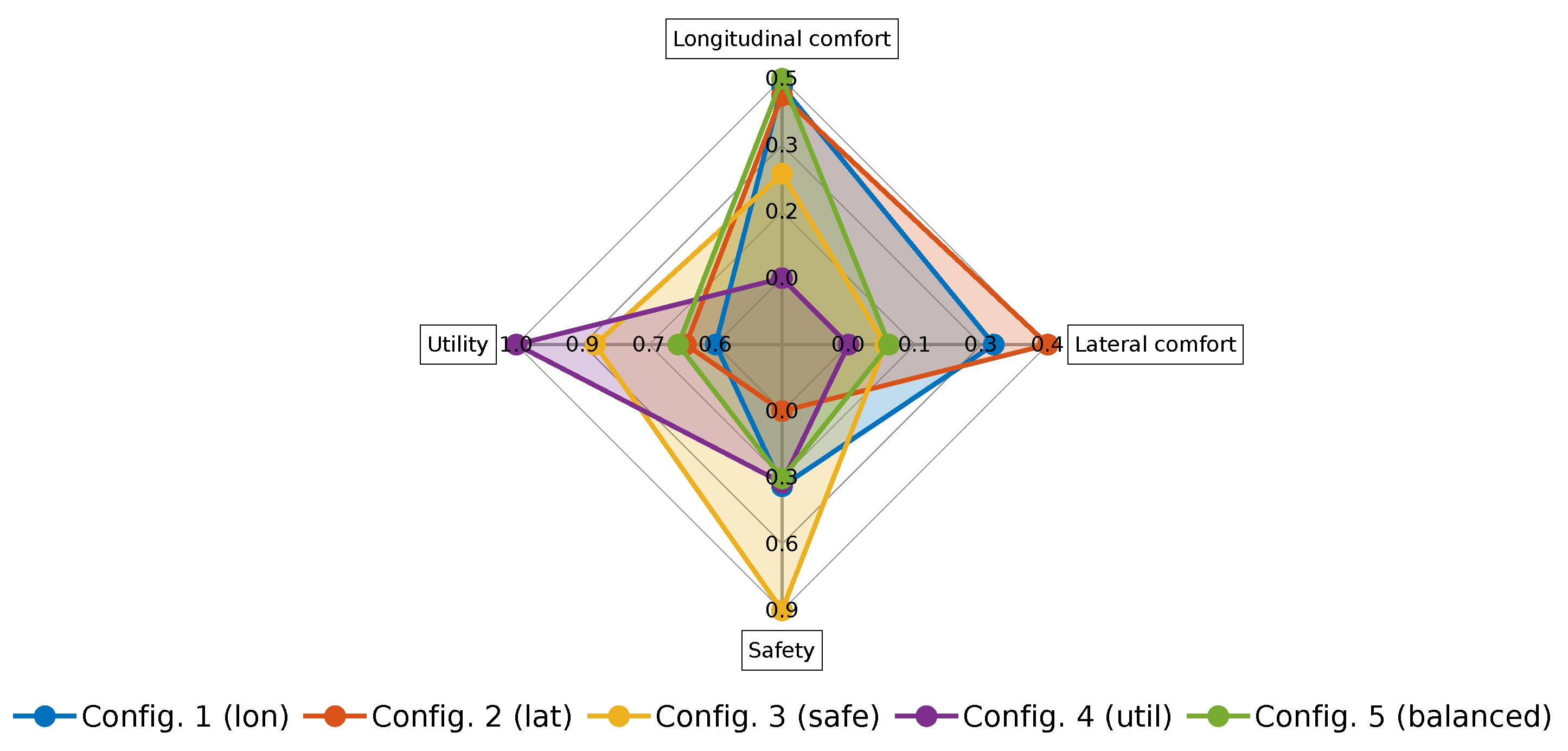
In order to show how the weight configuration affects decision making in the autonomous driving process, three different weight configurations (see
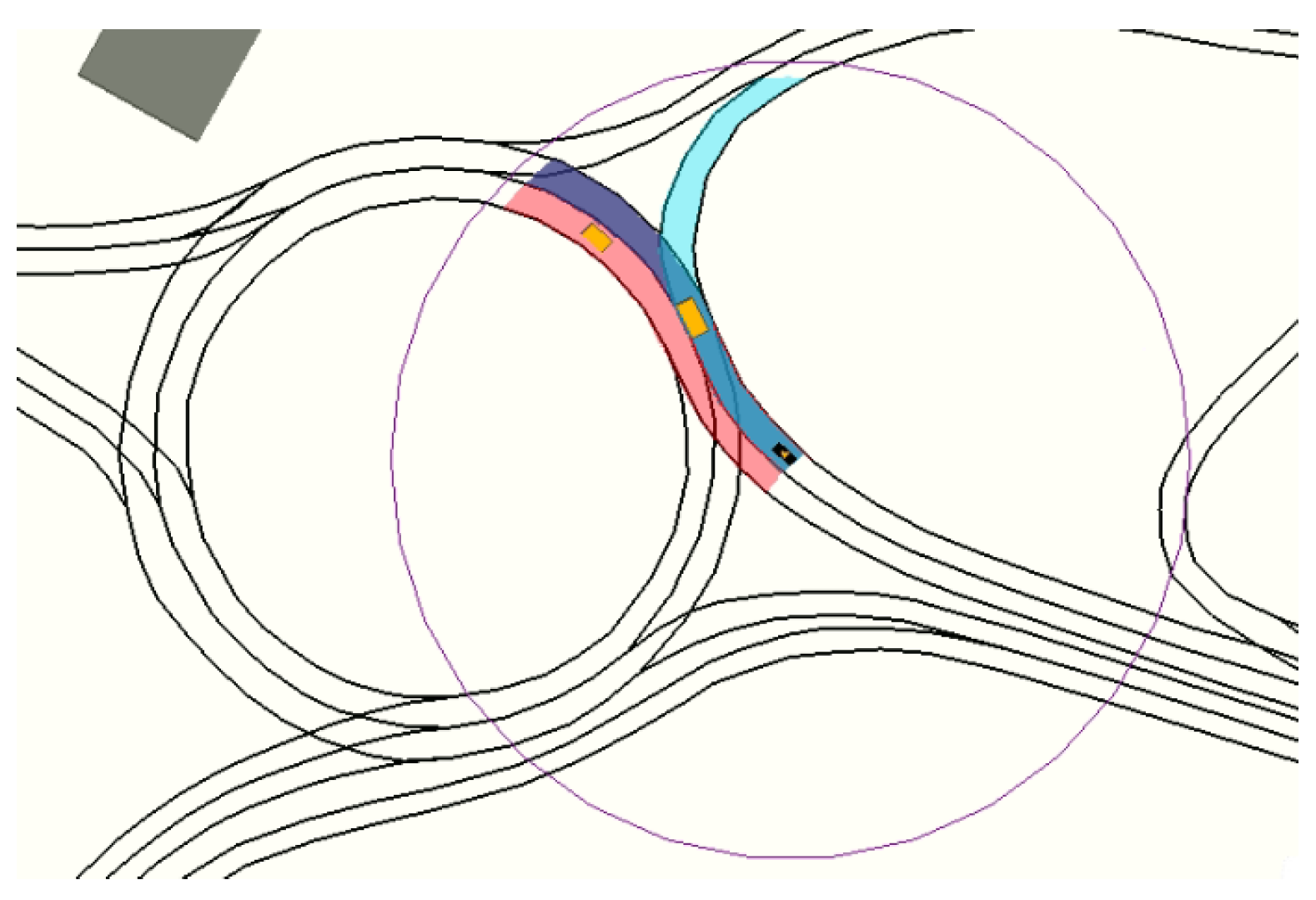
Table 2) were tested for the driving scenario of
Figure 6.
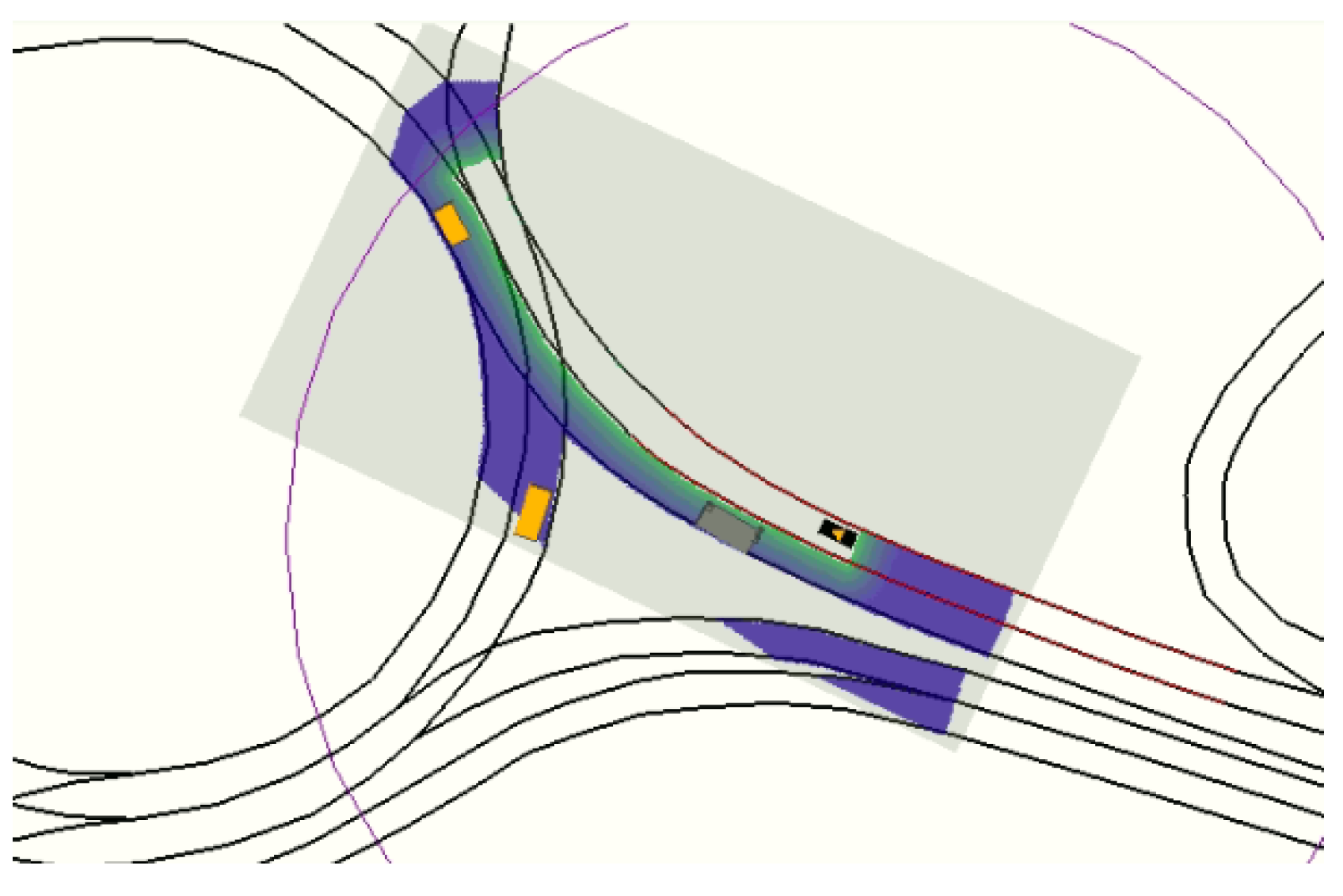
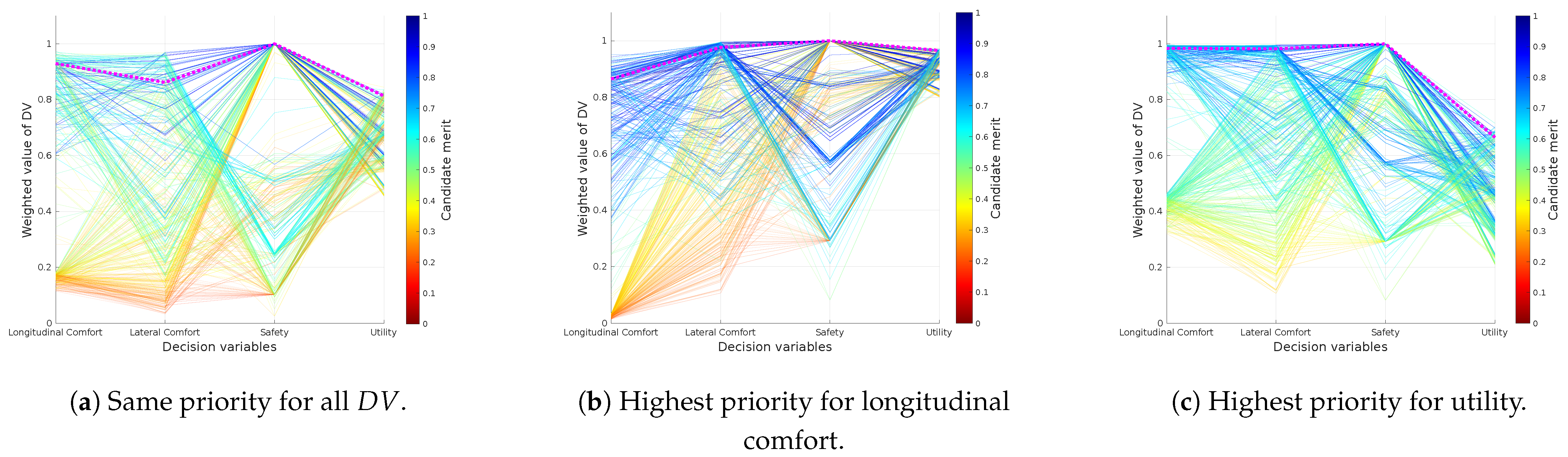
Figure 11 shows a reachability map where each candidate is represented as a vector, formed by four decision variables
and their correspondent weighted value. The final merit assigned to the candidates is plotted using a color-map. Alternatively,
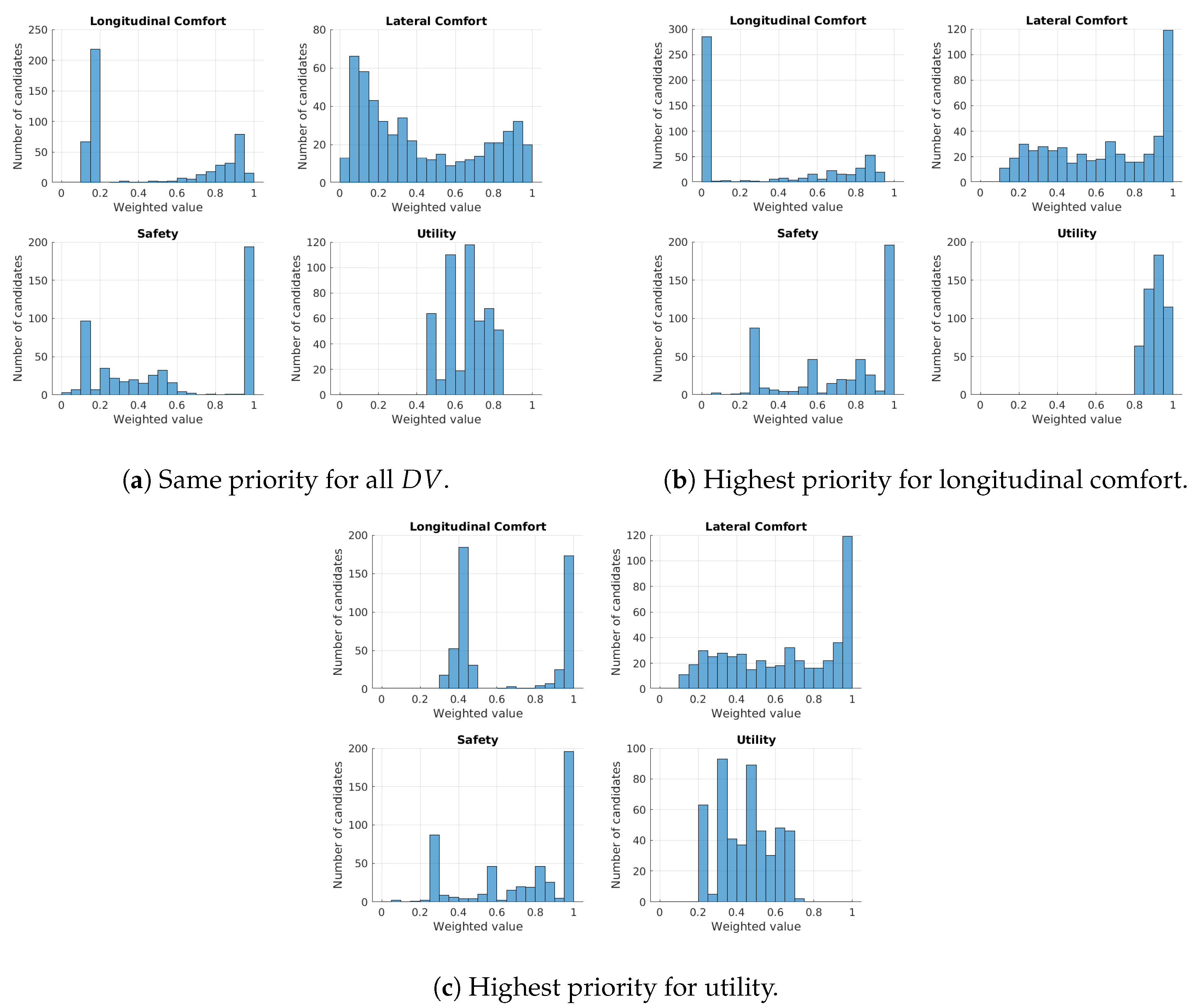
Figure 12 shows the distribution of the weighted
in a histogram representation.
The first configuration, where each
has a weight
, is used as baseline (see
Figure 11a and
Figure 12a to see its
distribution). The second configuration establishes the highest weight to the longitudinal comfort and sets the weights of the other
to 0.1. The effect of this configuration is that the system will be more selective with the candidates according to their longitudinal comfort, and the other
will not affect the final merit correspondingly. This behavior can be observed in the histogram distribution of the
Figure 12b. Note that in the case of the longitudinal comfort, a great number of candidates obtained a value lower than 0.05, while the performance of the other
was improved compared to the distributions of
Figure 12a (the number of candidates in the higher bins of the histograms increased).
Figure 11b shows that the overall merit of the candidates was increased and that candidates with poor longitudinal comfort performance tend to have low merits, while candidates with better longitudinal comfort performance have a higher merit. In the third configuration, the highest weight is assigned to utility; as a result, the system raises the bar with this
, and only the candidates with good utility performance maintain a good value after being weighted. Now the number of candidates tend to be more distributed along the utility histogram, as seen in
Figure 12c; besides, the performance of the candidates with regard to the longitudinal comfort increased considerably compared with
Figure 12b, and now it does not influence the final merit of candidates as much (there are no red candidates due to the low performance on the longitudinal comfort). In this case, the overall merit of the candidates improved because of the low influence of
such as safety or longitudinal comfort in this configuration.
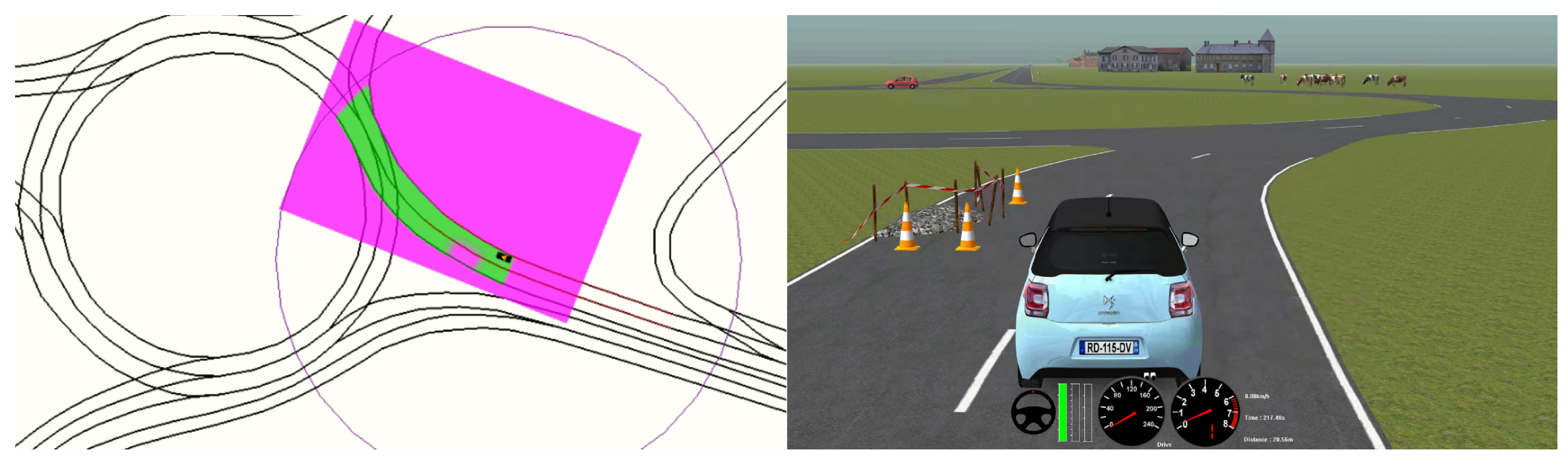
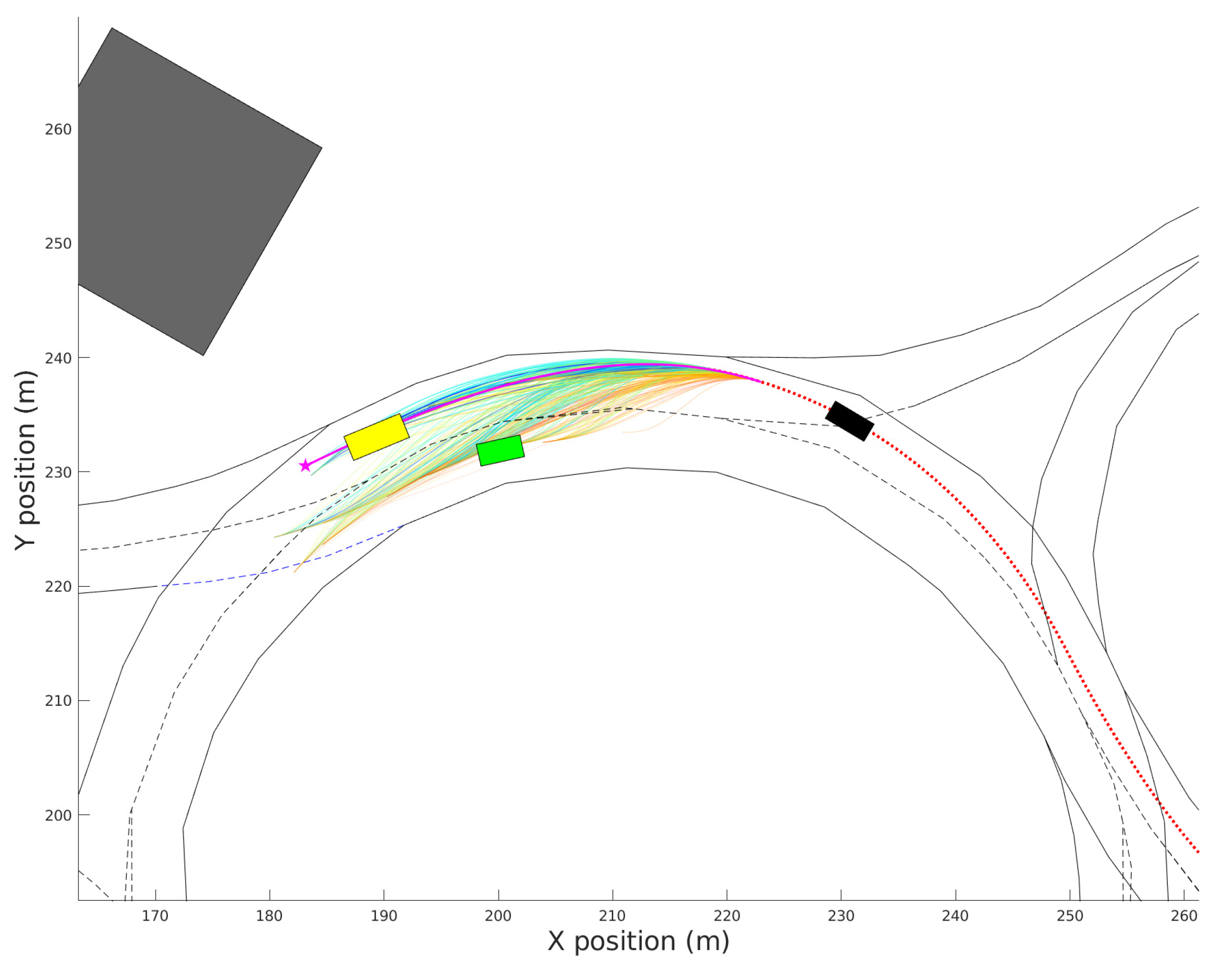
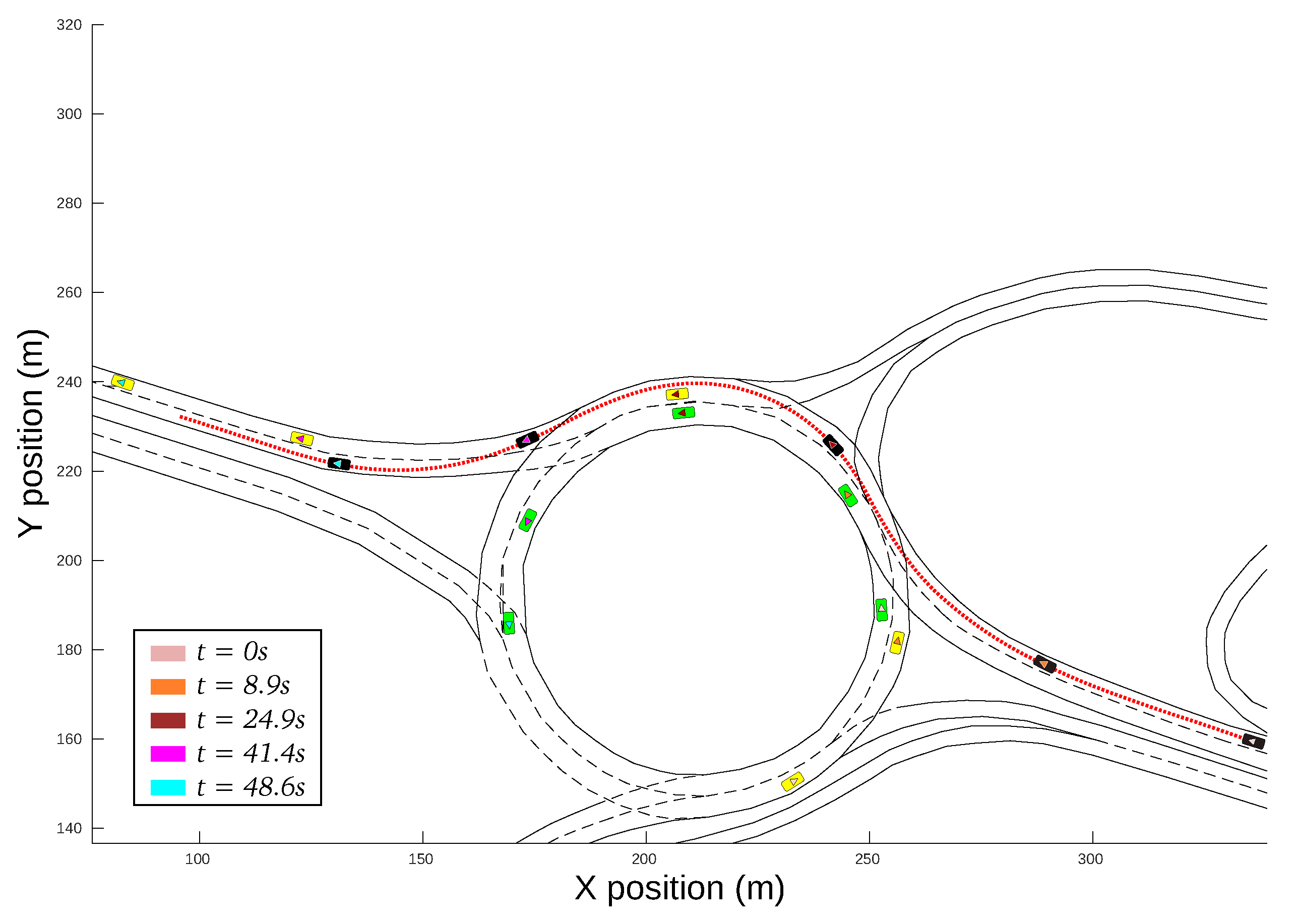
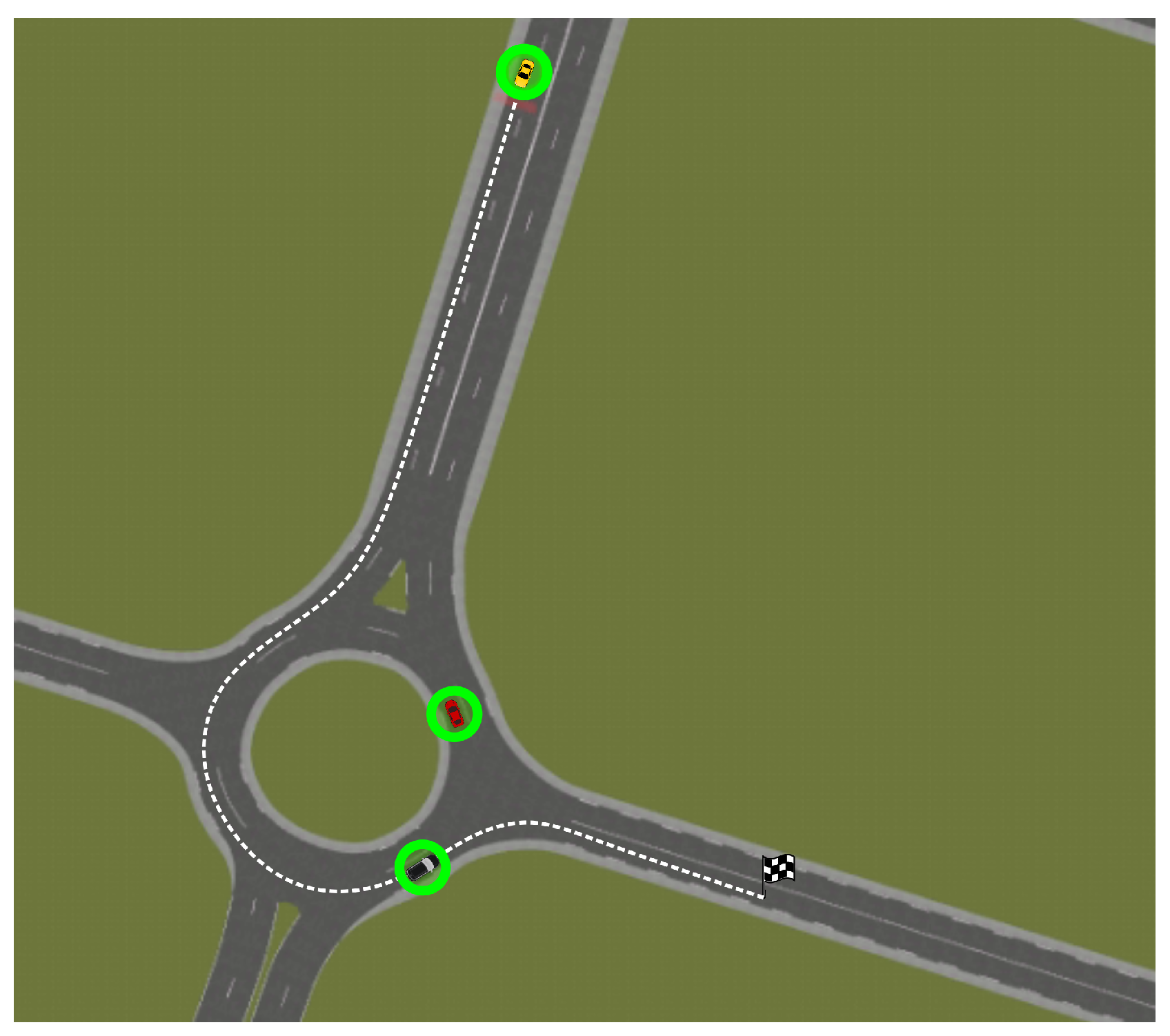
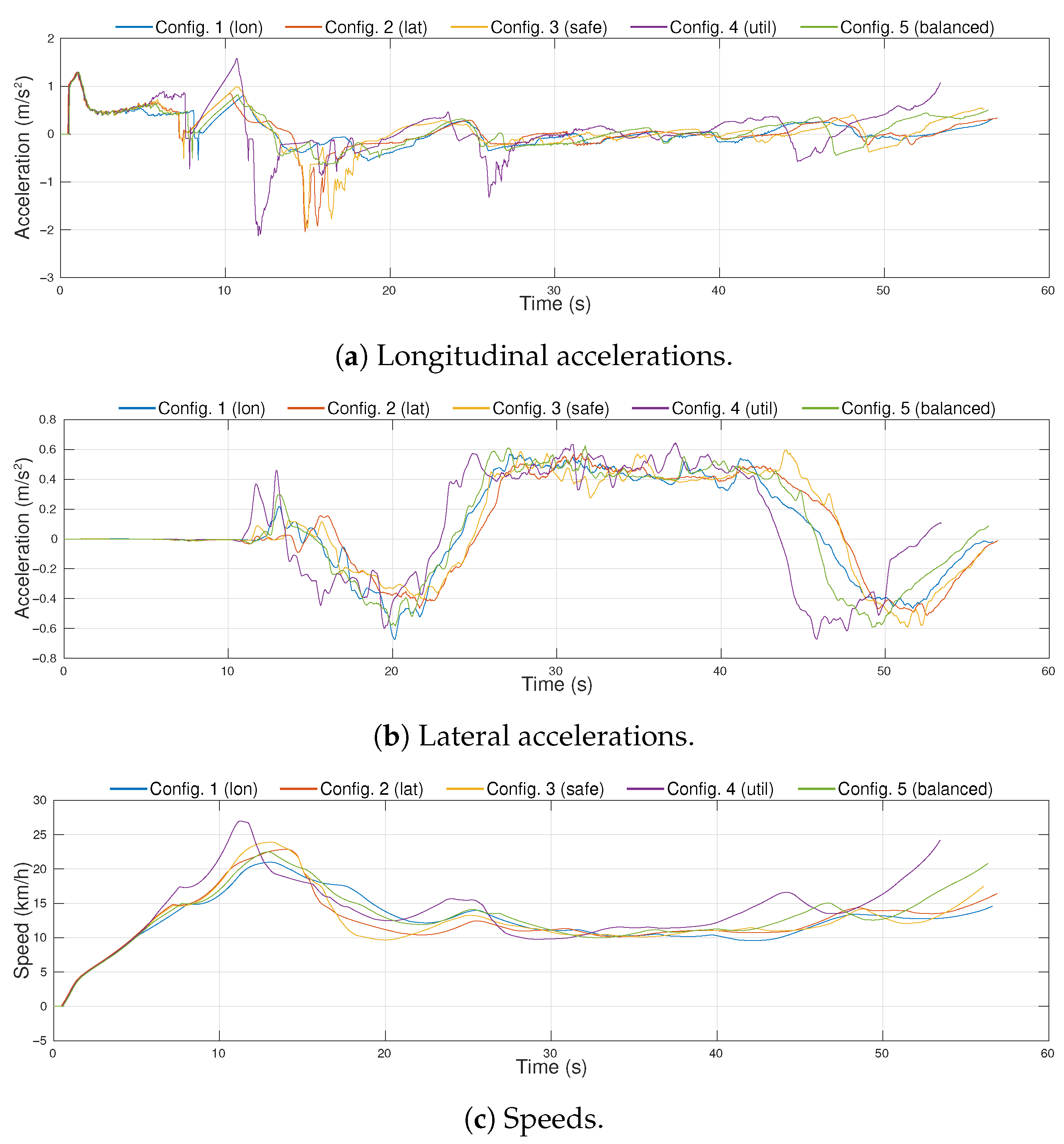
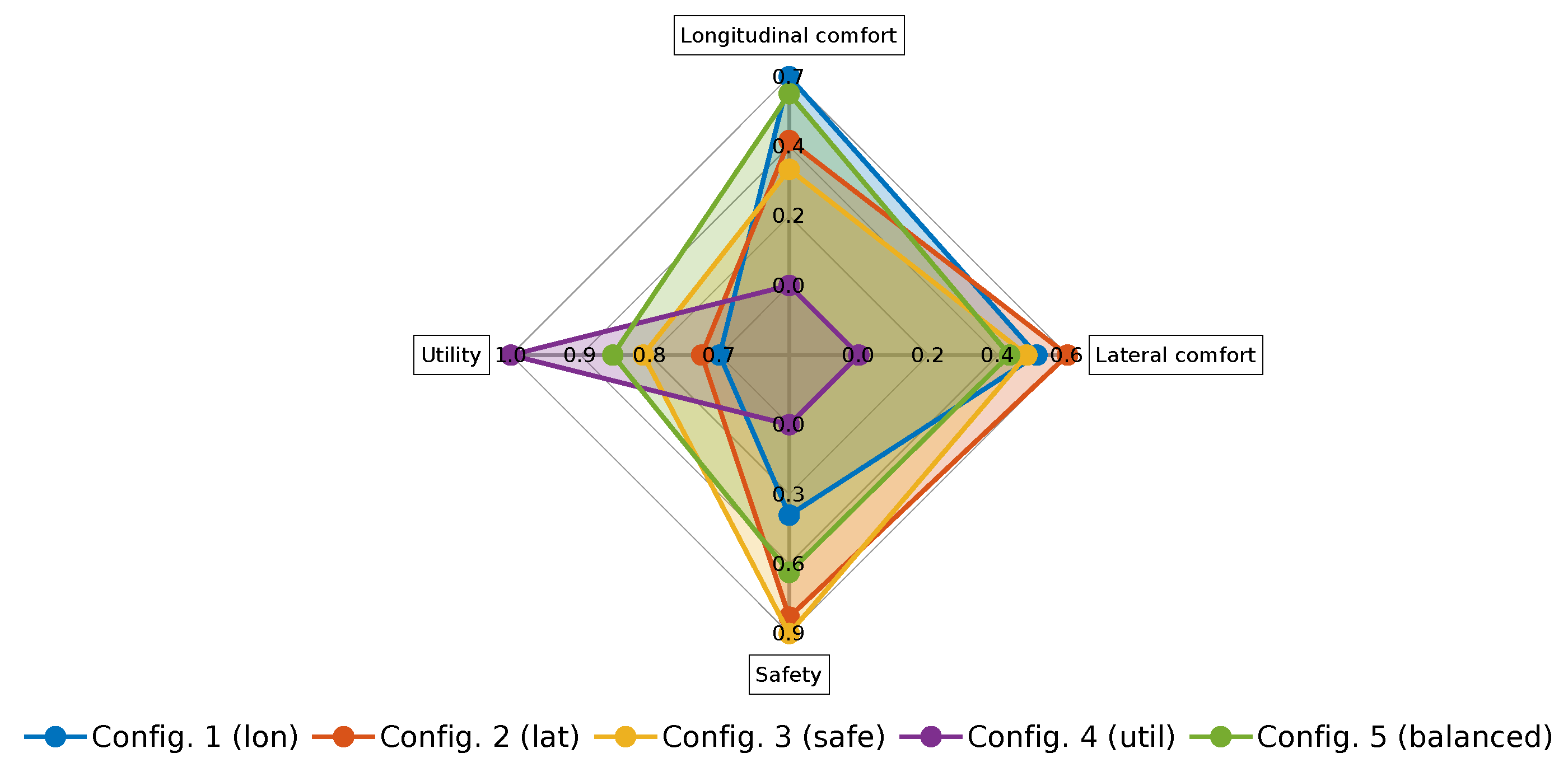
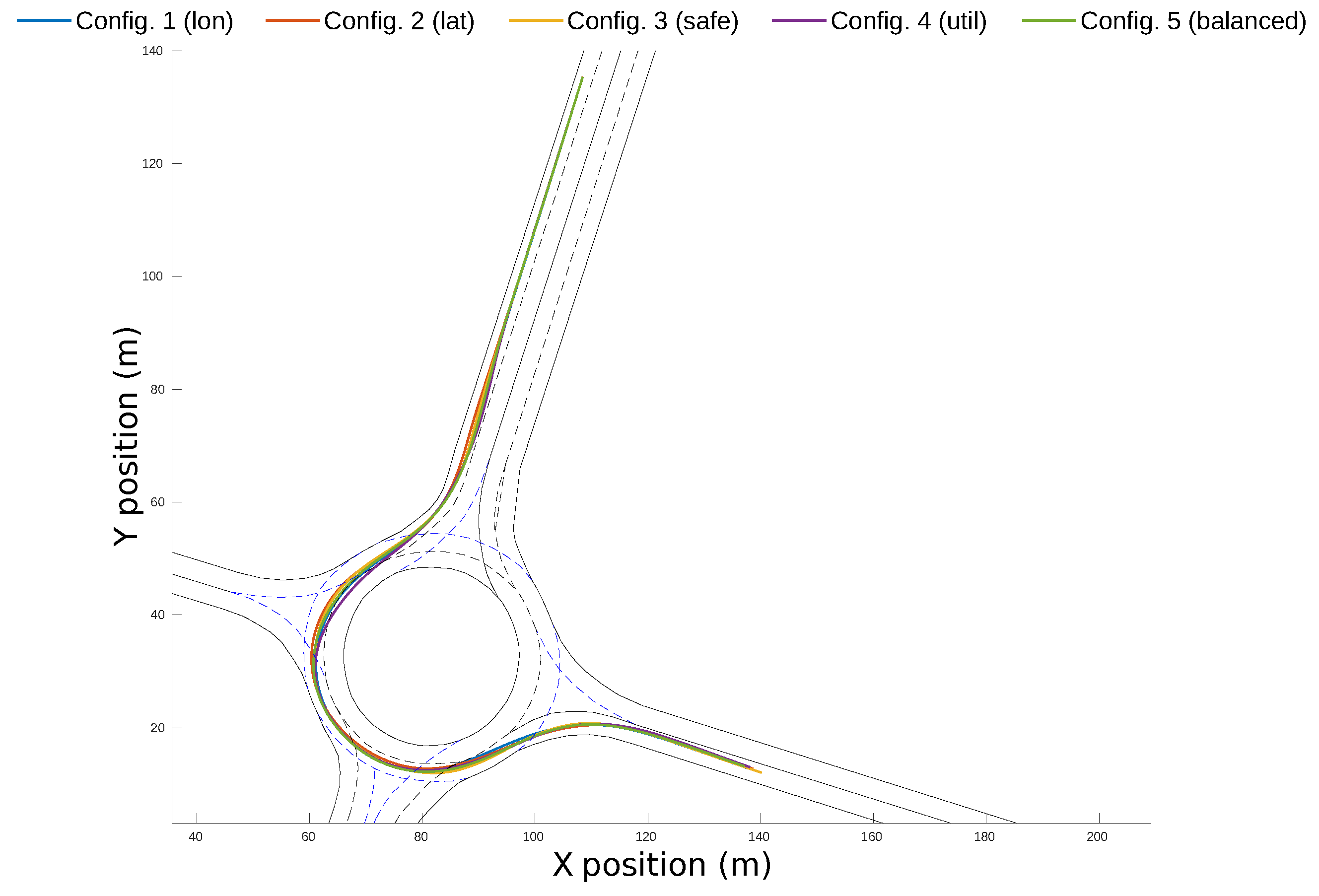
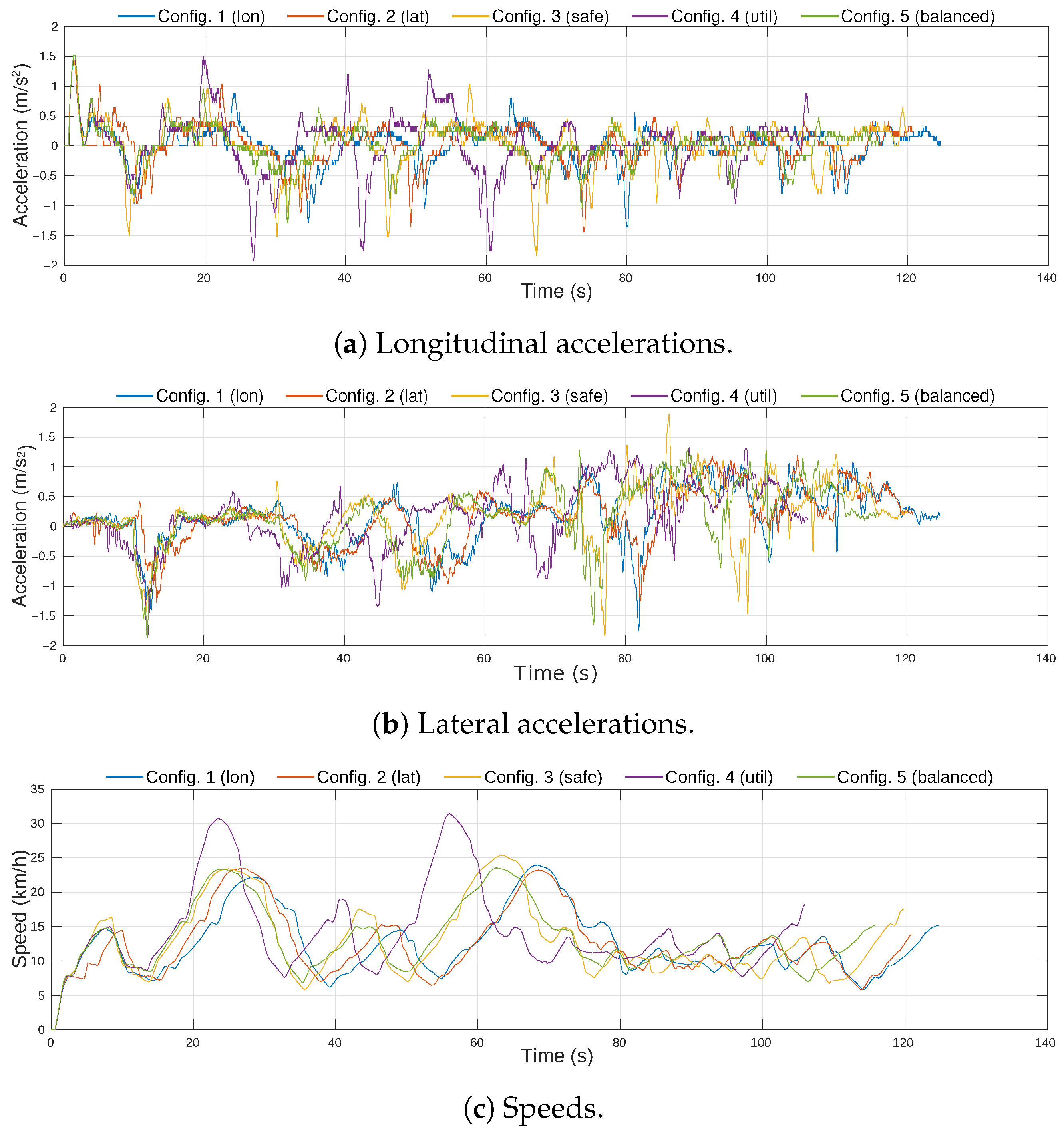
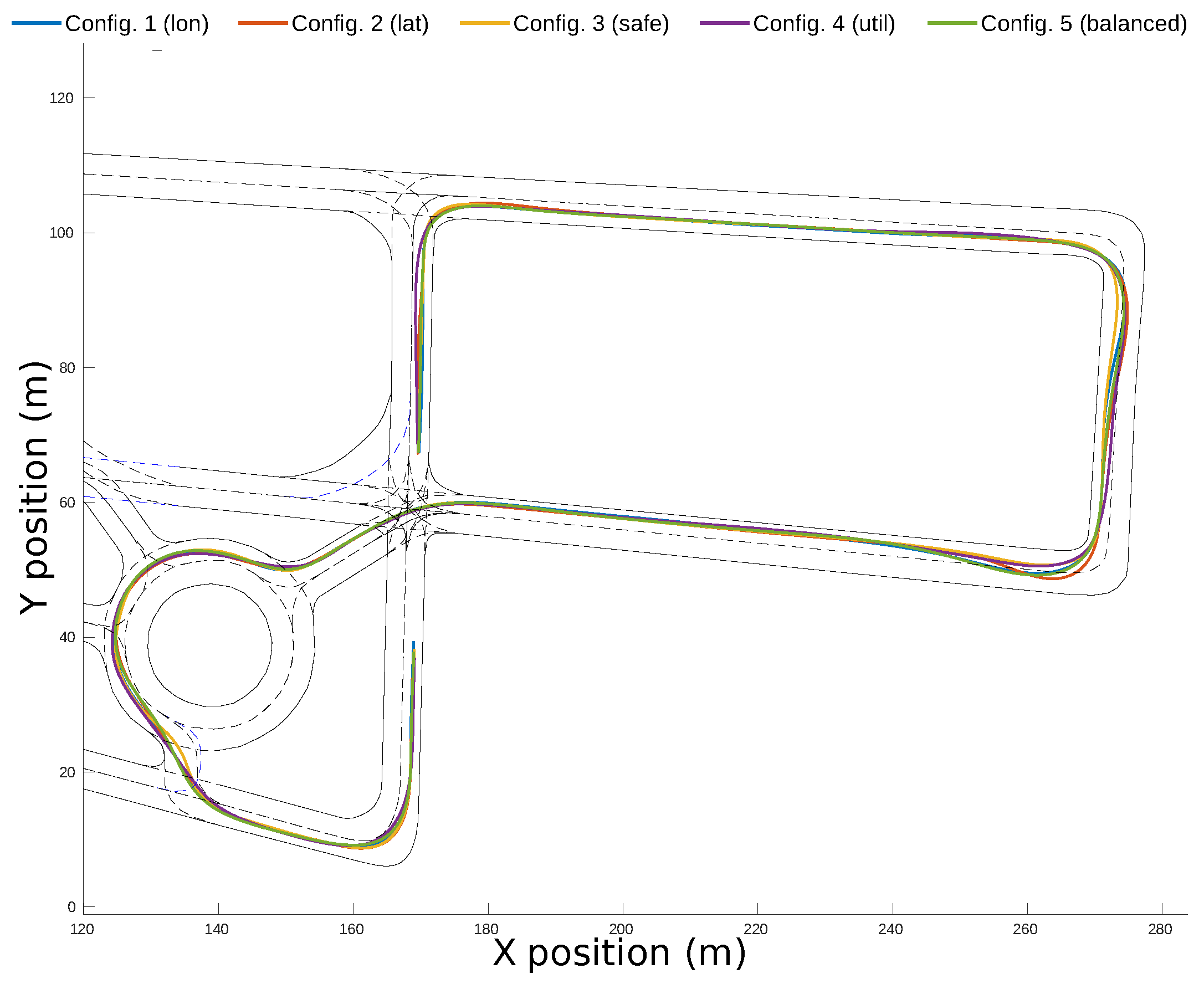
Figure 13 shows the vehicle’s evolution inside the roundabout during the complete driving scenario. It can be observed that the ego-vehicle keeps a distance with respect to the yellow vehicle inside the roundabout, and it performs a lane-change in the highway once outside the roundabout. The trajectory does not follow the centerline of the ego-lane in order to increase the lateral comfort, but it does not invade the adjacent lane because that would jeopardize safety. This experiment was carried out with a weight configuration
.