A Novel Versatile Approach for Underwater Conformal Volumetric Array Design
Abstract
1. Introduction
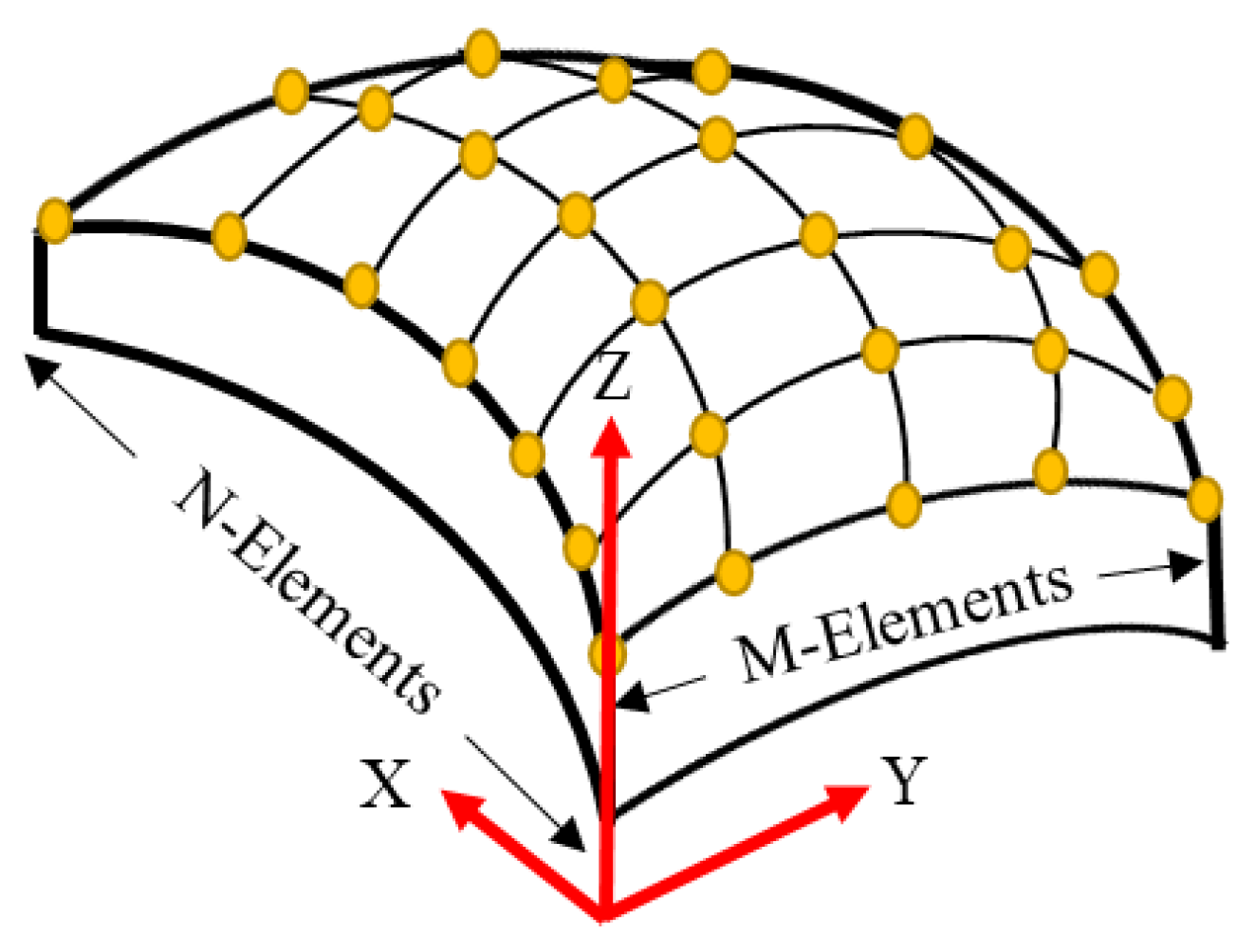
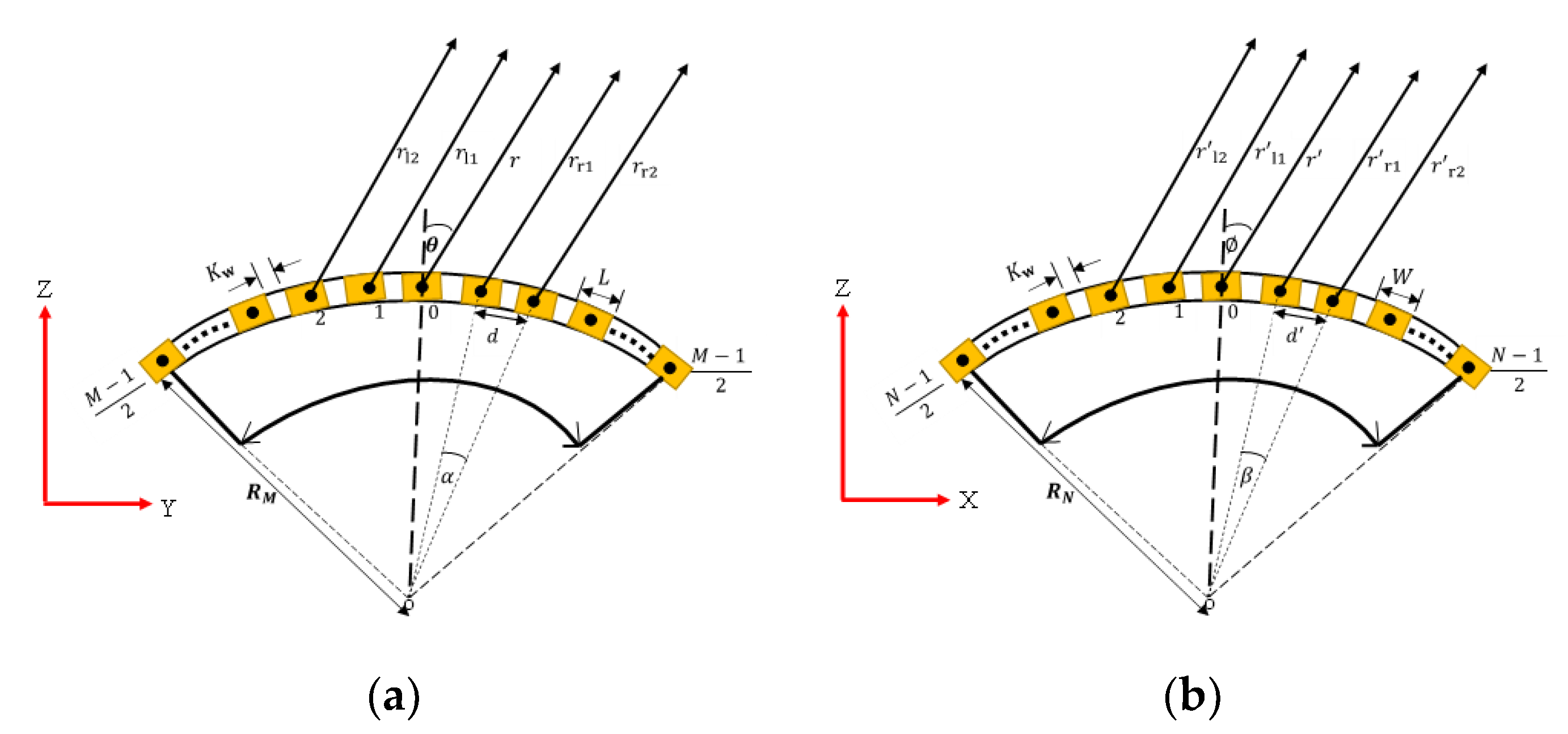
2. The Conformal Array Geometrical Parameters
3. Determination of the Far-Field
4. Derivation of the Directivity Function
5. The Working Frequency and the Maximum Array Aperture Size
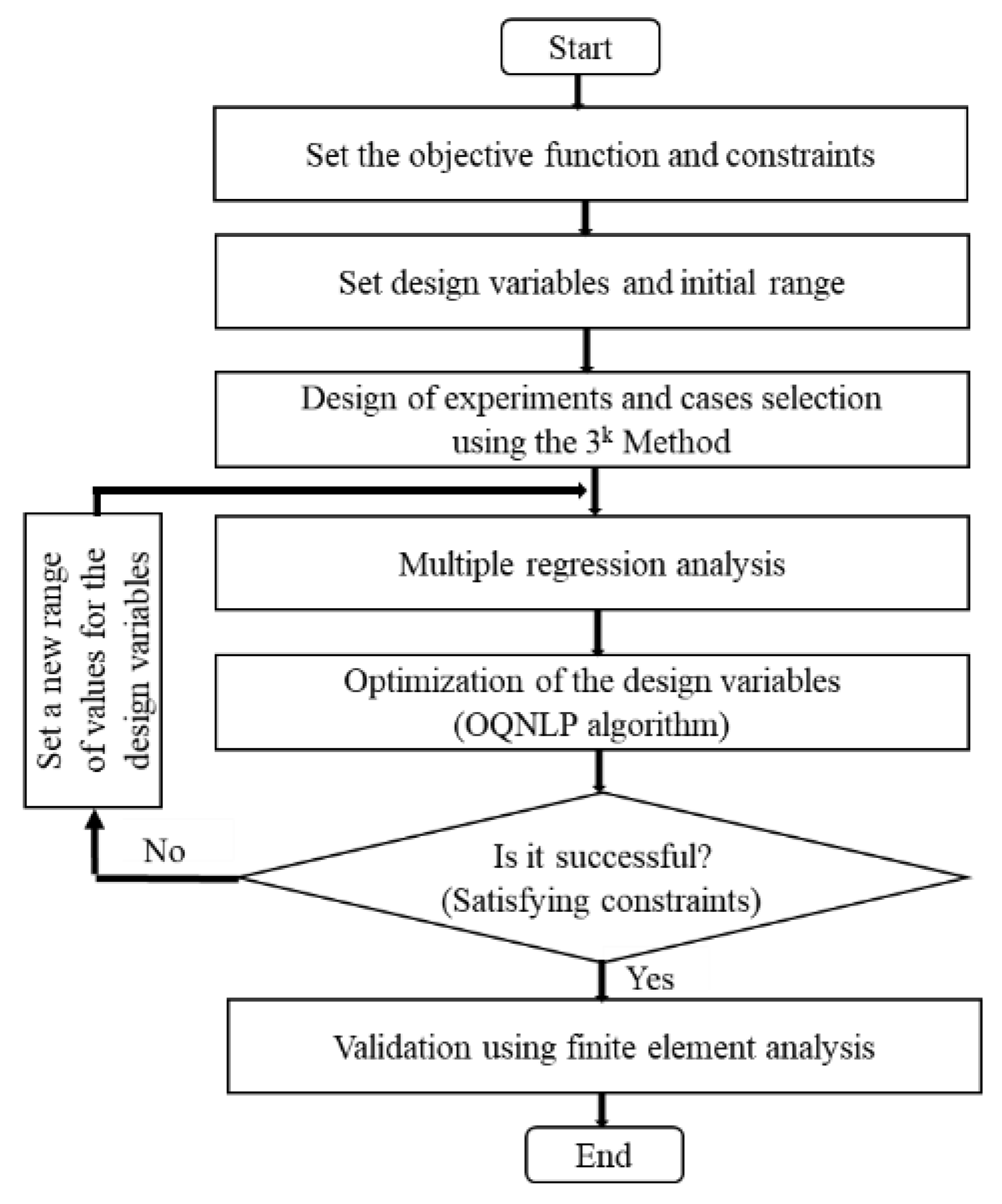
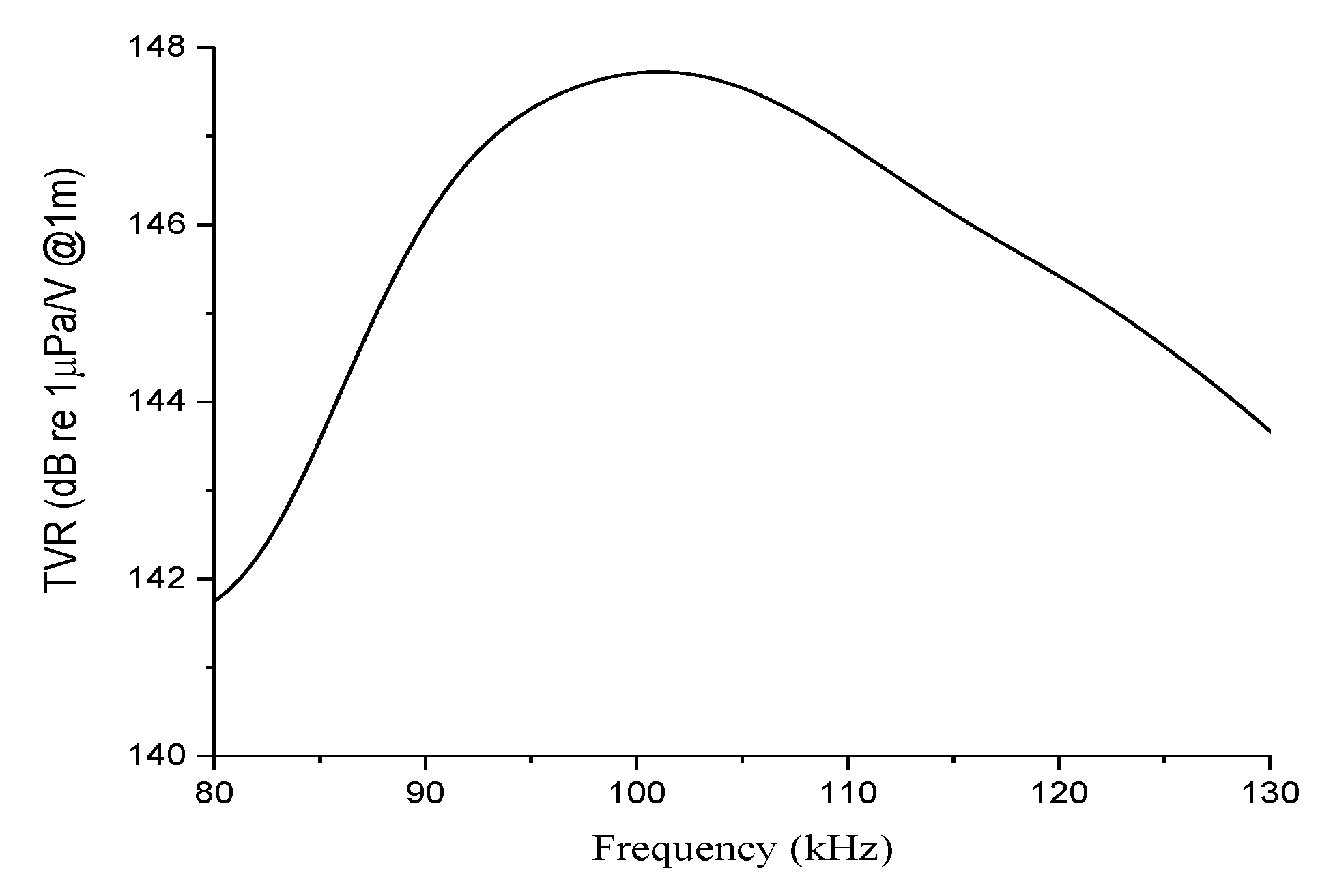
6. Design of the Conformal Volumetric Array
7. Validation of the Design
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, R.S.; Culjat, M.O.; Vampola, S.P.; Williams, K.; Taylor, Z.D.; Lee, H.; Grundfest, W.S.; Brown, E.R. P3D-6 simulation, fabrication, and characterization of a novel flexible, conformal ultrasound transducer array. In Proceedings of the 2007 IEEE Ultrasonics Symposium, New York, NY, USA, 28–31 October 2007; pp. 1824–1827. [Google Scholar]
- Culjat, M.O.; Singh, R.S.; Utley, C.D.; Vampola, S.P.; Sharareh, B.; Lee, H.; Brown, E.R.; Grundfest, W.S. A flexible, conformal ultrasound array for medical imaging. Stud. Health Technol. Inform. 2008, 132, 95–97. [Google Scholar] [PubMed]
- Zhou, T.; Lan, Y.; Zhang, Q.; Yuan, J.; Li, S.; Lu, W. A conformal driving class IV flextensional transducer. Sensors 2018, 18, 2102. [Google Scholar] [CrossRef]
- Evans, M.B.; Stutin, T.A. Anticipating the Waiting Weapon: U.S. Ports and Terrorist Sea Mining; US Merchant Marine Academy: Kings Point, NY, USA, 2006. [Google Scholar]
- Rios, J.J. Naval Mines in the 21st Century: Can NATO Navies Meet the Challenge? Naval Postgraduate School: Monterey, CA, USA, 2005. [Google Scholar]
- Tellez, O.L.L.; Borghgraef, A.; Mersch, E. The special case of sea mines. In Mine Action—The Research Experience of the Royal Military Academy of Belgium; Beumier, C., Closson, D., Lacroix, V., Milisavljevic, N., Yvinec, Y., Eds.; TechOpen: London, UK, 2017; pp. 251–279. [Google Scholar]
- Arimatsu, L. International Law Applicable to Naval Mines. In International Security Department Workshop Summary; Chatham Housethe Royal Institute of International Affairs: London, UK, 2014. [Google Scholar]
- Shimoyama, T.; Nanri, M.; Murakami, Y.; Tamakawa, K. Maritime infrastructure security using underwater sonar systems. Hitachi Rev. 2013, 62, 214–218. [Google Scholar]
- Köhntopp, D.; Lehmann, B.; Kraus, D.; Birk, A. Classification and localization of naval mines with superellipse active contours. IEEE J. Ocean. Eng. 2019, 44, 767–782. [Google Scholar] [CrossRef]
- Köhntopp, D.; Lehmann, B.; Kraus, D.; Birk, A. Seafloor Classification for Mine Counter Measure Operations using Synthetic Aperture Sonar Image. In Proceedings of the IEEE Oceans, Aberdeen, UK, 19–22 June 2017; pp. 1–5. [Google Scholar]
- Dura, E.; Bell, J.; Lane, D. Superellipse fitting for the recovery and classification of mine-like shapes in sidescan sonar images. IEEE J. Ocean. Eng. 2008, 33, 434–444. [Google Scholar] [CrossRef]
- Reed, S.; Petilot, Y.; Bell, J. A Model Based Approach to Mine Detection and Classification in Sidescan Sonar. In Proceedings of the IEEE Oceans, San Diego, CA, USA, 22–26 September 2003; Volume 3, pp. 1402–1407. [Google Scholar]
- Quidu, I.; Malkasse, J.P.; Burel, G.; Vilbe, P. Mine Classification Using a Hybrid Set of Descriptors. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition, Conference Proceedings (Cat. No.00CH37158), Providence, RI, USA, 11–14 September 2000; Volume 1, pp. 291–297. [Google Scholar]
- Dura, E.; Zhang, Y.; Liao, X.; Dobeck, G.J.; Carin, L. Active learning for detection of mine-like objects in side-scan sonar imagery. IEEE J. Ocean. Eng. 2005, 30, 360–371. [Google Scholar] [CrossRef]
- Dobeck, G.J. Algorithm Fusion for Automated Sea Mine Detection and Classification. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey. Conference (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; pp. 130–134. [Google Scholar]
- Phung, S.L.; Nguyen, T.N.A.; Le, H.T.; Chapple, P.B.; Ritz, C.H.; Bouzerdoum, A.; Tran, L.C. Mine-Like Object Sensing in Sonar Imagery with a Compact Deep Learning Architecture for Scarce Data. In Proceedings of the Digital Image Computing: Techniques and Applications (DICTA), Perth, Australia, 2–4 December 2019; pp. 1–7. [Google Scholar]
- Josefsson, L.; Persson, P. Conformal array antenna theory and design. In IEEE Press Series on Electromagnetic Wave Theory; El-Hawary, M.E., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 182. [Google Scholar]
- Knott, P.; Bertuch, T.; Wilden, H.; Peters, O.; Brenner, A.R.; Walterscheid, I. SAR experiments using a conformal antenna array radar demonstrator. Int. J. Antenn. Propag. 2012, 2012, 142542. [Google Scholar] [CrossRef]
- Gallaudet, T.C.; de Moustier, C.P. On optimal shading for arrays of irregularly-spaced or noncoplanar elements. IEEE J. Ocean. Eng. 2000, 25, 553–567. [Google Scholar] [CrossRef]
- Persson, P. Analysis and Design of Conformal Array Antennas; Universitetsservice US AB: Stockholm, Sweden, 2001; p. 66. [Google Scholar]
- Zhao, Y.Q.; Peng, Z. Three-Dimensional Phased Array Antenna Analysis and Simulation. In Proceedings of the 3rd IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 27–29 October 2009; pp. 538–542. [Google Scholar]
- Ito, Y. Design and performance of an acoustic antenna for a phased array Doppler sodar. Meteorol. Appl. 1997, 5, 149–156. [Google Scholar] [CrossRef]
- Saleh, K.Y.; Smith, N.B. Two-dimensional ultrasound phased array design for tissue ablation for treatment of benign prostatic hyperplasia. Int. J. Hyperth. 2004, 20, 7–31. [Google Scholar] [CrossRef]
- Sun, D.; Shen, R.; Yan, X.A. Broadband conformal phased array antenna on spherical surface. Int. J. Antennas Propag. 2014, 2014, 206736. [Google Scholar] [CrossRef]
- Ferreira, D.B.; de Paula, C.B.; Daniel, C.; Nascimento, D.C. Design techniques for conformal microstrip antennas and their arrays. In Advancement in Microstrip Antennas with Recent Applications; Kishk, A., Ed.; InTechOpen: London, UK, 2013; pp. 3–31. [Google Scholar]
- Pyo, S.; Lim, Y.; Roh, Y. Analysis of the transmitting characteristics of an acoustic conformal array of multimode tonpilz transducers by the equivalent circuit method. Sens. Actuator A Phys. 2021, 318, 112507. [Google Scholar] [CrossRef]
- Shankar, S.G.; Beenamole, K.S.; Tamilarasan; Sreejith, C.A.; Shanthi, P.; Singh, A.K. A Comparative Study on Arc Conformal Arrays for Different Curvatures. In Proceedings of the 10th International Radar Symposium India, NIMHANS Convention Centre, Bangalore, India, 15–19 December 2015; pp. 1–4. [Google Scholar]
- Wei, Z.; Junfeng, Y. A design of vertical polarized conformal antenna and its array based on UAV structure. Int. J. Antennas Propag. 2017, 2017, 9769815. [Google Scholar] [CrossRef]
- Han, R. Simulation of radiation characteristics for cylindrical conformal phased array. Comput. Inf. Sci. 2010, 3, 175–179. [Google Scholar] [CrossRef][Green Version]
- He, Q.Q.; Wang, B.Z. Radiation patterns synthesis for a conformal dipole antenna array. Prog. Electromagn. Res. 2007, 76, 327–340. [Google Scholar] [CrossRef][Green Version]
- Lei, J.; Yang, J.; Chen, X.; Zhang, Z.; Fu, G.; Hao, Y. Experimental demonstration of conformal phased array antenna via transformation optics. Sci. Rep. 2018, 8, 3807. [Google Scholar] [CrossRef]
- Deng, L.; Wu, Y.; Hong, W.; Zhu, J.; Peng, B.; Li, S. Conformal array design on arbitrary polygon surface with transformation optics. AIP Adv. 2016, 6, 065011. [Google Scholar] [CrossRef]
- Smiley, A.; Howell, M.; Clement, G.T.; Fleischman, A.J. Toward transcranial ultrasound tomography: Design of a 456-element low profile conformal array. Biomed. Phys. Eng. Express 2019, 5, 025025. [Google Scholar] [CrossRef]
- Kim, H.H.; Chang, J.H.; Cannata, J.M.; Shung, K.K. 2F-3 Design of 20 MHz Convex Array Transducers for High Frequency Ophthalmic Imaging. In Proceedings of the 2007 IEEE Ultrasonics Symposium Proceedings, New York, NY, USA, 28–31 October 2007; pp. 88–91. [Google Scholar]
- Freitag, L.; Grund, M.; Catipovic, J.; Nagle, D.; Pazol, B.; Glynn, J. Acoustic Communication with Small UUVs Using a Hull-Mounted Conformal Array. In Proceedings of the MTS/IEEE Oceans 2001. An Ocean Odyssey, Conference (IEEE Cat. No.01CH37295), Honolulu, HI, USA, 5–8 November 2001; pp. 2270–2275. [Google Scholar]
- Benjamin, K.C. Recent advances in 1–3 piezoelectric polymer composite transducer technology for AUV/UUV acoustic imaging applications. J. Electroceram. 2002, 8, 145–154. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, H.; Yan, B.; Sun, H.; Wu, C.; Shu, Y.; Wang, L.; Ren, T. A flexible piezoelectric micromachined ultrasound transducer. RSC Adv. 2013, 3, 24900–24905. [Google Scholar] [CrossRef]
- Zhu, S.; Yang, Y.; Wang, Y.; Yang, Q.; Yan, X. Performance of a Cylindrical Hydrophone Array for Practical Use. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing, Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Stepnowski, A.; Szczucka, J.; Pankiewicz, L. Computer simulation of beam patterns for a sonar phased cylindrical array. In Progress in Underwater Acoustics; Merklinger, H.M., Ed.; Springer: Boston, MA, USA, 1987; pp. 627–638. [Google Scholar]
- Huissoon, J.P. Multiobjective design of curved array sonar transducers. In Acoustical Imaging; Ermert, H., Harjes, H.P., Eds.; Springer: Boston, MA, USA, 1992; pp. 231–236. [Google Scholar]
- Lesniak, W. High-precision bearing estimation for active sonar with cylindrical array performed by interpolated array transformation. Hydroacoustic 2016, 19, 238–265. [Google Scholar]
- Bertilone, D.C.; Killeen, D.S.; Bao, C. Array gain for a cylindrical array with baffle scatter effects. J. Acoust. Soc. Am. 2007, 122, 2679–2685. [Google Scholar] [CrossRef]
- Yen, J.T.; Steinberg, J.P.; Smith, S.W. Sparse 2-D array design for real time rectilinear volumetric imaging. IEEE Trans. Ultrason Ferroelectr. Freq. Control 2000, 47, 93–110. [Google Scholar] [CrossRef]
- Barott, W.C.; Steffes, P.G. A Three-Dimensional Pattern-Space Representation for Volumetric Arrays. IEEE Antennas Wirel Propag. Lett. 2008, 7, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Qin, L.; Liao, Q.; Zhong, C.A. Doubly-Curved Piezoelectric Composite with 1–3 Connectivity for Underwater Transducer Applications. In Proceedings of the IOP Conferences Series: Materials Science and Engineering, 4th International Conference on Advanced Engineering and Technology, Shanghai, China, 15–17 December 2017; IOP Publishing Ltd.: Bristol, UK, 2018; Volume 317, pp. 1–6. [Google Scholar]
- Rigelsford, J.M. Design and Analysis of an Acoustic Random Spherical Volumetric Array. Ph.D. Thesis, The University of Hull, Cottingham, UK, 2001. [Google Scholar]
- Ahmad, K.A.; Abd Manaf, A.; Mohd Yaacob, M.H.; Rahman, M.F.A. Design of Polyimide based Piezoelectric Micromachined Ultrasonic Transducer for Underwater Imaging Application. In Proceedings of the International Conference on Imaging, Signal Processing and Communication, Penang, Malaysia, 26–28 July 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 63–66. [Google Scholar]
- Sonar. Available online: https://www.sciencedirect.com/topics/physics-and-astronomy/sonar (accessed on 8 April 2021).
- Wettergren, T.A.; Traweek, C.M. Optimization of conventional beamformer shading weights for conformal velocity sonar. IEEE J. Ocean. Eng. 2005, 30, 213–220. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2000; p. 195. [Google Scholar]
- Foote, K.G. Discriminating between the nearfield and the farfield of acoustic transducers. J. Acoust. Soc. Am. 2014, 136, 1511–1517. [Google Scholar] [CrossRef]
- Butler, J.L.; Sherman, C.H. Transducers and Arrays for Underwater Sound, 2nd ed.; Springer: Boston, MA, USA, 2008; p. 349. [Google Scholar]
- Lasdon, L.S.; Plummer, J.C. Multistart algorithms for seeking feasibility. Comput. Oper. Res. 2008, 35, 1379–1393. [Google Scholar] [CrossRef]
- Ugray, Z.; Lasdon, L.; Plummer, J.; Glover, F.; Kelly, J.; Martí, R. Scatter search and local NLP solvers: A multistart framework for global optimization. Inf. J. Comput. 2007, 19, 328–340. [Google Scholar] [CrossRef]
- Abazid, M.; Alkoud, D. A least-squares approach to prediction the future sales of pharmacy. Int. J. Innov. Technol. Explor. Eng. 2018, 7, 1–4. [Google Scholar]
- Koukouvinos, C. Orthogonal 2k and 3k factorial designs constructed using sequences with zero autocorrelation. Stat. Probab. Lett. 1996, 28, 59–63. [Google Scholar] [CrossRef]
- Dobson, J.; Tweedie, A.; Harvey, G.; O’Leary, R.; Mulholland, A.; Tant, K.; Gachagan, A. Finite element analysis simulations for ultrasonic array NDE inspections. AIP Conf. Proc. 2016, 1706, 040005. [Google Scholar]
- Augustyniak, M.; Usarek, Z. Finite element method applied in electromagnetic NDTE: A review. J. Nondestruct. Eval. 2016, 35, 39. [Google Scholar] [CrossRef]


| Design Variable | Lower Bound | Basic | Upper Bound |
|---|---|---|---|
| Radius of Curvature, RM (mm) | 182.5 | 202.8 | 223.1 |
| Length of Element, L (mm) | 5.0 | 5.2 | 5.4 |
| Model | Geometrical Parameters | Performance Parameters | |||
|---|---|---|---|---|---|
| M | RM (mm) | L (mm) | Ripple (dB) | Beamwidth (°) | |
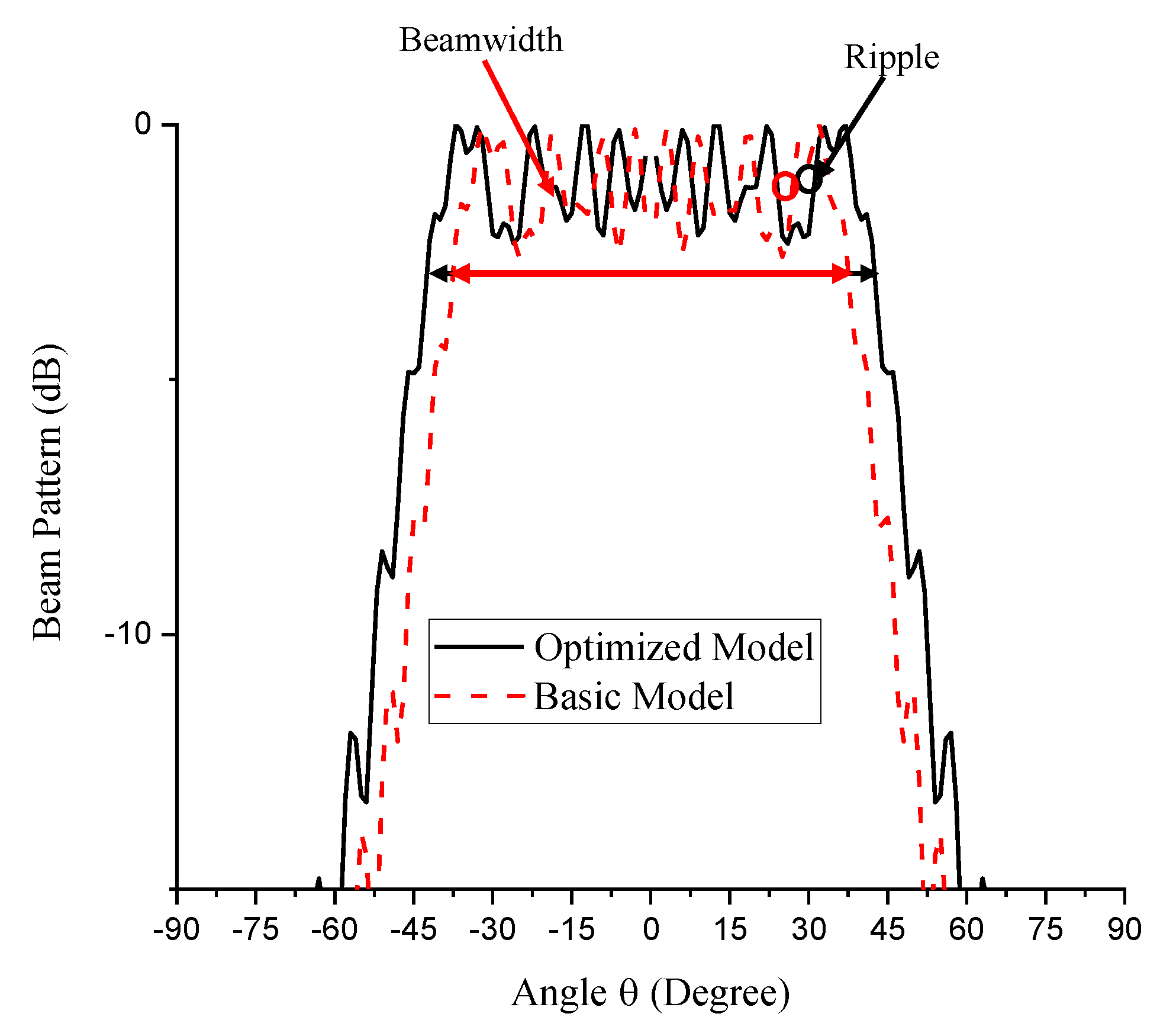
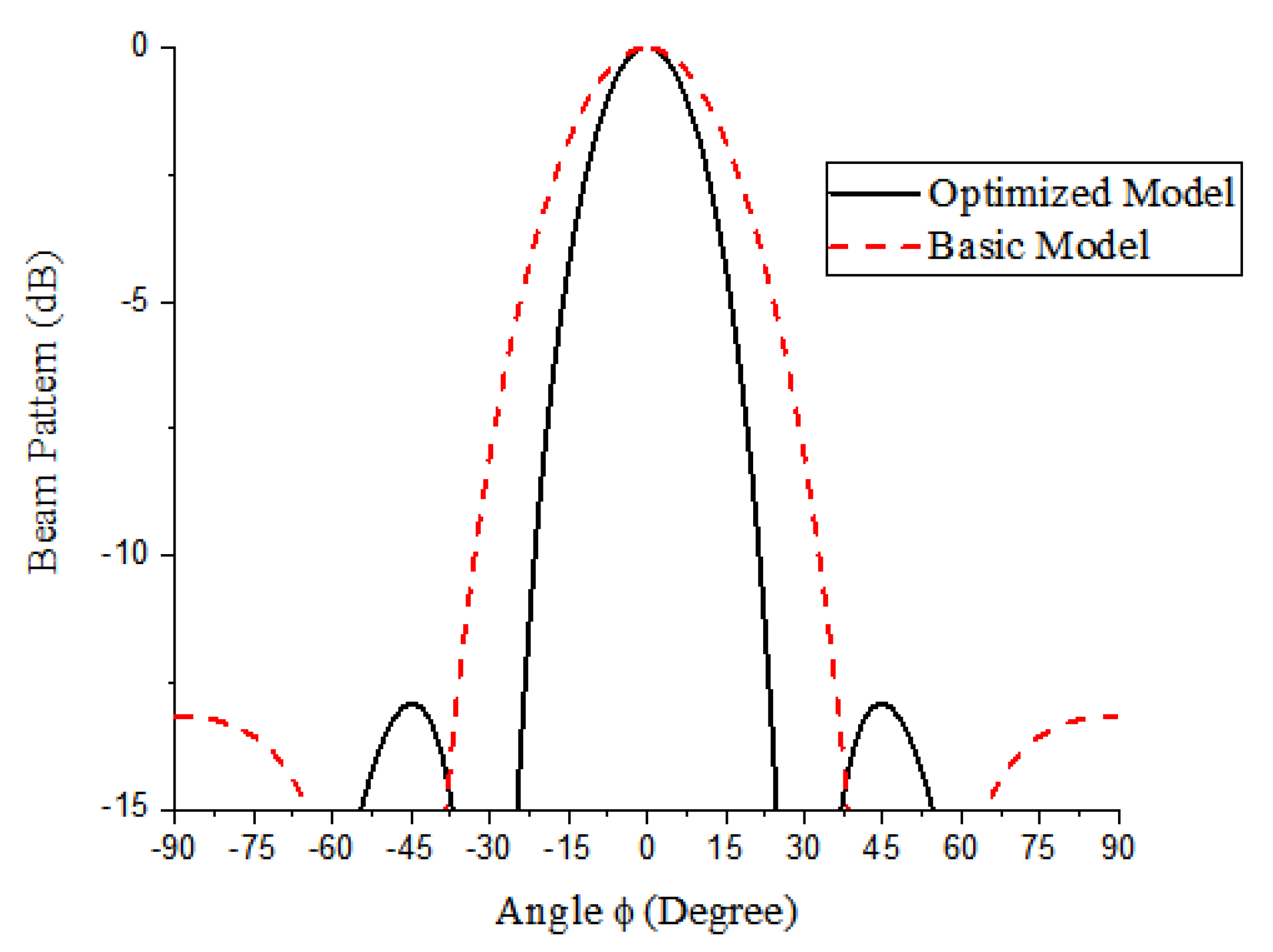
| Basic | 55 | 202.8 | 5.2 | 2.6 | 75.1 |
| Optimized | 55 | 182.5 | 5.2 | 2.3 | 85.1 |
| Design Variables | Lower Bound | Basic | Upper Bound |
|---|---|---|---|
| Radius of Curvature, RN (mm) | 80 | 120 | 160 |
| Width of Element, W (mm) | 1.6 | 3.6 | 5.6 |
| Model | Geometrical Parameters | Performance Parameters | |||
|---|---|---|---|---|---|
| N | RN (mm) | W (mm) | Ripple (dB) | Beamwidth (°) | |
| Basic | 5 | 120 | 3.6 | 0 | 38.0 |
| Optimized | 5 | 150 | 5.6 | 0 | 25.3 |
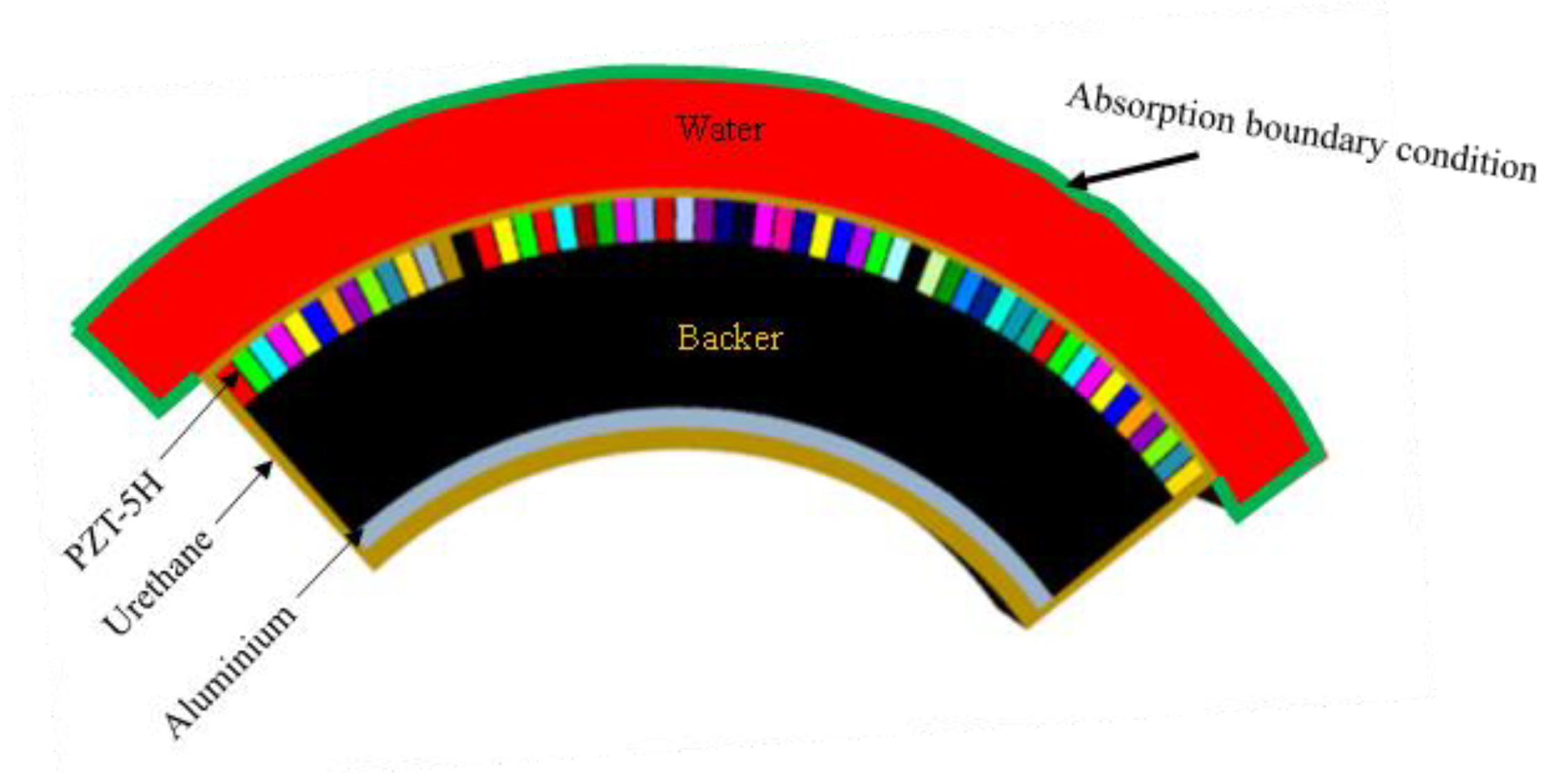
| Material | Density (kg/m3) | Longitudinal Velocity (m/s) | Shear Velocity (m/s) |
|---|---|---|---|
| Urethane/Kerf | 1065 | 1284 | 252 |
| Backer | 1712 | 1815 | 0 |
| Aluminum | 2700 | 6149 | 3097 |
| Water | 1000 | 1500 | 0 |
| M-Array Part | N-Array Part | |||
|---|---|---|---|---|
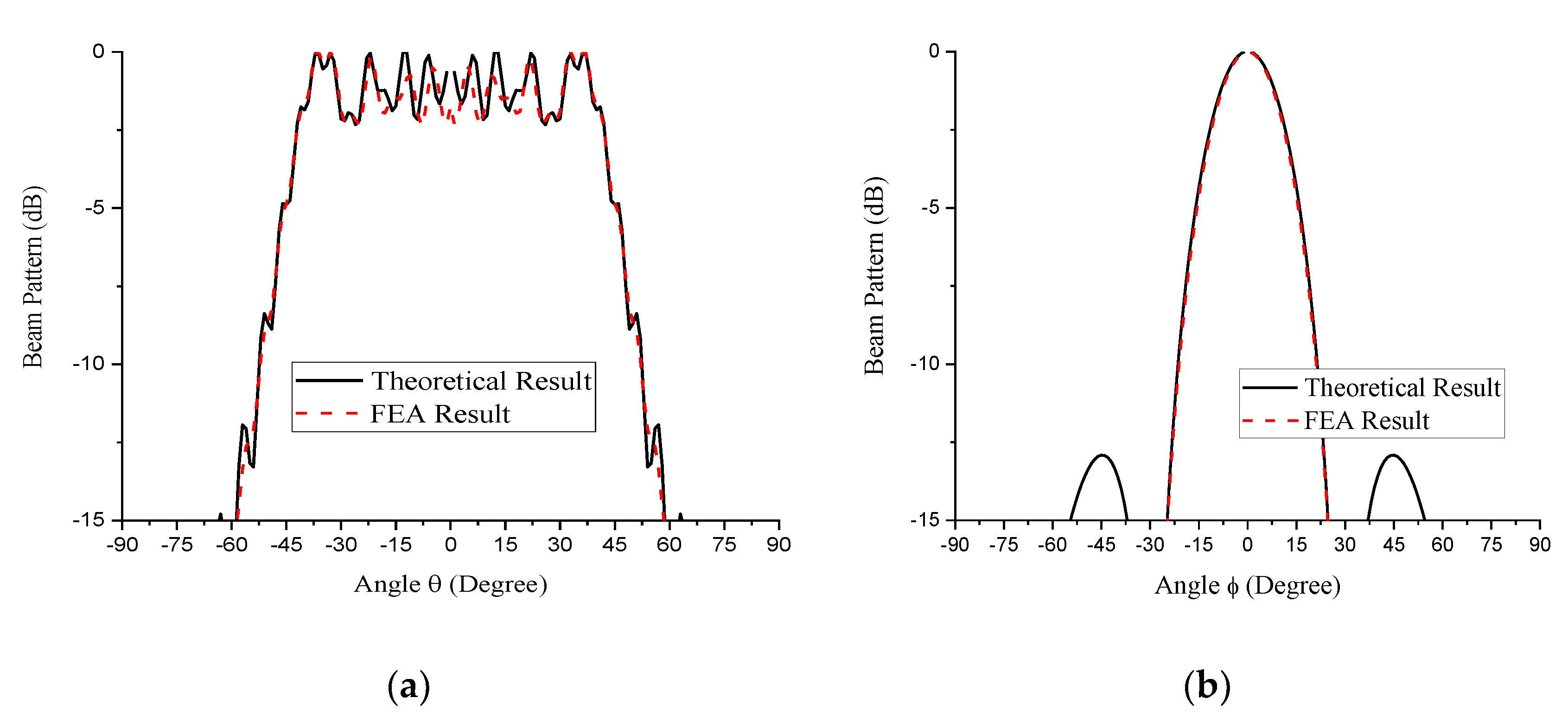
| Measured Parameters | Theoretical | FEA | Theoretical | FEA |
| −3 dB Beamwidth (°) | 85.1 | 85.2 | 25.3 | 24.5 |
| Ripple level (dB) | 2.3 | 2.3 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusuf, T.A.; Pyo, S.; Roh, Y. A Novel Versatile Approach for Underwater Conformal Volumetric Array Design. Sensors 2021, 21, 3591. https://doi.org/10.3390/s21113591
Yusuf TA, Pyo S, Roh Y. A Novel Versatile Approach for Underwater Conformal Volumetric Array Design. Sensors. 2021; 21(11):3591. https://doi.org/10.3390/s21113591
Chicago/Turabian StyleYusuf, Taofeek Ayotunde, Seonghun Pyo, and Yongrae Roh. 2021. "A Novel Versatile Approach for Underwater Conformal Volumetric Array Design" Sensors 21, no. 11: 3591. https://doi.org/10.3390/s21113591
APA StyleYusuf, T. A., Pyo, S., & Roh, Y. (2021). A Novel Versatile Approach for Underwater Conformal Volumetric Array Design. Sensors, 21(11), 3591. https://doi.org/10.3390/s21113591







