Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions
Abstract
1. Introduction
2. Methodology
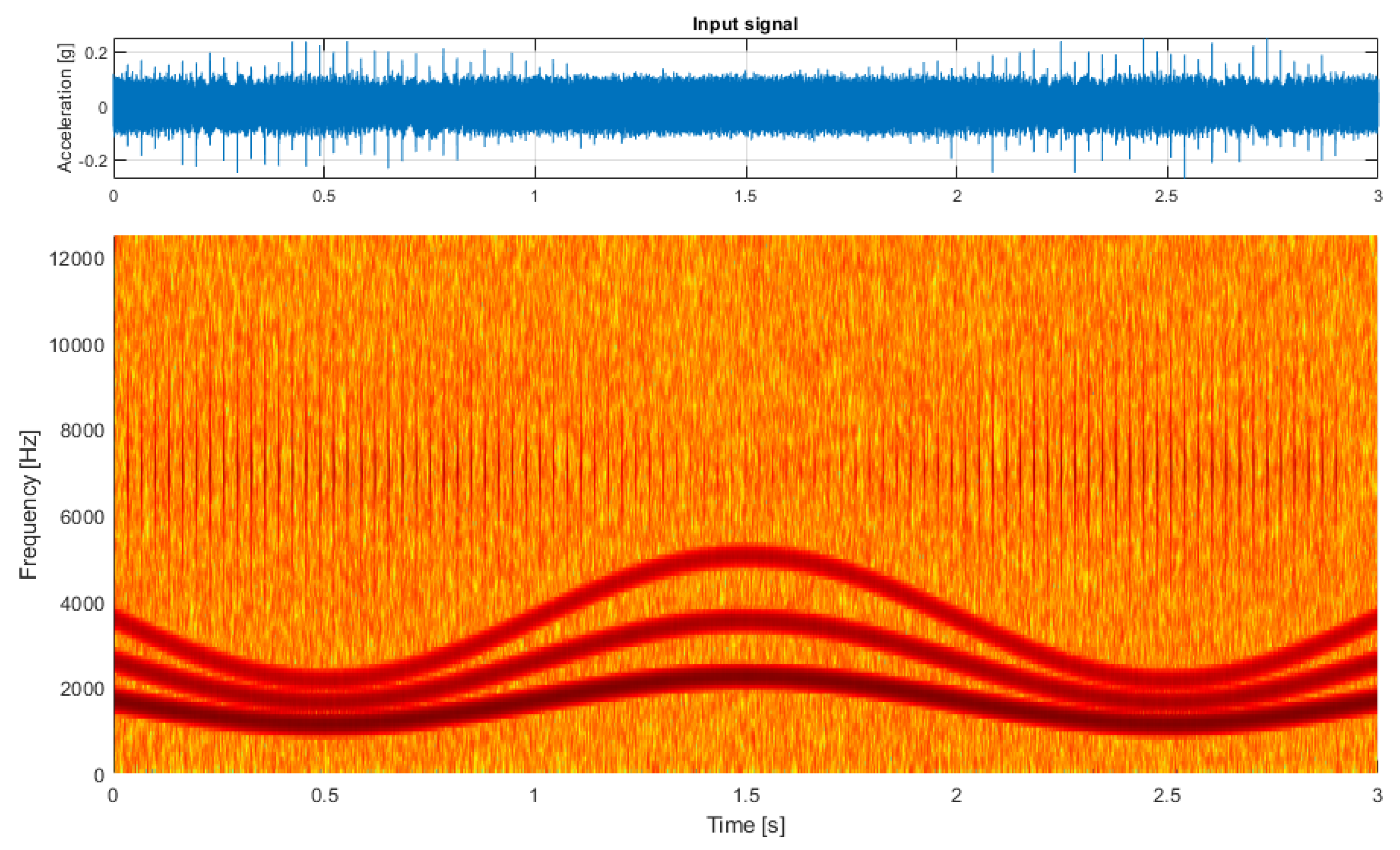
2.1. Simulated Signal Construction
- the fault component, which is an amplitude-modulated cyclic impulsive signal,
- a series of frequency-modulated sine waves representing time-invariant frequency components describing the ordinary behavior of machine operation, and
- Gaussian background noise.
2.2. Short-Time Fourier Transform
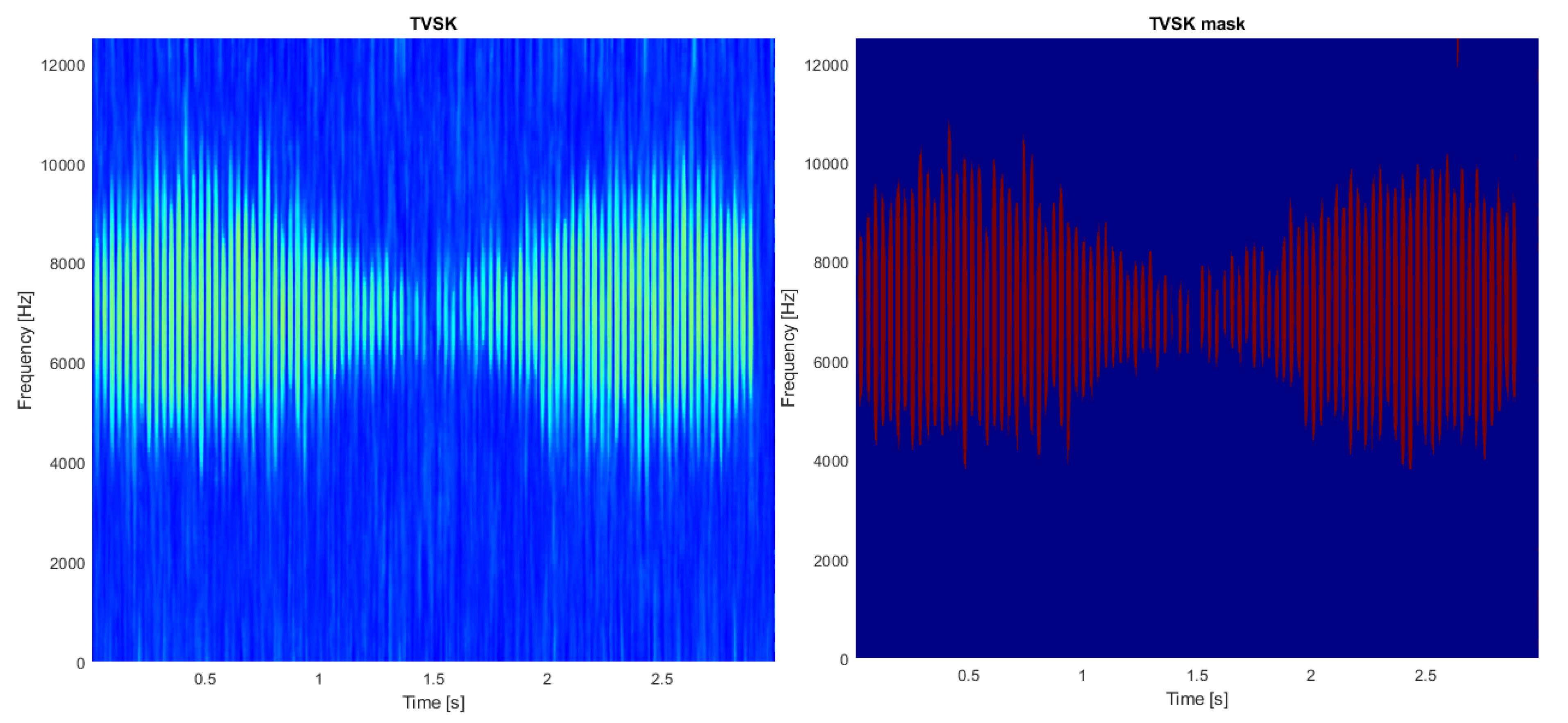
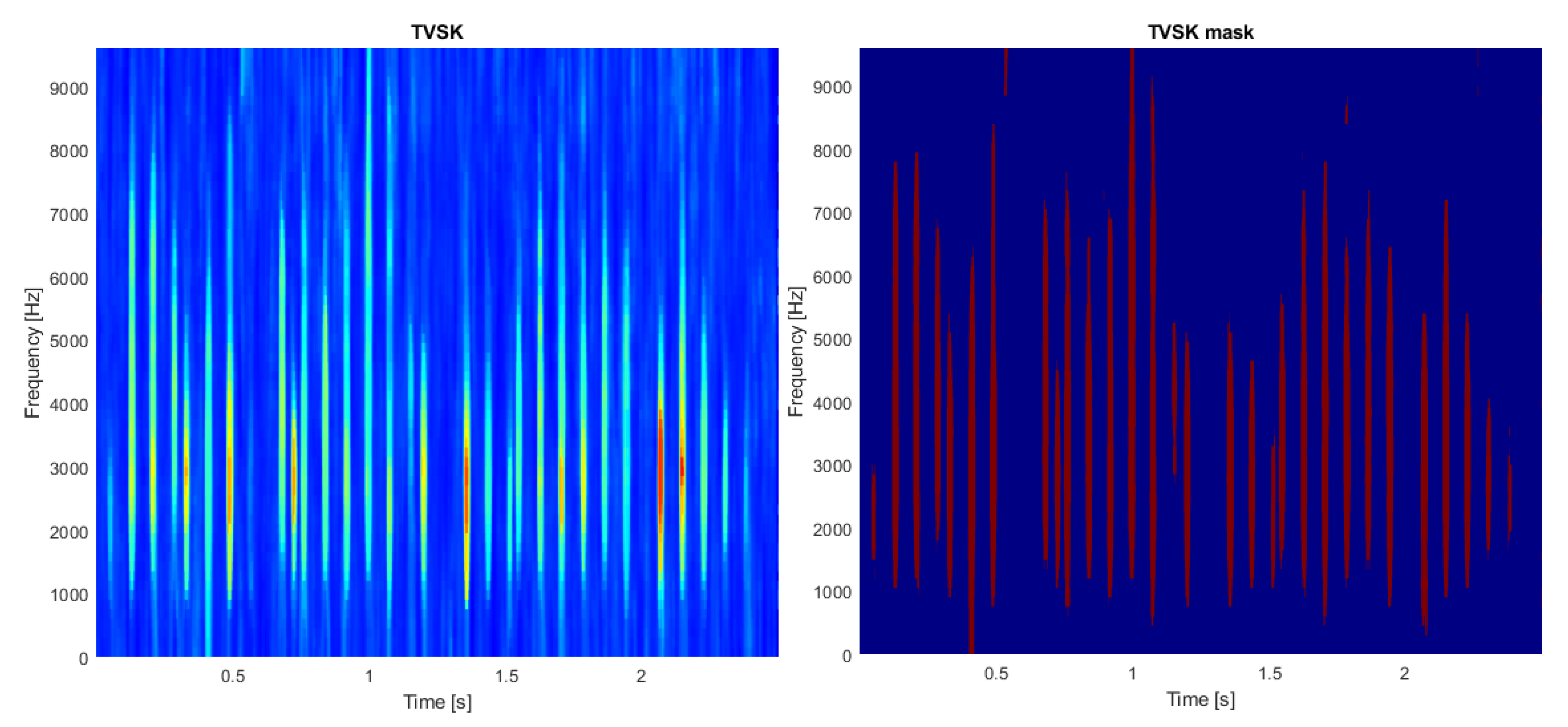
2.3. Time-Varying Spectral Kurtosis
2.4. Postprocessing: Median Filter and Resampling
- It produces undulations that find a balanced middle ground between ‘spline’ and ‘pchip’ (Piecewise Cubic Hermite Interpolating Polynomial) techniques.
- It increases the robustness of Akima’s formula in the edge case of equal side slopes.
- It eliminates a special type of overshoot occurring when the data is constant for more than two consecutive nodes, which is relevant after using a median filter that has a “piecewise-flattening” effect.
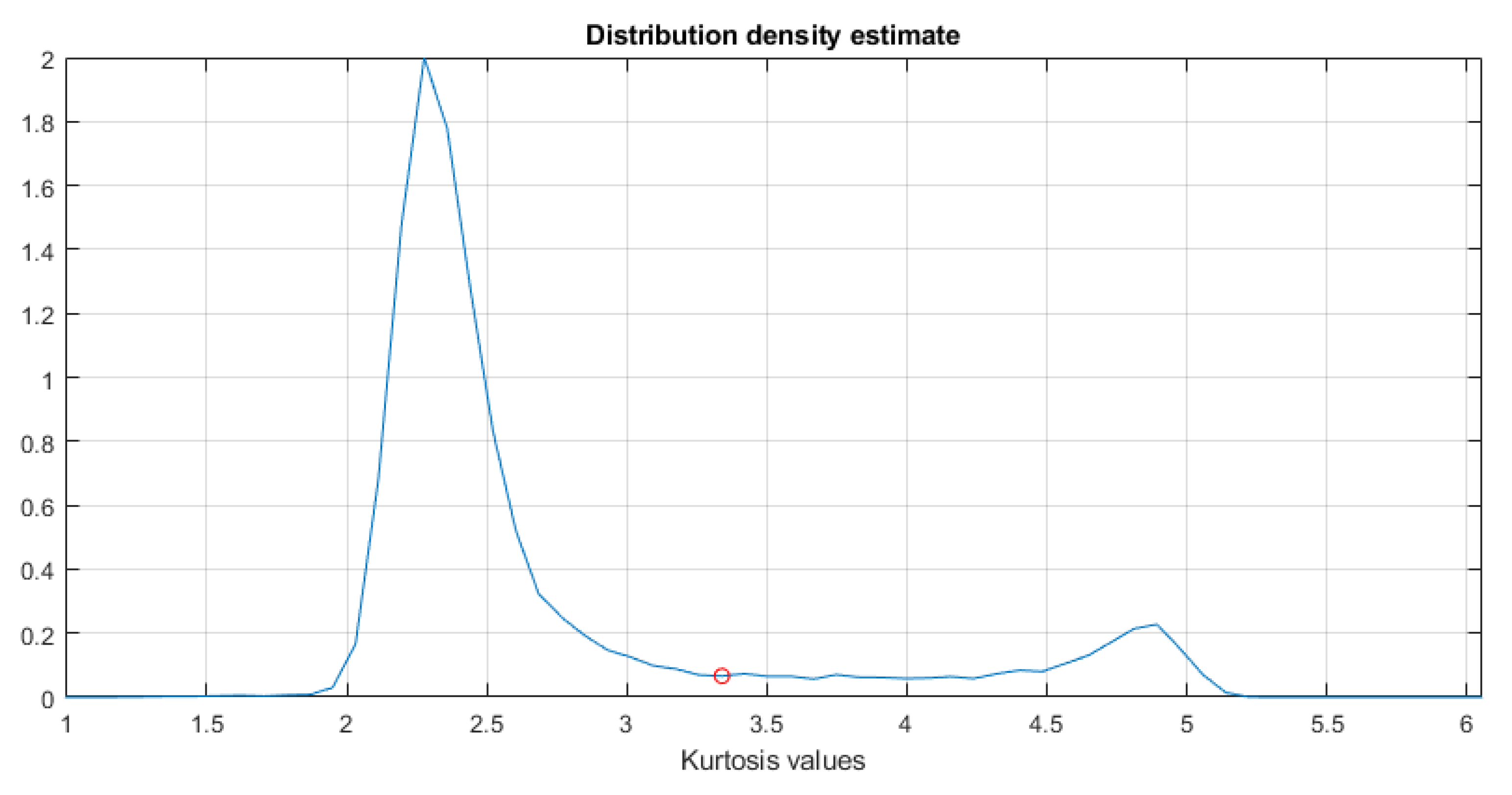
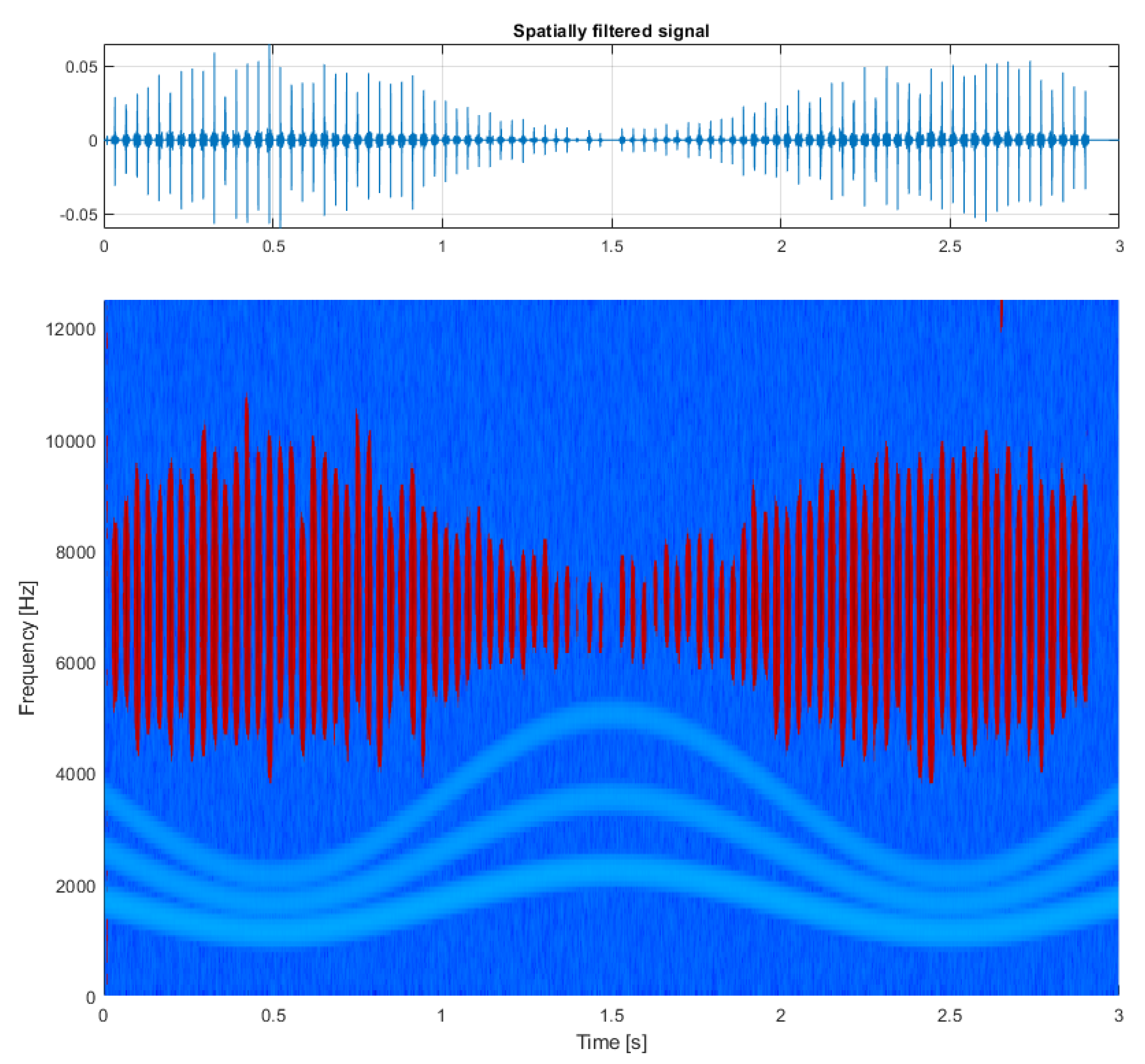
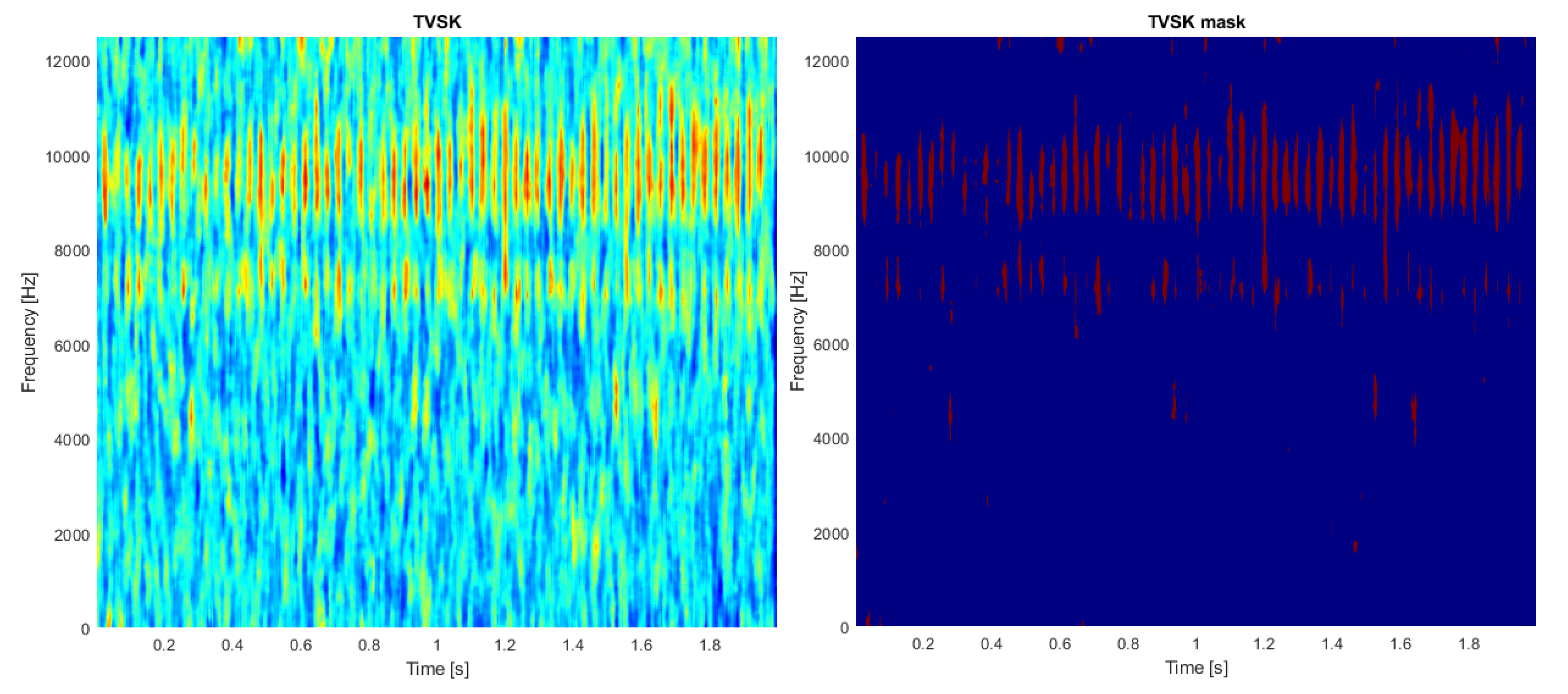
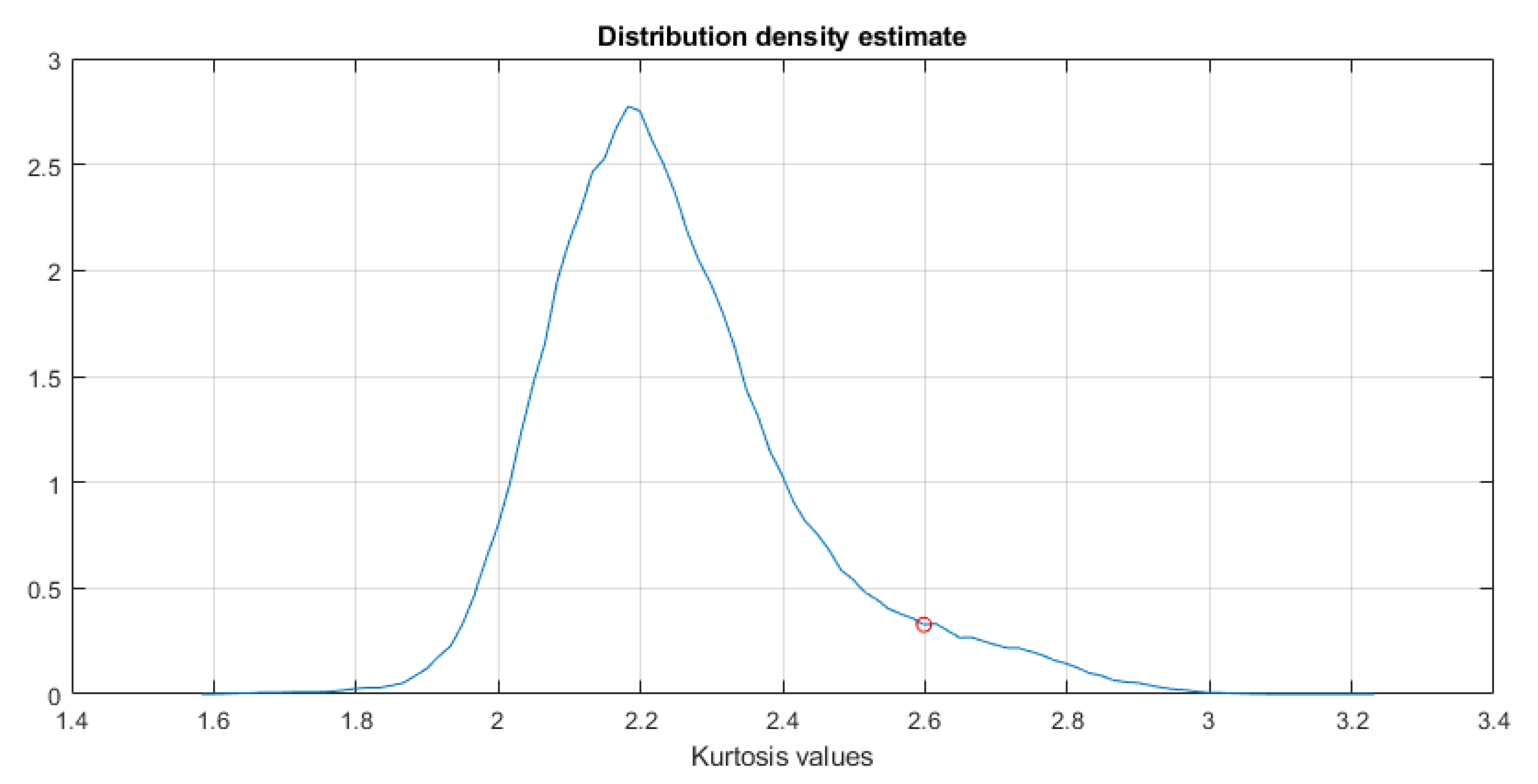
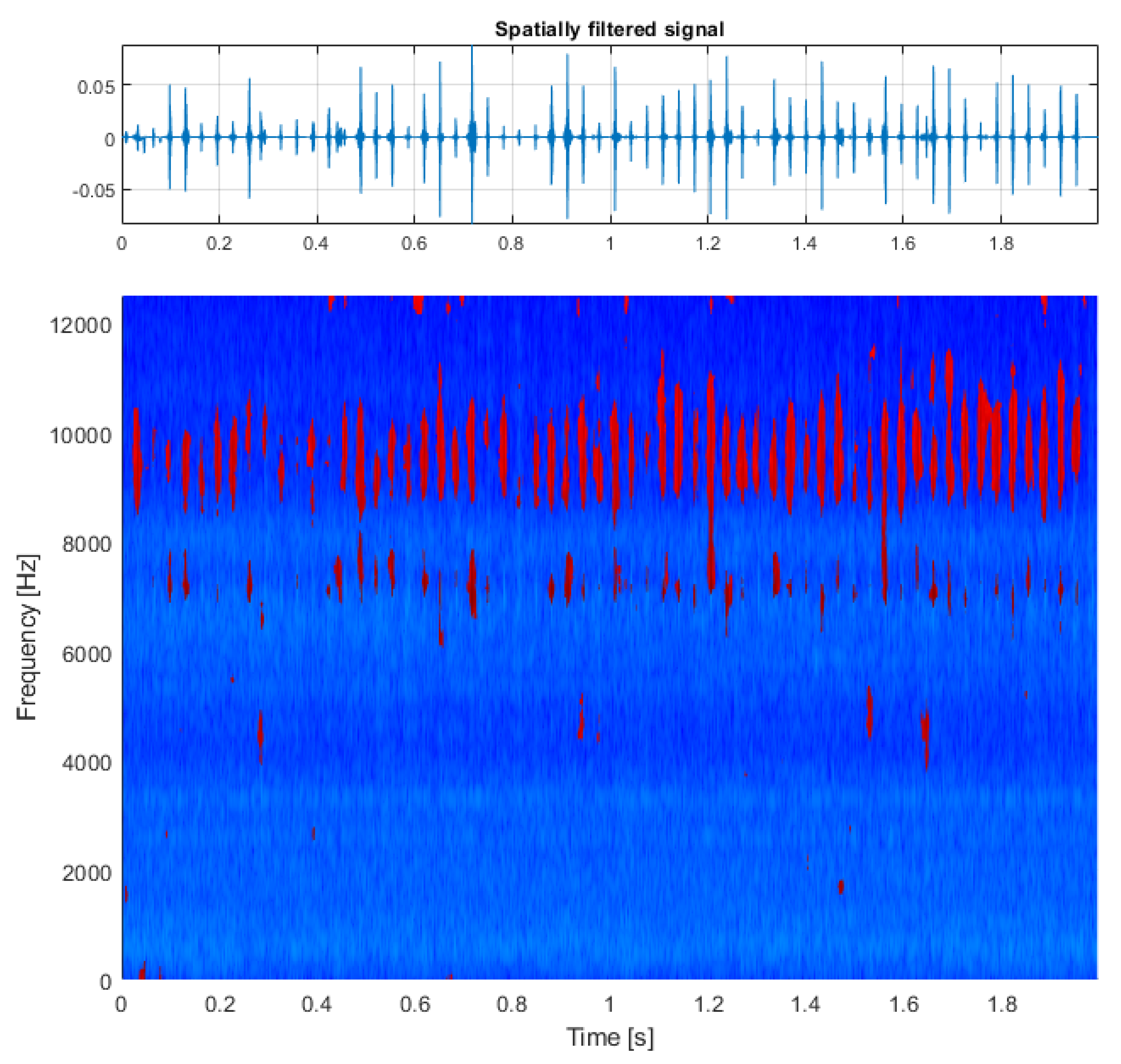
2.5. Binarization and Filtration
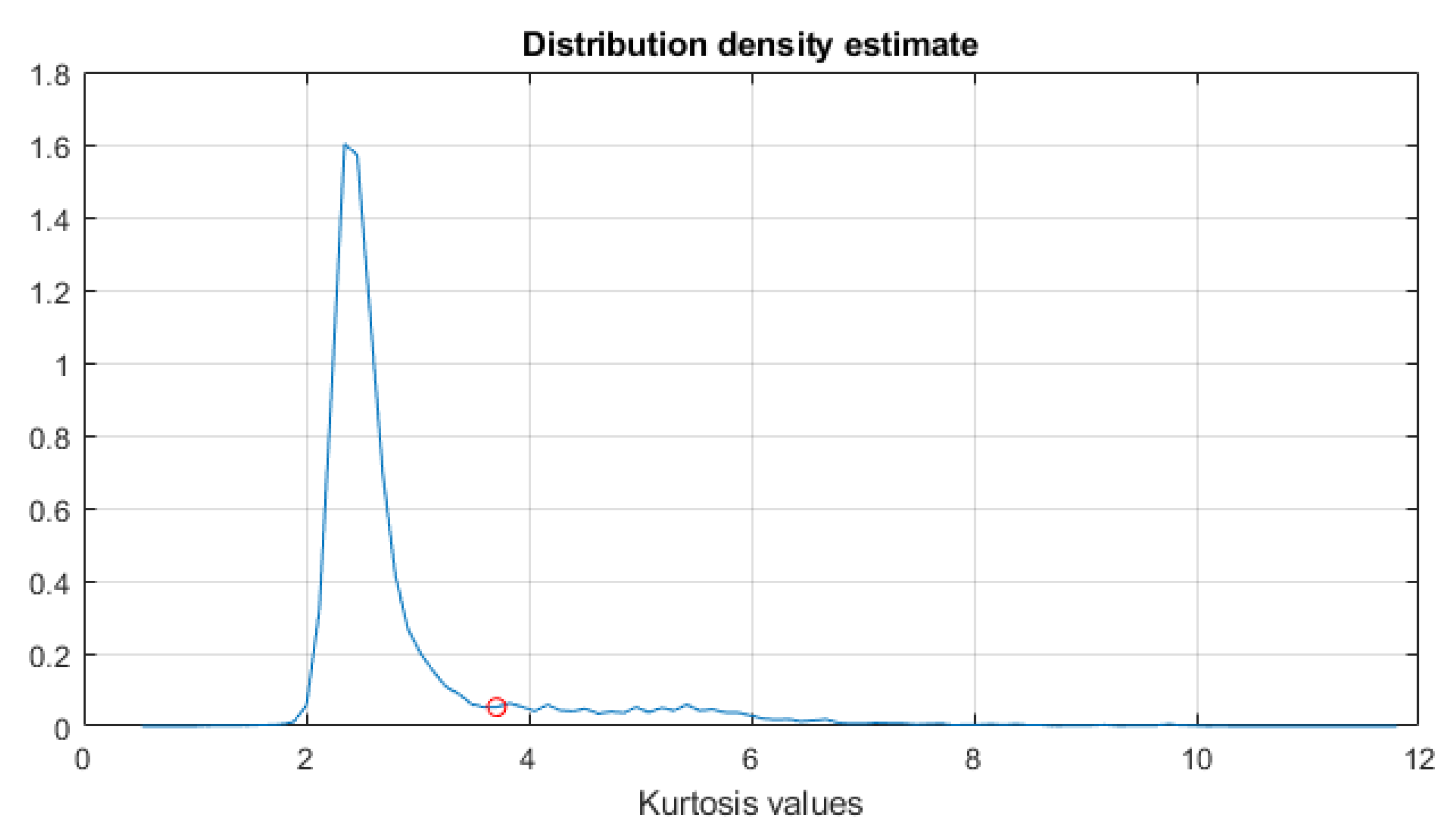
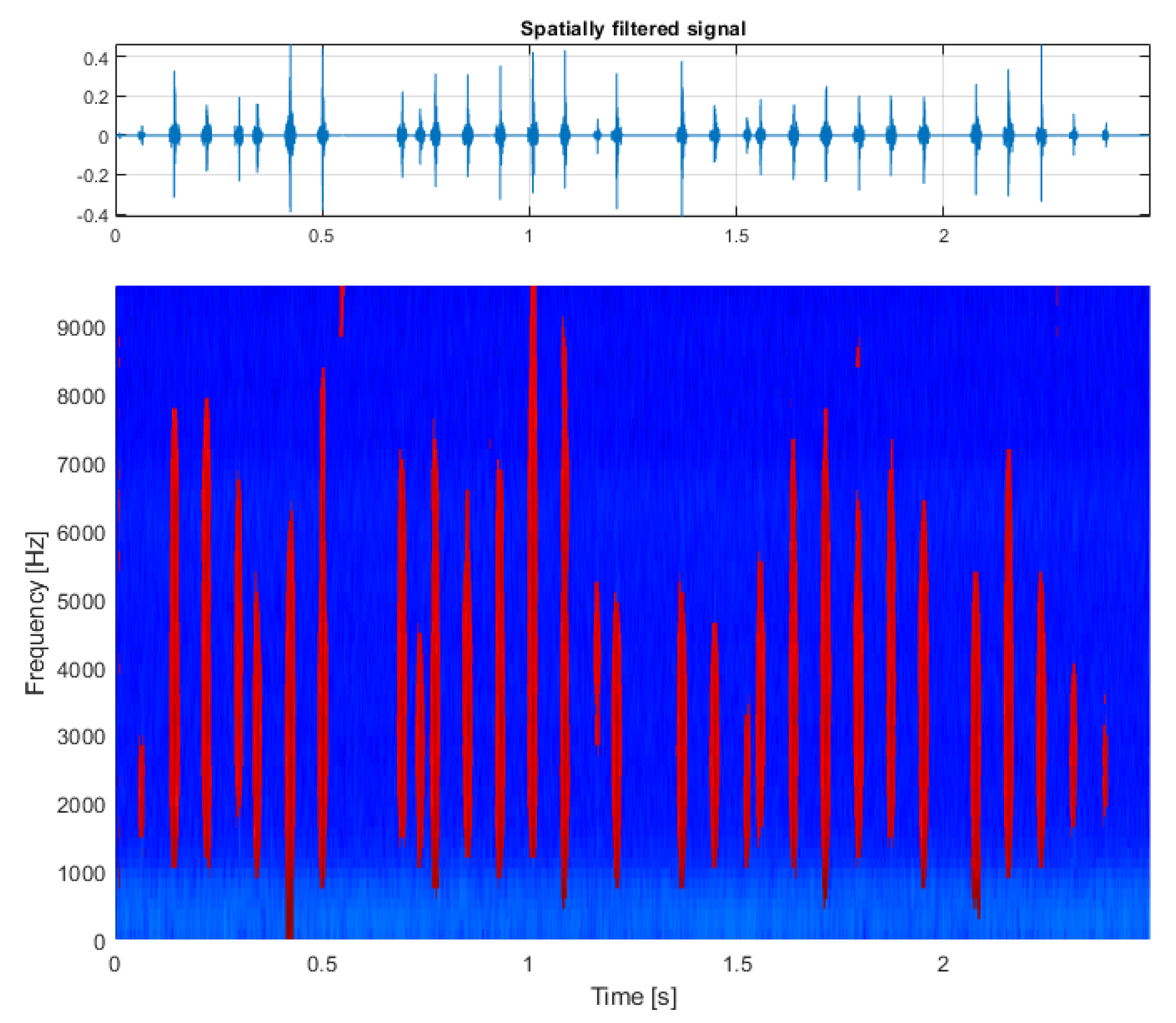
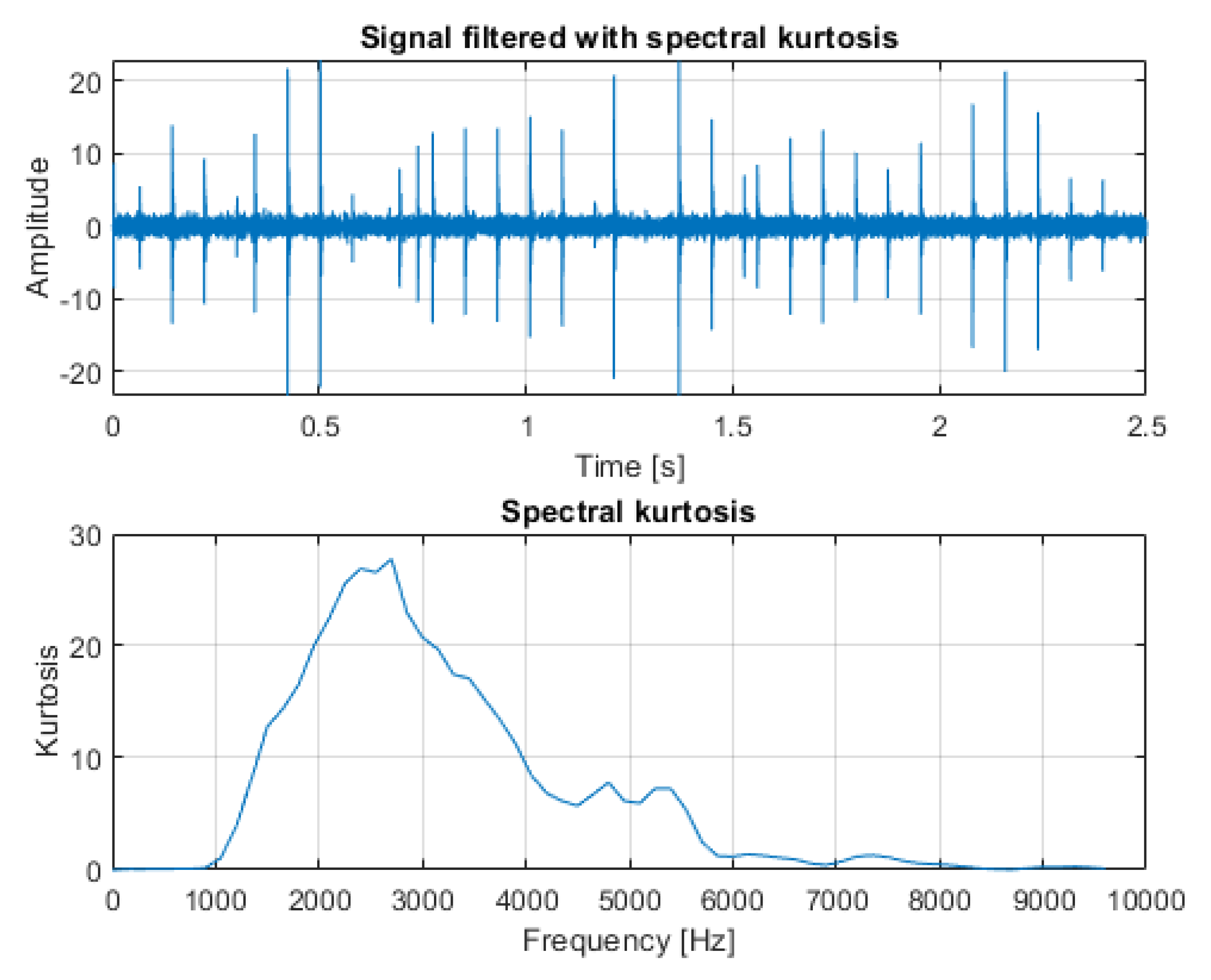
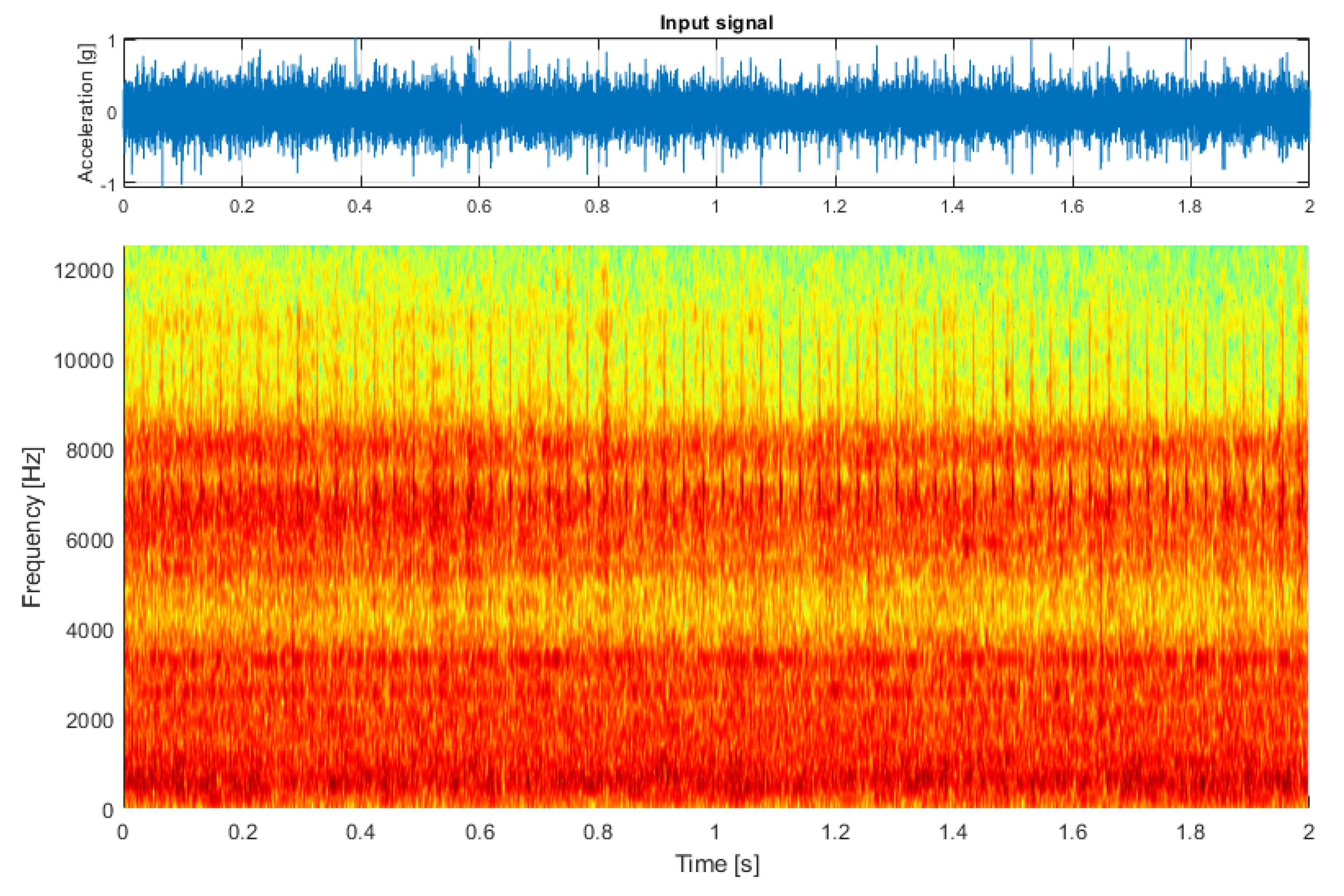
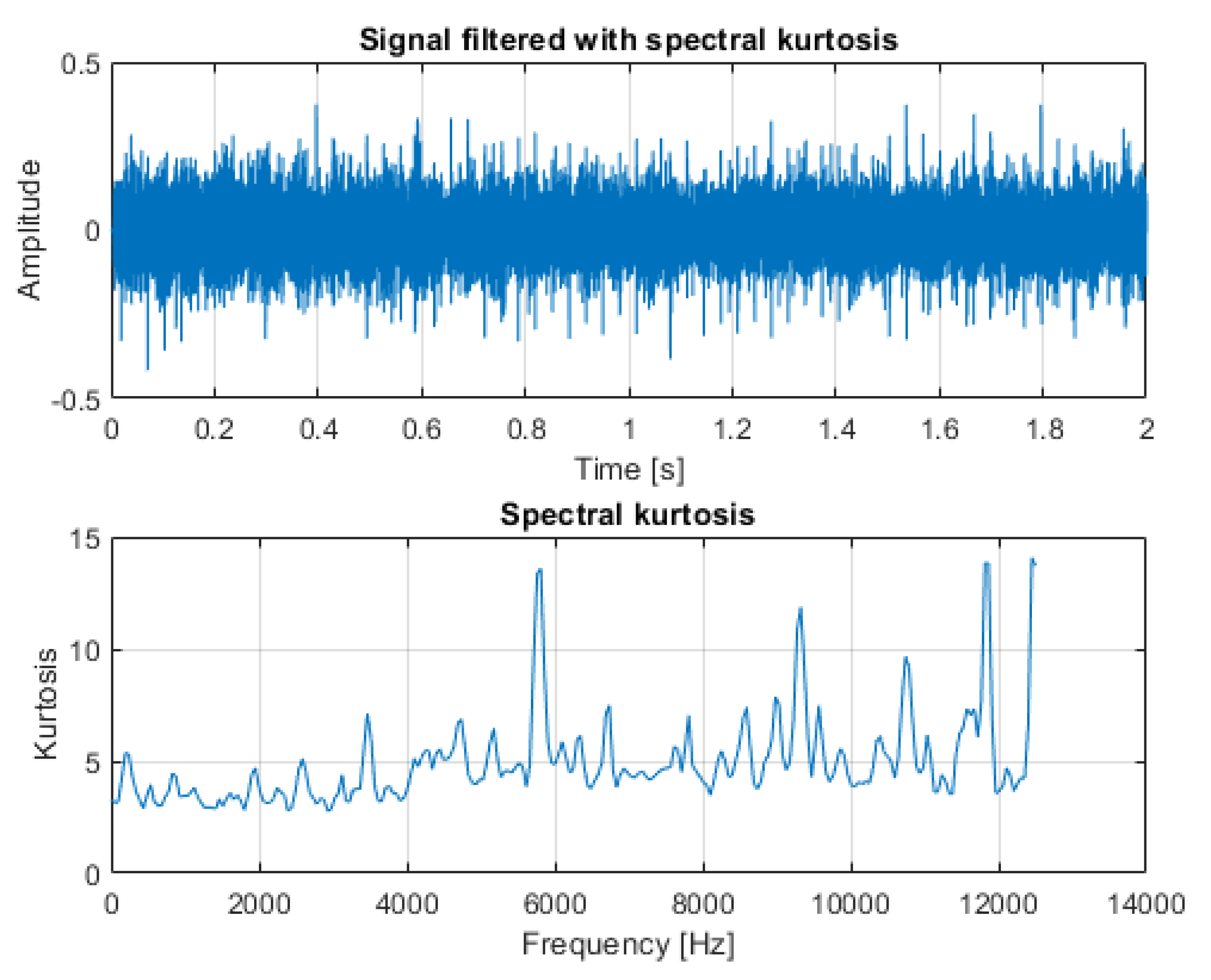
3. Results
3.1. Simulated Signal Analysis
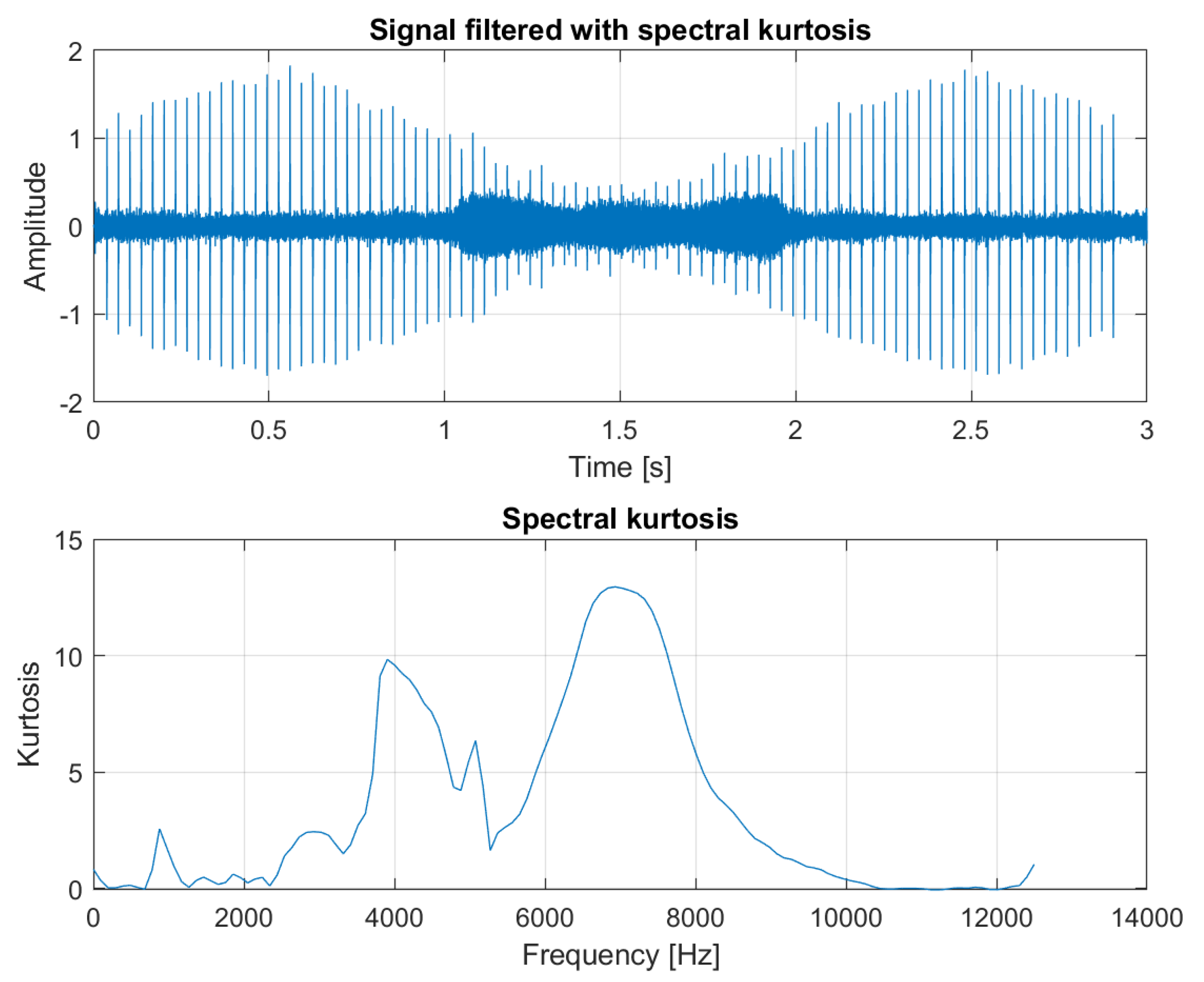
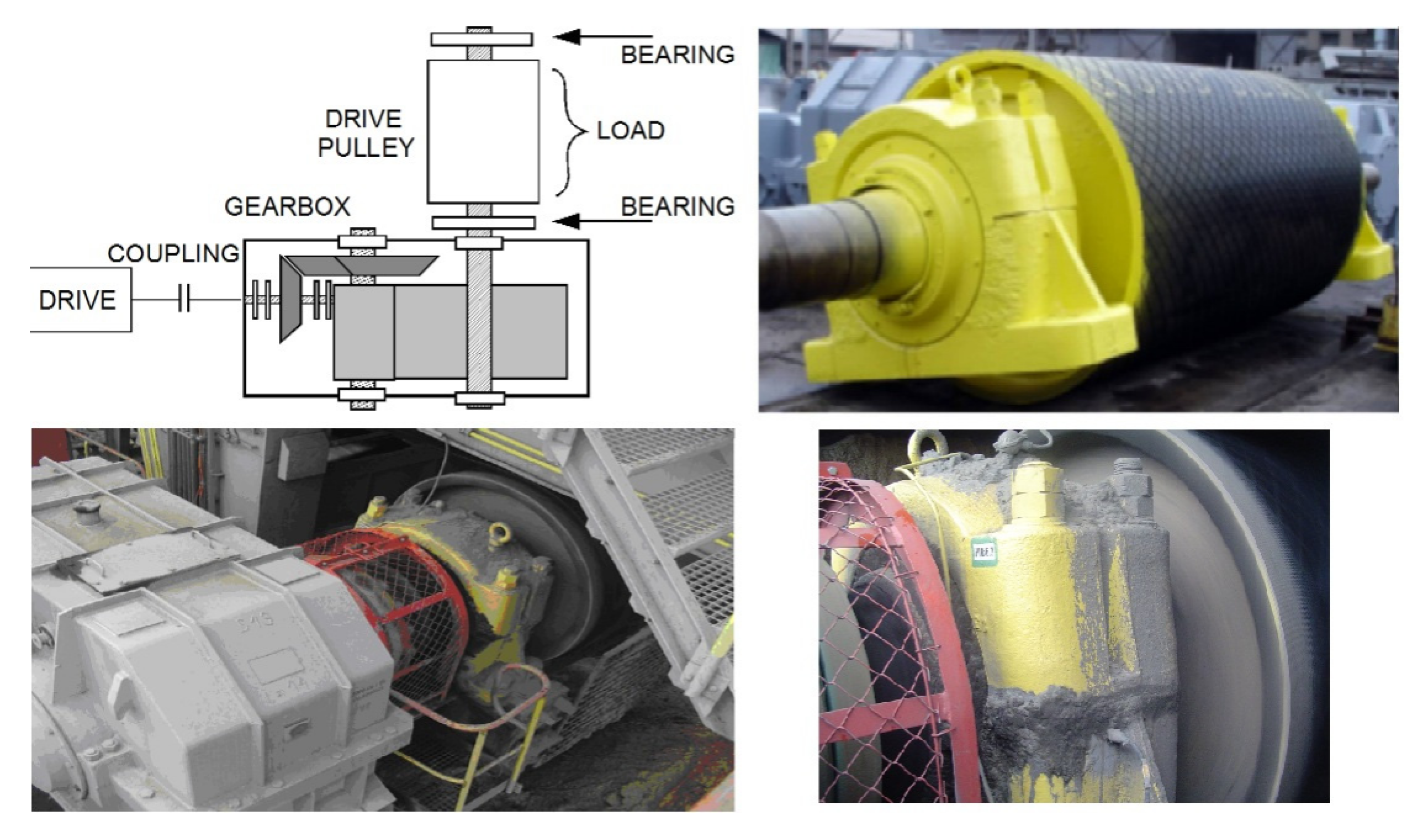
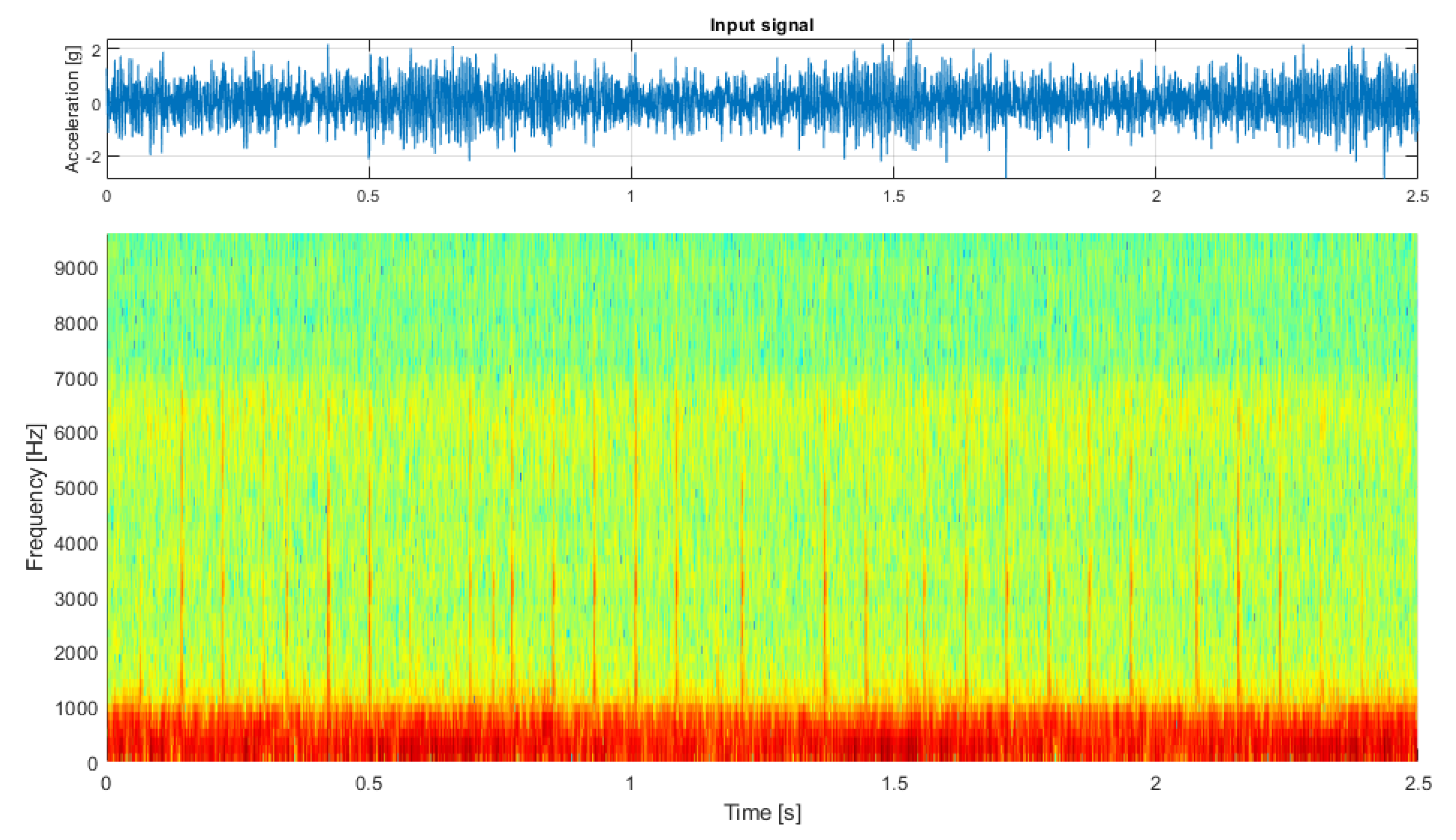
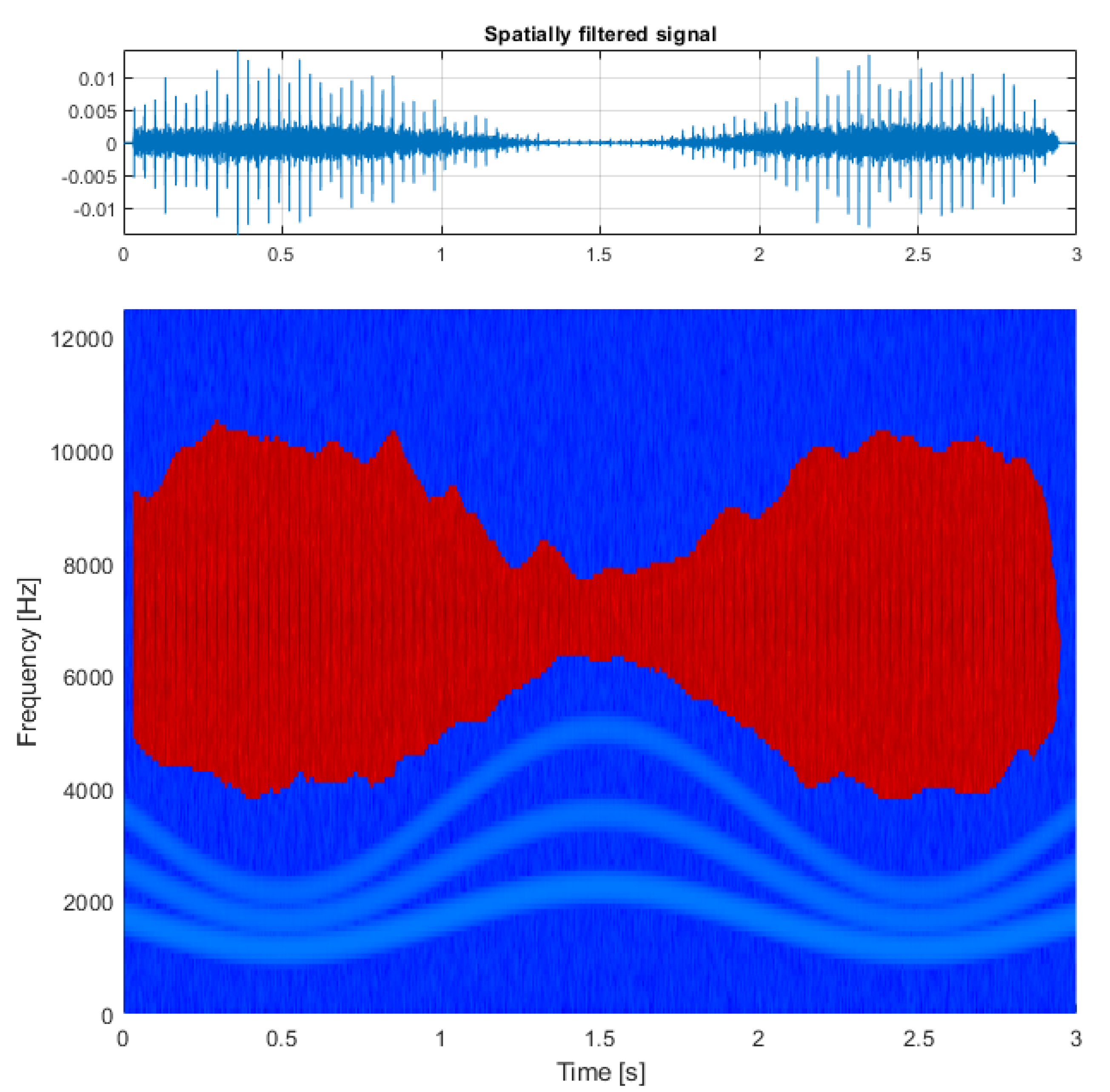
3.2. Real-Life Signal Analysis
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Merzoug, M.; Ait-Sghir, K.; Miloudi, A.; Dron, J.P.; Bolaers, F. Early detection of gear failure by vibration analysis. In Conference on Multiphysics Modelling and Simulation for Systems Design; Springer: Berlin/Heidelberg, Germany, 2014; pp. 69–79. [Google Scholar]
- Davis, F. Advanced Vibration Analysis Techniques for Fault Detection and Diagnosis in Geared Transmission Systems. Ph.D. Thesis, Swinburn University of Technology, Melbourne, Australia, 1996. [Google Scholar]
- Choy, F.; Polyshchuk, V.; Zakrajsek, J.; Handschuh, R.; Townsend, D. Analysis of the effects of surface pitting and wear on the vibration of a gear transmission system. Tribol. Int. 1996, 29, 77–83. [Google Scholar] [CrossRef]
- Staszewski, W.J.; Worden, K.; Tomlinson, G.R. Time–frequency analysis in gearbox fault detection using the Wigner–Ville distribution and pattern recognition. Mech. Syst. Signal Process. 1997, 11, 673–692. [Google Scholar] [CrossRef]
- Loutridis, S. Instantaneous energy density as a feature for gear fault detection. Mech. Syst. Signal Process. 2006, 20, 1239–1253. [Google Scholar] [CrossRef]
- Wang, W.; Wong, A.K. Autoregressive model-based gear fault diagnosis. J. Vib. Acoust. 2002, 124, 172–179. [Google Scholar] [CrossRef]
- Martin, N.; Jaussaud, P.; Combet, F. Close shock detection using time–frequency Prony modeling. Mech. Syst. Signal Process. 2004, 18, 235–261. [Google Scholar] [CrossRef]
- McFadden, P. Detecting fatigue cracks in gears by amplitude and phase demodulation of the meshing vibration. J. Vib. Acoust. Stress. Reliab. Des. 1986, 108, 165–170. [Google Scholar] [CrossRef]
- Chaari, F.; Bartelmus, W.; Zimroz, R.; Fakhfakh, T.; Haddar, M. Gearbox vibration signal amplitude and frequency modulation. Shock Vib. 2012, 19, 635–652. [Google Scholar] [CrossRef]
- El Badaoui, M.; Cahouet, V.; Guillet, F.; Daniere, J.; Velex, P. Modeling and detection of localized tooth defects in geared systems. J. Mech. Des. 2001, 123, 422–430. [Google Scholar] [CrossRef]
- Randall, R. A new method of modeling gear faults. J. Mech. Des. 1982, 104, 259–267. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Liu, B.; Riemenschneider, S.; Xu, Y. Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum. Mech. Syst. Signal Process. 2006, 20, 718–734. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Zimroz, R. Optimal filter design with progressive genetic algorithm for local damage detection in rolling bearings. Mech. Syst. Signal Process. 2018, 102, 102–116. [Google Scholar] [CrossRef]
- Hebda-Sobkowicz, J.; Zimroz, R.; Pitera, M.; Wylomanska, A. Informative frequency band selection in the presence of non-Gaussian noise—A novel approach based on the conditional variance statistic with application to bearing fault diagnosis. Mech. Syst. Signal Process. 2020, 145, 106971. [Google Scholar] [CrossRef]
- Obuchowski, J.; Wyłomańska, A.; Zimroz, R. Selection of informative frequency band in local damage detection in rotating machinery. Mech. Syst. Signal Process. 2014, 48, 138–152. [Google Scholar] [CrossRef]
- Wodecki, J.; Kruczek, P.; Wylomanska, A.; Bartkowiak, A.; Zimroz, R. Novel method of informative frequency band selection for vibration signal using Nonnegative Matrix Factorization of spectrogram matrix. Mech. Syst. Signal Process. 2019, 130, 585–596. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Zimroz, R. Local damage detection based on vibration data analysis in the presence of Gaussian and heavy-tailed impulsive noise. Measurement 2021, 169, 108400. [Google Scholar] [CrossRef]
- Smith, W.A.; Borghesani, P.; Ni, Q.; Wang, K.; Peng, Z. Optimal demodulation-band selection for envelope-based diagnostics: A comparative study of traditional and novel tools. Mech. Syst. Signal Process. 2019, 134, 106303. [Google Scholar] [CrossRef]
- Antoni, J. Fast computation of the kurtogram for the detection of transient faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y.; Gao, H. Rolling element bearing fault detection using PPCA and spectral kurtosis. Measurement 2015, 75, 180–191. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Improvement of kurtosis-guided-grams via Gini index for bearing fault feature identification. Meas. Sci. Technol. 2017, 28, 125001. [Google Scholar] [CrossRef]
- Schmidt, S.; Mauricio, A.; Heyns, P.S.; Gryllias, K.C. A methodology for identifying information rich frequency bands for diagnostics of mechanical components-of-interest under time-varying operating conditions. Mech. Syst. Signal Process. 2020, 142, 106739. [Google Scholar] [CrossRef]
- Antoni, J. The infogram: Entropic evidence of the signature of repetitive transients. Mech. Syst. Signal Process. 2016, 74, 73–94. [Google Scholar] [CrossRef]
- Bozchalooi, I.S.; Liang, M. A smoothness index-guided approach to wavelet parameter selection in signal de-noising and fault detection. J. Sound Vib. 2007, 308, 246–267. [Google Scholar] [CrossRef]
- Zhao, M.; Lin, J.; Miao, Y.; Xu, X. Detection and recovery of fault impulses via improved harmonic product spectrum and its application in defect size estimation of train bearings. Measurement 2016, 91, 421–439. [Google Scholar] [CrossRef]
- Borah, A.D.; Mondal, A.J.; Muchahary, D.; Majumder, A. Fir low pass filter design using craziness base particle swarm optimization technique. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015; pp. 870–874. [Google Scholar]
- Sarangi, S.; Sahidullah, M.; Saha, G. Optimization of data-driven filterbank for automatic speaker verification. Digit. Signal Process. 2020, 104, 102795. [Google Scholar] [CrossRef]
- Antoni, J. Cyclostationarity by examples. Mech. Syst. Signal Process. 2009, 23, 987–1036. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mech. Syst. Signal Process. 2006, 20, 308–331. [Google Scholar] [CrossRef]
- Barszcz, T.; Randall, R.B. Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine. Mech. Syst. Signal Process. 2009, 23, 1352–1365. [Google Scholar] [CrossRef]
- Makowski, R.; Zimroz, R. A procedure for weighted summation of the derivatives of reflection coefficients in adaptive Schur filter with application to fault detection in rolling element bearings. Mech. Syst. Signal Process. 2013, 38, 65–77. [Google Scholar] [CrossRef]
- Elasha, F.; Ruiz-Carcel, C.; Mba, D.; Chandra, P. A comparative study of the effectiveness of adaptive filter algorithms, spectral kurtosis and linear prediction in detection of a naturally degraded bearing in a gearbox. J. Fail. Anal. Prev. 2014, 14, 623–636. [Google Scholar] [CrossRef]
- Chaturved, G.; Thomas, D. Adaptive noise cancelling and condition monitoring. J. Sound Vib. 1981, 76, 391–405. [Google Scholar] [CrossRef]
- Zimroz, R.; Bartelmus, W. Application of adaptive filtering for weak impulsive signal recovery for bearings local damage detection in complex mining mechanical systems working under condition of varying load. Solid State Phenomena. Trans. Tech. Publ. 2012, 180, 250–257. [Google Scholar] [CrossRef]
- Allen, J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 235–238. [Google Scholar] [CrossRef]
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. JACM 1970, 17, 589–602. [Google Scholar] [CrossRef]
- Dan, E.L.; Dînşoreanu, M.; Mureşan, R.C. Accuracy of Six Interpolation Methods Applied on Pupil Diameter Data. In Proceedings of the 2020 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 21–23 May 2020; pp. 1–5. [Google Scholar]
- Ozdemir, H. Comparison of Linear, Cubic Spline and Akima Interpolation Methods. 2007. Available online: https://home.pilsfree.net/tonny/zcu/FAV/KIV/KIV.PPR/Apendix%20B%20-%20Comparison%20of%20linear%2C%20cubic%20spline%20and%20akima%20interpolation%20methods.pdf (accessed on 21 May 2021).
- Peter, D.H. Kernel estimation of a distribution function. Commun. Stat. Theory Methods 1985, 14, 605–620. [Google Scholar] [CrossRef]
- Silverman, B.W. Density estimation for statistics and data analysis. In Monographs on Statistics and Applied Probability; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Griffin, D.; Lim, J. Signal estimation from modified short-time Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 236–243. [Google Scholar] [CrossRef]
- Wodecki, J.; Michalak, A.; Zimroz, R.; Wyłomańska, A. Separation of multiple local-damage-related components from vibration data using Nonnegative Matrix Factorization and multichannel data fusion. Mech. Syst. Signal Process. 2020, 145, 106954. [Google Scholar] [CrossRef]
- Gelman, L.; Kolbe, S.; Shaw, B.; Vaidhianathasamy, M. Novel adaptation of the spectral kurtosis for vibration diagnosis of gearboxes in non-stationary conditions. Insight-Non-Destr. Test. Cond. Monit. 2017, 59, 434–439. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1750–1764. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, T. An adaptive spectral kurtosis method based on optimal filter. Shock Vib. 2017, 2017. [Google Scholar] [CrossRef]
- Combet, F.; Gelman, L. Optimal filtering of gear signals for early damage detection based on the spectral kurtosis. Mech. Syst. Signal Process. 2009, 23, 652–668. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wodecki, J. Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions. Sensors 2021, 21, 3590. https://doi.org/10.3390/s21113590
Wodecki J. Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions. Sensors. 2021; 21(11):3590. https://doi.org/10.3390/s21113590
Chicago/Turabian StyleWodecki, Jacek. 2021. "Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions" Sensors 21, no. 11: 3590. https://doi.org/10.3390/s21113590
APA StyleWodecki, J. (2021). Time-Varying Spectral Kurtosis: Generalization of Spectral Kurtosis for Local Damage Detection in Rotating Machines under Time-Varying Operating Conditions. Sensors, 21(11), 3590. https://doi.org/10.3390/s21113590





