FOCUSED–Short-Term Wind Speed Forecast Correction Algorithm Based on Successive NWP Forecasts for Use in Traffic Control Decision Support Systems
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
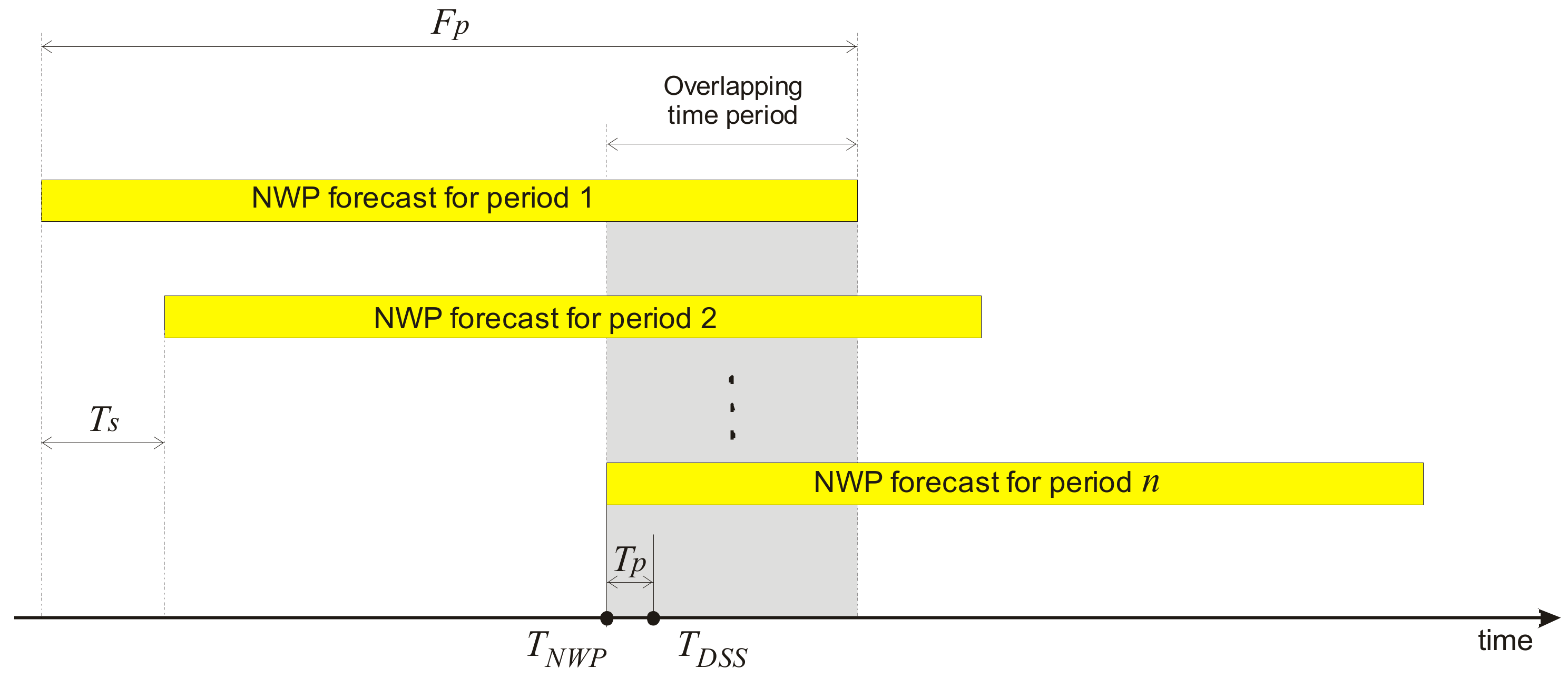
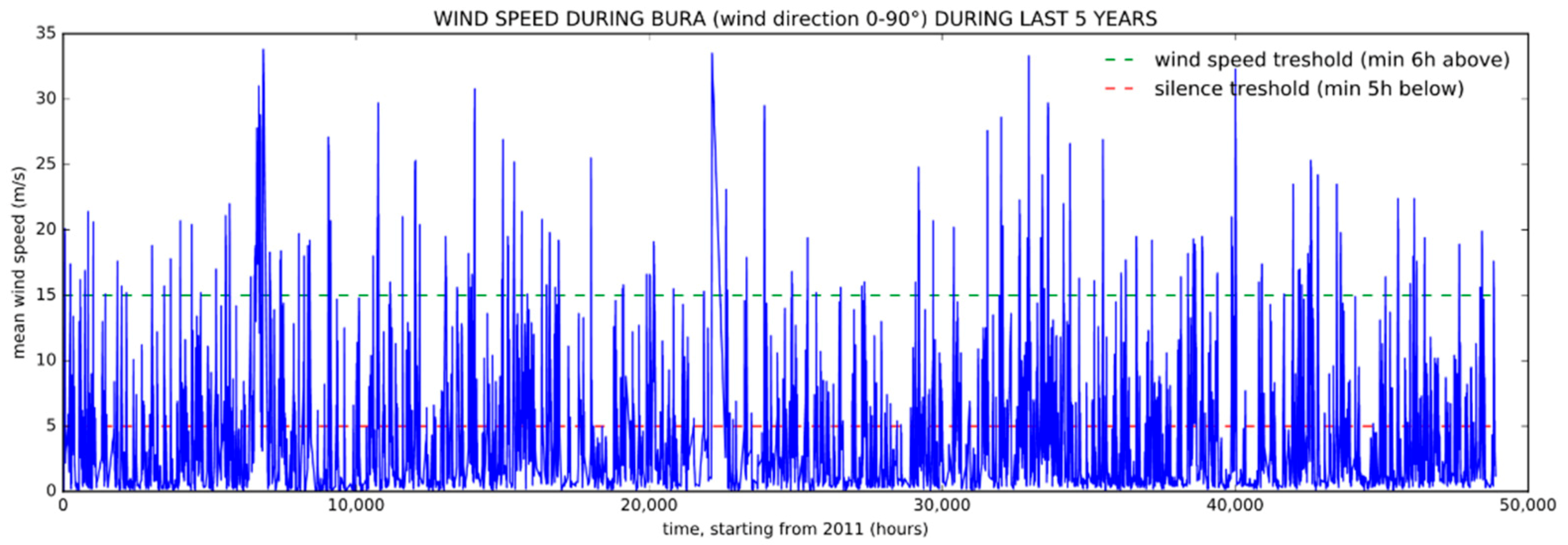
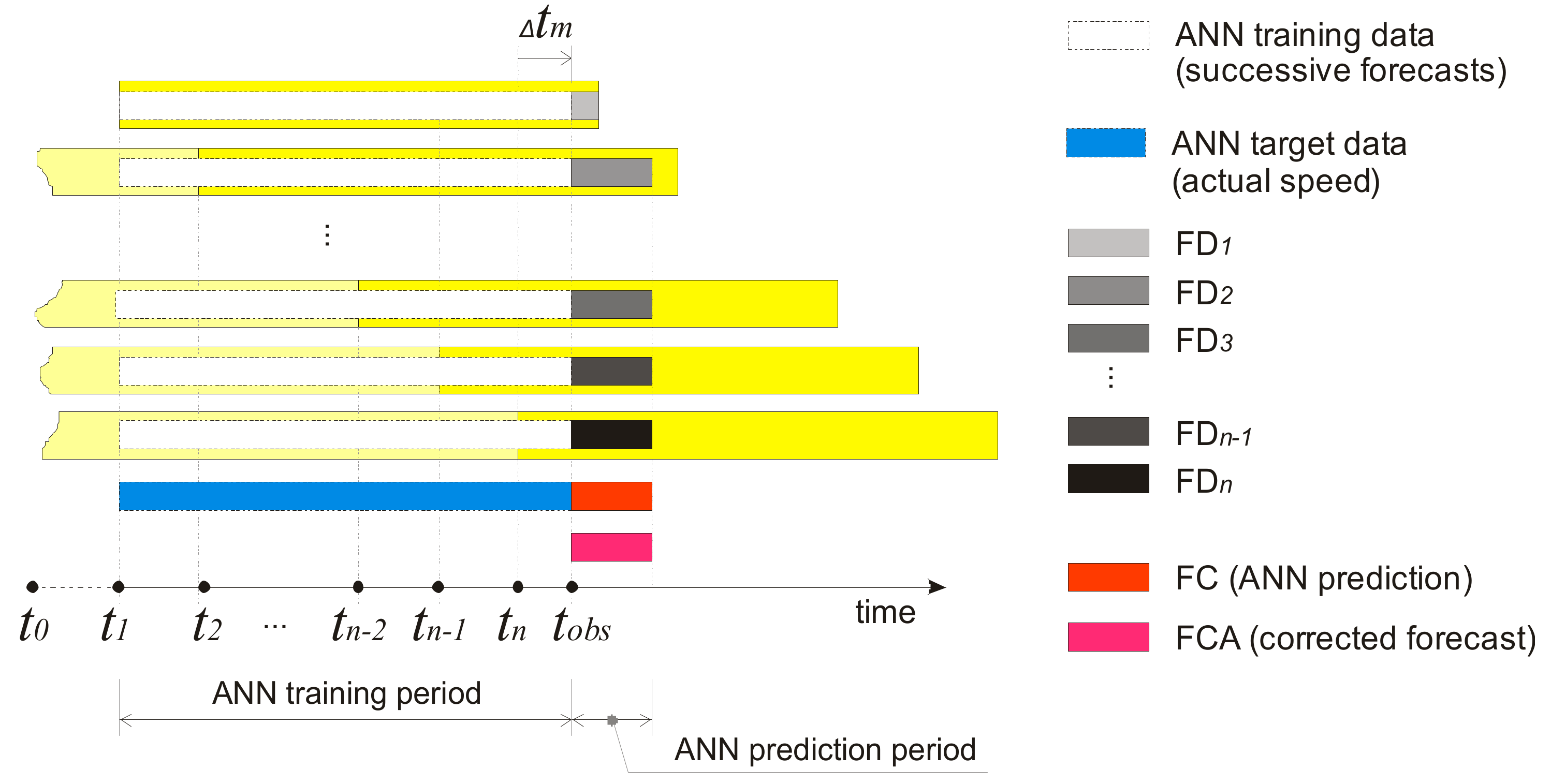
3.1. Forecasting Setup
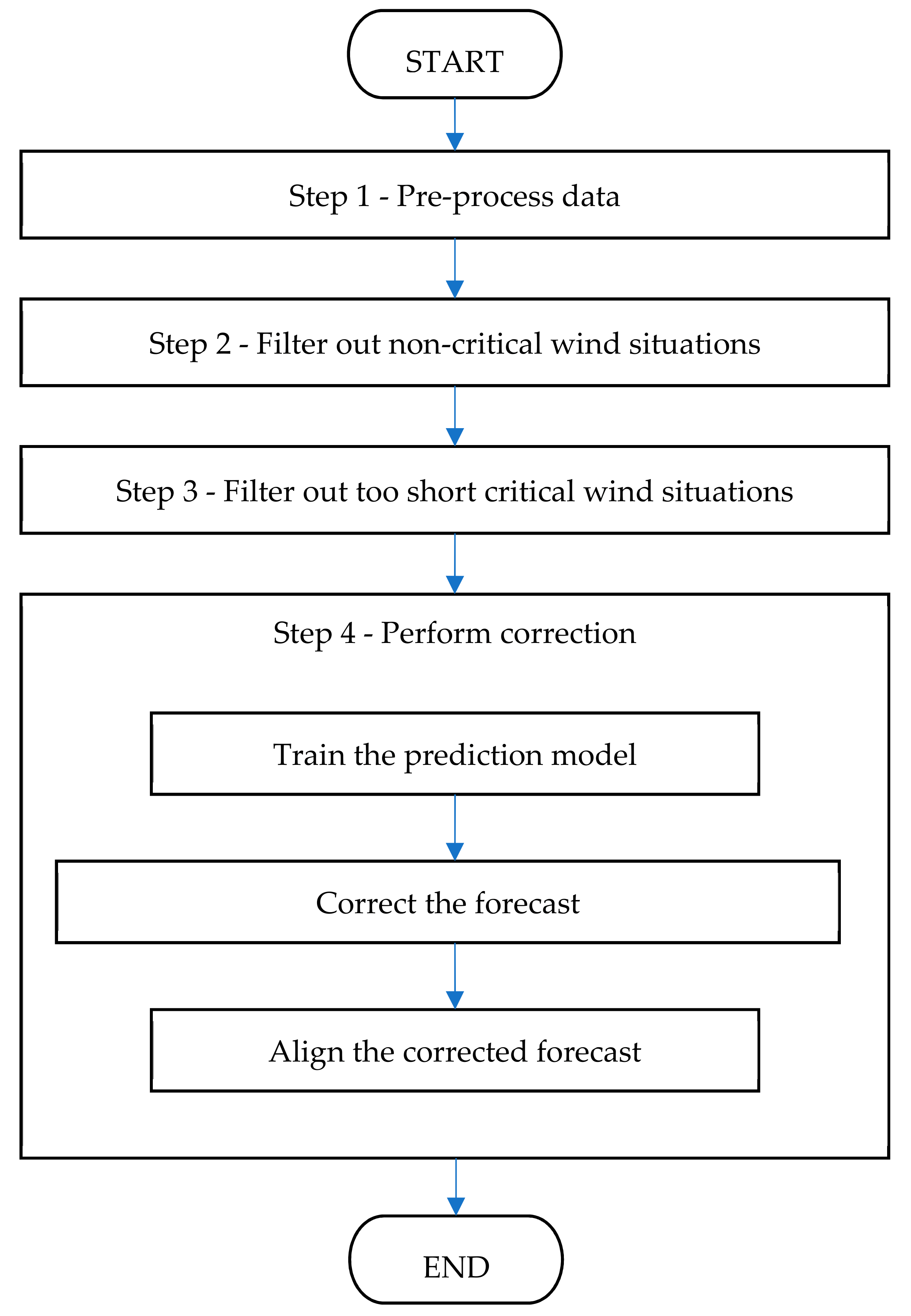
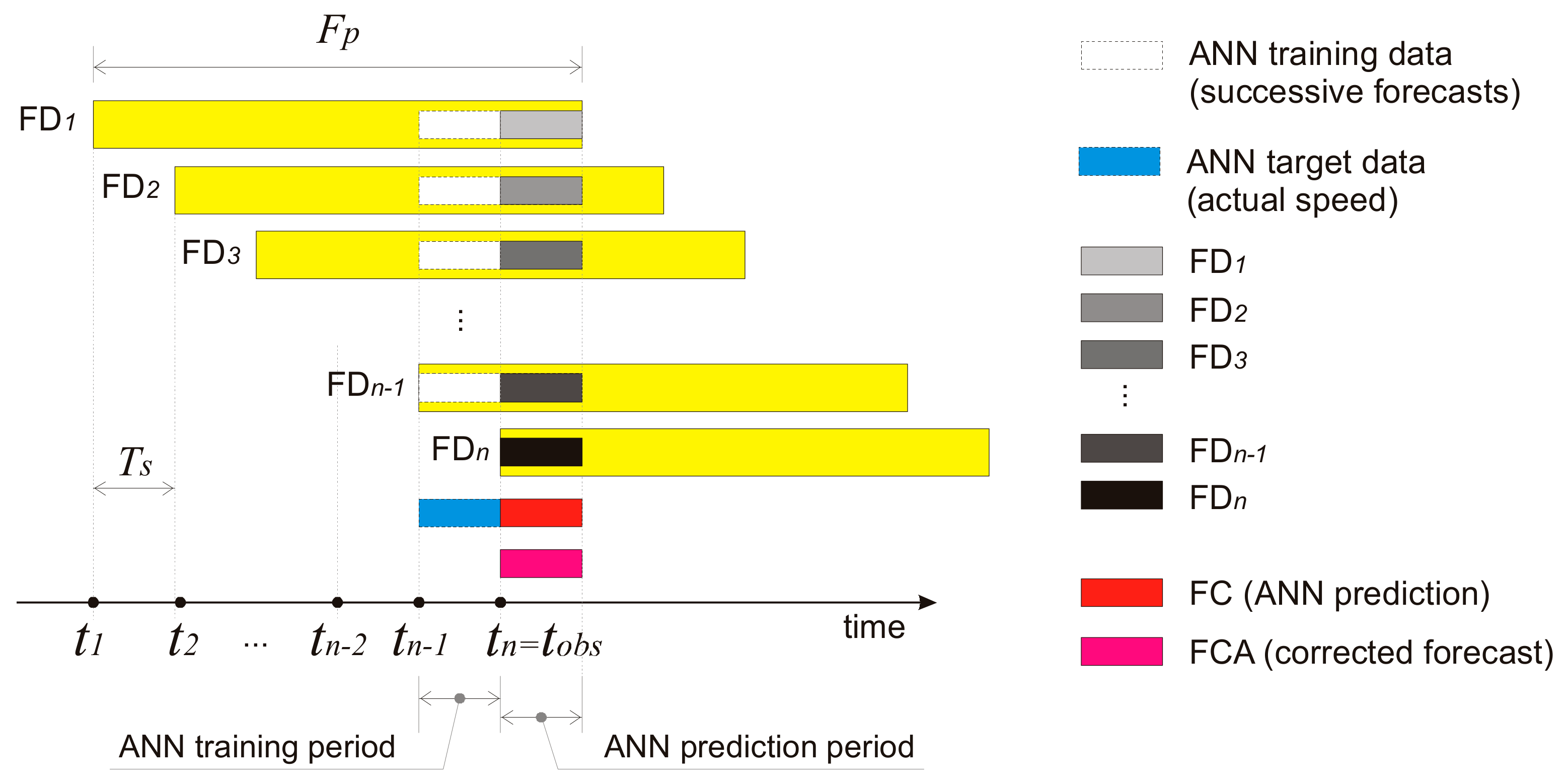
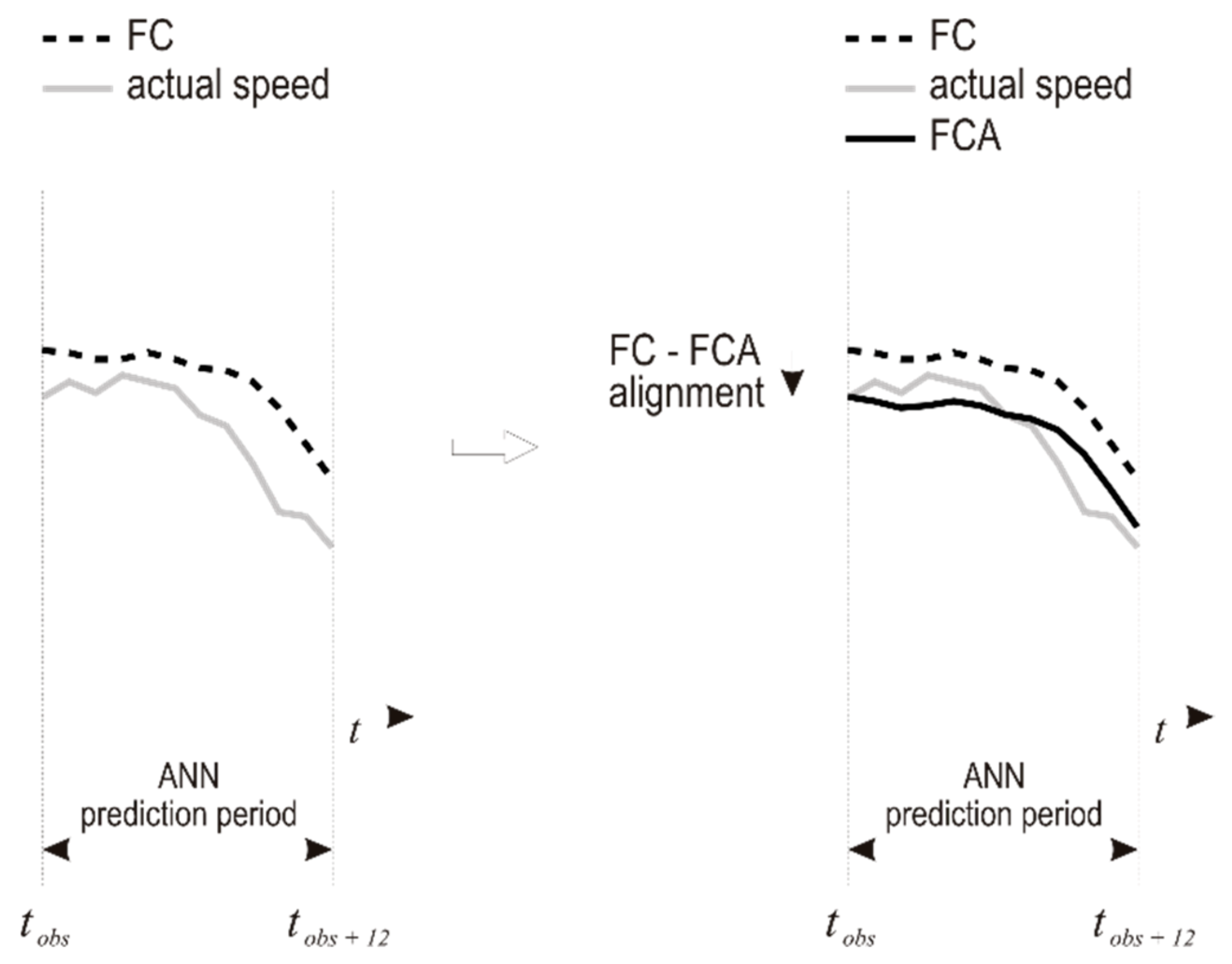
3.2. The FOCUSED Algorithm
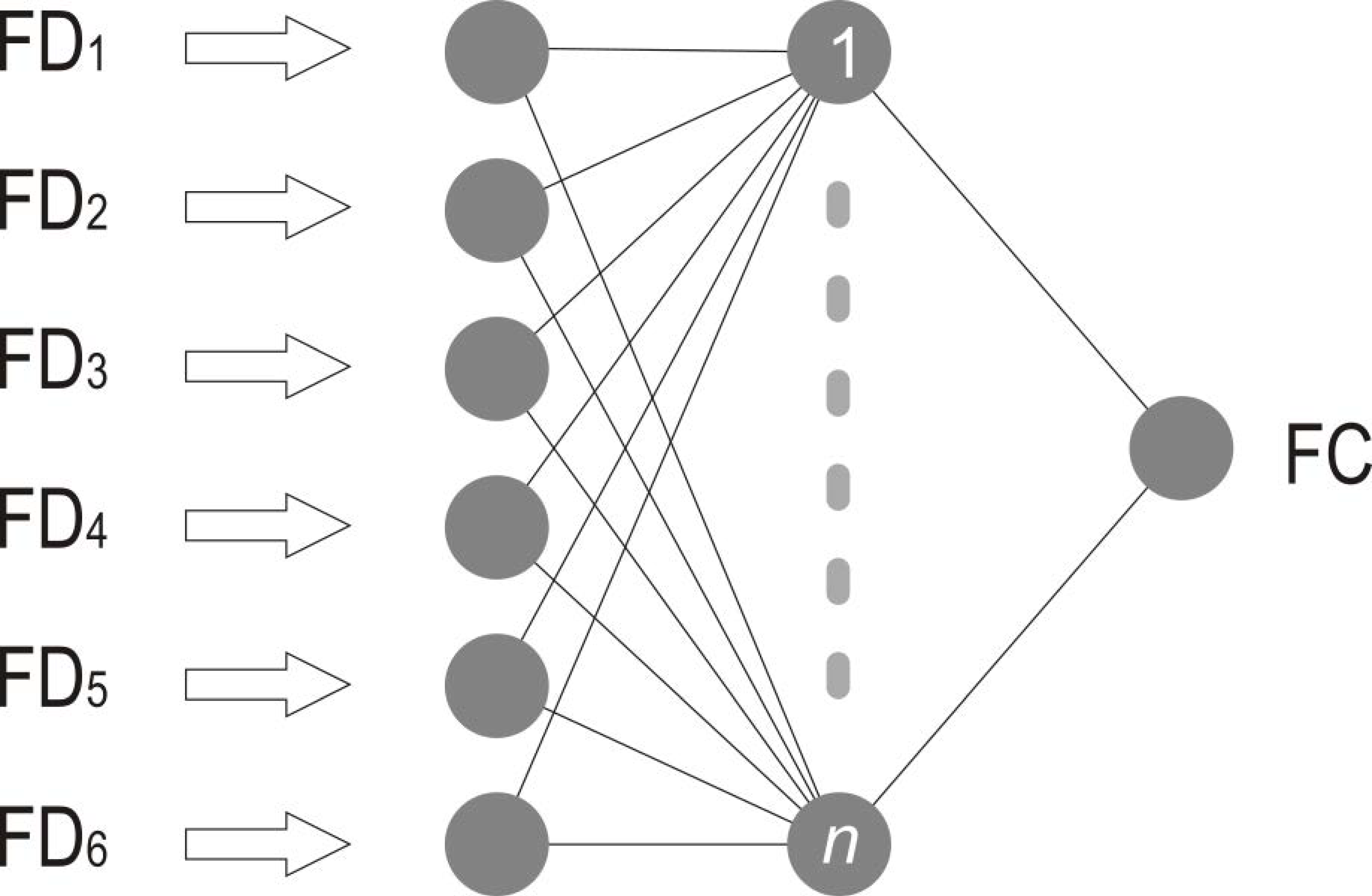
3.3. Training the Model (ANN Example)
- sigmoid
- 2.
- tanh
- 3.
- ReLU
4. Results
4.1. Statistical Evaluation of Using Successive Forecasts Instead of the Last Forecast
- H0 (null hypothesis): There is no tendency for ranks of corrected forecasts based on tested models to be significantly different than ranks of the original NWP (FD6).
- H1 (research hypothesis): The ranks of corrected forecasts are significantly different than those of the FD6.
4.2. Statistical Comparison with Autoregressive Moving Average (ARMA) Model
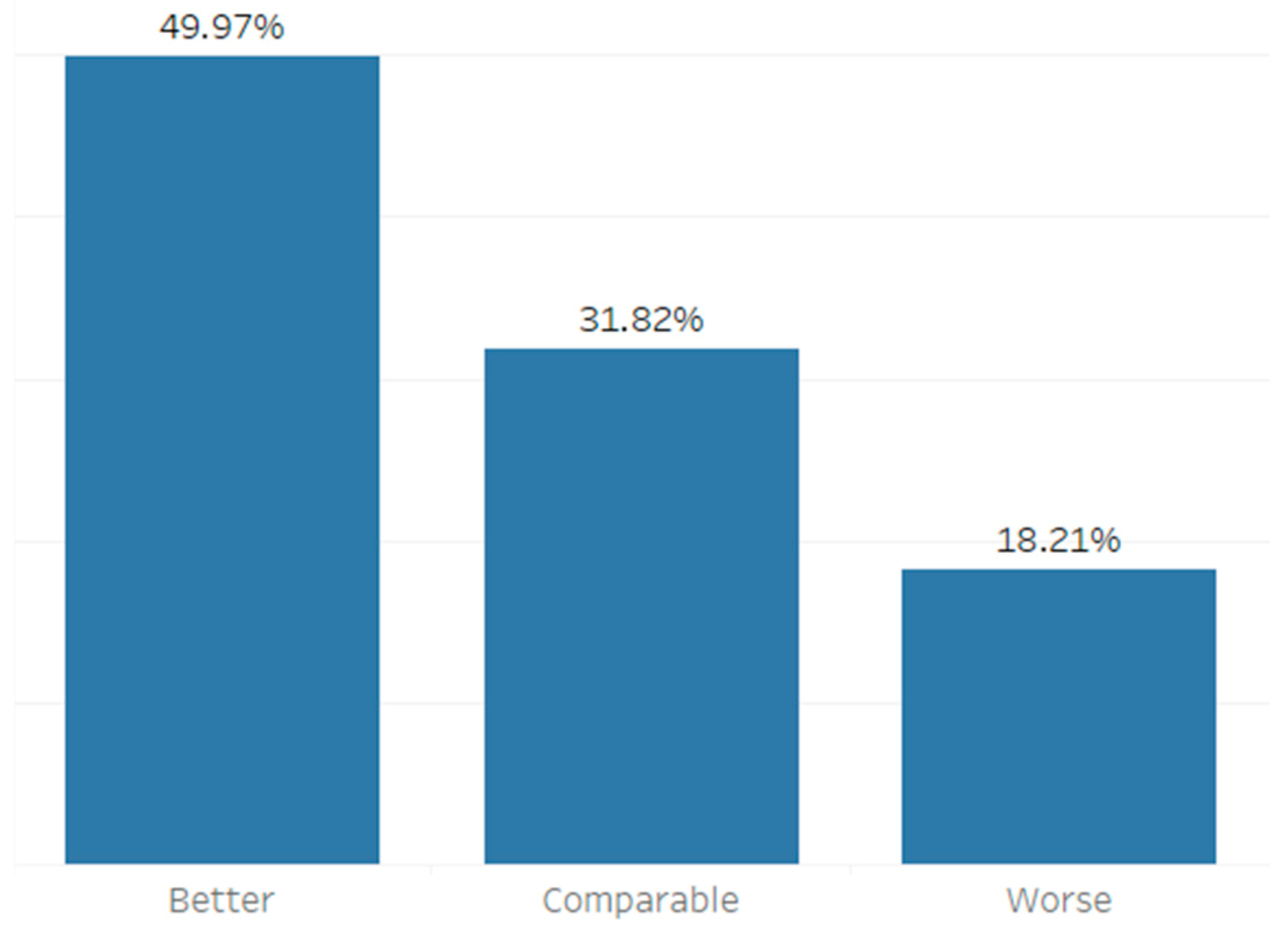
4.3. Empirical Evaluation
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bajić, A. Bora wind and road traffic safety. In Proceedings of the Fourth Croatian Road Maintenance Conference; Gospodarsko interesno udruženje trgovačkih društava za održavanje cesta Hrvatski cestar: Šibenik, Croatia, 2009; pp. 307–312. [Google Scholar]
- Bajić, A.; Ivatek-Šahdan, S.; Žibrat, Z. Anemo-alarm operational use of wind speed and direction forecast. In Proceedings of the GIU Hrvatski cestar Zagreb, Third Croatian Road Maintenance Conference, Šibenik, Croatia, 20–22 October 2008; pp. 109–114. [Google Scholar]
- Wang, X.; Guo, P.; Huang, X. A review of wind power forecasting models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef]
- ALADIN International Team The ALADIN Project: Mesoscale modelling seen as a basic tool for weather forecasting and atmospheric research. WMO Bull. 1997, 46, 317–324.
- Žibrat, Z.; Tomšić, D.; Jakopović, Z.; Kunić, Z. Meteorological measuring systems and software in the network of automatic weather stations in Meteorological and hydrological service of the Republic of Croatia. Hrvat. Meteoroloski Cas. 2012, 46, 69–84. [Google Scholar]
- Zjavka, L. Wind speed forecast correction models using polynomial neural networks. Renew. Energy 2015, 83, 998–1006. [Google Scholar] [CrossRef]
- Aimei, S.; Shuang, X.I.; Chongjian, Q.I.U. A variational method for correcting non-systematic errors in numerical weather prediction. Sci. China Ser. D Earth Sci. 2009, 52, 1650–1660. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; UNC: Chapel Hill, NC, USA, 2006; Volume 7, pp. 1–16. [Google Scholar]
- Libonati, R.; Trigo, I.; DaCamara, C.C. Correction of 2 m-temperature forecasts using Kalman Filtering technique. Atmos. Res. 2008, 87, 183–197. [Google Scholar] [CrossRef]
- Sweeney, C.P.; Lynch, P.; Nolan, P. Reducing errors of wind speed forecasts by an optimal combination of post-processing methods. Meteorol. Appl. 2013, 20, 32–40. [Google Scholar] [CrossRef]
- Zjavka, L. “Aladin” weather model local revisions using the differential polynomial neural network. Neural Netw. World 2014, 24, 143–156. [Google Scholar] [CrossRef]
- Shukur, O.B.; Lee, M.H. Daily wind speed forecasting through hybrid KF-ANN model based on ARIMA. Renew. Energy 2015, 76, 637–647. [Google Scholar] [CrossRef]
- Louka, P.; Galanis, G.; Siebert, N.; Kariniotakis, G.; Katsafados, P.; Pytharoulis, I.; Kallos, G. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2348–2362. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, J.; Wang, C.; Dong, X.; Miao, X. Short-term wind power combined forecasting based on error forecast correction. Energy Convers. Manag. 2016, 119, 215–226. [Google Scholar] [CrossRef]
- Ko, W.; Hur, D.; Park, J. Journal of International Council on Electrical Engineering Correction of wind power forecasting by considering wind speed forecast error. J. Int. Counc. Electr. Eng. 2015, 5, 47–50. [Google Scholar] [CrossRef]
- Nan, X.; Li, Q.; Qiu, D.; Zhao, Y.; Guo, X. Short-term wind speed syntheses correcting forecasting model and its application. Int. J. Electr. Power Energy Syst. 2013, 49, 264–268. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar] [CrossRef]
- Dong, L.; Ren, L.; Gao, S.; Gao, Y.; Liao, X. Studies on wind farms ultra-short term NWP wind speed correction methods. In Proceedings of the 2013 25th Chinese Control and Decision Confrence (CCDC), Guiyang, China, 25–27 May 2013; pp. 1576–1579. [Google Scholar]
- Xue, H.L.; Shen, X.S.; Chou, J.F. A forecast error correction method in numerical weather prediction by using recent multiple-time evolution data. Adv. Atmos. Sci. 2013, 30, 1249–1259. [Google Scholar] [CrossRef]
- Luo, J.; Hong, T.; Fang, S.-C. Benchmarking robustness of load forecasting models under data integrity attacks. Int. J. Forecast. 2018, 34, 89–104. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, F.; Wang, K. Robustness of Short-Term Wind Power Forecasting against False Data Injection Attacks. Energies 2020, 13, 3780. [Google Scholar] [CrossRef]
- Bajić, A. Gale-force wind in Croatia. In Proceedings of the Zbornik Radova s 2. Konferencije Hrvatske Platforme za Smanjenje Rizika od Katastrofa; Državna Uprava Za Zaštitu i Spašavanje: Zagreb, Croatia, 2011; pp. 141–147. [Google Scholar]
- da Silva, I.N.; Hernane Spatti, D.; Andrade Flauzino, R.; Liboni, L.H.B.; dos Reis Alves, S.F. Artificial Neural Networks; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-43161-1. [Google Scholar]
- Sharma, S.; Sharma, S.; Anidhya, A. Understanding Activation Functions in Neural Networks. Int. J. Eng. Appl. Sci. Technol. 2017, 4, 310–316. [Google Scholar]
- Zhao, G.; Zhang, Z.; Guan, H.; Tang, P.; Wang, J. Rethinking ReLU to Train Better CNNs. In Proceedings of the 2018 24th the International Conference Pattern Recognition, Beijing, China, 20–24 August 2018; pp. 603–608. [Google Scholar]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Klepac, G. Otkrivanje Zakonitosti Temeljem Jedinstvenoga Modela Transformacije Vremenske Serije, Doktorska Disertacija. Ph.D. Thesis, Sveučilište u Zagrebu, Fakultet Organizacije i Informatike Varaždin, Varaždin, Croatia, 2005. [Google Scholar]
- Klepac, G.; Kopal, R.; Mršić, L. REFII Model as a Base for Data Mining Techniques Hybridization with Purpose of Time Series Pattern Recognition; Springer: New Delhi, India, 2016; pp. 237–270. [Google Scholar]


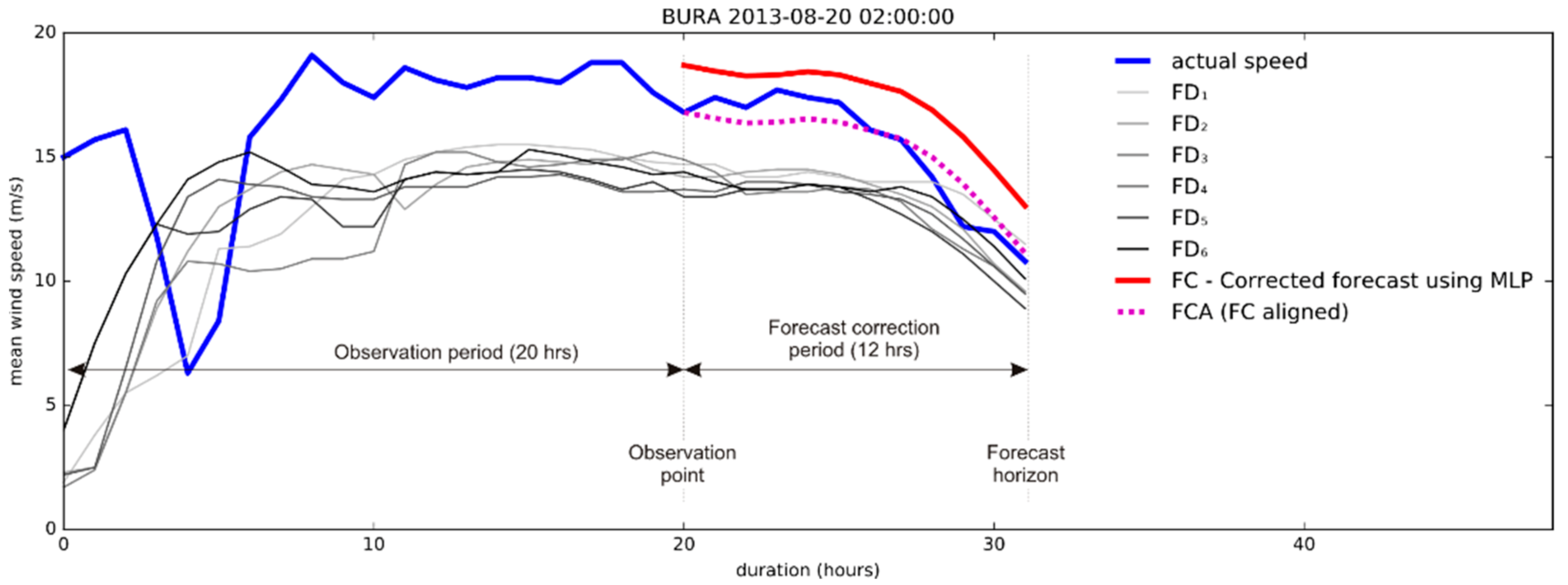

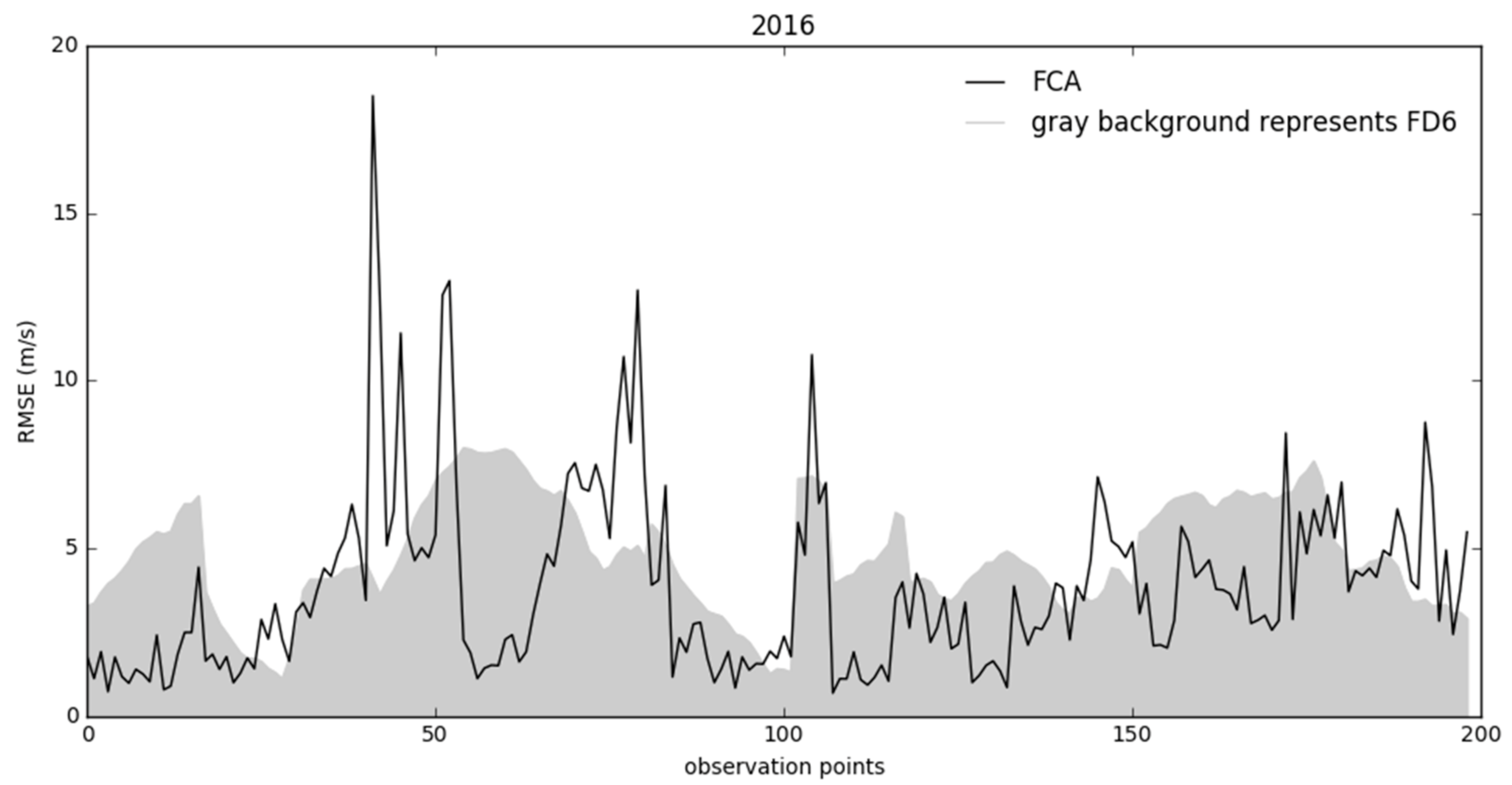

| Algorithm Run Number | Training Set Samples | Test Samples |
|---|---|---|
| 1 | 1–12 | 13–24 |
| 2 | 1–13 | 14–25 |
| 3 | 1–14 | 15–26 |
| 4 | 1–15 | 16–27 |
| Tested Model | p-Value | U1-FOCUSED | U2-FD6 |
|---|---|---|---|
| FCA_ANN | 0.0015 | 109,164 | 135,861 |
| FCA_RFR | 0.0017 | 109,366 | 135,659 |
| FCA_SVM | 0.0322 | 114,195 | 130,830 |
| FCA_LRM | 0.0348 | 114,348 | 130,677 |
| Tested Algorithm | p-Value | U1-FOCUSED | U2-ARMA |
|---|---|---|---|
| FOCUSED | 0.0015 | 109,164 | 135,861 |
| ARMA | 0.0139 | 113,076 | 132,940 |
| Category | Description |
|---|---|
| Better | RMSE FCA lower than any RMSE of original NWP forecasts |
| Comparable | RMSE FCA between lowest and highest RMSE of original NWP forecasts |
| Worse | RMSE FCA higher than any RMSE of original NWP forecasts |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunić, Z.; Ženko, B.; Boshkoska, B.M. FOCUSED–Short-Term Wind Speed Forecast Correction Algorithm Based on Successive NWP Forecasts for Use in Traffic Control Decision Support Systems. Sensors 2021, 21, 3405. https://doi.org/10.3390/s21103405
Kunić Z, Ženko B, Boshkoska BM. FOCUSED–Short-Term Wind Speed Forecast Correction Algorithm Based on Successive NWP Forecasts for Use in Traffic Control Decision Support Systems. Sensors. 2021; 21(10):3405. https://doi.org/10.3390/s21103405
Chicago/Turabian StyleKunić, Zdravko, Bernard Ženko, and Biljana Mileva Boshkoska. 2021. "FOCUSED–Short-Term Wind Speed Forecast Correction Algorithm Based on Successive NWP Forecasts for Use in Traffic Control Decision Support Systems" Sensors 21, no. 10: 3405. https://doi.org/10.3390/s21103405
APA StyleKunić, Z., Ženko, B., & Boshkoska, B. M. (2021). FOCUSED–Short-Term Wind Speed Forecast Correction Algorithm Based on Successive NWP Forecasts for Use in Traffic Control Decision Support Systems. Sensors, 21(10), 3405. https://doi.org/10.3390/s21103405







